High Q-Factor, High Contrast, and Multi-Band Optical Sensor Based on Plasmonic Square Bracket Dimer Metasurface
Abstract
1. Introduction
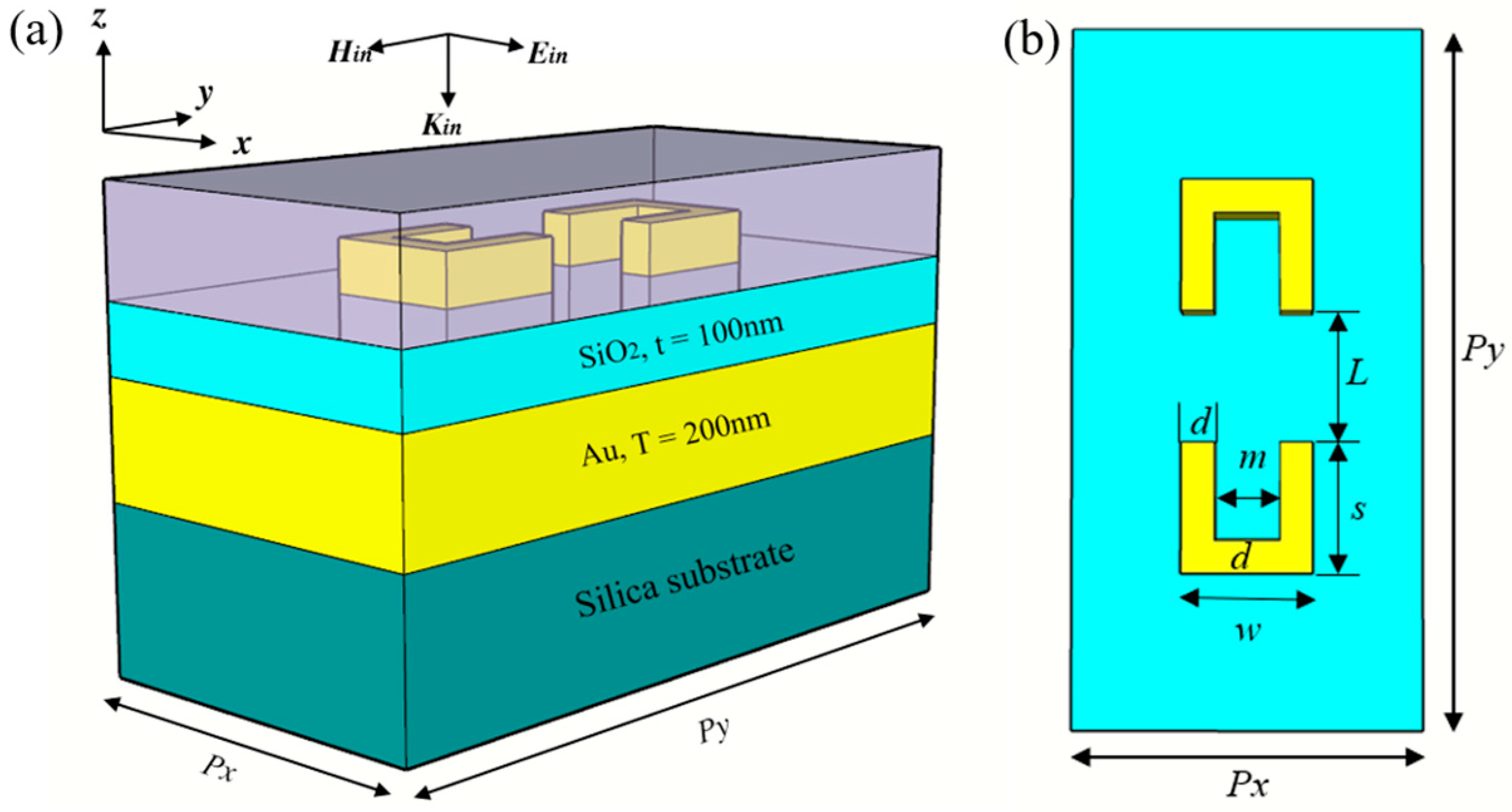
2. Structure and Simulation Setup
3. Results and Discussion
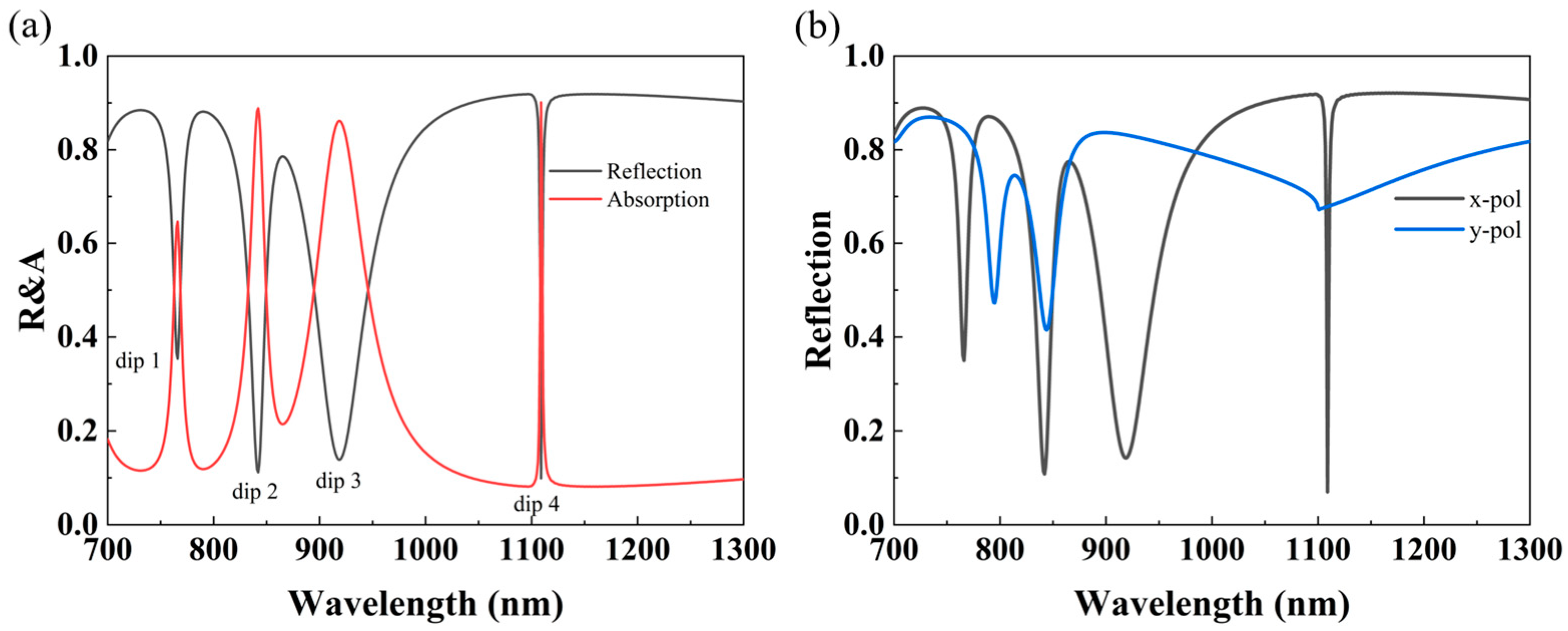
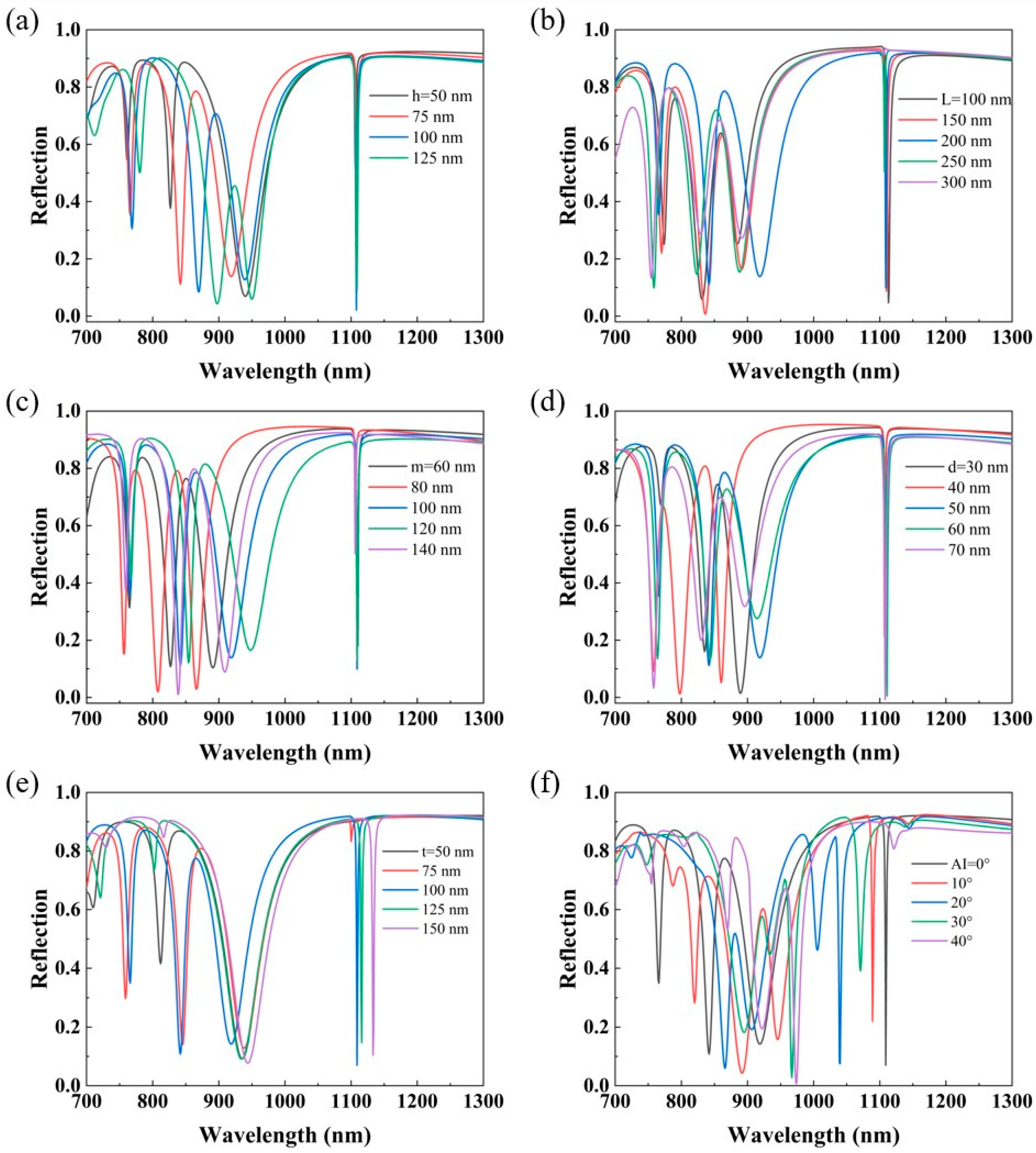
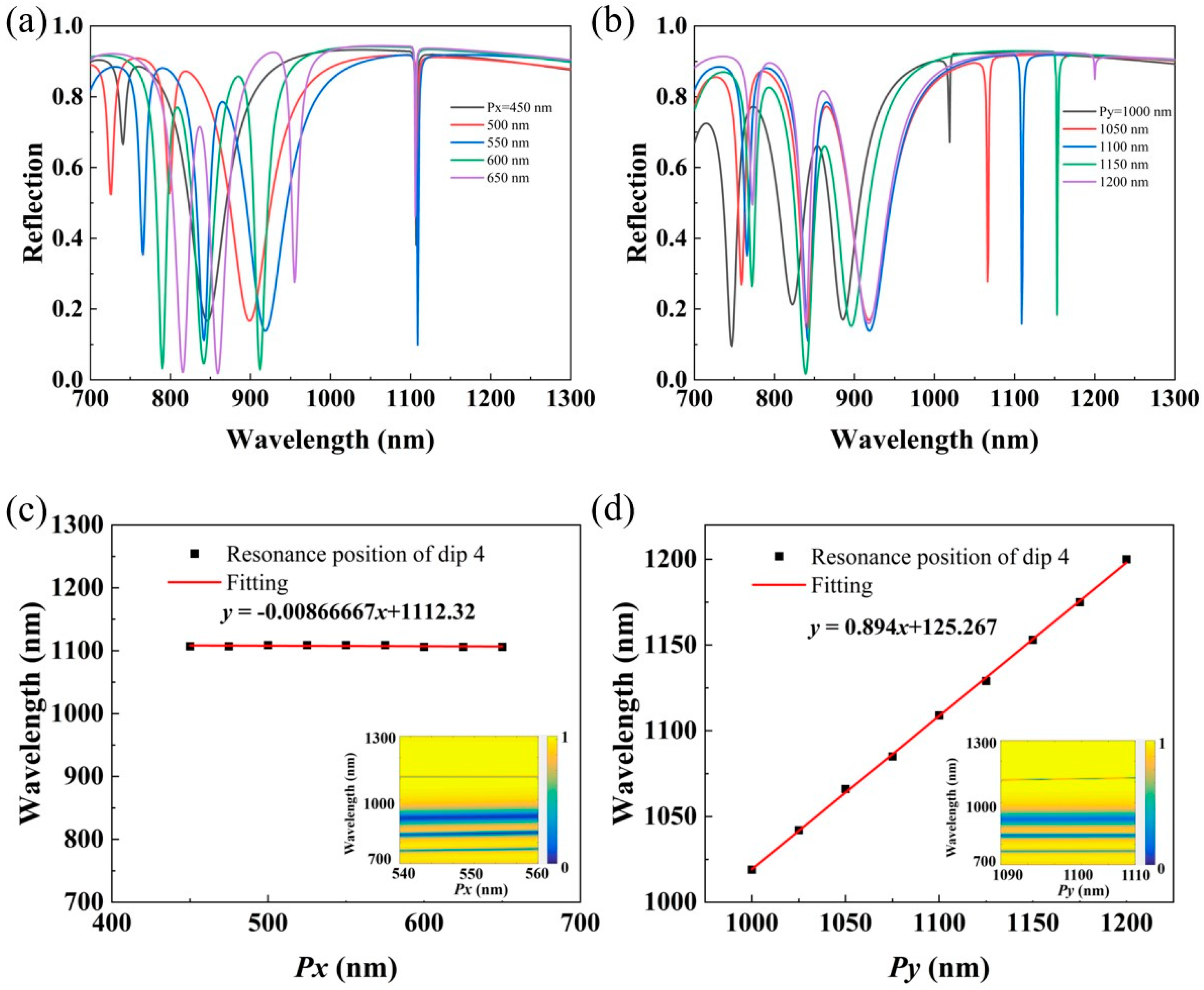
3.1. Structure Optimization and Feature Analysis
3.2. Underlying Mechanisms of Resonant Modes
3.3. Potential Application and Performance
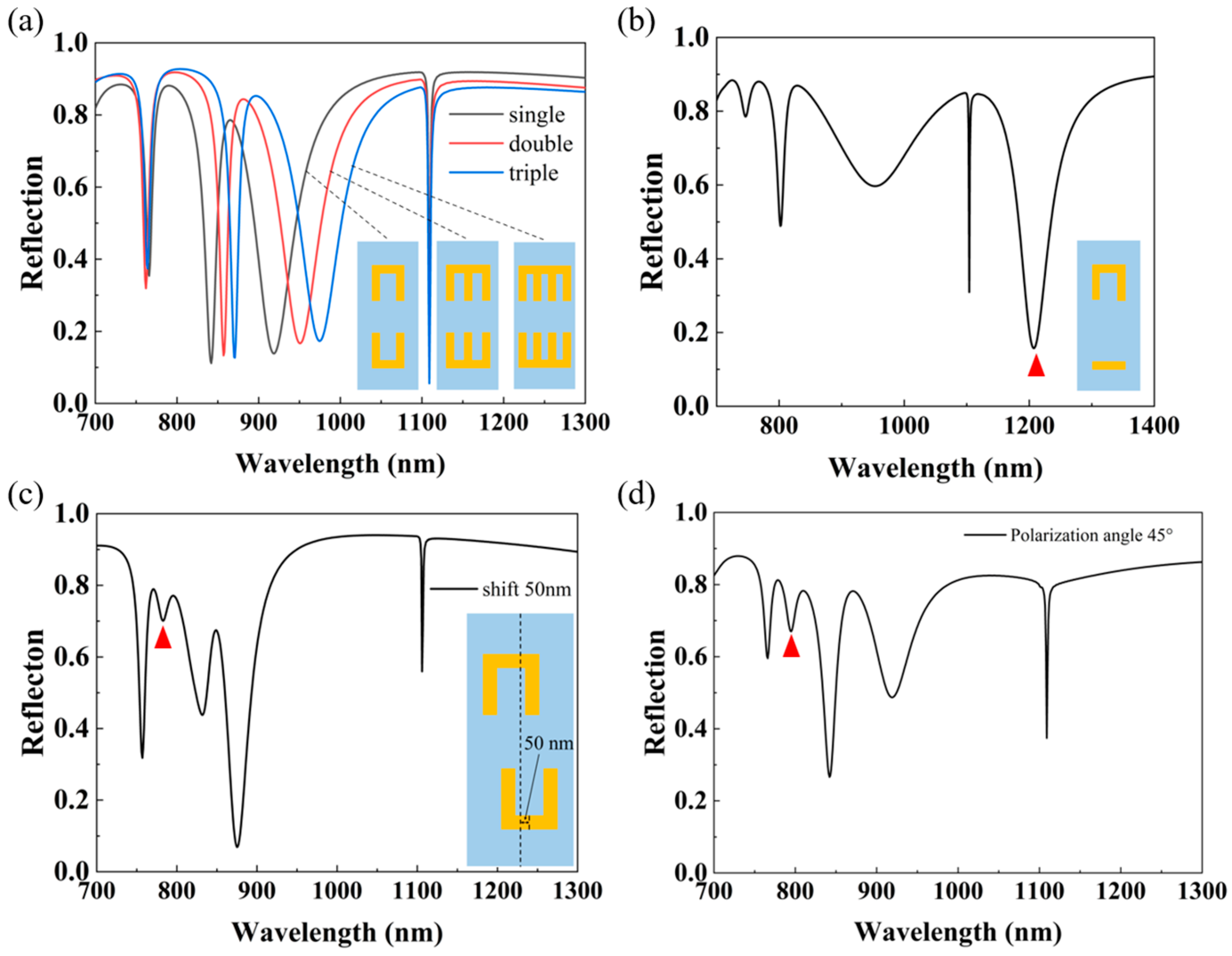
3.4. Realization of More Resonant Modes
3.5. Manufacturing Procedure of the Metasurface
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, Y.; Li, Z.; Cheng, Z. Terahertz perfect absorber based on InSb metasurface for both temperature and refractive index sensing. Opt. Mater. 2021, 117, 111129. [Google Scholar] [CrossRef]
- Vafapour, Z.; Ghahraloud, H.; Keshavarz, A.; Islam, S.; Rashidi, A.; Dutta, M.; Stroscio, M.A. The Potential of Refractive Index Nanobiosensing Using a Multi-Band Optically Tuned Perfect Light Metamaterial Absorber. IEEE Sens. J. 2021, 21, 13786–13793. [Google Scholar] [CrossRef]
- Khonina, S.N.; A Butt, M.; Kazanskiy, N.L. Numerical investigation of metasurface narrowband perfect absorber and a plasmonic sensor for a near-infrared wavelength range. J. Opt. 2021, 23, 065102. [Google Scholar] [CrossRef]
- Ye, Z.; Yang, M.; Zhu, L.; Chen, P.-Y. PTX-symmetric metasurfaces for sensing applications. Front. Optoelectron. 2021, 14, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Carbon dioxide gas sensor based on polyhexamethylene biguanide polymer deposited on silicon nano-cylinders metasurface. Sensors 2021, 21, 378. [Google Scholar] [CrossRef] [PubMed]
- Yanase, Y.; Hiragun, T.; Yanase, T.; Kawaguchi, T.; Ishii, K.; Hide, M. Application of SPR imaging sensor for detection of individual living cell reactions and clinical diagnosis of type I allergy. Allergol. Int. 2013, 62, 163–169. [Google Scholar] [CrossRef]
- Liang, H.; Miranto, H.; Granqvist, N.; Sadowski, J.W.; Viitala, T.; Wang, B.; Yliperttula, M. Surface plasmon resonance instrument as a refractometer for liquids and ultrathin films. Sens. Actuators B Chem. 2010, 149, 212–220. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Zhang, Y.; Bai, B.; Shao, Q. High-sensitive gas-mixture detection based on Mie resonance in slotted MDM metasurface. Optik 2021, 242, 167096. [Google Scholar] [CrossRef]
- Jiang, W.; Ma, Z.; Cao, F.; Hu, L.; Bao, L.; Chang, P.; Xu, C.; Lv, X.; Xie, Y. Label-free integrated microfluidic plasmonic biosensor from vertical-cavity surface-emitting lasers for SARS-CoV-2 receptor binding domain protein detection. Opt. Express 2023, 31, 12138–12149. [Google Scholar] [CrossRef] [PubMed]
- Cinel, N.A.; Bütün, S.; Özbay, E. Electron beam lithography designed silver nano-disks used as label free nano-biosensors based on localized surface plasmon resonance. Opt. Express 2012, 20, 2587–2597. [Google Scholar] [CrossRef]
- Wang, Z.; Singh, R.; Marques, C.; Jha, R.; Zhang, B.; Kumar, S. Taper-in-taper fiber structure-based LSPR sensor for alanine aminotransferase detection. Opt. Express 2021, 29, 43793–43810. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Alipour, A.; Mir, A.; Farmani, A. Ultra high-sensitivity and tunable dual-band perfect absorber as a plasmonic sensor. Opt. Laser Technol. 2020, 127, 106201. [Google Scholar] [CrossRef]
- Du, Y.X.; Ao, X.Y.; Cai, Y.J. High-Q Surface Lattice Resonances. Acta Optica Sin. 2023, 43, 1623005. [Google Scholar] [CrossRef]
- Jing, J.-Y.; Wang, Q.; Zhao, W.-M.; Wang, B.-T. Long-range surface plasmon resonance and its sensing applications: A review. Opt. Lasers Eng. 2019, 112, 103–118. [Google Scholar] [CrossRef]
- Chao, C.-T.C.; Chau, Y.-F.C.; Huang, H.J.; Kumara, N.T.R.N.; Kooh, M.R.R.; Lim, C.M.; Chiang, H.-P. Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods. Nanomaterials 2020, 10, 1399. [Google Scholar] [CrossRef] [PubMed]
- Kravets, V.G.; Wu, F.; Yu, T.; Grigorenko, A.N. Metal-Dielectric-Graphene Hybrid Heterostructures with Enhanced Surface Plasmon Resonance Sensitivity Based on Amplitude and Phase Measurements. Plasmonics 2022, 17, 973–987. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
- Yao, J.; Li, J.; Zhang, Y.; Li, J.; Yue, Z.; Xu, H.; Yang, F. Bound states in continuum in periodic optical systems. Chin. Opt. 2023, 16, 1–23. [Google Scholar] [CrossRef]
- Chen, W.; Li, M.; Zhang, W.; Chen, Y. Dual-resonance sensing for environmental refractive index based on quasi-BIC states in all-dielectric metasurface. Nanophotonics 2023, 12, 1147–1157. [Google Scholar] [CrossRef]
- Dudek, M.; Kowerdziej, R.; Pianelli, A.; Parka, J. Graphene-based tunable hyperbolic microcavity. Sci. Rep. 2021, 11, 74. [Google Scholar] [CrossRef]
- Pianelli, A.; Caligiuri, V.; Dudek, M.; Kowerdziej, R.; Chodorow, U.; Sielezin, K.; De Luca, A.; Caputo, R.; Parka, J. Active control of dielectric singularities in indium-tin-oxides hyperbolic metamaterials. Sci. Rep. 2022, 12, 16961. [Google Scholar] [CrossRef]
- Sreekanth, K.V.; Alapan, Y.; ElKabbash, M.; Ilker, E.; Hinczewski, M.; Gurkan, U.A.; De Luca, A.; Strangi, G. Extreme sensitivity biosensing platform based on hyperbolic metamaterials. Nat. Mater. 2016, 15, 621–627. [Google Scholar] [CrossRef]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic surface lattice resonances: A review of properties and applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef] [PubMed]
- Bin-Alam, M.S.; Reshef, O.; Mamchur, Y.; Alam, M.Z.; Carlow, G.; Upham, J.; Sullivan, B.T.; Ménard, J.-M.; Huttunen, M.J.; Boyd, R.W.; et al. Ultra-high-Q resonances in plasmonic metasurfaces. Nat. Commun. 2021, 12, 974. [Google Scholar] [CrossRef]
- Hu, J.; Tan, C.; Bai, W.; Li, Y.; Lin, Q.; Wang, L.-L. Dielectric nanocavity-coupled surface lattice resonances for high-efficiency plasmonic sensing. J. Phys. D Appl. Phys. 2022, 55, 075105. [Google Scholar] [CrossRef]
- Li, Z.; Prasad, C.S.; Wang, X.; Zhang, D.; Lach, R.; Naik, G.V. Balancing detectivity and sensitivity of plasmonic sensors with surface lattice resonance. Nanophotonics 2023, 12, 3721–3727. [Google Scholar] [CrossRef]
- Humphrey, A.D.; Barnes, W.L. Plasmonic surface lattice resonances on arrays of different lattice symmetry. Phys. Rev. B 2014, 90, 075404. [Google Scholar] [CrossRef]
- Yang, A.; Hryn, A.J.; Bourgeois, M.R.; Lee, W.-K.; Hu, J.; Schatz, G.C.; Odom, T.W. Programmable and reversible plasmon mode engineering. Proc. Natl. Acad. Sci. USA 2016, 113, 14201–14206. [Google Scholar] [CrossRef]
- Le-Van, Q.; Zoethout, E.; Geluk, E.; Ramezani, M.; Berghuis, M.; Rivas, J.G. Enhanced quality factors of surface lattice resonances in plasmonic arrays of nanoparticles. Adv. Opt. Mater. 2019, 7, 1801451. [Google Scholar] [CrossRef]
- Li, L.; Ouyang, Y.; Ma, L.; Sun, H.; Chen, Y.; Wu, M.; Qi, Z.-M.; Wu, W. Reflection-type surface lattice resonances in all-metal metasurfaces for refractive index sensing. Photon. Res. 2023, 11, 2210–2221. [Google Scholar] [CrossRef]
- Yao, J.; Ou, J.-Y.; Savinov, V.; Chen, M.K.; Kuo, H.Y.; Zheludev, N.I.; Tsai, D.P. Plasmonic anapole metamaterial for refractive index sensing. PhotoniX 2022, 3, 23. [Google Scholar] [CrossRef]
- He, M.; Wang, J.; Sun, S.; Mao, Y.; Li, R.; Tian, S.; Taqi, M.M.U.H.N.U.; Liang, E. Improved strong field enhancement and ultranarrow perfect absorption based on anapole mode in slotted Si nanodisk metamaterial. Results Phys. 2022, 40, 105809. [Google Scholar] [CrossRef]
- Song, S.; Yu, S.; Li, H.; Zhao, T. Ultra-high Q-factor toroidal dipole resonance and magnetic dipole quasi-bound state in the continuum in an all-dielectric hollow metasurface. Laser Phys. 2022, 32, 025403. [Google Scholar] [CrossRef]
- Hamans, R.F.; Parente, M.; Castellanos, G.W.; Ramezani, M.; Rivas, J.G.; Baldi, A. Super-resolution mapping of enhanced emission by collective plasmonic resonances. ACS Nano 2019, 13, 4514–4521. [Google Scholar] [CrossRef] [PubMed]
- Castellanos, G.W.; Bai, P.; Rivas, J.G. Lattice resonances in dielectric metasurfaces. J. Appl. Phys. 2019, 125, 213105. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. Recent Development in Metasurfaces: A Focus on Sensing Applications. Nanomaterials 2022, 13, 118. [Google Scholar] [CrossRef]
- Jeong, J.; Goldflam, M.D.; Campione, S.; Briscoe, J.L.; Vabishchevich, P.P.; Nogan, J.; Sinclair, M.B.; Luk, T.S.; Brener, I. High quality factor toroidal resonances in dielectric metasurfaces. ACS Photon. 2020, 7, 1699–1707. [Google Scholar] [CrossRef]
- Shen, Z.; Du, M. High-performance refractive index sensing system based on multiple Fano resonances in polarization-insensitive metasurface with nanorings. Opt. Express 2021, 29, 28287–28296. [Google Scholar] [CrossRef]
- Luo, M.; Hu, J.; Li, Y.; Bai, W.; Zhang, R.; Lin, Q.; Wang, L. Anapole-assisted ultra-narrow-band lattice resonance in slotted silicon nanodisk arrays. J. Phys. D Appl. Phys. 2023, 56, 375102. [Google Scholar] [CrossRef]
- Du, Z.; Zhou, R.; Luo, S.; Zhao, D.; Long, W.; Ling, Q.; Yu, Z.; Chen, D. Tunable multi-band absorbers based on graphene metasurfaces for infrared sensing and switching. Opt. Commun. 2023, 534, 129320. [Google Scholar] [CrossRef]
- Wang, B.-X.; Xu, C.; Zhou, H.; Duan, G.; Jiang, J.; Zhu, H. Design of triple-/six-spectral perfect absorber using multiple resonance responses of metallic split-ring resonator. Opt. Laser Technol. 2022, 156, 108530. [Google Scholar] [CrossRef]
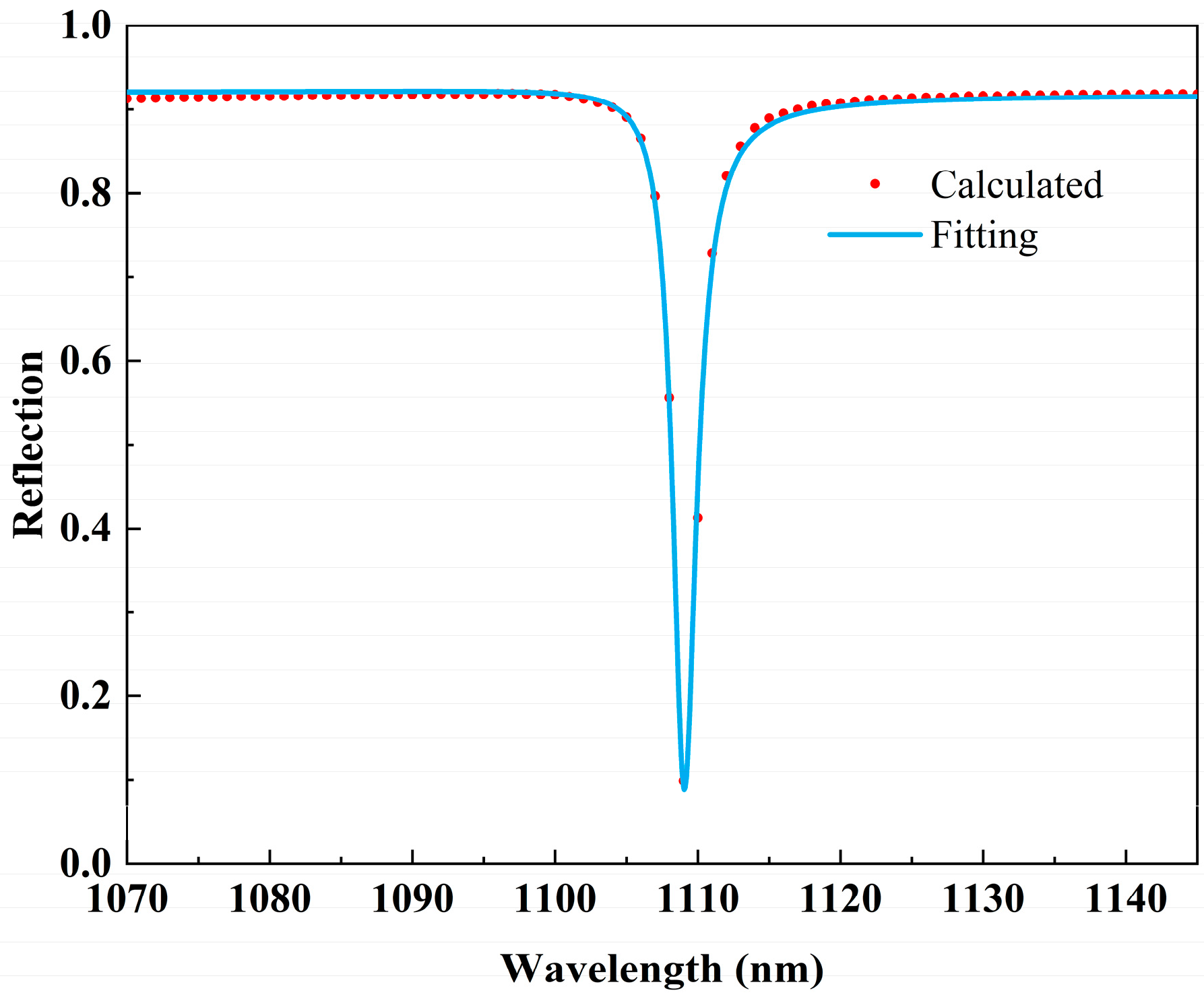

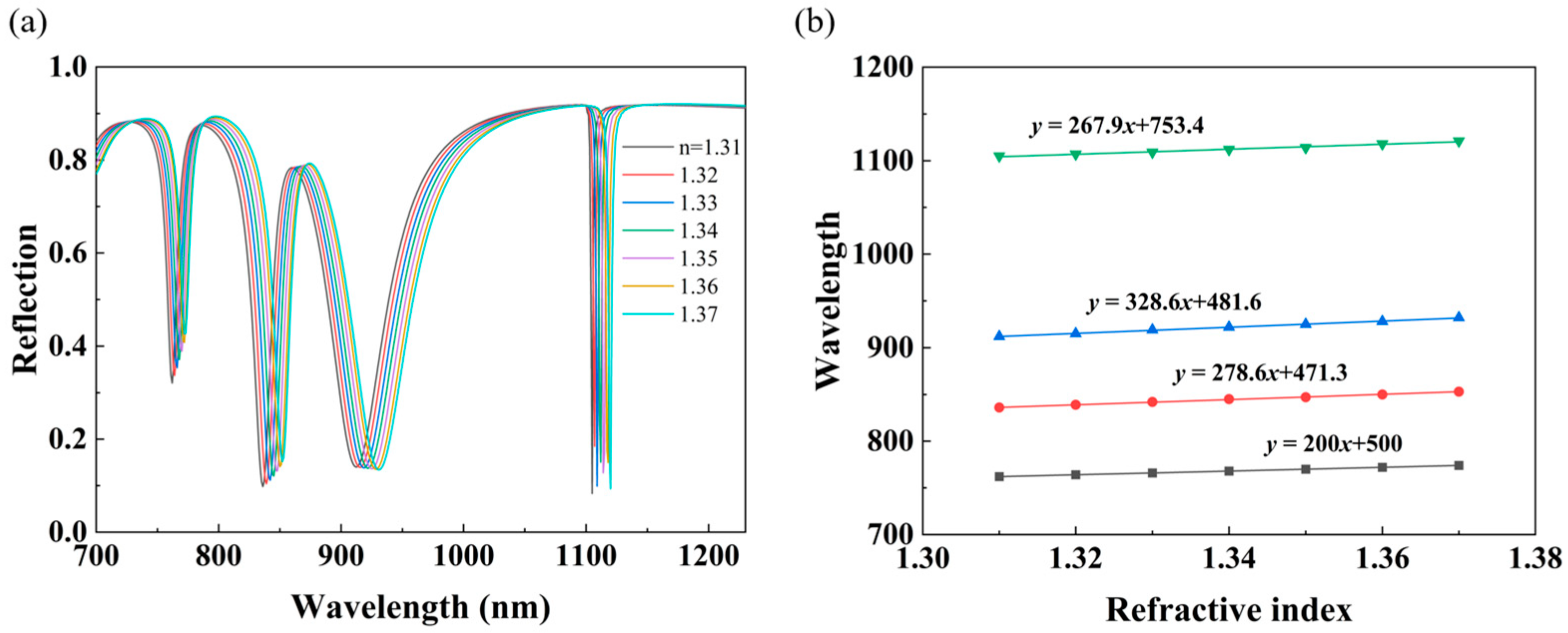


| Results | Dip 1 | Dip 2 | Dip 3 | Dip 4 |
|---|---|---|---|---|
| Resonance wavelength (nm) | 766 | 842 | 916 | 1109 |
| FWHM (nm) | 9.5 | 38.1 | 45.8 | 2 |
| Q-factor | 80.6 | 22.1 | 20.1 | 548 |
| Results | Dip 1 | Dip 2 | Dip 3 | Dip 4 |
|---|---|---|---|---|
| R2 | 1 | 0.99803 | 0.99811 | 0.98754 |
| RMSE (nm) | - | 0.2928 | 0.3380 | 0.7121 |
| RI error (RIU) | - | 1.05 × 10−3 | 1.03 × 10−3 | 2.66 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, B.; Chu, G.; Xu, Z.; Hou, L.; Liu, X.; Xiong, J. High Q-Factor, High Contrast, and Multi-Band Optical Sensor Based on Plasmonic Square Bracket Dimer Metasurface. Nanomaterials 2024, 14, 421. https://doi.org/10.3390/nano14050421
Ni B, Chu G, Xu Z, Hou L, Liu X, Xiong J. High Q-Factor, High Contrast, and Multi-Band Optical Sensor Based on Plasmonic Square Bracket Dimer Metasurface. Nanomaterials. 2024; 14(5):421. https://doi.org/10.3390/nano14050421
Chicago/Turabian StyleNi, Bin, Guanghu Chu, Zheyang Xu, Lianping Hou, Xuefeng Liu, and Jichuan Xiong. 2024. "High Q-Factor, High Contrast, and Multi-Band Optical Sensor Based on Plasmonic Square Bracket Dimer Metasurface" Nanomaterials 14, no. 5: 421. https://doi.org/10.3390/nano14050421
APA StyleNi, B., Chu, G., Xu, Z., Hou, L., Liu, X., & Xiong, J. (2024). High Q-Factor, High Contrast, and Multi-Band Optical Sensor Based on Plasmonic Square Bracket Dimer Metasurface. Nanomaterials, 14(5), 421. https://doi.org/10.3390/nano14050421






