Study on Crack Resistance Mechanism of Helical Carbon Nanotubes in Nanocomposites
Abstract
:1. Introduction
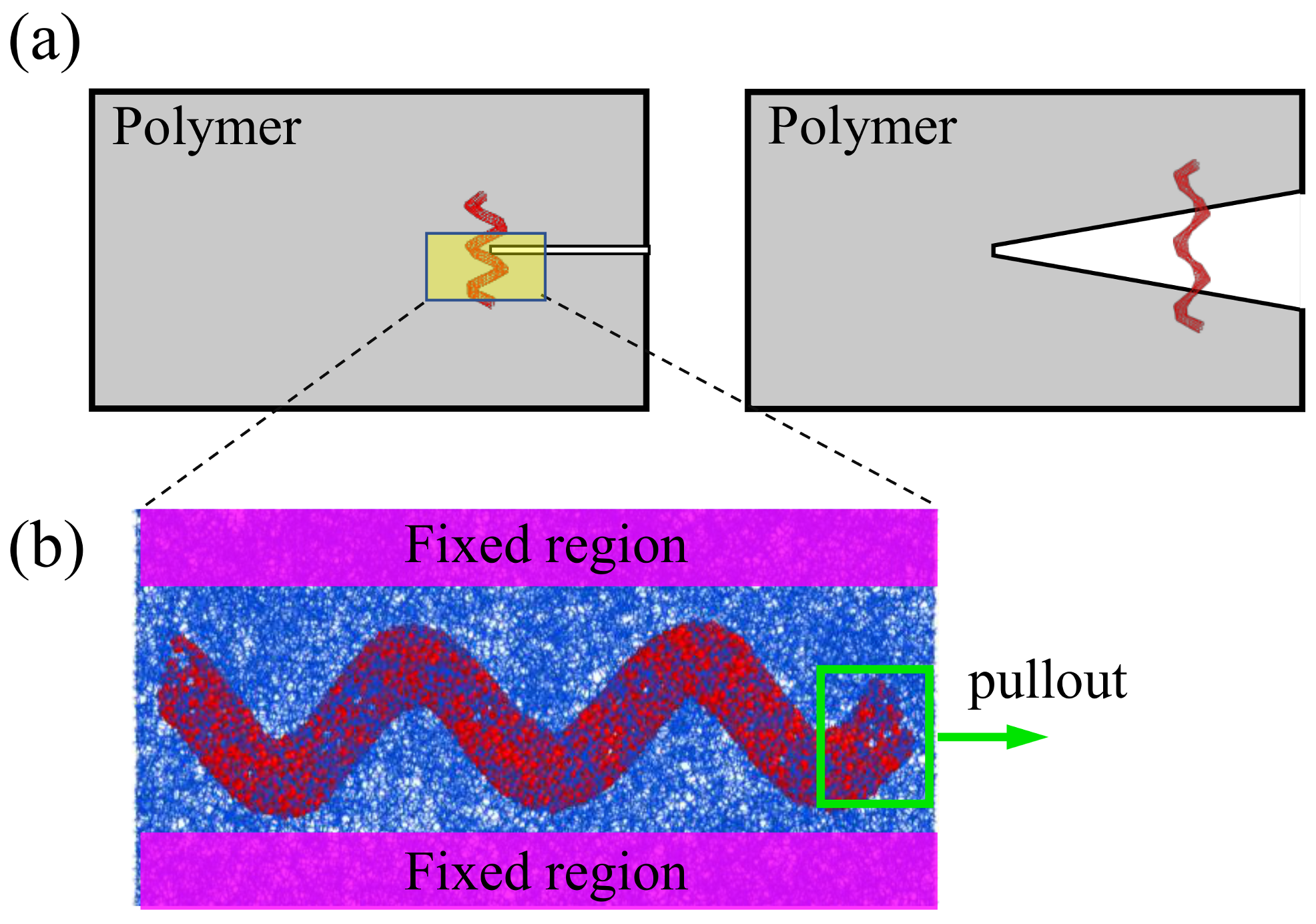
2. Model Construction in MD Simulation
3. Simulation Procedure
4. Results and Discussions
4.1. Mechanical Properties of Composites with HCNT, Snake-like HCNT, and CNT
4.2. The Effect of the Diameter of HCNTs on the Interfacial Properties
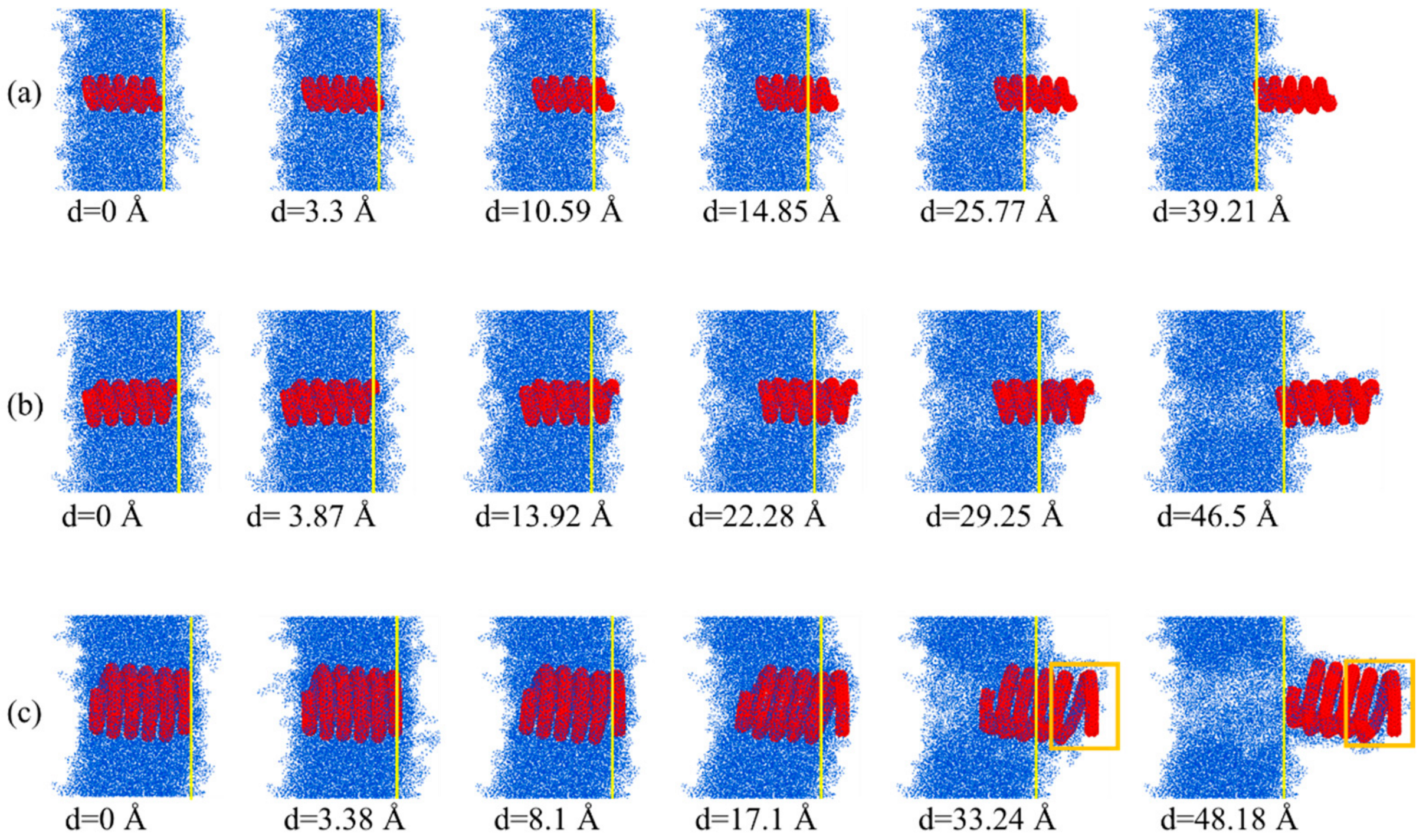
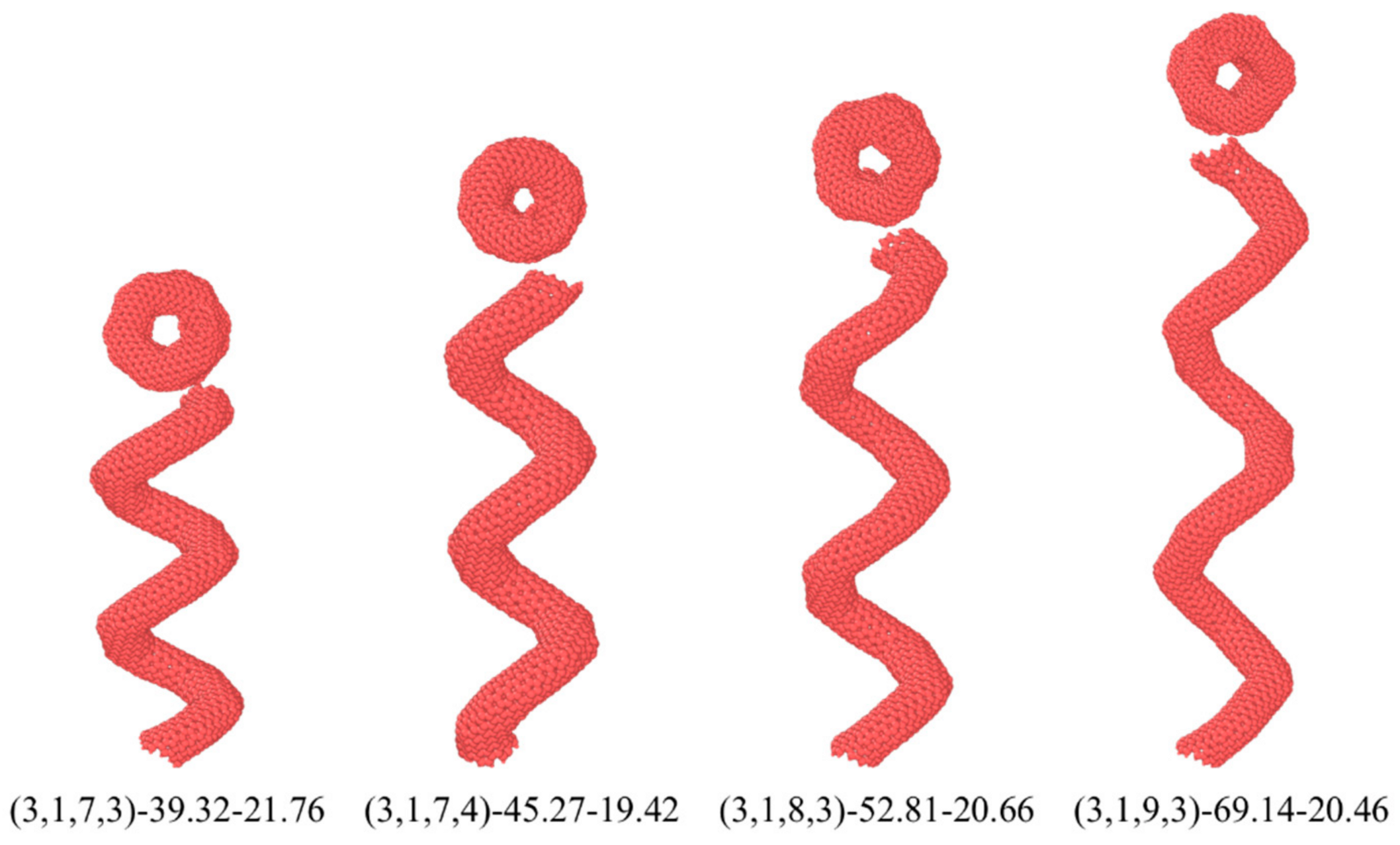
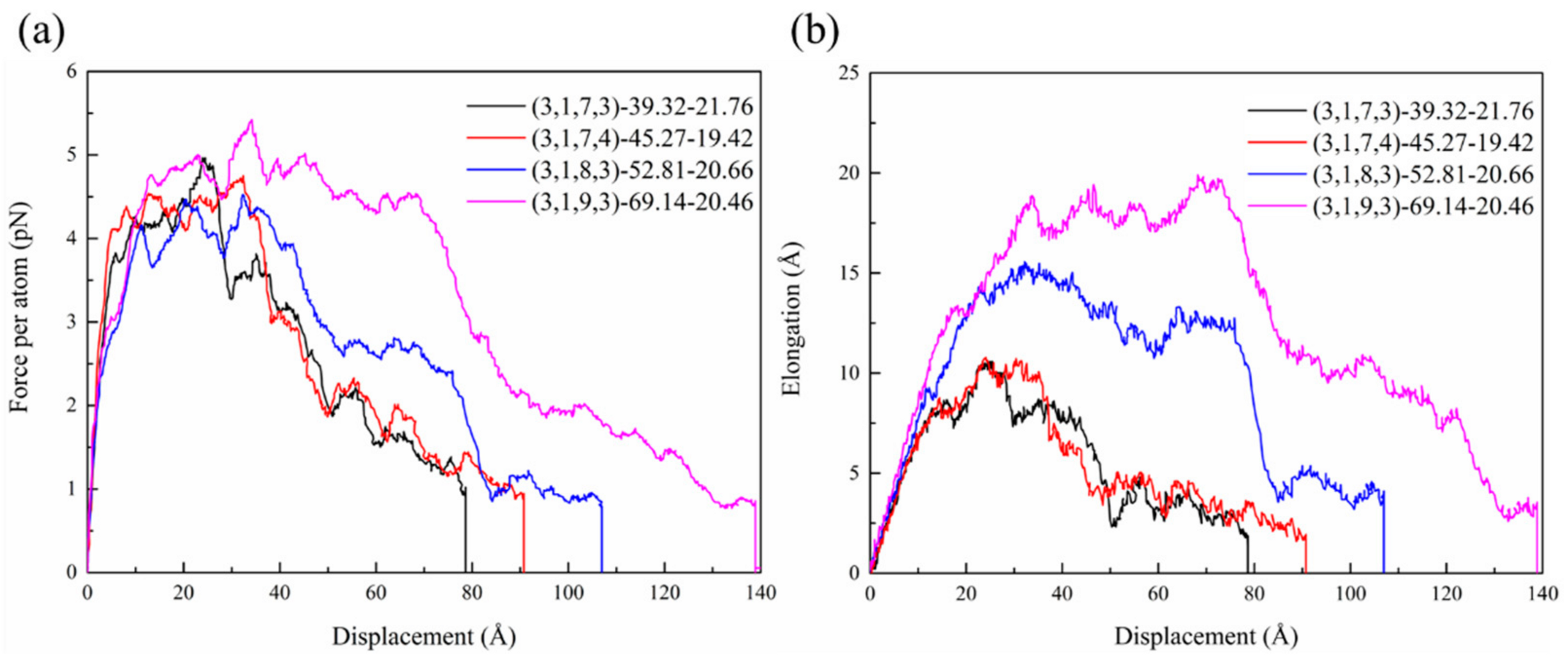
4.3. The Interfacial Properties of HCNTs with Different Pitch Lengths
5. Conclusions
- (a)
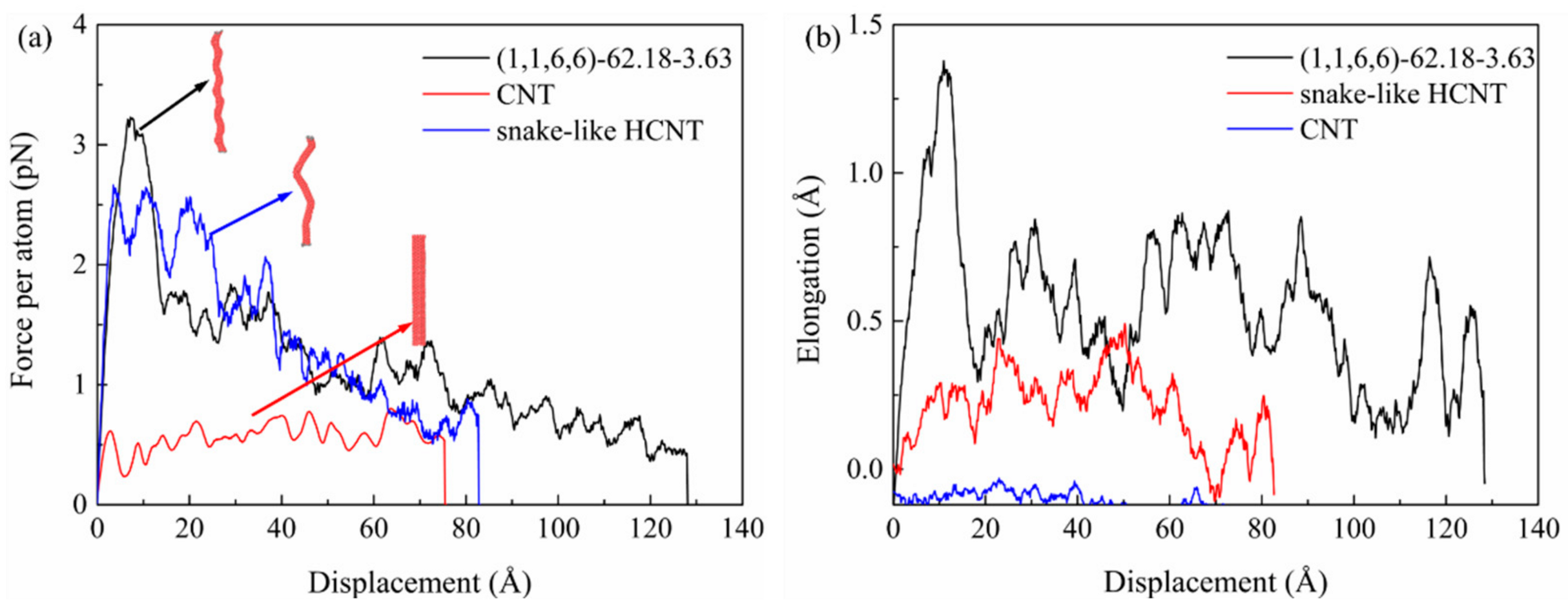
- The shear resistance of HCNTs is much better than that of straight CNTs during the pullout process, where the maximum pullout force per atom of the CNT is only 0.8 pN which is four times smaller than that of HCNTs (up to 3.23 pN). However, (1,1,2,0)-6.54-12.28 with both a small diameter and helix angle showed very poor interfacial mechanical properties, which are similar to CNTs.
- (b)
- As for the nanocomposites reinforced by HCNTs with different diameters, the friction coefficient showed a decreasing pattern with the increase in the diameter of HCNTs. And (1,1,3,0)-7.61-16.32 possessed the largest maximum pullout force (5.45 pN) while (1,1,6,0)-8.43-29.50 had the smallest maximum pullout force (2.57 pN). Furthermore, (1,1,2,0)-6.54-12.28 with the smallest diameter and inter-tube gap showed a similar pattern with straight CNTs where the interlocking strength was very weak and could be easily pulled out from the matrix.
- (c)
- Among the nanocomposites reinforced by HCNTs with different pitch lengths, (3,1,8,3)-52.81-20.66 with a pitch length of 52.81 Å had the ability to prevent the initiation and the growth of cracks since it simultaneously possessed a large friction coefficient, reversible force, and maximum force.
- (d)
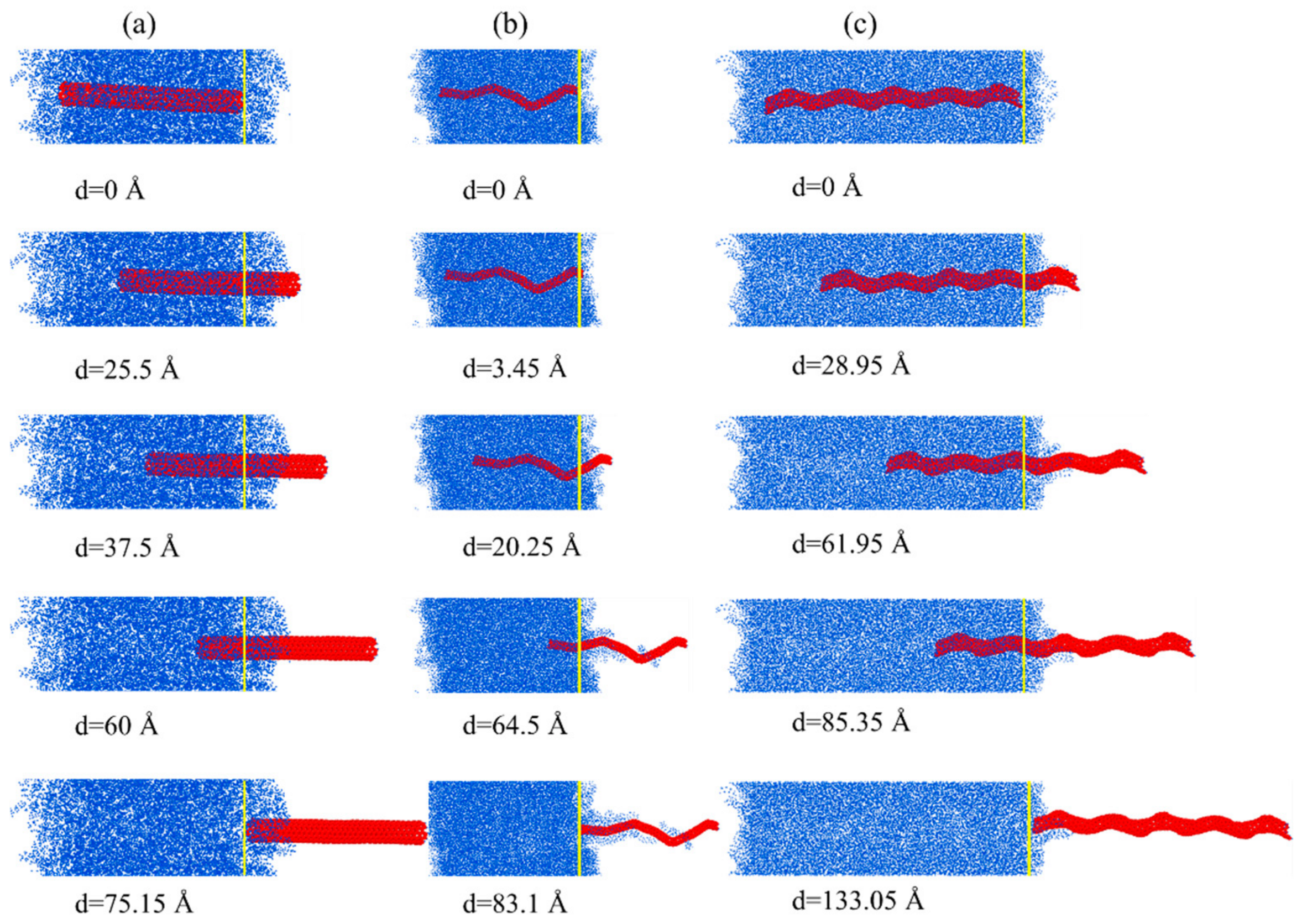
- During the pullout process, there was an obvious elongation of HCNTs, causing the high value and strong oscillation of the pullout force, indicating the efficient load transfer ability from the matrix to nanofillers. The elongation of HCNTs depends both on the helix angle and the stiffness of HCNTs. On the other hand, the length of straight CNTs remains unchanged during the process, which can also be observed for snake-like HCNTs and (1,1,2,0)-6.54-12.28 with both a small diameter and pitch length.
- (e)
- After the nanofillers are pulled out from the matrix, HCNTs can carry out the most polymer chains, and an even bigger void is generated inside the polymer matrix because of the biggest diameter being used while the CNT cannot capture polymer chains efficiently. This indicates that the shear fracture of nanocomposites for HCNTs always occurs inside the matrix, while fracture only occurs on the interface for nanocomposites reinforced by CNTs with a large helix angle.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, P.; Wu, J.; Zhang, J.; Shao, J.; Tang, W.; Hou, G.; Zhang, L.; Chen, X. Role of geometric shapes on the load transfer in graphene-PMMA nanocomposites. Comput. Mater. Sci. 2020, 184, 109863. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, K.; Dixit, A.R. A review on the mechanical and thermal properties of graphene and graphene-based polymer nanocomposites: Understanding of modelling and MD simulation. Mol. Simul. 2019, 46, 136–154. [Google Scholar] [CrossRef]
- Izadi, R.; Ghavanloo, E.; Nayebi, A. Elastic properties of polymer composites reinforced with C60 fullerene and carbon onion: Molecular dynamics simulation. Phys. B Condens. Matter 2019, 574, 311636. [Google Scholar] [CrossRef]
- Yang, S.; Yu, S.; Cho, M. Influence of Thrower–Stone–Wales defects on the interfacial properties of carbon nanotube/polypropylene composites by a molecular dynamics approach. Carbon 2013, 55, 133–143. [Google Scholar] [CrossRef]
- Nie, F.; Jian, W.; Lau, D. An atomistic study on the thermomechanical properties of graphene and functionalized graphene sheets modified asphalt. Carbon 2021, 182, 615–627. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Wang, Q.; Xing, M. A comparison study on mechanical properties of polymer composites reinforced by carbon nanotubes and graphene sheet. Compos. Part B Eng. 2018, 133, 35–41. [Google Scholar] [CrossRef]
- van de Werken, N.; Tekinalp, H.; Khanbolouki, P.; Ozcan, S.; Williams, A.; Tehrani, M. Additively manufactured carbon fiber-reinforced composites: State of the art and perspective. Addit. Manuf. 2020, 31, 100962. [Google Scholar] [CrossRef]
- Shen, S.; Yang, L.; Wang, C.; Wei, L. Effect of CNT orientation on the mechanical property and fracture mechanism of vertically aligned carbon nanotube/carbon composites. Ceram. Int. 2020, 46, 4933–4938. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, X.; Sui, G.; Yang, X. Improving interfacial and mechanical properties of carbon nanotube-sized carbon fiber/epoxy composites. Carbon 2019, 145, 629–639. [Google Scholar] [CrossRef]
- Abidin, M.S.Z.; Herceg, T.; Greenhalgh, E.S.; Shaffer, M.; Bismarck, A. Enhanced fracture toughness of hierarchical carbon nanotube reinforced carbon fibre epoxy composites with engineered matrix microstructure. Compos. Sci. Technol. 2019, 170, 85–92. [Google Scholar] [CrossRef]
- Zhang, L.W.; Ji, W.M.; Liew, K.M. Mechanical properties of diamond nanothread reinforced polymer composites. Carbon 2018, 132, 232–240. [Google Scholar] [CrossRef]
- Rouhi, S.; Alizadeh, Y.; Ansari, R. On the interfacial characteristics of polyethylene/single-walled carbon nanotubes using molecular dynamics simulations. Appl. Surf. Sci. 2014, 292, 958–970. [Google Scholar] [CrossRef]
- Duan, K.; Li, L.; Wang, F.; Liu, S.; Hu, Y.; Wang, X. New insights into interface interactions of CNT-reinforced epoxy nanocomposites. Compos. Sci. Technol. 2021, 204, 108638. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, P.H.; Tian, X.B.; Shi, S.Q.; Tam, L.-H. Molecular investigation on temperature-dependent mechanical properties of PMMA/CNT nanocomposite. Eng. Fract. Mech. 2023, 293, 109705. [Google Scholar] [CrossRef]
- Wang, J.F.; Shi, S.Q.; Liu, Y.Z.; Yang, J.P.; Tam, L.-H. Multiscale simulation of temperature- and pressure-dependent nonlinear dynamics of PMMA/CNT composite plates. Nonlinear Dyn. 2022, 109, 1517–1550. [Google Scholar] [CrossRef]
- Tang, L.-C.; Zhang, H.; Wu, X.-P.; Zhang, Z. A novel failure analysis of multi-walled carbon nanotubes in epoxy matrix. Polymer 2011, 52, 2070–2074. [Google Scholar] [CrossRef]
- Quan, D.; Urdániz, J.L.; Ivanković, A. Enhancing mode-I and mode-II fracture toughness of epoxy and carbon fibre reinforced epoxy composites using multi-walled carbon nanotubes. Mater. Des. 2018, 143, 81–92. [Google Scholar] [CrossRef]
- Zheng, Q.B.; Xue, Q.Z.; Yan, K.O.; Hao, L.Z.; Li, Q.; Gao, X.L. Investigation of molecular interactions between SWNT and polyethylene/polypropylene/polystyrene/polyaniline molecules. J. Phys. Chem. C 2007, 111, 4628–4635. [Google Scholar] [CrossRef]
- Liu, F.; Hu, N.; Ning, H.; Liu, Y.; Li, Y.; Wu, L. Molecular dynamics simulation on interfacial mechanical properties of polymer nanocomposites with wrinkled graphene. Comput. Mater. Sci. 2015, 108, 160–167. [Google Scholar] [CrossRef]
- Awasthi, A.P.; Lagoudas, D.C.; Hammerand, D.C. Modeling of graphene–polymer interfacial mechanical behavior using molecular dynamics. Model. Simul. Mater. Sci. Eng. 2009, 17, 015002. [Google Scholar] [CrossRef]
- Li, Y.; Seidel, G.D. Multiscale modeling of the effects of nanoscale load transfer on the effective elastic properties of unfunctionalized carbon nanotube–polyethylene nanocomposites. Model. Simul. Mater. Sci. Eng. 2014, 22, 025023. [Google Scholar] [CrossRef]
- Mahboob, M.; Islam, M.Z. Molecular dynamics simulations of defective CNT-polyethylene composite systems. Comput. Mater. Sci. 2013, 79, 223–229. [Google Scholar] [CrossRef]
- Islam, M.Z.; Mahboob, M.; Lowe, R.L. Mechanical properties of defective carbon nanotube/polyethylene nanocomposites: A molecular dynamics simulation study. Polym. Compos. 2016, 37, 305–314. [Google Scholar] [CrossRef]
- Peng, X.; Meguid, S.A. Molecular simulations of the influence of defects and functionalization on the shear strength of carbon nanotube-epoxy polymer interfaces. Comput. Mater. Sci. 2017, 126, 204–216. [Google Scholar] [CrossRef]
- Kai, M.F.; Zhang, L.W.; Liew, K.M. Carbon nanotube-geopolymer nanocomposites: A molecular dynamics study of the influence of interfacial chemical bonding upon the structural and mechanical properties. Carbon 2020, 161, 772–783. [Google Scholar] [CrossRef]
- Kai, M.F.; Zhang, L.W.; Liew, K.M. Graphene and graphene oxide in calcium silicate hydrates: Chemical reactions, mechanical behavior and interfacial sliding. Carbon 2019, 146, 181–193. [Google Scholar] [CrossRef]
- Jian, W.; Lau, D. Understanding the effect of functionalization in CNT-epoxy nanocomposite from molecular level. Compos. Sci. Technol. 2020, 191, 108076. [Google Scholar] [CrossRef]
- Sharma, K.; Kaushalyayan, K.S.; Shukla, M. Pull-out simulations of interfacial properties of amine functionalized multi-walled carbon nanotube epoxy composites. Comput. Mater. Sci. 2015, 99, 232–241. [Google Scholar] [CrossRef]
- Li, Y.; Seidel, G.D. Multiscale modeling of functionalized interface effects on the effective elastic material properties of CNT–polyethylene nanocomposites. Comput. Mater. Sci. 2015, 107, 216–234. [Google Scholar] [CrossRef]
- Karimi, M.R.; Abrinia, K.; Hamdia, K.M.; Hashemianzadeh, S.M.; Baniassadi, M. Effects of functional group type and coverage on the interfacial strength and load transfer of graphene-polyethylene nanocomposites: A molecular dynamics simulation. Appl. Phys. A 2022, 128, 341. [Google Scholar] [CrossRef]
- Yuan, Z.; Lu, Z.; Chen, M.; Yang, Z.; Xie, F. Interfacial properties of carboxylic acid functionalized CNT/polyethylene composites: A molecular dynamics simulation study. Appl. Surf. Sci. 2015, 351, 1043–1052. [Google Scholar] [CrossRef]
- Lau, K.-T.; Lu, M.; Liao, K. Improved mechanical properties of coiled carbon nanotubes reinforced epoxy nanocomposites. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1837–1840. [Google Scholar] [CrossRef]
- Yoshimura, K.; Nakano, K.; Miyake, T.; Hishikawa, Y.; Motojima, S. Effectiveness of carbon microcoils as a reinforcing material for a polymer matrix. Carbon 2006, 44, 2833–2838. [Google Scholar] [CrossRef]
- Li, X.; Lau, K.; Yin, Y. Mechanical properties of epoxy-based composites using coiled carbon nanotubes. Compos. Sci. Technol. 2008, 68, 2876–2881. [Google Scholar] [CrossRef]
- Sharifian, A.; Baghani, M.; Odegard, G.M.; Wu, J.; van Duin, A.C.T.; Baniassadi, M. How to characterize interfacial load transfer in spiral carbon-based nanostructure-reinforced nanocomposites: Is this a geometry-dependent process? Phys. Chem. Chem. Phys. 2019, 21, 23880–23892. [Google Scholar] [CrossRef] [PubMed]
- Vijayan, R.; Ghazinezami, A.; Taklimi, S.R.; Khan, M.Y.; Askari, D. The geometrical advantages of helical carbon nanotubes for high-performance multifunctional polymeric nanocomposites. Compos. Part B Eng. 2019, 156, 28–42. [Google Scholar] [CrossRef]
- Wang, Y.; Mei, Y.; Wang, Q.; Wei, W.; Huang, F.; Li, Y.; Li, J.; Zhou, Z. Improved fracture toughness and ductility of PLA composites by incorporating a small amount of surface-modified helical carbon nanotubes. Compos. Part B Eng. 2019, 162, 54–61. [Google Scholar] [CrossRef]
- Kadhim, N.; Mei, Y.; Wang, Y.; Li, Y.; Meng, F.; Jiang, M.; Zhou, Z. Remarkable Improvement in the Mechanical Properties of Epoxy Composites Achieved by a Small Amount of Modified Helical Carbon Nanotubes. Polymers 2018, 10, 1103. [Google Scholar] [CrossRef] [PubMed]
- Sharifian, A.; Baghani, M.; Wu, J.; Odegard, G.M.; Baniassadi, M. Insight into Geometry-Controlled Mechanical Properties of Spiral Carbon-Based Nanostructures. J. Phys. Chem. C 2019, 123, 3226–3238. [Google Scholar] [CrossRef]
- Sarapat, P.; Hill, J.; Baowan, D. A review of geometry, construction and modelling for carbon nanotori. Appl. Sci. 2019, 9, 2301. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, H.; Liu, J.; Zhang, Z.; Ning, F.; Liu, Y. Nanotube-chirality-controlled tensile characteristics in coiled carbon metastructures. Carbon 2018, 133, 335–349. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Q.S.; Liew, K.M.; He, X.Q. Superstretchability and stability of helical structures of carbon nanotube/polymer composite fibers: Coarse-grained molecular dynamics modeling and simulation. Carbon 2017, 115, 220–228. [Google Scholar] [CrossRef]
- Chang, X.; Xu, Q.; Lv, J.; Xu, L.; Zhu, Z.; Liu, S.; Liu, X.; Qin, J. Bioinspired 3D helical fibers toughened thermosetting composites. Compos. Part B Eng. 2021, 216, 108855. [Google Scholar] [CrossRef]
- Chuang, C.; Fan, Y.-C.; Jin, B.-Y. Generalized classification scheme of toroidal and helical carbon nanotubes. J. Chem. Inf. Model. 2009, 49, 361–368. [Google Scholar] [CrossRef]
- Haghighi, S.; Ansari, R.; Ajori, S. Influence of polyethylene cross-linked functionalization on the interfacial properties of carbon nanotube-reinforced polymer nanocomposites: A molecular dynamics study. J. Mol. Model. 2019, 25, 105. [Google Scholar] [CrossRef]
- Nikkhah, S.J.; Moghbeli, M.R.; Hashemianzadeh, S.M. Dynamic study of deformation and adhesion of an amorphous polyethylene/graphene interface: A simulation study. Macromol. Theory Simul. 2016, 25, 533–549. [Google Scholar] [CrossRef]
- Qin, R.; Zhou, A.; Yu, Z.; Wang, Q.; Lau, D. Role of carbon nanotube in reinforcing cementitious materials: An experimental and coarse-grained molecular dynamics study. Cem. Concr. Res. 2021, 147, 106517. [Google Scholar] [CrossRef]
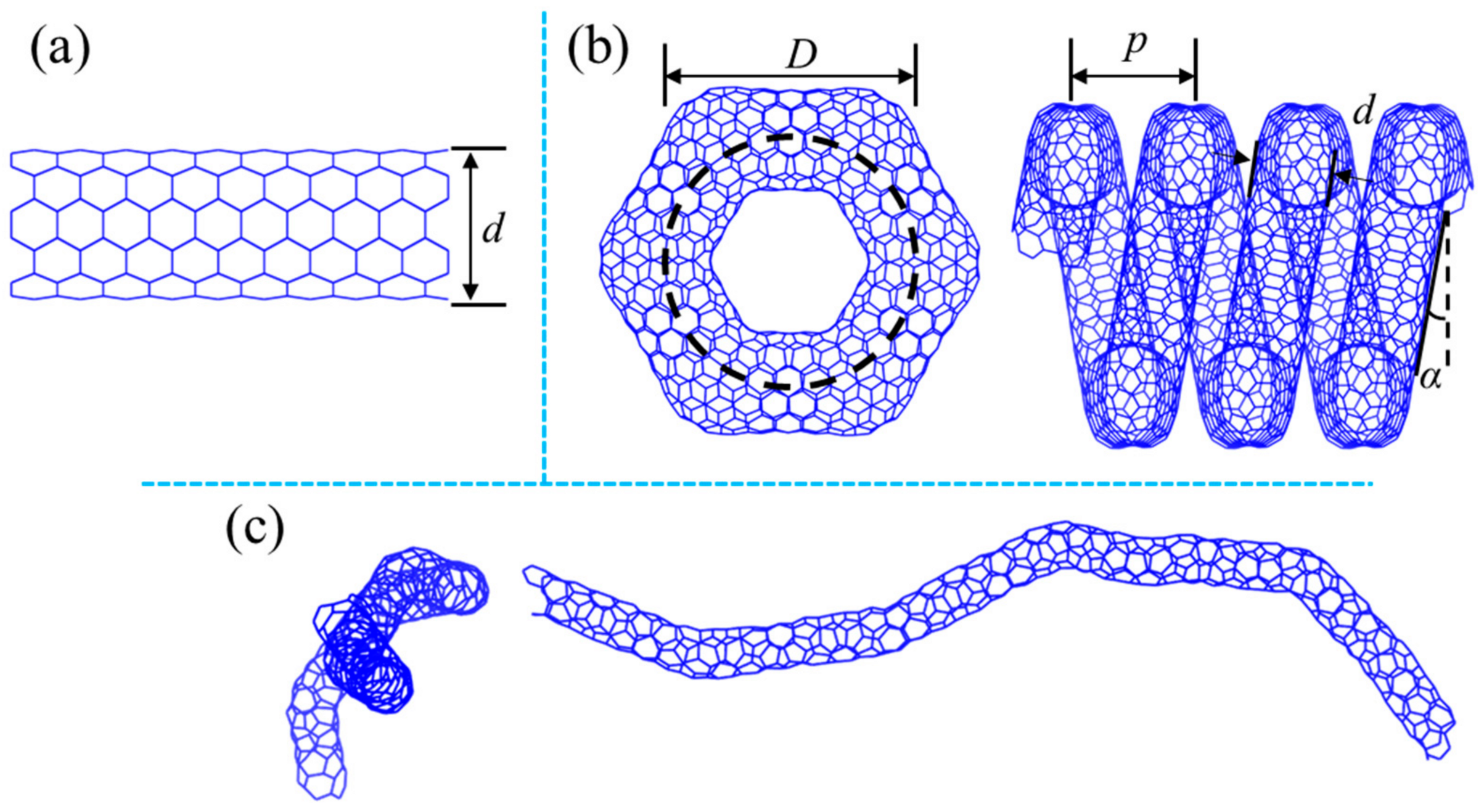



| HCNTs | Number of Atoms | Tube Radius d (Å) | Effective Diameter D (Å) | Pitch Length p (Å) | Helix Angle (°) |
|---|---|---|---|---|---|
| (1,1,2,0)-6.54-12.28 | 1164 | 2.7 | 12.28 | 6.54 | 4.84 |
| (1,1,3,0)-7.61-16.32 | 1744 | 2.7 | 16.32 | 7.61 | 4.24 |
| (1,1,4,0)-8.17-20.36 | 2320 | 2.7 | 20.36 | 8.17 | 3.65 |
| (1,1,5,0)-8.43-24.86 | 2896 | 2.7 | 24.86 | 8.43 | 3.09 |
| (1,1,6,0)-8.53-29.50 | 3472 | 2.7 | 29.50 | 8.53 | 2.63 |
| HCNTs | Reversible Displacement (Å) | Reversible Force (pN) | Friction Coefficient (pN/Å) | Maximum Pullout Force (pN) | Maximum Elongation (Å) |
|---|---|---|---|---|---|
| (1,1,2,0)-6.54-12.28 | 3.29 | 4.48 | 1.36 | 4.48 | 0.23 |
| (1,1,3,0)-7.61-16.32 | 3.86 | 5.45 | 1.41 | 5.45 | 2.01 |
| (1,1,4,0)-8.17-20.36 | 3.96 | 4.04 | 1.02 | 4.04 | 4.81 |
| (1,1,5,0)-8.43-24.86 | 4.78 | 4.33 | 0.91 | 4.33 | 5.02 |
| (1,1,6,0)-8.53-29.50 | 3.38 | 2.57 | 0.76 | 2.57 | 9.89 |
| HCNTs | Number of Atoms | Tube Radius d (Å) | Effective Diameter D (Å) | Pitch Length p (Å) | Helix Angle (°) |
|---|---|---|---|---|---|
| (3,1,7,3)-39.32-21.76 | 1754 | 4.2 | 21.76 | 39.32 | 16.05 |
| (3,1,7,4)-45.27-19.42 | 1754 | 4.2 | 19.42 | 45.27 | 20.35 |
| (3,1,8,3)-52.81-20.66 | 2042 | 4.2 | 20.66 | 52.81 | 22.13 |
| (3,1,9,3)-69.14-20.46 | 2330 | 4.2 | 20.46 | 69.14 | 28.27 |
| HCNTs | Reversible Displacement (Å) | Reversible Force (pN) | Friction Coefficient (pN/Å) | Maximum Pullout Force (pN) | Maximum Elongation (Å) |
|---|---|---|---|---|---|
| (3,1,7,3)-39.32-21.76 | 5.83 | 3.83 | 0.66 | 4.97 | 10.95 |
| (3,1,7,4)-45.27-19.42 | 8.06 | 4.11 | 0.51 | 4.75 | 11.08 |
| (3,1,8,3)-52.81-20.66 | 11.23 | 4.10 | 0.37 | 4.52 | 25.63 |
| (3,1,9,3)-69.14-20.46 | 13.15 | 4.76 | 0.36 | 5.42 | 19.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bie, Z.; Liu, X.; Deng, Y.; Shi, X.; He, X. Study on Crack Resistance Mechanism of Helical Carbon Nanotubes in Nanocomposites. Nanomaterials 2025, 15, 119. https://doi.org/10.3390/nano15020119
Bie Z, Liu X, Deng Y, Shi X, He X. Study on Crack Resistance Mechanism of Helical Carbon Nanotubes in Nanocomposites. Nanomaterials. 2025; 15(2):119. https://doi.org/10.3390/nano15020119
Chicago/Turabian StyleBie, Zhiwu, Xuefeng Liu, Yajie Deng, Xian Shi, and Xiaoqiao He. 2025. "Study on Crack Resistance Mechanism of Helical Carbon Nanotubes in Nanocomposites" Nanomaterials 15, no. 2: 119. https://doi.org/10.3390/nano15020119
APA StyleBie, Z., Liu, X., Deng, Y., Shi, X., & He, X. (2025). Study on Crack Resistance Mechanism of Helical Carbon Nanotubes in Nanocomposites. Nanomaterials, 15(2), 119. https://doi.org/10.3390/nano15020119






