Oscillations in Absorption from InGaN/GaN Quantum Well to Continuum
Abstract
:1. Introduction
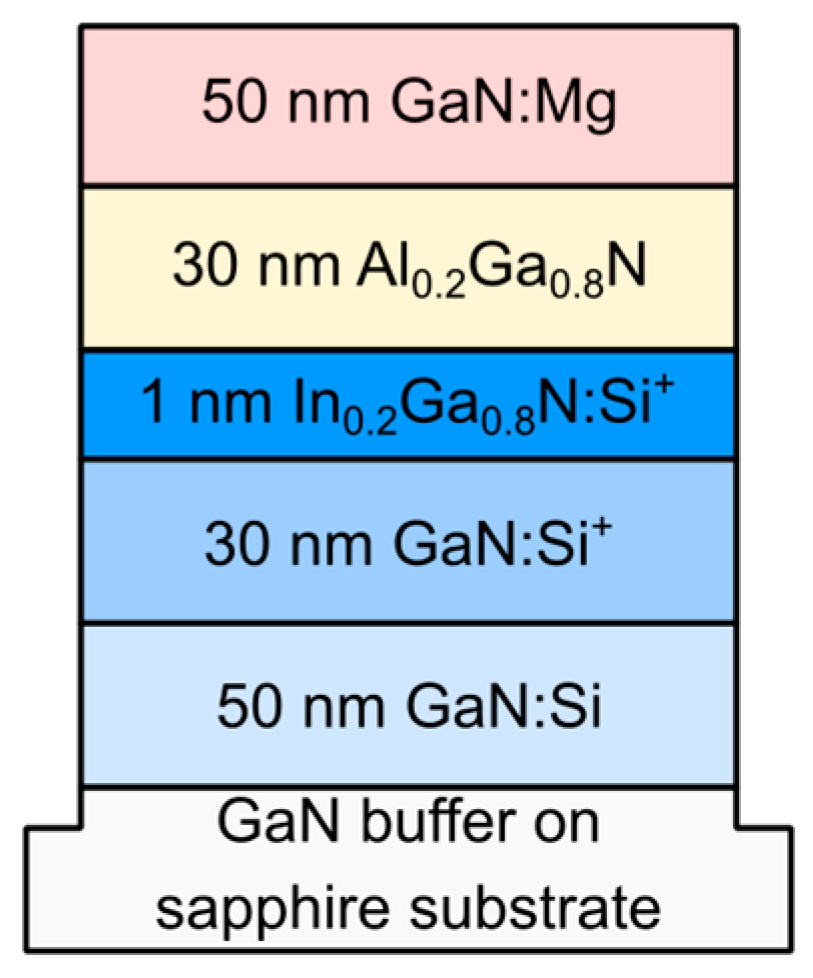
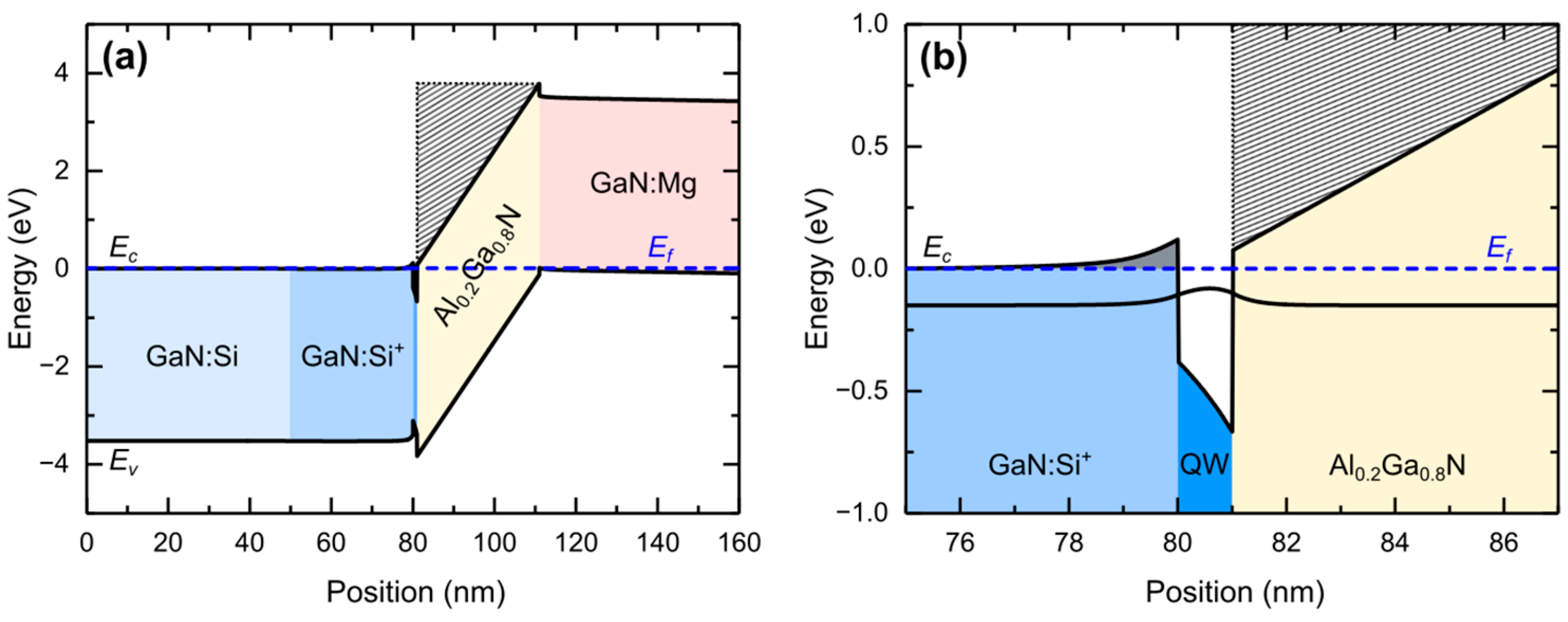
2. The Sample and Computational Methods
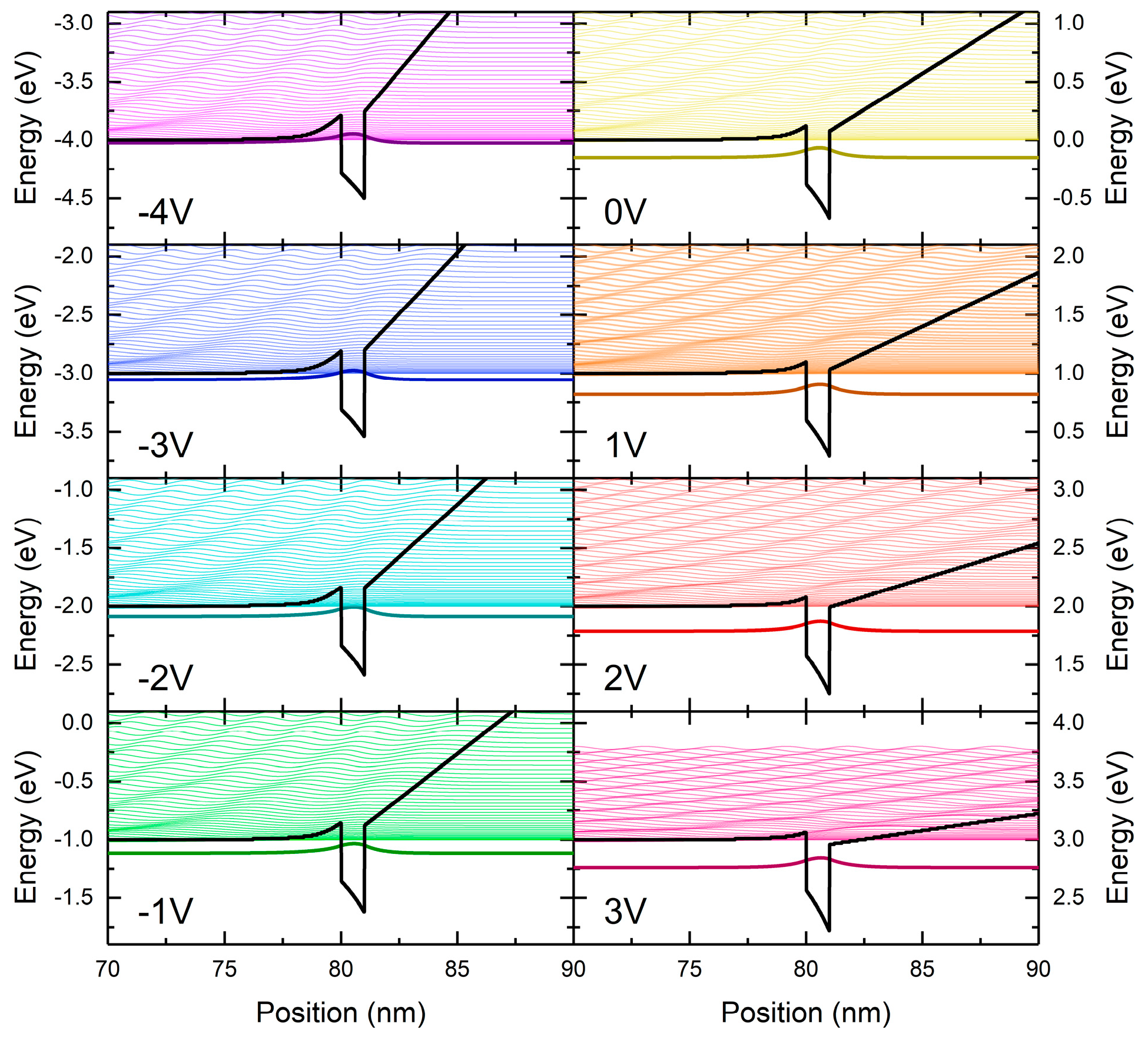
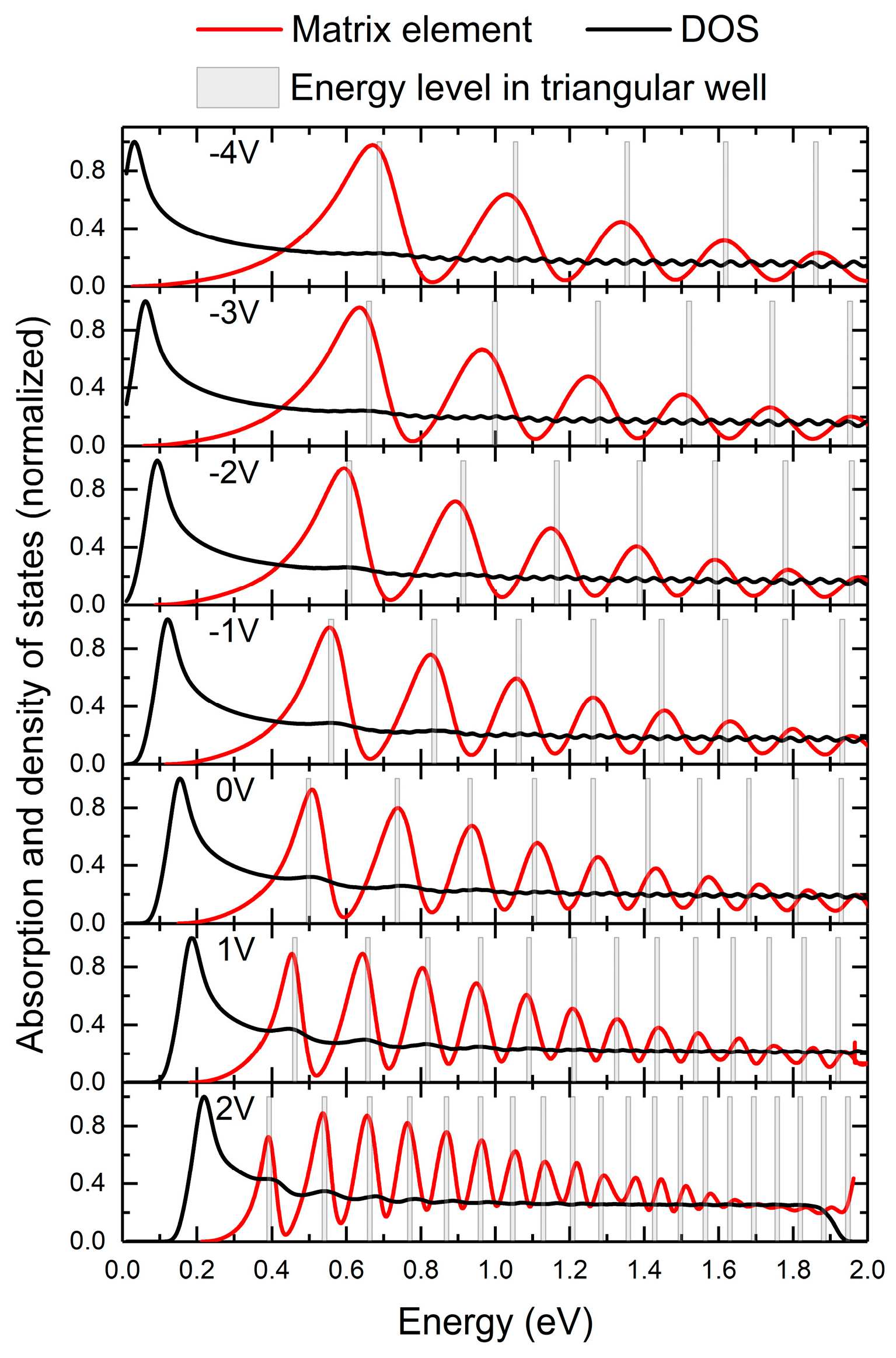
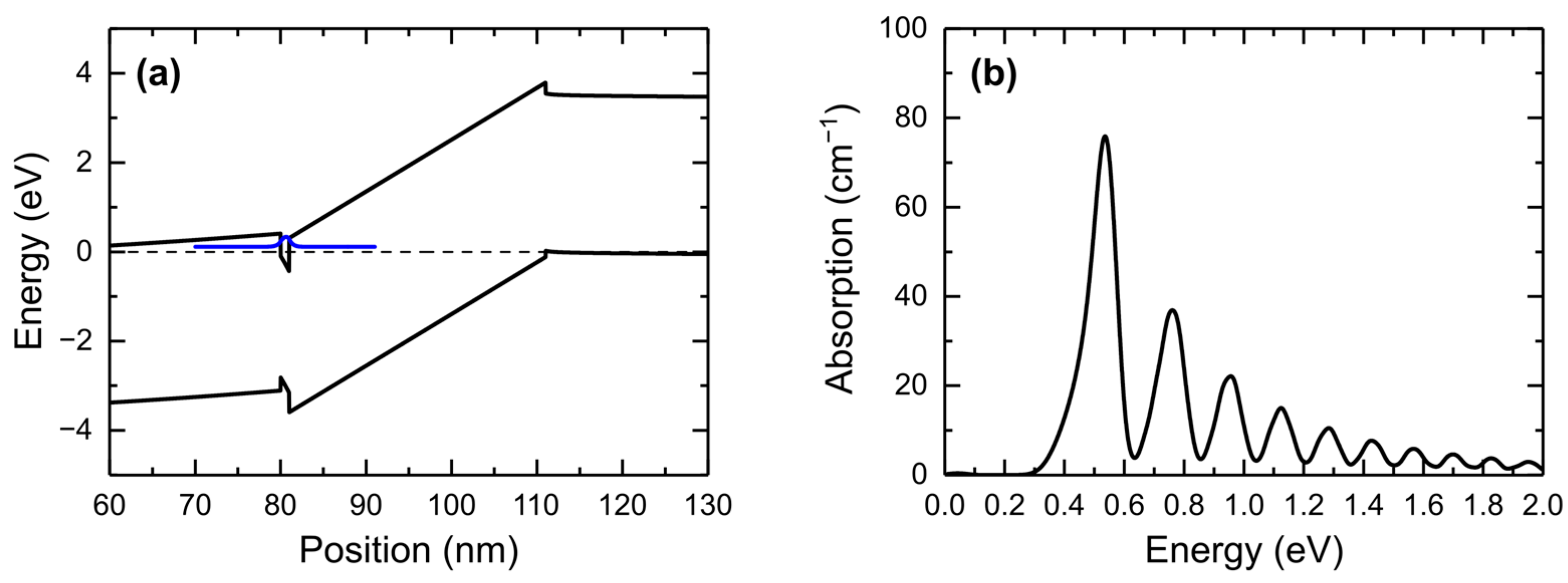
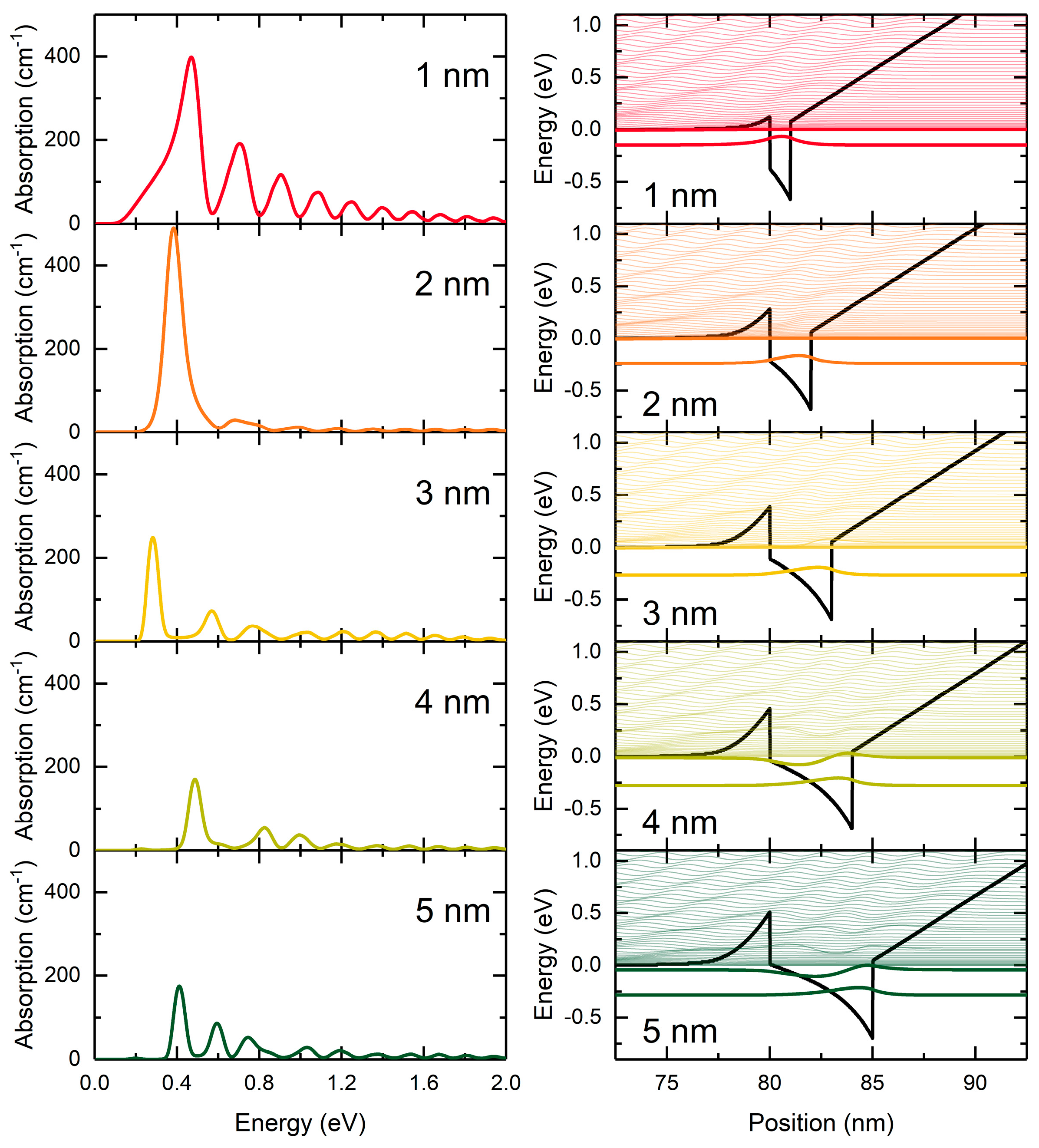
3. Results
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.C.; Capasso, F. Intersubband Transitions in Quantum Wells: Physics and Device Applications I; Semiconductors and Semimetals; Academic Press: San Diego, CA, USA, 2000; Volume 62. [Google Scholar]
- Fafard, S. Energy levels in quantum wells with capping barrier layer of finite size: Bound states and oscillatory behavior of the continuum states. Phys. Rev. B 1992, 46, 4659–4666. [Google Scholar] [CrossRef] [PubMed]
- Fafard, S.; Fortin, E.; Roth, A.P. Effects of an electric field on the continuum energy levels in InGaAs/GaAs quantum wells terminated with thin cap layers. Phys. Rev. B 1993, 47, 8089–10595. [Google Scholar] [CrossRef]
- Colocci, M.; Martinez-Pastor, J.; Gurioli, M. Above-barrier resonant transitions in AlGaAs/A1As/GaAs heterostructures. Phys. Rev. B 1993, 48, 8089–8094. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.D.; Son, J.S.; Leem, J.Y.; Noh, S.K.; Kyu-Seok Lee Lee, C.; Hwang, I.S.; Park, H.Y. Direct observation of above-barrier quasibound states in InGaAs/AlAs/GaAs quantum wells. Phys. Rev. B 1996, 54, 1541–1544. [Google Scholar] [CrossRef] [PubMed]
- Trzeciakowski, W.; Gurioli, M. Electric-field effects in semiconductor quantum wells. Phys. Rev. B 1991, 44, 3880–3890. [Google Scholar] [CrossRef] [PubMed]
- Kuo, D.M.-T.; Chang, Y.-C. Intersubband electroabsorption spectra of semiconductor quantum wells. J. Appl. Phys. 2000, 87, 2936–2940. [Google Scholar] [CrossRef]
- Vorob’ev, L.E.; Zibik, E.A.; Firsov, D.A.; Shalygin, V.A.; Nashchekina, O.N.; Saidashev, I.I. Modulation of optical absorption of GaAs/AlGaAs quantum wells in a transverse electric field. Semiconductors 1998, 32, 754–756. [Google Scholar] [CrossRef]
- Gmachl, C.; Ng, H.M.; Cho, A.Y. Intersubband absorption in GaN/AlGaN multiple quantum wells in the wavelength range of λ∼1.75–4.2 μm. Appl. Phys. Lett. 2000, 77, 334–336. [Google Scholar] [CrossRef]
- Machhadani, H.; Kandaswamy, P.; Sakr, S.; Vardi, A.; Wirtmüller, A.; Nevou, L.; Guillot, F.; Pozzovivo, G.; Tchernycheva, M.; Lupu, A.; et al. GaN/AlGaN intersubband optoelectronic devices. New J. Phys. 2009, 11, 125023. [Google Scholar] [CrossRef]
- Hofstetter, D.; Baumann, E.; Giorgetta, F.R.; Théron, R.; Wu, H.; Schaff, W.J.; Dawlaty, J.; George, P.A.; Eastman, L.F.; Rana, F.; et al. Intersubband transition-based processes and devices in AlN/GaN-based heterostructures. Proc. IEEE 2010, 98, 1234–1248. [Google Scholar] [CrossRef]
- Beeler, M.; Trichas, E.; Monroy, E. III-nitride semiconductors for intersubband optoelectronics: A review. Semicond. Sci. Technol. 2013, 28, 074022. [Google Scholar] [CrossRef]
- Gładysiewicz, M.; Kudrawiec, R. Random approach to determine the broadening of intersubband and interband transitions in (In)GaN/Al(In)N quantum wells. J. Phys. Condens. Matter 2010, 22, 485801. [Google Scholar] [CrossRef]
- Yıldırım, H.; Aslan, B. Intersubband transitions in InGaN/InGaN/GaN staggered quantum wells. J. Appl. Phys. 2014, 115, 164306. [Google Scholar] [CrossRef]
- Chen, G.; Wang, X.Q.; Rong, X.; Wang, P.; Xu, F.J.; Tang, N.; Qin, Z.X.; Chen, Y.H.; Shen, B. Intersubband Transition in GaN/InGaN Multiple Quantum Wells. Sci. Rep. 2015, 5, 11485. [Google Scholar] [CrossRef]
- Monavarian, M.; Xu, J.; Fireman, M.N.; Nookala, N.; Wu, F.; Bonef, B.; Qwah, K.S.; Young, E.C.; Belkin, M.A.; Speck, J.S. Structural and optical properties of nonpolar m- and a-plane GaN/AlGaN heterostructures for narrow-linewidth mid-infrared intersubband transitions. Appl. Phys. Lett. 2020, 116, 201103. [Google Scholar] [CrossRef]
- Wu, Y.-R.; Chiu, C.; Chang, C.-Y.; Yu, P.; Kuo, H.-C. Size-Dependent Strain Relaxation and Optical Characteristics of InGaN/GaN Nanorod LEDs. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1226–1233. [Google Scholar] [CrossRef]
- Wu, Y.-R.; Shivaraman, R.; Wang, K.-C.; Speck, J.S. Analyzing the physical properties of InGaN multiple quantum well light emitting diodes from nano scale structure. Appl. Phys. Lett. 2012, 101, 083505. [Google Scholar] [CrossRef]
- Ambacher, O.; Majewski, J.; Miskys, C.; Link, A.; Hermann, M.; Eickhoff, M.; Stutzmann, M.; Bernardini, F.; Fiorentini, V.; Tilak, V.; et al. Pyroelectric properties of Al(In)GaN/GaN hetero- and quantum well structures. J. Phys. Condens. Matter 2002, 14, 3399. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.R. Band parameters for nitrogen-containing semiconductors. J. Appl. Phys. 2003, 94, 3675–3696. [Google Scholar] [CrossRef]
- Chuang, S.L.; Chang, C.S. k·p method for strained wurtzite semiconductors. Phys. Rev. B 1996, 54, 2491. [Google Scholar] [CrossRef] [PubMed]
- BenDaniel, D.J.; Duke, C.B. Space-Charge Effects on Electron Tunneling. Phys. Rev. B 1966, 152, 683–692. [Google Scholar] [CrossRef]
- Salejda, W.; Tyc, M.; Andrzejewski, J.; Kubisa, M.; Misiewicz, J.; Just, M.; Ryczko, K. New Numerical Matrix Methods of Solving the Quasi-One-Dimensional Effective-Mass Equation. Acta Phys. Pol. A 1999, 95, 881–896. [Google Scholar] [CrossRef]
- Gładysiewicz, M.; Kudrawiec, R.; Muzioł, G.; Turski, H.; Skierbiszewski, C. Theoretical and Experimental Studies on Material Gain for Wide Polar InGaN Quantum Well-Mechanism Leading to Electric Field Screening and Lasing. Adv. Phys. Res. 2023, 2, 2200107. [Google Scholar] [CrossRef]
- Gladysiewicz, M.; Skierbiszewski, C.; Kudrawiec, R. Material Gain in Polar GaInN and AlGaN Quantum Wells: How to Overcome the ‘Dead’ Width for Light Emitters in These QW Systems? IEEE J. Sel. Top. Quantum Electron. 2022, 28, 1501509. [Google Scholar] [CrossRef]
- Jarema, M.; Gladysiewicz, M.; Janicki, L.; Zdanowicz, E.; Turski, H.; Muziol, G.; Skierbiszewski, C.; Kudrawiec, R. Inhomogeneous broadening of optical transitions observed in photoluminescence and modulated reflectance of polar and non-polar InGaN quantum wells. J. Appl. Phys. 2020, 127, 035702. [Google Scholar] [CrossRef]
- Baranowski, M.; Janicki, L.; Gladysiewicz, M.; Welna, M.; Latkowska, M.; Misiewicz, J.; Marona, L.; Schiavon, D.; Perlin, P.; Kudrawiec, R. Direct evidence of photoluminescence broadening enhancement by local electric field fluctuations in polar InGaN/GaN quantum wells. Jpn. J. Appl. Phys. 2018, 57, 9. [Google Scholar]
- Jarema, M.; Gladysiewicz, M.; Zdanowicz, E.A.; Bellet-Amalric, E.; Monroy, E.; Kudrawiec, R. On intrinsic Stokes shift in wide GaN/AlGaN polar quantum wells. Semicond. Sci. Technol. 2019, 34, 075021. [Google Scholar] [CrossRef]
- Chow, W.; Kira, M.; Koch, S.W. Microscopic theory of optical nonlinearities and spontaneous emission lifetime in group-III nitride quantum wells. Phys. Rev. B 1999, 60, 1947–1952. [Google Scholar] [CrossRef]
- Bin-He, W. Transient Intersubband Optical Absorption in Double Quantum Well Structure. Commun. Theor. Phys. 2005, 43, 759–764. [Google Scholar] [CrossRef]
- Ndebeka-Bandou, C.; Carosella, F.; Ferreira, R.; Wacker, A.; Bastard, G. Free carrier absorption and inter-subband transitions in imperfect heterostructures. Semicond. Sci. Technol. 2014, 29, 023001. [Google Scholar] [CrossRef]
- Smith, R.P.; Funk, A.C.; Mirin, R.P.; Cundiff, S.T.; Steiner, J.T.; Schafer, M.; Kira, M.; Koch, S.W. Extraction of Many-Body Configurations from Nonlinear Absorption in Semiconductor Quantum Wells. Phys. Rev. Lett. 2010, 104, 247401. [Google Scholar] [CrossRef] [PubMed]
- Sfuncia, G.; Nicotra, G.; Giannazzo, F.; Pécz, B.; Gueorguiev, G.K.; Kakanakova-Georgieva, A. 2D graphitic-like gallium nitride and other structural selectivity in confinement at the graphene/SiC interface. CrystEngComm 2023, 25, 5810. [Google Scholar] [CrossRef]
- Filho, M.A.M.; Hsiao, C.-L.; dos Santos, R.B.; Hultman, L.; Birch, J.; Gueorguiev, G.K. Self-Induced Core–Shell InAlN Nanorods: Formation and Stability Unraveled by Ab Initio Simulations. ACS Nanosci. Au 2023, 3, 84–93. [Google Scholar] [CrossRef]
- Scheibenzuber, W.G.; Schwarz, U.T.; Sulmoni, L.; Carlin, J.-F.; Castiglia, A.; Grandjean, N. Bias-dependent absorption coefficient of the absorber section in GaN-based multisection laser diodes. Appl. Phys. Lett. 2010, 97, 181103. [Google Scholar] [CrossRef]
- Yang, Z.-H.; Ullrich, C.A. Direct calculation of exciton binding energies with time-dependent density-functional theory. Phys. Rev. B 2013, 87, 195204. [Google Scholar] [CrossRef]
- Baeten, M.; Wouters, M. Many-body effects of a two-dimensional electron gas on trion-polaritons. Phys. Rev. B 2015, 91, 115313. [Google Scholar] [CrossRef]
- Hwang, E.H.; Throckmorton, R.E.; Sarma, S.D. Plasmon-pole approximation for many-body effects in extrinsic graphene. Phys. Rev. B 2018, 98, 195140. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gładysiewicz-Kudrawiec, M.; Żak, M.; Trzeciakowski, W. Oscillations in Absorption from InGaN/GaN Quantum Well to Continuum. Nanomaterials 2025, 15, 174. https://doi.org/10.3390/nano15030174
Gładysiewicz-Kudrawiec M, Żak M, Trzeciakowski W. Oscillations in Absorption from InGaN/GaN Quantum Well to Continuum. Nanomaterials. 2025; 15(3):174. https://doi.org/10.3390/nano15030174
Chicago/Turabian StyleGładysiewicz-Kudrawiec, Marta, Mikołaj Żak, and Witold Trzeciakowski. 2025. "Oscillations in Absorption from InGaN/GaN Quantum Well to Continuum" Nanomaterials 15, no. 3: 174. https://doi.org/10.3390/nano15030174
APA StyleGładysiewicz-Kudrawiec, M., Żak, M., & Trzeciakowski, W. (2025). Oscillations in Absorption from InGaN/GaN Quantum Well to Continuum. Nanomaterials, 15(3), 174. https://doi.org/10.3390/nano15030174






