Complex Refractive Index Spectrum of CsPbBr3 Nanocrystals via the Effective Medium Approximation
Abstract
1. Introduction
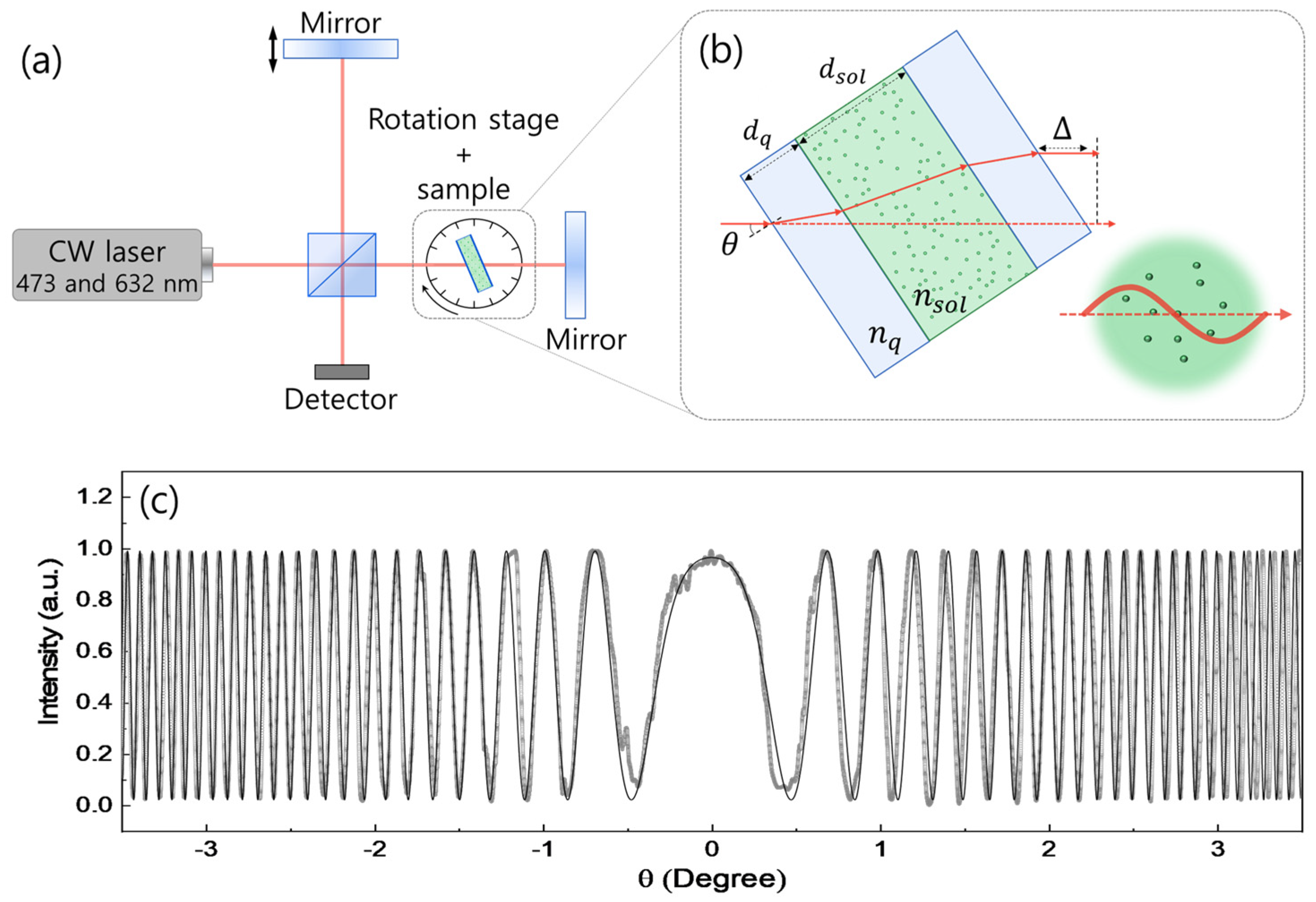
2. Experiment
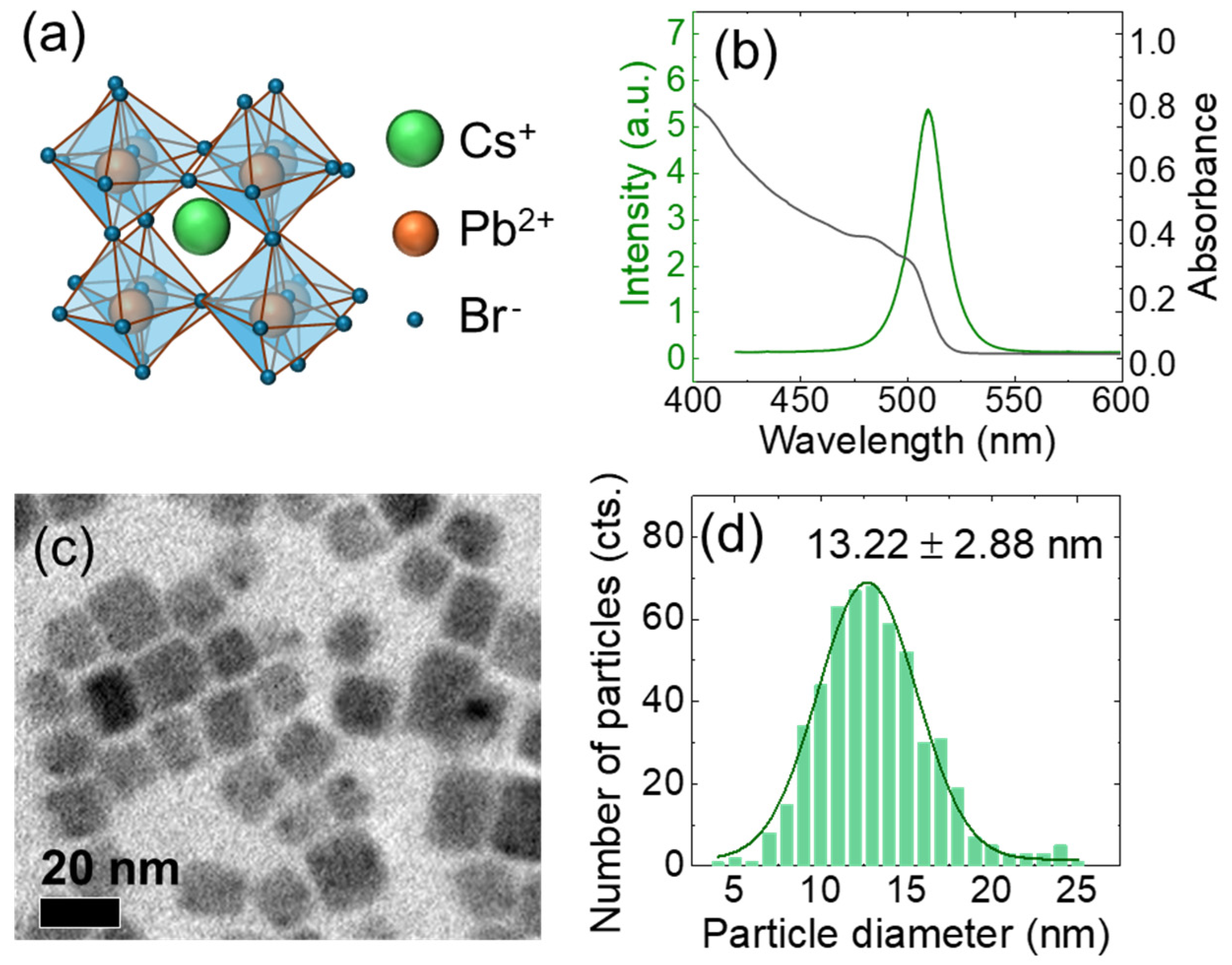
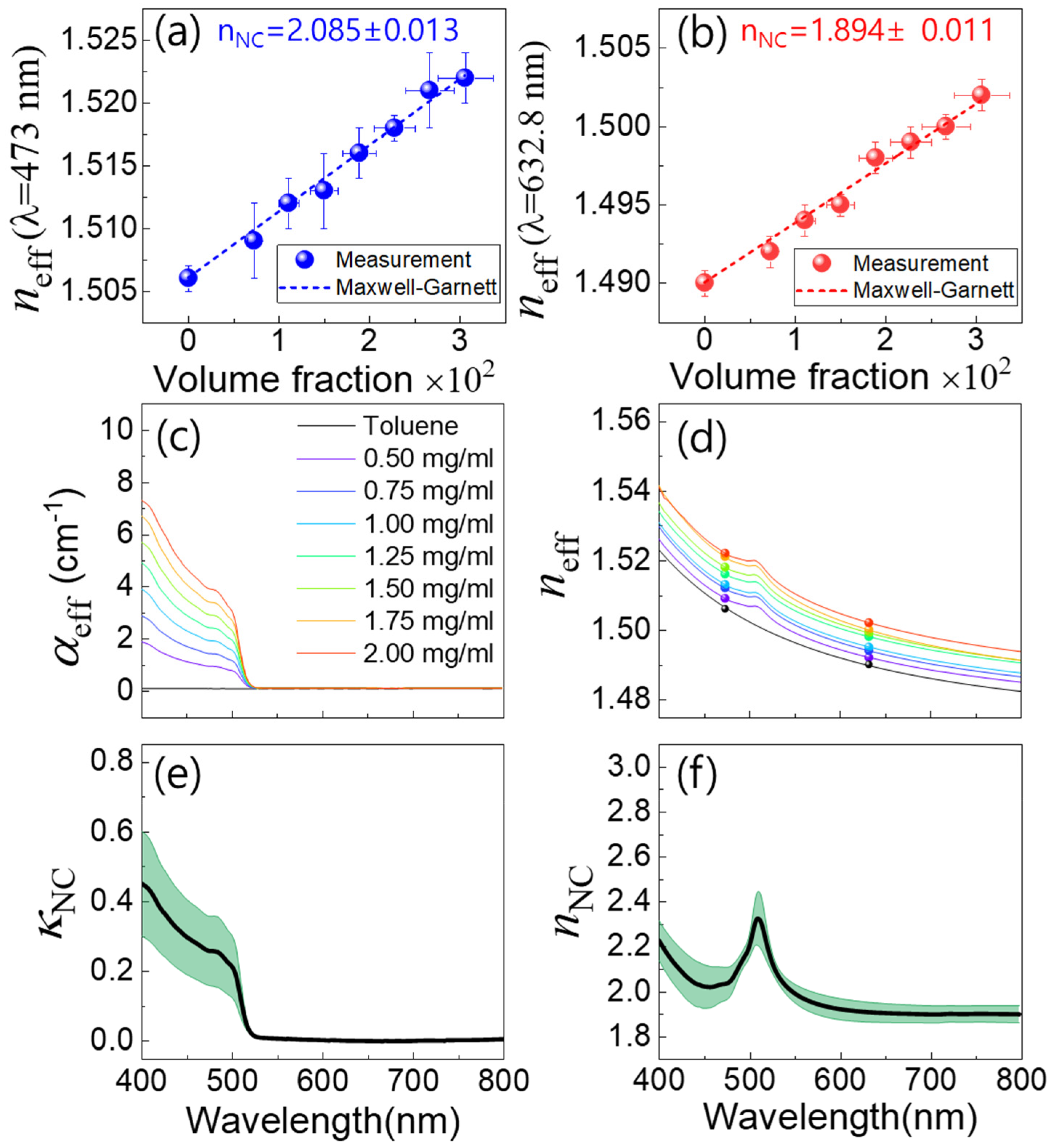
3. Result and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Zhong, H.; Chen, C.; Wu, X.g.; Hu, X.; Huang, H.; Han, J.; Zou, B.; Dong, Y. Brightly luminescent and color-tunable colloidal CH3NH3PbX3 (X = Br, I, Cl) quantum dots: Potential alternatives for display technology. ACS Nano 2015, 9, 4533–4542. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wu, Y.; Zhang, S.; Cai, B.; Gu, Y.; Song, J.; Zeng, H. CsPbX3 quantum dots for lighting and displays: Room-temperature synthesis, photoluminescence superiorities, underlying origins and white light-emitting diodes. Adv. Funct. Mater. 2016, 26, 2435–2445. [Google Scholar] [CrossRef]
- Kovalenko, M.V.; Protesescu, L.; Bodnarchuk, M.I. Properties and potential optoelectronic applications of lead halide perovskite nanocrystals. Science 2017, 358, 745–750. [Google Scholar] [CrossRef]
- Li, G.; Rivarola, F.W.R.; Davis, N.J.; Bai, S.; Jellicoe, T.C.; de la Peña, F.; Hou, S.; Ducati, C.; Gao, F.; Friend, R.H.; et al. Highly Efficient Perovskite Nanocrystal Light-Emitting Diodes Enabled by a Universal Crosslinking Method. Adv. Mater. 2016, 28, 3528–3534. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, C.; Zhang, Y.; Wu, H.; Ji, C.; Chuai, Y.; Wang, P.; Wen, S.; Zhang, C.; Yu, W.W. Bright perovskite nanocrystal films for efficient light-emitting devices. J. Phys. Chem. Lett. 2016, 7, 4602–4610. [Google Scholar] [CrossRef]
- Akkerman, Q.A.; Gandini, M.; Di Stasio, F.; Rastogi, P.; Palazon, F.; Bertoni, G.; Ball, J.M.; Prato, M.; Petrozza, A.; Manna, L. Strongly emissive perovskite nanocrystal inks for high-voltage solar cells. Nat. Energy 2016, 2, 1–7. [Google Scholar] [CrossRef]
- Jacak, J.E.; Jacak, W.A. Routes for Metallization of Perovskite Solar Cells. Materials 2022, 15, 2254. [Google Scholar] [CrossRef]
- Yang, W.; Jo, S.H.; Lee, T.W. Perovskite Colloidal Nanocrystal Solar Cells: Current Advances, Challenges and Future Perspectives. Adv. Mater. 2024, 36, 2401788. [Google Scholar] [CrossRef]
- Ramasamy, P.; Lim, D.H.; Kim, B.; Lee, S.H.; Lee, M.S.; Lee, J.S. All-inorganic cesium lead halide perovskite nanocrystals for photodetector applications. Chem. Commun. 2016, 52, 2067–2070. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.H.; Dursun, I.; Liu, G.; Sinatra, L.; Sun, X.; Kong, M.; Pan, J.; Maity, P.; Ooi, E.N.; Ng, T.K.; et al. High-speed colour-converting photodetector with all-inorganic CsPbBr3 perovskite nanocrystals for ultraviolet light communication. Light Sci. Appl. 2019, 8, 94. [Google Scholar] [CrossRef] [PubMed]
- Dey, A.; Ye, J.; De, A.; Debroye, E.; Ha, S.K.; Bladt, E.; Kshirsagar, A.S.; Wang, Z.; Yin, J.; Wang, Y.; et al. State of the art and prospects for halide perovskite nanocrystals. ACS Nano 2021, 15, 10775–10981. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Fu, Y.; Meng, F.; Wu, X.; Gong, Z.; Ding, Q.; Gustafsson, M.V.; Trinh, M.T.; Jin, S.; Zhu, X. Lead halide perovskite nanowire lasers with low lasing thresholds and high quality factors. Nat. Mater. 2015, 14, 636–642. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Niu, W.; Wang, A.L.; Fan, Z.; Chen, B.; Tan, C.; Lu, Q.; Zhang, H. Ultrathin two-dimensional organic–inorganic hybrid perovskite nanosheets with bright, tunable photoluminescence and high stability. Angew. Chem. 2017, 129, 4316–4319. [Google Scholar] [CrossRef]
- Sichert, J.A.; Tong, Y.; Mutz, N.; Vollmer, M.; Fischer, S.; Milowska, K.Z.; García Cortadella, R.; Nickel, B.; Cardenas-Daw, C.; Stolarczyk, J.K.; et al. Quantum size effect in organometal halide perovskite nanoplatelets. Nano Lett. 2015, 15, 6521–6527. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, D.; Fu, Y.; Poddar, S.; Shu, L.; Mo, X.; Fan, Z. Light out-coupling management in perovskite LEDs—What can we learn from the past? Adv. Funct. Mater. 2020, 30, 2002570. [Google Scholar] [CrossRef]
- Markina, D.I.; Pushkarev, A.P.; Shishkin, I.I.; Komissarenko, F.E.; Berestennikov, A.S.; Pavluchenko, A.S.; Smirnova, I.P.; Markov, L.K.; Vengris, M.; Zakhidov, A.A.; et al. Perovskite nanowire lasers on low-refractive-index conductive substrate for high-Q and low-threshold operation. Nanophotonics 2020, 9, 3977–3984. [Google Scholar] [CrossRef]
- Kumar, S.; Marcato, T.; Krumeich, F.; Li, Y.T.; Chiu, Y.C.; Shih, C.J. Anisotropic nanocrystal superlattices overcoming intrinsic light outcoupling efficiency limit in perovskite quantum dot light-emitting diodes. Nat. Commun. 2022, 13, 2106. [Google Scholar] [CrossRef] [PubMed]
- Manzoor, S.; Häusele, J.; Bush, K.A.; Palmstrom, A.F.; Carpenter III, J.; Yu, Z.J.; Bent, S.F.; Mcgehee, M.D.; Holman, Z.C. Optical modeling of wide-bandgap perovskite and perovskite/silicon tandem solar cells using complex refractive indices for arbitrary-bandgap perovskite absorbers. Opt. Express 2018, 26, 27441–27460. [Google Scholar] [CrossRef] [PubMed]
- Schlaus, A.P.; Spencer, M.S.; Zhu, X. Light–matter interaction and lasing in lead halide perovskites. Acc. Chem. Res. 2019, 52, 2950–2959. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Arenas, J.; Suárez, I.; Gualdrón-Reyes, A.F.; Mora-Seró, I.; Bisquert, J.; Martínez-Pastor, J.P. Recycled Photons Traveling Several Millimeters in Waveguides Based on CsPbBr3 Perovskite Nanocrystals. Adv. Opt. Mater. 2021, 9, 2100807. [Google Scholar] [CrossRef]
- Jellison, G., Jr. Spectroscopic ellipsometry data analysis: Measured versus calculated quantities. Thin Solid Film. 1998, 313, 33–39. [Google Scholar] [CrossRef]
- Tompkins, H. Handbook of Ellipsometry; William Andrew: Norwich, NY, USA, 2005. [Google Scholar]
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Loper, P.; Stuckelberger, M.; Niesen, B.; Werner, J.; Filipic, M.; Moon, S.J.; Yum, J.H.; Topic, M.; De Wolf, S.; Ballif, C. Complex refractive index spectra of CH3NH3PbI3 perovskite thin films determined by spectroscopic ellipsometry and spectrophotometry. J. Phys. Chem. Lett. 2015, 6, 66–71. [Google Scholar] [CrossRef]
- Malak, S.T.; Lafalce, E.; Jung, J.; Lin, C.H.; Smith, M.J.; Yoon, Y.J.; Lin, Z.; Vardeny, Z.V.; Tsukruk, V.V. Enhancement of optical gain characteristics of quantum dot films by optimization of organic ligands. J. Mater. Chem. C 2016, 4, 10069–10081. [Google Scholar] [CrossRef]
- Zhong, F.; Sheng, J.; Du, C.; He, Y.; Sun, Y.; Dong, F. Ligand-mediated exciton dissociation and interparticle energy transfer on CsPbBr3 perovskite quantum dots for efficient CO2-to-CO photoreduction. Sci. Bull. 2024, 69, 901–912. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, N.; Wang, D.; Tang, Z.; Yu, K.; Wei, W. Method for refractive index measurement of nanoparticles. Opt. Lett. 2014, 39, 4251–4254. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Lu, J.Q.; Brock, R.S.; Jacobs, K.M.; Yang, P.; Hu, X.H. Determination of complex refractive index of polystyrene microspheres from 370 to 1610 nm. Phys. Med. Biol. 2003, 48, 4165. [Google Scholar] [CrossRef] [PubMed]
- van der Pol, E.; van Leeuwen, T.G.; Yan, X. Misinterpretation of solid sphere equivalent refractive index measurements and smallest detectable diameters of extracellular vesicles by flow cytometry. Sci. Rep. 2021, 11, 24151. [Google Scholar] [CrossRef] [PubMed]
- Pleet, M.L.; Cook, S.; Tang, V.A.; Stack, E.; Ford, V.J.; Lannigan, J.; Do, N.; Wenger, E.; Fraikin, J.L.; Jacobson, S.; et al. Extracellular vesicle refractive index derivation utilizing orthogonal characterization. Nano Lett. 2023, 23, 9195–9202. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Xue, C.; Zhang, W.; Chen, C.; Ma, L.; Niu, Q.; Wu, L.; Yan, X. Refractive index determination of individual viruses and small extracellular vesicles in aqueous media using nano-flow cytometry. Anal. Chem. 2022, 94, 14299–14307. [Google Scholar] [CrossRef] [PubMed]
- Van Der Pol, E.; Coumans, F.A.; Sturk, A.; Nieuwland, R.; Van Leeuwen, T.G. Refractive index determination of nanoparticles in suspension using nanoparticle tracking analysis. Nano Lett. 2014, 14, 6195–6201. [Google Scholar] [CrossRef]
- Kashkanova, A.D.; Blessing, M.; Gemeinhardt, A.; Soulat, D.; Sandoghdar, V. Precision size and refractive index analysis of weakly scattering nanoparticles in polydispersions. Nat. Methods 2022, 19, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Alves-Santos, M.; Felice, R.D.; Goldoni, G. Dielectric functions of semiconductor nanoparticles from the optical absorption spectrum: The case of CdSe and CdS. J. Phys. Chem. C 2010, 114, 3776–3780. [Google Scholar] [CrossRef]
- Moreels, I.; Allan, G.; De Geyter, B.; Wirtz, L.; Delerue, C.; Hens, Z. Dielectric function of colloidal lead chalcogenide quantum dots obtained by a Kramers-Kronig analysis of the absorbance spectrum. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 235319. [Google Scholar] [CrossRef]
- Dement, D.B.; Puri, M.; Ferry, V.E. Determining the complex refractive index of neat CdSe/CdS quantum dot films. J. Phys. Chem. C 2018, 122, 21557–21568. [Google Scholar] [CrossRef]
- Rodriguez Ortiz, F.A.; Zhao, B.; Wen, J.R.; Yim, J.E.; Bauer, G.; Champ, A.; Sheldon, M.T. The Anisotropic Complex Dielectric Function of CsPbBr3 Perovskite Nanorods Obtained via an Iterative Matrix Inversion Method. J. Phys. Chem. C 2023, 127, 14812–14821. [Google Scholar] [CrossRef]
- Aspnes, D. Extending scanning ellipsometric spectra into experimentally inaccessible regions. Surf. Sci. 1976, 56, 322–333. [Google Scholar] [CrossRef]
- Jezierski, K. Improvements in the Kramers-Kronig analysis of reflection spectra. J. Phys. C Solid State Phys. 1986, 19, 2103. [Google Scholar] [CrossRef]
- Naegele, K.; Plieth, W. Kramers-Kronig analysis for the determination of the optical constants of thin surface films: II. Application to platinum oxide films. Surf. Sci. 1975, 50, 64–76. [Google Scholar] [CrossRef]
- Rodríguez-de Marcos, L.V.; Larruquert, J.I.; Méndez, J.A.; Aznárez, J.A. Self-consistent optical constants of SiO2 and Ta2O5 films. Opt. Mater. Express 2016, 6, 3622–3637. [Google Scholar] [CrossRef]
- He, S.; Kumar, N.; Lee, H.B.; Ko, K.J.; Jung, Y.J.; Kim, J.I.; Bae, S.; Lee, J.H.; Kang, J.W. Tailoring the refractive index and surface defects of CsPbBr3 quantum dots via alkyl cation-engineering for efficient perovskite light-emitting diodes. Chemical. Eng. J. 2021, 425, 130678. [Google Scholar] [CrossRef]
- Fiuza-Maneiro, N.; Sun, K.; López-Fernández, I.; Gomez-Grana, S.; Muller-Buschbaum, P.; Polavarapu, L. Ligand chemistry of inorganic lead halide perovskite nanocrystals. ACS Energy Lett. 2023, 8, 1152–1191. [Google Scholar] [CrossRef]
- Ye, J.; Byranvand, M.M.; Martínez, C.O.; Hoye, R.L.; Saliba, M.; Polavarapu, L. Defect passivation in lead-halide perovskite nanocrystals and thin films: Toward efficient LEDs and solar cells. Angew. Chem. 2021, 133, 21804–21828. [Google Scholar] [CrossRef]
- Smock, S.R.; Williams, T.J.; Brutchey, R.L. Quantifying the thermodynamics of ligand binding to CsPbBr3 quantum dots. Angew. Chem. Int. Ed. 2018, 57, 11711–11715. [Google Scholar] [CrossRef]
- Yang, D.; Li, X.; Zeng, H. Surface chemistry of all inorganic halide perovskite nanocrystals: Passivation mechanism and stability. Adv. Mater. Interfaces 2018, 5, 1701662. [Google Scholar] [CrossRef]
- Abbas, B.; Alshikh Khalil, M. An experimental method for determination of the refractive index of liquid samples using Michelson interferometer. Acta Phys. Pol. A 2016, 129, 59–63. [Google Scholar] [CrossRef]
- Maxwell-Garnett, J.C. XII. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. Lond. Ser. A 1904, 203, 385–420. [Google Scholar]
- Bruggeman, V.D. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitatskonstanten und Leitfahigkeiten der Mischkorper aus isotropen Substanzen. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Hens, Z.; Moreels, I. Light absorption by colloidal semiconductor quantum dots. J. Mater. Chem. 2012, 22, 10406–10415. [Google Scholar] [CrossRef]
- Zhao, X.; Tang, T.; Xie, Q.; Gao, L.; Lu, L.; Tang, Y. First-principles study on the electronic and optical properties of the orthorhombic CsPbBr3 and CsPbI3 with Cmcm space group. New J. Chem. 2021, 45, 15857–15862. [Google Scholar] [CrossRef]
- Mannino, G.; Deretzis, I.; Smecca, E.; La Magna, A.; Alberti, A.; Ceratti, D.; Cahen, D. Temperature-dependent optical band gap in CsPbBr3, MAPbBr3, and FAPbBr3 single crystals. J. Phys. Chem. Lett. 2020, 11, 2490–2496. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Sun, L.; Wu, T.; Chu, T.; Deng, W.; Han, K. First-principles screening of all-inorganic lead-free ABX3 perovskites. J. Phys. Chem. C 2018, 122, 7670–7675. [Google Scholar] [CrossRef]
- Ghaithan, H.M.; Alahmed, Z.A.; Qaid, S.M.; Hezam, M.; Aldwayyan, A.S. Density functional study of cubic, tetragonal, and orthorhombic CsPbBr3 perovskite. ACS Omega 2020, 5, 7468–7480. [Google Scholar] [CrossRef] [PubMed]
- Brennan, M.C.; Zinna, J.; Kuno, M. Existence of a size-dependent Stokes shift in CsPbBr3 perovskite nanocrystals. ACS Energy Lett. 2017, 2, 1487–1488. [Google Scholar] [CrossRef]
- Chen, J.; Zidek, K.; Chábera, P.; Liu, D.; Cheng, P.; Nuuttila, L.; Al-Marri, M.J.; Lehtivuori, H.; Messing, M.E.; Han, K.; et al. Size-and wavelength-dependent two-photon absorption cross-section of CsPbBr3 perovskite quantum dots. J. Phys. Chem. Lett. 2017, 8, 2316–2321. [Google Scholar] [CrossRef]
- Cheng, O.H.C.; Qiao, T.; Sheldon, M.; Son, D.H. Size-and temperature-dependent photoluminescence spectra of strongly confined CsPbBr3 quantum dots. Nanoscale 2020, 12, 13113–13118. [Google Scholar] [CrossRef]
- Brennan, M.C.; Herr, J.E.; Nguyen-Beck, T.S.; Zinna, J.; Draguta, S.; Rouvimov, S.; Parkhill, J.; Kuno, M. Origin of the size- dependent stokes shift in CsPbBr3 perovskite nanocrystals. J. Am. Chem. Soc. 2017, 139, 12201–12208. [Google Scholar] [CrossRef]
- Mulder, J.T.; Du Fossé, I.; Alimoradi Jazi, M.; Manna, L.; Houtepen, A.J. Electrochemical p-doping of CsPbBr3 perovskite nanocrystals. ACS Energy Lett. 2021, 6, 2519–2525. [Google Scholar] [CrossRef]
- Ha, S.T.; Su, R.; Xing, J.; Zhang, Q.; Xiong, Q. Metal halide perovskite nanomaterials: Synthesis and applications. Chem. Sci. 2017, 8, 2522–2536. [Google Scholar] [CrossRef] [PubMed]
- Worku, M.; Tian, Y.; Zhou, C.; Lin, H.; Chaaban, M.; Xu, L.j.; He, Q.; Beery, D.; Zhou, Y.; Lin, X.; et al. Hollow metal halide perovskite nanocrystals with efficient blue emissions. Sci. Adv. 2020, 6, eaaz5961. [Google Scholar] [CrossRef]
- Yan, W.; Mao, L.; Zhao, P.; Mertens, A.; Dottermusch, S.; Hu, H.; Jin, Z.; Richards, B.S. Determination of complex optical constants and photovoltaic device design of all-inorganic CsPbBr3 perovskite thin films. Opt. Express 2020, 28, 15706–15717. [Google Scholar] [CrossRef]
- Chen, C.; Wu, D.; Yuan, M.; Yu, C.; Zhang, J.; Li, C.; Duan, Y. Spectroscopic ellipsometry study of CsPbBr3 perovskite thin films prepared by vacuum evaporation. J. Phys. D Appl. Phys. 2021, 54, 224002. [Google Scholar] [CrossRef]
- Zhao, M.; Shi, Y.; Dai, J.; Lian, J. Ellipsometric study of the complex optical constants of a CsPbBr3 perovskite thin film. J. Mater. Chem. C 2018, 6, 10450–10455. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-H.; Kim, J.; Kim, M.J.; Kim, M.W.; Taylor, R.A.; Kyhm, K. Complex Refractive Index Spectrum of CsPbBr3 Nanocrystals via the Effective Medium Approximation. Nanomaterials 2025, 15, 181. https://doi.org/10.3390/nano15030181
Park S-H, Kim J, Kim MJ, Kim MW, Taylor RA, Kyhm K. Complex Refractive Index Spectrum of CsPbBr3 Nanocrystals via the Effective Medium Approximation. Nanomaterials. 2025; 15(3):181. https://doi.org/10.3390/nano15030181
Chicago/Turabian StylePark, Sang-Hyuk, Jungwon Kim, Min Ju Kim, Min Woo Kim, Robert A. Taylor, and Kwangseuk Kyhm. 2025. "Complex Refractive Index Spectrum of CsPbBr3 Nanocrystals via the Effective Medium Approximation" Nanomaterials 15, no. 3: 181. https://doi.org/10.3390/nano15030181
APA StylePark, S.-H., Kim, J., Kim, M. J., Kim, M. W., Taylor, R. A., & Kyhm, K. (2025). Complex Refractive Index Spectrum of CsPbBr3 Nanocrystals via the Effective Medium Approximation. Nanomaterials, 15(3), 181. https://doi.org/10.3390/nano15030181





