Dual-Task Optimization Method for Inverse Design of RGB Micro-LED Light Collimator
Abstract
1. Introduction
2. Materials and Methods
2.1. Design Parameters
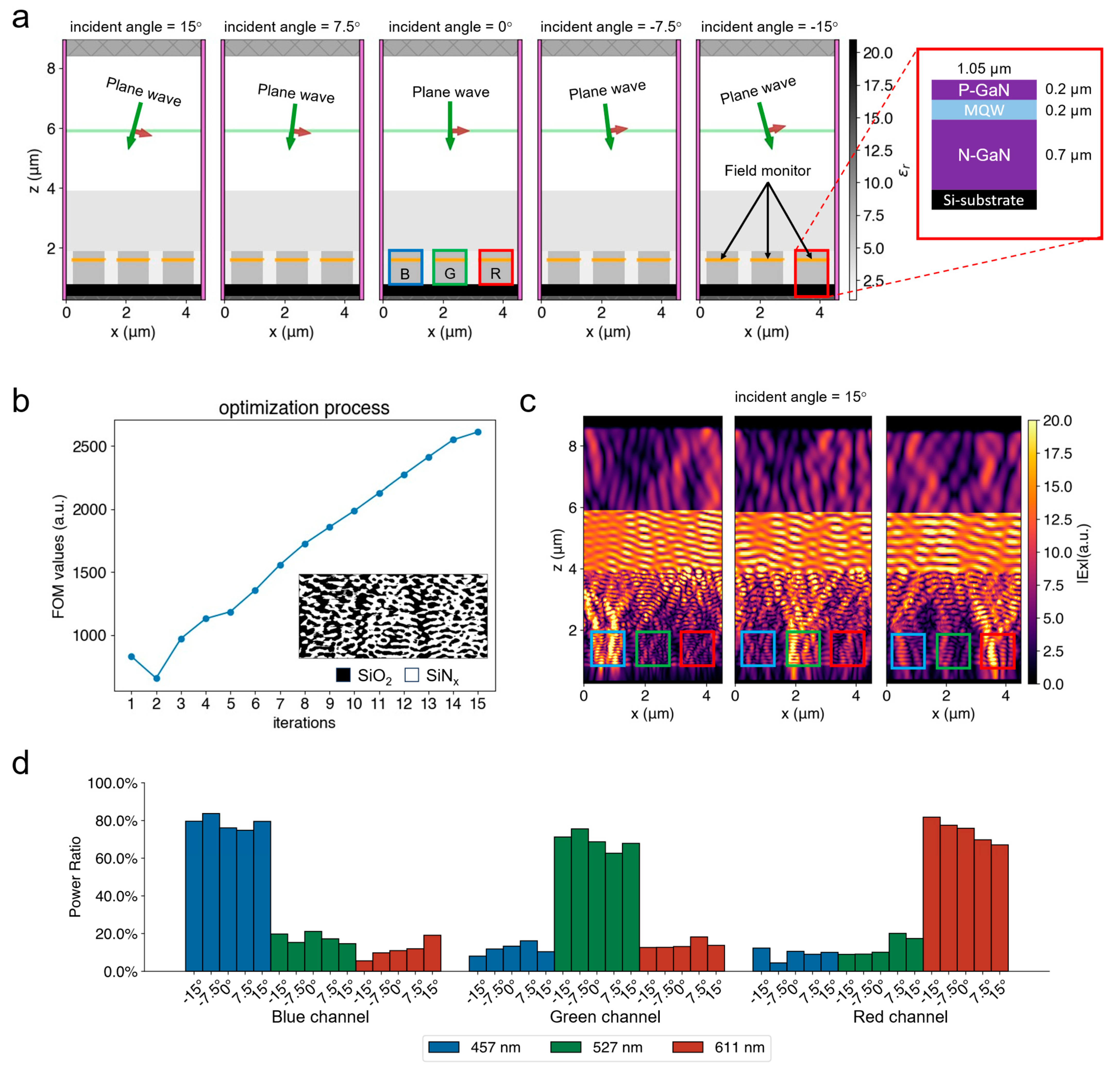
2.2. Micro-LED Pixel Structure
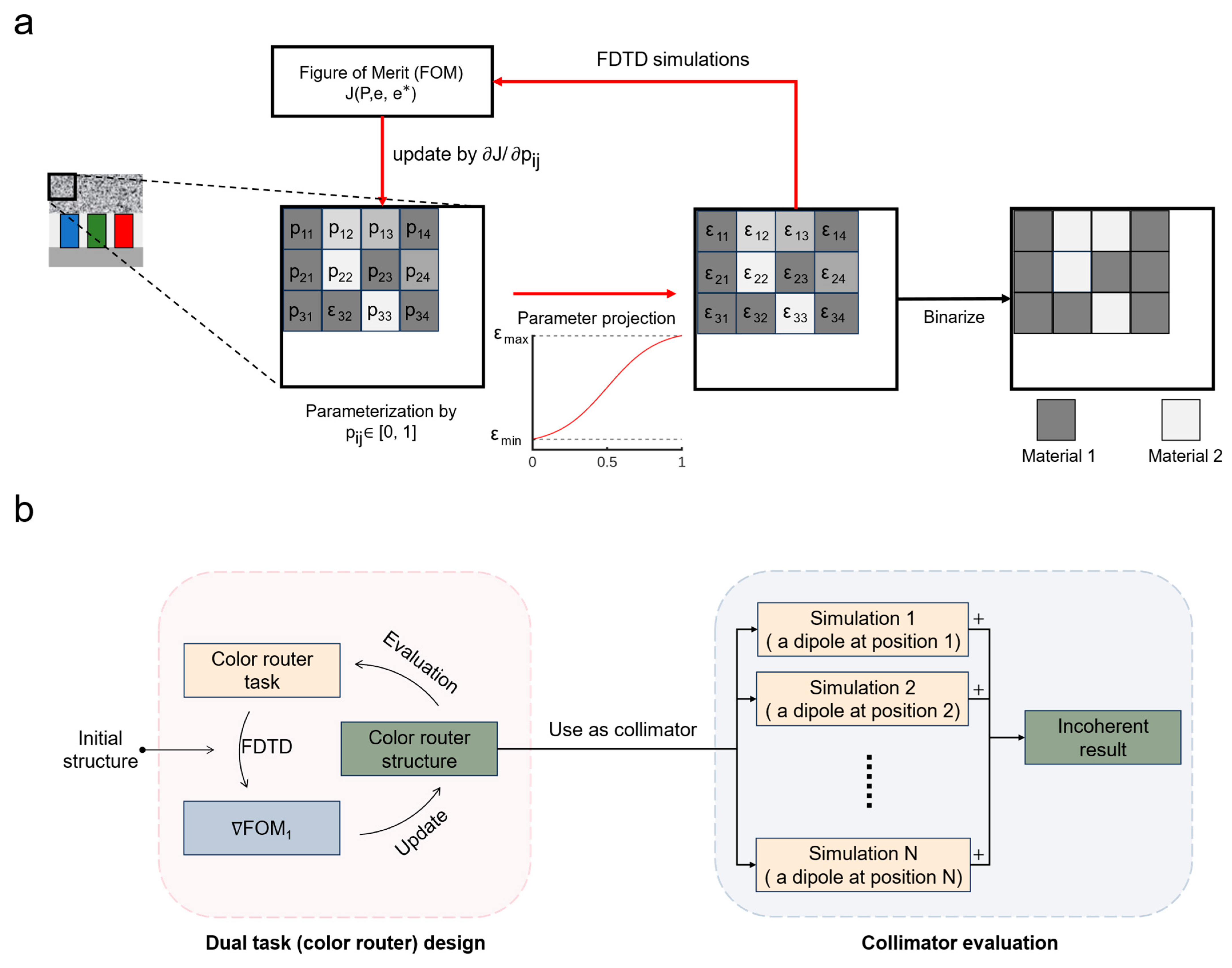
2.3. Figure of Merit
2.4. Collimation Evaluation Using Multiple-Dipole Method
3. Results
3.1. Results of Designing in Dual Task
3.2. Results of Collimation Evaluation
4. Discussion
5. Conclusions
6. Patents
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoffman, C.; Driggers, R. (Eds.) Encyclopedia of Optical and Photonic Engineering. , 2nd ed.CRC Press: Boca Raton, FL, USA, 2015; ISBN 9781439850992.
- Yang, Z.; Luo, Z.; Ding, Y.; Qian, Y.; Chen, S.C.; Lin, C.L.; Wu, S.T. Advances and Challenges in Microdisplays and Imaging Optics for Virtual Reality and Mixed Reality. Device 2024, 2, 100398. [Google Scholar] [CrossRef]
- Yang, Q.; Hsiang, E.-L.; Wu, S.-T.; Lai, P.-C.; Yang, Z.; Lin, C.-L. AR/VR Light Engines: Perspectives and Challenges. Adv. Opt. Photonics 2022, 14, 783–861. [Google Scholar] [CrossRef]
- Chae, M.; Bang, K.; Jo, Y.; Yoo, C.; Lee, B. Occlusion-Capable See-through Display without the Screen-Door Effect Using a Photochromic Mask. Opt. Lett. 2021, 46, 4554. [Google Scholar] [CrossRef] [PubMed]
- LaRussa, J.A.; Gill, A.T. The Holographic Pancake Window TM. Soc. Photo-Opt. Instrum. Eng. 1978, 162, 120–129. [Google Scholar] [CrossRef]
- Kress, B.C. Optical Architectures for Augmented-, Virtual-, and Mixed-Reality Headsets; SPIE: Bellingham, WA, USA, 2020; ISBN 9781510634343. [Google Scholar]
- Lin, C.-M.; Chen, Y.-T.; Lin, P.-H.; Chou, C.-H.; Wang, K.-J.; Whang, A.J.-W.; Chen, H.-C.; Chen, Y.-Y.; Wu, X.-R. Innovative Design of Light Collimator Based on a Freeform Microlens Array. Appl. Opt. 2014, 53, H35–H43. [Google Scholar] [CrossRef]
- Zhu, L.; Lai, P.T.; Choi, H.W. Microlens Array on Flip-Chip LED Patterned with an Ultraviolet Micro-Pixelated Emitter. IEEE Photonics Technol. Lett. 2011, 23, 1067–1069. [Google Scholar] [CrossRef][Green Version]
- Hsiang, E.-L.; Lan, Y.-F.; Wu, S.-T.; He, Z.; Yang, Z. Tailoring the Light Distribution of Micro-LED Displays with a Compact Compound Parabolic Concentrator and an Engineered Diffusor. Opt. Express 2021, 29, 39859–39873. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Brongersma, M.L.; Yao, J.; Chen, M.K.; Levy, U.; Tsai, D.P.; Zheludev, N.I.; Faraon, A.; Arbabi, A.; Yu, N.; et al. Roadmap for Optical Metasurfaces. ACS Photonics 2024, 11, 816–865. [Google Scholar] [CrossRef]
- Nielsen, K.E.S.; Nielsen, K.E.S.; Carlsen, M.A.; Zambrana-Puyalto, X.; Raza, S. Non-Imaging Metasurface Design for Collimated Beam Shaping. Opt. Express 2023, 31, 37861–37870. [Google Scholar] [CrossRef]
- Avayu, O.; Eisenbach, O.; Ellenbogen, T.; Ditcovski, R. Optical Metasurfaces for Polarization-Controlled Beam Shaping. Opt. Lett. 2014, 39, 3892–3895. [Google Scholar] [CrossRef]
- Briggs, R.M.; Bagheri, M.; Horie, Y.; Arbabi, A.; Faraon, A. Efficient Dielectric Metasurface Collimating Lenses for Mid-Infrared Quantum Cascade Lasers. Opt. Express 2015, 23, 33310–33317. [Google Scholar] [CrossRef]
- Singh, R.; Nie, Y.; Gao, M.; Agarwal, A.M.; Anthony, B.W. Inverse Design of Photonic Meta-Structure for Beam Collimation in on-Chip Sensing. Sci. Rep. 2021, 11, 5343. [Google Scholar] [CrossRef] [PubMed]
- Chen, E.; Chen, E.; Fan, Z.; Zhang, K.; Zhang, K.; Zhang, K.; Huang, C.; Xu, S.; Xu, S.; Ye, Y.; et al. Broadband Beam Collimation Metasurface for Full-Color Micro-LED Displays. Opt. Express 2024, 32, 10252–10264. [Google Scholar] [CrossRef]
- Yang, K.Y.; Shirpurkar, C.; White, A.D.; Zang, J.; Chang, L.; Ashtiani, F.; Guidry, M.A.; Lukin, D.M.; Pericherla, S.V.; Yang, J.; et al. Multi-Dimensional Data Transmission Using Inverse-Designed Silicon Photonics and Microcombs. Nat. Commun. 2022, 13, 7862. [Google Scholar] [CrossRef]
- Sapra, N.V.; Piggott, A.Y.; Su, L.; Vercruysse, D.; Trivedi, R.; Vučković, J. Fully-Automated Optimization of Grating Couplers. Opt. Express 2018, 26, 4023–4034. [Google Scholar] [CrossRef]
- Su, L.; Piggott, A.Y.; Sapra, N.V.; Petykiewicz, J.; Vučković, J. Inverse Design and Demonstration of a Compact On-Chip Narrowband Three-Channel Wavelength Demultiplexer. ACS Photonics 2018, 5, 301–305. [Google Scholar] [CrossRef]
- Yang, K.Y.; Skarda, J.; Cotrufo, M.; Dutt, A.; Ahn, G.H.; Sawaby, M.; Vercruysse, D.; Arbabian, A.; Fan, S.; Alù, A.; et al. Inverse-Designed Non-Reciprocal Pulse Router for Chip-Based LiDAR. Nat. Photonics 2020, 14, 369–374. [Google Scholar] [CrossRef]
- White, A.D.; Su, L.; Shahar, D.I.; Yang, K.Y.; Ahn, G.H.; Skarda, J.L.; Ramachandran, S.; Vučković, J. Inverse Design of Optical Vortex Beam Emitters. ACS Photonics 2022, 10, 803–807. [Google Scholar] [CrossRef]
- Vercruysse, D.; Sapra, N.V.; Yang, K.Y.; Vučković, J. Inverse-Designed Photonic Crystal Circuits for Optical Beam Steering. ACS Photonics 2021, 8, 3085–3093. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Hughes, T.W.; Minkov, M.; Williamson, I.A.D.; Fan, S. Adjoint Method and Inverse Design for Nonlinear Nanophotonic Devices. ACS Photonics 2018, 5, 4781–4787. [Google Scholar] [CrossRef]
- Minkov, M.; Williamson, I.A.D.; Andreani, L.C.; Gerace, D.; Lou, B.; Song, A.Y.; Hughes, T.W.; Fan, S. Inverse Design of Photonic Crystals through Automatic Differentiation. ACS Photonics 2020, 7, 1729–1741, Inverse Design of Photonic Crystals through Automatic Differentiation | ACS Photonics. [Google Scholar] [CrossRef]
- Catrysse, P.B.; Zhao, N.; Jin, W.; Fan, S. Subwavelength Bayer RGB Color Routers with Perfect Optical Efficiency. Nanophotonics 2022, 11, 2381–2387, Subwavelength Bayer RGB color routers with perfect optical efficiency. [Google Scholar] [CrossRef]
- Zhao, N.; Catrysse, P.B.; Fan, S. Perfect RGB-IR Color Routers for Sub-Wavelength Size CMOS Image Sensor Pixels. Adv. Photonics Res. 2021, 2, 202000048. [Google Scholar] [CrossRef]
- Ahn, S.; Catrysse, P.B.; Mun, S.; Cho, C.; Lim, M.; Roh, S.; Yun, S.; Fan, S. Polarization Independent Freeform Color Router for Subwavelength-Pixel CMOS Image Sensors. In Proceedings of the High Contrast Metastructures XII, San Francisco, CA, USA, 30 January–1 February 2023; Fan, J.A., Chang-Hasnain, C.J., Zhou, W., Eds.; SPIE: Bellingham, WA, USA, 2023; p. 10. [Google Scholar]
- Liu, Z.; Wang, K.; Luo, X.; Liu, S. Precise Optical Modeling of Blue Light-Emitting Diodes by Monte Carlo Ray-Tracing. Opt. Express 2010, 18, 9398. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Elsevier: Amsterdam, The Netherlands, 1985; ISBN 9780080547213. [Google Scholar]
- Qian, Y.; Yang, Z.; Huang, Y.; Lin, K.; Wu, S. High-efficiency Nanowire Light-emitting Diodes for Augmented Reality and Virtual Reality Displays. J. Soc. Inf. Disp. 2023, 31, 211–219. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2014. [Google Scholar]
- Schubert, M.F.; Cheung, A.K.C.; Williamson, I.A.D.; Spyra, A.; Alexander, D.H. Inverse Design of Photonic Devices with Strict Foundry Fabrication Constraints. ACS Photonics 2022, 9, 2327–2336. [Google Scholar] [CrossRef]
- Ali, A.; Mitra, A.; Aïssa, B. Metamaterials and Metasurfaces: A Review from the Perspectives of Materials, Mechanisms and Advanced Metadevices. Nanomaterials 2022, 12, 1027. [Google Scholar] [CrossRef]

| Materials | Blue (457 nm) | Green (527 nm) | Red (611 nm) | |||
|---|---|---|---|---|---|---|
| n | k | n | k | n | k | |
| GaN | 2.49 | \ | 2.38 | \ | 2.35 | \ |
| MQW | 2.51 | \ | 2.41 | \ | 2.37 | \ |
| Polyimide | 1.5 | \ | 1.5 | \ | 1.5 | \ |
| SiO2 | 1.465 | \ | 1.4609 | \ | 1.4577 | \ |
| SiNx | 2.0475 | \ | 2.0279 | \ | 2.0133 | \ |
| Silicon | 4.583 | 0.13 | 4.215 | 0.048 | 3.906 | 0.022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Li, Z.; Wang, P.; Wu, S.; Li, W.; Wang, J.; Cao, Y.; Mortazavi, M.; Peng, L.; Wu, P. Dual-Task Optimization Method for Inverse Design of RGB Micro-LED Light Collimator. Nanomaterials 2025, 15, 190. https://doi.org/10.3390/nano15030190
Chen L, Li Z, Wang P, Wu S, Li W, Wang J, Cao Y, Mortazavi M, Peng L, Wu P. Dual-Task Optimization Method for Inverse Design of RGB Micro-LED Light Collimator. Nanomaterials. 2025; 15(3):190. https://doi.org/10.3390/nano15030190
Chicago/Turabian StyleChen, Liming, Zhuo Li, Purui Wang, Sihan Wu, Wen Li, Jiechen Wang, Yue Cao, Masood Mortazavi, Liang Peng, and Pingfan Wu. 2025. "Dual-Task Optimization Method for Inverse Design of RGB Micro-LED Light Collimator" Nanomaterials 15, no. 3: 190. https://doi.org/10.3390/nano15030190
APA StyleChen, L., Li, Z., Wang, P., Wu, S., Li, W., Wang, J., Cao, Y., Mortazavi, M., Peng, L., & Wu, P. (2025). Dual-Task Optimization Method for Inverse Design of RGB Micro-LED Light Collimator. Nanomaterials, 15(3), 190. https://doi.org/10.3390/nano15030190






