Study on the Superhydrophobic Properties of Micro/Nano Hole Structure on the Surface of Glass Fiber Reinforced Plastics Based on Femtosecond Laser Etching
Abstract
:1. Introduction
2. Materials and Methods
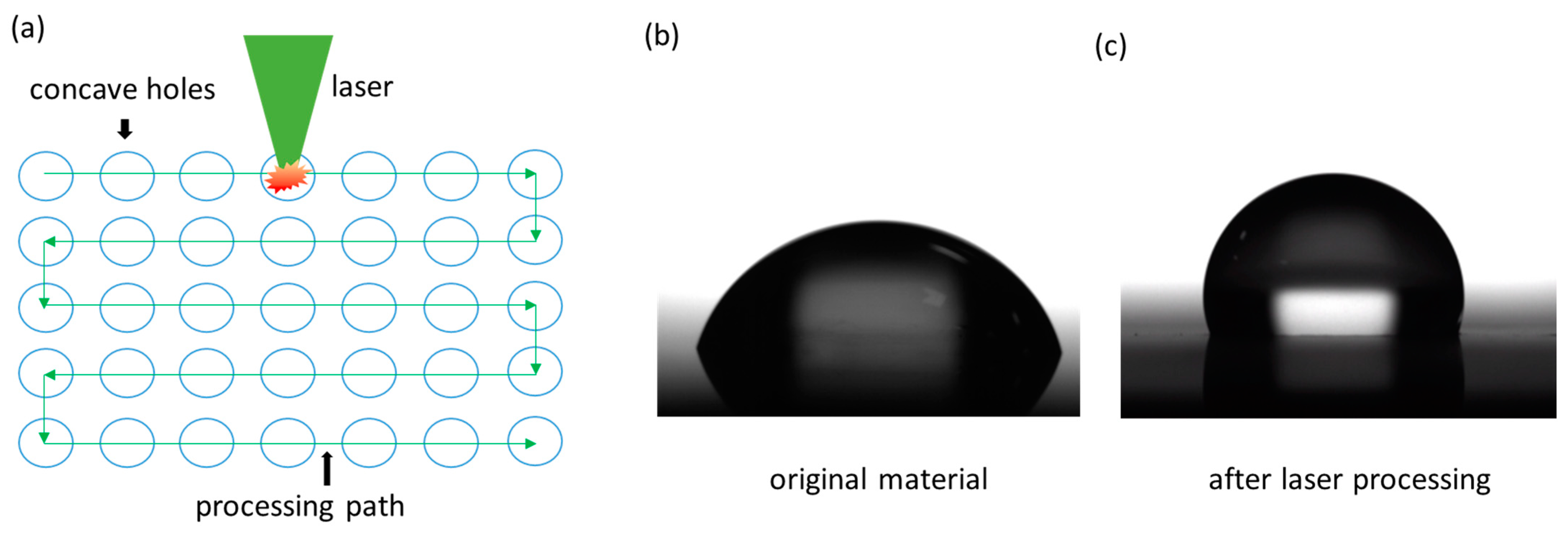
2.1. Method and Experimental Setup
2.2. Materials
2.3. Instruments and Data Processing
3. Results
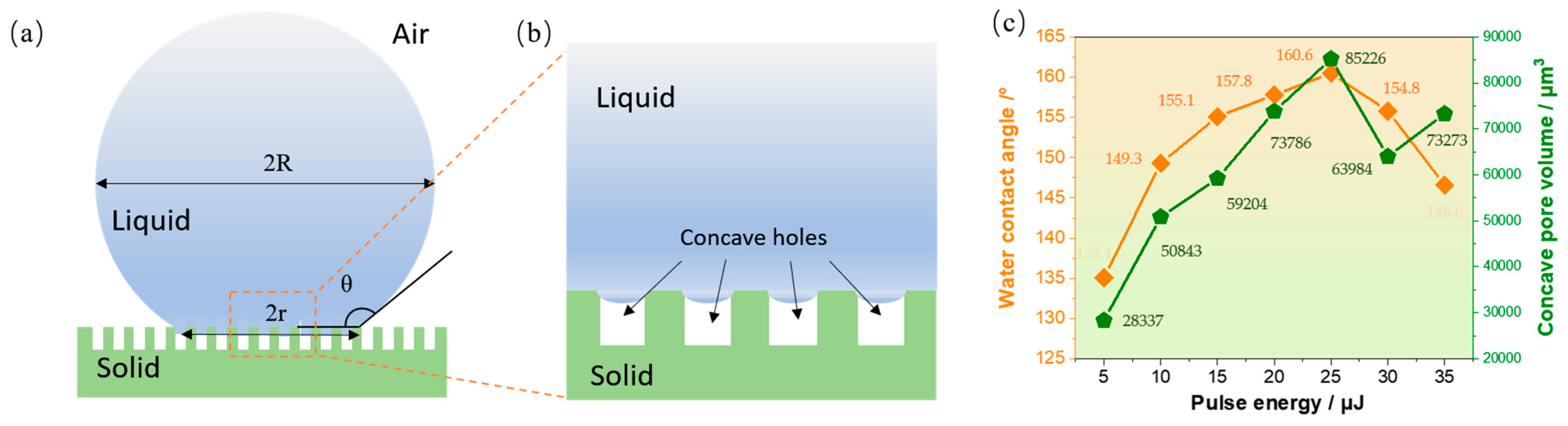
3.1. Influence of Pulse Energy
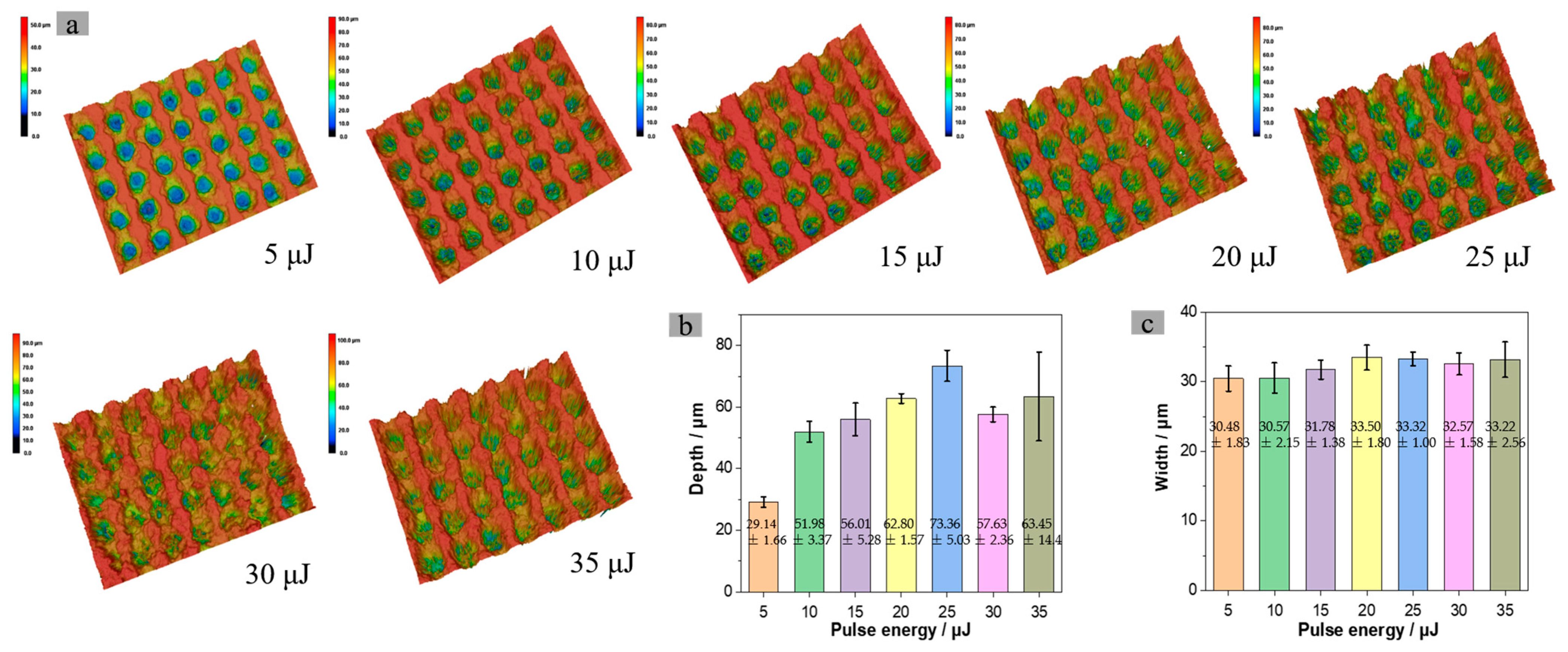
3.1.1. Influence of Pulse Energy on Surface Microstructure
3.1.2. Ablation Effect of Excessive Energy on Surface Structure
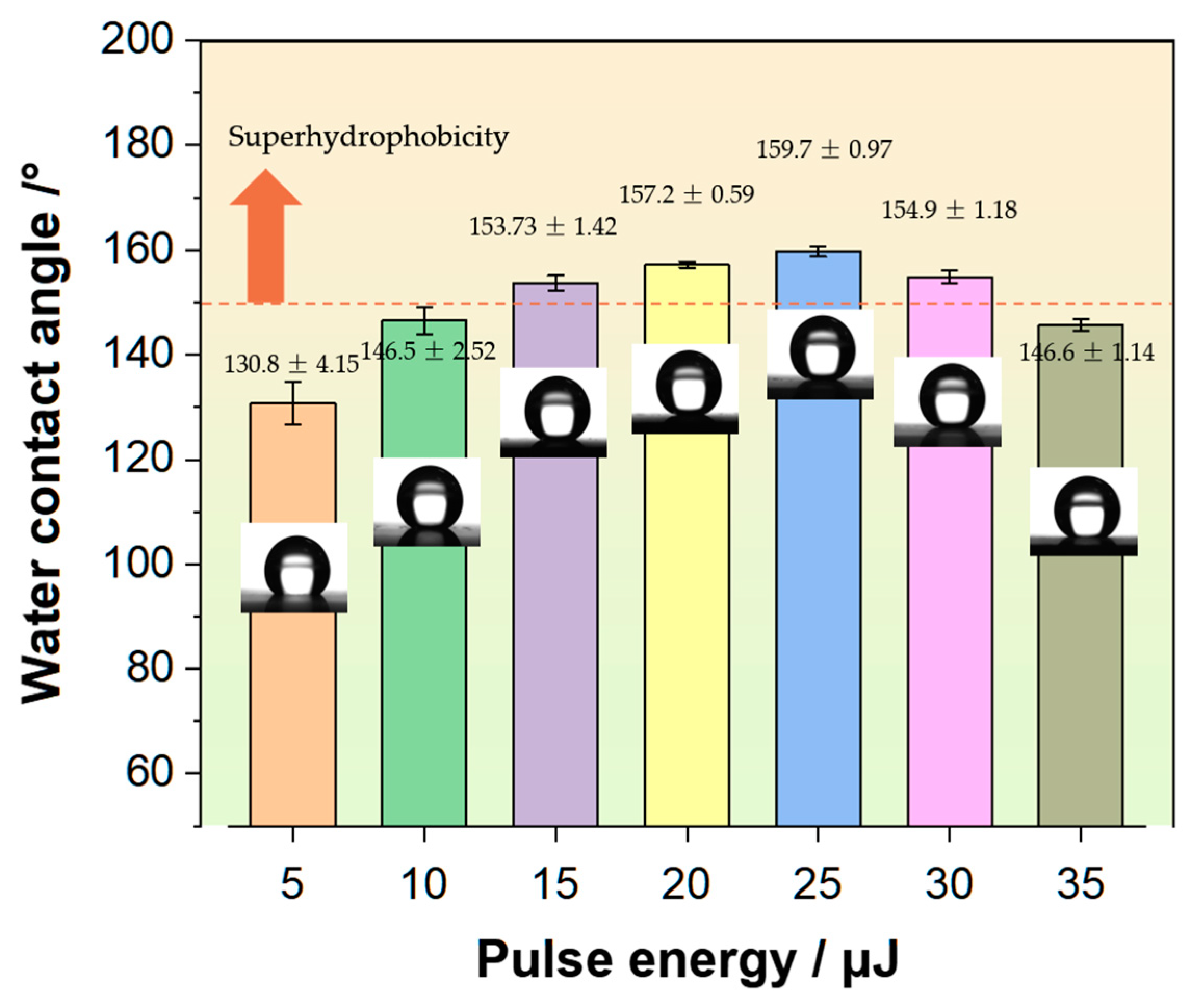
3.1.3. Effect of Laser Energy on Wettability of the Concave Hole Surface
3.2. Influence of Pulse Number
3.2.1. Influence of Laser Pulse Number on Surface Microstructure
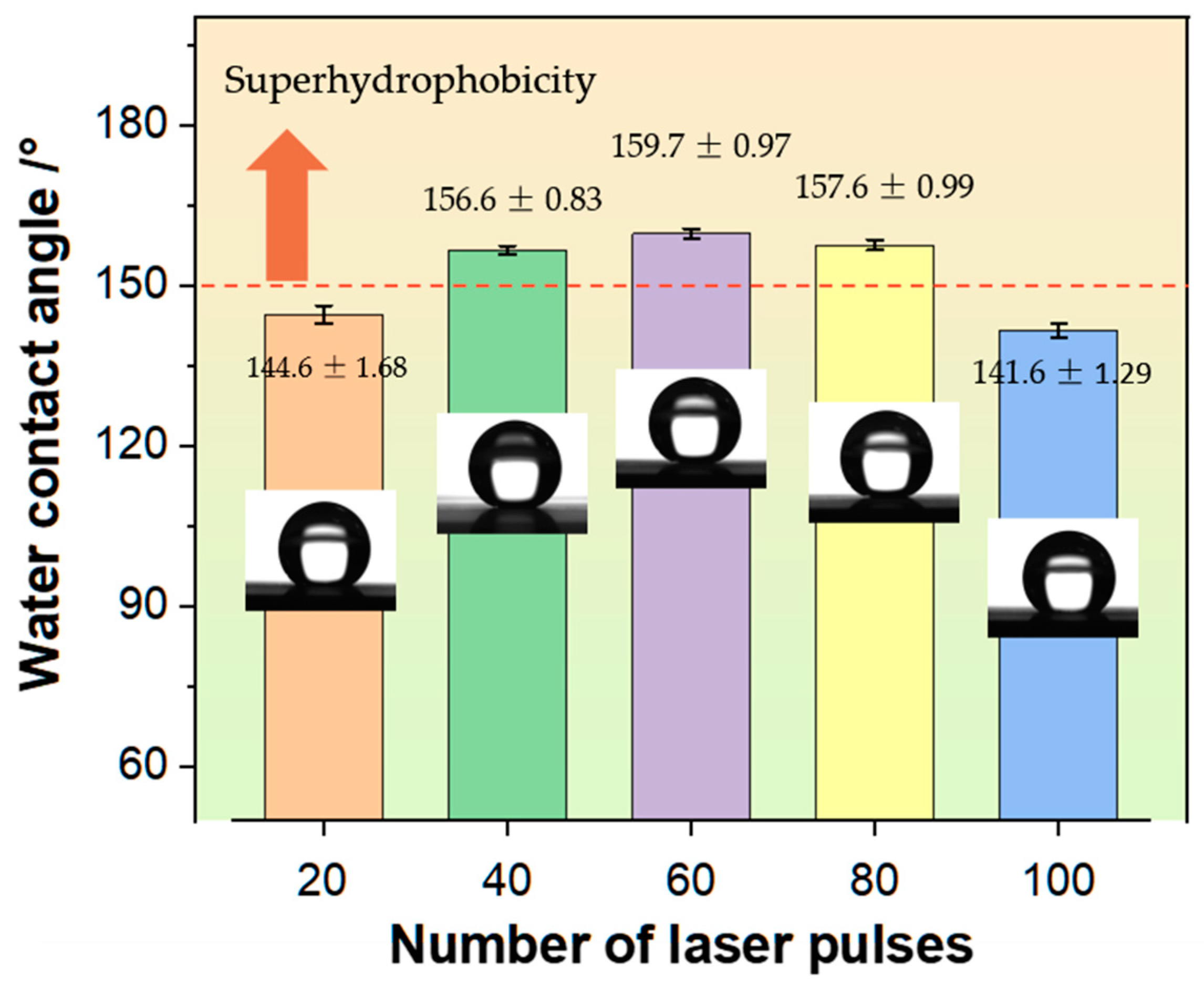
3.2.2. Effect of Laser Pulse Number on Wettability of the Concave Hole Surface
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sá, M.F.; Gomes, A.M.; Correia, J.R.; Silvestre, N. Creep behavior of pultruded GFRP elements–Part 1: Literature review and experimental study. Compos. Struct. 2011, 93, 2450–2459. [Google Scholar] [CrossRef]
- Karataş, M.A.; Gökkaya, H. A review on machinability of carbon fiber reinforced polymer (CFRP) and glass fiber reinforced polymer (GFRP) composite materials. Def. Technol. 2018, 14, 318–326. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, M.; Liu, Y.; Wang, A.; Zhou, B.; Hu, J. Structural health monitoring of glass fiber-reinforced polymer laminates with carbon nanotube-coated glass fiber sensing layer after low-velocity impact using electrical resistance tomography. Nanomaterials 2024, 14, 1462. [Google Scholar] [CrossRef]
- Lafuma, A.; Quéré, D. Superhydrophobic states. Nat. Mater. 2003, 2, 457–460. [Google Scholar] [CrossRef]
- Ye, H.; Zhu, L.; Li, W.; Liu, H.; Chen, H. Simple spray deposition of a water-based superhydrophobic coating with high stability for flexible applications. J. Mater. Chem. A 2017, 5, 9882–9890. [Google Scholar] [CrossRef]
- Barthwal, S.; Barthwal, S. A highly robust, non-fluorinated, and economical PDMS-based superhydrophobic flexible surface with repairable and flame-retardant properties. J. Appl. Polym. Sci. 2023, 140, e53766. [Google Scholar] [CrossRef]
- Wang, X.; Tang, L.; Fan, S.; Fan, W. Novel self-healing superhydrophobic coating with oil-water separation and anti-icing properties. Nanomaterials 2024, 14, 1981. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Kumar, S.; Samal, S.K.; Mohanty, S.; Nayak, S.K. A review on superhydrophobic polymer nanocoatings: Recent development and applications. Ind. Eng. Chem. Res. 2018, 57, 2727–2745. [Google Scholar] [CrossRef]
- Sojoudi, H.; Wang, M.; Boscher, N.D.; McKinley, G.H.; Gleason, K.K. Durable and scalable icephobic surfaces: Similarities and distinctions from superhydrophobic surfaces. Soft Matter 2016, 12, 1927–2232. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.M.; Kim, K.; Kim, S.; Lee, D.G.; An, T.; Kim, G.H. Synthesis of hierarchical superhydrophilic/superhydrophobic nanostructured surfaces for oil/water separation. Adv. Mater. Interfaces 2024, 11, 2300627. [Google Scholar] [CrossRef]
- Ye, Y.; Li, T.; Zhao, Y.; Liu, J.; Lu, D.; Wang, J.; Wang, K.; Zhang, Y.; Ma, J.; Drioli, E.; et al. Engineering environmentally friendly nanofiber membranes with superhydrophobic surface and intrapore interfaces for ultrafast oil-water separation. Sep. Purif. Technol. 2023, 317, 123885. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, J.; Peng, Y.; Li, Y.; Guo, W.; Liao, C. Fabrication of non-wetting Mg(OH)2 composites with photoresponsive capabilities and their environmental restoration performance. Nanomaterials 2024, 14, 1240. [Google Scholar] [CrossRef] [PubMed]
- Van den Berg, D.; Asker, D.; Kim, J.; Kim, H.; Aizenberg, J.; Hatton, B. Tuning the topography of non-wetting surfaces to reduce short-term microbial contamination within hospitals. Adv. Funct. Mater. 2024, 34, 2315957. [Google Scholar] [CrossRef]
- Chen, Y.; Ao, J.; Zhang, J.; Gao, J.; Hao, L.; Jiang, R.; Zhang, Z.; Liu, Z.; Zhao, J.; Ren, L. Bioinspired superhydrophobic surfaces, inhibiting or promoting microbial contamination? Mater. Today 2023, 67, 468–494. [Google Scholar] [CrossRef]
- Wang, Z.; Du, M.; Fang, H.; Zhao, P.; Yao, X.; Chen, S. The development of high-strength, anticorrosive, and strongly adhesive polyaspartate polyurea coating suitable for pipeline spray repairs. J. Appl. Polym. Sci. 2024, 141, e55668. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Q.; Han, J.; Chen, X.; Min, Y. A novel combination approach for the preparation of superhydrophobic surface on copper and the consequent corrosion resistance. Eval. Program Plann. 2016, 110, 105–113. [Google Scholar] [CrossRef]
- Wang, T.; Sun, T.; Feng, L.; Aizenberg, J. Interfacial materials with special wettability. MRS Bull. 2013, 38, 366–371. [Google Scholar] [CrossRef]
- Sun, J.; Wang, J. The fabrication of superhydrophobic glass fiber-reinforced plastic surfaces with tunable adhesion based on hydrophobic silica nanoparticle aggregates. Colloid Polym. Sci. 2015, 293, 2815–2821. [Google Scholar] [CrossRef]
- Feng, G.; Li, F.; Xue, W.; Sun, K.; Yang, H.; Pan, Q.; Cao, Y. Laser textured GFRP superhydrophobic surface as an underwater acoustic absorption metasurface. Appl. Surf. Sci. 2019, 463, 741–746. [Google Scholar] [CrossRef]
- Cai, Z.; Lin, J.; Hong, X. Transparent superhydrophobic hollow films (TSHFs) with superior thermal stability and moisture resistance. RSC Adv. 2018, 8, 491–498. [Google Scholar] [CrossRef]
- Kudaibergenova, R.M.; Roman, F.F.; Silva, A.S.; Sugurbekova, G.K. Carbon-Nanotube-Based Superhydrophobic Magnetic Nanomaterial as Absorbent for Rapid and Efficient Oil/Water Separation. Nanomaterials 2024, 14, 1942. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; He, Y.; Zhang, J.F.; Li, Z.; Zhuo, W.; Yang, D.; Sacher, E. Preparation of large-scale, durable, superhydrophobic PTFE films using rough glass templates. Surf. Interface Anal. 2017, 49, 1422–1430. [Google Scholar] [CrossRef]
- Fang, Z.; Luo, W.; Hu, H.; Xia, M.; Sun, Z.; Zhang, Y.; He, P. Ice-template triggered roughness: A facile method to prepare robust superhydrophobic surface with versatile performance. Prog. Org. Coat. 2019, 135, 345–351. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, M.; Duan, Y.; Hao, H. Superhydrophobic coatings based on raspberry-like nanoparticles and their applications on cotton. Colloids Surf. A Physicochem. Eng. Asp. 2020, 602, 125039. [Google Scholar] [CrossRef]
- Zakerizadeh, M.; Dogolsar, M.A.; Jamshidi, Z.; Haghi, A.K. Non-fluorinated sol-gel processing of hydrophobic coating on cotton fabric. Mater. Chem. Phys. 2021, 114, 63–68. [Google Scholar] [CrossRef]
- Wang, J.; Chen, C.; Wang, G.; Chen, K.; Zhang, W. Efficient coupling of dual beam combined laser into micro water jet for deep processing. Sci. Rep. 2025, 15, 1083. [Google Scholar] [CrossRef]
- Wan, Z.; Liu, Z.; Zhang, Q.; Zhang, Q.; Gu, M. Laser Technology for Perovskite: Fabrication and Applications. Adv. Mater. Technol. 2024, 9, 2302033. [Google Scholar] [CrossRef]
- Zhu, Z.; Wu, P.; Juodkazis, S.; Wang, J.; Yao, S.; Yao, J.; Zhang, W. Superhydrophobic and anti-icing surface by femtosecond laser direct writing. Adv. Eng. Mater. 2023, 25, 2300575. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, H. Femtosecond laser processed superhydrophobic surface. J. Manuf. Process. 2024, 109, 250–287. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, M.; Zhang, Z.; Lu, J.; Xu, K.; Zhu, H.; Wu, Y.; Wang, B.; Lei, W. A review on applications of functional superhydrophobic surfaces prepared by laser biomimetic manufacturing. J. Mater. Sci. 2023, 58, 3421–3459. [Google Scholar] [CrossRef]
- Cheng, K.; Wang, J.; Wang, G.; Yang, K.; Zhang, W. Controllable Preparation of Fused Silica Micro Lens Array through Femtosecond Laser Penetration-Induced Modification Assisted Wet Etching. Materials 2024, 17, 4231. [Google Scholar] [CrossRef]
- Yan, D.; Xu, W.; Zou, T.; Li, L.; Xu, J.; Zhang, R.; Hu, L.; Yang, X.; Ma, H.; Yang, J. Durable Organic Coating-Free Superhydrophobic Metal Surface by Paracrystalline State Formation. Adv. Mater. 2024, 37, e2412850. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Zhou, C.; Su, J.; Tang, S. Enhanced anti-icing performance of novel superhydrophobic F-L@KH-SiO2/OTMS coating synergistic preparation with bionic micro-nano structures and modified nanoparticles. Chem. Eng. J. 2024, 498, 155264. [Google Scholar] [CrossRef]
- Wang, H.; He, M.; Liu, H.; Guan, Y. One-step fabrication of robust superhydrophobic steel surfaces with mechanical durability, thermal stability, and anti-icing function. ACS Appl. Mater. Interfaces 2019, 11, 25586–25594. [Google Scholar] [CrossRef] [PubMed]
- Lang, Y.; Sun, X.; Zhang, M.; Sun, X. Femtosecond laser patterned alumina ceramics surface towards enhanced superhydrophobic performance. Ceram. Int. 2024, 50, 15426–15434. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Li, J.; Zhao, S.; Du, F.; Zhou, Y.; Yu, H. One-step fabrication of superhydrophobic surfaces with different adhesion via laser processing. J. Alloys Compd. 2018, 739, 489–498. [Google Scholar] [CrossRef]
- Maharana, H.S.; Katiyar, P.K.; Mondal, K. Structure dependent super-hydrophobic and corrosion resistant behavior of electrodeposited Ni-MoSe2-MWCNT coating. Appl. Surf. Sci. 2019, 478, 26–37. [Google Scholar] [CrossRef]
- Bai, X.; Gou, X.; Zhang, J.; Liang, J.; Yang, L.; Wang, S. A review of smart superwetting surfaces based on shape-memory micro/nanostructures. Small 2023, 19, 2206463. [Google Scholar] [CrossRef] [PubMed]
- Moghadam, S.G.; Parsimehr, H.; Ehsani, A. Multifunctional superhydrophobic surfaces. Adv. Colloid Interface Sci. 2021, 290, 102397. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Feng, X.; Wang, Z.; Zhu, D.; Chu, J.; Zhu, X.; Hu, Y.; Tian, G. Superhydrophobic Surfaces with Excellent Ice Prevention and Drag Reduction Properties Inspired by Iridaceae Leaf. Langmuir 2024, 40, 7192–7204. [Google Scholar] [CrossRef] [PubMed]
- Kreder, M.J.; Alvarenga, J.; Kim, P.; Aizenberg, J. Design of anti-icing surfaces: Smooth, textured or slippery? Nat. Rev. Mater. 2016, 1, 15003. [Google Scholar] [CrossRef]
- Wang, G.; Wang, J.; Cheng, K.; Yang, K.; Zhang, W. Nano hierarchical hill-like structure with TA1 surface manufactured by LIPSS for anti-corrosion and anti-icing. J. Mater. Res. Technol. 2025, 35, 3655–3667. [Google Scholar] [CrossRef]
- Lee, C.; Choi, H.-J.; Jeong, K.; Lee, K.; Cho, H. Formation of Wrinkled Nanostructures via Surface–Bulk Curing Disparity in Ethyl Cyanoacrylate: Toward Superhydrophobic Surface Applications. Nanomaterials 2025, 15, 12. [Google Scholar] [CrossRef]
- Shoaib, M.; Jamshaid, H.; Mishra, R.K.; Ali, M.; Chandan, V.; Kolar, V.; Nazari, S.; TM, A.; Jirku, P.; Muller, M.; et al. Facile-Solution-Processed Silicon Nanofibers Formed on Recycled Cotton Nonwovens as Multifunctional Porous Sustainable Materials. Materials 2024, 17, 412. [Google Scholar] [CrossRef] [PubMed]
- Xuan, S.; Yin, H.; Li, G.; Zhang, Z.; Jiao, Y.; Liao, Z.; Li, J.; Liu, S.; Wang, Y.; Tang, C.; et al. Trifolium repens L.-Like Periodic Micronano Structured Superhydrophobic Surface with Ultralow Ice Adhesion for Efficient Anti-Icing/Deicing. ACS Nano 2023, 17, 21749–21760. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, B.; Jung, Y.C.; Koch, K. Micro-, nano- and hierarchical structures for super-hydrophobicity, self-cleaning and low adhesion. Philos. Trans. R. Soc. A 2009, 367, 1631–1672. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Yin, K.; Pei, J.; He, Y.; Duan, J.; Arnusch, J.C. Femtosecond laser-textured superhydrophilic coral-like structures spread AgNWs enable strong thermal camouflage and anti-counterfeiting. Appl. Phys. Lett. 2024, 124, 161602. [Google Scholar] [CrossRef]
- Wang, W.; Chang, J.; Chen, L.; Weng, D.; Yu, Y.; Hou, Y. A laser-processed micro/nanostructures surface and its photothermal de-icing and self-cleaning performance. J. Colloid Interface Sci. 2024, 655, 307–318. [Google Scholar] [CrossRef] [PubMed]
- Patankar, N.A. Mimicking the lotus effect: Influence of double roughness structures and slender pillars. Langmuir 2004, 20, 8209–8213. [Google Scholar] [CrossRef] [PubMed]
- Drelich, J.W.; Boinovich, L.; Chibowski, E.; Della Volpe, C.; Hołysz, L.; Marmur, A.; Siboni, S. Contact angles: History of over 200 years of open questions. Surf. Innov. 2020, 8, 3–27. [Google Scholar] [CrossRef]
- Kietzig, A.-M.; Hatzikiriakos, S.G.; Englezos, P. Patterned superhydrophobic metallic surfaces. Langmuir 2009, 25, 4821–4827. [Google Scholar] [CrossRef] [PubMed]
- Fu, D.; Zheng, H.; Sheng, W.; Hao, X.; Zhang, X.; Chang, S.; Song, M. An experimental study on the influence of humidity on ice adhesion strength on superhydrophobic surfaces with microstructures. Appl. Therm. Eng. 2024, 24, 122732. [Google Scholar] [CrossRef]






| Physical Quantity | Data | Physical Quantity | Data |
|---|---|---|---|
| wavelength/nm | 516 | M2 | x: 1.09; y: 1.15 |
| repetition frequency/kHz | 100 | pulse width/fs | 373 |
| pulse energy/μJ | 5–35 | pulse number | 20–100 |
| scanning speed/mm/s | 1 | scanning spacing/μm | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, G.; Zhu, Z.; Zhang, W. Study on the Superhydrophobic Properties of Micro/Nano Hole Structure on the Surface of Glass Fiber Reinforced Plastics Based on Femtosecond Laser Etching. Nanomaterials 2025, 15, 287. https://doi.org/10.3390/nano15040287
Wang J, Wang G, Zhu Z, Zhang W. Study on the Superhydrophobic Properties of Micro/Nano Hole Structure on the Surface of Glass Fiber Reinforced Plastics Based on Femtosecond Laser Etching. Nanomaterials. 2025; 15(4):287. https://doi.org/10.3390/nano15040287
Chicago/Turabian StyleWang, Ji, Guolong Wang, Zhenkai Zhu, and Wenwu Zhang. 2025. "Study on the Superhydrophobic Properties of Micro/Nano Hole Structure on the Surface of Glass Fiber Reinforced Plastics Based on Femtosecond Laser Etching" Nanomaterials 15, no. 4: 287. https://doi.org/10.3390/nano15040287
APA StyleWang, J., Wang, G., Zhu, Z., & Zhang, W. (2025). Study on the Superhydrophobic Properties of Micro/Nano Hole Structure on the Surface of Glass Fiber Reinforced Plastics Based on Femtosecond Laser Etching. Nanomaterials, 15(4), 287. https://doi.org/10.3390/nano15040287






