Merging of Accidental Bound States in the Continuum in Symmetry and Symmetry-Broken Terahertz Photonic Crystal Slabs
Abstract
1. Introduction
2. Result and Discussion
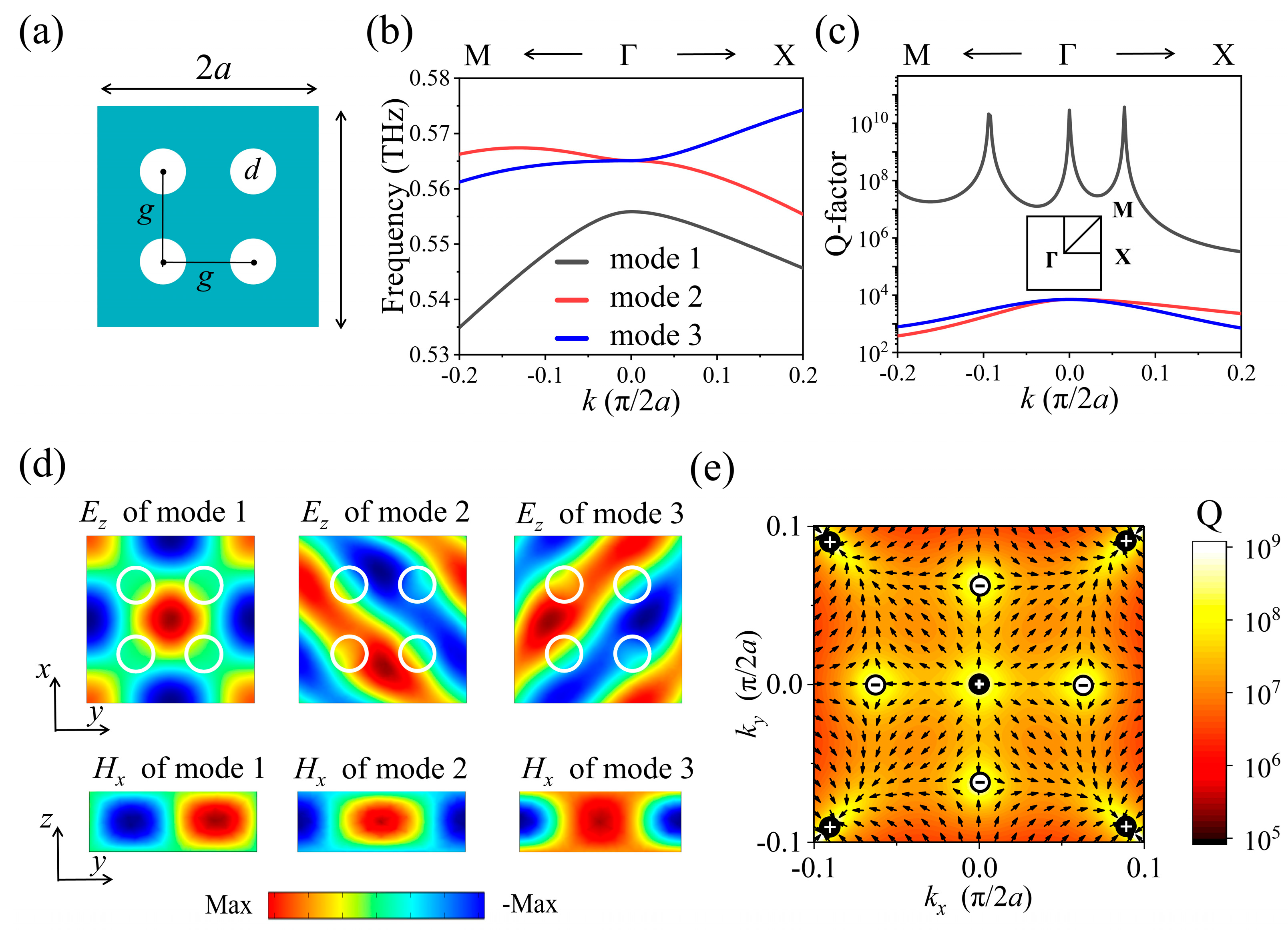
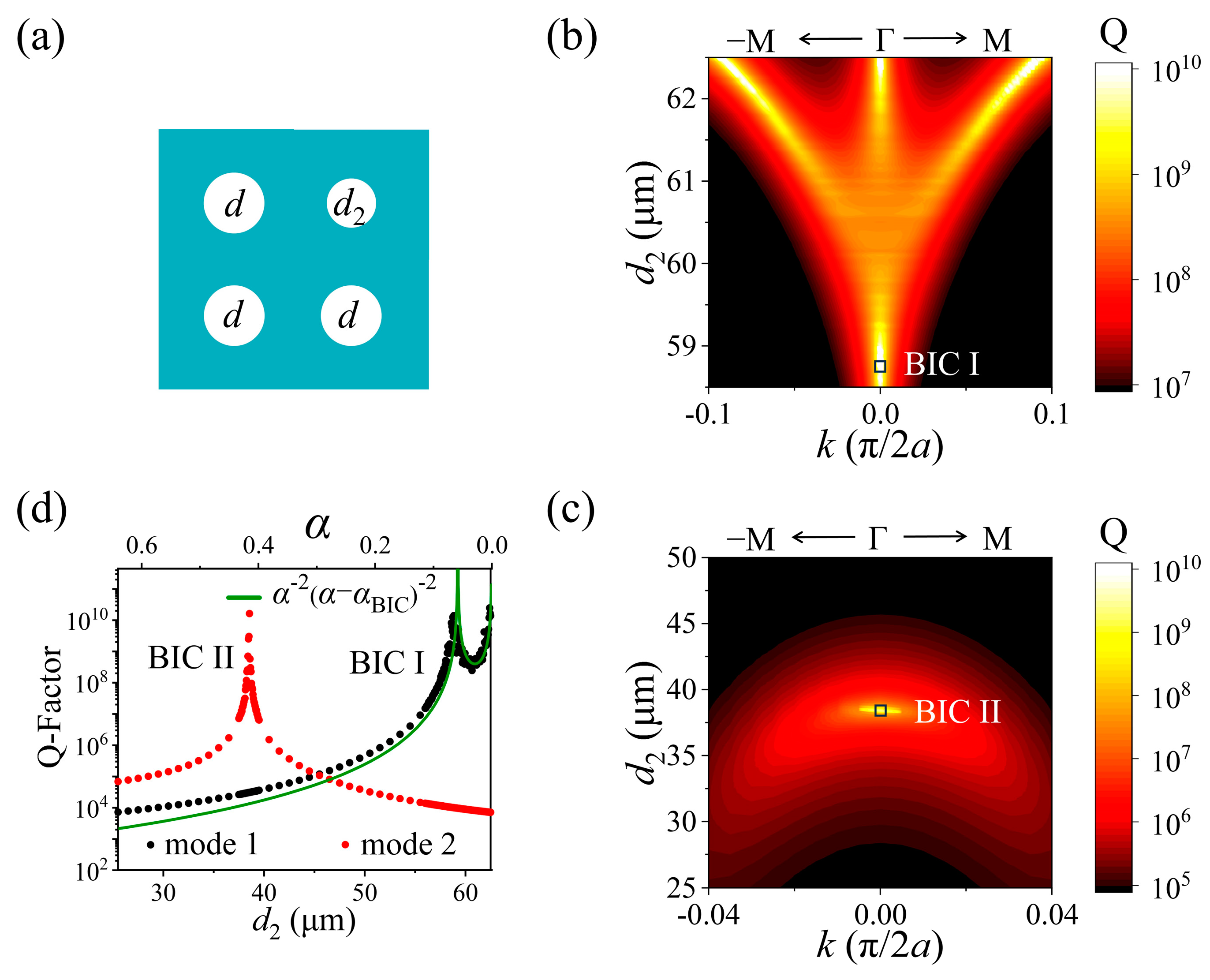
2.1. Accidental BICs in a Perturbed PhC Slab with C4 Symmetry
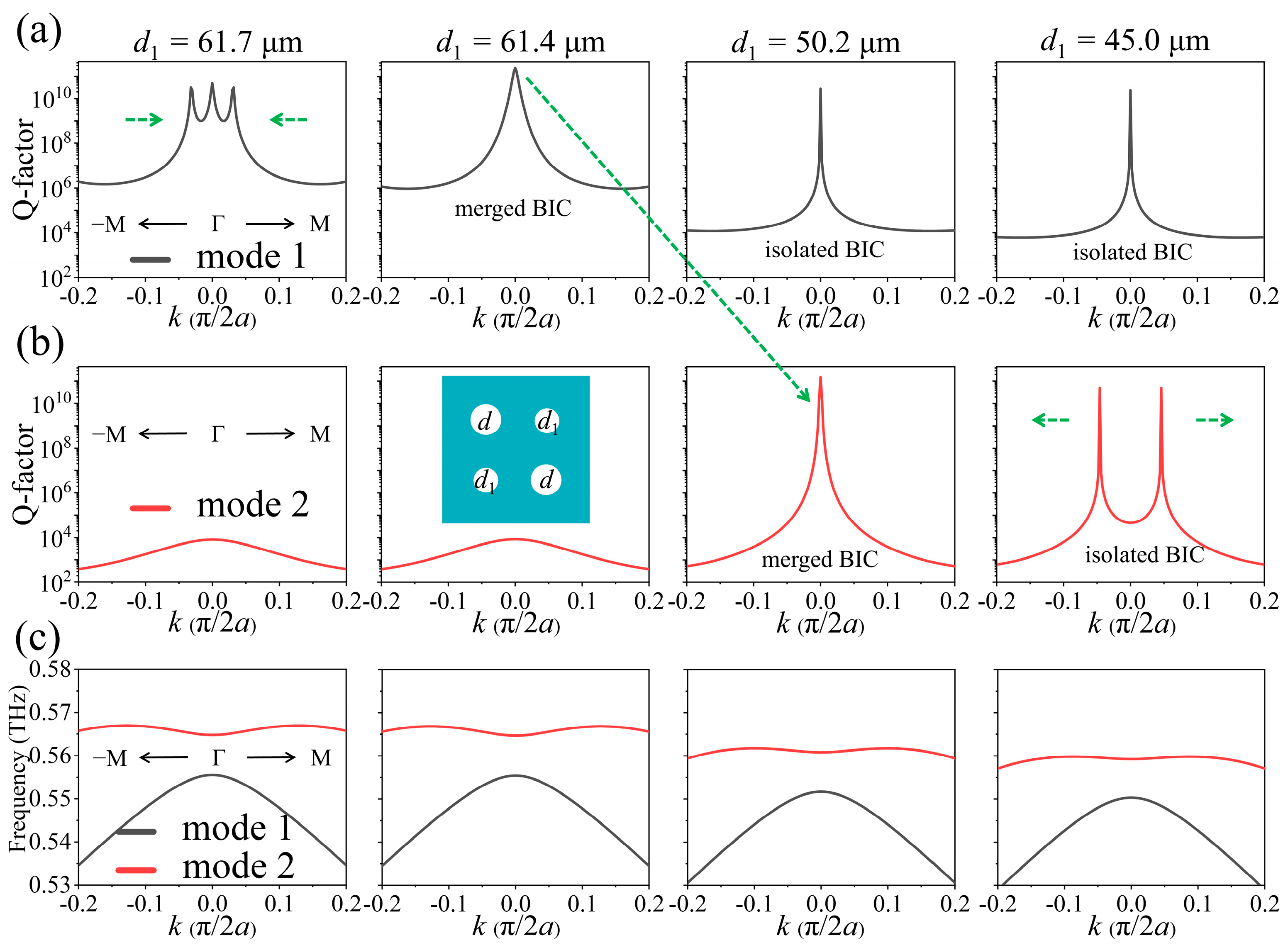
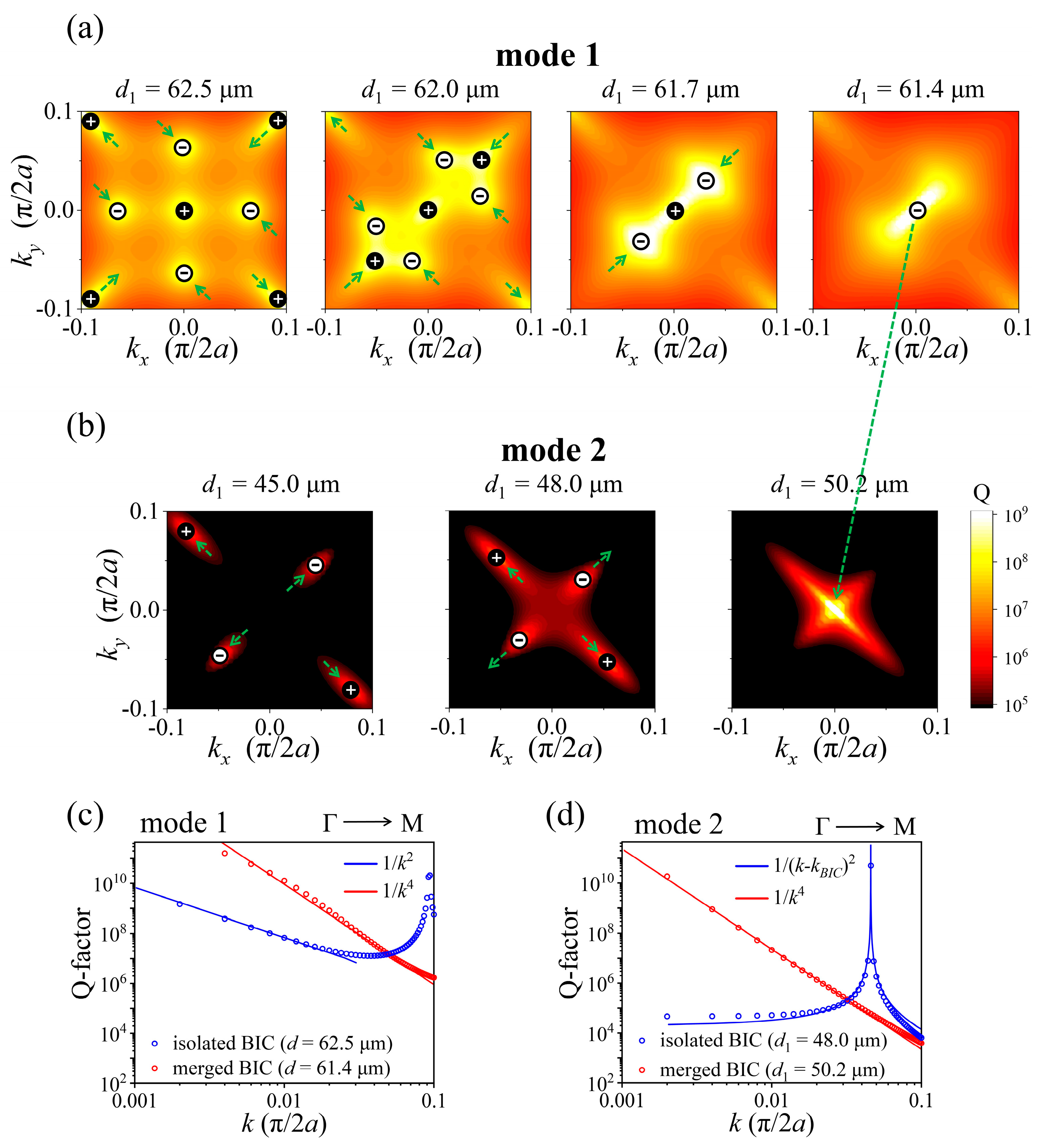
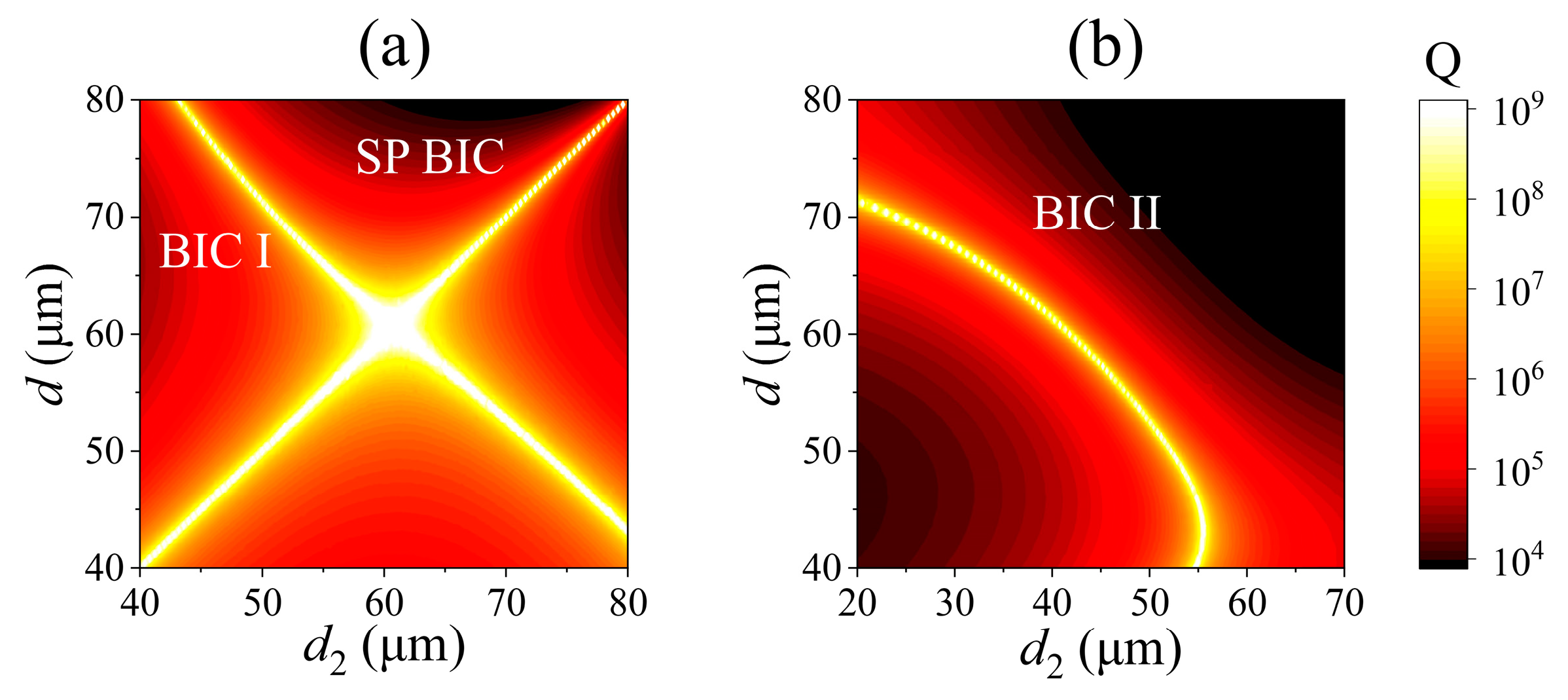
2.2. Merging and Band Transition of Accidental BICs in a PhC Slab with C2 Symmetry
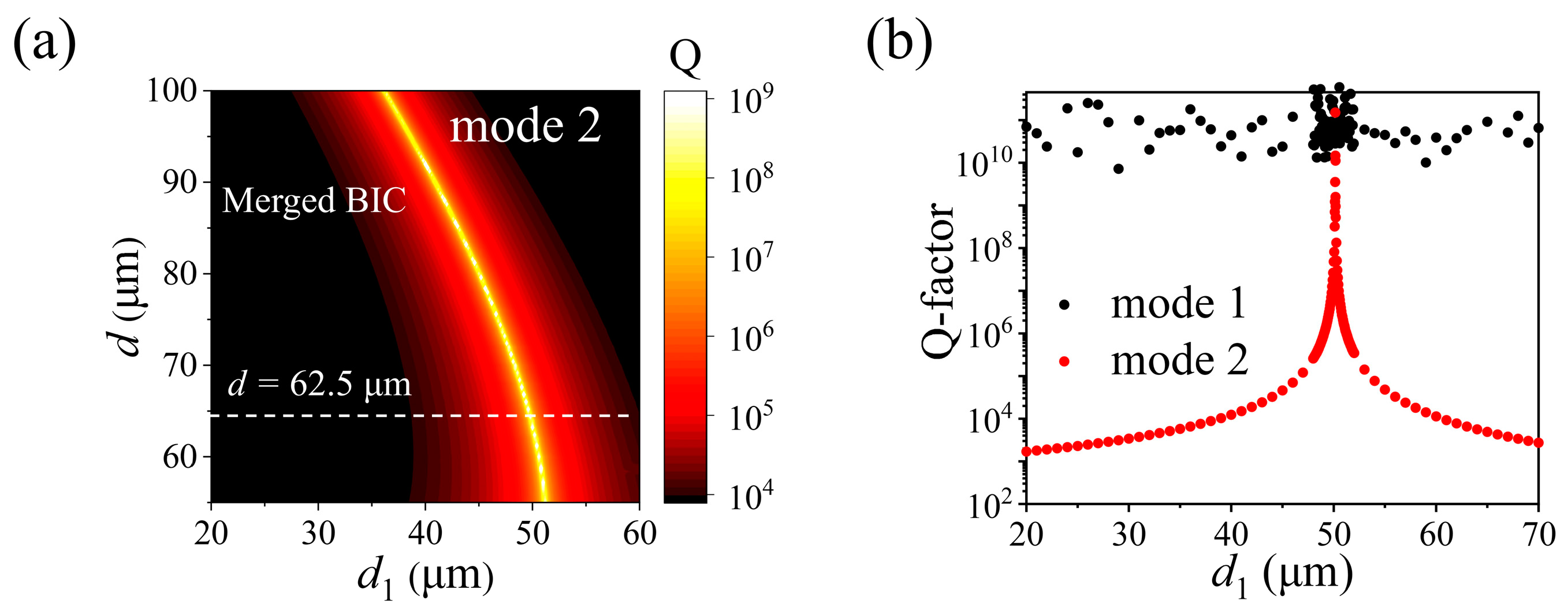
2.3. Accidental BICs in a PhC Slab with C2 Broken Symmetry
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Azzam, S.I.; Kildishev, A.V. Photonic Bound States in the Continuum: From Basics to Applications. Adv. Opt. Mater. 2021, 9, 2001469. [Google Scholar] [CrossRef]
- Koshelev, K.; Favraud, G.; Bogdanov, A.; Kivshar, Y.; Fratalocchi, A. Nonradiating photonics with resonant dielectric nanostructures. Nanophotonics 2019, 8, 725–745. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Wang, J.; Li, P.; Zhao, X.; Qian, Z.; Wang, X.; Wang, F.; Zhou, X.; Han, D.; Peng, C.; Shi, L.; et al. Optical bound states in the continuum in periodic structures: Mechanisms, effects, and applications. Photonics Insights 2024, 3, R01. [Google Scholar] [CrossRef]
- Koshelev, K.; Tang, Y.; Li, K.; Choi, D.Y.; Li, G.; Kivshar, Y. Nonlinear Metasurfaces Governed by Bound States in the Continuum. ACS Photonics 2019, 6, 1639–1644. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Y.; Lin, Y.; Xiang, J.; Feng, T.; Cao, Q.; Li, J.; Lan, S.; Liu, J. High-Q Quasibound States in the Continuum for Nonlinear Metasurfaces. Phys. Rev. Lett. 2019, 123, 253901. [Google Scholar] [CrossRef] [PubMed]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing action from photonic bound states in continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, C.; Xiao, S.; Wang, Y.; Fan, Y.; Liu, Y.; Zhang, N.; Qu, G.; Ji, H.; Han, J.; et al. Ultrafast control of vortex microlasers. Science 2020, 367, 1018–1021. [Google Scholar] [CrossRef]
- Tittl, A.; Leitis, A.; Liu, M.; Yesilkoy, F.; Choi, D.-Y.; Neshev, D.N.; Kivshar, Y.S.; Altug, H. Imaging-based molecular barcoding with pixelated dielectric metasurfaces. Science 2018, 360, 1105–1109. [Google Scholar] [CrossRef]
- Yesilkoy, F.; Arvelo, E.R.; Jahani, Y.; Liu, M.; Tittl, A.; Cevher, V.; Kivshar, Y.; Altug, H. Ultrasensitive hyperspectral imaging and biodetection enabled by dielectric metasurfaces. Nat. Photonics 2019, 13, 390–396. [Google Scholar] [CrossRef]
- Azzam, S.I.; Shalaev, V.M.; Boltasseva, A.; Kildishev, A.V. Formation of bound states in the continuum in hybrid plasmonic-photonic systems. Phys. Rev. Lett. 2018, 121, 253901. [Google Scholar] [CrossRef] [PubMed]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef] [PubMed]
- Yoda, T.; Notomi, M. Generation and annihilation of topologically protected bound states in the continuum and circularly polarized states by symmetry breaking. Phys. Rev. Lett. 2020, 125, 053902. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of trapped light within the radiation continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Chen, Y.; Liu, W. Singularities and poincaré indices of electromagnetic multipoles. Phys. Rev. Lett. 2019, 122, 153907. [Google Scholar] [CrossRef]
- Sadrieva, Z.; Frizyuk, K.; Petrov, M.; Kivshar, Y.; Bogdanov, A. Multipolar origin of bound states in the continuum. Phys. Rev. B 2019, 100, 115303. [Google Scholar] [CrossRef]
- Zhen, B.; Hsu, C.W.; Lu, L.; Stone, A.D.; Soljačić, M. Topological Nature of Optical Bound States in the Continuum. Phys. Rev. Lett. 2014, 113, 257401. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, A.; Liu, W.; Hsu, C.W.; Wang, B.; Guan, F.; Liu, X.; Shi, L.; Lu, L.; Zi, J. Observation of Polarization Vortices in Momentum Space. Phys. Rev. Lett. 2018, 120, 186103. [Google Scholar] [CrossRef]
- Dai, S.; Liu, L.; Han, D.; Zi, J. From topologically protected coherent perfect reflection to bound states in the continuum. Phys. Rev. B 2018, 98, 081405. [Google Scholar] [CrossRef]
- Doeleman, H.M.; Monticone, F.; den Hollander, W.; Alù, A.; Koenderink, A.F. Experimental observation of a polarization vortex at an optical bound state in the continuum. Nat. Photonics 2018, 12, 397–401. [Google Scholar] [CrossRef]
- Jiang, Q.; Hu, P.; Wang, J.; Han, D.; Zi, J. General Bound States in the Continuum in Momentum Space. Phys. Rev. Lett. 2023, 131, 013801. [Google Scholar] [CrossRef]
- Kang, M.; Zhang, S.; Xiao, M.; Xu, H. Merging Bound States in the Continuum at Off-High Symmetry Points. Phys. Rev. Lett. 2021, 126, 117402. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.; Mao, L.; Zhang, S.; Xiao, M.; Xu, H.; Chan, C.T. Merging bound states in the continuum by harnessing higher-order topological charges. Light: Sci. Appl. 2022, 11, 228. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Qu, L.; Gu, Z.; Zhang, D.; Wu, W.; Cai, W.; Ren, M.; Xu, J. Boosting second harmonic generation by merging bound states in the continuum. Phys. Rev. B 2023, 107, 245408. [Google Scholar] [CrossRef]
- Qi, X.; Wu, J.; Wu, F.; Ren, M.; Wei, Q.; Wang, Y.; Jiang, H.; Li, Y.; Guo, Z.; Yang, Y.; et al. Steerable merging bound states in the continuum on a quasi-flatband of photonic crystal slabs without breaking symmetry. Photonics Res. 2023, 11, 1262–1274. [Google Scholar] [CrossRef]
- Han, S.; Pitchappa, P.; Wang, W.; Srivastava, Y.K.; Rybin, M.V.; Singh, R. Extended Bound States in the Continuum with Symmetry-Broken Terahertz Dielectric Metasurfaces. Adv. Opt. Mater. 2021, 9, 2002001. [Google Scholar] [CrossRef]
- Jin, J.; Yin, X.; Ni, L.; Soljačić, M.; Zhen, B.; Peng, C. Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scattering. Nature 2019, 574, 501–504. [Google Scholar] [CrossRef]
- Chen, Z.; Yin, X.; Jin, J.; Zheng, Z.; Zhang, Z.; Wang, F.; He, L.; Zhen, B.; Peng, C. Observation of miniaturized bound states in the continuum with ultra-high quality factors. Sci. Bull. 2022, 67, 359–366. [Google Scholar] [CrossRef]
- Hwang, M.S.; Lee, H.C.; Kim, K.H.; Jeong, K.Y.; Kwon, S.H.; Koshelev, K.; Kivshar, Y.; Park, H.G. Ultralow-threshold laser using super-bound states in the continuum. Nat. Commun. 2021, 12, 4135. [Google Scholar] [CrossRef]
- Ren, Y.; Li, P.; Liu, Z.; Chen, Z.; Chen, Y.-L.; Peng, C.; Liu, J. Low-threshold nanolasers based on miniaturized bound states in the continuum. Sci. Adv. 2022, 8, eade8817. [Google Scholar] [CrossRef]
- Zhong, H.; Yu, Y.; Zheng, Z.; Ding, Z.; Zhao, X.; Yang, J.; Wei, Y.; Chen, Y.; Yu, S. Ultra-low threshold continuous-wave quantum dot mini-BIC lasers. Light Sci. Appl. 2023, 12, 100. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.; Chen, Z.; Yin, X.; Zhang, Z.; Hu, W.; Peng, C. High-Sensitive Refractive Index Sensing Enabled by Topological Charge Evolution. IEEE Photonics J. 2020, 12, 4501610. [Google Scholar] [CrossRef]
- Lee, S.G.; Kim, S.H.; Lee, W.J. Merging and Band Transition of Bound States in the Continuum in Leaky-Mode Photonic Lattices. Laser Photonics Rev. 2023, 17, 2300550. [Google Scholar] [CrossRef]
- Lee, S.G.; Kim, S.H.; Suk Hong, K.; Lee, W.J. Merging of TM-polarized bound states in the continuum in leaky-mode photonic lattices. J. Appl. Phys. 2024, 135, 153105. [Google Scholar] [CrossRef]
- Light: Science & ApplicationsYu, S.; Li, Z.; Chai, R.; Liu, W.; Zhou, W.; Cheng, H.; Chen, S. Merging bound states in the continuum in the geometrical parameter space. Phys. Rev. B 2024, 109, 115109. [Google Scholar]
- Song, Z.; Wang, Y.; Liu, J.; Pan, G.; Shu, F.; Du, Y.; Fang, B.; Hong, Z. Tailoring bound states in the continuum in symmetric-breaking terahertz photonic crystal slab. Chin. Opt. Lett. 2025, 23, 023601. [Google Scholar] [CrossRef]
- Zhou, C.; Huang, L.; Jin, R.; Xu, L.; Li, G.; Rahmani, M.; Chen, X.; Lu, W.; Miroshnichenko, A.E. Bound States in the Continuum in Asymmetric Dielectric Metasurfaces. Laser Photonics Rev. 2023, 17, 2200564. [Google Scholar] [CrossRef]
- Wang, P.; He, F.; Liu, J.; Shu, F.; Fang, B.; Lang, T.; Jing, X.; Hong, Z. Ultra-high-Q resonances in terahertz all-silicon metasurfaces based on bound states in the continuum. Photonics Res. 2022, 10, 2743–2750. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, P.; Liu, J.; Shu, F.; Pan, G.; Jin, Z.; Jing, X.; Hong, Z. High-Q resonances in terahertz all-silicon metasurface with imperforated air-hole array. Chin. Opt. Lett. 2023, 21, 113601. [Google Scholar] [CrossRef]
- Wang, W.; Srivastava, Y.K.; Tan, T.C.; Wang, Z.; Singh, R. Brillouin zone folding driven bound states in the continuum. Nat. Commun. 2023, 14, 2811. [Google Scholar] [CrossRef]
- Kazarinov, R.; Henry, C. Second-order distributed feedback lasers with mode selection provided by first-order radiation losses. IEEE J. Quantum Electron. 1985, 21, 144–150. [Google Scholar] [CrossRef]
- Ko, Y.H.; Lee, K.J.; Simlan, F.A.; Magnusson, R. Singular states of resonant nanophotonic lattices. Nanophotonics 2023, 12, 263–272. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Liu, J.; Shu, F.; Du, Y.; Hong, Z. Merging of Accidental Bound States in the Continuum in Symmetry and Symmetry-Broken Terahertz Photonic Crystal Slabs. Nanomaterials 2025, 15, 451. https://doi.org/10.3390/nano15060451
Chen J, Liu J, Shu F, Du Y, Hong Z. Merging of Accidental Bound States in the Continuum in Symmetry and Symmetry-Broken Terahertz Photonic Crystal Slabs. Nanomaterials. 2025; 15(6):451. https://doi.org/10.3390/nano15060451
Chicago/Turabian StyleChen, Jiale, Jianjun Liu, Fangzhou Shu, Yong Du, and Zhi Hong. 2025. "Merging of Accidental Bound States in the Continuum in Symmetry and Symmetry-Broken Terahertz Photonic Crystal Slabs" Nanomaterials 15, no. 6: 451. https://doi.org/10.3390/nano15060451
APA StyleChen, J., Liu, J., Shu, F., Du, Y., & Hong, Z. (2025). Merging of Accidental Bound States in the Continuum in Symmetry and Symmetry-Broken Terahertz Photonic Crystal Slabs. Nanomaterials, 15(6), 451. https://doi.org/10.3390/nano15060451





