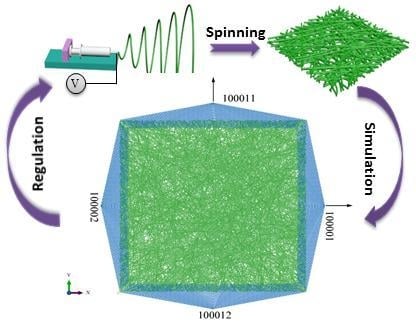
Finite Element Analysis of Electrospun Nanofibrous Mats under Biaxial Tension
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Test Methods
3. Experimental Results
3.1. Characterization of the Mats
3.2. Mechanical Behavior
4. Constitutive Relationship
- Electrospun nanofibrous mats are assumed to be homogeneous and continuous on the macroscopic scale.
- Single nanofibers are assumed to be incompressible and deform following the deformation of the mat.
- Because electrospun nanofibrous mats are made by stacking many fiber layers with similar properties from one layer to the other, the deformation characteristics of the entire nanofibrous mat can be described by considering only a single layer. The material is transversely isotropic.
4.1. Uniaxial Tension
4.2. Biaxial Tension
5. Results and Discussion
5.1. Uniform Nanofiber Distribution
5.1.1. Finite Element Modeling
5.1.2. Biaxial Tensile Analysis
5.1.3. Stochastic Effect Analysis
5.1.4. Parameter Analysis
5.2. Non-uniform Nanofiber Distribution
5.2.1. Finite Element Model
- The rand(1) function generates a 0–1 random number, prob is a randomly generated 0–1 random number, and the probability of being generated in the 0–1 range is the same;
- The 0–1 range is divided into 12 sectors according to Table 1, and the probability in the 12 sectors is the probability of each fibrous angle;
- When the random number prob falls in a certain zone, the corresponding fibrous angle of the zone is generated. For example, if prob = 0.5 falls into the (prob > 0.2993 && prob ≤ 0.7898) zone, then θ = π*(rand(1)*0.0833 + 0.0833*5), where θ is randomly generated in the 0.4165π–0.4998π (75°–90°) zone.
5.2.2. Biaxial Tension Analysis
6. Conclusions
- (1)
- The FE models of the SF/PCL nanofibrous mats (uniform fiber distribution and oriented fiber distribution) were built, and the model membranes were analyzed under biaxial tension to obtain stress-strain curves, which were similar to the test results.
- (2)
- The mats with a random distribution of electrospun nanofibers presented the same mechanical response in both biaxial tension directions. This confirmed the preliminary theoretical formula of biaxial tension. In addition, multiple sets of stochastic models were built, and the FE analysis showed that the simulation results did not depend on the randomness of modeling.
- (3)
- With an increase in the aspect ratio, the modulus of the nanofibrous mats decreases due to the upward tension along the long direction of the fibrous mats. In contrast, the modulus increases due to upward tension of the fibrous mats along the short direction of the membranes. The porosity has a negative effect on the modulus of the nanofibrous mats;
- (4)
- FE models of oriented nanofibrous mats were established. The orientation distribution of the fibers shows clear anisotropy in their mechanical tensile properties. The simulation results are consistent with the experimental results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weng, L.; Xie, J. Smart Electrospun Nanofibers for Controlled Drug Release: Recent Advances and New Perspectives. Curr. Pharm. Des. 2015, 21, 1944–1959. [Google Scholar] [CrossRef] [PubMed]
- Salifu, A.A.; Lekakou, C.; Labeed, F.H. Electrospun oriented gelatin-hydroxyapatite fiber scaffolds for bone tissue engineering. J. Biomed. Mater. Res. A. 2017, 105, 1911–1926. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, B.K.; Mousa, H.M.; Tiwari, A.P.; Ko, S.W.; Park, C.H.; Kim, C.S. Development of polyamide-6,6/chitosan electrospun hybrid nanofibrous scaffolds for tissue engineering application. Carbohydr. Polym. 2016, 148, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Hussain, T.; Garg, T.; Goyal, A.K.; Rath, G. Biomedical Applications of Nanofiber Scaffolds in Tissue Engineering. J. Biomater. Tissue Eng. 2014, 4, 600–623. [Google Scholar] [CrossRef]
- Gnavi, S.; Fornasari, B.E.; Tondaturo, C.; Laurano, R.; Zanetti, M.; Ciardelli, G.; Geuna, S. The Effect of Electrospun Gelatin Fibers Alignment on Schwann Cell and Axon Behavior and Organization in the Perspective of Artificial Nerve Design. Int. J. Mol. Sci. 2015, 16, 12925–12942. [Google Scholar] [CrossRef] [PubMed]
- Gentile, P.; Ferreira, A.M.; Callaghan, J.T.; Miller, C.A.; Atkinson, J.; Freeman, C.; Hatton, P.V. Multilayer Nanoscale Encapsulation of Biofunctional Peptides to Enhance Bone Tissue Regeneration In Vivo. Adv. Healthc. Mater. 2017, 6. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Wang, R.; Tian, M.; Qiu, C.; Fane, A.G. Fabrication of polyvinylidene fluoride (PVDF) nanofiber membranes by electro-spinning for direct contact membrane distillation. J. Membr. Sci. 2013, 425–426, 30–39. [Google Scholar] [CrossRef]
- Obaid, M.; Barakat, N.A.M.; Fadali, O.A.; Motlak, M.; Almajid, A.A.; Khalil, K.A. Effective and reusable oil/water separation membranes based on modified polysulfone electrospun nanofiber mats. Chem. Eng. J. 2015, 259, 449–456. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L. Cellulose Nanowhiskers and Fiber Alignment Greatly Improve Mechanical Properties of Electrospun Prolamin Protein Fibers. ACS Appl. Mater. Interfaces 2014, 6, 1709–1718. [Google Scholar] [CrossRef] [PubMed]
- Huan, S.; Liu, G.; Cheng, W.; Han, G.; Bai, L. Electrospun Poly(lactic acid)-Based Fibrous Nanocomposite Reinforced by Cellulose Nanocrystals: Impact of Fiber Uniaxial Alignment on Microstructure and Mechanical Properties. Biomacromolecules 2018, 19, 1037–1046. [Google Scholar] [CrossRef] [PubMed]
- Ding, B.; Wang, M.; Wang, X.; Yu, J.; Sun, G. Electrospun nanomaterials for ultrasensitive sensors. Mater. Today 2010, 13, 16–27. [Google Scholar] [CrossRef]
- Zou, B.; Guo, Y.; Shen, N.; Xiao, A.; Li, M.; Zhu, L.; Wan, P.; Sun, X. Sulfophenyl-Functionalized Reduced Graphene Oxide Networks on Electrospun 3D Scaffold for Ultrasensitive NO2 Gas Sensor. Sensors 2017, 17, 2954. [Google Scholar] [CrossRef] [PubMed]
- Merklein, M.; Biasutti, M. Development of a biaxial tensile machine for characterization of sheet metals. J. Mater. Process. Technol. 2013, 213, 939–946. [Google Scholar] [CrossRef]
- Stylianopoulos, T.; Bashur, C.A.; Goldstein, A.S.; Guelcher, S.A.; Barocas, V.H. Computational predictions of the tensile properties of electrospun fibre meshes: Effect of fibre diameter and fibre orientation. J. Mech. Behav. Biomed. Mater. 2008, 1, 326–335. [Google Scholar] [CrossRef] [PubMed]
- Cozza, E.S.; Monticelli, O.; Marsano, E.; Cebe, P. On the electrospinning of PVDF: Influence of the experimental conditions on the nanofiber properties. Polym. Int. 2013, 62, 41–48. [Google Scholar] [CrossRef]
- Gao, J.; Zhu, J.; Luo, J.; Xiong, J. Investigation of microporous composite scaffolds fabricated by embedding sacrificial polyethylene glycol microspheres in nanofibrous membrane. Compos. Part A 2016, 91, 20–29. [Google Scholar] [CrossRef]
- Nouri, M.; Mokhtari, J.; Rostamloo, M. Electrospun Poly(ε-caprolactone)/Nanoclay Nanofibrous Mats for Tissue Engineering. Fibers Polym. 2013, 14, 957–964. [Google Scholar] [CrossRef]
- Backer, S.; Petterson, D.R. Some Principles of Nonwoven Fabrics. Text. Res. J. 1960, 30, 704–711. [Google Scholar] [CrossRef]
- Dupaix, R.B.; Hosmer, J.E.D. Mechanical characterization and finite strain constitutive modeling of electrospun polycaprolactone under cyclic loading. Int. J. Struct. Changes Solids 2010, 2, 9–17. [Google Scholar]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Silberstein, M.N.; Pai, C.L.; Rutledge, G.C.; Boyce, M.C. Elastic–plastic behavior of non-woven fibrous mats. J. Mech. Phys. Solids 2012, 60, 295–318. [Google Scholar] [CrossRef]
- Hou, X.; Acar, M.; Silberschmidt, V.V. 2D finite element analysis of thermally bonded nonwoven materials: Continuous and discontinuous models. Comput. Mater. Sci. 2009, 46, 700–707. [Google Scholar] [CrossRef]
- Hou, X.; Acar, M.; Silberschmidt, V.V. Finite element simulation of low-density thermally bonded nonwoven materials: Effect of orientation distribution function and arrangement of bond points. Comput. Mater. Sci. 2011, 50, 1292–1298. [Google Scholar] [CrossRef]
- Hou, X.; Acar, M.; Silberschmidt, V.V. Non-uniformity of deformation in low-density thermally bonded nonwoven material: Effect of microstructure. J. Mater. Sci. 2011, 46, 307–315. [Google Scholar] [CrossRef]
- Sabuncuoglu, B.; Acar, M.; Silberschmidt, V.V. A parametric finite element analysis method for low-density thermally bonded nonwovens. Comput. Mater. Sci. 2012, 52, 164–170. [Google Scholar] [CrossRef]
- Farukh, F.; Demirci, E.; Sabuncuoglu, B.; Acar, M.; Pourdeyhimi, B.; Silberschmidt, V.V. Numerical modelling of damage initiation in low-density thermally bonded nonwovens. Comput. Mater. Sci. 2012, 64, 112–115. [Google Scholar] [CrossRef]
- Farukh, F.; Demirci, E.; Sabuncuoglu, B.; Acar, M.; Pourdeyhimi, B.; Silberschmidt, V.V. Numerical analysis of progressive damage in nonwoven fibrous networks under tension. Int. J. Solids Struct. 2014, 51, 1670–1685. [Google Scholar] [CrossRef]
- Ridruejo, A.; González, C.; Llorca, J. Micromechanisms of deformation and fracture of polypropylene nonwoven fabrics. Int. J. Solids Struct. 2011, 48, 153–162. [Google Scholar] [CrossRef]
- Isaksson, P.; Dumont, P.J.J.; Roscoat, S.R.D. Crack growth in planar elastic fiber materials. Int. J. Solids Struct. 2012, 49, 1900–1907. [Google Scholar] [CrossRef]
- Wilbrink, D.V.; Beex, L.A.A.; Peerlings, R.H.J. A discrete network model for bond failure and frictional sliding in fibrous materials. Int. J. Solids Struct. 2013, 50, 1354–1363. [Google Scholar] [CrossRef]
- Yin, Y.; Pan, Z.; Xiong, J. A Tensile Constitutive Relationship and a Finite Element Model of Electrospun Nanofibrous Mats. Nanomaterials 2018, 8, 29. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Rigueiro, J.; Viney, C.; Llorca, J.; Elices, M. Mechanical properties of single-brin silkworm silk. J. Appl. Polym. Sci. 2000, 75, 1270–1277. [Google Scholar] [CrossRef]
- Vepari, C.; Kaplan, D.L. Silk as a biomaterial. Prog. Polym. Sci. 2007, 32, 991–1007. [Google Scholar] [CrossRef] [PubMed]
- Kundu, B.; Kurland, N.E.; Bano, S.; Patra, C.; Engel, F.B.; Yadavalli, V.K.; Kundu, S.C. Silk proteins for biomedical applications: Bioengineering perspectives. Prog. Polym. Sci. 2014, 39, 251–267. [Google Scholar] [CrossRef]
- Koh, L.D.; Cheng, Y.; Teng, C.P.; Khin, Y.W.; Loh, X.J.; Tee, S.Y.; Low, M.; Ye, E.; Yu, H.D.; Zhang, Y.W.; et al. Structures, mechanical properties and applications of silk fibroin materials. Prog. Polym. Sci. 2015, 46, 86–110. [Google Scholar] [CrossRef]
- Lee, H.; Jang, C.H.; Kim, G.H. A polycaprolactone/silk-fibroin nanofibrous composite combined with human umbilical cord serum for subacute tympanic membrane perforation; an in vitro and in vivo study. J. Mater. Chem. B 2014, 2, 2703–2713. [Google Scholar] [CrossRef]
- Kharaziha, M.; Fathi, M.H.; Edris, H. Development of novel aligned nanofibrous composite membranes for guided bone regeneration. J. Mech. Behav. Biomed. 2013, 24, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Xiong, J. Effect of the Distribution of Fiber Orientation on the Mechanical Properties of Silk Fibroin/Polycaprolactone Nanofiber Mats. J. Eng. Fibers Fabr. 2017, 12, 17–28. [Google Scholar]
- Rutledge, G.C.; Lowery, J.L.; Pai, C.L. Characterization by Mercury Porosimetry of Nonwoven Fiber Media with Deformation. J. Eng. Fibers Fabr. 2009, 4, 1–13. [Google Scholar]
- Kwon, I.K.; Kidoaki, S.; Matsuda, T. Electrospun nano to microfiber fabrics made of biodegradable copolyesters: Structural characteristics, mechanical properties and cell adhesion potential. Biomaterials 2005, 26, 3929–3939. [Google Scholar] [CrossRef] [PubMed]
- Plastics-Determination of Tensile Properties—Part 1: General Principles. Available online: https://www.iso.org/standard/56045.html (accessed on 29 April 2018).
- Plastics-Determination of Tensile Properties—Part 3: Test Conditions for Films and Sheets. Available online: https://www.iso.org/standard/4594.html (accessed on 29 April 2018).
- Beachley, V.; Katsanevakis, E.; Zhang, N.; Wen, X.J. Highly Aligned Polymer Nanofiber Structures: Fabrication and Applications in Tissue Engineering. Adv. Polym. Sci. 2012, 246, 171–212. [Google Scholar]
















| Section | Angle (°) | Percentage (%) | Section | Angle (°) | Percentage (%) |
|---|---|---|---|---|---|
| 1 | 15 | 0.27 | 7 | 105 | 17.13 |
| 2 | 30 | 0.25 | 8 | 120 | 1.17 |
| 3 | 45 | 1.46 | 9 | 135 | 1.04 |
| 4 | 60 | 1.45 | 10 | 150 | 0.37 |
| 5 | 75 | 26.5 | 11 | 165 | 1.23 |
| 6 | 90 | 49.05 | 12 | 180 | 0.08 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Xiong, J. Finite Element Analysis of Electrospun Nanofibrous Mats under Biaxial Tension. Nanomaterials 2018, 8, 348. https://doi.org/10.3390/nano8050348
Yin Y, Xiong J. Finite Element Analysis of Electrospun Nanofibrous Mats under Biaxial Tension. Nanomaterials. 2018; 8(5):348. https://doi.org/10.3390/nano8050348
Chicago/Turabian StyleYin, Yunlei, and Jie Xiong. 2018. "Finite Element Analysis of Electrospun Nanofibrous Mats under Biaxial Tension" Nanomaterials 8, no. 5: 348. https://doi.org/10.3390/nano8050348
APA StyleYin, Y., & Xiong, J. (2018). Finite Element Analysis of Electrospun Nanofibrous Mats under Biaxial Tension. Nanomaterials, 8(5), 348. https://doi.org/10.3390/nano8050348