Flat-Band in Pyrochlore Oxides: A First-Principles Study
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
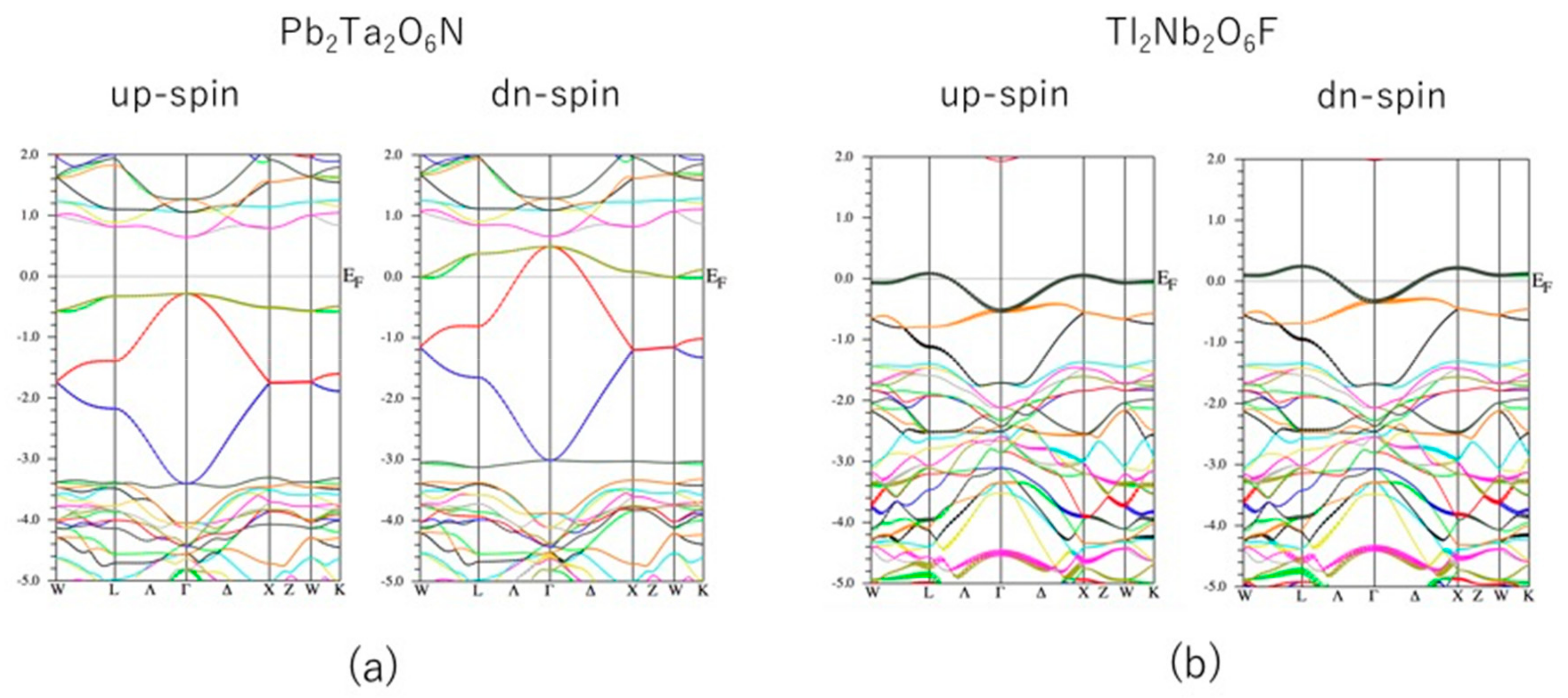
3.1. Band Structure and Quasi Flat Band
3.2. Ferromagnetic State
3.3. Comparison with Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pullar, R.C. Hexagonal Ferrites: A Review of the Synthesis, Properties and Applications of Hexaferrite Ceramics. Prog. Mater. Sci. 2012, 57, 1191–1334. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Slimani, Y.; Güngüne, H.; Baykal, A.; Trukhanov, S.V.; Trukhanov, A.V. Manganese/Yttrium Codoped Strontium Nanohexaferrites: Evaluation of Magnetic Susceptibility and Møssbbauer Spectra. Nanomaterials 2019, 24, 18. [Google Scholar] [CrossRef] [PubMed]
- Almessiere, M.A.; Slimani, Y.; El Sayed, H.S.; Baykal, A.; Ercan, I. Microstructural and Magnetic Investigation of Vanadium-Substituted Sr-nanohexaferrite. J. Magn. Magn. Mater. 2019, 471, 124–132. [Google Scholar] [CrossRef]
- Goodenough, J.B. Electronic and Ionic Transport Properties and Other Physical Aspects of Perovskites. Rep. Prog. Phys. 2004, 67, 1915. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Troyanchuk, I.O.; Fita, I.M.; Szymczak, H.; Bärner, K. Comparative Study of the Magnetic and Electrical Properties of Pr1-xBaxMnO3-δ Manganites Depending on the Preparation Conditions. J. Magn. Magn. Mater. 2001, 237, 276–282. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Vasiliev, A.N.; Szymczak, H. Frustrated Exchange Interactions Formation at Low Temperatures and High Hydrostatic Pressures in La0.70Sr0.30MnO2.85. JETP 2010, 111, 209–214. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Lobanovski, L.S.; Bushinsky, M.V.; Troyanchuk, I.O.; Szymczak, H. Magnetic Phase Transitions in the Anion-Deficient La1-xBaxMnO3-x/2 (0 ≤ x ≤ 0.50) Manganites. J. Phys. Condens. Mater. 2003, 15, 1783–1795. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Vasiliev, A.N.; Balagurov, A.M.; Szymczak, H. Magnetic State of the Structural Separated Anion-Deficient La0.70Sr0.30MnO2.85 Manganite. JETP 2011, 113, 819–825. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Szymczak, H.; Botez, C.E.; Adair, A. Magnetotransport Properties and Mechanism of the A-site Ordering in the Nd-Ba Optimal-Doped Manganites. J. Low Temp. Phys. 2007, 149, 185–199. [Google Scholar] [CrossRef]
- Doroshev, V.D.; Borodin, V.A.; Kamenev, V.I.; Mazur, A.S.; Tarasenko, T.N.; Tovstolytkin, A.I.; Trukhanov, S.V. Self-Doped Lanthanum Manganites as a Phase-Separated System: Transformation of Magnetic Resonance, and Transport Properties with Doping and Hydrostatic Compression. J. Appl. Phys. 2008, 104, 093909. [Google Scholar] [CrossRef]
- Subramanian, M.A.; Aravamudan, G.; Subba Rao, G.V. Oxides Pyrochlore—A Review. Prog. Solid State Chem. 1983, 15, 55–143. [Google Scholar] [CrossRef]
- Gardner, J.S.; Gingras, M.J.P.; Greedan, J.E. Magnetic Pyrochlore Oxides. Rev. Mod. Phys. 2010, 82, 53. [Google Scholar] [CrossRef]
- Ramirez, A.P. Strongly Geometrically Frustrated Magnets. Annu. Rev. Mater. Sci. 1994, 24, 453–480. [Google Scholar] [CrossRef]
- Canals, B.; Lacriox, C. Pyrochlore Antiferromagnet: A Three-Dimensional Quantum Spin Liquid. Phys. Rev. Lett. 1998, 80, 2933. [Google Scholar] [CrossRef]
- Ramirez, A.P.; Hayashi, A.; Cava, R.J.; Siddharthan, R.; Shastry, B.S. Zero-Point Entropy in ‘Spin Ice’. Nature (London) 1999, 399, 333–335. [Google Scholar] [CrossRef]
- Castelnovo, C.; Moessner, R.; Sondhi, S. Magnetic Monopoles in Spin Ice. Nature (London) 2007, 451, 42–45. [Google Scholar] [CrossRef]
- Kadowaki, H.; Doi, N.; Aoki, Y.; Tabata, Y.; Sato, T.J.; Lynn, J.W.; Matsuhira, K.; Hiroi, Z. Observation of Magnetic Monopoles in Spin Ice. J. Phys. Soc. Jpn. 2009, 78, 103706. [Google Scholar] [CrossRef] [Green Version]
- Hanawa, M.; Muraoka, Y.; Tayama, T.; Sakakibara, T.; Yamaura, J.; Hiroi, Z. Superconductivity at 1K in Cd2Re2O7. Phys. Rev. Lett. 2001, 87, 187001. [Google Scholar] [CrossRef]
- Hiroi, Z.; Yamaura, J.; Kobayashi, C.T.; Matsubayashi, Y.; Hirai, D. Pyrochlore Oxide Superconductor Cd2Re2O7 Revisited. J. Phys. Sco. Jpn. 2018, 87, 024702. [Google Scholar] [CrossRef]
- Guo, H.-M.; Franz, M. Three Dimensional Topological Insulators on the Pyrochlore Lattice. Phys. Rev. Lett. 2009, 103, 206805. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, F.; Wu, Y.-S. Exotic Electronic States in the World of Flat Bands: From Theory to Material. Chin. Phys. Lett. B 2014, 23, 077308. [Google Scholar] [CrossRef]
- Derzhko, O.; Richter, J.; Maksymenko, M. Strongly Correlated Flat Band Systems: The Route from Heisenberg Spins to Hubbard Electrons. Int. J. Mod. Phys. B 2015, 29, 1530007. [Google Scholar] [CrossRef]
- Mielke, A. Ferromagnetic Ground States for the Hubbard model on the Line Graphs. J. Phys. A Math. Gen. 1991, 24, L73. [Google Scholar] [CrossRef]
- Mielke, A. Ferromagnetism in the Hubbard model on Line Graphs and Further Considerations. J. Phys. A Math. Gen. 1991, 24, 3311. [Google Scholar] [CrossRef]
- Kobayashi, K.; Okumura, M.; Yamada, S.; Machida, M.; Aoki, H. Superconductivity in Repulsively Interacting Fermion on a Diamond Chain: Flat-Band Induced Pairing. Phys. Rev. B 2016, 94, 214501. [Google Scholar] [CrossRef]
- Hatsugai, Y.; Maruyama, I. ZQ Topological Invariants in Polyacetylene, Kagome, and Pyrochlore Lattice. Europhys. Lett. 2011, 95, 20003. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, H.; Gu, Z.; Gong, C.; Sheng, D.-N. Non-Abelian Quantum Hall Effect in Topological Flat Band. Phys. Rev. Lett. 2012, 108, 126805. [Google Scholar] [CrossRef] [PubMed]
- Hase, I.; Yanagisawa, T.; Kawashima, K. Computational Design of Flat Band System. Nanoscale Res. Lett. 2018, 13, 63. [Google Scholar] [CrossRef] [PubMed]
- Hase, I.; Yanagisawa, T.; Aiura, Y.; Kawashima, K. Possibility of Flat-Band Ferromagnetism in Hold-Doped Pyrochlore Oxides Sn2Nb2O7 and Sn2Ta2O7. Phys. Rev. Lett. 2018, 120, 196401. [Google Scholar] [CrossRef]
- Anderson, P.W. Model for the Electronic Structure of Amorphous Semiconductors. Phys. Rev. Lett. 1975, 34, 953–955. [Google Scholar] [CrossRef]
- Dzero, M.; Schmalian, J. Superconductivity in Charge Kondo System. Phys. Rev. Lett. 2005, 941, 157003. [Google Scholar] [CrossRef] [PubMed]
- Matsushita, Y.; Bluhm, H.; Geballe, T.H.; Fisher, I.R. Evidence of Charge Kondo Effect in Superconducting Tl-Doped PbTe. Phys. Rev. Lett. 1988, 61, 2713–2716. [Google Scholar] [CrossRef] [PubMed]
- Taraphder, A.; Krishnamurthy, H.R.; Pandit, R.; Ramakrishnan, T.V. Negative-U Extended Hubbard Model for Doped Barium Bismathates. Phys. Rev. B 1981, 52, 1368. [Google Scholar] [CrossRef]
- Varma, C.M. Missing Valence States, Diamagnetic Insulators, and Superconductors. Phys. Rev. Lett. 1988, 61, 2713–2716. [Google Scholar] [CrossRef] [PubMed]
- Hase, I.; Tanagisawa, T. Madelung Energy of the Valence-Skipping Compound BaBiO3. Phys. Rev. B 2007, 76, 174103. [Google Scholar] [CrossRef]
- Hase, I.; Tanagisawa, T. Electronic States of Valence-Skipping Compounds. J. Phys. Conf. Ser. 2008, 108, 012011. [Google Scholar] [CrossRef]
- Sleight, A.W. Valency, Valence Degeneracy, Ferroelectricity and Superconductivity. Prog. Solid State Chem. 2009, 37, 251–261. [Google Scholar] [CrossRef]
- Micnas, R.; Ranninger, D.; Robaszkievicz. Superconductivity in Narrow-Band Systems with local Nonretarded Attractive Interaction. Rev. Mod. Phys. 1990, 62, 113–171. [Google Scholar] [CrossRef]
- Moreo, A.; Scalapino, D.J. Two-Dimensional Negative-U Hubbard Model. Phys. Rev. Lett. 1991, 66, 946–948. [Google Scholar] [CrossRef]
- Mizoguchi, H.; Kawazoe, H.; Ueda, T.; Hayashi, S.; Hosono, H.; Ueda, N. Formation and Optical Absorbtion Spectra of Mixed Valence State of Tl in Tl2Nb2O6+x with Pyrochlore Structure. Bull. Chem. Soc. Jpn. 1996, 69, 111–115. [Google Scholar] [CrossRef]
- Fourquet, J.L.; Duroy, H.; Lacorre, P. Tl2Nb2O6+x (0 ≦ x ≦ 1): A Continuous Cubic Pyrochlore Type Solid Solution. J. Solid State Chem. 1995, 114, 575–584. [Google Scholar] [CrossRef]
- Ramadass, N.; Palanisamy, N.; Gopalakrishnan, J.; Aravamudan, G.; Sastri, M.V.C. Some ABO3 Oxides with Defect Pyrochlore Structure. Solid State Commun. 1975, 17, 545–575. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. WIEN2k, an Augmented Plane Wave + local orbitals Program for Calculating Crystal Properties; Vienna Univ. of Technology: Vienna, Austria, 2001. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3875. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Belyaev, I.N.; Lupeiko, T.G.; Nalbandyan, V.B.; Abanina, E.V. Exchange Reactions in Systems Comprising Alkali Metal, Silver, and Thallium Sulphates, Niobates, and Tantalates. Russ. J. Inorg. Chem. 1978, 23, 18–22. [Google Scholar]
- Kusakabe, K.; Aoki, H. Robustness of the Ferromagnetism of in Flat Band. Phys. (Amst.) B 1994, 194–195, 215–216. [Google Scholar] [CrossRef]
- Soulairol, R.; Fu, C.-C.; Barreteau, C. Structure and Magnetism of Bulk Fe and Cr: From Plane Waves to LCAO methods. J. Phys. Condens. Matter 2010, 22, 295502. [Google Scholar] [CrossRef]
- Friak, M.; Sob, M.; Vitek, V. Ab-initio Calculation of Phase Boundaries in Iron along the BCC-FCC Transformation Path. Phys. Rev. B 2001, 63, 052405. [Google Scholar] [CrossRef]
- Kikuchi, N.; Samizo, A.; Ikeda, S.; Aiura, Y.; Mibu, K.; Nishio, K. Carrier Generation in a p-type Oxide Semiconductor Sn2(Nb2-xTax)O7. Phys. Rev. Mater. 2017, 1, 021601R. [Google Scholar] [CrossRef]
- Aiura, Y.; Ozawa, K.; Hase, I.; Bando, K.; Haga, H.; Kawanaka, H.; Samizo, A.; Kikuchi, N.; Mase, K. Disappearance of Localized Valence Bond Maximum in Ternary Tin Oxide with Pyrochlore Structure, Sn2Nb2O7. J. Phys. Chem. C 2017, 121, 9480–9488. [Google Scholar] [CrossRef]
- Ubic, R.; Reaney, I.M. Structure and Dielectric Properties of Lead Pyrochlores. J. Am. Ceram. Soc. 2012, 85, 2472–2478. [Google Scholar] [CrossRef]



| Compound | Magnetic Moment (μB cell) |
|---|---|
| Sn2Nb2O6N | 2.000 |
| Sn2Ta2O6N | 2.001 |
| Pb2Nb2O6N | 2.001 |
| Pb2Ta2O6N | 2.000 |
| Tl2Nb2O6F | 1.522 |
| Tl2Ta2O6F | 1.507 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hase, I.; Yanagisawa, T.; Kawashima, K. Flat-Band in Pyrochlore Oxides: A First-Principles Study. Nanomaterials 2019, 9, 876. https://doi.org/10.3390/nano9060876
Hase I, Yanagisawa T, Kawashima K. Flat-Band in Pyrochlore Oxides: A First-Principles Study. Nanomaterials. 2019; 9(6):876. https://doi.org/10.3390/nano9060876
Chicago/Turabian StyleHase, Izumi, Takashi Yanagisawa, and Kenji Kawashima. 2019. "Flat-Band in Pyrochlore Oxides: A First-Principles Study" Nanomaterials 9, no. 6: 876. https://doi.org/10.3390/nano9060876
APA StyleHase, I., Yanagisawa, T., & Kawashima, K. (2019). Flat-Band in Pyrochlore Oxides: A First-Principles Study. Nanomaterials, 9(6), 876. https://doi.org/10.3390/nano9060876





