Steric Interference in Bilayer Graphene with Point Dislocations
Abstract
:1. Introduction
2. Validation of the Theoretical Model
2.1. Harmonic Response
2.2. Lattice Defects
2.2.1. Method of Analysis
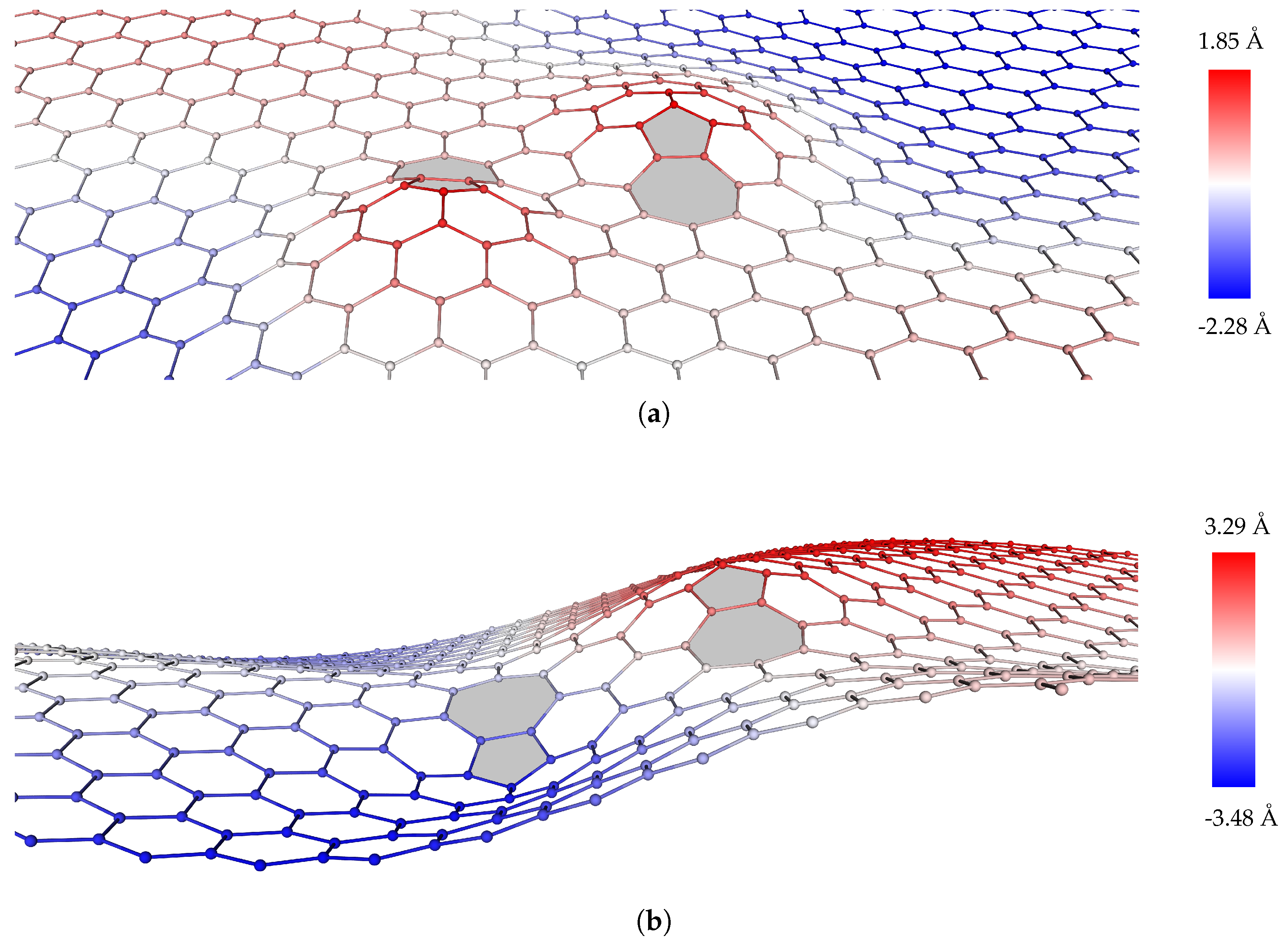
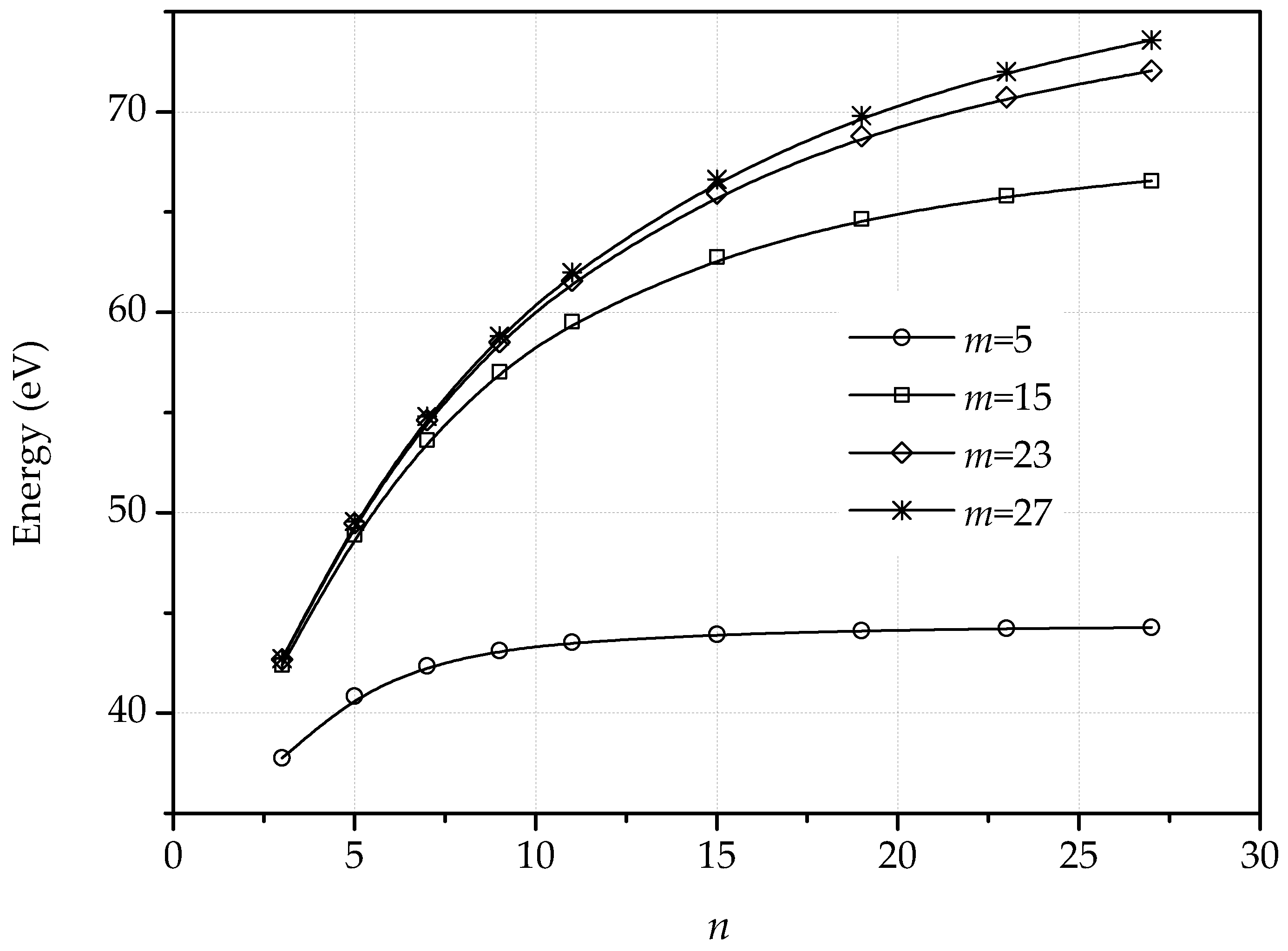
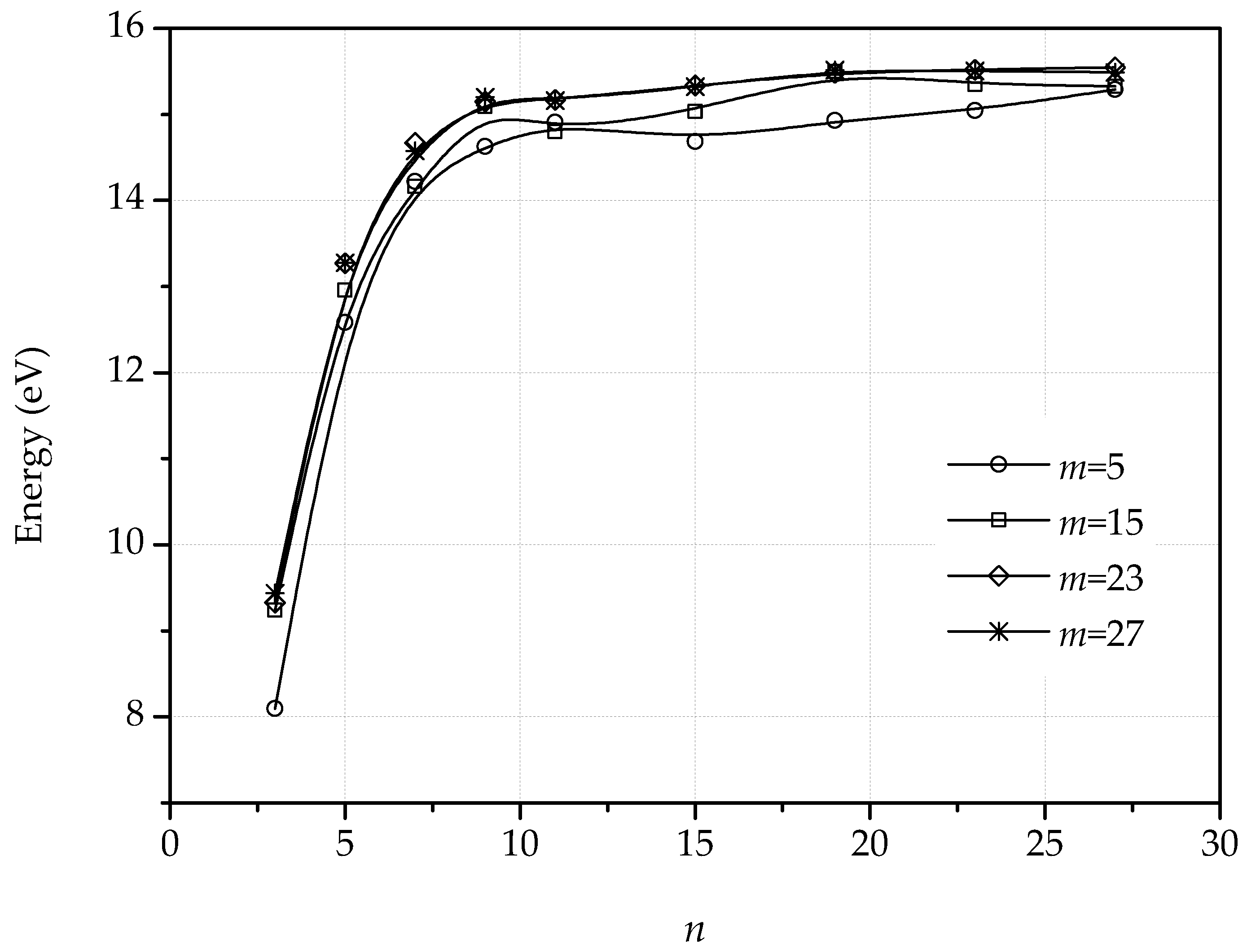
2.2.2. Dislocation Dipoles
2.2.3. Dislocation Quadrupole
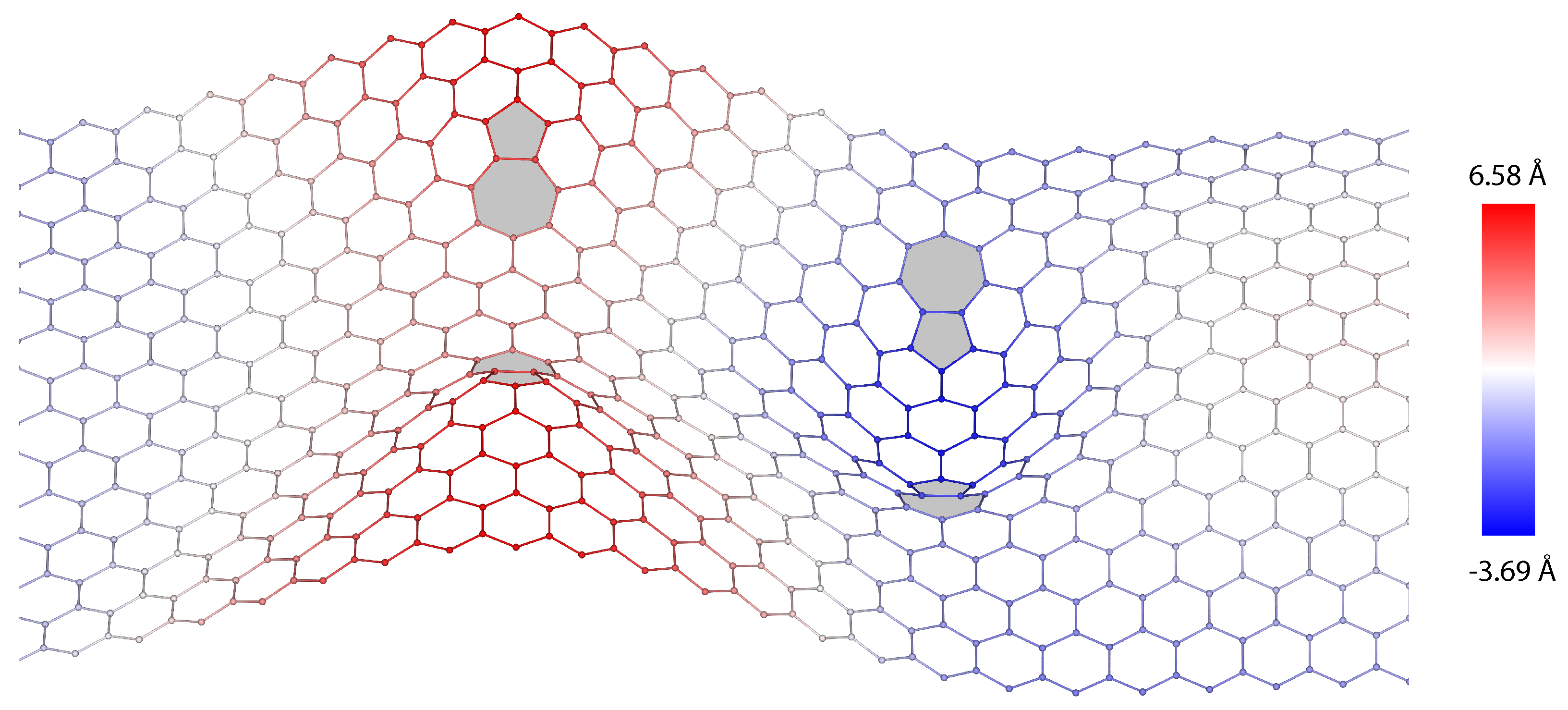
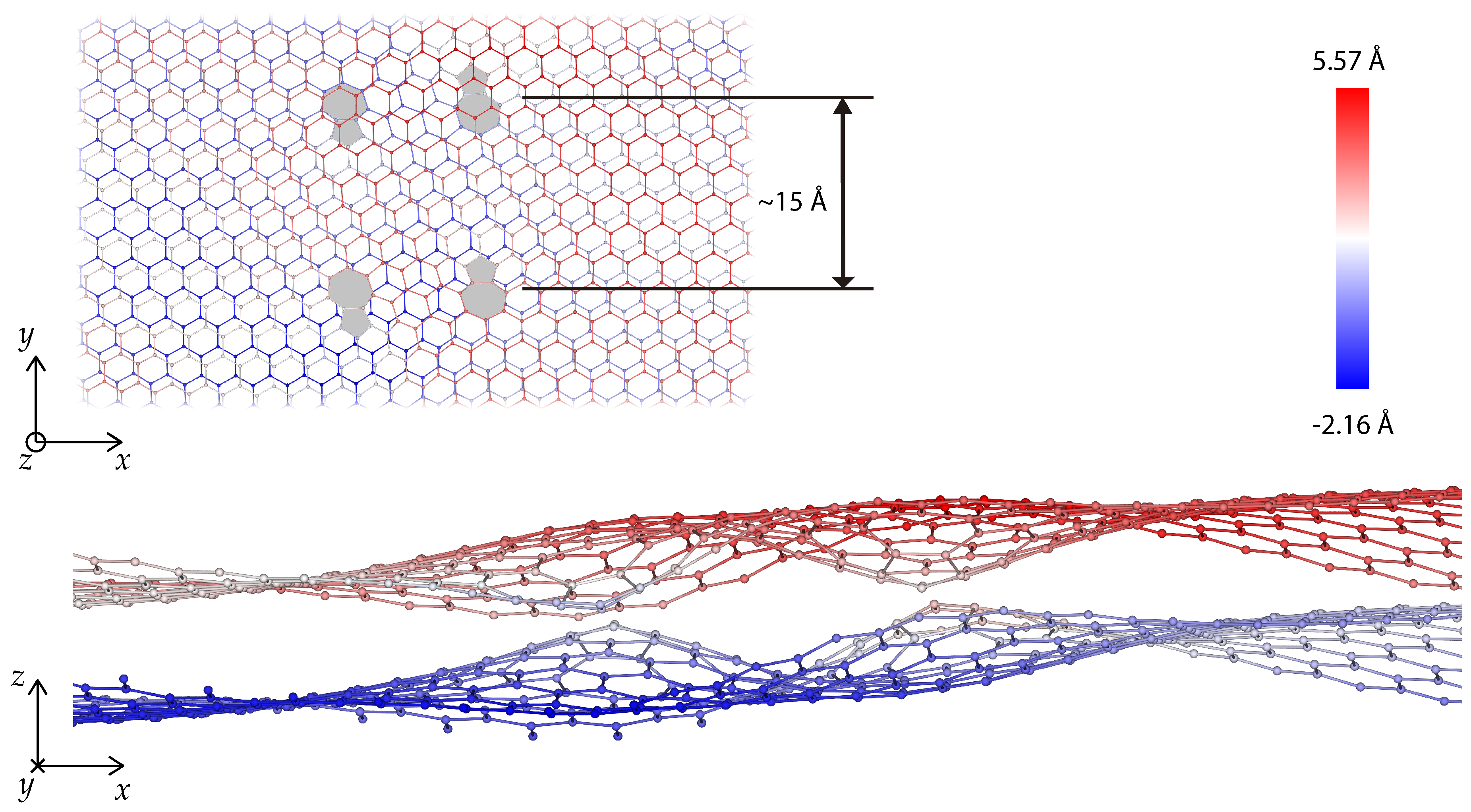
3. Dislocations in Bilayer Graphene
4. Summary and Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Frank, I.W.; Tanenbaum, D.M.; Van der Zande, A.M.; McEuen, P.L. Mechanical properties of suspended graphene sheets. J. Vacuum Sci. Technol. B 2007, 25, 2558–2561. [Google Scholar] [CrossRef]
- McCann, E.; Koshino, M. The electronic properties of bilayer graphene. Rep. Prog. Phys. 2013, 76, 056503. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.; Kim, H.; Lee, Y.; Xu, X.; Park, J.; Zheng, Y.; Balakrishnan, J.; Lei, T.; Kim, H.R.; Song, Y.I.; et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nat. Nanotechnol. 2010, 5, 574–578. [Google Scholar] [CrossRef] [Green Version]
- Jung, Y.; Park, K.; Hur, S.; Choi, S.; Kang, S. High-transmittance liquid-crystal displays using graphene conducting layers. Liq. Cryst. 2013, 41, 1–5. [Google Scholar] [CrossRef]
- Shallcross, S.; Sharma, S.; Weber, H.B. Anomalous Dirac point transport due to extended defects in bilayer graphene. Nat. Commun. 2017, 8, 342. [Google Scholar] [CrossRef]
- Kisslinger, F.; Ott, C.; Heide, C.; Kampert, E.; Butz, B.; Spiecker, E.; Shallcross, S.; Weber, H.B. Linear magnetoresistance in mosaic-like bilayer graphene. Nat. Phys. 2015, 11, 650. [Google Scholar] [CrossRef]
- Mirzakhani, M.; Zarenia, M.Z.; Peeters, F.M. Edge states in gated bilayer-monolayer graphene ribbons and bilayer domain walls. J. Appl. Phys. 2018, 123, 204301. [Google Scholar] [CrossRef]
- Stone, A.; Wales, D. Theoretical studies of icosahedral C60 and some related species. Chem. Phys. Lett. 1986, 128, 501–503. [Google Scholar] [CrossRef]
- Meyer, J.C.; Kisielowski, C.; Erni, R.; Rossell, M.D.; Crommie, M.F.; Zettl, A. Direct Imaging of Lattice Atoms and Topological Defects in Graphene Membranes. Nano Lett. 2008, 8, 3582–3586. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Reich, S.; Robertson, J. Defect energies of graphite: Density-functional calculations. Phys. Rev. B 2005, 72, 184109. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.; Staniszewski, J.; Gillespie, J. Tensile behaviors of graphene sheets and carbon nanotubes with multiple Stone–Wales defects. Mater. Sci. Eng. A 2010, 527, 715–723. [Google Scholar] [CrossRef]
- Qin, X.; Meng, Q.; Zhao, W. Effects of Stone–Wales defect upon adsorption of formaldehyde on graphene sheet with or without Al dopant: A first principle study. Surf. Sci. 2011, 605, 930–933. [Google Scholar] [CrossRef]
- Mendez, J.P.; Ariza, M.P. Harmonic model of graphene based on a tight binding interatomic potential. J. Mech. Phys. Solids 2016, 93, 198–223. [Google Scholar] [CrossRef]
- Mendez, J.P.; Arca, F.; Ramos, J.; Ortiz, M.; Ariza, M.P. Charge carrier transport across grain boundaries in graphene. Acta Mater. 2018, 154, 199–206. [Google Scholar] [CrossRef] [Green Version]
- Hashimoto, A.; Suenaga, K.; Gloter, A.; Urita, K.; Iijima, S. Direct evidence for atomic defects in graphene layers. Nature 2004, 430, 870. [Google Scholar] [CrossRef]
- Lehtinen, O.; Kurash, S.; Krasheninnikov, A.; Kaiser, U. Atomic scale study of the life cycle of a dislocation in graphene from birth to annihilation. Nat. Commun. 2013, 4, 2098. [Google Scholar] [CrossRef] [PubMed]
- Warner, J.H.; Margine, E.R.; Mukai, M.; Robertson, A.W.; Giustino, F.; Kirkland, A.I. Dislocation-Driven Deformations in Graphene. Science 2012, 337, 209–212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeong, B.; Ihm, J.; Lee, G. Stability of dislocation defect with two pentagon-heptagon pairs in graphene. Phys. Rev. B 2008, 78, 165403. [Google Scholar] [CrossRef]
- Aizawa, T.; Souda, R.; Otani, S.; Ishizawa, Y.; Oshima, C. Bond softening in monolayer graphite formed on transition-metal carbide surfaces. Phys. Rev. B 1990, 42, 11469–11478. [Google Scholar] [CrossRef] [PubMed]
- Wirtz, L.; Rubio, A. The phonon dispersion of graphite revisited. Solid State Commun. 2004, 131, 141–152. [Google Scholar] [CrossRef] [Green Version]
- Tersoff, J. Empirical Interatomic Potential for Carbon, with Applications to Amorphous Carbon. Phys. Rev. Lett. 1988, 61, 2879–2882. [Google Scholar] [CrossRef] [Green Version]
- Tewary, V.K.; Yang, B. Parametric interatomic potential for graphene. Phys. Rev. B 2009, 79, 075442. [Google Scholar] [CrossRef] [Green Version]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458–9471. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Los, J.H.; Fasolino, A. Intrinsic long-range bond-order potential for carbon: Performance in Monte Carlo simulations of graphitization. Phys. Rev. B 2003, 68, 024107. [Google Scholar] [CrossRef] [Green Version]
- Los, J.H.; Ghiringhelli, L.M.; Meijer, E.J.; Fasolino, A. Improved long-range reactive bond-order potential for carbon. I. Construction. Phys. Rev. B 2005, 72, 214102. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, C. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Siebentritt, S.; Pues, R.; Rieder, K.H.; Shikin, A.M. Surface phonon dispersion in graphite and in a lanthanum graphite intercalation compound. Phys. Rev. B 1997, 55, 7927–7934. [Google Scholar] [CrossRef]
- Oshima, C.; Aizawa, T.; Souda, R.; Ishizawa, Y.; Sumiyoshi, Y. Surface phonon dispersion curves of graphite (0001) over the entire energy region. Solid State Commun. 1988, 65, 1601–1604. [Google Scholar] [CrossRef]
- Nicklow, R.; Wakabayashi, N.; Smith, H.G. Lattice Dynamics of Pyrolytic Graphite. Phys. Rev. B 1972, 5, 4951–4962. [Google Scholar] [CrossRef]
- Yanagisawa, H.; Tanaka, T.; Ishida, Y.; Matsue, M.; Rokuta, E.; Otani, S.; Oshima, C. Analysis of phonons in graphene sheets by means of HREELS measurement and ab initio calculation. Surf. Interface Anal. 2005, 37, 133–136. [Google Scholar] [CrossRef]
- Arca, F. Estudio de defectos topológicos en grafeno mediante un método no lineal basado en el potencial LCBOP. Ph.D. Thesis, University of Seville, Sevilla, Spain, 2019. [Google Scholar]
- Ariza, M.P.; Ortiz, M. Discrete dislocations in graphene. J. Mech. Phys. Solids 2010, 58, 710–734. [Google Scholar] [CrossRef]
- Musgrave, M.J.P. Crystal Acoustics; Introduction to the Study of Elastic Waves and Vibrations in Crystals; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Ariza, M.P.; Ventura, C.; Ortiz, M. Force constants model for graphene from Airebo potential. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 2011, 27, 105–116. [Google Scholar]
- Mura, T. Micromechanics of Defects in Solids; Kluwer Academic Publishers: Boston, MA, USA, 1987. [Google Scholar]
- Ariza, M.P.; Ortiz, M. Discrete Crystal Elasticity and Discrete Dislocations in Crystals. Arch. Ration. Mech. Anal. 2005, 178, 149–226. [Google Scholar] [CrossRef]
- Ariza, M.P.; Serrano, R.; Mendez, J.P.; Ortiz, M. Stacking faults and partial dislocations in graphene. Philos. Mag. 2012, 92, 2004–2021. [Google Scholar] [CrossRef]
- Jain, S.; Barkema, G.; Mousseau, N.; Fang, C.; Huis, M. Strong Long-Range Relaxations of Structural Defects in Graphene Simulated Using a New Semiempirical Potential. J. Phys. Chem. C 2015, 119, 9646–9655. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Alfè, D.; Michaelides, A.; Wang, E. Stone-Wales defects in graphene and other planar sp2-bonded materials. Phys. Rev. B 2009, 80, 033407. [Google Scholar] [CrossRef]
- Jalali, S.; Jomehzadeh, E.; Pugno, N. Influence of out-of-plane defects on vibration analysis of graphene: Molecular Dynamics and Non-local Elasticity approaches. Superlattices Microstruct. 2016, 91, 331–344. [Google Scholar] [CrossRef]
- Chen, S.; Chrzan, D. Continuum theory of dislocations and buckling in graphene. Phys. Rev. 2011, 84, 214103. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, J. Mechanical properties of bilayer graphene with twist and grain boundaries. J. Appl. Phys. 2013, 113, 043514. [Google Scholar] [CrossRef]
- Jiang, B.Y.; Ni, G.X.; Addison, Z.; Shi, J.K.; Liu, X.; Zhao, S.Y.F.; Kim, P.; Mele, E.J.; Basov, D.N.; Fogler, M.M. Plasmon Reflections by Topological Electronic Boundaries in Bilayer Graphene. Nano Lett. 2017, 17, 7080–7085. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoo, H.; Engelke, R.; Carr, S.; Fang, S.; Zhang, K.; Cazeaux, P.; Sung, S.H.; Hovden, R.; Tsen, A.W.; Taniguchi, T.; et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Mater. 2019, 18, 448–453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, S.; Kim, K.; Efimkin, D.K.; Lovorn, T.; Taniguchi, T.; Watanabe, K.; MacDonald, A.H.; Tutuc, E.; LeRoy, B.J. Topologically Protected Helical States in Minimally Twisted Bilayer Graphene. Phys. Rev. Lett. 2018, 121, 037702. [Google Scholar] [CrossRef] [Green Version]











| [25] | [27] | [38] | [40] | [18] | Present Work | |
|---|---|---|---|---|---|---|
| 399.0 | 409.7 | 364.0 | 527.7 | 497.2 | 423.6 | |
| 135.7 | 145.0 | 247.0 | 68.1 | 173.7 | 144.3 | |
| 292.8 | 98.9 | 100.5 | 118.3 | 106.9 | 75.7 | |
| −79.6 | −40.8 | −30.8 | 5.8 | −41.43 | −6.5 | |
| 67.8 | 74.2 | 72.3 | 32.7 | 58.1 | 29.9 | |
| 39.2 | −9.1 | −17.8 | 26.7 | −3.0 | −23.7 | |
| 0.9 | −8.2 | −11.5 | −16.9 | −15.9 | −8.8 | |
| 0.0 | −33.2 | 0.0 | −20.64 | 4.0 | ||
| 0.0 | 50.1 | 0.0 | 34.51 | −0.8 | ||
| −34.3 | 5.8 | 3.7 | 9.1 | −0.8 | ||
| 0.0 | 10.5 | 0.0 | 0.3 | |||
| 0.0 | 5.0 | 0.0 | 0.0 | |||
| 0.0 | 2.2 | 0.0 | 0.1 | |||
| 0.0 | −2.2 | 0.0 | 0.1 | |||
| 17.1 | −5.2 | −1.8 | 0.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arca, F.; Mendez, J.P.; Ortiz, M.; Ariza, P. Steric Interference in Bilayer Graphene with Point Dislocations. Nanomaterials 2019, 9, 1012. https://doi.org/10.3390/nano9071012
Arca F, Mendez JP, Ortiz M, Ariza P. Steric Interference in Bilayer Graphene with Point Dislocations. Nanomaterials. 2019; 9(7):1012. https://doi.org/10.3390/nano9071012
Chicago/Turabian StyleArca, Francisco, Juan Pedro Mendez, Michael Ortiz, and Pilar Ariza. 2019. "Steric Interference in Bilayer Graphene with Point Dislocations" Nanomaterials 9, no. 7: 1012. https://doi.org/10.3390/nano9071012
APA StyleArca, F., Mendez, J. P., Ortiz, M., & Ariza, P. (2019). Steric Interference in Bilayer Graphene with Point Dislocations. Nanomaterials, 9(7), 1012. https://doi.org/10.3390/nano9071012





