Porous Silicon Bragg Reflector and 2D Gold-Polymer Nanograting: A Route Towards a Hybrid Optoplasmonic Platform
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Porous Silicon Photonic Crystals
2.2. Preparation of Plasmonic Nanostructured Surfaces
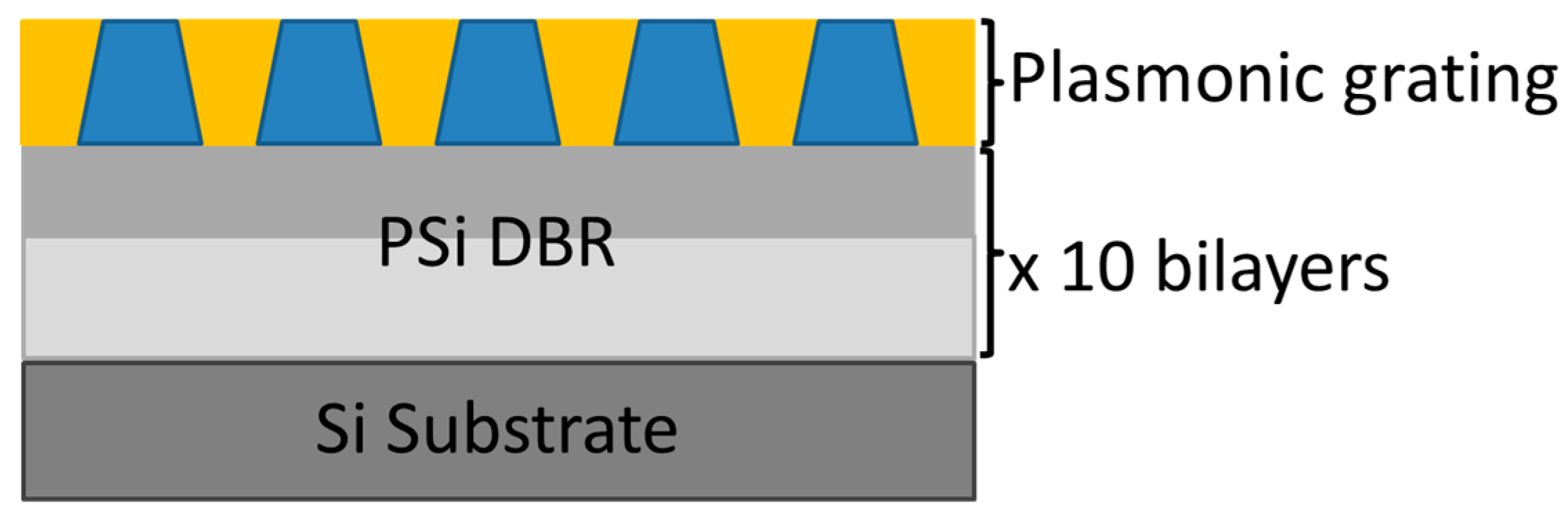
2.3. Preparation of Hybrid Plasmonic–Photonic Structures
2.4. Characterization of the Structures
2.5. Polyelectrolyte Probing
3. Results and Discussion
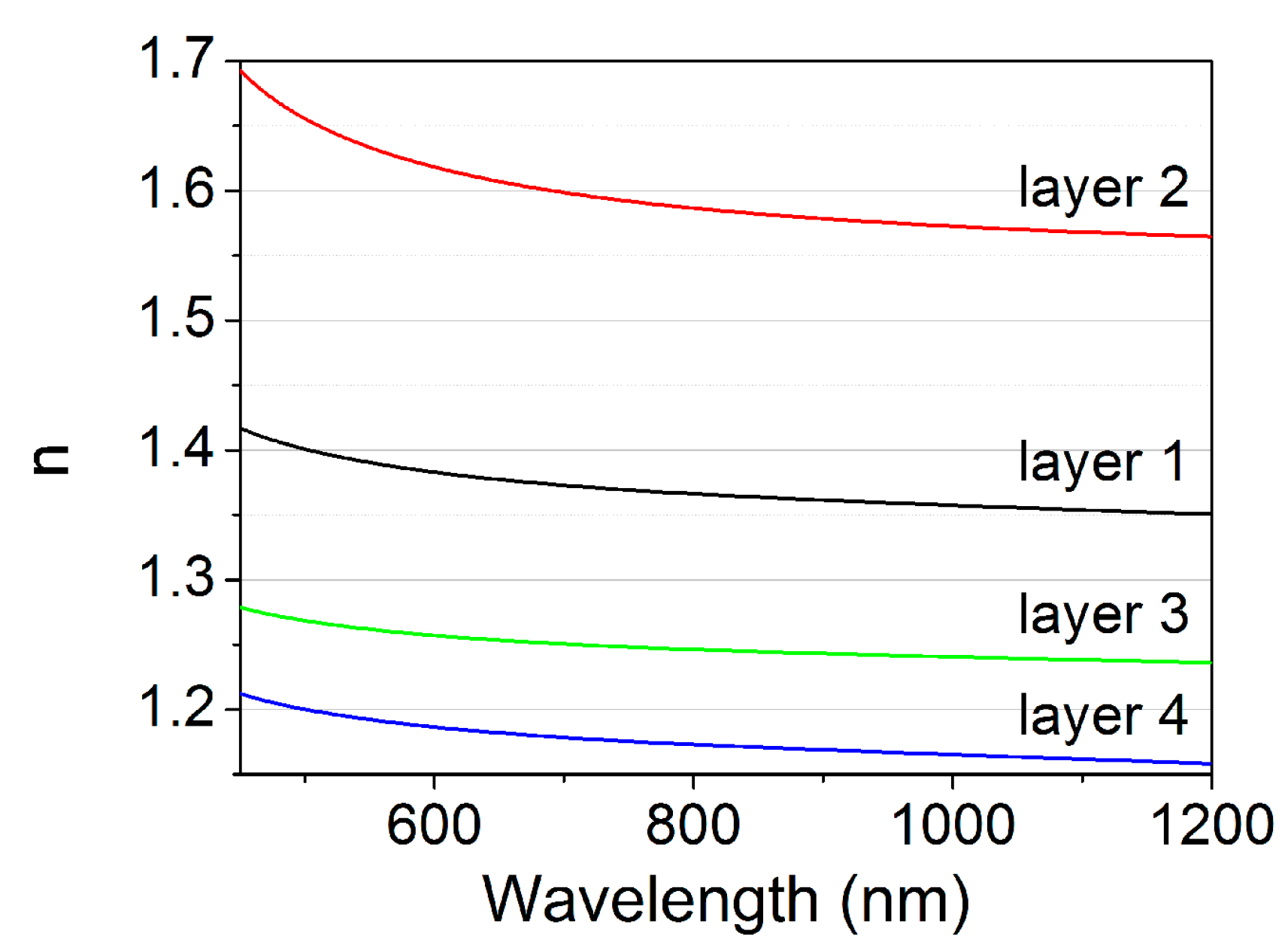
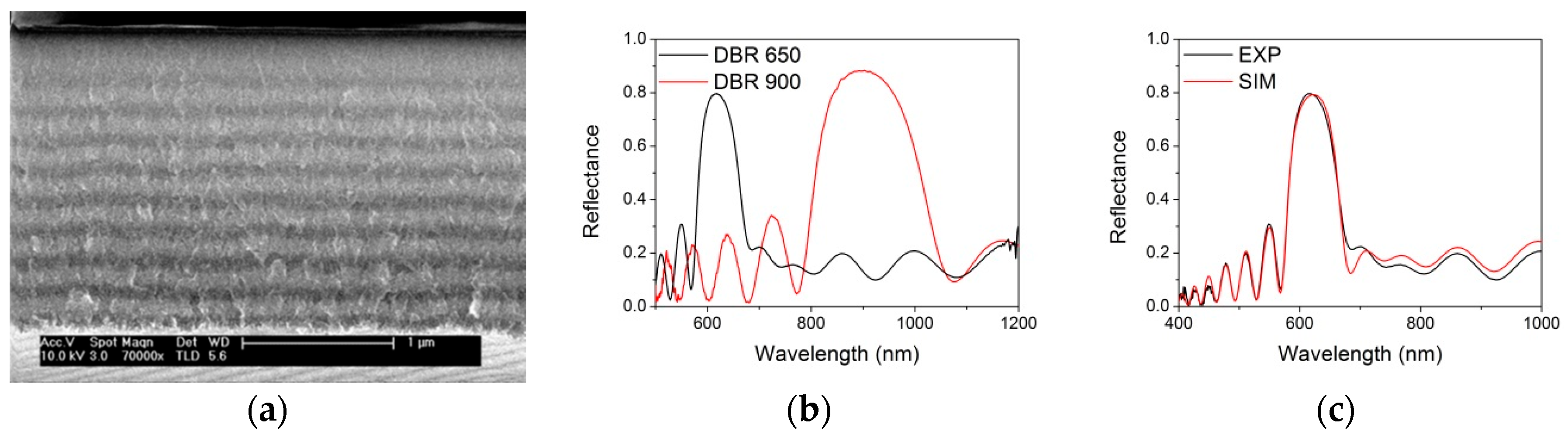
3.1. Porous Silicon Photonic Crystals
3.2. Porous Silicon Photonic Crystals
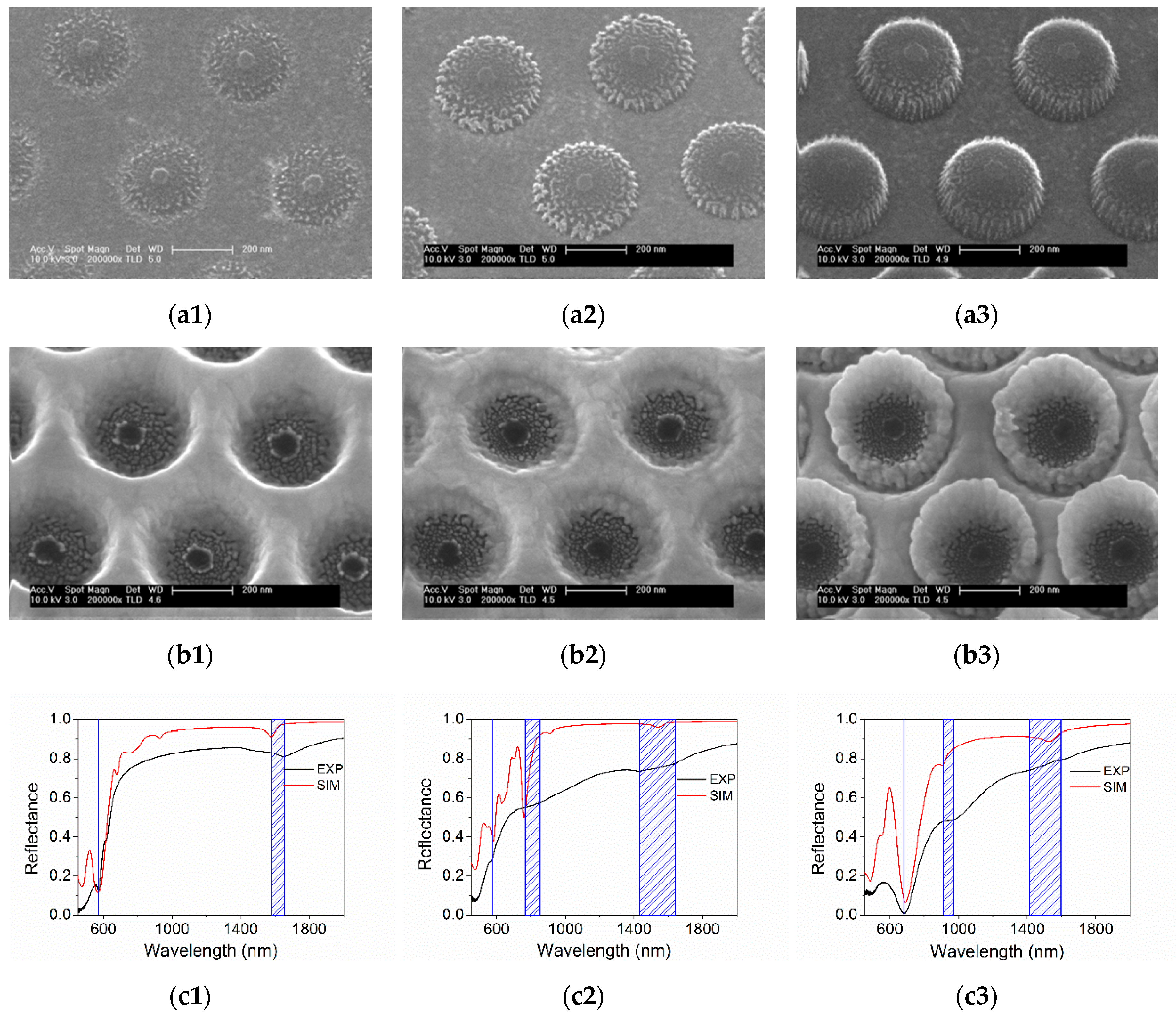
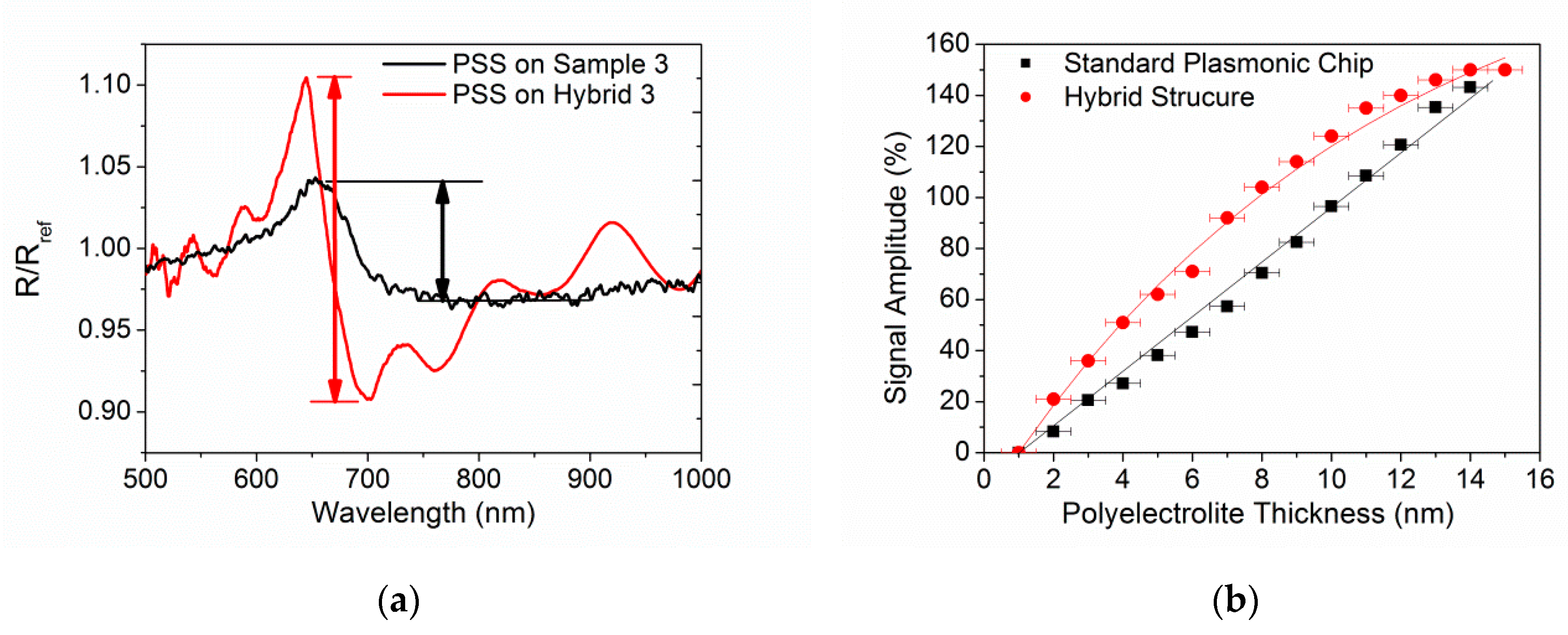
3.3. Hybrid Plasmonic–Photonic Structure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B

| Parameter | Sample 1 | Sample 2 | Sample 3 |
|---|---|---|---|
| h1 | 150 | 150 | 150 |
| h2 | 40 | 70 | 110 |
| h3 | 10 | 30 | 40 |
| h4 | 110 | 30 | 40 |
| h5 | 30 | ||
| D1 | 300 | 320 | 340 |
| D2 | 200 | 260 | 260 |
| D3 | 330 | 180 | 340 |
| D4 | 320 | ||
| Rint | 340 | ||
| Rext | 420 |
References
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Park, J.E.; Kim, J.; Nam, J.M. Emerging plasmonic nanostructures for controlling and enhancing photoluminescence. Chem. Sci. 2017, 8, 4696–4704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brolo, A.G.; Gordon, R.; Leathem, B.; Kavanagh, K.L. Surface plasmon sensor based on the enhanced light transmission through arrays of nanoholes in gold films. Langmuir 2004, 20, 4813–4815. [Google Scholar] [CrossRef] [PubMed]
- Gillibert, R.; Sarkar, M.; Bryche, J.F.; Yasukuni, R.; Moreau, J.; Besbes, M.; Barbillon, G.; Bartenlian, B.; Canva, M.; Lamy de La Chapelle, M. Directional surface enhanced Raman scattering on gold nano-gratings. Nanotechnology 2016, 27, 115202. [Google Scholar] [CrossRef] [PubMed]
- Kauranen, M.; Zayats, A.V. Nonlinear plasmonics. Nat. Photonics 2012, 6, 737–748. [Google Scholar] [CrossRef]
- Wang, W.; Ramezani, M.; Väkeväinen, A.I.; Törmä, P.; Gómez Rivas, J.; Odom, T.W. The rich photonic world of plasmonic nanoparticle arrays. Mater. Today 2018, 21, 303–314. [Google Scholar] [CrossRef]
- Rodrigo, D.; Tittl, A.; John-Herpin, A.; Limaj, O.; Altug, H. Self-Similar Multiresonant Nanoantenna Arrays for Sensing from Near- to Mid-Infrared. ACS Photonics 2018, 5, 4903–4911. [Google Scholar] [CrossRef]
- Munday, J.N.; Atwater, H.A. Large Integrated Absorption Enhancement in Plasmonic Solar Cells by Combining Metallic Gratings and Antireflection Coatings. Nano Lett. 2011, 11, 2195–2201. [Google Scholar] [CrossRef]
- Wen, L.; Sun, F.; Chen, Q. Cascading Metallic Gratings for Broadband Absorption Enhancement in Ultrathin Plasmonic Solar Cells. Appl. Phys. Lett. 2014, 104, 151106. [Google Scholar] [CrossRef]
- Jang, Y.H.; Jang, Y.J.; Kim, S.; Quan, L.N.; Chung, K.; Kim, D.H. Plasmonic Solar Cells: From Rational Design to Mechanism Overview. Chem. Rev. 2016, 116, 14982–15034. [Google Scholar] [CrossRef] [PubMed]
- Enrichi, F.; Quandt, A.; Righini, G.C. Plasmonic enhanced solar cells: Summary of possible strategies and recent results. Renew. Sustain. Energy Rev. 2018, 82, 2433–2439. [Google Scholar] [CrossRef]
- Wu, X.; Hao, C.; Kumar, J.; Kuang, H.; Kotov, N.A.; Liz-Marzán, L.M.; Xu, C. Environmentally responsive plasmonic nanoassemblies for biosensing. Chem. Soc. Rev. 2018, 47, 4677–4696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mejía-Salazar, J.R.; Oliveira, O.N. Plasmonic Biosensing. Chem. Rev. 2018, 118, 10617–10625. [Google Scholar] [CrossRef] [PubMed]
- Bog, U.; Huska, K.; Maerkle, F.; Nesterov-Mueller, A.; Lemmer, U.; Mappes, T. Design of Plasmonic Grating Structures towards Optimum Signal Discrimination for Biosensing Applications. Opt. Express 2012, 20, 11357–11369. [Google Scholar] [CrossRef] [PubMed]
- Dhawan, A.; Canva, M.; Vo-Dinh, T. Narrow Groove Plasmonic Nano-Gratings for Surface Plasmon Resonance Sensing. Opt. Express 2011, 19, 787–813. [Google Scholar] [CrossRef]
- Kuo, W.K.; Chang, C.H.; Wu, C.J.; Yu, H.H. Phase Detection-Sensitivity Enhancement of Grating-Coupled Surface Plasmon Resonance Sensor with Light Incident at Nonzero Azimuth Angle. J. Nanophoton. 2012, 6, 063524. [Google Scholar] [CrossRef]
- Giudicatti, S.; Valsesia, A.; Marabelli, F.; Colpo, P.; Rossi, F. Plasmonic resonances in nanostructured gold/polymer surfaces by colloidal lithography. Phys. Status Solidi A 2010, 207, 935–942. [Google Scholar] [CrossRef]
- Bottazzi, B.; Fornasari, L.; Frangolho, A.; Giudicatti, S.; Mantovani, A.; Marabelli, F.; Marchesini, G.; Pellacani, P.; Therisod, R.; Valsesia, A. Multiplexed label-free optical biosensor for medical diagnostics. J. Biomed. Opt. 2014, 19, 017006. [Google Scholar] [CrossRef]
- Carpignano, F.; Bombera, R.; Frangolho, A.; Pellacani, P.; Fornasari, L.; Schafer-Nielsen, C.; Marabelli, F.; Marchesini, G.; Colpo, P. Nanoplasmonic platform for multiparametric and high throughput biosensing. In Proceedings of the 18th Italian National Conference on Photonic Technologies (Fotonica 2016), Rome, Italy, 6–8 June 2016. [Google Scholar]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Gal, M.; Reece, P.J.; Zheng, W.; Lerondel, G. Porous silicon: A versatile optical material. In Proceedings of the Microelectronics, Mems, and Nanotechnology, Perth, Australia, 10–12 December 2003. [Google Scholar] [CrossRef]
- Lehmann, V.; Gösele, U. Porous silicon formation: A quantum wire effect. Appl. Phys. Lett. 1991, 58, 856–858. [Google Scholar] [CrossRef]
- Frohnhoff, S.; Berger, M.G. Porous silicon superlattices. Adv. Mater. 1994, 6, 963–965. [Google Scholar] [CrossRef]
- Vincent, G. Optical properties of porous silicon superlattices. Appl. Phys. Lett. 1994, 64, 2367–2369. [Google Scholar] [CrossRef]
- Lorenzo, E.; Oton, C.J.; Capuj, N.E.; Ghulinyan, M.; Navarro-Urrios, D.; Gaburro, Z.; Pavesi, L. Porous silicon-based rugate filters. Appl. Opt. 2005, 44, 5415–5421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ilyas, S.; Böcking, T.; Kilian, K.; Reece, P.J.; Gooding, J.; Gaus, K.; Gal, M. Porous silicon based narrow line-width rugate filters. Opt. Mater. 2007, 29, 619–622. [Google Scholar] [CrossRef]
- Pellegrini, V.; Tredicucci, A.; Mazzoleni, C.; Pavesi, L. Enhanced optical properties in porous silicon microcavities. Phys. Rev. B 1995, 52, R14328–R14331. [Google Scholar] [CrossRef] [PubMed]
- Krueger, N.A.; Holsteen, A.L.; Kang, S.-K.; Ocier, C.R.; Zhou, W.; Mensing, G.; Rogers, J.A.; Brongersma, M.L.; Braun, P.V. Porous Silicon Gradient Refractive Index Micro-Optics. Nano Lett. 2016, 16, 7402–7407. [Google Scholar] [CrossRef] [PubMed]
- Pacholski, C. Photonic Crystal Sensors Based on Porous Silicon. Sensors 2013, 13, 4694–4713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Gaur, G.; Retterer, S.T.; Laibinis, P.E.; Weiss, S.M. Flow-Through Porous Silicon Membranes for Real-Time Label-Free Biosensing. Anal. Chem. 2016, 88, 10940–10948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Jia, Z.; Lv, G.; Wen, H.; Li, P.; Zhang, H.; Wang, J. Detection of Echinococcus granulosus antigen by a quantum dot/porous silicon optical biosensor. Biomed. Opt. Express 2017, 8, 3458–3469. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.H.; Pei, Y.; Zhang, D.; Li, Y.; Kilian, K.A. Patterned porous silicon photonic crystals with modular surface chemistry for spatial control of neural stem cell differentiation. Nanoscale 2016, 8, 10891–10895. [Google Scholar] [CrossRef] [PubMed]
- Zhong, F.; Wu, Z.; Guo, J.; Jia, D. Porous Silicon Photonic Crystals Coated with Ag Nanoparticles as Efficient Substrates for Detecting Trace Explosives Using SERS. Nanomaterials 2018, 8, 872. [Google Scholar] [CrossRef] [PubMed]
- Arshavsky-Graham, S.; Massad-Ivanir, N.; Segal, E.; Weiss, S. Porous Silicon-Based Photonic Biosensors: Current Status and Emerging Applications. Anal. Chem. 2019, 91, 441–467. [Google Scholar] [CrossRef]
- Rodriguez, C.; Torres Costa, V.; Ahumada, O.; Cebrián, V.; Gómez-Abad, C.; Díaz, A.; Manso Silván, M. Gold nanoparticle triggered dual optoplasmonic-impedimetric sensing of prostate-specific antigen on interdigitated porous silicon platforms. Sens. Actuator B Chem. 2018, 267, 559–564. [Google Scholar] [CrossRef] [Green Version]
- Oulton, R.F.; Sorger, V.J.; Genov, D.A.; Pile, D.F.P.; Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photonics 2008, 2, 496–500. [Google Scholar] [CrossRef] [Green Version]
- De Angelis, F.; Patrini, M.; Das, G.; Maksymov, I.; Galli, M.; Businaro, L.; Andreani, L.C.; Di Fabrizio, E. A hybrid plasmonic− photonic nanodevice for label-free detection of a few molecules. Nano Lett. 2008, 8, 2321–2327. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Chamanzar, M.; Apuzzo, A.; Salas-Montiel, R.; Nguyen, K.N.; Blaize, S.; Adibi, A. On-Chip Hybrid Photonic–Plasmonic Light Concentrator for Nanofocusing in an Integrated Silicon Photonics Platform. Nano Lett. 2015, 15, 849–856. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-N.; Huang, Q.; Liu, K.-K.; Singamaneni, S.; Cunningham, B.T. Nanoantenna–Microcavity Hybrids with Highly Cooperative Plasmonic–Photonic Coupling. Nano Lett. 2017, 17, 7569–7577. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, F. Hybrid plasmonic-photonic resonators. In Proceedings of the SPIE Photonics Europe Nanophotonics VII, Strasbourg, France, 23 May 2018; Volume 106720. [Google Scholar] [CrossRef]
- Mirlou, F.; Soofi, H. Hybrid Plasmonic–Photonic–Organic Modulators With Low Insertion Loss and High Modulation Depth. J. Lightwave Technol. 2018, 36, 2471–2477. [Google Scholar] [CrossRef]
- Bozzola, A.; Perotto, S.; De Angelis, F. Hybrid plasmonic–photonic whispering gallery mode resonators for sensing: A critical review. Analyst 2017, 142, 883–898. [Google Scholar] [CrossRef]
- Barth, M.; Schietinger, S.; Fischer, S.; Becker, J.; Nüsse, N.; Aichele, T.; Löchel, B.; Sönnichsen, C.; Benson, O. Nanoassembled Plasmonic-Photonic Hybrid Cavity for Tailored Light-Matter Coupling. Nano Lett. 2010, 10, 891–895. [Google Scholar] [CrossRef]
- Conteduca, D.; Reardon, C.; Scullion, M.G.; Dell’Olio, F.; Armenise, M.N.; Krauss, T.F.; Ciminelli, C. Ultra-high Q/V hybrid cavity for strong light-matter interaction. APL Photonics 2017, 2, 086101. [Google Scholar] [CrossRef] [Green Version]
- Vasa, P.; Lienau, C. Strong Light–Matter Interaction in Quantum Emitter/Metal Hybrid Nanostructures. ACS Photonics 2018, 5, 2–23. [Google Scholar] [CrossRef]
- Khokhlov, N.E.; Prokopov, A.R.; Shaposhnikov, A.N.; Berzhansky, V.N.; Kozhaev, M.A.; Andreev, S.N.; Ravishankar, A.P.; Gopal, A.V.; Bykov, D.A.; Zvezdin, A.K. Photonic crystals with plasmonic patterns: Novel type of the heterostructures for enhanced magneto-optical activity. J. Phys. D Appl. Phys. 2015, 48, 095001. [Google Scholar] [CrossRef]
- Badugu, R.; Descrovi, E.; Lakowicz, J. Radiative decay engineering 7: Tamm state-coupled emission using a hybrid plasmonic–photonic structure. Anal. Biochem. 2014, 445, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Frimmer, M.; Koenderink, F. Spontaneous Emission Control in a Tunable Hybrid Photonic System. Phys. Rev. Lett. 2013, 110, 217405. [Google Scholar] [CrossRef]
- Dezfouli, M.K.; Gordon, R.; Hughes, S. Modal theory of modified spontaneous emission of a quantum emitter in a hybrid plasmonic photonic-crystal cavity system. Phys. Rev. A 2017, 95, 013846. [Google Scholar] [CrossRef] [Green Version]
- Lan, Y.; Wang, S.; Yin, X.; Liang, Y.; Dong, H.; Gao, N.; Li, J.; Wang, H.; Li, G. 2D-ordered dielectric sub-micron bowls on a metal surface: A useful hybrid plasmonic–photonic structure. Nanoscale 2016, 8, 13454–13462. [Google Scholar] [CrossRef] [PubMed]
- Hameed, M.F.O.; Saadeldin, A.S.; Elkaramany, E.M.A.; Obayya, S.S.A. Label-Free Highly Sensitive Hybrid Plasmonic Biosensor for the Detection of DNA Hybridization. J. Lightwave Technol. 2017, 35, 4851–4858. [Google Scholar] [CrossRef]
- Zhu, S.; Li, H.; Yang, M.; Pang, S.W. Highly sensitive detection of exosomes by 3D plasmonic photonic crystal biosensor. Nanoscale 2018, 10, 19927–19936. [Google Scholar] [CrossRef] [PubMed]
- Manso Silván, M.; Arroyo Hernández, M.; Torres Costa, V.; Martín Palma, R.J.; Martínez Duart, J.M. Structured porous silicon sub-micrometer wells grown by colloidal lithography. Europhys. Lett. 2006, 76, 690–695. [Google Scholar] [CrossRef]
- Torres-Costa, V.; Martin-Palma, R.J.; Martinez-Duart, J.M. Optical characterization of porous silicon films and multilayer filters. J. Appl. Phys. A 2004, 79, 1919–1923. [Google Scholar] [CrossRef]
- Gedig, E.T. Handbook of Surface Plasmon Resonance, 2nd ed.; Richard, B.M.S., Ed.; The Royal Society of Chemistry: London, UK, 2017; p. 176. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellacani, P.; Fornasari, L.; Rodriguez, C.; Torres-Costa, V.; Marabelli, F.; Manso Silván, M. Porous Silicon Bragg Reflector and 2D Gold-Polymer Nanograting: A Route Towards a Hybrid Optoplasmonic Platform. Nanomaterials 2019, 9, 1017. https://doi.org/10.3390/nano9071017
Pellacani P, Fornasari L, Rodriguez C, Torres-Costa V, Marabelli F, Manso Silván M. Porous Silicon Bragg Reflector and 2D Gold-Polymer Nanograting: A Route Towards a Hybrid Optoplasmonic Platform. Nanomaterials. 2019; 9(7):1017. https://doi.org/10.3390/nano9071017
Chicago/Turabian StylePellacani, Paola, Lucia Fornasari, Chloé Rodriguez, Vicente Torres-Costa, Franco Marabelli, and Miguel Manso Silván. 2019. "Porous Silicon Bragg Reflector and 2D Gold-Polymer Nanograting: A Route Towards a Hybrid Optoplasmonic Platform" Nanomaterials 9, no. 7: 1017. https://doi.org/10.3390/nano9071017






