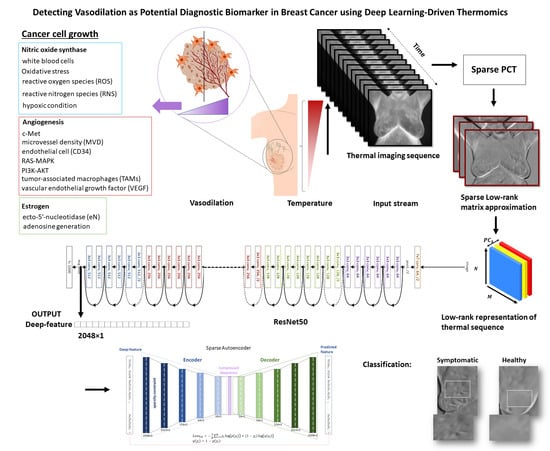
Detecting Vasodilation as Potential Diagnostic Biomarker in Breast Cancer Using Deep Learning-Driven Thermomics
Abstract
:1. Introduction
2. Thermography and Biological Rationale as an Alternative Imaging Modality
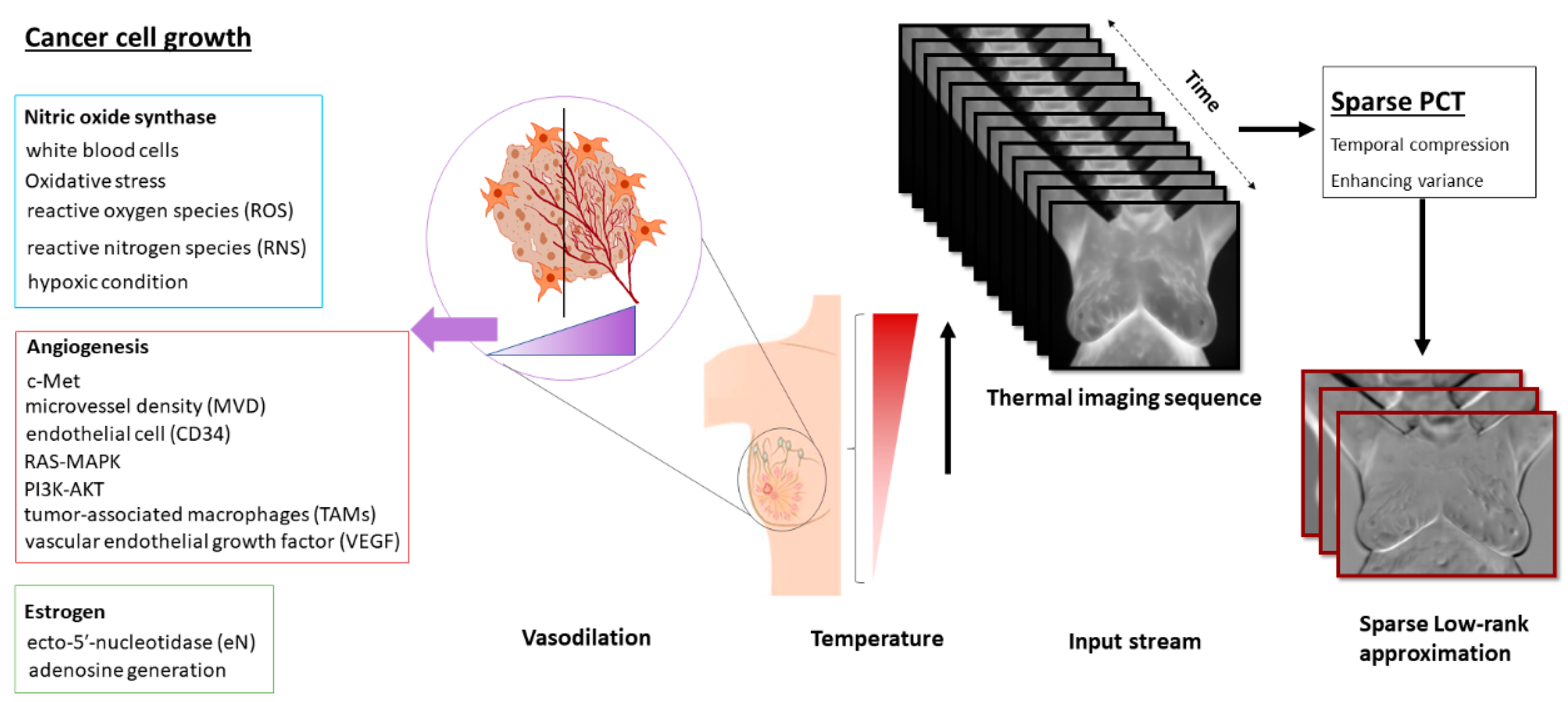
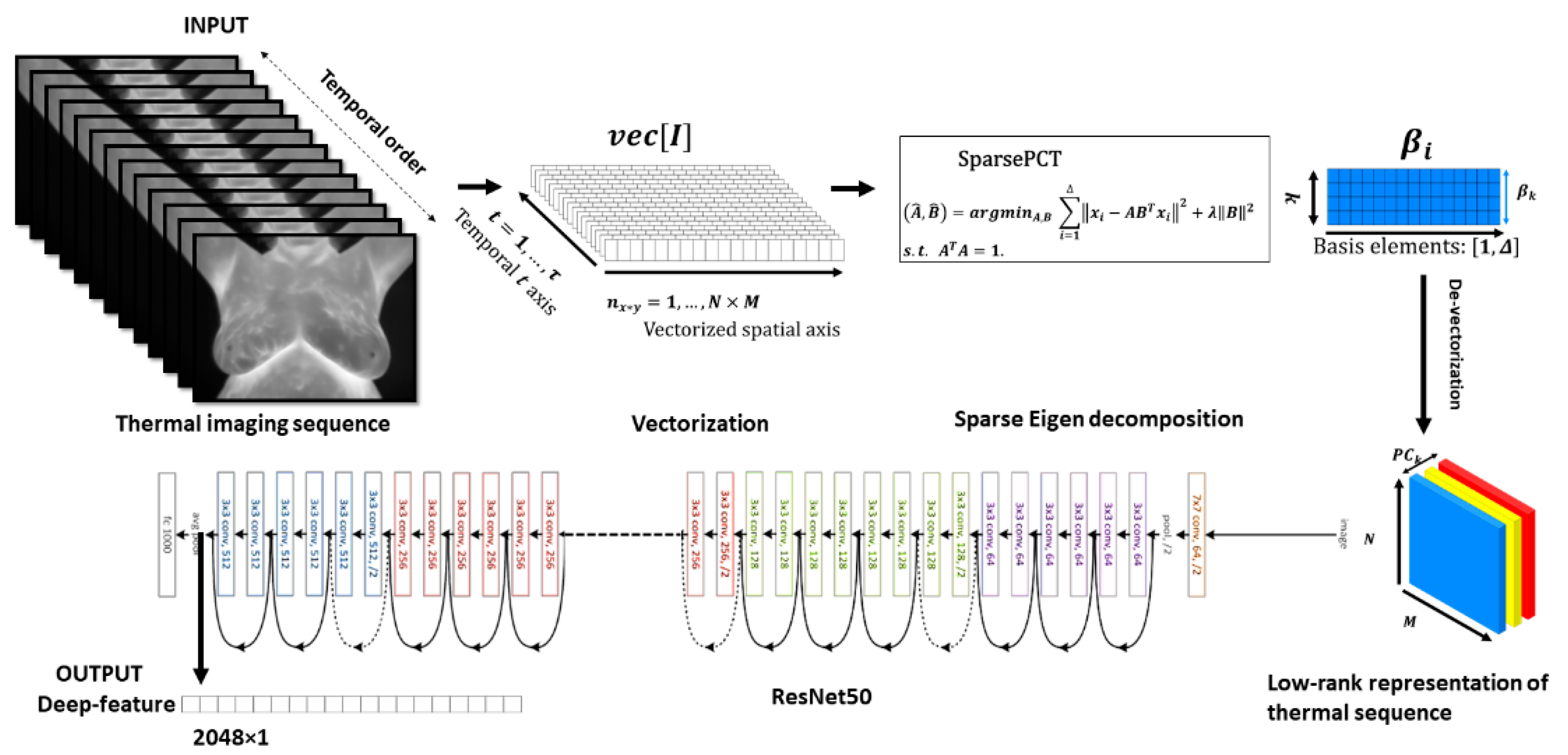
- The sparse principal component analysis in the thermography (Sparse PCT) is used to compress the input thermal sequence and capture high temporal variance across the acquisitions. This leads to capture thermal heterogeneity patterns in three first initial bases, called avatars, which concatenate in three different channels similar to a red, green and blue (RGB) image as the input for our pretrained model.
- Deep thermal features, called deep-thermomics inspired by radiomics, are extracted to measure thermal heterogeneity in breast cancer screening using infrared thermography.
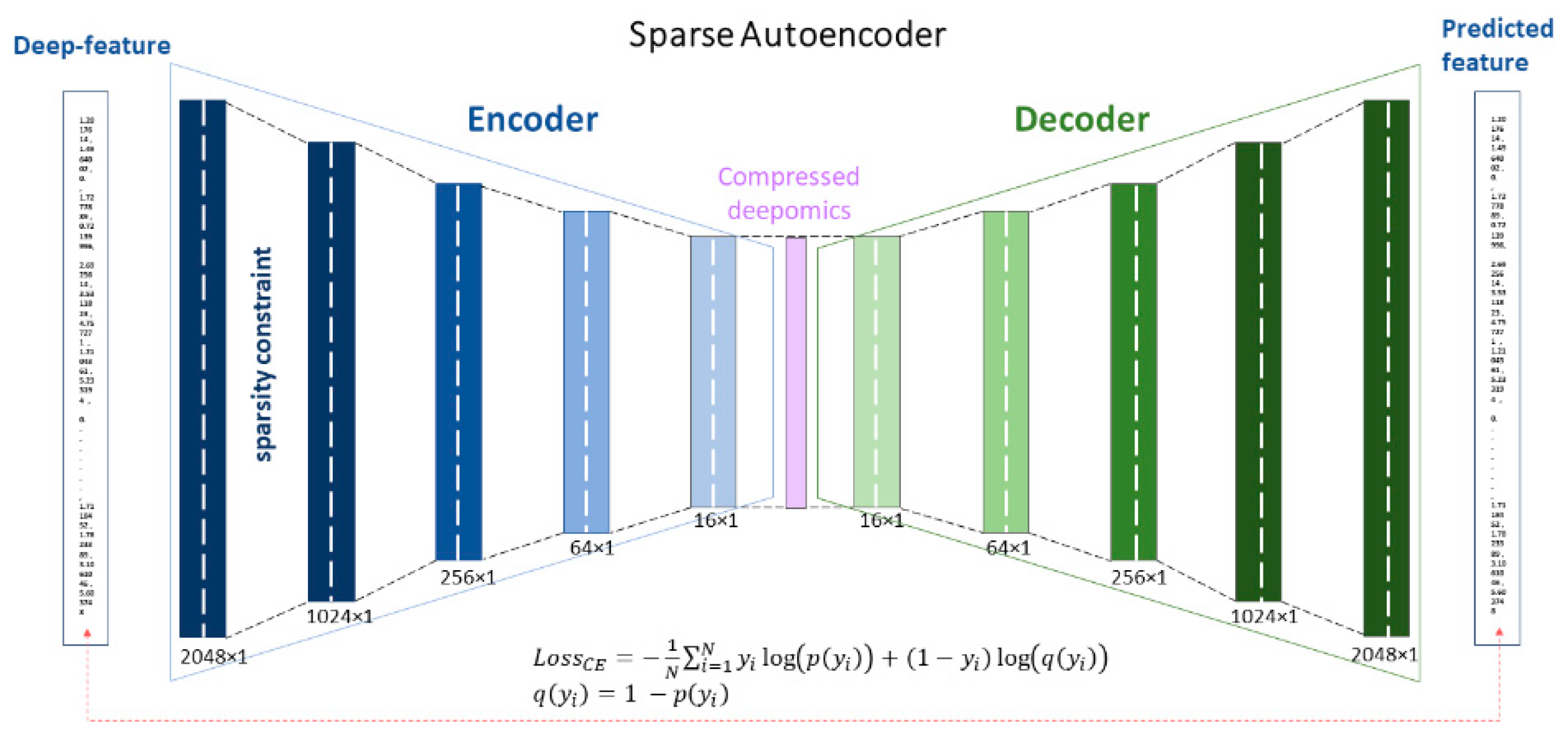
- The proposed approach tackles the problem of the curse of dimensionality in deep-thermomics using a sparse deep autoencoder without using traditional human-engineered feature selection methods.
- The multivariate models trained and validated using the obtained descriptors successfully classify between symptomatic and non-symptomatic subjects. We also provided a comparative analysis using a non-sparse PCT.
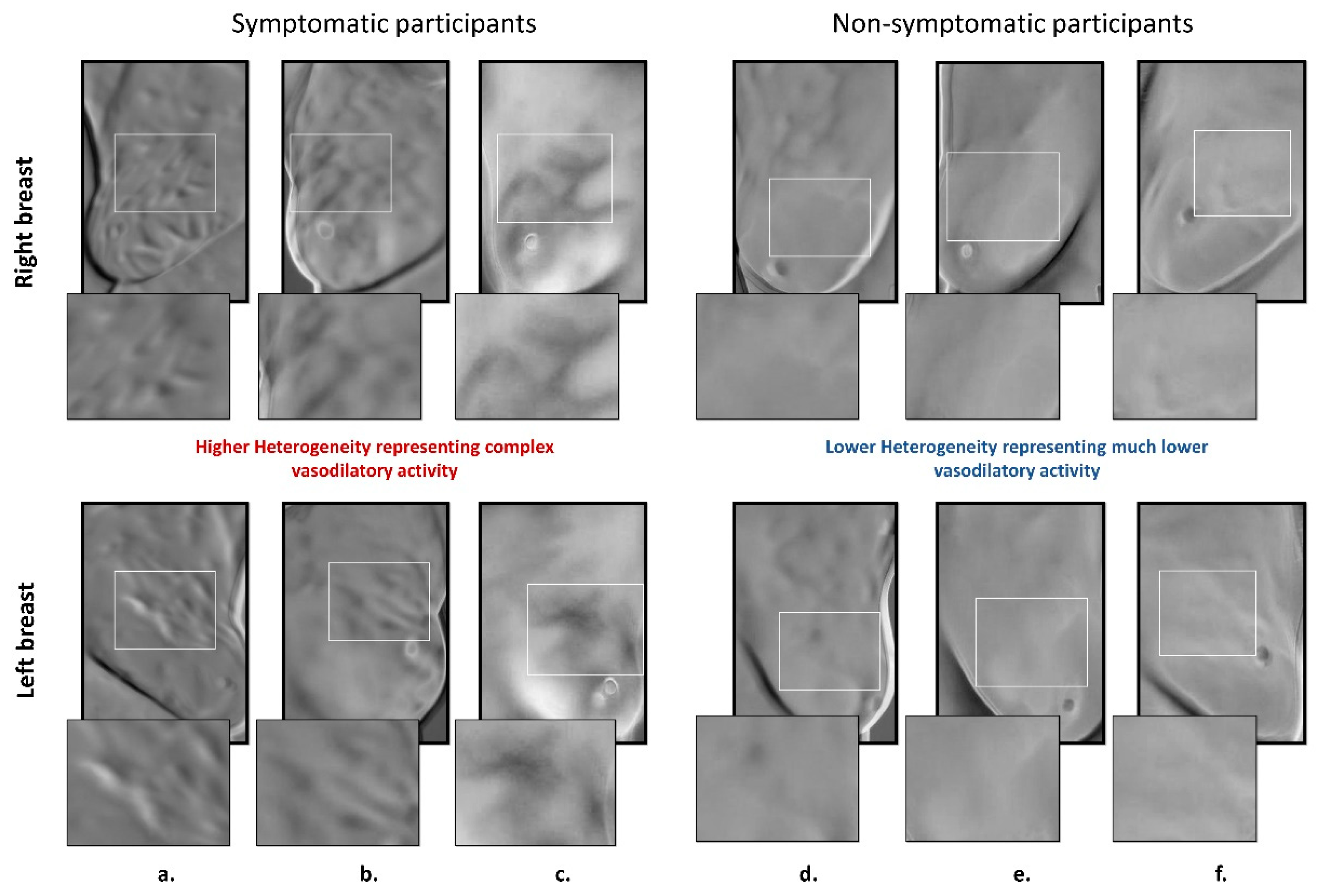
- This study shows the association between thermal heterogeneous patterns and potential vasodilation in the breast area, as a new potential imaging biomarker.
3. Thermal Transfer in Thermography
4. Methodology
4.1. Low-Rank Approximation of Thermal Stream
4.2. Deep Thermomics
4.3. Sparse Autoencoder for Dimensionality Reduction for Deep Thermomics
5. Results
5.1. Patient Population and Infrared Breast Cancer Study Data
5.2. Results of Low-Rank Sparse PCT (Principal Component Analysis)
5.3. Deep-Thermomic Features
5.4. Result of the Sparse Autoencoder and Dimensionality Reduction
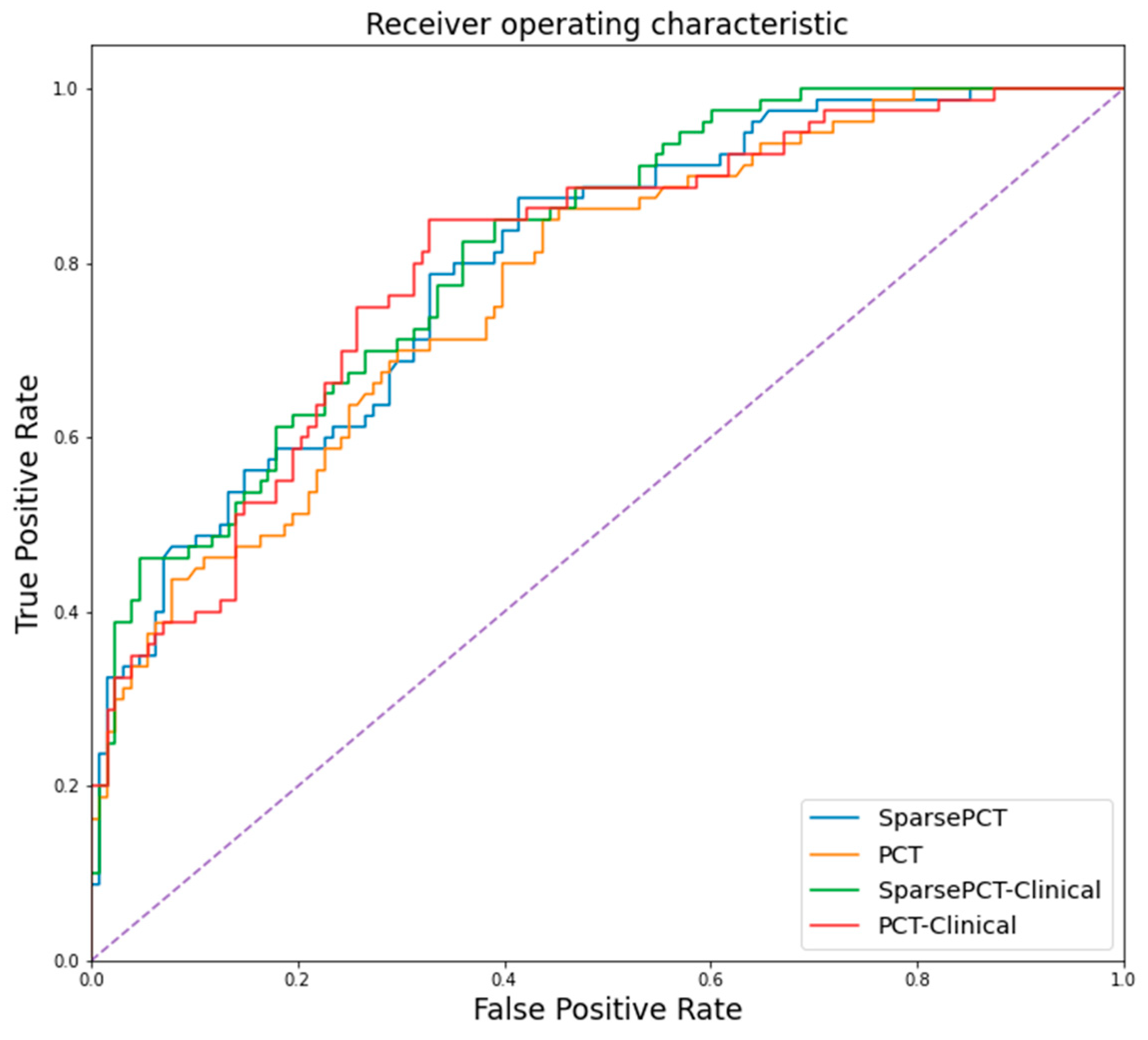
5.5. Result of Random Forest Classification of Symptomatic and Non-Symptomatic Participants
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2019. CA Cancer J. Clin. 2019, 69, 7–34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crystal, P.; Strano, S.D.; Shcharynski, S.; Koretz, M.J. Using Sonography to Screen Women with Mammographically Dense Breasts. Am. J. Roentgenol. 2003, 181, 177–182. [Google Scholar] [CrossRef] [Green Version]
- Kerlikowske, K.; Grady, D.; Barclay, J.; Sickles, E.A.; Ernster, V. Effect of age, breast density, and family history on the sensitivity of first screening mammography. JAMA 1996, 276, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Song, S.Y.; Park, B.; Suh, M.; Choi, K.S.; Jung, S.E.; Kim, M.J.; Lee, E.H.; Lee, C.W.; Jun, J.K. Effect of Digital Mammography for Breast Cancer Screening: A Comparative Study of More than 8 Million Korean Women. Radiology 2020, 294, 247–255. [Google Scholar] [CrossRef]
- Kennedy, D.A.; Lee, T.; Seely, D. A comparative review of thermography as a breast cancer screening technique. Integr. Cancer Ther. 2009, 8, 9–16. [Google Scholar] [CrossRef]
- Fletcher, S.W.; Elmore, J.G. Mammographic Screening for Breast Cancer. N. Engl. J. Med. 2003, 348, 1672–1680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osako, T.; Iwase, T.; Takahashi, K.; Lijima, K.; Miyagi, Y.; Nishimura, S.; Tada, K.; Makita, M.; Akiyama, F.; Sakamoto, G.; et al. Diagnostic mammography and ultrasonography for palpable and nonpalpable breast cancer in women aged 30 to 39 years. Breast Cancer 2007, 14, 255–259. [Google Scholar] [CrossRef] [PubMed]
- Duffy, S.W.; Vulkan, D.; Cuckle, H.; Parmar, D.; Sheikh, S.; Smith, R.A.; Evans, A.; Blyuss, O.; Johns, L.; Ellis, I.O.; et al. Effect of mammographic screening from age 40 years on breast cancer mortality (UK Age trial): Final results of a randomised, controlled trial. Lancet Oncol. 2020, 21, 1165–1172. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Nguyen, N.T.; Dixon III, L.; Monetto, F.E.P.; Robinson, A.S. Spontaneously Disappearing Calcifications in the Breast: A Rare Instance Where a Decrease in Size on Mammogram Is Not Good. Cureus 2020, 12, e8753. [Google Scholar] [CrossRef]
- De González, A.B.; Reeves, G. Mammographic screening before age 50 years in the UK: Comparison of the radiation risks with the mortality benefits. Br. J. Cancer 2005, 93, 590–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoekstra, P. Quantitive digital thermology: 21st century imaging systems. In Proceedings of the OAND Conference, Hamilton, ON, Canada, 18–21 June 2001. [Google Scholar]
- Law, J.; Faulkner, K.; Young, K.C. Risk factors for induction of breast cancer by X-rays and their implications for breast screening. Br. J. Radiol. 2007, 80, 261–266. [Google Scholar] [CrossRef] [PubMed]
- Hendrick, R.E. Radiation Doses and Risks in Breast Screening. J. Breast Imaging 2020, 2, 188–200. [Google Scholar] [CrossRef]
- Chowdhury, A.S.; Tamanna, S. Radiation-induced side effects in breast cancer patients and factors affecting them. Asian J. Med Biol. Res. 2020, 6, 138–148. [Google Scholar] [CrossRef]
- Nelson, H.D.; Pappas, M.; Cantor, A.; Griffin, J.; Daeges, M.; Humphrey, L. Harms of breast cancer screening: Systematic review to update the 2009 US Preventive Services Task Force recommendation. Ann. Intern. Med. 2016, 164, 256–267. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, U.; Das, D.; Banerjee, R.K. Reactive oxygen species: Oxidative damage and pathogenesis. Curr. Sci. 1999, 77, 658–666. [Google Scholar]
- Yang, Y.; Bazhin, A.V.; Werner, J.; Karakhanova, S. Reactive Oxygen Species in the Immune System. Int. Rev. Immunol. 2013, 32, 249–270. [Google Scholar] [CrossRef]
- Friedenson, B. Is mammography indicated for women with defective BRCA genes? Implications of recent scientific advances for the diagnosis, treatment, and prevention of hereditary breast cancer. MedGenMed 2000, 2, E9. [Google Scholar] [PubMed]
- Narod, S.A.; Lubinski, J.; Ghadirian, P.; Lynch, H.T.; Moller, P.; Foulkes, W.; Rosen, B.; Kim-Sing, C.; Isaacs, C.; Domcheck, S.; et al. Screening mammography and risk of breast cancer in BRCA1 and BRCA2 mutation carriers: A case-control study. Lancet Oncol. 2006, 7, 402–406. [Google Scholar] [CrossRef]
- Khalkhali, I.; Vargas, H. Practical use of ultrasound at a dedicated breast center. Breast J. 2005, 11, 165–166. [Google Scholar] [CrossRef]
- Burkett, B.J.; Hanemann, C.W. A Review of Supplemental Screening Ultrasound for Breast Cancer. Acad. Radiol. 2016, 23, 1604–1609. [Google Scholar] [CrossRef]
- Berg, W.A.; Zhang, Z.; Lehrer, D.; Jong, R.A.; Pisano, E.D.; Barr, R.G.; Böhm-Vélez, M.; Mahoney, M.C.; Evans, W.P.; Larsen, L.H.; et al. Detection of Breast Cancer With Addition of Annual Screening Ultrasound or a Single Screening MRI to Mammography in Women With Elevated Breast Cancer Risk. JAMA 2012, 307, 1394–1404. [Google Scholar] [CrossRef] [Green Version]
- Morris, E.A. Screening for breast cancer with MRI. In Seminars in Ultrasound, CT and MRI. WB Saunders 2003, 24, 45–54. [Google Scholar]
- Ibrahim, A.; Mohammed, S.; Ali, H.A. Breast Cancer Detection and Classification Using Thermography: A Review. In Proceedings of the International Conference on Advanced Machine Learning Technologies and Applications, Cairo, Egypt, 22–24 February 2018; Springer: Cham, Switzerland, 2018; pp. 496–505. [Google Scholar]
- Ahern, C.H.; Shih, Y.-C.T.; Dong, W.; Parmigiani, G.; Shen, Y. Cost-effectiveness of alternative strategies for integrating MRI into breast cancer screening for women at high risk. Br. J. Cancer 2014, 111, 1542–1551. [Google Scholar] [CrossRef] [Green Version]
- Barton, M.B.; Harris, R.; Fletcher, S.W. Does This Patient Have Breast Cancer? JAMA 1999, 282, 1270–1280. [Google Scholar] [CrossRef]
- Oestreicher, N.; Lehman, C.D.; Seger, D.J.; Buist, D.S.M.; White, E. The Incremental Contribution of Clinical Breast Examination to Invasive Cancer Detection in a Mammography Screening Program. Am. J. Roentgenol. 2005, 184, 428–432. [Google Scholar] [CrossRef]
- Freed, D.; Golden, J.; Chu, M.; Carrillo, O.; Chin, Y.; Adams, M.; Abramov, V. Medical Devices and Systems. U.S. Patent Application No.11/388,247, 23 March 2006. [Google Scholar]
- Kirimtat, A.; Krejcar, O.; Selamat, A.; Herrera-Viedma, E. FLIR vs SEEK thermal cameras in biomedicine: Comparative diagnosis through infrared thermography. BMC Bioinform. 2020, 21, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moore, G. Breast cancer: Early detection needed. Bus. Heal. 2001, 19, 39. [Google Scholar]
- Feig, S.A.; Shaber, G.S.; Schwartz, G.F.; Patchefsky, A.; Libshitz, H.I.; Edeiken, J.; Nerlinger, R.; Curley, R.F.; Wallace, J.D. Thermography, Mammography, and Clinical Examination in Breast Cancer Screening. Radiology 1977, 122, 123–127. [Google Scholar] [CrossRef]
- Keyserlingk, J.; Ahlgren, P.; Yu, E.; Belliveau, N.; Yassa, M. Functional infrared imaging of the breast. IEEE Eng. Med. Boil. Mag. 2000, 19, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Anbar, M. Clinical thermal imaging today. IEEE Eng. Med. Boil. Mag. 1998, 17, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Gautherie, M. Thermopathology of breast cancer: Measurement and analysis of in vivo temperature and blood flow. Ann. N. Y. Acad. Sci. 1980, 335, 383–415. [Google Scholar] [CrossRef]
- Recinella, A.N.; Gonzalez-Hernandez, J.-L.; Kandlikar, S.G.; Dabydeen, D.; Medeiros, L.; Phatak, P. Clinical Infrared Imaging in the Prone Position for Breast Cancer Screening—Initial Screening and Digital Model Validation. J. Eng. Sci. Med. Diagn. Ther. 2020, 3. [Google Scholar] [CrossRef]
- Mc Donald, D. Mechanism of Tumour Leakiness Proceeding Angiogenesis and Cancer. From Basic Mechanisms to Therapeutic Applications. In Proceedings of the American Association of Cancer Research Conference (AACR), San Francisco, CA, USA, 1–5 April 2000; pp. 11–15. [Google Scholar]
- Gamagami, P. Indirect Signs of Breast Cancer: Angiogenesis Study. In Atlas of Mammography; Blackwell Science: Cambridge, MA, USA, 1996; pp. 321–326. [Google Scholar]
- Yoshida, S.; Nakagawa, S.; Yahara, T.; Koga, T.; Deguchi, H.; Shirouzu, K. Relationship Between Microvessel Density and Thermographic Hot Areas in Breast Cancer. Surg. Today 2003, 33, 243–248. [Google Scholar] [CrossRef]
- Mitra, S.; Bal, A.; Kashyap, D.; Kumar, S.; Shrivastav, S.; Das, A.; Singh, G. Tumour angiogenesis and c-Met pathway activation—Implications in breast cancer. APMIS 2020, 128, 316–325. [Google Scholar] [CrossRef]
- Tsutsui, S.; Yasuda, K.; Suzuki, K.; Tahara, K.; Higashi, H.; Era, S. Macrophage infiltration and its prognostic implications in breast cancer: The relationship with VEGF expression and microvessel density. Oncol. Rep. 2005, 14, 425–431. [Google Scholar] [CrossRef]
- Buckley, D.L.; Drew, P.J.; Mussurakis, S.; Monson, J.R.; Horsman, A. Microvessel density in invasive breast cancer assessed by dynamic gd-dtpa enhanced MRI. J. Magn. Reson. Imaging 1997, 7, 461–464. [Google Scholar] [CrossRef]
- Anbar, M.; Brown, C.; Milescu, L.; Babalola, J.; Gentner, L. The potential of dynamic area telethermometry in assessing breast cancer. IEEE Eng. Med. Boil. Mag. 2000, 19, 58–62. [Google Scholar] [CrossRef] [PubMed]
- Thomsen, L.L.; Miles, D.W.; Happerfield, L.; Bobrow, L.G.; Knowles, R.G.; Moncada, S. Nitric oxide synthase activity in human breast cancer. Br. J. Cancer 1995, 72, 41–44. [Google Scholar] [CrossRef]
- Arnedos, M.; Vicier, C.; Loi, S.; Lefebvre, C.; Michiels, S.; Bonnefoi, H.; Andre, F. Precision medicine for metastatic breast cancer—Limitations and solutions. Nat. Rev. Clin. Oncol. 2015, 12, 693. [Google Scholar] [CrossRef]
- Di Meo, S.; Reed, T.T.; Venditti, P.; Victor, V.M. Role of ROS and RNS Sources in Physiological and Pathological Conditions. Oxidative Med. Cell. Longev. 2016, 2016, 1–44. [Google Scholar] [CrossRef]
- Moldogazieva, N.T.; Lutsenko, S.V.; Terentiev, A.A. Reactive Oxygen and Nitrogen Species–Induced Protein Modifications: Implication in Carcinogenesis and Anticancer Therapy. Cancer Res. 2018, 78, 6040–6047. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, K.A.; Waypa, G.B.; Schumacker, P.T. Redox signaling during hypoxia in mammalian cells. Redox Biol. 2017, 13, 228–234. [Google Scholar] [CrossRef]
- Xu, W.; Liu, L.Z.; Loizidou, M.; Ahmed, M.J.U.; Charles, I.G. The role of nitric oxide in cancer. Cell Res. 2002, 12, 311–320. [Google Scholar] [CrossRef] [Green Version]
- Choudhari, S.K.; Chaudhary, M.; Bagde, S.; Gadbail, A.R.; Joshi, V. Nitric oxide and cancer: A review. World J. Surg. Oncol. 2013, 11, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Martínez, M.C.; Andriantsitohaina, R. Reactive Nitrogen Species: Molecular Mechanisms and Potential Significance in Health and Disease. Antioxidants Redox Signal. 2009, 11, 669–702. [Google Scholar] [CrossRef]
- Xing, F.; Liu, Y.; Sharma, S.; Wu, K.; Chan, M.D.; Lo, H.-W.; Carpenter, R.L.; Metheny-Barlow, L.J.; Zhou, X.; Qasem, S.A.; et al. Activation of the c-Met Pathway Mobilizes an Inflammatory Network in the Brain Microenvironment to Promote Brain Metastasis of Breast Cancer. Cancer Res. 2016, 76, 4970–4980. [Google Scholar] [CrossRef] [Green Version]
- Changchun, K.; Pengchao, H.; Ke, S.; Ying, W.; Wei, L. Interleukin-17 augments tumor necrosis factor α-mediated increase of hypoxia-inducible factor-1α and inhibits vasodilator-stimulated phosphoprotein expression to reduce the adhesion of breast cancer cells. Oncol. Lett. 2017, 13, 3253–3260. [Google Scholar] [CrossRef] [Green Version]
- Maher, E.A.; Mietz, J.; Arteaga, C.L.; DePinho, R.A.; Mohla, S. Brain metastasis: Opportunities in basic and translational research. Cancer Res. 2009, 69, 6015–6020. [Google Scholar] [CrossRef] [Green Version]
- Ganong, W.F. Review of Medical Physiology, 2nd ed.; Lange Medical Books/McGraw-Hill: San Francisco, CA, USA, 2005. [Google Scholar]
- Spychala, J.; Lazarowski, E.; Ostapkowicz, A.; Ayscue, L.H.; Jin, A.; Mitchell, B.S. Role of estrogen receptor in the regulation of ecto-5′-nucleotidase and adenosine in breast cancer. Clin. Cancer Res. 2004, 10, 708–717. [Google Scholar] [CrossRef] [Green Version]
- Lozano, A.; Hayes, J.C.; Compton, L.M.; Azarnoosh, J.; Hassanipour, F. Determining the thermal characteristics of breast cancer based on high-resolution infrared imaging, 3D breast scans, and magnetic resonance imaging. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef] [PubMed]
- FDA Safety Communication, FDA Warns Thermography Should Not Be Used in Place of Mammography to Detect, Diagnose, or Screen for Breast Cancer. 2019. Available online: www.fda.gov (accessed on 25 February 2019).
- FDA Consumer Update, Breast Cancer Screening: Thermogram No Substitute for Mammogram, U.S. Food and Drug Administration. 2017. Available online: www.fda.gov (accessed on 30 October 2017).
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Yousefi, B.; Sfarra, S.; Ibarra-Castanedo, C.; Maldague, X.P. Comparative analysis on thermal non-destructive testing imagery applying Candid Covariance-Free Incremental Principal Component Thermography (CCIPCT). Infrared Phys. Technol. 2017, 85, 163–169. [Google Scholar] [CrossRef]
- Yousefi, B.; Sfarra, S.; Sarasini, F.; Castanedo, C.I.; Maldague, X.P. Low-rank sparse principal component thermography (sparse-PCT): Comparative assessment on detection of subsurface defects. Infrared Phys. Technol. 2019, 98, 278–284. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Sfarra, S.; Yao, Y. Sparse Principal Component Thermography for Subsurface Defect Detection in Composite Products. IEEE Trans. Ind. Inform. 2018, 14, 5594–5600. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Mokhtari, Y.; Ibarra-Castanedo, C.; Klein, M.; Genest, M.; Maldague, X. Automated Dynamic Inspection Using Active Infrared Thermography. IEEE Trans. Ind. Inform. 2018, 14, 5648–5657. [Google Scholar] [CrossRef]
- Marinetti, S.; Finesso, L.; Marsilio, E. Matrix factorization methods: Application to thermal NDT/E. NDT E Int. 2006, 39, 611–616. [Google Scholar] [CrossRef]
- Cramer, K.E.; Winfree, W. Fixed eigenvector analysis of thermographic NDE data. SPIE 2011, 225–235. [Google Scholar] [CrossRef] [Green Version]
- Yousefi, B.; Sharifipour, H.M.; Eskandari, M.; Castanedo, C.I.; Laurendeau, D.; Watts, R.; Klein, M.; Maldague, X. Incremental Low Rank Noise Reduction for Robust Infrared Tracking of Body Temperature during Medical Imaging. Electronics 2019, 8, 1301. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, J.; Gao, B.; Woo, W.L. Wavelet-Integrated Alternating Sparse Dictionary Matrix Decomposition in Thermal Imaging CFRP Defect Detection. IEEE Trans. Ind. Inform. 2018, 15, 4033–4043. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse principal component analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef] [Green Version]
- FeCun, Y. LeNet-5, Convolutional Neural Networks. 2015. Available online: http://yann.lecun.com/exdb/lenet (accessed on 31 October 2020).
- Aghdam, H.H.; Heravi, E.J. Guide to Convolutional Neural Networks: A Practical Application to Traffic-Sign Detection and Classification; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. arXiv 2016, arXiv:1603.05027v3. [Google Scholar]
- Liang, L.; Liu, M.; Sun, W. A deep learning approach to estimate chemically-treated collagenous tissue nonlinear anisotropic stress-strain responses from microscopy images. Acta Biomater. 2017, 63, 227–235. [Google Scholar] [CrossRef]
- Akbari, H.; Rathore, S.; Bakas, S.; Nasrallah, M.P.; Shukla, G.; Mamourian, E.; Rozycki, M.; Bagley, S.J.; Rudie, J.D.; Flanders, A.E.; et al. Histopathology-validated machine learning radiographic biomarker for noninvasive discrimination between true progression and pseudo-progression in glioblastoma. Cancer 2020, 126, 2625–2636. [Google Scholar] [CrossRef]
- Yousefi, B.; Kalhor, D.; Usamentiaga, R.; Lei, L.; Ibarra-Castanedo, C.; Maldague, X. Application of Deep Learning in Infrared Non-Destructive Testing. Quant. InfraRed Thermogr. 2018. [Google Scholar] [CrossRef]
- Chaves, E.; Gonçalves, C.B.; Albertini, M.K.; Lee, S.; Jeon, G.; Fernandes, H.C. Evaluation of transfer learning of pre-trained CNNs applied to breast cancer detection on infrared images. Appl. Opt. 2020, 59, E23–E28. [Google Scholar] [CrossRef]
- Acharya, S.; Alsadoon, A.; Prasad, P.W.C.; Abdullah, S.; Deva, A. Deep convolutional network for breast cancer classification: Enhanced loss function (ELF). J. Supercomput. 2020, 76, 1–18. [Google Scholar] [CrossRef]
- Fernández-Ovies, F.J.; Alférez-Baquero, E.S.; De Andrés-Galiana, E.J.; Cernea, A.; Fernández-Muñiz, Z.; Fernández-Martínez, J.L. Detection of Breast Cancer Using Infrared Thermography and Deep Neural Networks. In Proceedings of the International Work-Conference on Bioinformatics and Biomedical Engineering, Granada, Spain, 8–10 May 2019; Springer: Cham, Switzerland, 2019; pp. 514–523. [Google Scholar]
- Zuluaga-Gomez, J.; Al Masry, Z.; Benaggoune, K.; Meraghni, S.; Zerhouni, N. A CNN-based methodology for breast cancer diagnosis using thermal images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2020, 1–15. [Google Scholar] [CrossRef]
- Ekici, S.; Jawzal, H. Breast cancer diagnosis using thermography and convolutional neural networks. Med. Hypotheses 2020, 137, 109542. [Google Scholar] [CrossRef]
- Mambou, S.J.; Maresova, P.; Krejcar, O.; Selamat, A.; Kuca, K. Breast Cancer Detection Using Infrared Thermal Imaging and a Deep Learning Model. Sensors 2018, 18, 2799. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Gillies, R.J.; Kinahan, P.E.; Hricak, H. Radiomics: Images Are More than Pictures, They Are Data. Radiology 2016, 278, 563–577. [Google Scholar] [CrossRef] [Green Version]
- Chollet, F. Building Autoencoders in Keras. 2016. Available online: https://blog.keras.io/building-autoencoders-in-keras.html (accessed on 14 March 2017).
- Olshausen, B.A.; Field, D.J. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vis. Res. 1997, 37, 3311–3325. [Google Scholar] [CrossRef] [Green Version]
- Arpit, D.; Zhou, Y.; Ngo, H.; Govindaraju, V. Why regularized auto-encoders learn sparse representation? In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 136–144. [Google Scholar]
- Hinton, G.E. Distributed Representations. 1984. Available online: https://web.stanford.edu/~jlmcc/papers/PDP/ (accessed on 18 July 2005).
- Silva, L.F.; Saade, D.C.M.; Sequeiros, G.O.; Silva, A.C.; Paiva, A.C.; Bravo, R.S.; Conci, A. A New Database for Breast Research with Infrared Image. J. Med Imaging Heal. Inform. 2014, 4, 92–100. [Google Scholar] [CrossRef]
- Python 3 Google Compute Engine Backend, T4, and P100 GPU and 27.4 Gb RAM, Google 2020.
- Mortazi, A.; Khosravan, N.; Torigian, E.A.; Kurugol, S.; Bagci, U. Weakly Supervised Segmentation by a Deep Geodesic Prior. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; pp. 238–246. [Google Scholar]
- Yousefi, B.; Castanedo, C.I.; Maldague, X.P. Measuring heterogeneous thermal patterns in infrared-based diagnostic systems using sparse low-rank matrix approximation: Comparative study. IEEE Trans. Instrum. Meas. 2020. [Google Scholar] [CrossRef]
- Yousefi, B.; Castanedo, C.I.; Maldague, X.P.V. Low-rank Convex/Sparse Thermal Matrix Approximation for Infrared-based Diagnostic System. arXiv 2020, arXiv:2010.06784. [Google Scholar]
- Kirimtat, A.; Krejcar, O. A review of infrared thermography for the investigation of building envelopes: Advances and prospects. Energy Build. 2018, 176, 390–406. [Google Scholar] [CrossRef]

| DMR—Database for Mastology Research | ||
|---|---|---|
| Age | Median (±IQR) | 60 (25,120) |
| Race | Caucasian | 77 (37%) |
| African | 57 (27.4%) | |
| Pardo | 72 (34.6%) | |
| Mulatto | 1 (0.5%) | |
| Indigenous | 1 (0.5%) | |
| Diagnosis 1 | Healthy 2 | 128 (61.5%) |
| Symptomatic (with and without cancer) | 80 (38.5%) | |
| Sick 3 | 36 (17.3%) | |
| Family history | Diabetes | 52 (25%) |
| Hypertensive | 5 (2.4%) | |
| Leukemia | 1 (0.5%) | |
| None | 150 (72.1%) | |
| Hormone therapy (HT) | Hormone replacement | 38 (18.3%) |
| None | 170 (81.7%) | |
| Methods | Cross-Validated Accuracy |
|---|---|
| Sparse PCT | 75.24 (72.33–77.67)% |
| PCT | 73.27 (71.84–76.21)% |
| Clinical information * | 71.36 (69.42–73.3)% |
| Sparse PCT with clinical information * | 78.16 (73.3–81.07)% |
| PCT with clinical information * | 73.79 (72.33–76.7)% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousefi, B.; Akbari, H.; Maldague, X.P.V. Detecting Vasodilation as Potential Diagnostic Biomarker in Breast Cancer Using Deep Learning-Driven Thermomics. Biosensors 2020, 10, 164. https://doi.org/10.3390/bios10110164
Yousefi B, Akbari H, Maldague XPV. Detecting Vasodilation as Potential Diagnostic Biomarker in Breast Cancer Using Deep Learning-Driven Thermomics. Biosensors. 2020; 10(11):164. https://doi.org/10.3390/bios10110164
Chicago/Turabian StyleYousefi, Bardia, Hamed Akbari, and Xavier P.V. Maldague. 2020. "Detecting Vasodilation as Potential Diagnostic Biomarker in Breast Cancer Using Deep Learning-Driven Thermomics" Biosensors 10, no. 11: 164. https://doi.org/10.3390/bios10110164
APA StyleYousefi, B., Akbari, H., & Maldague, X. P. V. (2020). Detecting Vasodilation as Potential Diagnostic Biomarker in Breast Cancer Using Deep Learning-Driven Thermomics. Biosensors, 10(11), 164. https://doi.org/10.3390/bios10110164