Theoretical Model for a Highly Sensitive Near Infrared Biosensor Based on Bloch Surface Wave with Dirac Semimetal
Abstract
:1. Introduction
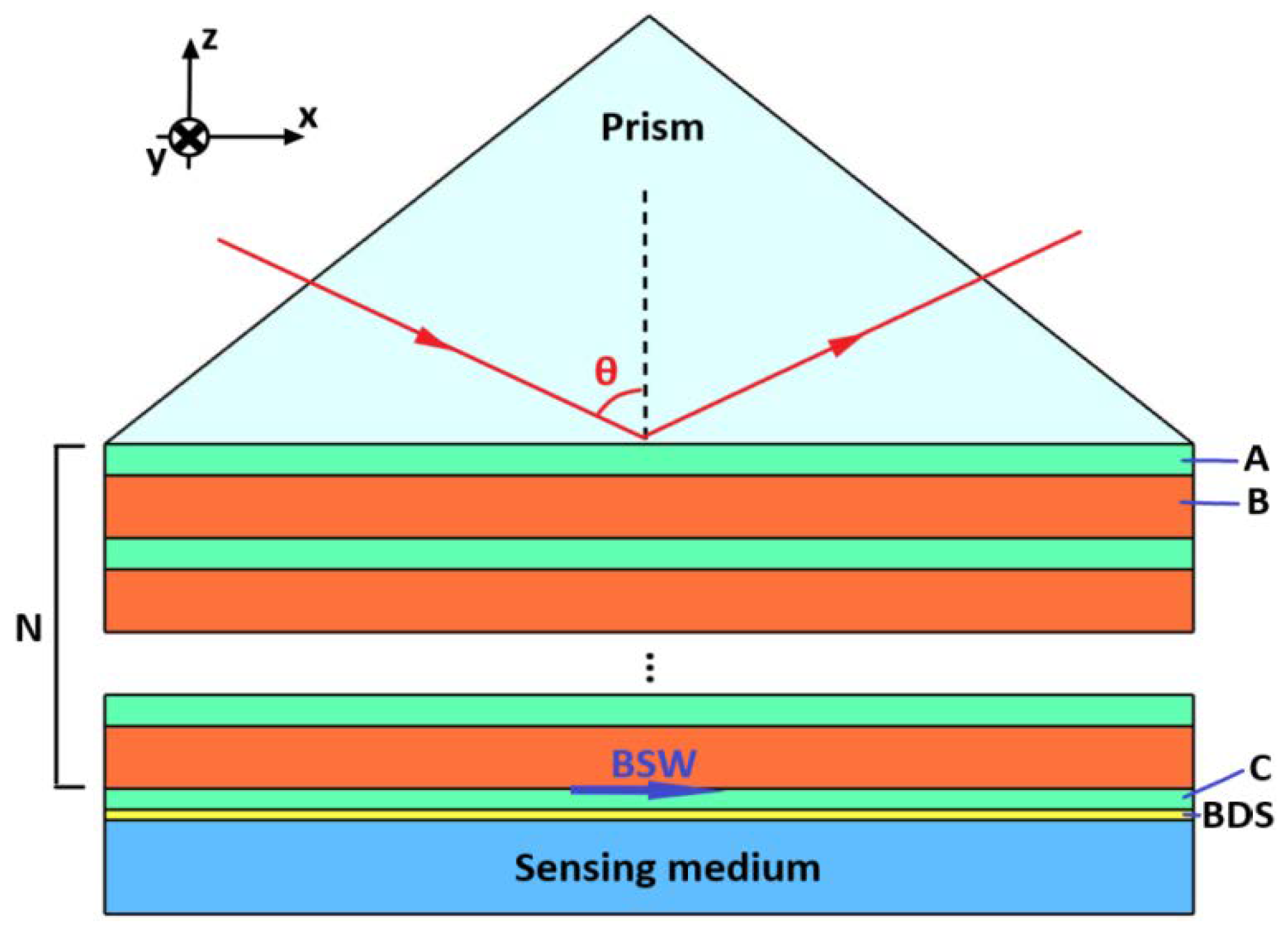
2. Theoretical Model and Method
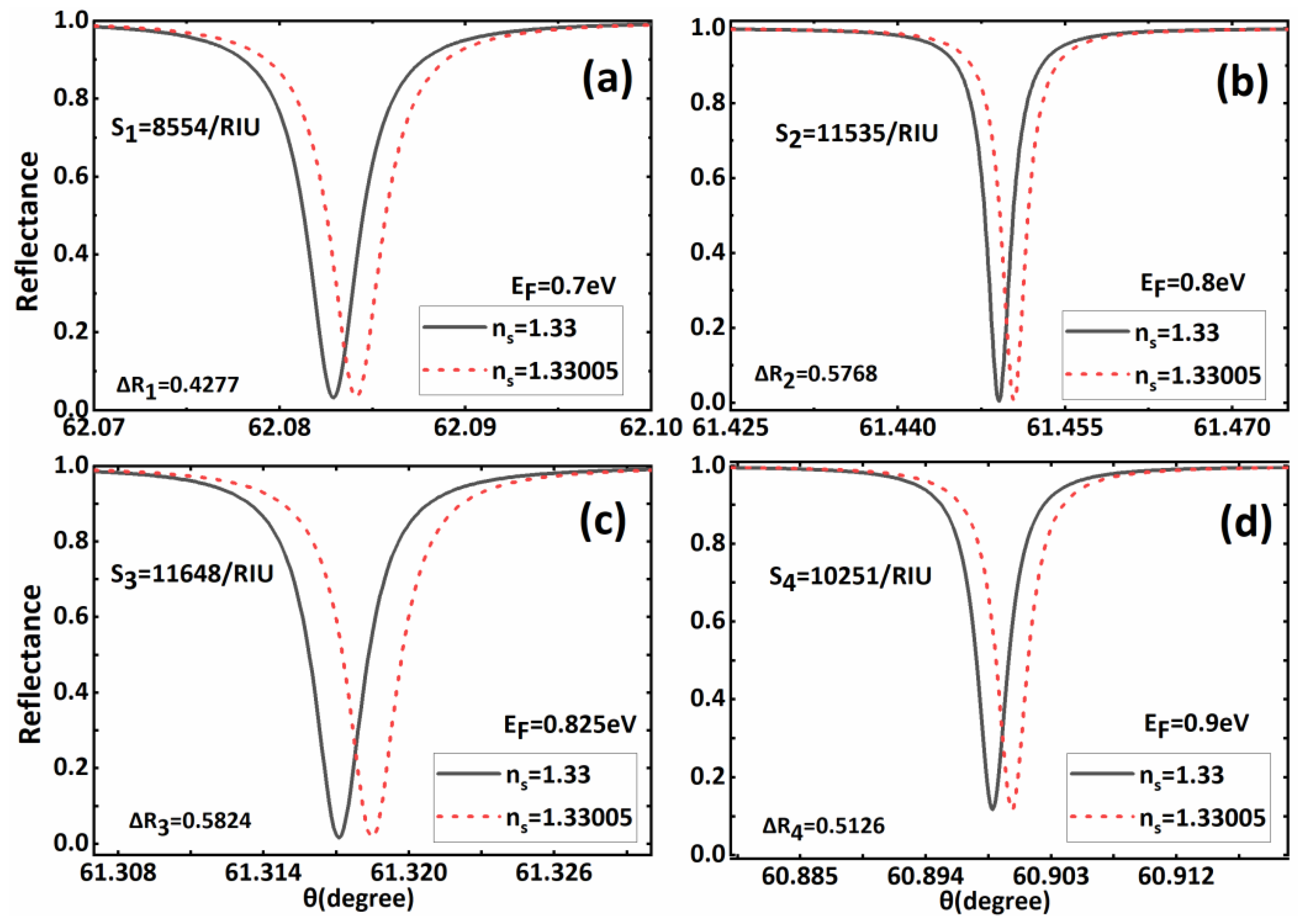
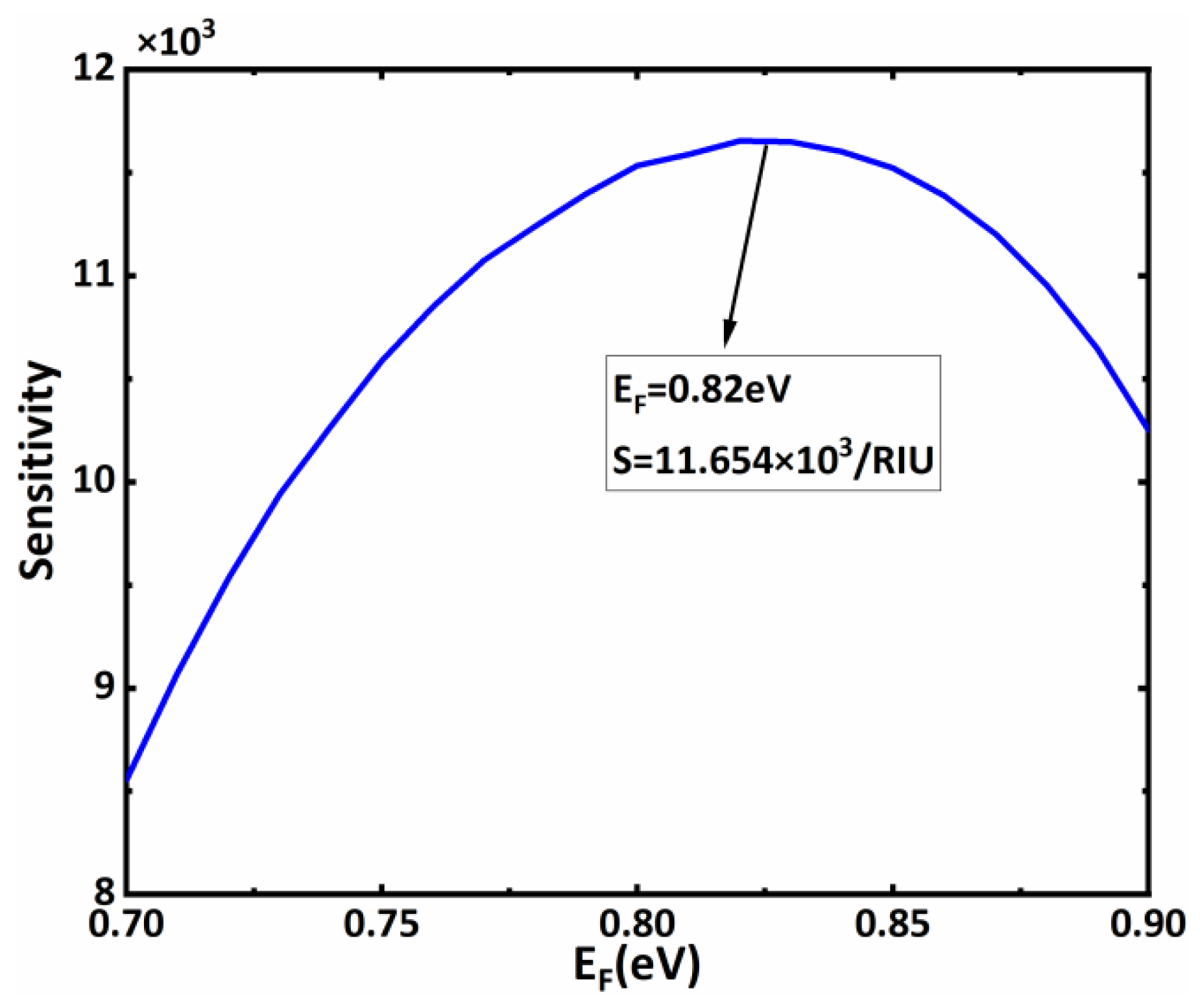
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Turner, A. Biosensors—Sense and sensitivity. Science 2000, 290, 1315–1317. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.J.; Chung, M.F. Detection of cadmium by a fiber-optic biosensor based on localized surface plasmon resonance. Biosens. Bioelectron. 2009, 24, 1213–1218. [Google Scholar] [CrossRef] [PubMed]
- Silalahi, H.M.; Chen, Y.P.; Shih, Y.H.; Chen, Y.S.; Lin, X.Y.; Liu, J.H.; Huang, C.Y. Floating terahertz metamaterials with extremely large refractive index sensitivities. Photonics Res. 2021, 9, 1970–1978. [Google Scholar] [CrossRef]
- Singh, V.V.; Gupta, G.; Batra, A.; Nigam, A.K.; Boopathi, M.; Gutch, P.K.; Tripathi, B.K.; Srivastava, A.; Samuel, M.; Agarwal, G.S.; et al. Greener electrochemical synthesis of high quality graphene nanosheets directly from pencil and its SPR sensing application. Adv. Funct. Mater. 2012, 22, 2352–2362. [Google Scholar] [CrossRef]
- Zhang, N.; Li, K.; Shum, P.P.; Yu, X.; Zeng, S.; Wu, Z.; Wang, Q.J.; Yong, K.T.; Wei, L. Hybrid graphene/gold plasmonic fiber-optic biosensor. Adv. Mater. Technol. 2017, 2, 1600185. [Google Scholar] [CrossRef]
- Verma, R.; Gupta, B.D. Fiberoptic SPR sensor for the detection of 3-pyridinecarboxamide (vitamin B3) using molecularly imprinted hydrogel. Sens. Actuators B Chem. 2013, 177, 279–285. [Google Scholar] [CrossRef]
- Leung, A.; Shankar, P.M.; Mutharasan, R. A review of fiber-optic biosensors. Sens. Actuators B Chem. 2007, 125, 688–703. [Google Scholar] [CrossRef]
- Lo, S.M.; Hu, S.; Gaur, G.; Kostoulas, Y.; Fauchet, P.M. Photonic crystal microring resonator for label-free biosensing. Opt. Express 2017, 25, 7046–7054. [Google Scholar] [CrossRef]
- Baghdouche, L.K.; Cassan, E. Sensitivity analysis of ring-shaped slotted photonic crystal waveguides for mid-infrared refractive index sensing. Opt. Quantum Electron. 2019, 51, 328. [Google Scholar] [CrossRef]
- Levy, R.; Ruschin, S. SPR waveguide sensor based on transition of modes at abrupt discontinuity. Sens. Actuators B Chem. 2007, 124, 459–465. [Google Scholar] [CrossRef]
- Cai, D.; Lu, Y.; Lin, K.; Wang, P.; Ming, H. Improving the sensitivity of SPR sensors based on gratings by double-dips method (DDM). Opt. Express 2008, 16, 14597–14602. [Google Scholar] [CrossRef] [PubMed]
- Akter, S.; Rahman, M.Z.; Mahmud, S. Highly sensitive open-channels based plasmonic biosensor in visible to near-infrared wavelength. Results Phys. 2019, 13, 102328. [Google Scholar] [CrossRef]
- Zeng, S.; Sreekanth, K.V.; Shang, J.; Yu, T.; Chen, C.K.; Yin, F.; Baillargeat, D.; Coquet, P.; Ho, H.P.; Kabashin, A.V. Graphene–gold metasurface architectures for ultrasensitive plasmonic biosensing. Adv. Mater. 2015, 27, 6163–6169. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.A.; Hwang, T.; Dugasani, S.R.; Amin, R.; Kulkarni, A.; Park, S.H.; Kim, T. Graphene based fiber optic surface plasmon resonance for bio-chemical sensor applications. Sens. Actuators B Chem. 2013, 187, 426–433. [Google Scholar] [CrossRef] [Green Version]
- Ubeid, M.F.; Shabat, M.M. Numerical investigation of a D-shape optical fiber sensor containing graphene. Appl. Phys. A 2015, 118, 1113–1118. [Google Scholar] [CrossRef]
- Maharana, P.K.; Srivastava, T.; Jha, R. On the performance of highly sensitive and accurate graphene-on-aluminum and silicon-based SPR biosensor for visible and near infrared. Plasmonics 2014, 9, 1113–1120. [Google Scholar] [CrossRef]
- Sadeghi, Z.; Shirkani, H. Highly sensitive mid-infrared SPR biosensor for a wide range of biomolecules and biological cells based on graphene-gold grating. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 119, 114005. [Google Scholar] [CrossRef]
- Baghbadorani, H.K.; Barvestani, J. Sensing improvement of 1D photonic crystal sensors by hybridization of defect and Bloch surface modes. Appl. Surf. Sci. 2020, 537, 147730. [Google Scholar] [CrossRef]
- Tu, T.; Pang, F.; Shan, Z.; Cheng, J.; Wang, T. Excitation of Bloch surface wave on tapered fiber coated with one-dimensional photonic crystal for refractive index sensing. Opt. Express 2017, 25, 9019. [Google Scholar] [CrossRef]
- Farmer, A.; Friedli, A.C.; Wright, S.M.; Robertson, W.M. Biosensing using surface electromagnetic waves in photonic band gap multilayers. Sens. Actuators B Chem. 2012, 173, 79–84. [Google Scholar] [CrossRef]
- Li, S.; Kong, W.; Zheng, Z.; Wan, Y.; Liu, J. High-sensitivity sensing based on intensity-interrogated Bloch surface wave sensors. Sens. Actuators B Chem. 2014, 193, 467–471. [Google Scholar]
- Sinibaldi, A.; Danz, N.; Descrovi, E.; Munzert, P.; Schulz, U.; Sonntag, F.; Dominici, L.; Michelotti, F. Direct comparison of the performance of Bloch surface wave and surface plasmon polariton sensors. Sens. Actuators B Chem. 2012, 174, 292–298. [Google Scholar] [CrossRef]
- Kang, X.B.; Liu, L.J.; Lu, H.; Li, H.D.; Wang, Z.G. Guided Bloch surface wave resonance for biosensor designs. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2016, 33, 997–1003. [Google Scholar] [CrossRef] [PubMed]
- Toma, K.; Descrovi, E.; Toma, M.; Ballarini, M.; Dostálek, J. Bloch surface wave-enhanced fluorescence biosensor. Biosens. Bioelectron. 2012, 43C, 108–114. [Google Scholar] [CrossRef] [PubMed]
- Gryga, M.; Ciprian, D.; Hlubina, P. Bloch surface wave resonance based sensors as an alternative to surface plasmon resonance sensors. Sensors 2020, 20, 5119. [Google Scholar] [CrossRef]
- Ma, J.; Kang, X.B.; Wang, Z.G. Sensing performance optimization of the Bloch surface wave biosensor based on the Bloch impedance-matching method. Opt. Lett. 2018, 43, 5375–5378. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Gembalova, L.; Hlubina, P. Sensing based on Bloch surface wave and self-referenced guided mode resonances employing a one-dimensional photonic crystal. Opt. Express 2021, 29, 12996–13010. [Google Scholar] [CrossRef]
- Lin, Z.; Yue, J.; Qian, M.; Wu, L.; Ruan, B.; Zhu, J.; Dai, X.; Xiang, Y. High sensitivity intensity-interrogated Bloch surface wave biosensor with graphene. Sens. J. IEEE 2018, 18, 106–110. [Google Scholar] [CrossRef]
- Zou, X.J.; Zheng, G.G.; Chen, Y.Y. Confinement of Bloch surface waves in a graphene-based one-dimensional photonic crystal and sensing applications. Chin. Phys. B 2018, 27, 5. [Google Scholar] [CrossRef]
- Liu, G.D.; Xiang, Z.; Meng, H.Y.; Lin, Q.; Wang, L.L. Dirac semimetals based tunable narrowband absorber at terahertz frequencies. Opt. Express 2018, 26, 11471–11480. [Google Scholar] [CrossRef]
- Liu, Z.K.; Jiang, J.; Zhou, B.; Wang, Z.J.; Zhang, Y.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Peng, H.; Dudin, P.; et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 2014, 13, 677–681. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Timusk, T.; Carbotte, J.P.; Homes, C.C.; Basov, D.N.; Sharapov, S.G. Three-dimensional Dirac fermions in quasicrystals as seen via optical conductivity. Phys. Rev. B Condens. Matter 2013, 87, 3249–3253. [Google Scholar] [CrossRef] [Green Version]



| dBDS = 5 nm | dBDS = 10 nm | dBDS = 15 nm | dBDS = 20 nm | dBDS = 25 nm | dBDS = 30 nm | dBDS = 35 nm | |
|---|---|---|---|---|---|---|---|
| dc = 80 nm | 11,675 | 15,342 | 13,398 | 10,037 | 7222 | 5342 | 4276 |
| dc = 90 nm | 15,656 | 15,362 | 11,497 | 8216 | 6126 | 5005 | 4499 |
| dc = 100 nm | 17,234 | 14,018 | 10,001 | 7450 | 6066 | 5167 | 3684 |
| dc = 110 nm | 17,159 | 12,930 | 9420 | 7236 | 5140 | 2304 | 443 |
| dc = 120 nm | 16,010 | 11,654 | 7657 | 3744 | 899 | 112 | 15 |
| dc = 130 nm | 11,229 | 5879 | 1699 | 240 | 28 | 4.83 | 1.34 |
| dc = 140 nm | 2324 | 458 | 54 | 7.71 | 1.82 | 0.81 | 0.49 |
| dc = 150 nm | 72.75 | 11.43 | 2.4 | 0.76 | 0.52 | 0.31 | 0.19 |
| Reference | Mechanism | Structure | Sensitivity | FOM (RIU−1) | Frequency Range |
|---|---|---|---|---|---|
| [1] | SPR sensor | Photonic crystal fibers (PCFs) structure with open-channels | 396/RIU | 47 | Near Infrared |
| [2] | SPR biosensor | Aluminum and Silicon-Graphene structure | 550/RIU | / | Near Infrared |
| [3] | Mode coupling sensor | Otto structure | 3260/RIU | / | THz |
| [25] | BSW biosensor | Prism-photonic crystal composite structure with graphene | 35,000/RIU | / | Near Infrared |
| [4] | Mode coupling sensor | Bragg reflector structure(with defect layer) | 810 nm/RIU | 9679 | Near Infrared |
| [5] | SPR biosensor | Grating- coupled structure | 1782 nm/RIU | 21,214 | Near Infrared |
| [6] | BSW biosensor | Grating/Bragg mirror structure | 128°/RIU | / | Visible |
| This work | BSW biosensor | Prism-coupled structure(with defect layer) | 17,406/RIU | / | Near Infrared |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Q.; Liu, Y.; Lu, W.; Dai, X.; Tian, H.; Jiang, L. Theoretical Model for a Highly Sensitive Near Infrared Biosensor Based on Bloch Surface Wave with Dirac Semimetal. Biosensors 2021, 11, 390. https://doi.org/10.3390/bios11100390
Zheng Q, Liu Y, Lu W, Dai X, Tian H, Jiang L. Theoretical Model for a Highly Sensitive Near Infrared Biosensor Based on Bloch Surface Wave with Dirac Semimetal. Biosensors. 2021; 11(10):390. https://doi.org/10.3390/bios11100390
Chicago/Turabian StyleZheng, Qiwen, Yamei Liu, Wenguang Lu, Xiaoyu Dai, Haishan Tian, and Leyong Jiang. 2021. "Theoretical Model for a Highly Sensitive Near Infrared Biosensor Based on Bloch Surface Wave with Dirac Semimetal" Biosensors 11, no. 10: 390. https://doi.org/10.3390/bios11100390
APA StyleZheng, Q., Liu, Y., Lu, W., Dai, X., Tian, H., & Jiang, L. (2021). Theoretical Model for a Highly Sensitive Near Infrared Biosensor Based on Bloch Surface Wave with Dirac Semimetal. Biosensors, 11(10), 390. https://doi.org/10.3390/bios11100390








