Enhanced Blood Plasma Extraction Utilising Viscoelastic Effects in a Serpentine Microchannel
Abstract
:1. Introduction
2. Theoretical Background
3. Materials and Methods
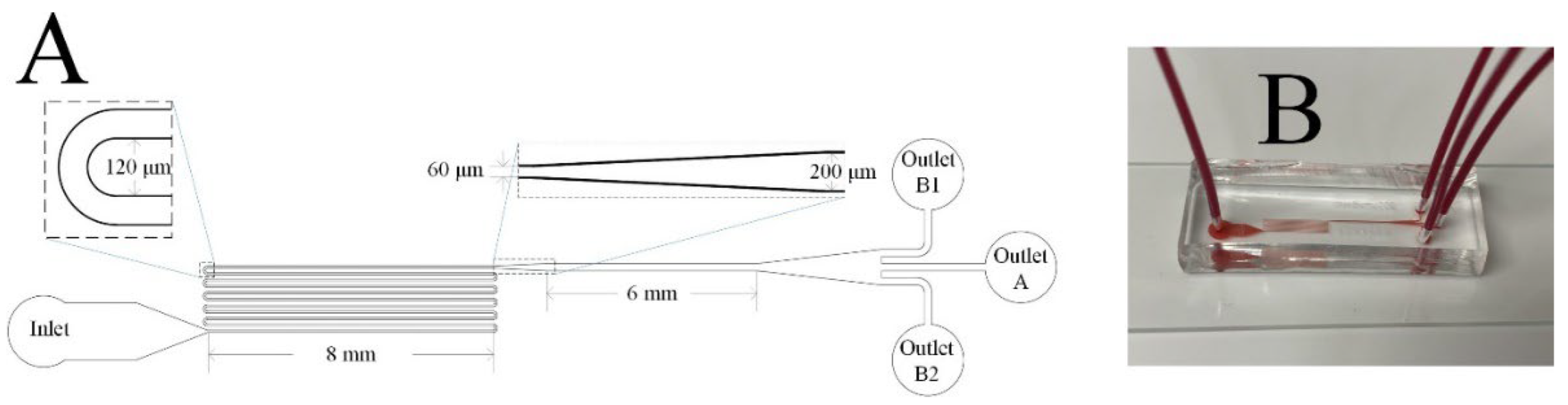
3.1. Design and Fabrication of Microfluidic Devices
3.2. Preparation of Viscoelastic Fluids
3.3. Preparation of Blood Cells
3.4. Flow Cytometry and Haemoglobin Analysis
3.5. Experimental Setup and Data Analysis
4. Results and Discussions
4.1. Blood Plasma Extraction Mechanism
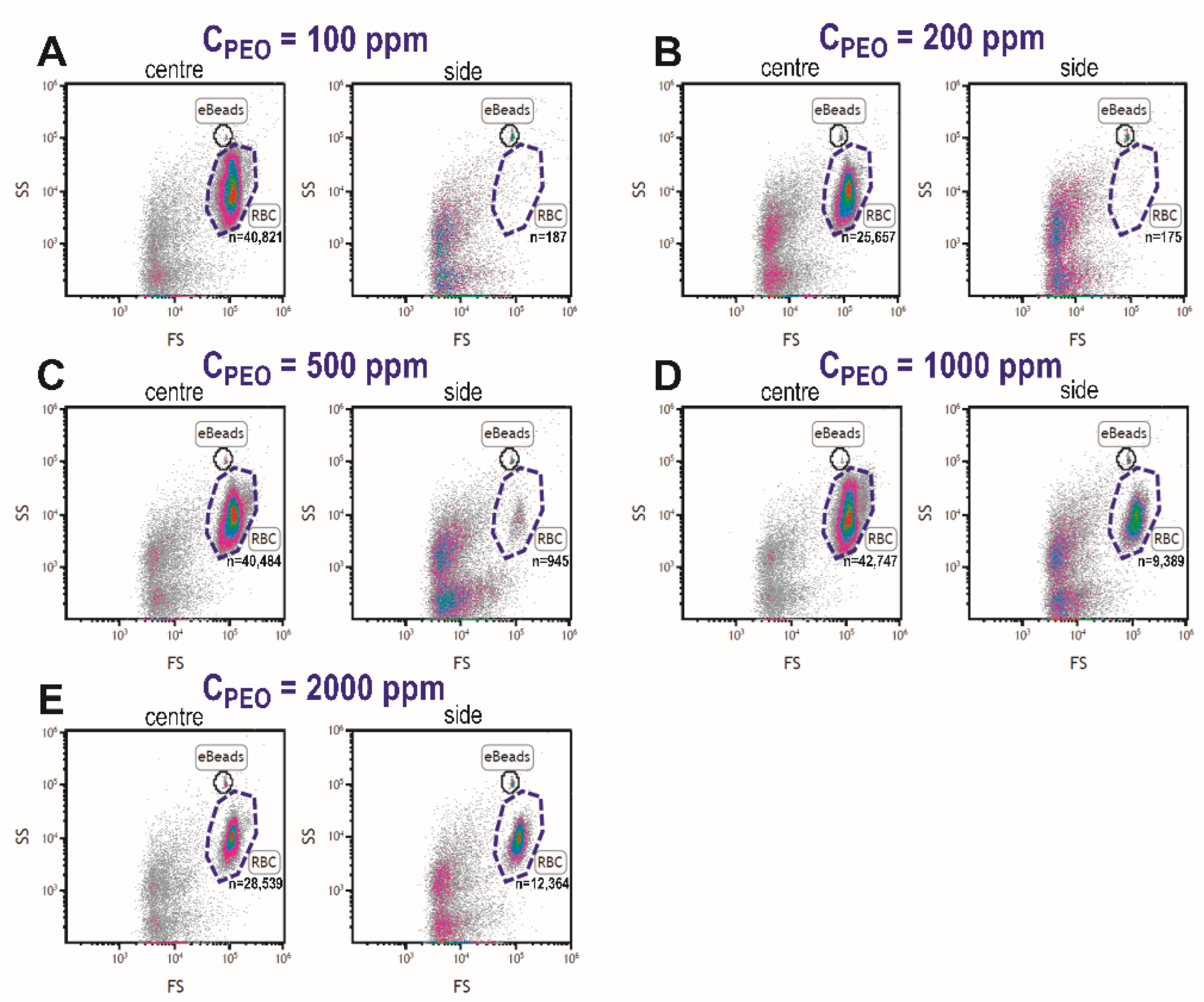
4.2. Fluid Viscoelastic Enhanced Focusing of Blood Cells
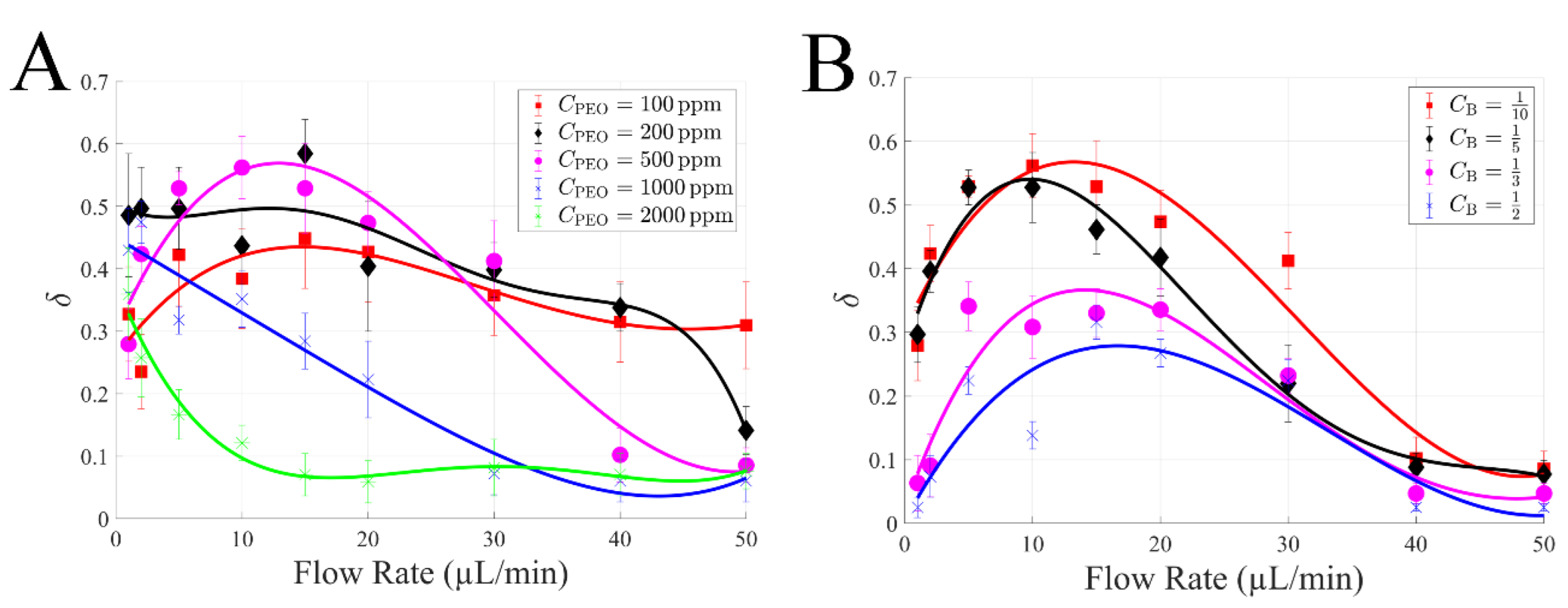
4.3. Effects of PEO Concentration and Blood Dilution
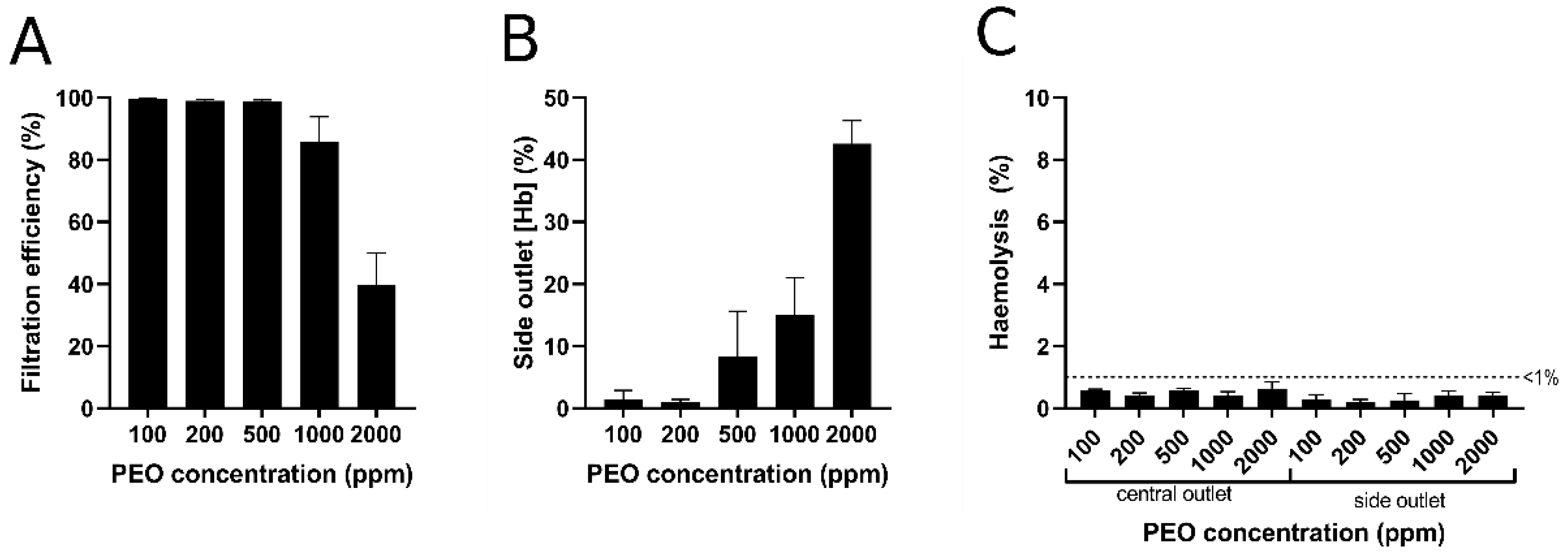
4.4. Blood Plasma Extraction and Haemoglobin Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lippi, G.; Plebani, M.; di Somma, S.; Cervellin, G. Hemolyzed specimens: A major challenge for emergency departments and clinical laboratories. Crit. Rev. Clin. Lab. Sci. 2011, 48, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.T.F.; Yong, K.M.A.; Fu, J. Microfluidic blood cell sorting: Now and beyond. Small 2014, 10, 1687–1703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tripathi, S.; Kumar, Y.B.V.; Prabhakar, A.; Joshi, S.S.; Agrawal, A. Passive blood plasma separation at the microscale: A review of design principles and microdevices. J. Micromech. Microeng. 2015, 25, 083001. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, D.; Sluyter, R.; Yan, S.; Zhao, Q.; Xia, H.; Tan, S.H.; Nguyen, N.-T.; Li, W. High-throughput separation of white blood cells from whole blood using inertial microfluidics. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 1422–1430. [Google Scholar] [CrossRef] [Green Version]
- Kuan, D.-H.; Wu, C.-C.; Su, W.-Y.; Huang, N.-T. A microfluidic device for simultaneous extraction of plasma, red blood cells, and on-chip white blood cell trapping. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Çetin, B.; Li, D. Dielectrophoresis in microfluidics technology. Electrophoresis 2011, 32, 2410–2427. [Google Scholar] [CrossRef] [Green Version]
- Forbes, T.P.; Forry, S.P. Microfluidic magnetophoretic separations of immunomagnetically labeled rare mammalian cells. Lab Chip 2012, 12, 1471–1479. [Google Scholar] [CrossRef]
- Kersaudy-Kerhoas, M.; Sollier, E. Micro-scale blood plasma separation: From acoustophoresis to egg-beaters. Lab Chip 2013, 13, 3323–3346. [Google Scholar] [CrossRef] [Green Version]
- Crowley, T.A.; Pizziconi, V. Isolation of plasma from whole blood using planar microfilters for lab-on-a-chip applications. Lab Chip 2005, 5, 922–929. [Google Scholar] [CrossRef]
- di Carlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Yan, S.; Yuan, D.; Alici, G.; Nguyen, N.-T.; Warkiani, M.E.; Li, W. Fundamentals and applications of inertial microfluidics: A review. Lab Chip 2016, 16, 10–34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fallahi, H.; Yadav, S.; Phan, H.-P.; Ta, H.; Zhang, J.; Nguyen, N.-T. Size-tuneable isolation of cancer cells using stretchable inertial microfluidics. Lab Chip 2021, 21, 2008–2018. [Google Scholar] [CrossRef] [PubMed]
- Yuan, D.; Zhao, Q.; Yan, S.; Tang, S.-Y.; Alici, G.; Zhang, J.; Li, W. Recent progress of particle migration in viscoelastic fluids. Lab Chip 2018, 18, 551–567. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, X.; Liu, C.; Hu, G.; Xuan, X. Particle manipulations in non-Newtonian microfluidics: A review. J. Colloid Interface Sci. 2017, 500, 182–201. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Papautsky, I. Viscoelastic microfluidics: Progress and challenges. Microsyst. Nanoeng. 2020, 6, 1–24. [Google Scholar] [CrossRef]
- D’Avino, G.; Greco, F.; Maffettone, P.L. Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices. Annu. Rev. Fluid Mech. 2017, 49, 341–360. [Google Scholar] [CrossRef]
- Yuan, D.; Yadav, S.; Ta, H.T.; Fallahi, H.; An, H.; Kashaninejad, N.; Ooi, C.H.; Nguyen, N.T.; Zhang, J. Investigation of viscoelastic focusing of particles and cells in a zigzag microchannel. Electrophoresis 2021, 42, 2230–2237. [Google Scholar] [CrossRef]
- Leshansky, A.M.; Bransky, A.; Korin, N.; Dinnar, U. Tunable nonlinear viscoelastic “focusing” in a microfluidic device. Phys. Rev. Lett. 2007, 98, 234501. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Kim, J.Y.; Lee, S.J.; Lee, S.S.; Kim, J.M. Sheathless elasto-inertial particle focusing and continuous separation in a straight rectangular microchannel. Lab Chip 2011, 11, 266–273. [Google Scholar] [CrossRef]
- Nam, J.; Lim, H.; Kim, D.; Jung, H.; Shin, S. Continuous separation of microparticles in a microfluidic channel via the elasto-inertial effect of non-Newtonian fluid. Lab Chip 2012, 12, 1347–1354. [Google Scholar] [CrossRef]
- Liu, C.; Xue, C.; Chen, X.; Shan, L.; Tian, Y.; Hu, G. Size-based separation of particles and cells utilizing viscoelastic effects in straight microchannels. Anal. Chem. 2015, 87, 6041–6048. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nam, J.; Shin, Y.; Tan, J.K.S.; Lim, Y.B.; Lim, C.T.; Kim, S. High-throughput malaria parasite separation using a viscoelastic fluid for ultrasensitive PCR detection. Lab Chip 2016, 16, 2086–2092. [Google Scholar] [CrossRef] [PubMed]
- Yuan, D.; Tan, S.H.; Zhao, Q.; Yan, S.; Sluyter, R.; Nguyen, N.-T.; Zhang, J.; Li, W. Sheathless Dean-flow-coupled elasto-inertial particle focusing and separation in viscoelastic fluid. RSC Adv. 2017, 7, 3461–3469. [Google Scholar] [CrossRef] [Green Version]
- Yuan, D.; Zhao, Q.; Yan, S.; Tang, S.-Y.; Zhang, Y.; Yun, G.; Nguyen, N.-T.; Zhang, J.; Li, M.; Li, W. Sheathless separation of microalgae from bacteria using a simple straight channel based on viscoelastic microfluidics. Lab Chip 2019, 19, 2811–2821. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Xuan, X. Elasto-inertial pinched flow fractionation for continuous shape-based particle separation. Anal. Chem. 2015, 87, 11523–11530. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Zhu, L.; Hua, R.-M.; Xuan, X. Continuous sheath-free separation of particles by shape in viscoelastic fluids. Appl. Phys. Lett. 2015, 107, 264102. [Google Scholar] [CrossRef]
- Valero, A.; Braschler, T.; Rauch, A.; Demierre, N.; Barral, Y.; Renaud, P. Tracking and synchronization of the yeast cell cycle using dielectrophoretic opacity. Lab Chip 2011, 11, 1754–1760. [Google Scholar] [CrossRef] [Green Version]
- Sugaya, S.; Yamada, M.; Seki, M. Observation of nonspherical particle behaviors for continuous shape-based separation using hydrodynamic filtration. Biomicrofluidics 2011, 5, 024103. [Google Scholar] [CrossRef] [Green Version]
- Beech, J.P.; Holm, S.H.; Adolfsson, K.; Tegenfeldt, J.O. Sorting cells by size, shape and deformability. Lab Chip 2012, 12, 1048–1051. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Zielinski, J.; Kozubowski, L.; Xuan, X. Continuous sheath-free separation of drug-treated human fungal pathogen Cryptococcus neoformans by morphology in biocompatible polymer solutions. Electrophoresis 2018, 39, 2362–2369. [Google Scholar] [CrossRef]
- Nam, J.; Jee, H.; Jang, W.S.; Yoon, J.; Park, B.G.; Lee, S.J.; Lim, C.S. Sheathless shape-based separation of Candida albicans using a Viscoelastic non-Newtonian fluid. Micromachines 2019, 10, 817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, D.; Yan, S.; Zhang, J.; Guijt, R.M.; Zhao, Q.; Li, W. Sheathless Separation of Cyanobacterial Anabaena by Shape Using Viscoelastic Microfluidics. Anal. Chem. 2021, 93, 12648–12654. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Lee, S.S.; Ahn, S.W.; Kang, K.; Shim, W.; Lee, G.; Hyun, K.; Kim, J.M. Deformability-selective particle entrainment and separation in a rectangular microchannel using medium viscoelasticity. Soft Matter 2012, 8, 5011–5019. [Google Scholar] [CrossRef]
- di Carlo, D.; Edd, J.F.; Humphry, K.J.; Stone, H.A.; Toner, M. Particle segregation and dynamics in confined flows. Phys. Rev. Lett. 2009, 102, 094503. [Google Scholar] [CrossRef] [Green Version]
- Gossett, D.R.; Carlo, D.D. Particle focusing mechanisms in curving confined flows. Anal. Chem. 2009, 81, 8459–8465. [Google Scholar] [CrossRef]
- Yuan, D.; Zhang, J.; Sluyter, R.; Zhao, Q.; Yan, S.; Alici, G.; Li, W. Continuous plasma extraction under viscoelastic fluid in a straight channel with asymmetrical expansion–contraction cavity arrays. Lab Chip 2016, 16, 3919–3928. [Google Scholar] [CrossRef]
- Asmolov, E.S. The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech. 1999, 381, 63–87. [Google Scholar] [CrossRef]
- di Carlo, D. Inertial microfluidics. Lab Chip 2009, 9, 3038–3046. [Google Scholar] [CrossRef]
- Rodd, L.; Cooper-White, J.; Boger, D.; McKinley, G.H. Role of the elasticity number in the entry flow of dilute polymer solutions in micro-fabricated contraction geometries. J. Non-Newton. Fluid Mech. 2007, 143, 170–191. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Fluid mechanics. In Dynamics of Polymeric Liquids; Wiley: Hoboken, NJ, USA, 1987; Volume 1. [Google Scholar]
- Magda, J.; Lou, J.; Baek, S.; DeVries, K. Second normal stress difference of a Boger fluid. Polymer 1991, 32, 2000–2009. [Google Scholar] [CrossRef]
- Tehrani, M. An experimental study of particle migration in pipe flow of viscoelastic fluids. J. Rheol. 1996, 40, 1057–1077. [Google Scholar] [CrossRef]
- Duffy, D.C.; McDonald, J.C.; Schueller, O.J.; Whitesides, G.M. Rapid prototyping of microfluidic systems in poly (dimethylsiloxane). Anal. Chem. 1998, 70, 4974–4984. [Google Scholar] [CrossRef] [PubMed]
- Yuan, D.; Sluyter, R.; Zhao, Q.; Tang, S.; Yan, S.; Yun, G.; Li, M.; Zhang, J.; Li, W. Dean-flow-coupled elasto-inertial particle and cell focusing in symmetric serpentine microchannels. Microfluid. Nanofluid. 2019, 23, 41. [Google Scholar] [CrossRef] [Green Version]
- Harboe, M. A method for determination of hemoglobin in plasma by near-ultraviolet spectrophotometry. Scand. J. Clin. Lab. Investig. 1959, 11, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Cookson, P.; Sutherland, J.; Cardigan, R. A simple spectrophotometric method for the quantification of residual haemoglobin in platelet concentrates. Vox Sang. 2004, 87, 264–271. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Y.; Cha, H.; Simmonds, M.J.; Fallahi, H.; An, H.; Ta, H.T.; Nguyen, N.-T.; Zhang, J.; McNamee, A.P. Enhanced Blood Plasma Extraction Utilising Viscoelastic Effects in a Serpentine Microchannel. Biosensors 2022, 12, 120. https://doi.org/10.3390/bios12020120
Dai Y, Cha H, Simmonds MJ, Fallahi H, An H, Ta HT, Nguyen N-T, Zhang J, McNamee AP. Enhanced Blood Plasma Extraction Utilising Viscoelastic Effects in a Serpentine Microchannel. Biosensors. 2022; 12(2):120. https://doi.org/10.3390/bios12020120
Chicago/Turabian StyleDai, Yuchen, Haotian Cha, Michael J. Simmonds, Hedieh Fallahi, Hongjie An, Hang T. Ta, Nam-Trung Nguyen, Jun Zhang, and Antony P. McNamee. 2022. "Enhanced Blood Plasma Extraction Utilising Viscoelastic Effects in a Serpentine Microchannel" Biosensors 12, no. 2: 120. https://doi.org/10.3390/bios12020120
APA StyleDai, Y., Cha, H., Simmonds, M. J., Fallahi, H., An, H., Ta, H. T., Nguyen, N.-T., Zhang, J., & McNamee, A. P. (2022). Enhanced Blood Plasma Extraction Utilising Viscoelastic Effects in a Serpentine Microchannel. Biosensors, 12(2), 120. https://doi.org/10.3390/bios12020120











