New Generation Dielectrophoretic-Based Microfluidic Device for Multi-Type Cell Separation
Abstract
:1. Introduction
2. Theory
2.1. Dielectrophoresis
2.2. Electroporation
3. Methodology
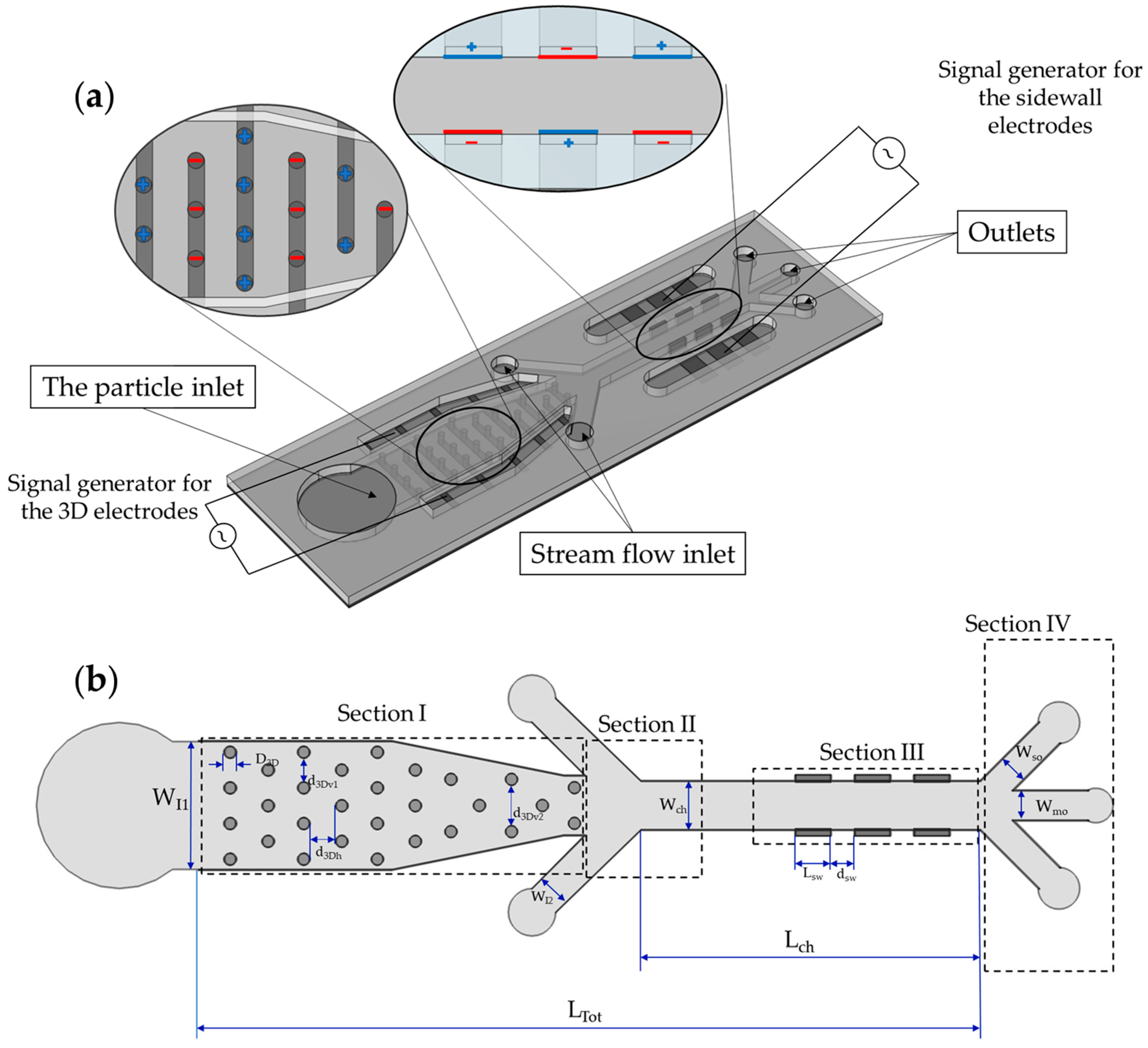
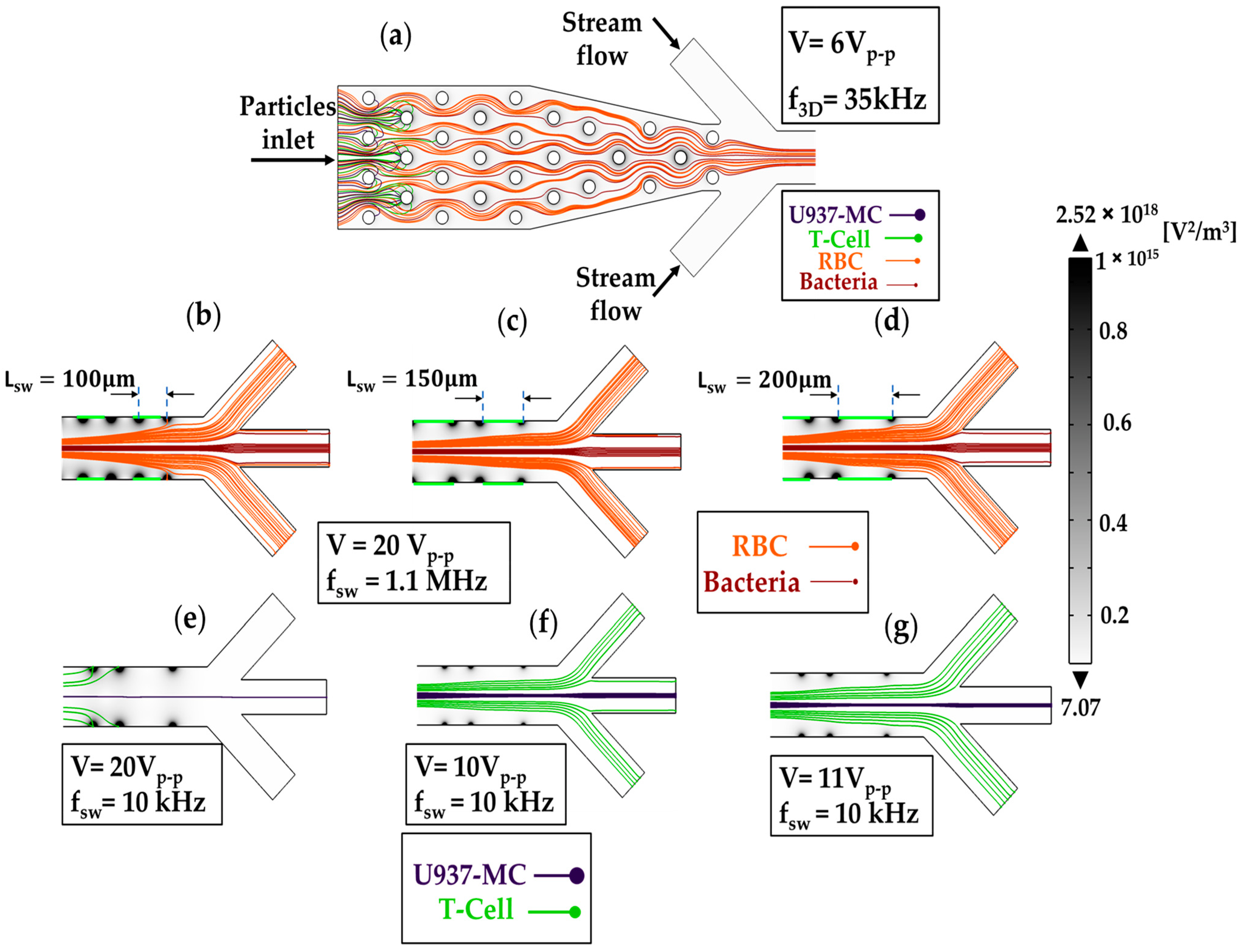
3.1. The Microfluidic Device
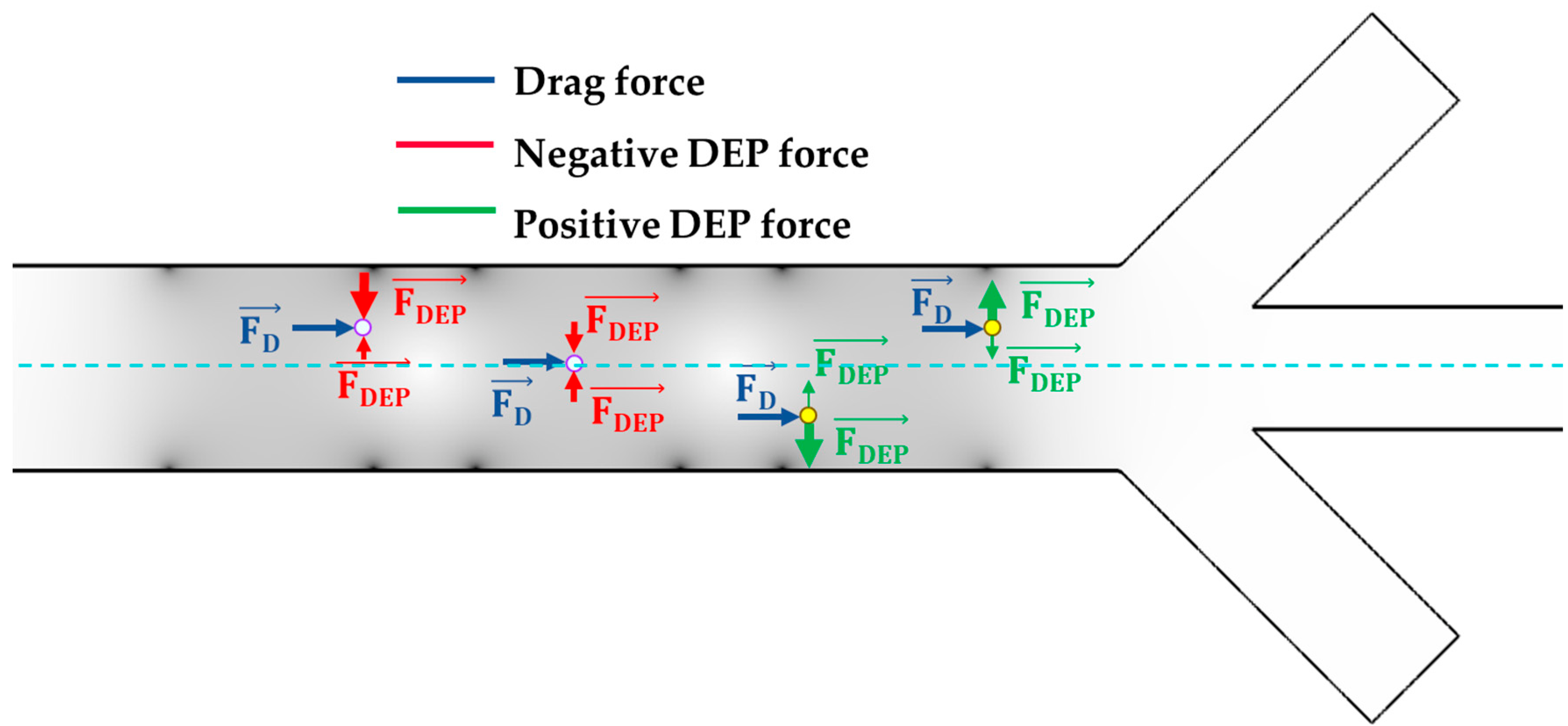
3.2. Working Principle of the Microfluidic Device
3.3. Governing Equations
3.3.1. Electric Field
3.3.2. Creeping Flow
3.3.3. Particle Tracing
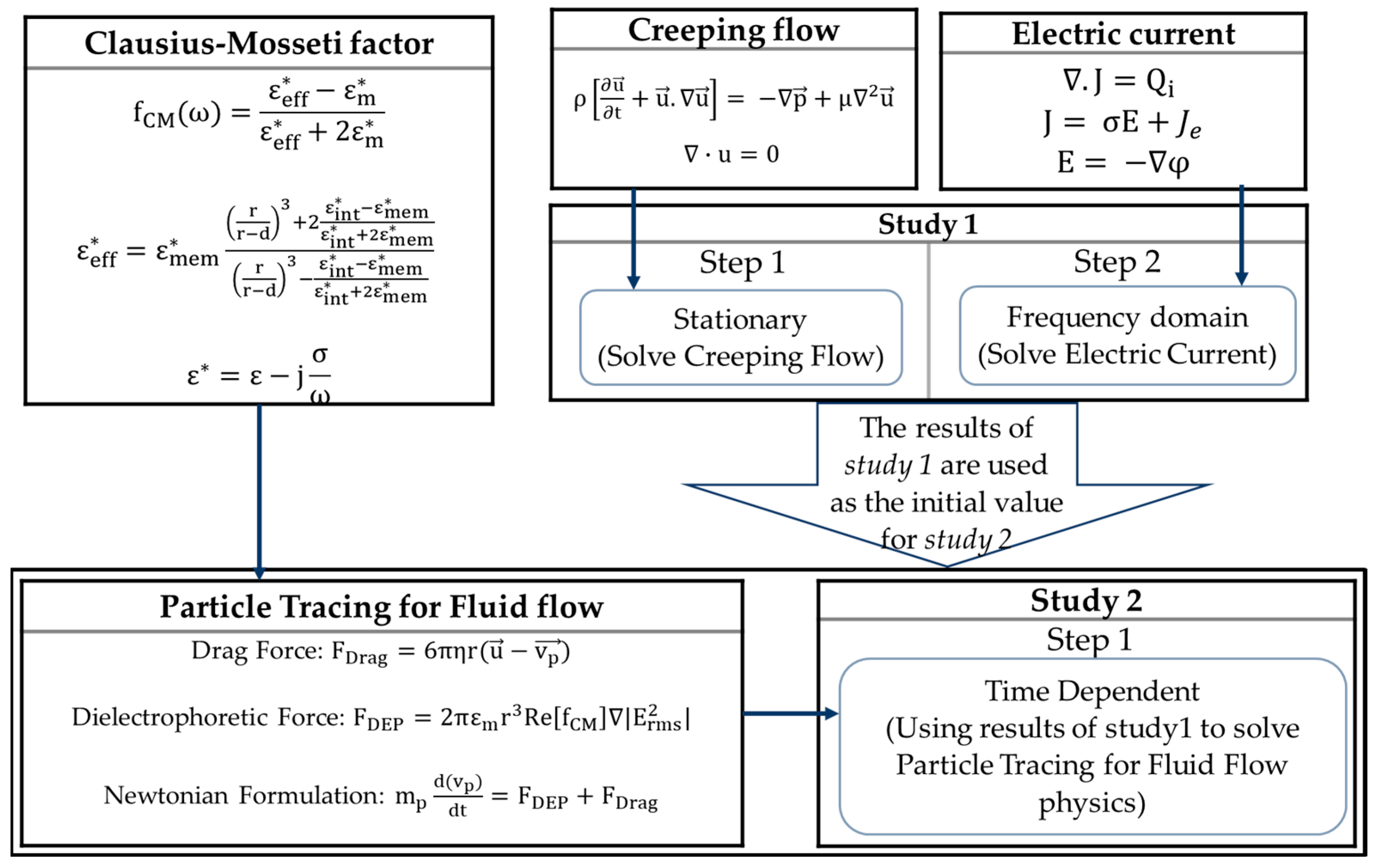
3.4. Numerical Modeling
3.4.1. Simulation
3.4.2. Validation and Mesh Independency
4. Results and Discussion
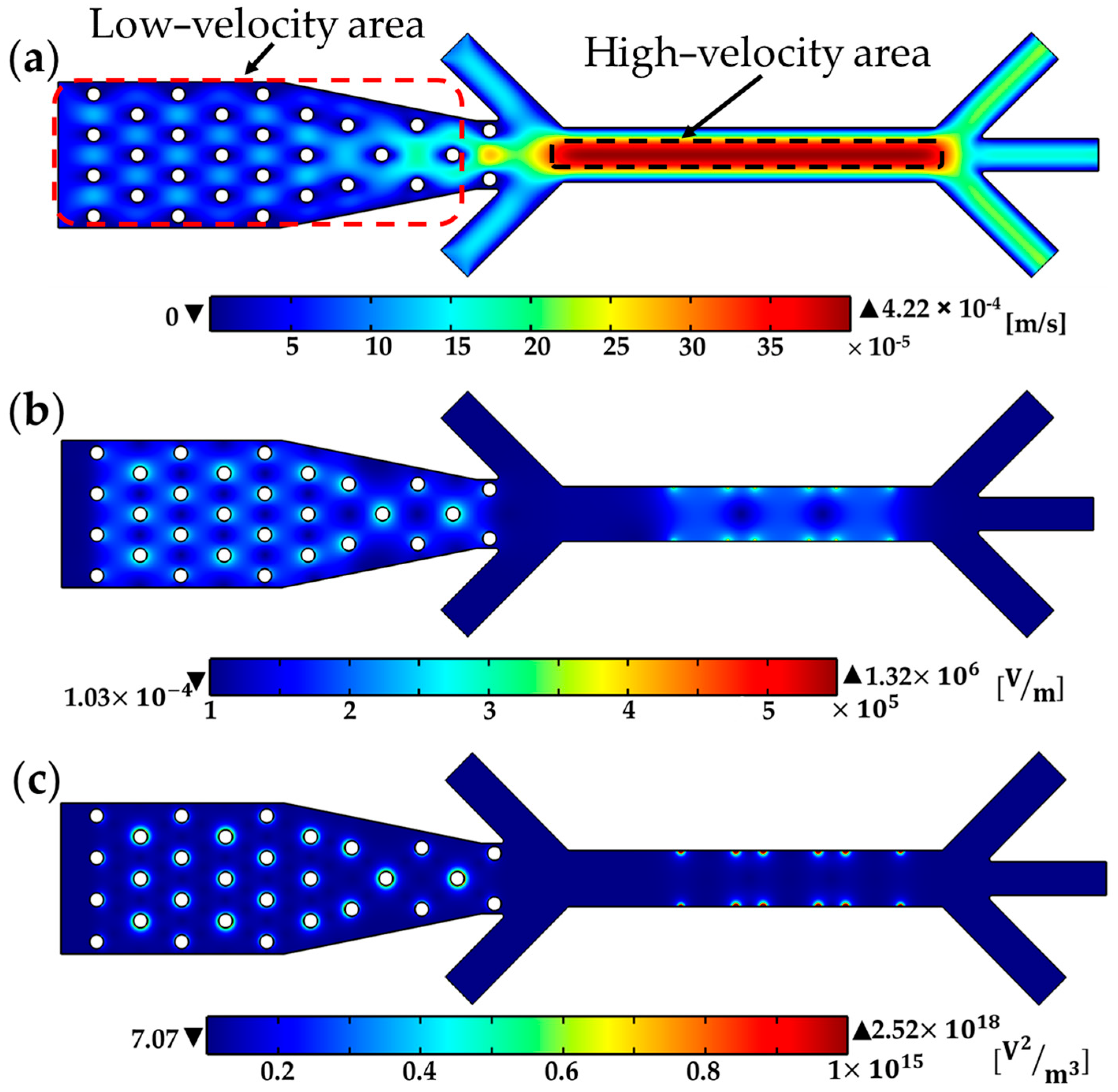
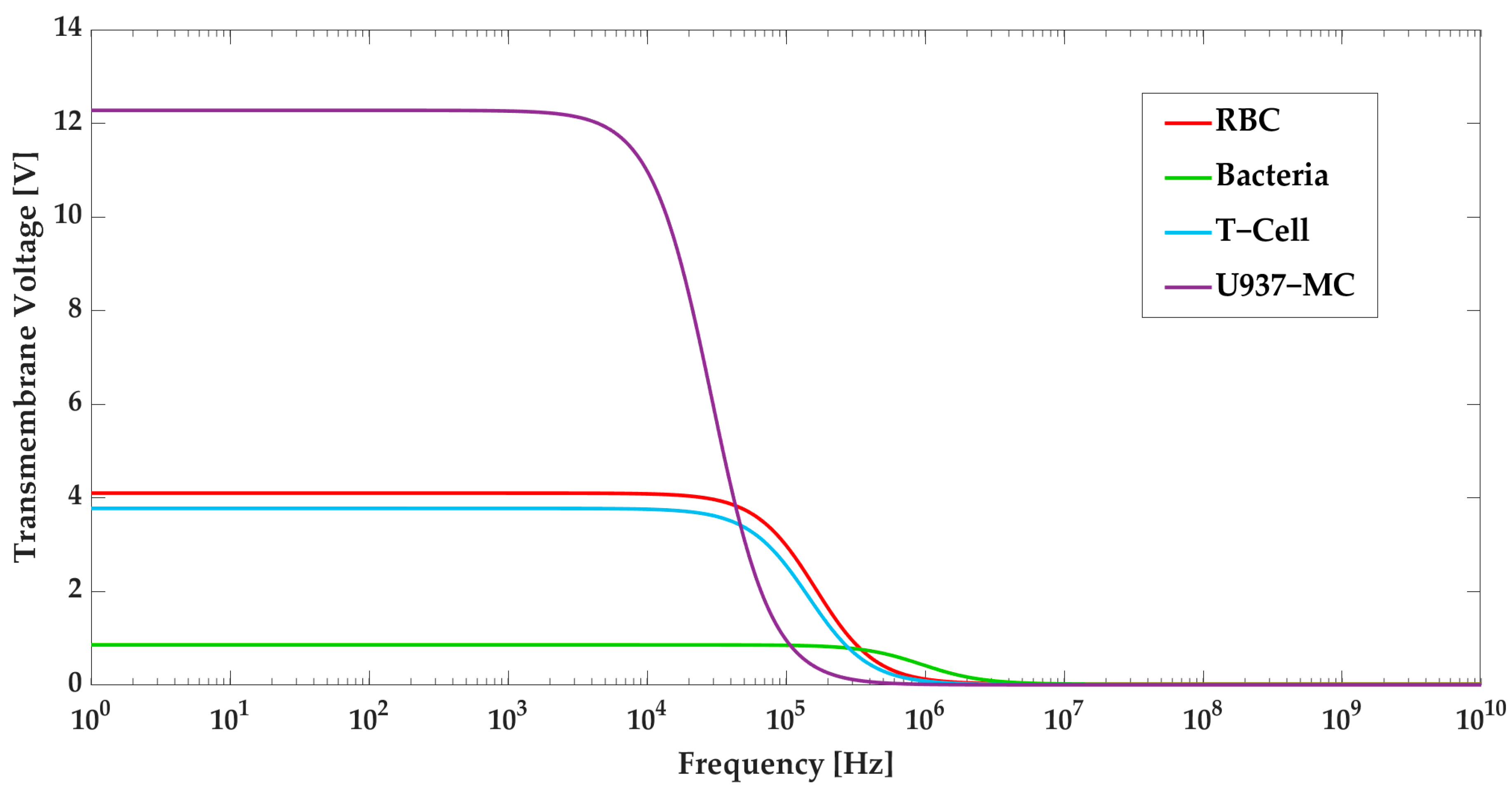
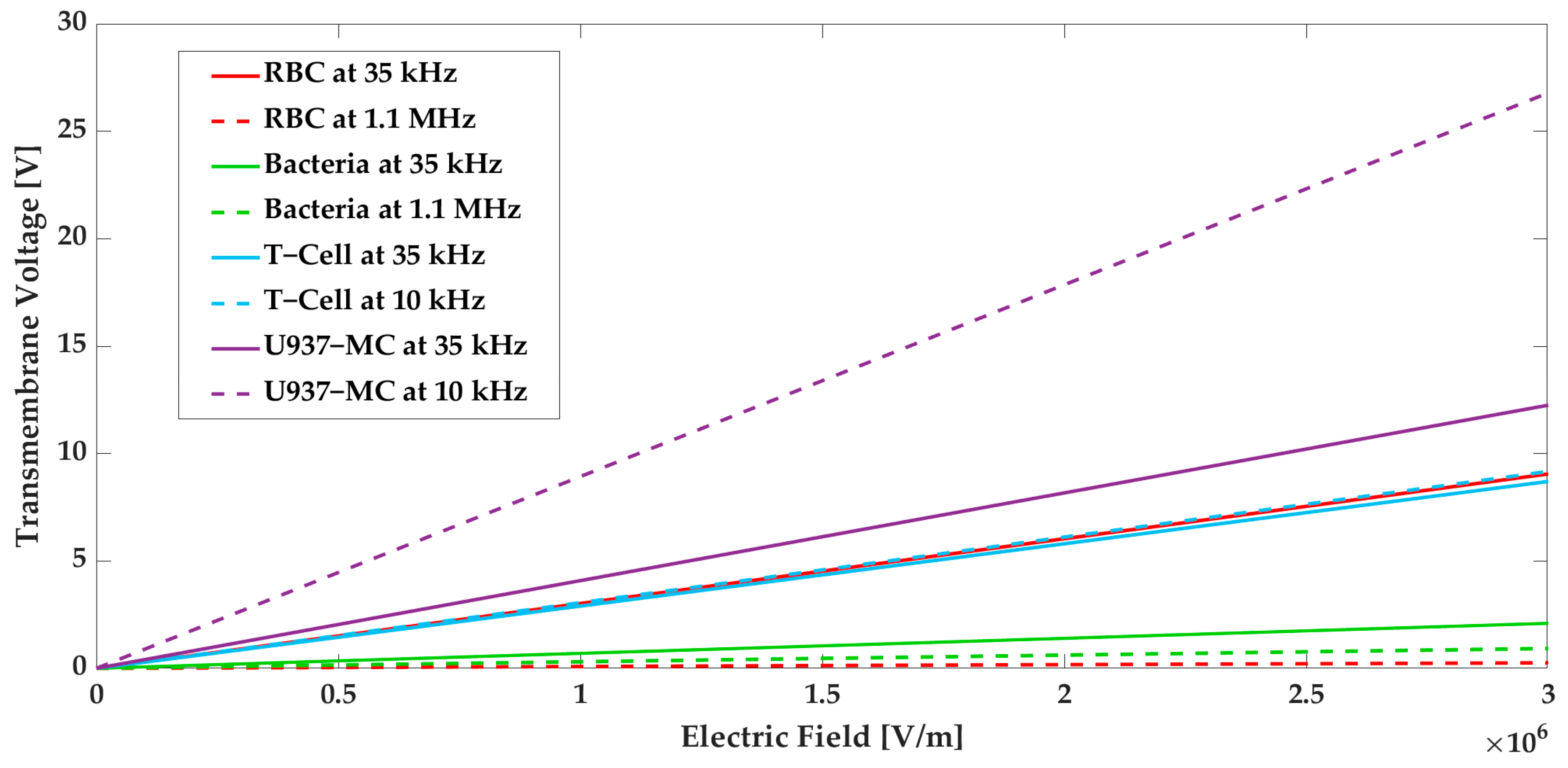
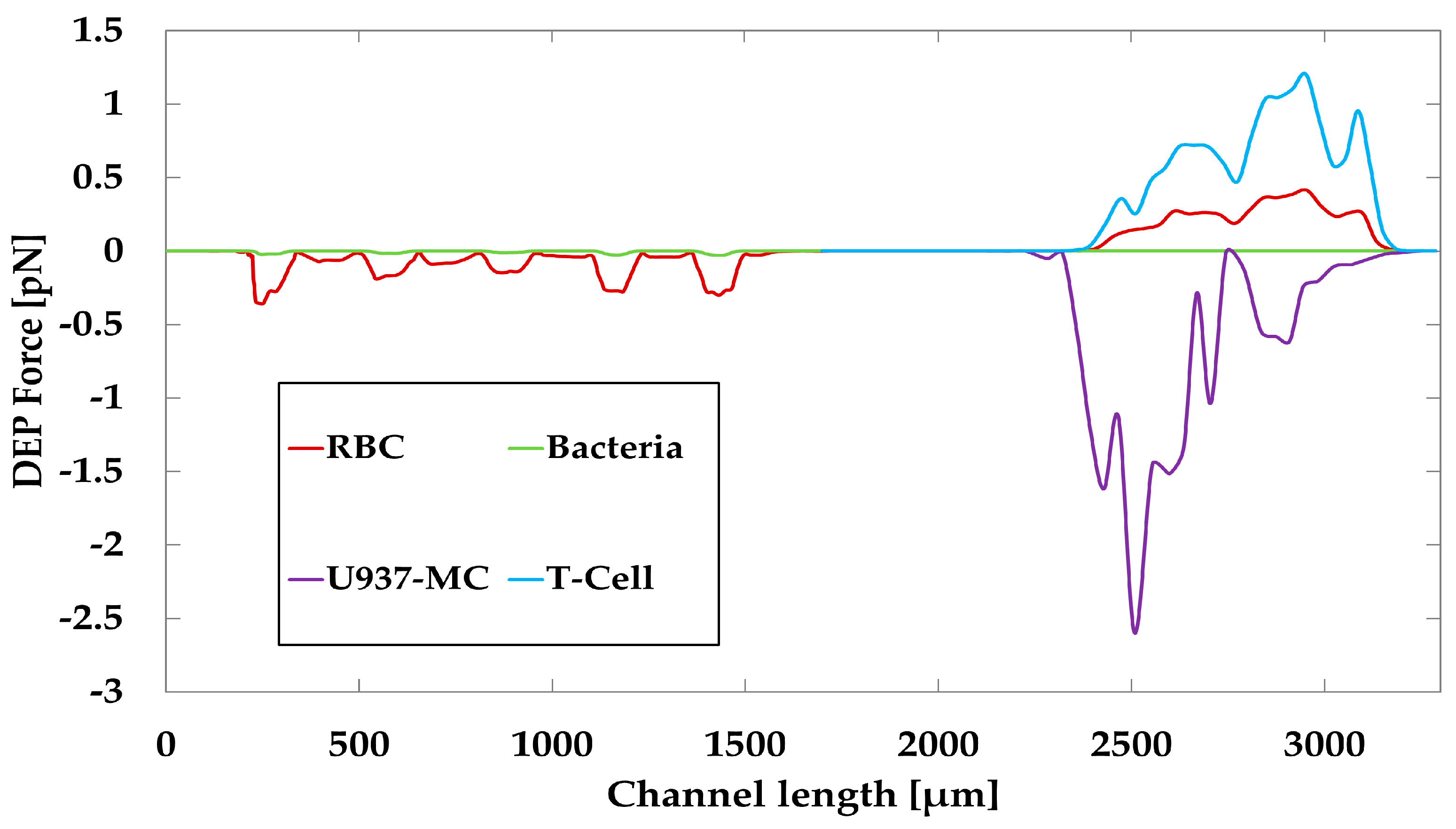
4.1. Numerical Modeling
4.2. Cell-Throuput Optimization of the Microfluidic Device
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| r | Radius | J | Current density |
| CM | Clausius–Mossotti | Q | Charge density |
| fCM | Clausius–Mossotti factor | P | Pressure |
| Re | Real | u | Velocity vector |
| E | Electric field | vp | Particle velocity |
| FDEP | DEP force | m | mass |
| FDrag | Drag force | DEP | Dielectrophoresis |
| D | Diameter | AC | Alternating current |
| d | Thickness of the membrane | nDEP | Negative DEP |
| h | Height of electrodes | pDEP | Posetive DEP |
| L | Microchannel length | RBC | Red blood cells |
| W | Microchannel width | CTC | Circulating tumor cell |
| Vp-p | Pick to pick voltage | d3D | Distance between 3D electrodes |
| f | Applied frequency | dsw | Distance between planar electrodes |
| t | Time | ||
| Greek | |||
| ε | Permittivity | Notation for gradient | |
| σ | Conductivity | φ | Applied potential |
| ω | Angular frequency | η | Dynamic viscosity |
| µ | Dynamic viscosity | ||
References
- Rahman, N.A.; Ibrahim, F.; Yafouz, B. Dielectrophoresis for Biomedical Sciences Applications: A Review. Sensors 2017, 17, 449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, F.C.; Liao, C.S.; Lee, G.B. An Integrated Microfluidic Chip for DNA/RNA Amplification, Electrophoresis Separation and On-Line Optical Detection. Electrophoresis 2006, 27, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Ou, X.; Chen, P.; Huang, X.; Li, S.; Liu, B.F. Microfluidic Chip Electrophoresis for Biochemical Analysis. J. Sep. Sci. 2020, 43, 258–270. [Google Scholar] [CrossRef] [PubMed]
- Sengul, E.; Sharbati, P.; Elitas, M.; Islam, M.; Korvink, J.G. Analysis of U87 Glioma Cells by Dielectrophoresis. Electrophoresis 2022, 43, 1357–1365. [Google Scholar] [CrossRef]
- Farasat, M.; Aalaei, E.; Kheirati Ronizi, S.; Bakhshi, A.; Mirhosseini, S.; Zhang, J.; Nguyen, N.T.; Kashaninejad, N. Signal-Based Methods in Dielectrophoresis for Cell and Particle Separation. Biosensors 2022, 12, 510. [Google Scholar] [CrossRef]
- Tian, L.; Ye, Z.; Gui, L. A Study of Dielectrophoresis-Based Liquid Metal Droplet Control Microfluidic Device. Micromachines 2021, 12, 340. [Google Scholar] [CrossRef]
- Zaman, M.A.; Wu, M.; Padhy, P.; Jensen, M.A.; Hesselink, L.; Davis, R.W. Modeling Brownian Microparticle Trajectories in Lab-on-a-Chip Devices with Time Varying Dielectrophoretic or Optical Forces. Micromachines 2021, 12, 1265. [Google Scholar] [CrossRef]
- Altay, R.; Yapici, M.K.; Koşar, A. A Hybrid Spiral Microfluidic Platform Coupled with Surface Acoustic Waves for Circulating Tumor Cell Sorting and Separation: A Numerical Study. Biosensors 2022, 12, 171. [Google Scholar] [CrossRef]
- Alnaimat, F.; Dagher, S.; Mathew, B.; Hilal-Alnqbi, A.; Khashan, S. Microfluidics Based Magnetophoresis: A Review. Chem. Rec. 2018, 18, 1596–1612. [Google Scholar] [CrossRef]
- Shamloo, A.; Yazdani, A.; Saghafifar, F. Investigation of a Two-Step Device Implementing Magnetophoresis and Dielectrophoresis for Separation of Circulating Tumor Cells from Blood Cells. Eng. Life Sci. 2020, 20, 296–304. [Google Scholar] [CrossRef]
- Atajanov, A.; Zhbanov, A.; Yang, S. Sorting and Manipulation of Biological Cells and the Prospects for Using Optical Forces. Micro Nano Syst. Lett. 2018, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Pereira, D.; Panão, M.O. Photophoresis of Spherical Particles in Slip-Flow Regime. Phys. Fluids 2022, 34, 103307. [Google Scholar] [CrossRef]
- Pethig, R.; Menachery, A.; Pells, S.; de Sousa, P. Dielectrophoresis: A Review of Applications for Stem Cell Research. J. Biomed. Biotechnol. 2010, 2010, 182581. [Google Scholar] [CrossRef]
- Pethig, R.; Markx, G.H. Applications of Dielectrophoresis in Biotechnology. Trends Biotechnol. 1997, 15, 426–432. [Google Scholar] [CrossRef]
- Cheng, I.-F.; Froude, V.E.; Zhu, Y.; Chang, H.-C.; Chang, H.-C. A Continuous High-Throughput Bioparticle Sorter Based on 3D Traveling-Wave Dielectrophoresis†. Lab Chip 2009, 9, 3193–3201. [Google Scholar] [CrossRef]
- Bhatt, G.; Mishra, K.; Ramanathan, G.; Bhattacharya, S. Dielectrophoresis Assisted Impedance Spectroscopy for Detection of Gold-Conjugated Amplified DNA Samples. Sens. Actuators B Chem. 2019, 288, 442–453. [Google Scholar] [CrossRef]
- Giraud, G.; Pethig, R.; Schulze, H.; Henihan, G.; Terry, J.G.; Menachery, A.; Ciani, I.; Corrigan, D.; Campbell, C.J.; Mount, A.R.; et al. Dielectrophoretic Manipulation of Ribosomal RNA. Biomicrofluidics 2011, 5, 024116. [Google Scholar] [CrossRef] [Green Version]
- Mohamad, A.S.; Hamzah, R.; Hoettges, K.F.; Hughes, M.P. A Dielectrophoresis-Impedance Method for Protein Detection and Analysis. AIP Adv. 2017, 7, 015202. [Google Scholar] [CrossRef] [Green Version]
- Kumar, N.; Wang, W.; Ortiz-Marquez, J.C.; Catalano, M.; Gray, M.; Biglari, N.; Hikari, K.; Ling, X.; Gao, J.; van Opijnen, T.; et al. Dielectrophoresis Assisted Rapid, Selective and Single Cell Detection of Antibiotic Resistant Bacteria with G-FETs. Biosens. Bioelectron. 2020, 156, 112123. [Google Scholar] [CrossRef]
- Vykoukal, D.M.; Gascoyne, P.R.C.; Vykoukal, J. Dielectric Characterization of Complete Mononuclear and Polymorphonuclear Blood Cell Subpopulations for Label-Free Discrimination. Integr. Biol. 2009, 1, 477–484. [Google Scholar] [CrossRef]
- Russo, G.I.; Musso, N.; Romano, A.; Caruso, G.; Petralia, S.; Lanzanò, L.; Broggi, G.; Camarda, M. The Role of Dielectrophoresis for Cancer Diagnosis and Prognosis. Cancers 2021, 14, 198. [Google Scholar] [CrossRef] [PubMed]
- Obeng, Y.S.; Nablo, B.J.; Reyes, D.R.; Poster, D.L.; Postek, M.T. Broadband Dielectric Spectroscopy as a Potential Label-Free Method to Rapidly Verify Ultraviolet-C Radiation Disinfection. J. Res. Natl. Inst. Stand. Technol. 2021, 126, 126022. [Google Scholar] [CrossRef] [PubMed]
- Gascoyne, P.R.C.; Vykoukal, J. Particle Separation by Dielectrophoresis. Electrophoresis 2002, 23, 1973–1983. [Google Scholar] [CrossRef]
- Li, X.; Duan, J.; Qu, Z.; Wang, J.; Ji, M.; Zhang, B. Continuous Particle Separation Driven by 3D Ag-PDMS Electrodes with Dielectric Electrophoretic Force Coupled with Inertia Force. Micromachines 2022, 13, 117. [Google Scholar] [CrossRef] [PubMed]
- Qian, C.; Huang, H.; Chen, L.; Li, X.; Ge, Z.; Chen, T.; Yang, Z.; Sun, L. Dielectrophoresis for Bioparticle Manipulation. Int. J. Mol. Sci. 2014, 15, 18281–18309. [Google Scholar] [CrossRef] [Green Version]
- Turcan, I.; Olariu, M.A. Dielectrophoretic Manipulation of Cancer Cells and Their Electrical Characterization. ACS Comb. Sci. 2020, 22, 554–578. [Google Scholar] [CrossRef]
- Wolff, A.; Leiterer, C.; Csaki, A.; Fritzsche, W. Dielectrophoretic Manipulation of DNA in Microelectrode Gaps for Single-Molecule Constructs. Front. Biosci. 2008, 13, 6834–6840. [Google Scholar] [CrossRef] [Green Version]
- Ettehad, H.M.; Wenger, C. Characterization and Separation of Live and Dead Yeast Cells Using Cmos-Based Dep Microfluidics. Micromachines 2021, 12, 270. [Google Scholar] [CrossRef]
- Kung, Y.C.; Niazi, K.R.; Chiou, P.Y. Tunnel Dielectrophoresis for Ultra-High Precision Size-Based Cell Separation. Lab Chip 2021, 21, 1049–1060. [Google Scholar] [CrossRef]
- Varmazyari, V.; Habibiyan, H.; Ghafoorifard, H.; Ebrahimi, M.; Ghafouri-Fard, S. A Dielectrophoresis-Based Microfluidic System Having Double-Sided Optimized 3D Electrodes for Label-Free Cancer Cell Separation with Preserving Cell Viability. Sci. Rep. 2022, 12, 12100. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Le Manh, T.; Nguyen, T.S.; Le, V.T.; Van Hieu, N. Applied Electric Field Analysis and Numerical Investigations of the Continuous Cell Separation in a Dielectrophoresis-Based Microfluidic Channel. J. Sci. Adv. Mater. Devices 2021, 6, 11–18. [Google Scholar] [CrossRef]
- Kazemi, B.; Darabi, J. Numerical Simulation of Dielectrophoretic Particle Separation Using Slanted Electrodes. Phys. Fluids 2018, 30, 102003. [Google Scholar] [CrossRef]
- Han, S.I.; Lee, S.M.; Joo, Y.D.; Han, K.H. Lateral Dielectrophoretic Microseparators to Measure the Size Distribution of Blood Cells. Lab Chip 2011, 11, 3864–3872. [Google Scholar] [CrossRef] [PubMed]
- Büyükkoçak, S.; Özer, M.B.; Çetin, B. Numerical Modeling of Ultrasonic Particle Manipulation for Microfluidic Applications. Microfluid. Nanofluid. 2014, 17, 1025–1037. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, Y.; Pesch, G.R.; Baune, M.; Du, F.; Liu, X. Rational Design and Numerical Analysis of a Hybrid Floating CIDE Separator for Continuous Dielectrophoretic Separation of Microparticles at High Throughput. Micromachines 2022, 13, 582. [Google Scholar] [CrossRef] [PubMed]
- Shirmohammadli, V.; Manavizadeh, N. Application of Differential Electrodes in a Dielectrophoresis-Based Device for Cell Separation. IEEE Trans. Electron. Devices 2019, 66, 4075–4080. [Google Scholar] [CrossRef]
- Zackria Ansar Babu Irshad, M.; Tirth, V.; Yousuff, C.M.; Shukla, N.K.; Islam, S.; Irshad, K.; Aarif, K.O.M. Simulation Guided Microfluidic Design for Multitarget Separation Using Dielectrophoretic Principle. Biochip J. 2020, 14, 390–404. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Van Manh, H.; Van Hieu, N. Numerical Simulation-Based Performance Improvement of the Separation of Circulating Tumor Cells from Bloodstream in a Microfluidic Platform by Dielectrophoresis. Korea Aust. Rheol. J. 2022, 34, 335–347. [Google Scholar] [CrossRef]
- Pimbley, D.W.; Patel, P.D.; Robertson, C.J. Dielectrophoresis; Wiley: Hoboken, NJ, USA, 2015; Volume 12, ISBN 9781118671450. [Google Scholar]
- Pethig, R. Dielectrophoresis: Status of the Theory, Technology, and Applications. Biomicrofluidics 2010, 4, 022811. [Google Scholar] [CrossRef] [Green Version]
- Valero, A.; Braschler, T.; Renaud, P. A Unified Approach to Dielectric Single Cell Analysis: Impedance and Dielectrophoretic Force Spectroscopy. Lab Chip 2010, 10, 2216–2225. [Google Scholar] [CrossRef]
- Kotnik, T.; Miklavčič, D. Theoretical Evaluation of the Distributed Power Dissipation in Biological Cells Exposed to Electric Fields. Bioelectromagnetics 2000, 21, 385–394. [Google Scholar] [CrossRef]
- Miklavčič, D. (Ed.) Handbook of Electroporation; Springer International Publishing: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X. Blood Cells Separation Microfluidic Chip Based on Dielectrophoretic Force. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 206. [Google Scholar] [CrossRef]
- Pallavi, K. Dielectrophoresis (DEP) and Travelling Wave Dielectrophoresis (TWDEP) Based Cell Manipulation Using Microfluidics. Master’s Thesis, Indian Institute of Technology Hyderabad, Sangareddy, India, 2015. [Google Scholar]
- Punjiya, M.; Nejad, H.R.; Mathews, J.; Levin, M.; Sonkusale, S. A Flow through Device for Simultaneous Dielectrophoretic Cell Trapping and AC Electroporation. Sci. Rep. 2019, 9, 11988. [Google Scholar] [CrossRef] [Green Version]
- Lewpiriyawong, N.; Yang, C.; Lam, Y.C. Continuous Sorting and Separation of Microparticles by Size Using AC Dielectrophoresis in a PDMS Microfluidic Device with 3-D Conducting PDMS Composite Electrodes. Electrophoresis 2010, 31, 2622–2631. [Google Scholar] [CrossRef]
- Numerical Methods: Using MATLAB—George Lindfield, John Penny—Google Books. Available online: https://books.google.com.tr/books?hl=en&lr=&id=JWhyDwAAQBAJ&oi=fnd&pg=PP1&dq=matlab+numerical+methods&ots=jnONbb6K6z&sig=AQlcwBE7cAvnw2-fpbFu8wL8UFo&redir_esc=y#v=onepage&q&f=false (accessed on 11 October 2022).
- Erdem, N.; Yildizhan, Y.; Elitas, M. A Numerical Approach for Dielectrophoretic Characterization and Separation of Human Hematopoietic Cells. Int. J. Eng. Res. 2017, 6, 1079–1082. [Google Scholar] [CrossRef]
- Martinez-Duarte, R.; Camacho-Alanis, F.; Renaud, P.; Ros, A. Dielectrophoresis of Lambda-DNA Using 3D Carbon Electrodes. Electrophoresis 2013, 34, 1113–1122. [Google Scholar] [CrossRef]
- Emmerich, M.E.P.; Sinnigen, A.-S.; Neubauer, P.; Birkholz, M. Dielectrophoretic Separation of Blood Cells. Biomed. Microdevices 2022, 24, 30. [Google Scholar] [CrossRef]
- Alnaimat, F.; Mathew, B.; Hilal-Alnaqbi, A. Modeling a Dielectrophoretic Microfluidic Device with Vertical Interdigitated Transducer Electrodes for Separation of Microparticles Based on Size. Micromachines 2020, 11, 563. [Google Scholar] [CrossRef]
- Wang, L.; Lu, J.; Marchenko, S.A.; Monuki, E.S.; Flanagan, L.A.; Lee, A.P. Dual Frequency Dielectrophoresis with Interdigitated Sidewall Electrodes for Microfluidic Flow-Through Separation of Beads and Cells. Electrophoresis 2009, 30, 782–791. [Google Scholar] [CrossRef]
- Yildizhan, Y.; Erdem, N.; Islam, M.; Martinez-Duarte, R.; Elitas, M. Dielectrophoretic Separation of Live and Dead Monocytes Using 3D Carbon-Electrodes. Sensors 2017, 17, 2691. [Google Scholar] [CrossRef] [Green Version]
- Siani, O.Z.; Sojoodi, M.; Targhi, M.Z.; Movahedin, M. Blood Particle Separation Using Dielectrophoresis in a Novel Microchannel: A Numerical Study. Cell J. 2019, 22, 218–226. [Google Scholar] [CrossRef]



| Study Objective | Simulation Software | System Efficiency | Ref. |
|---|---|---|---|
| Optimization of a DEP-base microfluidic device for cancer cell separation with preserving cell viability. | COMSOL Multiphysics | 95% | [30] |
| Numerical modeling of an ultrasonic-based system for microparticles separation. | COMSOL Multiphysics | 100% | [34] |
| Design and numerical analysis of a novel DEP-based microparticle separator device. | COMSOL Multiphysics | Close to 100% | [35] |
| Optimization of a microfluidic device based on direct current dielectrophoresis to separate breast cancer cells from red and white blood cells. | COMSOL Multiphysics | 100% | [36] |
| Numerical investigation of a novel hybrid microfluidic design for cell sorting and continuous separation of CTCs from RBCs. | COMSOL Multiphysics | 97% | [31] |
| Numerical optimization of a multistage hybrid microfluidics platform that utilizes inertial and acoustic forces for particle separation. | COMSOL Multiphysics | - | [8] |
| Numerical optimization of a DEP-based cell separation device | Open FOAM, COMSOL Multiphysics | - | [32] |
| Modeling and optimization of a novel DEP-based multitarget cell separation microfluidic device | COMSOL Multiphysics | - | [37] |
| Numerical investigation and optimization of a DEP-based microfluidic platform for continuous CTC separation from blood stream | COMSOL Multiphysics | 100% | [38] |
| The Parameter | Symbol | Value |
|---|---|---|
| Height of microfluidic channel [µm] | hch | 100 |
| Height of 3D cylindrical electrodes [µm] | h3D | 90 |
| Height of sidewall electrodes [µm] | hsw | 100 |
| Total length of the device [µm] | LTot | 3200 |
| Length of the microchannel from the buffer inlets to the outlet [µm] | Lch | 1350 |
| Width of the sample inlet [µm] | WI1 | 540 |
| Width of buffer inlets [µm] | WI2 | 140 |
| Width of the microchannel in Section III [µm] | Wch | 200 |
| Width of side outlets [µm] | Wso | 140 |
| Width of the outlet in the middle [µm] | Wmo | 130 |
| Diameter of 3D cylindrical electrodes [µm] | D3D | 50 |
| Edge to edge horizontal distance between 3D cylindrical electrodes [µm] | d3Dh | 100 |
| Edge to edge vertical distance between 3D cylindrical electrodes (column 1–6 and 11) [µm] | d3Dv1 | 100 |
| Edge to edge vertical distance between 3D cylindrical electrodes (column 7 and 9) [µm] | d3Dv2 | 170 |
| Length of 3D sidewall electrodes [µm] | Lsw | 200 |
| Edge to edge distance between 3D sidewall electrodes [µm] | dsw | 100 |
| Cell Group to Separate | Separation Route | Separation Step | Particle Trajectory | |||
|---|---|---|---|---|---|---|
| Group #1 | Group #2 | Group #n | ||||
| 3D Electrode Frequency [Hz] | Sidewall Electrode Frequency [Hz] |  Cell #1−1 Cell #1−1 Cell #1−2 Cell #1−2 |  Cell #2−1 Cell #2−1 Cell #2−2 Cell #2−2 |  Cell #n−1 Cell #n−1 Cell #n−2 Cell #n−2 | ||
| Group #1 | f3D,1 | fsw,1 | Step I | 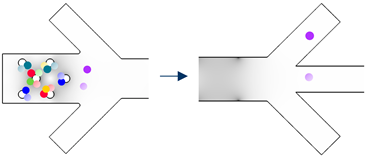 | ||
| Group #2 | f3D,2 | fsw,2 | Step II |  | ||
| Group #n | off | fsw,n | Step n | 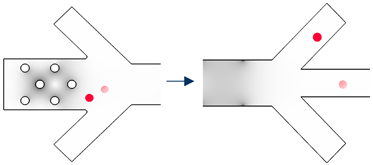 | ||
| Bio Particle | Radius [mm] | Membrane Thickness [nm] | Cytoplasm Permittivity [-] | Cytoplasm Conductivity [S/m] | Membrane Permittivity [-] | Membrane Conductivity [S/m] |
|---|---|---|---|---|---|---|
| RBC | 2.8 | 4.5 | 59 | 0.31 | 4.44 | 10 × 10−6 |
| Bacteria | 0.5 | 9 | 55 | 0.46 | 7 | 2.5 × 10−5 |
| T-cell | 3.29 | 7.5 | 103.9 | 0.73 | 8.89 | 2.7 × 10−5 |
| U937-MC | 7 | 7 | 50 | 0.5 | 12.5 | 1 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharbati, P.; Sadaghiani, A.K.; Koşar, A. New Generation Dielectrophoretic-Based Microfluidic Device for Multi-Type Cell Separation. Biosensors 2023, 13, 418. https://doi.org/10.3390/bios13040418
Sharbati P, Sadaghiani AK, Koşar A. New Generation Dielectrophoretic-Based Microfluidic Device for Multi-Type Cell Separation. Biosensors. 2023; 13(4):418. https://doi.org/10.3390/bios13040418
Chicago/Turabian StyleSharbati, Pouya, Abdolali K. Sadaghiani, and Ali Koşar. 2023. "New Generation Dielectrophoretic-Based Microfluidic Device for Multi-Type Cell Separation" Biosensors 13, no. 4: 418. https://doi.org/10.3390/bios13040418
APA StyleSharbati, P., Sadaghiani, A. K., & Koşar, A. (2023). New Generation Dielectrophoretic-Based Microfluidic Device for Multi-Type Cell Separation. Biosensors, 13(4), 418. https://doi.org/10.3390/bios13040418






