An Amplitude Analysis-Based Magnetoelastic Biosensing Method for Quantifying Blood Coagulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Description of the Relationship Between the Magnetoelastic Resonant Amplitude and the Liquid Viscosity
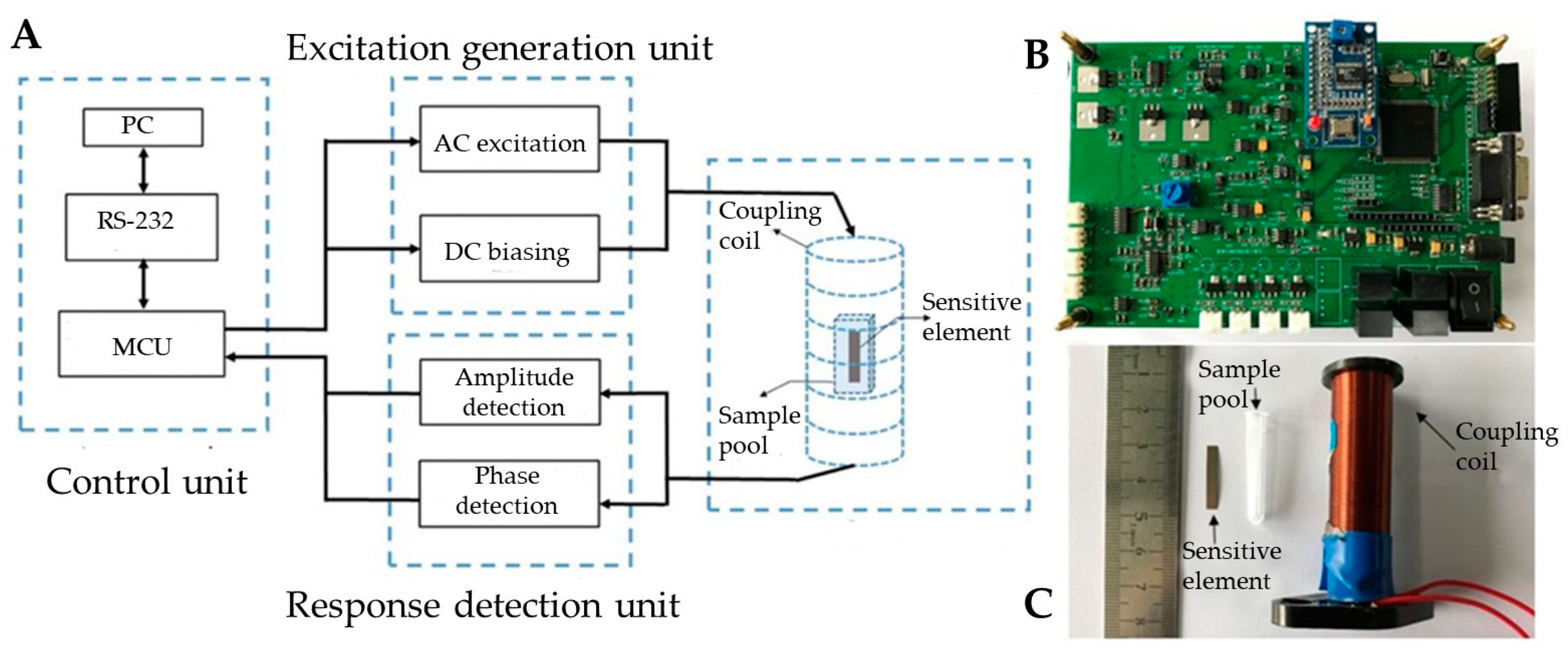
2.2. Magnetoelastic Measurement Device and Sensitive Element Fabrication
2.3. Chemicals and Apparatus
2.4. Measurements of Glycerol Solutions by Amplitude Analysis
2.5. Monitoring the Blood Coagulation
3. Results and Discussion
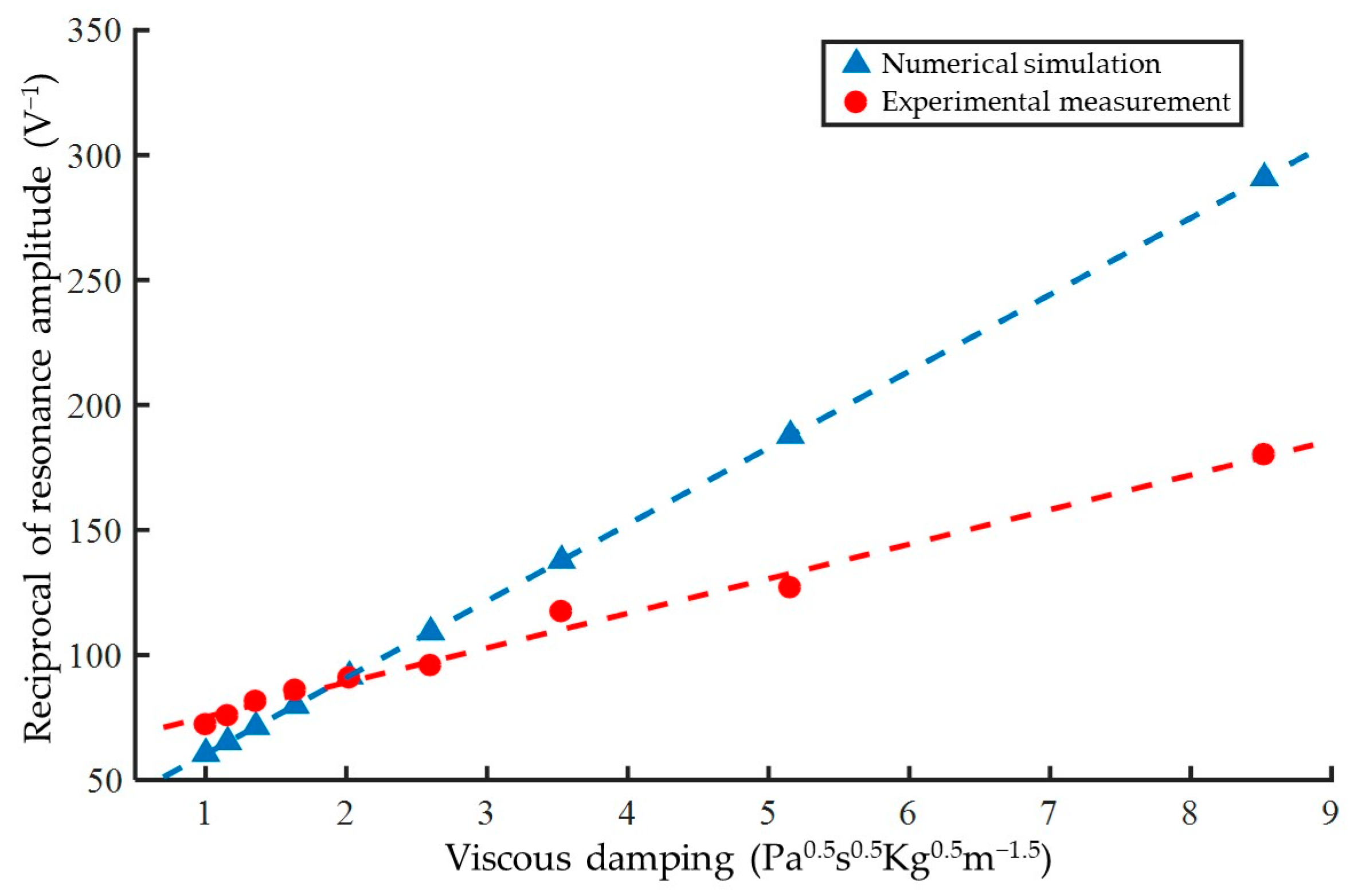
3.1. Verification of Amplitude Analysis Method Based on Glycerol Samples
3.2. Quantitative Assessment of Viscosity Variations During Coagulation
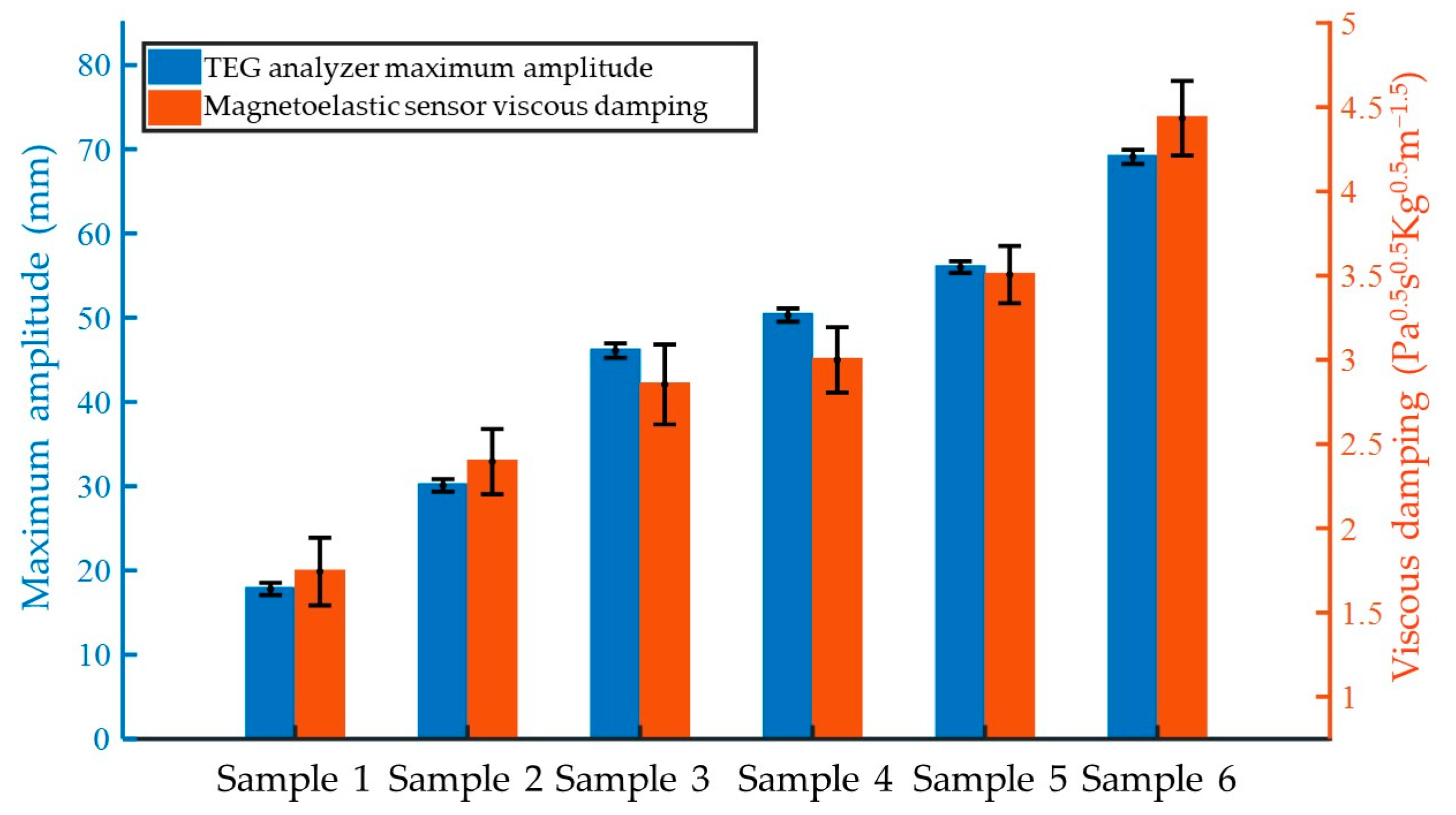
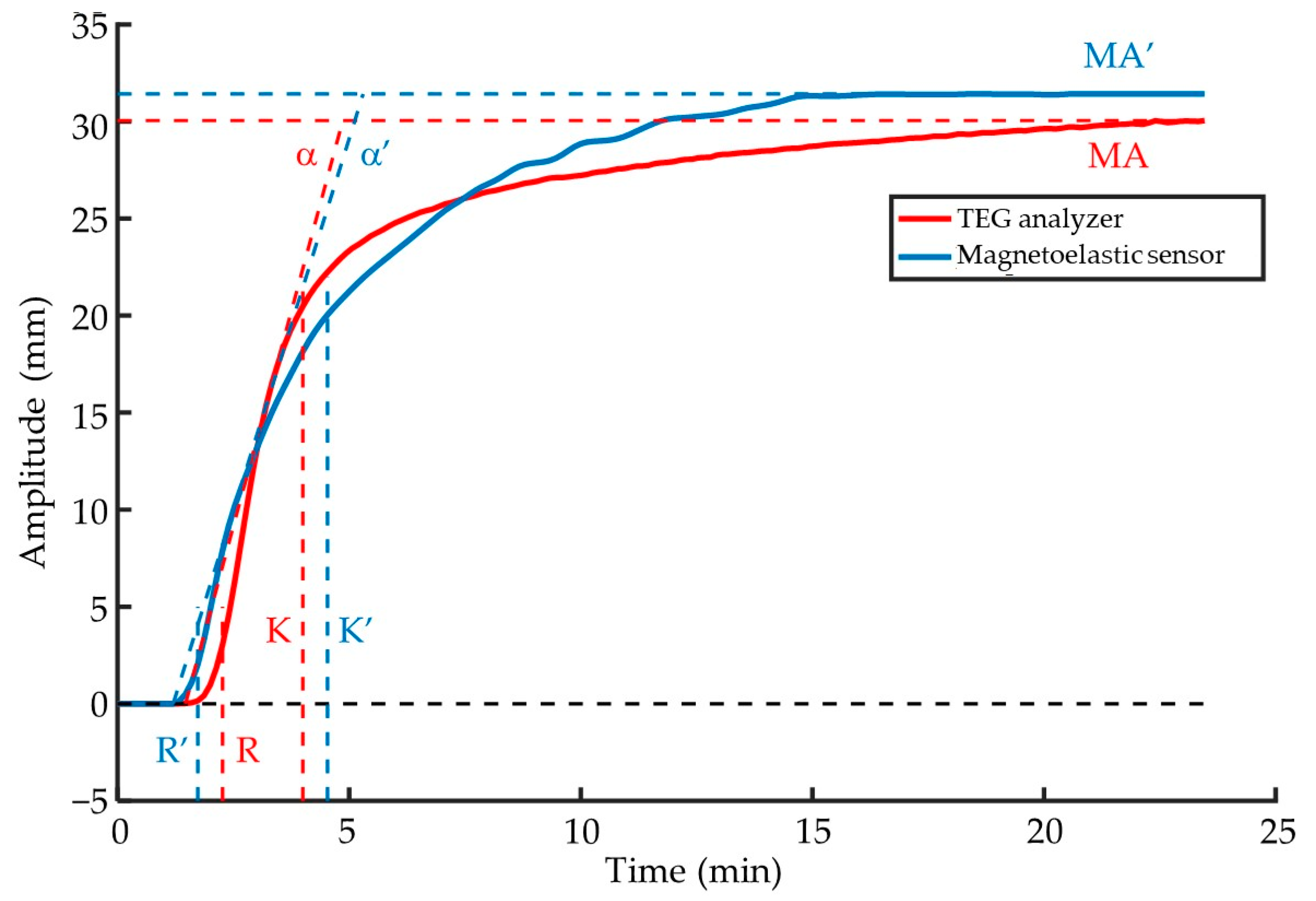
3.3. Comparison with the TEG Analyzer
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Münzel, T.; Hahad, O.; Daiber, A. Soil and water pollution and cardiovascular disease. Nat. Rev. Cardiol. 2025, 22, 71–89. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.S.; Du, Z.L.; Hu, G.F.; Ma, Y.T.; Li, C.B. Coagulation factors VIII and factors IX testing practices in China: Results of the 5-year external quality assessment program. Clin. Chim. Acta 2025, 565, 119950. [Google Scholar] [CrossRef] [PubMed]
- Macfarlane, R.G. An enzyme cascade in the blood clotting mechanism, and its function as a biochemical amplifier. Nature 1964, 202, 498–499. [Google Scholar] [CrossRef]
- Xu, T.; Ji, H.F.; Xu, L.; Cheng, S.J.; Liu, X.D.; Li, Y.P.; Zhong, R.; Zhao, W.F.; Kizhakkedathu, J.N.; Zhao, C.S. Self-anticoagulant sponge for whole blood auto-transfusion and its mechanism of coagulation factor inactivation. Nat. Commun. 2023, 14, 4875. [Google Scholar] [CrossRef] [PubMed]
- Nath, S.S.; Pandey, C.K.; Kumar, S. Clinical application of viscoelastic point-of-care tests of coagulation-shifting paradigms. Ann. Card. Anaesth. 2022, 25, 1–10. [Google Scholar] [CrossRef]
- Qin, D.; Cai, H.F.; Liu, Q.; Lu, T.Y.; Tang, Z.; Shang, Y.H.; Cui, Y.B.; Wang, R. Nomogram model combined thrombelastography for venous thromboembolism risk in patients undergoing lung cancer surgery. Front. Physiol. 2023, 14, 1242132. [Google Scholar] [CrossRef]
- Wang, Q.N.; Cao, Y.M.; Yuan, Z.Y.; Han, M.S.; Zhang, Y.X.; Zhuo, K.; Sun, L.; Guo, X.; Zhang, H.P.; Jin, H. Magnetoelastic immunosensor for the rapid detection of SARS-CoV-2 in bioaerosols. ACS Sens. 2024, 9, 5936–5944. [Google Scholar] [CrossRef]
- Li, D.H.; Yuan, Z.Y.; Huang, X.R.; Li, H.M.; Guo, X.; Zhang, H.L.; Sang, S.B. Surface functionalization, bioanalysis, and applications: Progress of new magnetoelastic biosensors. Adv. Eng. Mater. 2022, 24, 2101216. [Google Scholar] [CrossRef]
- Sisniega, B.; de Luis, R.F.; Gutiérrez, J.; García-Arribas, A. Magnetoelastic resonators functionalized with metal-organic framework water harvesters as wireless humidity sensors. APL Mater. 2024, 12, 071123. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, D.L.; Yan, X.L.; Zhang, E.C.; Wang, X. Distinguish abnormal tensile and torsional stresses of steel wire rope using magnetoelastic effect. IEEE Trans. Instrum. Meas. 2023, 72, 6007110. [Google Scholar] [CrossRef]
- Samourgkanidis, G.; Kouzoudis, D. Magnetoelastic ribbons as vibration sensors for real-time health monitoring of rotating metal beams. Sensors 2021, 21, 8122. [Google Scholar] [CrossRef] [PubMed]
- Balcioglu, S.; Inan, O.O.; Kolak, S.; Ates, B.; Atalay, S. Diagnosis, bacterial density, food, and agricultural applications of magnetoelastic biosensors: Theory, instrumentation, and progress. J. Supercond. Nov. Magn 2024, 37, 1299–1322. [Google Scholar] [CrossRef]
- Skinner, W.S.; Zhang, S.Y.; Guldberg, R.E.; Ong, K.G. Magnetoelastic sensor optimization for improving mass monitoring. Sensors 2022, 22, 827. [Google Scholar] [CrossRef] [PubMed]
- Saiz, P.G.; de Luis, R.F.; Bartolome, L.; Gutiérrez, J.; Arriortua, M.I.; Lopes, A.C. Rhombic-magnetoelastic/metal-organic framework functionalized resonators for highly sensitive toluene detection. J. Mater. Chem. C 2020, 8, 13743–13753. [Google Scholar] [CrossRef]
- Liu, Y.H.; Sang, S.B.; Zhao, D.; Ge, Y.; Xue, J.J.; Duan, Q.Q.; Guo, X. Novel flexible magnetoelastic biosensor based on PDMS/FeSiB/QD composite film for the detection of African swine fever virus P72 protein. Anal. Methods 2024, 16, 5441–5449. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, H.X.; Qian, J.; Song, Y.; Wang, B.D.; Sun, H.X. Equivalent circuit models for magnetoelastic resonance sensors with various surface loadings. IEEE Sens. J. 2023, 23, 3675–3684. [Google Scholar] [CrossRef]
- Beltrami, L.V.R.; Beltrami, M.; Roesch-Ely, M.; Kunst, S.R.; Missell, F.P.; Birriel, E.J.; Malfatti, C.D. Magnetoelastic sensors with hybrid films for bacteria detection in milk. J. Food Eng. 2017, 212, 18–28. [Google Scholar] [CrossRef]
- Karuppuswami, S.; Kaur, A.; Arangali, H.; Chahal, P. A hybrid magnetoelastic wireless sensor for detection of food adulteration. IEEE Sens. J. 2017, 17, 1706–1714. [Google Scholar] [CrossRef]
- Dai, Z.Y.; Wang, M.R.; Wang, Y.; Yu, Z.C.; Li, Y.; Qin, W.D.; Qian, K. A smart finger patch with coupled magnetoelastic and resistive bending sensors. J. Semicond. 2025, 46, 012601. [Google Scholar] [CrossRef]
- Huang, X.R.; Sang, S.B.; Yuan, Z.Y.; Duan, Q.Q.; Guo, X.; Zhang, H.P.; Zhao, C. Magnetoelastic immunosensor via antibody immobilization for the specific detection of lysozymes. ACS Sens. 2021, 6, 3933–3939. [Google Scholar] [CrossRef]
- Peña, A.; Aguilera, J.D.; Matatagui, D.; de la Presa, P.; Horrillo, C.; Hernando, A.; Marín, P. Real-Time monitoring of breath biomarkers with a magnetoelastic contactless gas sensor: A proof of concept. Biosensors 2022, 12, 871. [Google Scholar] [CrossRef] [PubMed]
- Khan, W.U.; Alissa, M.; Allemailem, K.S.; Alrumaihi, F.; Alharbi, H.O.; Almansour, N.M.; Aldaiji, L.A.; Albalawi, M.J.; Abouzied, A.S.; Almousa, S.; et al. Navigating sensor-skin coupling challenges in magnetic-based blood pressure monitoring: Innovations and clinical implications for hypertension and aortovascular disease management. Curr. Probl. Cardiol. 2025, 50, 102964. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.Y.; Han, M.S.; Li, D.H.; Hao, R.F.; Guo, X.; Sang, S.B.; Zhang, H.P.; Ma, X.Y.; Jin, H.; Xing, Z.J.; et al. A cost-effective smartphone-based device for rapid C-reaction protein (CRP) detection using magnetoelastic immunosensor. Lab Chip 2023, 23, 2048–2056. [Google Scholar] [CrossRef]
- Xu, J.; Tat, T.; Zhao, X.; Zhou, Y.H.; Ngo, D.; Xiao, X.; Chen, J. A programmable magnetoelastic sensor array for self-powered human-machine interface. Appl. Phys. Rev. 2022, 9, 031404. [Google Scholar] [CrossRef]
- Lin, M.H.; Anderson, J.; Pinnaratip, R.; Meng, H.; Konst, S.; DeRouin, A.J.; Rajachar, R.; Ong, K.G.; Lee, B.P. Monitoring the long-term degradation behavior of biomimetic bioadhesive using wireless magnetoelastic sensor. IEEE Trans. Biomed. Eng. 2015, 62, 1838–1842. [Google Scholar] [CrossRef]
- Wu, P.X. Magnetostrictive strip sensors to identify the nonlinearity of viscosity. IEEE Sens. J. 2024, 24, 23599–23604. [Google Scholar] [CrossRef]
- Skinner, W.S.; Zhang, S.; Garcia, J.R.; Guldberg, R.E.; Ong, K.G. Magnetoelastic monitoring system for tracking growth of human mesenchymal stromal cells. Sensors 2023, 23, 1832. [Google Scholar] [CrossRef]
- Ren, L.M.; Zhang, X.; Li, Z.; Sun, Y.C.; Tan, Y.S. A novel negative Poisson’s ratio structure with high Poisson’s ratio and high compression resistance and its application in magnetostrictive sensors. Compos. Struct. 2025, 351, 118599. [Google Scholar] [CrossRef]
- Cao, Y.M.; Wang, Q.N.; Han, M.S.; Zhang, Y.X.; Yuan, Z.Y.; Zhuo, K.; Zhang, H.P.; Xing, Z.J.; Jin, H.; Zhao, C. A smartphone-based multichannel magnetoelastic immunosensor for acute aortic dissection supplementary diagnosis. Talanta 2025, 281, 126915. [Google Scholar] [CrossRef]
- Lasheras, A.; Garitaonandia, J.S.; Quintana, I.; Vilas, J.L.; Lopes, A.C. Development of nanocrystallized magnetoelastic sensors with self-biased effect and improved mass sensitivity. Sens. Actuator Rep. 2024, 8, 100251. [Google Scholar] [CrossRef]
- Silva, W.R.F.; Cunha, R.O.R.R.; Mendes, J.B.S. Development of an integrated device based on the gain/phase detector and Arduino platform for measuring magnetoelastic resonance. Measurement 2025, 242, 115819. [Google Scholar] [CrossRef]
- Guo, X.; Gao, S.; Sang, S.B.; Jian, A.Q.; Duan, Q.Q.; Ji, J.L.; Zhang, W.D. Detection system based on magnetoelastic sensor for classical swine fever virus. Biosens. Bioelectron. 2016, 82, 127–131. [Google Scholar] [CrossRef] [PubMed]
- Saiz, P.G.; de Luis, R.F.; Lasheras, A.; Arriortua, M.I.; Lopes, A.C. Magnetoelastic resonance sensors: Principles, applications, and perspectives. ACS Sens. 2022, 7, 1248–1268. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.Q.; Huang, W.M.; Guo, P.P.; Yang, H.W.; Weng, L.; Wang, B.W. Nonlinear model for magnetostrictive vibration energy harvester considering dynamic forces. IEEE Sens. J. 2024, 24, 16270–16278. [Google Scholar] [CrossRef]
- Saiz, P.G.; Gutiérrez, J.; Arriortua, M.I.; Lopes, A.C. Theoretical and experimental analysis of novel rhombus shaped magnetoelastic sensors with enhanced mass sensitivity. IEEE Sens. J. 2020, 20, 13332–13340. [Google Scholar] [CrossRef]
- Liang, C.; Morshed, S.; Prorok, B.C. Correction for longitudinal mode vibration in thin slender beams. Appl. Phys. Lett. 2007, 90, 221912. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw Hill: Boston, MA, USA, 2005. [Google Scholar]
- De Jesús, M.G.; Panduranga, M.K.; Shirazi, P.; Keller, S.; Jackson, M.; Wang, K.L.; Lynch, C.S.; Carman, G.P. Micro-magnetoelastic modeling of Terfenol-D for spintronics. J. Appl. Phys. 2022, 131, 234101. [Google Scholar] [CrossRef]
- Ramezani, Z.; Khizroev, S. Equivalent circuit model of magnetoelectric composite nanoparticles. J. Electron. Mater. 2024, 53, 6124–6139. [Google Scholar] [CrossRef]
- Luo, Y.M.; Yu, B.L.; Yu, H.Y.; Li, K.H. GaN integrated optical devices for glycerol viscosity measurement. Opt. Lett. 2024, 49, 2261–2264. [Google Scholar] [CrossRef]
- Volk, A.; Kähler, C.J. Density model for aqueous glycerol solutions Andreas. Exp. Fluids 2018, 59, 75. [Google Scholar] [CrossRef]





| Concentration (wt%) | Viscosity ηL (10−3 Pa·s) | Resonant Frequency (Hz) | Resonant Amplitude (mV) | |
|---|---|---|---|---|
| 0 | 1.01 | 998.23 | 120,898.3 ± 9.1 | 13.8837 ± 0.0350 |
| 10 | 1.31 | 1022.10 | 120,643.3 ± 17.3 | 13.2270 ± 0.0561 |
| 20 | 1.76 | 1046.90 | 120,308.3 ± 23.1 | 12.2919 ± 0.0563 |
| 30 | 2.50 | 1072.70 | 119,950.0 ± 13.1 | 11.6586 ± 0.0227 |
| 40 | 3.72 | 1099.30 | 119,441.7 ± 19.0 | 11.0223 ± 0.0415 |
| 50 | 6.00 | 1126.30 | 118,940.0 ± 24.2 | 10.4544 ± 0.0221 |
| 60 | 10.80 | 1153.80 | 118,470.0 ± 28.2 | 8.5304 ± 0.0167 |
| 70 | 22.50 | 1181.25 | 117,686.4 ± 23.4 | 7.8858 ± 0.0194 |
| 80 | 60.10 | 1208.50 | 116,390.5 ± 30.1 | 5.5546 ± 0.0029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wang, Q.; Deng, J.; Hu, N.; Liao, Y.; Yang, J. An Amplitude Analysis-Based Magnetoelastic Biosensing Method for Quantifying Blood Coagulation. Biosensors 2025, 15, 219. https://doi.org/10.3390/bios15040219
Chen X, Wang Q, Deng J, Hu N, Liao Y, Yang J. An Amplitude Analysis-Based Magnetoelastic Biosensing Method for Quantifying Blood Coagulation. Biosensors. 2025; 15(4):219. https://doi.org/10.3390/bios15040219
Chicago/Turabian StyleChen, Xi, Qiong Wang, Jinan Deng, Ning Hu, Yanjian Liao, and Jun Yang. 2025. "An Amplitude Analysis-Based Magnetoelastic Biosensing Method for Quantifying Blood Coagulation" Biosensors 15, no. 4: 219. https://doi.org/10.3390/bios15040219
APA StyleChen, X., Wang, Q., Deng, J., Hu, N., Liao, Y., & Yang, J. (2025). An Amplitude Analysis-Based Magnetoelastic Biosensing Method for Quantifying Blood Coagulation. Biosensors, 15(4), 219. https://doi.org/10.3390/bios15040219






