Study of Paclitaxel-Treated HeLa Cells by Differential Electrical Impedance Flow Cytometry
Abstract
:1. Introduction
2. Experimental Section
2.1. Detection and Chip Design
2.2. HeLa Cell Culturing and Treatment

2.3. Staining of Cells
2.4. Chip Fabrication and Measurement Setup
2.5. EIS Measurements
2.6. Theoretical Calculations
 , where j2 = −1, l is the length of the electrodes, w is the width of the electrodes, k is the cell constant of the electrode layout, emixc is the complex permittivity of a cell in the volume between a pair of electrodes and emed is the complex permittivity of the liquid. An equivalent circuit model can be used as a complementary model to the MMT model [19]. Figure 2 illustrates the equivalent circuit model, where Rm is the resistance of the medium, Ri is the resistance of the cytoplasm, Rmem is the resistance of the membrane, Cmem is the capacitance of the membrane and Cm is the capacitance of the medium.
, where j2 = −1, l is the length of the electrodes, w is the width of the electrodes, k is the cell constant of the electrode layout, emixc is the complex permittivity of a cell in the volume between a pair of electrodes and emed is the complex permittivity of the liquid. An equivalent circuit model can be used as a complementary model to the MMT model [19]. Figure 2 illustrates the equivalent circuit model, where Rm is the resistance of the medium, Ri is the resistance of the cytoplasm, Rmem is the resistance of the membrane, Cmem is the capacitance of the membrane and Cm is the capacitance of the medium.

3. Results and Discussion
3.1. System Resolution and Bead Separation

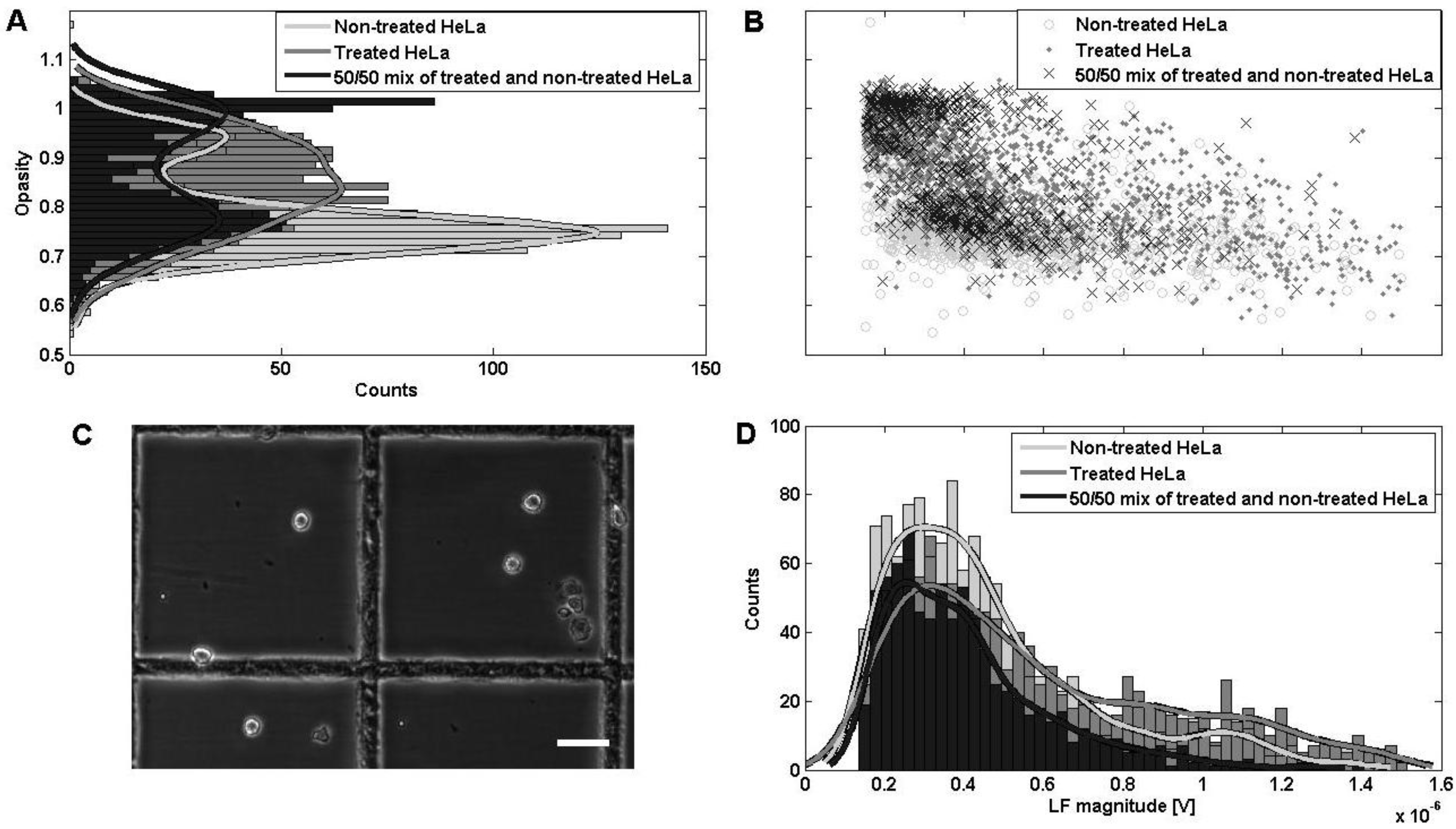
3.2. Impedance Response of Paclitaxel-Treated Cells


4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Riss, T.L.; Moravec, R.A. Use of multiple assay endpoints to investigate the effects of incubation time, dose of toxin, and plating density in cell-based cytotoxicity assays. Assay Drug Dev. Technol. 2004, 2, 51–62. [Google Scholar]
- Decker, T.; Lohmann-Matthes, M.L. A quick and simple method for the quantitation of lactate dehydrogenase release in measurements of cellular cytotoxicity and tumor necrosis factor (TNF) activity. J. Immunol. Meth. 1988, 115, 61–69. [Google Scholar] [CrossRef]
- Stachowiak, J.C.; Schmid, E.M.; Ryan, C.J.; Ann, H.S.; Sasaki, D.Y.; Sherman, M.B.; Geissler, P.L.; Fletcher, D.A.; Hayden, C.C. Membrane bending by protein-protein crowding. Nat. Cell Biol. 2012, 14, 944–949. [Google Scholar]
- Hulett, H.R.; Bonner, W.A.; Barrett, J.; Herzenberg, L.A. Cell sorting—Automated separation of mammalian cells as a function of intracellular fluorescence. Science 1969, 166, 747–749. [Google Scholar]
- Coulter, W.H. Means for Counting Particles Suspended in a Fluid. U.S. Patent 2,656,508, 1953. [Google Scholar]
- Pethig, R.; Kell, D.B. The passive electrical-properties of biological-systems—Their significance in physiology, biophysics and biotechnology. Phys. Med. Biol. 1987, 32, 933–970. [Google Scholar]
- Gawad, S.; Schild, L.; Renaud, P.H. Micromachined impedance spectroscopy flow cytometer for cell analysis and particle sizing. Lab on a Chip 2001, 1, 76–82. [Google Scholar] [CrossRef]
- Holmes, D.; Pettigrew, D.; Reccius, C.H.; Gwyer, J.D.; van Berkel, C.; Holloway, J.; Davies, D.E.; Morgan, H. Leukocyte analysis and differentiation using high speed microfluidic single cell impedance cytometry. Lab on a Chip 2009, 9, 2881–2889. [Google Scholar]
- Sun, T.; Morgan, H. Single-cell microfluidic impedance cytometry: A review. Microfluid Nanofluid 2010, 8, 423–443. [Google Scholar] [CrossRef]
- Ayliffe, H.E.; Frazier, A.B.; Rabbitt, R.D. Electric impedance spectroscopy using microchannels with integrated metal electrodes. J. Microelectromech. Syst. 1999, 8, 50–57. [Google Scholar] [CrossRef]
- Rodriguez-Trujillo, R.; Ajine, M.A.; Orzan, A.; Mar, M.D.; Larsen, F.; Clausen, C.H.; Svendsen, W.E. Label-free protein detection using a microfluidic Coulter-counter device. Sens. Actuator B Chem. 2014, 190, 922–927. [Google Scholar] [CrossRef]
- Lin, R.; Simon, M.G.; Lee, A.P.; Lopez-Prieto, J. Label-Free Detection of DNA Amplification in Droplets Using Electrical Impedance. In Proceedings of the 15th International Conference on Miniaturized Systems for Chemistry and Life Sciences 2011 (MicroTAS 2011), Seattle, WA, USA, 2–6 October 2011; pp. 1683–1685.
- Haandbaek, N.; Burgel, S.C.; Heer, F.; Hierlemann, A. Characterization of subcellular morphology of single yeast cells using high frequency microfluidic impedance cytometer. Lab on a Chip 2014, 14, 369–377. [Google Scholar] [CrossRef]
- Holmes, D.; Morgan, H. Single cell impedance cytometry for identification and counting of CD4 T-cells in human blood using impedance labels. Anal. Chem. 2010, 82, 1455–1461. [Google Scholar]
- Evander, M.; Ricco, A.J.; Morser, J.; Kovacs, G.T.A.; Leung, L.L.K.; Giovangrandi, L. Microfluidic impedance cytometer for platelet analysis. Lab on a Chip 2013, 13, 722–729. [Google Scholar] [CrossRef]
- Schade-Kampmann, G.; Huwiler, A.; Hebeisen, M.; Hessler, T.; Di Berardino, M. On-chip non-invasive and label-free cell discrimination by impedance spectroscopy. Cell Prolif. 2008, 41, 830–840. [Google Scholar] [CrossRef]
- Mernier, G.; Hasenkamp, W.; Piacentini, N.; Renaud, P. Multiple-frequency impedance measurements in continuous flow for automated evaluation of yeast cell lysis. Sens. Actuaor B Chem. 2012, 170, 2–6. [Google Scholar] [CrossRef]
- Sun, T.; Bernabini, C.; Morgan, H. Single-colloidal particle impedance spectroscopy: Complete equivalent circuit analysis of polyelectrolyte microcapsules. Langmuir 2010, 26, 3821–3828. [Google Scholar]
- Morgan, H.; Sun, T.; Holmes, D.; Gawad, S.; Green, N.G. Single cell dielectric spectroscopy. J. Phys. D Appl. Phys. 2007, 40, 61–70. [Google Scholar] [CrossRef]
- Giulian, D.; Diacumakos, E.G. Electrophysiological mapping of compartments within a mammalian-cell. J. Cell Biol. 1977, 72, 86–103. [Google Scholar] [CrossRef]
- Kim, K.S.; Cho, C.H.; Park, E.K.; Jung, M.H.; Yoon, K.S.; Park, H.K. AFM-detected apoptotic changes in morphology and biophysical property caused by paclitaxel in Ishikawa and Hela cells. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
- Jordan, M.A.; Wendell, K.; Gardiner, S.; Derry, W.B.; Copp, H.; Wilson, L. Mitotic block induced in HeLa cells by low concentrations of paclitaxel (Taxol) results in abnormal mitotic exit and apoptotic cell death. Cancer Res. 1996, 56, 816–825. [Google Scholar]
- Demierre, N.; Braschler, T.; Linderholm, P.; Seger, U.; van Lintel, H.; Renaud, P. Characterizationand optimization of liquid electrodes for lateral dielectrophoresis. Lab on a Chip 2007, 7, 355–365. [Google Scholar]
- Moresco, J.; Clausen, C.H.; Svendsen, W. Improved anti-stiction coating of SU-8 molds. Sens. Actuator B Chem. 2010, 145, 698–701. [Google Scholar] [CrossRef]
- Gawad, S.; Cheung, K.; Seger, U.; Bertsch, A.; Renaud, P. Dielectric spectroscopy in a micromachined flow cytometer: Theoretical and practical considerations. Lab on a Chip 2004, 4, 241–251. [Google Scholar] [CrossRef]
- Linderholm, P.; Renaud, P. Comment on “AC frequency characteristics of coplanar impedance sensors as design parameters” by Jongin Hong, Dae Sung Yoon, Sung Kwan Kim, Tae Song Kim, Sanghyo Kim, Eugene Y. Pak and Kwangsoo No, Lab Chip, 2005, 5, 270. Lab on a Chip 2005, 5, 1416–1417, author reply 1418. [Google Scholar] [CrossRef]
Appendix
Electrical Impedance Spectroscopy: Viability Study of Paclitaxel Treated HeLa Cells in Continuous Flow
Frequency Selection
Data Normalization Using Beads


Theoretical Model

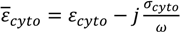
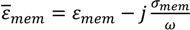
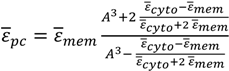

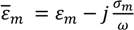
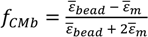
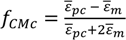
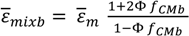

 is the empty channel. The calculations were done with the following parameters: j2 = −1, l = 30 µm, w = 30 µm, ε0 = 8.854e−12 F·m−1, rbead = 2.5 µm, σbead = 1e−3 S·m−1, εbead = 2.6ε0, rcell = 7.5 µm, dcell = 5 nm, σmem = 10e−8 S·m−1, µmem 8.3µ0, σm = 1.6 S·m−1, µbead = 80µ0, σi = 0.6 S·m−1, µi = 60µ0, k = 1.3713; where the frequency f is given as f = 2πω and was varied from 60 kHz to 10 kHz.
is the empty channel. The calculations were done with the following parameters: j2 = −1, l = 30 µm, w = 30 µm, ε0 = 8.854e−12 F·m−1, rbead = 2.5 µm, σbead = 1e−3 S·m−1, εbead = 2.6ε0, rcell = 7.5 µm, dcell = 5 nm, σmem = 10e−8 S·m−1, µmem 8.3µ0, σm = 1.6 S·m−1, µbead = 80µ0, σi = 0.6 S·m−1, µi = 60µ0, k = 1.3713; where the frequency f is given as f = 2πω and was varied from 60 kHz to 10 kHz.© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kirkegaard, J.; Clausen, C.H.; Rodriguez-Trujillo, R.; Svendsen, W.E. Study of Paclitaxel-Treated HeLa Cells by Differential Electrical Impedance Flow Cytometry. Biosensors 2014, 4, 257-272. https://doi.org/10.3390/bios4030257
Kirkegaard J, Clausen CH, Rodriguez-Trujillo R, Svendsen WE. Study of Paclitaxel-Treated HeLa Cells by Differential Electrical Impedance Flow Cytometry. Biosensors. 2014; 4(3):257-272. https://doi.org/10.3390/bios4030257
Chicago/Turabian StyleKirkegaard, Julie, Casper Hyttel Clausen, Romen Rodriguez-Trujillo, and Winnie Edith Svendsen. 2014. "Study of Paclitaxel-Treated HeLa Cells by Differential Electrical Impedance Flow Cytometry" Biosensors 4, no. 3: 257-272. https://doi.org/10.3390/bios4030257
APA StyleKirkegaard, J., Clausen, C. H., Rodriguez-Trujillo, R., & Svendsen, W. E. (2014). Study of Paclitaxel-Treated HeLa Cells by Differential Electrical Impedance Flow Cytometry. Biosensors, 4(3), 257-272. https://doi.org/10.3390/bios4030257



