1. Introduction
Bacteriostatic action, i.e., the inhibition of bacterial growth, is useful, and required in numerous application fields, such as drug delivery to prevent tissue infections (e.g., antibacterial plasters), inhibition of biofilm formation on food packaging, or on membranes used for water and air treatments [
1,
2,
3,
4,
5,
6,
7]. The bacteriostatic efficiency depends on several factors, such as the antibacterial agent used, its concentration, the bacterial strains, the bacterial concentration involved, and the kinetics (i.e., transport of the bacteriostatic agent, bacterial growth and antibacterial action), resulting in a certain contact time between bacteria and the antibacterial agent [
8]. As an example, a too slow transport of the biocidal agent may not prevent bacteria from growing since bacteria can multiply faster than they die. On the contrary, a too fast transport can induce an excessive consumption of biocidal agent and expose the receiving environment to high concentrations that can be possibly harmful [
9,
10]. Thus, it is very important to determine kinetics of antibacterial agent transfer, bacterial growth, and antibacterial action.
In this study, a usual and visual agar diffusion test was chosen to illustrate a bacteriostatic system where kinetics characterizations could be done. Silver ions (Ag
+) are a well-known biocidal agent [
11,
12] and were so selected for this test. Silver ions have indeed powerful antibacterial properties that were demonstrated and characterized by numerous studies [
1,
2,
13,
14,
15,
16,
17,
18,
19]. In particular, Ag
+ is able to (i) interact with the thiol groups (-SH) of the membrane cell proteins to form S-Ag bonds, leading to the inhibition of the biologic activity of these proteins (it is notably the case of the respiratory chain proteins), and (ii) induce protein agglomeration around DNA as a defense mechanism when it has penetrated in the cell, thus inhibiting DNA replication [
1,
2,
13,
14,
15,
16,
17,
18,
19]. These processes could lead to cell death. Herein, silver ions were deposited in a well, made in the center of a nutritive agar plate that was priorly inoculated on its surface by a non-pathogenic
Escherichia coli bacterium exhibiting similar shapes and biochemical properties as pathogenic
E. coli. In this configuration, different coupled kinetics occur: bacterial growth on the nutritive agar (inducing a biofilm formation), Ag
+ diffusion in the agar and in the biofilm formed and antibacterial action of the diffused Ag
+. Under certain conditions, the cumulative effect of these kinetics can result in the formation of inhibition halos (or inhibition zones) around the silver well that are enlarged over time due to silver diffusion. These inhibition halos are zones where bacteria were prevented from growing on the agar by action of silver. They correspond to agar solely, by opposition to the colonized agar where a bacterial biofilm has formed.
To the best of our knowledge, the modeling currently used to assess the evolution of the inhibition zones radii is based on a diffusive model (Fick’s law) traducing the antibacterial agent diffusion within the agar and on the experimental determinations of (i) the Minimum Inhibitory Concentration (MIC), i.e., the minimal concentration of antibacterial agent for which an inhibition zone appears after a given incubation period of the agar plates (usually 24 h or 48 h), and (ii) the critical time (T
c) that is the incubation time from which the bacterial cells become more numerous than what the MIC can inhibit [
20,
21,
22]. However, the MIC already couples the different kinetics and the diffusion approach does not take into account the bacterial growth that can impact the diffusive transport [
20,
21,
22]. This work aimed to distinguish experimentally and by the model the different kinetics (diffusion vs. bacterial growth and biocidal action) to get an overview of the system dynamics and identify the limiting phenomenon over the test duration. Thus, in this study, experiments were first designed to study independently the kinetics of silver diffusion, bacterial growth, and antibacterial action of silver. In addition, kinetics models were implemented. The correlation between experiments and models allowed notably to (i) obtain Ag
+ diffusivities (in agar but overall in the biofilm formed) and the kinetic constants for bacterial growth and Ag
+ biocidal action; (ii) identify the limiting phenomenon over time; and finally (iii) propose an innovative model combining all the kinetics that allows to simulate the coupling as a function of time and space. More generally, such an approach could be also envisaged to obtain models describing other bacteriostatic systems that involve diffusive materials.
2. Results and Discussion
Pure diffusion, pure bacterial growth, and pure antibacterial action of silver ions will be first decoupled and characterized by both experience and model to propose consistent kinetic models for each of this phenomenon. Then, these kinetics will be combined in a global model that will be compared to experimental data (i.e., inhibition zones radii).
2.1. Pure Diffusion of Silver Ions in the Agar
2.1.1. Modeling the Concentration Profile of Ag+ Diffusing in the Agar Plate
The diffusion of the antibacterial agent (Ag
+) in the agar exempt of bacteria was first studied in order to test the reliability for this specific application of both the COMSOL module used and the experiments carried out. Agar can be considered as a continuous and homogenous static medium, whose dynamic viscosity was fixed to 2.2 Pa s [
23] and density to 0.799 g mL
−1 (obtained in this study by weighting a known agar volume). Thus, diffusion transport follows the Fick’s Laws [
20] and the flow density J
Ag+ of Ag
+ diffusing in the agar medium was modeled by the first Fick’s Law (Equation (1)):
where:
JAg+ (mol m−2 s−1) is the flow density of Ag+ diffusing in the agar medium;
CAg+ (mol m−3) is the concentration of Ag+ at a position r and at a time t;
DAg+ (m2 s−1) is the diffusivity of Ag+ in the agar medium.
Diffusion is a microscopic phenomenon and a microscopic mass balance carried out on a portion of agar plate in mole of Ag
+ per second gives the second Fick’s Law (Equation (2)):
By replacing the expression of the flow density
in Equation (2), Equation (3) comes:
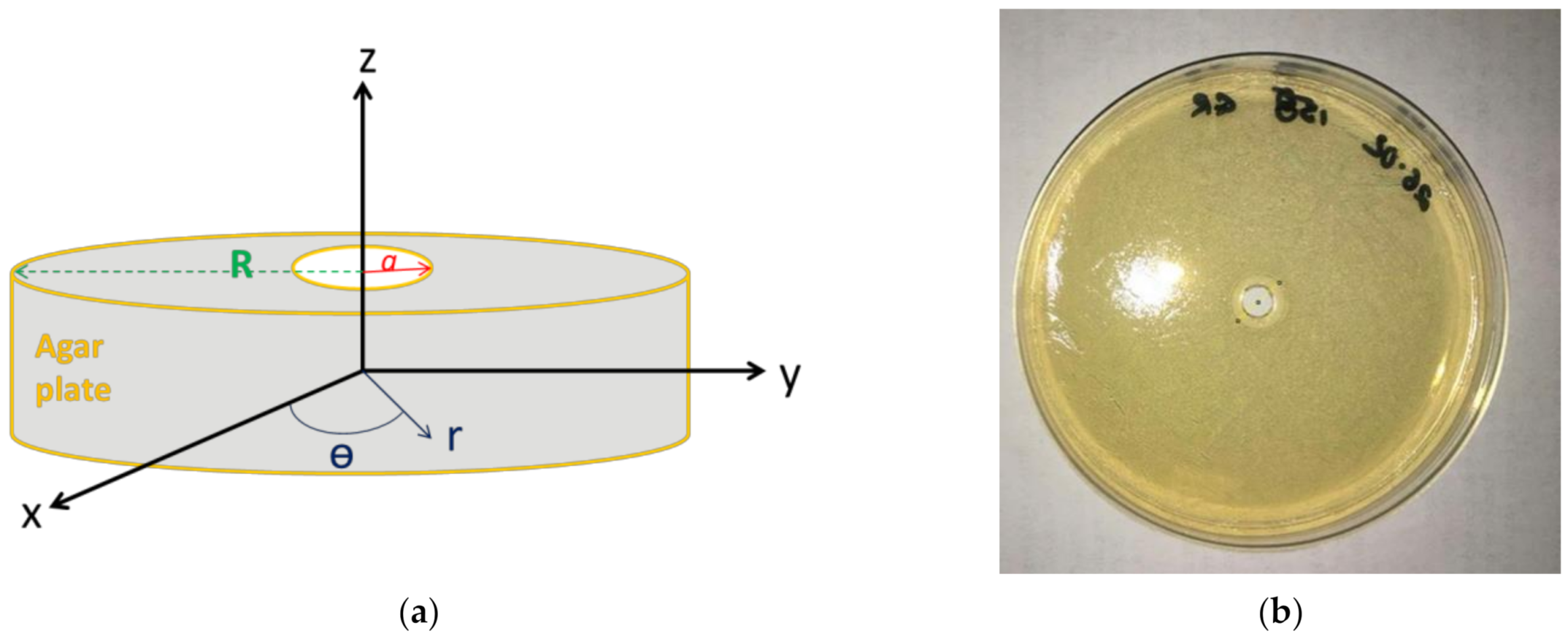
In agreement with the experimental system, a cylindrical geometry of the agar plate was considered (
Figure 1) with a cylindrical coordinate system. We looked for a C
Ag+ (r, t) solution that has to satisfy the initial conditions (IC) and boundary conditions (BC) given by Equations (4) and (5) respectively:
where:
a (m) is the radius of the well made in the agar plate center (
Figure 1) and C
Ag0+ (mol m
−3) the initial concentration of the Ag
+ solution that was deposited in the well
where R (m) is the radius of the agar plate (
Figure 1)
This first model was implemented in the COMSOL mass transfer module. From the modeling of Ag+ concentration profile, a modeling of halo radius was determined by considering the halo as the zone where the Ag+ concentration was different from zero.
2.1.2. Experiments: Measuring the Radius of the Diffusion Halos over Time
Experiments were carried out as described in
Section 3.3.1. Silver solution was stained with a red food dye before being deposited in the well of the agar plate that was not seeded; the concentration of silver ions was fixed to 100 mg L
−1. Then the formation and progression of the dyed halos around the wells were monitored over time. The radius of the dyed halos corresponds to the diffusion radius since diffusion was the only phenomenon occurring in the experiment.
Figure 2 shows the results obtained for the two experiment replicates (Experiment 1 (Exp 1) and Experiment (Exp 2), respectively). Diffusion radii (L) were measured on plate pictures by using the ImageJ software; images illustrating the evolution of the dyed halos over time are given in the
supplementary data (Figure S1). Initially, the radius of the halo is equal to the well radius (a).
The uncertainty on the measures was determined by summing three sources of experimental errors on: (i) the graduations of the measuring ruler (
Figure S1); (ii) the delimitation between the dyed halo and the agar (
Figure S1); and (iii) the distance and residual angle of the camera from the agar plate plane. The calculation of the standard deviation on the ruler graduations is based on the smallest measurable distance (i.e., 0.03 cm) while the other deviations were assessed by Student tests. For the Student tests, the size of the dyed halos were measured twenty times on the first hand, and on the second hand, the size of an object whose the real size is known (for example the ruler) was measured by Image J. An uncertainty of 0.09 cm was obtained.
2.1.3. Comparison between the Model and Experiments
The comparison between the model and experiments is intended to determine the D
Ag+ value, which appears in Equation (3), i.e., the diffusivity of silver ions in Lysogeny Broth (LB) agar (at 15 g
agar L
−1 and 37 °C). The radii (L) of the diffusion halos measured experimentally and obtained by the model were reported against time in
Figure 2. For the model, a similar silver concentration as in the experiments was used (i.e., 100 mg L
−1) and the silver diffusivity D
Ag+ in the agar was fixed to 2.7 × 10
−9 m
2 s
−1 in order to fit the model with the experiment.
With the fitted value of silver diffusivity,
Figure 2 shows a quite good correlation between both experimental and modeling values. In addition, the D
Ag+ value of 2.7 × 10
−9 m
2 s
−1 is in accordance with the magnitude order of values reported in the literature for silver ions diffusion in agar gel, i.e., about 10
−9 m
2 s
−1 [
24]. This result confirms the reliability of the COMSOL mass transfer module for this study. However, staining the silver solution might have induced chemical composition changes that are likely to interfere with silver diffusion, and could explain some relative deviations observed from 300 min (
Figure 2). Staining could obviously interact even more with bacterial growth and biocidal action. Such an approach, thus, appears to be not rigorous enough to conclude on the diffusion phenomenon when it will be coupled with bacterial growth and silver action. This justifies why no staining of the silver solution will be done to determine experimentally the inhibition zones. Nevertheless, the same COMSOL mass transfer module will be used to simulate the diffusion kinetics when bacterial growth and biocidal kinetics will also be considered. The coupling is expected to allow the determination of the silver diffusivity D
Ag+ biofilm in the bacterial biofilm formed.
2.2. Pure Bacterial Growth
2.2.1. Model
According to Equation (6), the flow of bacteria produced can be defined as the growth rate μ (min
−1) multiplied by the bacterial concentration N, where the growth rate is a specific rate. The bacterial concentration N is usually expressed in colonies forming units (CFU) mL
−1, but it can also be expressed in g
dry cell L
−1 or in mol L
−1. Indeed, the number of bacteria is directly proportional to the mass of dried bacterial cells and the mass can be converted to a mole number since
E. coli bacteria exhibit a known molecular weight (22 ± 12 kDa, [
25]).
The growth rate varies with time and usually depends on the concentration of the substrate S in the culture medium limiting the bacterial growth. In this case, the growth rate adopts the Monod law described by Equation (7) [
26]:
where:
μ (min−1) is the growth rate;
μmax (min−1) is the maximal growth rate;
[S] (mol L−1) is the concentration of the limiting substrate S;
KM (mol L−1) is the Monod constant. KM is the concentration of the substrate S for which the growth rate μ is equal to μmax/2. Thus, the more KM is small and the more the affinity of the bacteria for the substrate S is important.
When the concentration [S] of the limiting substrate is in large excess compared to KM, it comes that the growth rate is maximal (μ = μmax). At the opposite, the growth rate is proportional to [S].
2.2.2. Experiments
Experiments were carried out as detailed in
Section 3.3.2. The optical density at 600 nm (OD
600) of the bacterial culture was measured over time during the exponential growth phase.
Table 1 shows the results obtained for four independent experiments.
2.2.3. Comparison between the Model and the Experiments
According to
Section 3.3.2, the growth rate of the
E. coli culture was measured in the exponential phase on a rich culture medium (i.e., LB). Thus, in the LB medium, all nutrient substrates were in large excess. In addition, oxygen (O
2) was continuously provided by air, as was the case for the growth on LB plates. In these conditions, the growth rate was considered maximal (μ
max). Consequently, Equation (6) becomes Equation (8):
which gives after integration:
where
In a preliminary work carried out at the Lab, a linear correlation between the bacterial concentration and OD
600 was established during the exponential phase (Equation (10)):
Equation (9) can thus also be written as describes in Equation (11):
where
Figure 3 plots the experimental results obtained.
As predicted by the model, the evolution of ln (OD
600) is linear with time, with regression coefficients R
2 ranging from 0.9684 to 0.9961 (
Figure 3 and
Table 2) and consistent OD
600i values. The experimental data were thus used to determine the maximal growth rate µ
max.
Replicates were reproducible and the mean value of µmax was fixed to 0.78 ± 0.06 h−1 in the rest of the study.
2.3. Pure Antibacterial Action of Silver Ions
2.3.1. Modeling the Kinetics of Silver Antibacterial Action
The reaction between bacteria and silver ions can be schematized as follows:
Equation (12) traduces that silver remains linked to the bacterial cell (when agglomerated around DNA) or linked to its cellular compounds, due to a redox reaction between Ag
+ and the proteins thiol groups (-SH) [
14,
15,
16,
17,
18]. The most widespread kinetic law to describe the biocidal action of an antibacterial agent is the Chick–Watson law [
27]. For silver ions, the flow of inactivated bacteria given by the phenomenological law of Chick–Watson adopts the following form:
where
CAg0+ (mol L−1) is the initial concentration of silver ions;
N (mol L−1) is the bacterial concentration at a time t;
n (-) is an order to determine that is called the dilution coefficient [
28];
k is a kinetic constant whose units depends on n
Equation (13) can be integrated and gives:
where
N0 (CFU mL−1 or gdry cell L−1 or mol L−1) is the initial bacterial concentration;
N (CFU mL−1 or gdry cell L−1 or mol L−1) is the bacterial concentration at a time t;
log(N/N0) (-) is the bacterial log-removal value. A log-removal value of −1 means that 90 % of the bacteria were removed, while a log-removal value of −2 means that 99% of the bacteria were inactivated, and so on. In the particular case of a total removal (N = 0 CFU mL−1), a value of –log(N0) was attributed.
In the case of silver ions, the dilution coefficient n was reported to be 1.038, i.e., close to 1 [
27]. However, the Chick–Watson law does not take into account the time dependence of the silver concentration C
Ag+ due to the biocidal action of Ag
+ ions. Indeed, silver ions might be quenched when they are fixed to cellular thiol groups (by the formation of SH–Ag bonds) or confined in the bacterial cell (Equation (12)), leading to a decrease of free Ag
+ ions in solution available to induce a biocidal action. This explains why the linear model of Chick–Watson is commonly not used for silver ions. The Hom model and the Intrinsic Quenching (IQ) model were therefore developed with an exponential decrease of the silver concentration with time [
27] according to Equation (15):
with k
2 (min
−1) a kinetic constant traducing the quenching of Ag
+ ions.
In the particular case of Ag
+ provided by silver nitrates in water at an initial concentration C
Ag0+ of 3.0 mg L
−1 (corresponding to the experimental concentration), the kinetic laws are respectively [
27]:
These models were designed for low silver concentrations (from 0.25 to 2 mg L
−1) against the Gram-positive
Staphylococcus aureus bacterium. In a first approach, these laws could be extended to Gram negative bacteria, such as
E. coli, since studies reported that the action mechanism of silver ions is similar for both Gram bacteria [
13,
29,
30].
2.3.2. Experiments
The goal of the experiments was to determine the kinetics of the silver ions antibacterial action in a continuous stirred tank reactor whose liquid medium was exempt of nutriments. In this configuration, bacterial growth was avoided and the constant agitation allowed the contact between Ag
+ ions and bacteria by convection movements of the liquid. The mass transfer of silver toward bacteria was thus expected to be not limiting, which, thus, should induce a limitation by the biocidal phenomenon. Due to the high antibacterial efficiency of Ag
+ ions [
1], a small concentration of silver (i.e., 3.0 mg L
−1) was chosen for the experiments to permit (i) the monitoring of the bacterial concentration decrease over time, and (ii) the further use of the models presented in
Section 2.3.1. The bacterial concentration N was measured over time (
Table 3) and the log-removal values were plotted against time in
Figure 4.
Table 3 and
Figure 4 put in evidence a clear action of the silver ions against bacteria. Indeed, the bacterial concentration remained quasi-constant in the control reactor (i.e., 1.1 ± 0.4 × 10
9 CFU mL
−1 on average), whereas it was reduced by 6 log (i.e., by 99.9999%) after 120 min when Ag
+ ions were present.
Figure 4 evidences that the log-removal decreased quickly over the first 62 min and that the values were proportional to time (R
2 = 0.9815). Then, the variations of the log-removal values with time became less significant but still adopted a linear behavior (R
2 = 0.9713). A comparison between the experiments and the different models is presented in the next section.
2.3.3. Comparison between the Models and Experiments
Figure 5 shows the log-removal values obtained by the experiments on one hand and on the other hand by the three models (i.e., Chick–Watson, Hom and Intrinsic Quenching ones). It clearly appears that the linear Chick–Watson model (Equation (14)) could suit the experiment data over the first hour but do not describe the whole experiment. As expected, the phenomenological Chick–Watson law is, thus, not adapted in the case of antibacterial action of silver ions. For the Hom model and the Intrinsic Quenching model (IQ), Equations (16) and (17) were plotted. For the Chick–Watson model (Equation (14)), the dilution coefficient n was taken equal to 1.038 [
27] and the kinetic constant k (k = 6.6 × 10
−2 min L mol
−1) was determined in this study by fitting the experimental data over the first 62 min (
Figure 5).
The Chick–Watson model is thus consistent with the experiment beginning only (
Figure 5). The Hom model is attractive since the latest log-removal values obtained matches the measured ones (at 92 and 120 min respectively, with log–removal values of about 6,
Figure 5). However, the behavior of the Hom model at the beginning of the kinetics (i.e., up to 62 min) is not in agreement with the experiments. Finally, the Intrinsic Quenching (IQ) model seems to be relevant only with the measures over the first 15 min and then adopts a profile completely different (
Figure 5). As a conclusion, none of the models reported in the literature for the antibacterial action of Ag
+ ions are satisfactory enough to describe the experimental results.
Paying attention to the kinetic profile of the log-removal values measured (
Figure 4), two affine regressions are distinguishable: one from 0 to 62 min and another from 62 to 120 min. This profile is quite similar to the one observed for chlorine in wastewaters for which the model of Haas and Karra was proposed [
31]. Like the Hom and IQ laws, this model takes also into account that the biocidal agent (chlorine or silver ions) can be quenched during the biocidal process, leading to a decrease of its concentration during time. In that case, the quenching of the Ag
+ ions is done at two different rates (linked to the two linear regressions) and the silver concentration in the reaction medium can be described by Equation (18) [
32]:
where
The kinetic modeling of the Ag
+ concentration in the reaction medium is thus given in
Figure 6:
Based on this curve (
Figure 6), the bacterial removal can be divided in three zones:
Second zone: an intermediate and quick zone where free and quenched Ag+ ions coexist in the reaction medium; the concentration CAg+ depends on time according to Equation (18),
Third zone: the Ag+ concentration is strongly reduced and remains constant at CAg+ ≃ 0.1 CAg0+ ≃ 0.3 mg L−1:
with k’ = 0.1 k’’
By integrating the Equations (19) and (20), two linear laws are obtained:
where
k and k’ (L mg−1 min−1) are kinetic constants at 37 °C for the Ag+ antibacterial action;
Climit (mol L−1) is a concentration limiting the first and the third zones ( ≈ 0.3 mg L−1);
b (-) is an integration constant.
Table 4 gives the parameters of the Haas and Karra model determined by fitting the linear laws corresponding to Equations (21) and (22) with the respective linear regressions observed for the experiments. The fitting is showed in
Figure 7.
A mean value of 6.60 ± 0.10 × 10
-2 L mg
-1 min
-1 was thus obtained for k and 1.75 ± 0.05 × 10
-2 L mg
-1 min
-1 for k’.
Figure 7 shows the adequacy between the experiments and the Haas and Karra model, with both regression coefficients R
2 and
χ2reduce close to 1 (
Table 4). To the best of our knowledge, the implementation of the Haas and Karra model to describe the biocidal action of silver ions is innovative, and was not reported yet in the literature.
2.4. Coupling of Silver Diffusion, Bacterial Growth, and Silver Antibacterial Action
Modeling and dissociated experiments have allowed determining the different kinetics of pure silver diffusion, bacterial growth, and biocidal action. In the next section, these kinetics will be combined to propose a global model simulating inhibition zones radii that will be confronted with experimental measurements.
2.4.1. Model
The kinetics, thus, were coupled to simulate both diffusion and action of silver ions in the bacterial biofilm forming on the LB plate. For the simulation, two species were defined: silver ions (Ag
+) and
E. coli bacteria. Bacteria were admitted to grow on the agar only since the LB agar gel used is too viscous for bacteria diffusion inside the agar. As determined in
Section 2.2, the bacterial growth rate was fixed to 0.78 h
−1. Like silver diffusion within LB agar (
Section 2.1.1), Ag
+ ions were supposed to diffuse in the biofilm according to Fick’s Law (Equation (3)) with an unknown diffusivity D
Ag+ biofilm. Bacteria were assumed to react with silver ions following the Haas and Karra kinetics defined in
Section 2.3.3. Equation (20) was retained since inhibition halos were measured after at least 6 h of experiment and over 24 h in total.
The global bacterial rate resulted from two reactions (i.e., bacteria growth and biocidal action caused by silver ions) and was defined by Equation (23):
where:
CAg0+ is the initial silver concentration, ranging from 2 to 155 mg L−1 (i.e., from 0.19 to 1.44 mol m−3); testing different initial silver concentrations aimed to assess the robustness of the model;
N is the bacterial concentration expressed in the same unit as CAg0+ (i.e., mg L−1 or mol m−3);
t (min) is the time;
k’ was fixed to 1.75 ± 0.05 L mg
−1 min
−1 (according to
Section 2.3.3);
µ
max was fixed to 0.78 ± 0.06 h
−1 (according to
Section 2.2).
These pieces of information were entered in the Chemical Reaction Engineering module of COMSOL. The mass transfer module was also completed to consider the diffusion kinetics, i.e., with the initial bacterial concentration, the density, viscosity, and thickness of the biofilm formed and the diffusivity D
Ag+ biofilm of the silver ions in the biofilm. The density of an
E. coli biofilm made of living cells in an aqueous media was found to be 1.1 g mL
−1 [
33], while the dynamic viscosity was taken equal to 0.1 Pa s since this data were reported for a Gram-negative bacterium after 24 h incubation [
34]. The initial bacterial concentration and biofilm thickness were determined on the basis of experimental results (detailed in
Section 2.4.2). The diffusivity D
Ag+ biofilm, i.e., the only unknown parameter, was assessed by fitting the model with the experiment to obtain similar bacterial inhibition.
Figure 8 shows the geometry that was retained for the COMSOL simulation. It was the same as the cylindrical geometry used for pure diffusion (
Section 2.1.1,
Figure 1), which explains that initial and bound conditions were similar. Contrary to pure diffusion, the modeling was however focused on the biofilm only.
The implementation in COMSOL of the global model combining the reaction and diffusion kinetics was first intended to predict the respective concentration profiles of Ag+ (CAg+) and E. coli (N) in the biofilm formed on the plate over time and space. The radius of the resulting inhibition halo (Linhibition) can be then assessed by considering the inhibition halo as the zone where the E. coli concentration was zero.
Fitting the global model (coupling all the kinetics involved) with the experiment to obtain similar inhibition radii should allow determining the DAg+ biofilm value. Depending on this value, two behaviors could be possible:
Diffusion is the limiting phenomenon and a slight variation of DAg+ biofilm would cause strong shift between simulated and experimental results;
Diffusion is not the limiting phenomenon and the simulation results would not be very sensitive to the DAg+ biofilm value (over a consistent range).
2.4.2. Experiments
Experiments were carried out as described in
Section 3.3.4. The radius of the inhibition halo (L
inhibition) was measured over time (
Figure 9).
Figure S2 illustrates the plates obtained for two initial silver concentrations tested (20 and 155 mg L
−1) after 24 h incubation. As expected, the biofilm was only visible on the surface of the agar whatever the tested conditions. The measures of the inhibition halo radii were first done at 24 h to compare the influence of the presence of NaCl in the agar culture medium (
Figure 9). Thus, two agar media were implemented for these tests: usual LB medium (
Figure 9a) and medium with similar composition than LB, except for NaCl, was removed (
Figure 9b).
Results were reproducible and evidenced in both cases that a minimal silver concentration of 20 mg L
−1 was required to observe an action of silver against bacteria over 24 h (
Figure 9). However, the liquid tests carried out to determine the antibacterial activity of Ag
+ (
Section 2.3.2 and
Section 3.3.3) showed that a concentration of 3 mg L
−1 was already sufficient. One hypothesis was that the presence of chlorides in the LB medium (that were not present in the phosphate buffer used for the liquid tests) could lead to Ag
+ precipitation into AgCl and decrease the antibacterial activity of Ag
+ [
1]. Nevertheless, similar results were obtained for LB medium and LB medium exempt of NaCl (
Figure 9a,b). Thus, chlorides were not responsible for the shift and results obtained on LB agar only will be presented in the rest of the study. Another explanation can be that the mass transfer of silver ions to bacteria was not limited in the liquid tests (where convection occurred), but limited in the biofilm formed on the agar. Therefore, these results suggest that diffusion could be the limiting phenomenon. This assumption is consistent with the fact that the inhibition halos radii were quasi similar from 100 to 155 mg L
−1 (
Figure 9).
The inhibition zones radii (L
inhibition) were then measured on LB agar medium after 6 h, 16 h and 24 h of incubation (
Figure 10). Diffusion radii clearly increase with time and concentration. The inhibition zones reached a steady state after 6 h for the lowest silver concentration (20 mg mL
−1) and after 16 h for the rest of the concentrations. It is worth noticing that no significant differences were observed from 100 and 150 mg mL
−1.
Other experimental results are the initial bacterial concentration and the bacteria quantity forming the biofilm after 24 h incubation. The initial concentration of the bacteria spotted on the plate was 1.0 ± 0.2 × 10
9 CFU mL
−1, which corresponds to a mean mass concentration of 3.0 × 10
−4 g
dried cell.mL
−1 (knowing that the mean weight of one dried bacteria is about 3 × 10
−13 g, [
25]) and finally to a mean molar concentration of 1.36 × 10
−2 mol m
−3 (since the average molar mass of a bacteria is 22 ± 12 kDa, [
25]). Besides, the enumeration of bacteria in the biofilm recovered after 24 h incubation was found to be 3.2 ± 0.5 × 10
10 CFU. According to literature, the bacterial density in the biofilm is about 3.6 × 10
10 CFU mL
−1 [
33]. Thus, it was possible to determine the volume of the biofilm after 24 h (i.e., 3.2 × 10
10 CFU/3.6 × 10
10 CFU mL
−1 = 0.9 mL). Knowing that the surface of the agar plate was 62 cm
2, it comes a biofilm thickness around 145 µm, which is in accordance with literature [
33].
2.4.3. Comparison between the Model and the Experiments
The COMSOL simulation gave access to the concentration profiles for Ag
+ (C
Ag+) and
E. coli (N) in the biofilm formed on the agar. These profiles are available over time and over space (along r axis). An overview of these spatial distributions after 24 h of contact is given in
Figure 11.
The radius of the inhibition zone was defined as the smallest distance from the well center for which the
E. coli concentration (N) was zero. After 24 h,
Figure 11 shows that the bacterial concentration was zero up to a radius about 0.5 cm. In order to determine with precision the inhibition halos radii from the concentration profile of bacteria (
Figure 11), a minimum of the curve giving N with time t (and thus with the r axis) was searched according to Equation (24). The solving of Equation (24) gave a silver concentration, which allowed to precise the radial distance since the profile of silver concentration was known with time and space.
Different values of D
Ag+ biofilm were tested to fit the COMSOL simulations with the experimental results and a value of 7.0 ± 0.1 × 10
−12 m
2 s
−1 was selected for the simulations. Results, as a function of time and silver concentrations, are presented in
Figure 10.
A good correspondence between experimental results and simulation (
Figure 10) tend to validate the model over 24 h for the highest concentrations (i.e., from 50 to 150 mg L
−1) since the difference observed were included in the experimental error. Only the radii obtained for 20 mg L
−1 show a significant difference. This can be explained by (i) the fact that the Minimum Inhibitory Concentration (MIC) of silver to observe inhibition is closed to this concentration, around which discontinuity in the inhibition size could be experimentally evidenced, which is not taken into account by the model; (ii) the small size of the experimental halo (
Figure S2) inducing imprecision on the measures. The value of D
Ag+ biofilm (7.0 ± 0.1 × 10
−12 m
2 s
−1) is nearly 400-times lower than the silver diffusivity in the agar (D
Ag+). This is consistent with the presence of bacteria that hinder the silver transport. In addition, the predictions were much affected by slight variations on the value of D
Ag+ biofilm in the range tested (data not shown), which confirms the limitation by silver diffusion.