Time-Kill Analysis of Canine Skin Pathogens: A Comparison of Pradofloxacin and Marbofloxacin
Abstract
1. Introduction
2. Results
2.1. Descriptive Time-Kill Analysis
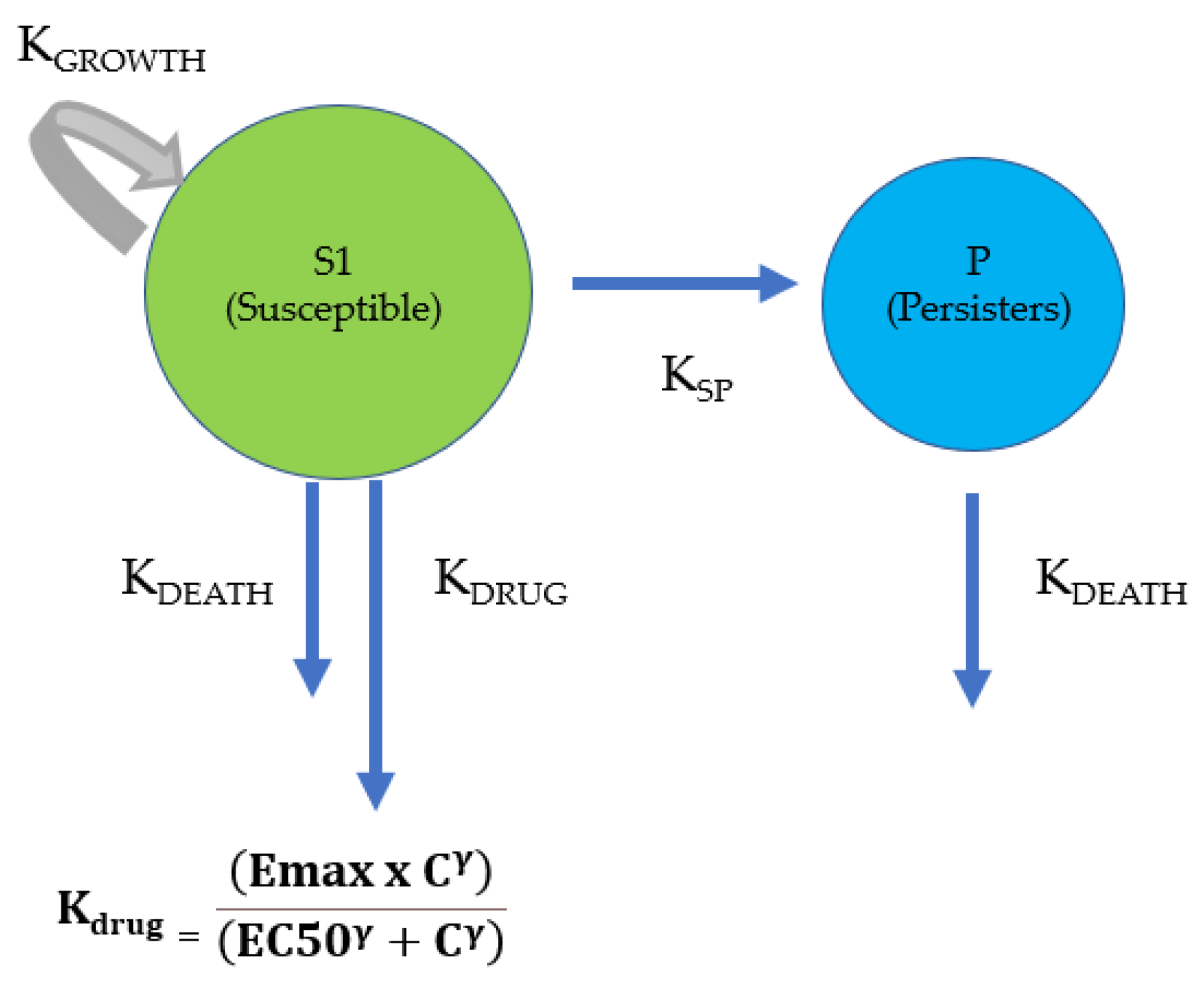
2.2. Time-Kill Curve Mathematical Modelling
2.3. Time-Kill Curve Analysis
2.4. Comparison of Predicted In Vivo Effects
2.5. Confirmation of PK/PD Index Target Value
3. Discussion
4. Materials and Methods
4.1. Selection of Bacterial Isolates and Antimicrobial Susceptibility
4.2. MIC Measurement and Time-Kill Curve Technique
4.3. Pharmacodynamic Data Analysis and Modelling
4.4. Pre-Existing Heterogenous Population Model
4.5. Covariate Analyses
4.6. Comparison of In Vivo Drug Effects Predicted from Licensed Dosage Regimens
4.7. In Silico Dose Fractionation Experiments
- -
- As a single dose over 24 h
- -
- Split in 2 half-doses, given every 12 h
- -
- Split in 4 quarter-doses, given every 6 h
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EUCAST. European Committee on Antimicrobial Susceptibility Testing. 2023. Available online: https://www.eucast.org/fileadmin/src/media/PDFs/EUCAST_files/Breakpoint_tables/v_13.0_Breakpoint_Tables.pdf (accessed on 1 July 2023).
- Andrews, J.M. Determination of minimum inhibitory concentrations. J. Antimicrob. Chemother. 2001, 48, 5–16. [Google Scholar] [CrossRef] [PubMed]
- Mouton, J.W.; Muller, A.E.; Canton, R.; Giske, C.G.; Kahlmeter, G.; Turnidge, J. MIC-based dose adjustment: Facts and fables. J. Antimicrob. Chemother. 2018, 73, 564–568. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, M.; Grégoire, N.; Couet, W.; Bulitta, J.B. Distinguishing antimicrobial models with different resistance mechanisms via population pharmacodynamic modeling. PLoS Comput. Biol. 2016, 12, e1004782. [Google Scholar] [CrossRef]
- Toutain, P.L.; Pelligand, L.; Lees, P.; Bousquet-Mélou, A.; Ferran, A.A.; Turnidge, J.D. The pharmacokinetic/pharmacodynamic paradigm for antimicrobial drugs in veterinary medicine: Recent advances and critical appraisal. J. Vet. Pharmacol. Ther. 2021, 44, 172–200. [Google Scholar] [CrossRef]
- Foerster, S.; Unemo, M.; Hathaway, L.J.; Low, N.; Althaus, C.L. Time-kill curve analysis and pharmacodynamic modelling for in vitro evaluation of antimicrobials against Neisseria gonorrhoeae. BMC Microbiol. 2016, 16, 216. [Google Scholar] [CrossRef] [PubMed]
- Pelligand, L.; Lees, P.; Sidhu, P.K.; Toutain, P.-L. Semi-mechanistic modeling of florfenicol time-kill curves and in silico dose fractionation for calf respiratory pathogens. Front. Microbiol. 2019, 10, 1237. [Google Scholar] [CrossRef] [PubMed]
- Minichmayr, I.K.; Aranzana-Climent, V.; Friberg, L.E. Pharmacokinetic/pharmacodynamic models for time courses of antibiotic effects. Int. J. Antimicrob. Agents 2022, 60, 106616. [Google Scholar] [CrossRef]
- Regoes, R.R.; Wiuff, C.; Zappala, R.M.; Garner, K.N.; Baquero, F.; Levin, B.R. Pharmacodynamic functions: A multiparameter approach to the design of antibiotic treatment regimens. Antimicrob. Agents Chemother. 2004, 48, 3670–3676. [Google Scholar] [CrossRef]
- Toutain, P.-L.; Bousquet-Mélou, A.; Damborg, P.; Ferran, A.A.; Mevius, D.; Pelligand, L.; Veldman, K.T.; Lees, P. En route towards European clinical breakpoints for veterinary antimicrobial susceptibility testing: A position paper explaining the VetCAST approach. Front. Microbiol. 2017, 8, 2344. [Google Scholar] [CrossRef]
- Mead, A.; Toutain, P.-L.; Richez, P.; Pelligand, L. Quantitative Pharmacodynamic Characterization of Resistance versus Heteroresistance of Colistin in E. coli Using a Semimechanistic Modeling of Killing Curves. Antimicrob. Agents Chemother. 2022, 66, e00793-22. [Google Scholar] [CrossRef]
- Lorenzutti, A.M.; San Andrés-Larrea, M.I.; Fernández-Varón, E.; Zarazaga, M.d.P.; Molina-López, A.M.; Serrano-Rodríguez, J.M. Effects of Growth Medium and Inoculum Size on Pharmacodynamics Activity of Marbofloxacin against Staphylococcus aureus Isolated from Caprine Clinical Mastitis. Antibiotics 2021, 10, 1290. [Google Scholar] [CrossRef] [PubMed]
- Blondeau, J.M.; Shebelski, S.D. Comparative in vitro killing of canine strains of Staphylococcus pseudintermedius and Escherichia coli by cefovecin, cefazolin, doxycycline and pradofloxacin. Vet. Dermatol. 2016, 27, 267-e63. [Google Scholar] [CrossRef] [PubMed]
- Blondeau, J.M.; Fitch, S.D. In vitro killing of canine strains of Staphylococcus pseudintermedius and Escherichia coli by cefazolin, cefovecin, doxycycline and pradofloxacin over a range of bacterial densities. Vet. Dermatol. 2020, 31, 187-e39. [Google Scholar] [CrossRef] [PubMed]
- Yohannes, S.; Awji, E.G.; Lee, S.-J.; Park, S.-C. Pharmacokinetics and pharmacokinetic/pharmacodynamic integration of marbofloxacin after intravenous and intramuscular administration in beagle dogs. Xenobiotica 2015, 45, 264–269. [Google Scholar] [CrossRef] [PubMed]
- Körber-Irrgang, B.; Wetzstein, H.G.; Bagel-Trah, S.; Hafner, D.; Kresken, M. Comparative activity of pradofloxacin and marbofloxacin against coagulase-positive staphylococci in a pharmacokinetic–pharmacodynamic model based on canine pharmacokinetics. J. Veter. Pharmacol. Ther. 2012, 35, 571–579. [Google Scholar] [CrossRef]
- Boothe, D.M.; Bush, K.M.; Boothe, H.W.; Davis, H.A. Pharmacokinetics and pharmacodynamics of oral pradofloxacin administration in dogs. Am. J. Veter-Res. 2018, 79, 1268–1276. [Google Scholar] [CrossRef]
- Schneider, M.; Thomas, V.; Boisrame, B.; Deleforge, J. Pharmacokinetics of marbofloxacin in dogs after oral and parenteral administration. J. Vet. Pharmacol. Ther. 1996, 19, 56–61. [Google Scholar] [CrossRef]
- Nielsen, E.I.; Friberg, L.E. Pharmacokinetic-pharmacodynamic modeling of antibacterial drugs. Pharmacol. Rev. 2013, 65, 1053–1090. [Google Scholar] [CrossRef]
- Campion, J.J.; McNamara, P.J.; Evans, M.E. Pharmacodynamic modeling of ciprofloxacin resistance in Staphylococcus aureus. Antimicrob. Agents Chemother. 2005, 49, 209–219. [Google Scholar] [CrossRef]
- Hauschild, G.; Rohn, K.; Engelhardt, E.; Sager, M.; Hardes, J.; Gosheger, G. Pharmacokinetic study on pradofloxacin in the dog–Comparison of serum analysis, ultrafiltration and tissue sampling after oral administration. BMC Vet. Res. 2013, 9, 32. [Google Scholar] [CrossRef]
- Zeniquin®. Product Monograph. Available online: https://www2.zoetisus.com/content/_assets/docs/vmips/package-inserts/zeniquin.pdf (accessed on 1 July 2023).
- Bregante, M.A.; de Jong, A.; Aramayona, J.J.; Garcia, M.A.; Solans, C.; Rueda, S. Protein binding of fluoroquinolones applied to live stock and companion animals. In Proceedings of the 8th International Congress European Asssociation for Veterinary Pharmacology and Toxicology (EAVPT), Jerusalem, Israel, 30 July–3 August 2000; p. 88. [Google Scholar]
- Papich, M.G. Pharmacokinetic–pharmacodynamic (PK–PD) modeling and the rational selection of dosage regimes for the prudent use of antimicrobial drugs. Vet. Microbiol. 2014, 171, 480–486. [Google Scholar] [CrossRef] [PubMed]
- Wright, D.H.; Brown, G.H.; Peterson, M.L.; Rotschafer, J.C. Application of fluoroquinolone pharmacodynamics. J. Antimicrob. Chemother. 2000, 46, 669–683. [Google Scholar] [CrossRef] [PubMed]
- WHO. World Health Organisation. 2023. Available online: https://www.who.int/news-room/fact-sheets/detail/antimicrobial-resistance (accessed on 1 July 2023).
- Drusano, G.L. Pharmacokinetics and pharmacodynamics of antimicrobials. Clin. Infect. Dis. 2007, 45, S89–S95. [Google Scholar] [CrossRef]
- Broussou, D.C.; Toutain, P.-L.; Woehrlé, F.; El Garch, F.; Bousquet-Melou, A.; Ferran, A.A. Comparison of in vitro static and dynamic assays to evaluate the efficacy of an antimicrobial drug combination against Staphylococcus aureus. PLoS ONE 2019, 14, e0211214. [Google Scholar] [CrossRef] [PubMed]
- Ferran, A.; Dupouy, V.; Toutain, P.-L.; Bousquet-Mélou, A. Influence of inoculum size on the selection of resistant mutants of Escherichia coli in relation to mutant prevention concentrations of marbofloxacin. Antimicrob. Agents Chemother. 2007, 51, 4163–4166. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, J.; Hao, H.; Huang, L.; Liu, Z.; Chen, D.; Yuan, Z. Pharmacokinetic and pharmacodynamic integration and modeling of enrofloxacin in swine for Escherichia coli. Front. Microbiol. 2016, 7, 36. [Google Scholar] [CrossRef]
- Potter, T.; Illambas, J.; Pelligand, L.; Rycroft, A.; Lees, P. Pharmacokinetic and pharmacodynamic integration and modelling of marbofloxacin in calves for Mannheimia haemolytica and Pasteurella multocida. Vet. J. 2013, 195, 53–58. [Google Scholar] [CrossRef]
- Illambas, J.; Potter, T.; Cheng, Z.; Rycroft, A.; Fishwick, J.; Lees, P. Pharmacodynamics of marbofloxacin for calf pneumonia pathogens. Res. Vet. Sci. 2013, 94, 675–681. [Google Scholar] [CrossRef]
- AliAbadi, F.S.; Lees, P. Pharmacokinetics and pharmacokinetic/pharmacodynamic integration of marbofloxacin in calf serum, exudate and transudate. J. Vet. Pharmacol. Ther. 2002, 25, 161–174. [Google Scholar] [CrossRef]
- Singh, R.; Ledesma, K.R.; Chang, K.-T.; Hou, J.-G.; Prince, R.A.; Tam, V.H. Pharmacodynamics of moxifloxacin against a high inoculum of Escherichia coli in an in vitro infection model. J. Antimicrob. Chemother. 2009, 64, 556–562. [Google Scholar] [CrossRef]
- Gebru, E.; Choi, M.-J.; Lee, S.-J.; Damte, D.; Park, S.C. Mutant-prevention concentration and mechanism of resistance in clinical isolates and enrofloxacin/marbofloxacin-selected mutants of Escherichia coli of canine origin. J. Med. Microbiol. 2011, 60, 1512–1522. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.B.; Park, C.H.; Kim, C.J.; Kim, E.-C.; Jacoby, G.A.; Hooper, D.C. Prevalence of plasmid-mediated quinolone resistance determinants over a 9-year period. Antimicrob. Agents Chemother. 2009, 53, 639–645. [Google Scholar] [CrossRef] [PubMed]
- Intorre, L.; Vanni, M.; Di Bello, D.; Pretti, C.; Meucci, V.; Tognetti, R.; Soldani, G.; Cardini, G.; Jousson, O. Antimicrobial susceptibility and mechanism of resistance to fluoroquinolones in Staphylococcus intermedius and Staphylococcus schleiferi. J. Vet. Pharmacol. Ther. 2007, 30, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Schmitz, F.-J.; Jones, M.E.; Hofmann, B.; Hansen, B.; Scheuring, S.; Lückefahr, M.; Fluit, A.; Verhoef, J.; Hadding, U.; Heinz, H.-P. Characterization of grlA, grlB, gyrA, and gyrB mutations in 116 unrelated isolates of Staphylococcus aureus and effects of mutations on ciprofloxacin MIC. Antimicrob. Agents Chemother. 1998, 42, 1249–1252. [Google Scholar] [CrossRef]
- Robicsek, A.; Strahilevitz, J.; Sahm, D.F.; Jacoby, G.A.; Hooper, D.C. qnr prevalence in ceftazidime-resistant Enterobacteriaceae isolates from the United States. Antimicrob. Agents Chemother. 2006, 50, 2872–2874. [Google Scholar] [CrossRef]
- Ciesielczuk, H.; Hornsey, M.; Choi, V.; Woodford, N.; Wareham, D.W. Development and evaluation of a multiplex PCR for eight plasmid-mediated quinolone-resistance determinants. J. Med. Microbiol. 2013, 62, 1823–1827. [Google Scholar] [CrossRef]
- CLSI-VET01-A4; Performance Standards for Antimicrobial Disk and Dilution Susceptibility Tests for Bacteria Isolated From Animals: Approved Standard. 4th ed. Clinical and Laboratory Standards Institute: Wayne, PA, USA, 2013.
- Aliabadi, F.S.; Lees, P. Pharmacokinetics and pharmacodynamics of danofloxacin in serum and tissue fluids of goats following intravenous and intramuscular administration. Am. J. Vet. Res. 2001, 62, 1979–1989. [Google Scholar] [CrossRef]
- CLSI-M26-A; M26-A: Methods for Determining Bactericidal Activity of Antimicrobial Agents; Approved Guideline. Clinical and Laboratory Standards Institute: Wayne, PA, USA, 1999.
- Azzariti, S.; Bond, R.; Loeffler, A.; Zendri, F.; Timofte, D.; Chang, Y.-M.; Pelligand, L. Investigation of In Vitro Susceptibility and Resistance Mechanisms in Skin Pathogens: Perspectives for Fluoroquinolone Therapy in Canine Pyoderma. Antibiotics 2022, 11, 1237. [Google Scholar] [CrossRef]
- Bregante, M.A.; De Jong, A.; Calvo, A.; Hernandez, E.; Rey, R.; Garcia, M.A. Protein binding of pradofloxacin, a novel 8-cyanofluoroquinolone, in dog and cat plasma. J. Vet. Pharmacol. Ther. 2003, 26, 87–88. [Google Scholar]
- Toutain, P.-L.; Bousquet-mélou, A. Plasma terminal half-life. J. Vet. Pharmacol. Ther. 2004, 27, 427–439. [Google Scholar] [CrossRef]
- CLSI-VET01S; Performance Standards for Antimicrobial Disk and Dilution Susceptibility Tests for Bacteria Isolated From Animals. 5th ed. Clinical and Laboratory Standards Institute: Wayne, PA, USA, 2020.
- Marbocyl®. Product Monograph. Available online: https://www.noahcompendium.co.uk/?id=-459540 (accessed on 1 July 2023).
- Nielsen, E.I.; Cars, O.; Friberg, L.E. Pharmacokinetic/pharmacodynamic (PK/PD) indices of antibiotics predicted by a semimechanistic PKPD model: A step toward model-based dose optimization. Antimicrob. Agents Chemother. 2011, 55, 4619–4630. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, E.I.; Viberg, A.; Löwdin, E.; Cars, O.; Karlsson, M.O.; Sandström, M. Semimechanistic pharmacokinetic/pharmacodynamic model for assessment of activity of antibacterial agents from time-kill curve experiments. Antimicrob. Agents Chemother. 2007, 51, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Khan, D.D.; Lagerbäck, P.; Cao, S.; Lustig, U.; Nielsen, E.I.; Cars, O.; Hughes, D.; Andersson, D.I.; Friberg, L.E. A mechanism-based pharmacokinetic/pharmacodynamic model allows prediction of antibiotic killing from MIC values for WT and mutants. J. Antimicrob. Chemother. 2015, 70, 3051–3060. [Google Scholar] [CrossRef] [PubMed]
- Mouton, J.W.; Vinks, A.A. Relationship between minimum inhibitory concentration and stationary concentration revisited: Growth rates and minimum bactericidal concentrations. Clin. Pharmacokinet. 2005, 44, 767–769. [Google Scholar] [CrossRef] [PubMed]


| Bacterial Growth System Parameters S. pseudintermedius | Bootstrap (n = 30) | |||
| Estimate | Median | 2.5% CI | 97.5% CI | |
| KGROWTHMAX (h−1) | 1.41 | 1.36 | 1.22 | 1.56 |
| KDEATH (h−1) | 0.179 | Fixed | ||
| Alpha (h−1) | 0.39 | 0.41 | 0.33 | 0.52 |
| BMAX (CFU/mL) | 6.02 × 10+09 | 6.72 × 10+09 | 5.45 × 10+09 | 8.91 × 10+09 |
| CV% BMAX (inter-strain variability) | 130% | |||
| Bacterial growth system parameters S. aureus | Bootstrap (n = 30) | |||
| Estimate | Median | 2.5% CI | 97.5% CI | |
| KGROWTHMAX (h−1) | 1.36 | 1.36 | 1.23 | 1.50 |
| KDEATH (h−1) | 0.179 | Fixed | ||
| Alpha (h−1) | 0.77 | 0.79 | 0.58 | 9.99 |
| BMAX (CFU/mL) | 6.60 × 10+09 | 7.16 × 10+09 | 5.59 × 10+09 | 1.07 × 10+10 |
| CV% BMAX (inter-strain variability) | 124% | |||
| Bacterial growth System parameters E. coli | Jacobian estimate | |||
| Estimate | CV% | 2.5% CI | 97.5% CI | |
| KGROWTHMAX (h−1) | 2.00 | 2.57 | 1.90 | 2.10 |
| KDEATH (h−1) | 0.179 | Fixed | ||
| BMAX (CFU/mL) | 6.84 × 10+09 | 15.96 | 4.70 × 10+09 | 8.98 × 10+09 |
| Isolate | PRADOFLOXACIN | MARBOFLOXACIN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimates | Bootstrap (n = 30) | Estimates | Bootstrap (n = 30) | |||||||
| Susceptible | Resistant | Median | 2.5% CI | 97.5% CI | Susceptible | Resistant | Median | 2.5% CI | 97.5% CI | |
| EC50_Pradofloxacin (mg/L) | EC50_Marbofloxacin (mg/L) | |||||||||
| MSSP_22219 | 0.037 | - | 0.036 | 0.029 | 0.049 | 0.17 | - | 0.18 | 0.15 | 0.21 |
| MSSP_108 | 0.041 | - | 0.041 | 0.032 | 0.054 | 0.49 | - | 0.45 | 0.41 | 0.53 |
| MRSP_1726 | 0.033 | - | 0.039 | 0.030 | 0.054 | 0.18 | - | 0.19 | 0.15 | 0.21 |
| MRSP_41 | 0.031 | - | 0.034 | 0.026 | 0.048 | 0.18 | - | 0.17 | 0.12 | 0.19 |
| MSSP_98 | - | 0.25 | 0.25 | 0.22 | 0.28 | - | 2.63 | 2.79 | 2.58 | 3.06 |
| MSSP_115 | - | 0.82 | 0.82 | 0.69 | 0.90 | - | 8.41 | 8.58 | 7.70 | 11.38 |
| MRSP_38 | - | 1.49 | 1.72 | 1.46 | 1.84 | - | 19.94 | 22.21 | 19.71 | 32.26 |
| MRSP_67 | - | 1.21 | 1.30 | 1.07 | 1.64 | - | 22.83 | 24.00 | 22.02 | 25.42 |
| Emax_Pradofloxacin (h−1) | Emax_Marbofloxacin (h−1) | |||||||||
| 2.23 | - | 2.36 | 1.74 | 2.87 | 1.85 | - | 1.91 | 1.53 | 2.04 | |
| - | 1.80 | 1.72 | 1.54 | 2.03 | - | 1.64 | 1.61 | 1.44 | 1.86 | |
| Gamma_Pradofloxacin (scalar) | Gamma_Marbofloxacin (scalar) | |||||||||
| 1.90 | 1.87 | 1.67 | 2.54 | 2.58 | 2.58 | 2.30 | 3.01 | |||
| Isolate | PRADOFLOXACIN | MARBOFLOXACIN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimates | Bootstrap (n = 30) | Estimates | Bootstrap (n = 30) | |||||||
| Susceptible | Resistant | Median | 2.5% CI | 97.5% CI | Susceptible | Resistant | Median | 2.5% CI | 97.5% CI | |
| EC50_Pradofloxacin (mg/L) | EC50_Marbofloxacin (mg/L) | |||||||||
| MSSA_476 | 0.061 | - | 0.062 | 0.058 | 0.085 | 0.32 | - | 0.317 | 0.297 | 0.359 |
| MSSA_B98 | 0.072 | - | 0.076 | 0.069 | 0.103 | 0.31 | - | 0.31 | 0.29 | 0.36 |
| MRSA_A53 | 0.051 | - | 0.052 | 0.040 | 0.066 | 0.28 | - | 0.28 | 0.26 | 0.32 |
| MRSA_A54 | 0.031 | - | 0.031 | 0.024 | 0.052 | 0.25 | - | 0.25 | 0.22 | 0.28 |
| MSSA_B53 | - | 1.29 | 1.28 | 1.24 | 1.48 | - | 15.47 | 15.74 | 14.78 | 16.85 |
| MSSA_B94 | - | 1.34 | 1.34 | 1.29 | 1.90 | - | 17.05 | 17.77 | 16.15 | 19.16 |
| MRSA_A009 | - | 1.34 | 1.33 | 1.26 | 1.87 | - | 16.30 | 16.72 | 15.53 | 17.65 |
| MRSA_A69 | - | 4.46 | 4.20 | 4.10 | 5.30 | - | 60.60 | 62.30 | 57.22 | 65.31 |
| Emax_Pradofloxacin (h−1) | Emax_Marbofloxacin (h−1) | |||||||||
| 2.17 | 2.30 | 1.88 | 2.69 | 1.97 | 2.01 | 1.67 | 2.23 | |||
| Gamma_Pradofloxacin (scalar) | Gamma_Marbofloxacin (scalar) | |||||||||
| 2.06 | 1.98 | 1.14 | 2.68 | 2.34 | 2.28 | 1.80 | 2.86 | |||
| Isolate | PRADOFLOXACIN | MARBOFLOXACIN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimates | Precision of Estimates | Estimates | Precision of Estimates | |||||||
| Susceptible | Resistant | CV% | 2.5% CI | 97.5% CI | Susceptible | Resistant | CV% | 2.5% CI | 97.5% CI | |
| EC50_Pradofloxacin_S1 (mg/L) | EC50_Marbofloxacin_S1 (mg/L) | |||||||||
| E. coli 14L_1510 | 0.047 | - | 8.72 | 0.04 | 0.05 | 0.119 | - | 9.01 | 0.10 | 0.14 |
| E. coli 16L_1242 | 0.052 | - | 9.13 | 0.04 | 0.06 | 0.178 | - | 9.80 | 0.14 | 0.21 |
| E. coli 17L_0826 | 0.033 | - | 9.43 | 0.03 | 0.04 | 0.157 | - | 9.74 | 0.13 | 0.19 |
| E. coli 17L_1562 | 0.076 | - | 9.29 | 0.06 | 0.09 | 0.642 | - | 9.88 | 0.52 | 0.77 |
| E. coli 2443 | - | 1.81 | 5.62 | 1.61 | 2.01 | - | 4.03 | 4.40 | 3.69 | 4.38 |
| E. coli 10L_2253 | - | 2.07 | 5.88 | 1.83 | 2.30 | - | 7.81 | 3.50 | 7.27 | 8.34 |
| E. coli 10L_3690 | - | 7.43 | 6.69 | 6.45 | 8.41 | - | 23.55 | 4.55 | 21.45 | 25.66 |
| E. coli 15L_3275 | - | 13.38 | 5.37 | 11.97 | 14.80 | - | 15.91 | 4.43 | 14.53 | 17.29 |
| EC50_Pradofloxacin_S2 = 1.97 × EC50_Pradofloxacin_S1 (mg/L) | EC50_Marbofloxacin_S2 = 1.67 × EC50_Marbofloxacin _S1 (mg/L) | |||||||||
| Emax_ Pradofloxacin (h−1) | Emax_Marbofloxacin (h−1) | |||||||||
| 8.73 | - | 3.63 | 8.11 | 9.35 | 17.14 | - | 4.22 | 15.72 | 18.56 | |
| - | 3.11 | 3.03 | 2.93 | 3.30 | - | 2.85 | 2.64 | 2.71 | 3.00 | |
| Gamma_Pradofloxacin (scalar) | Gamma_Marbofloxacin (scalar) | |||||||||
| 1.17 | 5.58 | 1.04 | 1.30 | 1.12 | 3.91 | 1.03 | 1.20 | |||
| 2.37 | 10.08 | 1.90 | 2.84 | 2.80 | 8.22 | 2.35 | 3.25 | |||
| Isolate | PRADOFLOXACIN | MARBOFLOXACIN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Average Free Plasma Concentration (µg/mL) | Kdrug (h−1) | Average Free Plasma Concentration (µg/mL) | Kdrug (h−1) | |||||||
| Experimental MIC (µg/mL) | First Dose | Steady State | First Dose | Steady State | Experimental MIC (µg/mL) | First Dose | Steady State | First Dose | Steady State | |
| MSRP 41 (susceptible) | 0.025 | 0.45 | 0.51 | 2.21 | 2.21 | 0.20 | 0.61/0.51 | 0.83/0.68 | 1.78/1.73 | 1.82/1.79 |
| MRSP 67 (resistant) | 0.9 | 0.24 | 0.29 | 11.2 | No efficacy (0.0001/0.0001) | No efficacy (0.0003/0.0002) | ||||
| MSSA B98 (susceptible) | 0.056 | 0.45 | 0.51 | 2.12 | 2.14 | 0.4 | 0.61/0.51 | 0.83/0.68 | 1.64/1.50 | 1.79/1.70 |
| MSSA B53 (resistant) | 1.8 | 0.22 | 0.28 | 12.8 | No efficacy (0.001/0.0006) | No efficacy (0.002/0.001) | ||||
| E. coli 14L-1510 (susceptible) | 0.0218 | 0.45 | 0.51 | 8.15 | 8.23 | 0.025 | 0.61/0.51 | 0.83/0.68 | 14.74/14.29 | 15.78/14.98 |
| E. coli 10L-2253 (resistant) | 2.8 | 0.081 | 0.11 | 14.4 | No efficacy (0.002/0.001) | No efficacy (0.005/0.0030) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azzariti, S.; Mead, A.; Toutain, P.-L.; Bond, R.; Pelligand, L. Time-Kill Analysis of Canine Skin Pathogens: A Comparison of Pradofloxacin and Marbofloxacin. Antibiotics 2023, 12, 1548. https://doi.org/10.3390/antibiotics12101548
Azzariti S, Mead A, Toutain P-L, Bond R, Pelligand L. Time-Kill Analysis of Canine Skin Pathogens: A Comparison of Pradofloxacin and Marbofloxacin. Antibiotics. 2023; 12(10):1548. https://doi.org/10.3390/antibiotics12101548
Chicago/Turabian StyleAzzariti, Stefano, Andrew Mead, Pierre-Louis Toutain, Ross Bond, and Ludovic Pelligand. 2023. "Time-Kill Analysis of Canine Skin Pathogens: A Comparison of Pradofloxacin and Marbofloxacin" Antibiotics 12, no. 10: 1548. https://doi.org/10.3390/antibiotics12101548
APA StyleAzzariti, S., Mead, A., Toutain, P.-L., Bond, R., & Pelligand, L. (2023). Time-Kill Analysis of Canine Skin Pathogens: A Comparison of Pradofloxacin and Marbofloxacin. Antibiotics, 12(10), 1548. https://doi.org/10.3390/antibiotics12101548






