Numerical Analysis of an Inline Metal-Organic Chemical Vapour Deposition Process Based on Sliding-Mesh Modelling
Abstract
:1. Introduction
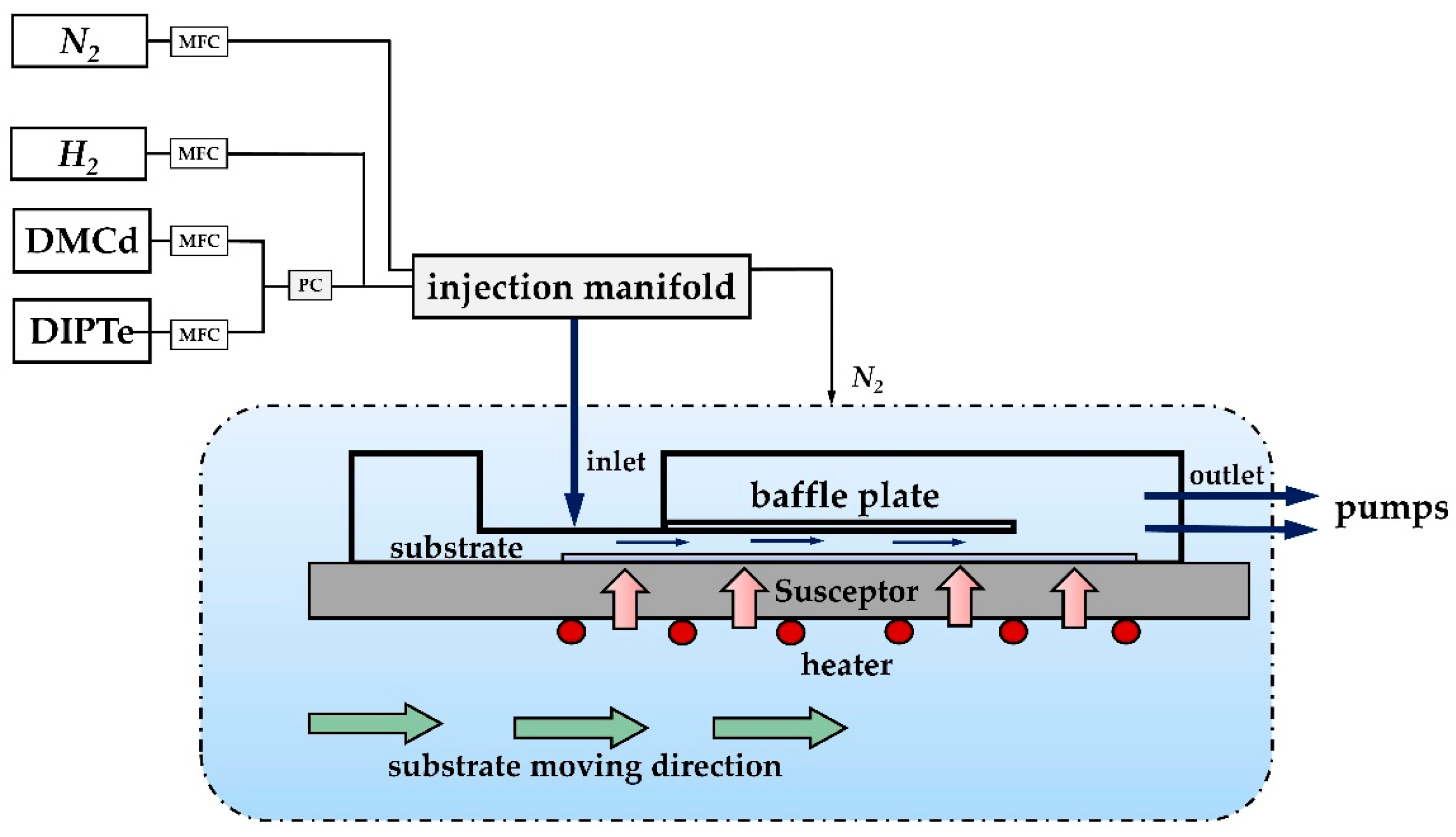
2. Experimental Parameters
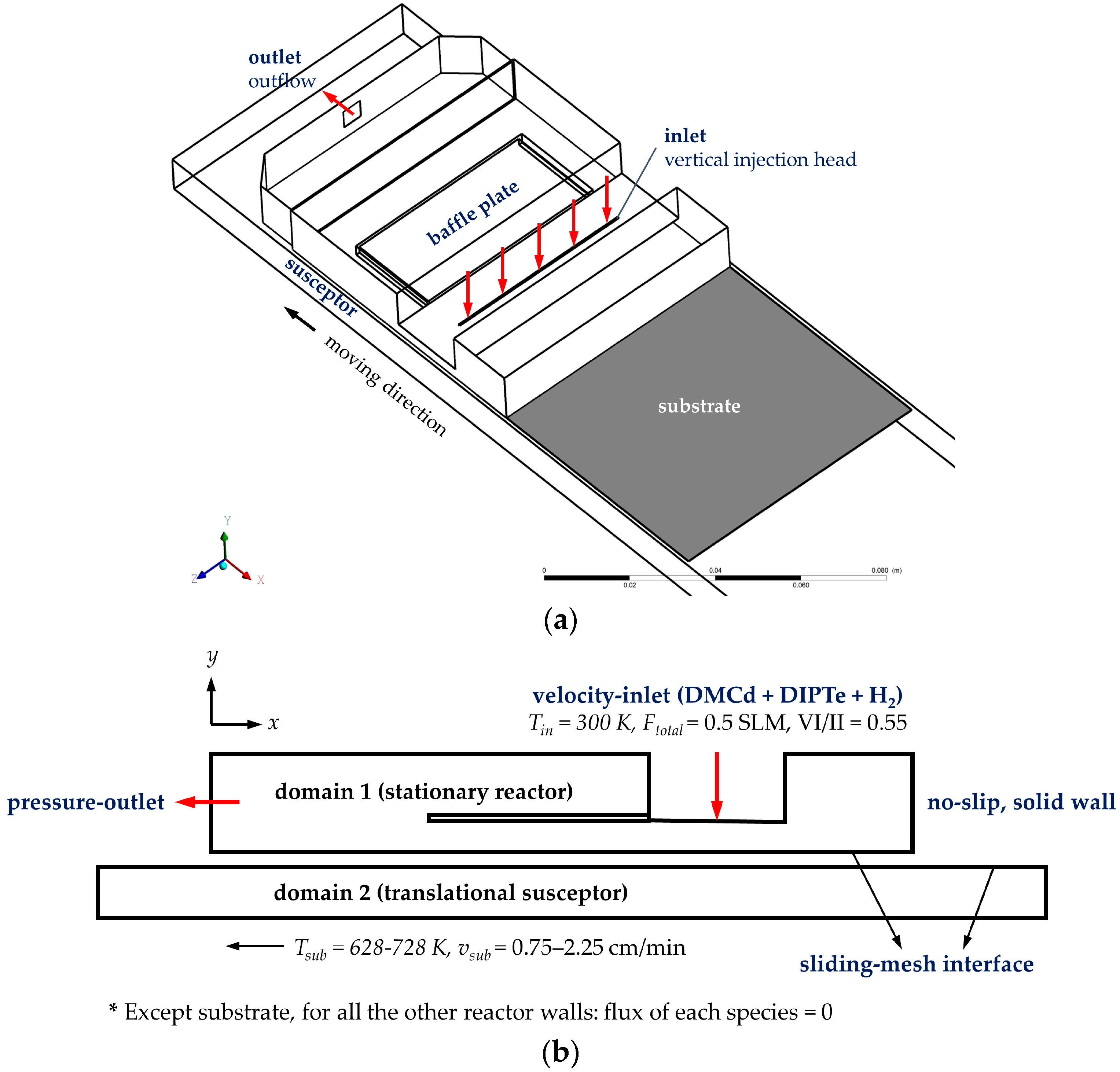
3. Numerical Model Description
4. Computational Grid Resolution
5. Results and Discussion
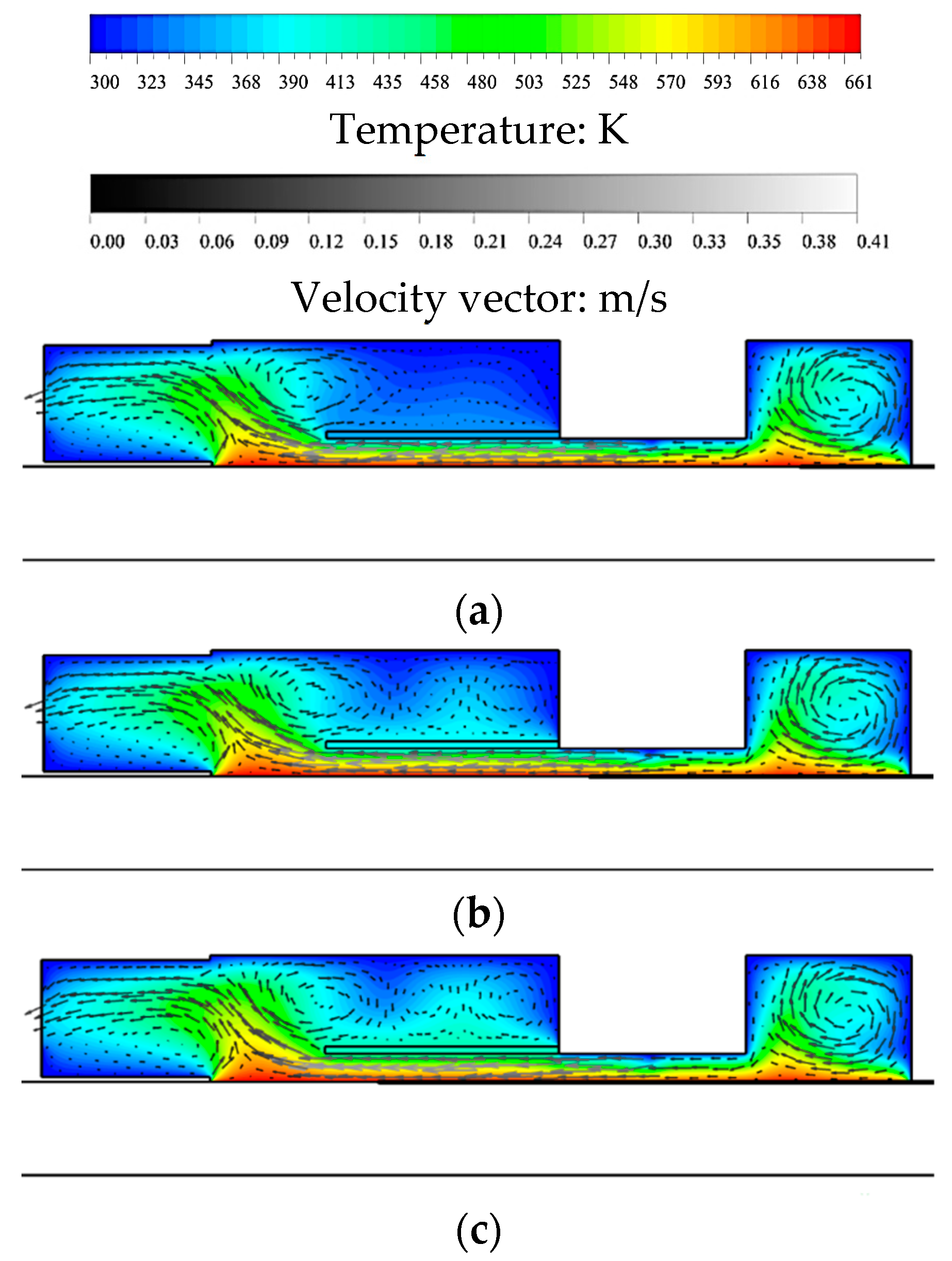
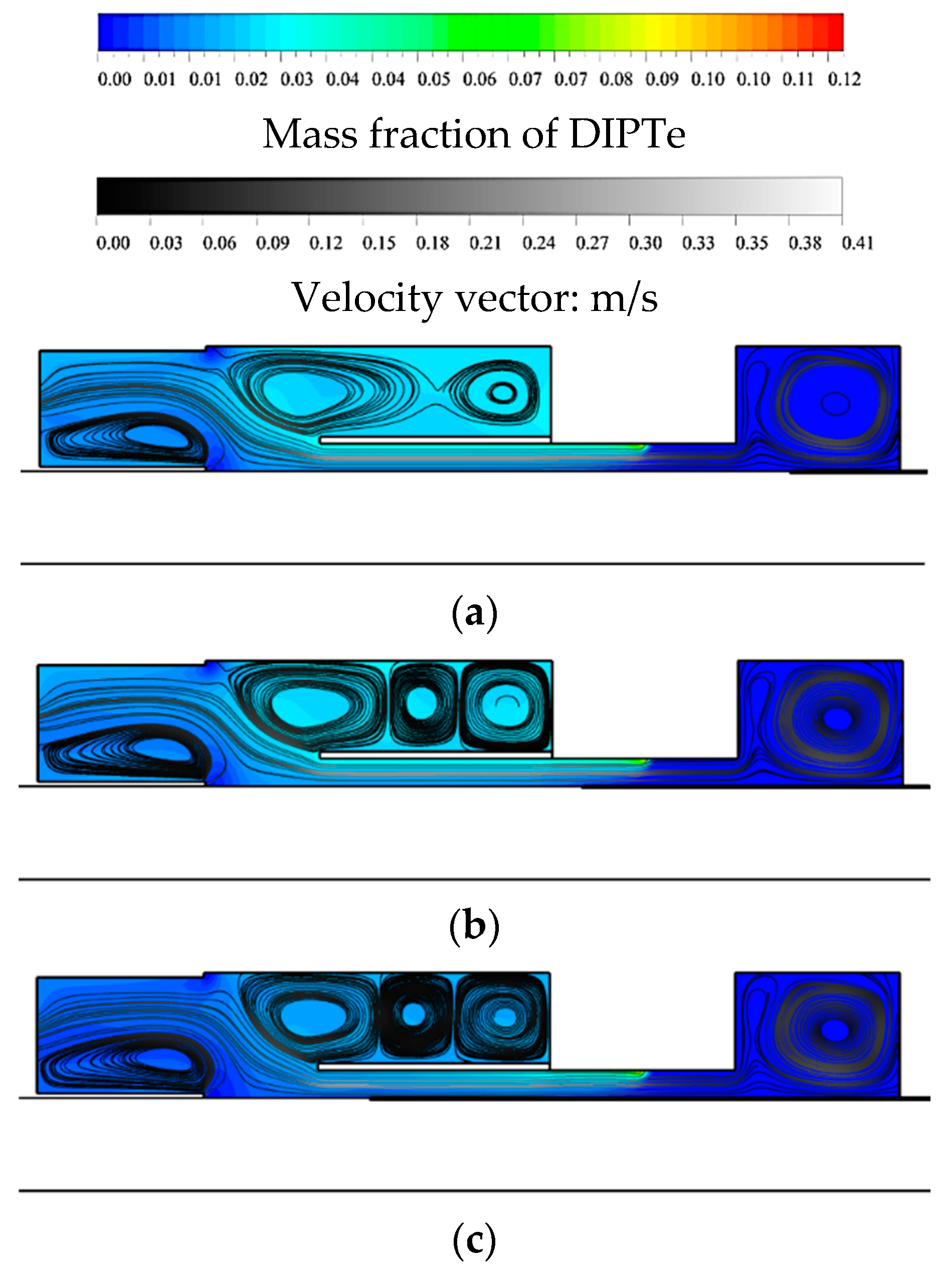
5.1. Sliding Mesh Technique
5.2. Susceptor Travelling Speed
6. Conclusions
- The grid sensitive study shows that the use of hexahedral mesh performs better both in simulation accuracy and convergence speed than the tetrahedral mesh. The number of 173,400 imposed in the stationary domain (reactor chamber) is found to be favourable in this study.
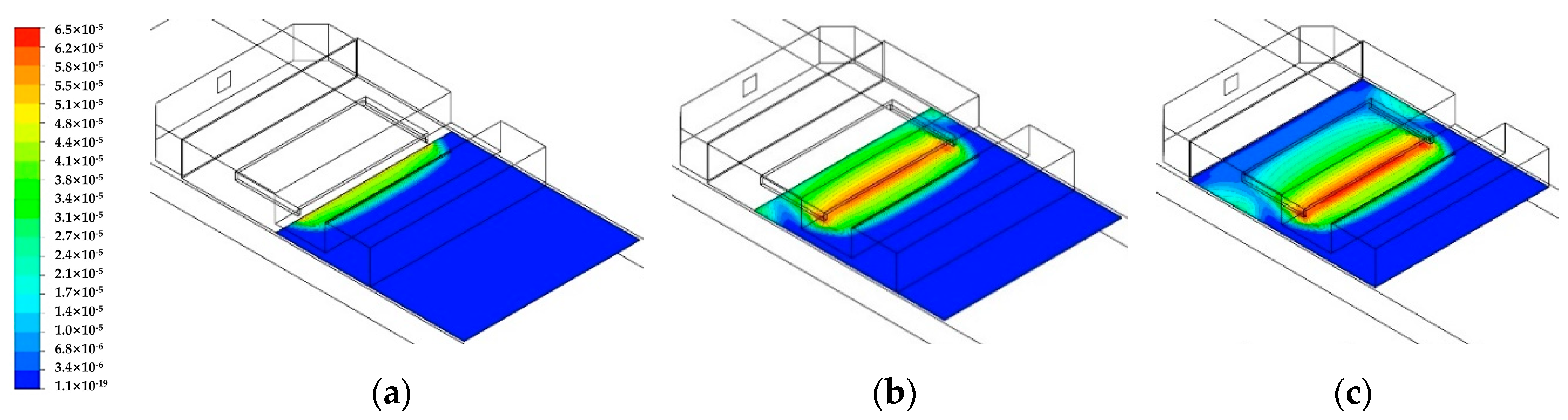
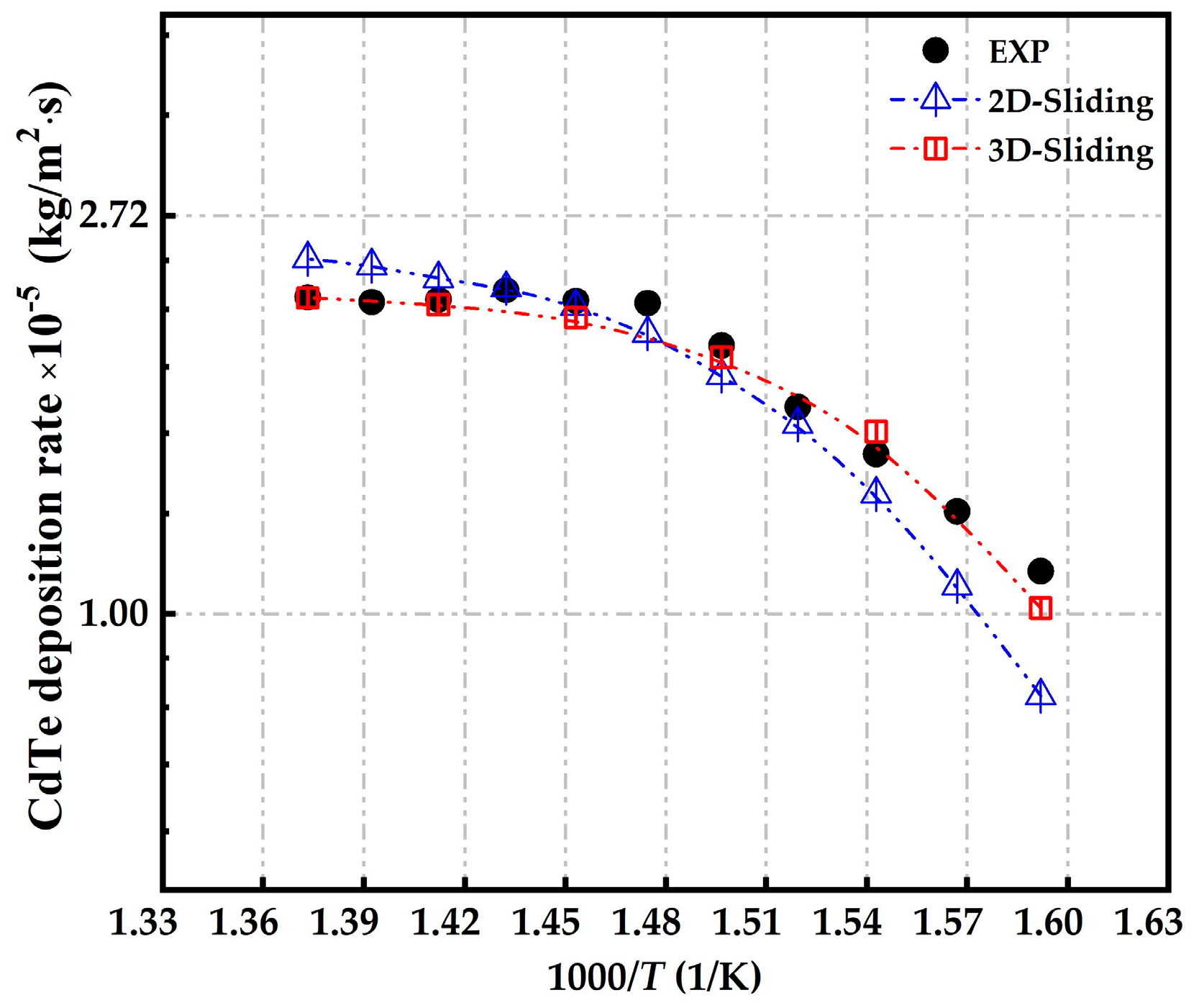
- Both 2D and 3D simulations are performed based on the proposed sliding mesh method, and the results show that 3D modelling fits better with the experimental data, which also demonstrates the feasibility of the sliding mesh method. The use of this method is able to provide a solution which can well interpret the transport phenomena inside the MOCVD reactor from the perspective of transient mass transfer of deposition dynamics. Such time-dependent simulations show that the laminar flow is quickly developed after the gas mixture has been injected into the reactor chamber, which ensures a uniform deposition of CdTe thin film. However, the uniformity on both edges of the substrate are influenced due to the buoyancy-driven recirculation rolls above the baffle plate.
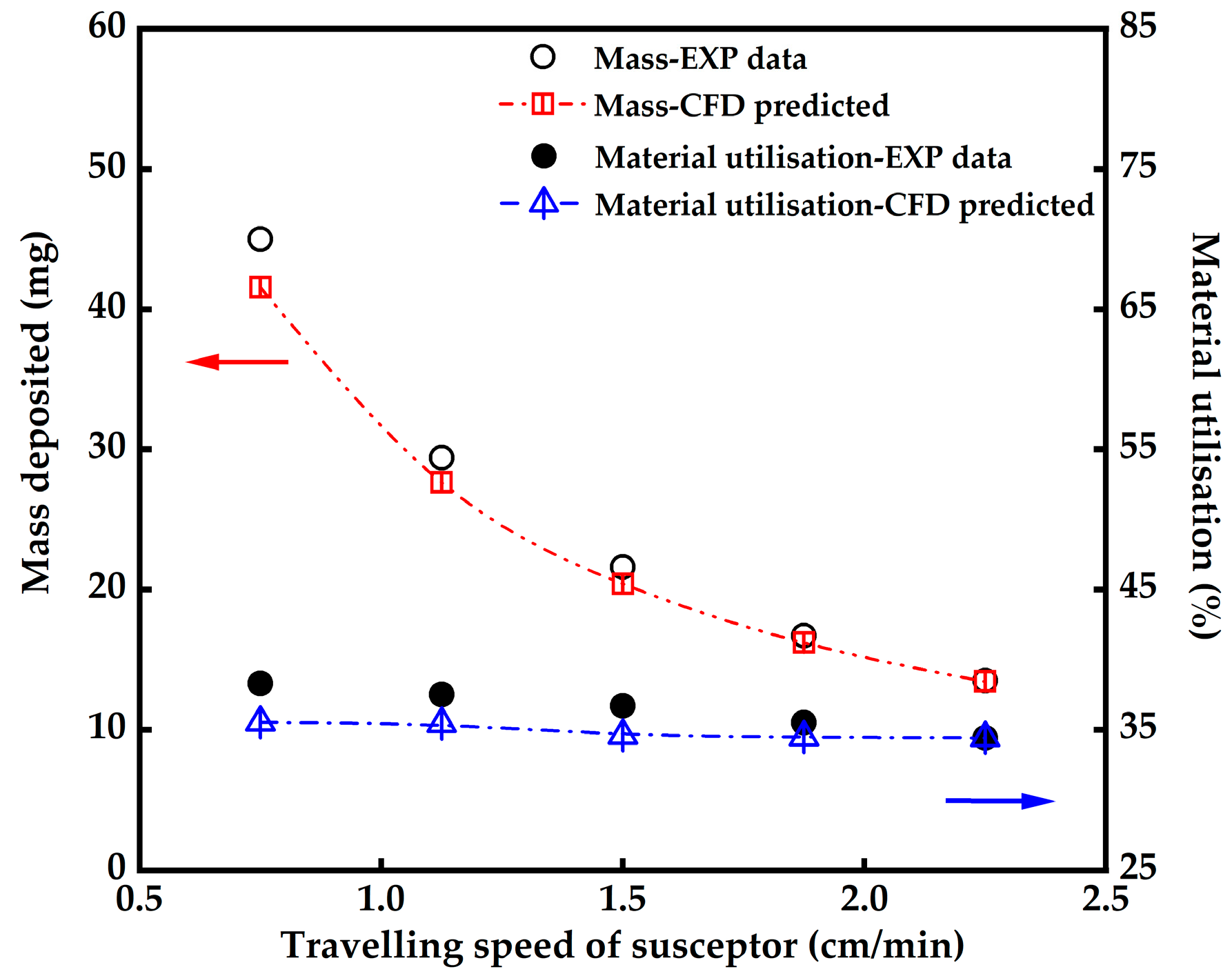
- On basis of the sliding mesh method, the adoption of transient simulations also makes it possible to investigate the influence of susceptor moving speed on the thin film deposition. By varying the susceptor moving speed from 0.75 to 2.25 cm/min, it has been found that the mass deposited on the substrate decreases with the increase in the moving speed, whereas the material utilisation is slightly changed because of a shorter residence time. This finding indicates that a susceptor moving speed between 0.75 and 1.13 cm/min is effectively beneficial in terms of CdTe mass deposition.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a0 | Å | lattice parameter |
| Asub | m2 | substrate area |
| cp | J/kg·K | specific heat capacity at constant pressure |
| C | mol/m3 | concentration |
| C0 | mol/m3 | initial concentration |
| D | m2/s | mass diffusion coefficient |
| DT | m2/s | thermal diffusion coefficient |
| Ftotal | L/min (standard), SLM | total flow rate |
| g | m/s2 | gravitational acceleration |
| mdeposit | kg | deposited mass |
| mpredict | kg | predicted mass of deposit |
| mtheory | kg | theoretical mass of deposit |
| Ṁlimit | kg/s | mass flow rate of the limiting precursor |
| NA | – | avagadro’s number |
| p | Pa | pressure |
| plimit | Pa | partial pressure of the limiting precursor |
| t | s | time |
| td | s | deposition time |
| T | K | temperature |
| Tin | K | inlet temperature |
| Tsub | K | substrate temperature |
| U | m/s | velocity of gas flow |
| Um | m/s | velocity component of the motion of moving mesh |
| vsub | m/s | substrate moving speed |
| η | – | material utilisation |
| κ | W/m·K | thermal conductivity |
| ρ | kg/m3 | density of gas flow |
| ρCdTe | kg/m3 | density of CdTe |
| τij | Pa | viscous stress tensor between species i and j |
| ωi | – | mass fraction of species i |
| CdTe | – | cadmium telluride |
| CFD | – | computational fluid dynamics |
| DIPTe | – | diisopropyltelluride |
| DMCd | – | dimethylcadmium |
| DR | – | deposition rate |
| HG | – | hexahedral grid |
| MOCVD | – | metal-organic chemical vapour deposition |
| RSD | – | relative standard deviation |
| TG | – | tetrahedral grid |
| SLM | – | standard litre per minute |
| SIMPLE | – | semi-implicit method for pressure-linked equations |
References
- Lee, T.D.; Ebong, A.U. A review of thin film solar cell technologies and challenges. Renew. Sustain. Energy Rev. 2017, 70, 1286–1297. [Google Scholar] [CrossRef]
- Bosio, A.; Pasini, S.; Romeo, N. The History of photovoltaics with emphasis on CdTe solar cells and modules. Coatings 2020, 10, 344. [Google Scholar] [CrossRef] [Green Version]
- Kartopu, G.; Phillips, L.J.; Barrioz, V.; Irvine, S.J.C.; Hodgson, S.D.; Tejedor, E.; Dupin, D.; Clayton, A.J.; Rugen-Hankey, S.L.; Durose, K. Progression of metalorganic chemical vapour-deposited CdTe thin-film PV devices towards modules. Prog. Photovolt. Res. Appl. 2016, 24, 283–291. [Google Scholar] [CrossRef]
- Mohanty, D.; Lu, Z.; Sun, X.; Xiang, Y.; Gao, L.; Shi, J.; Zhang, L.; Kisslinger, K.; Washington, M.; Wang, G.C.; et al. Growth of epitaxial CdTe thin films on amorphous substrates using single crystal graphene buffer. Carbon 2019, 144, 519–524. [Google Scholar] [CrossRef]
- Barrioz, V.; Clayton, A.; Brooks, W.S.M.; Yang, X.; Irvine, S.J.C.; Rugen-Hankey, S. CdTe Devices by AP-MOCVD: Evolution from Horizontal to Inline Reactors. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition/5th World Conference on Photovoltaic Energy Conversion, Valencia, Spain, 6–10 September 2010. [Google Scholar]
- Jones, A.C.; Hitchman, M.L. Overview of Chemical Vapour Deposition. In Chemical Vapour Deposition: Precursors, Processes and Applications; Royal Society of Chemistry: London, UK, 2009; pp. 1–36. [Google Scholar]
- Kumarasinghe, P.K.K.; Dissanayake, A.; Pemasiri, B.M.K.; Dassanayake, B.S. Effect of post deposition heat treatment on microstructure parameters, optical constants and composition of thermally evaporated CdTe thin films. Mater. Sci. Semicond. Process. 2017, 58, 51–60. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, J.; Pei, Y.; Wang, G. Study on the uniformity of ZnO films grown by MOCVD. Ceram. Int. 2019, 45, 3971–13978. [Google Scholar] [CrossRef]
- Li, H. Mass transport analysis of a showerhead MOCVD reactor. J. Semicond. 2011, 32, 033006. [Google Scholar] [CrossRef]
- Gu, C.Y.; Lee, C.M.; Liu, X.L. Design of a three-layer hot-wall horizontal flow MOCVD reactor. J. Semicond. 2012, 33, 093005. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Cai, J.; Xu, Y.; Fan, B.; Wang, G. Numerical simulation and analysis of process parameters of GaN-MOCVD reactor. Int. Commun. Heat Mass Transf. 2018, 91, 64–76. [Google Scholar] [CrossRef]
- Li, J.; Fei, Z.; Xu, Y.; Wang, J.; Fan, B.; Ma, X.; Wang, G. Study on the optimization of the deposition rate of planetary GaN-MOCVD films based on CFD simulation and the corresponding surface model. R. Soc. Open Sci. 2018, 5, 171757. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Cai, J.; Wu, Z.; Wang, J.; Pei, Y.; Wang, G. Numerical simulation and study of the metal-organic chemical vapor deposition growth of ZnO film. Phys. Fluids 2019, 31, 027104. [Google Scholar]
- Li, X.G.; Xiao, W.D. Model on transport phenomena and control of rod growth uniformity in siemens CVD reactor. Comput. Chem. Eng. 2018, 117, 351–358. [Google Scholar] [CrossRef]
- Tang, G.Q.; Chen, C.; Cai, Y.F.; Zong, B.; Cai, Y.G.; Wang, T.H. Numerical simulations of a 96-rod polysilicon CVD reactor. J. Cryst. Growth 2018, 489, 68–71. [Google Scholar]
- Ramadan, Z.; Im, I.T. Optimization of operating parameters in a planetary CVD reactor using response surface methodology. Silicon 2019, 11, 2067–2074. [Google Scholar] [CrossRef]
- Amirkhalili, A.; Barrioz, V.; Irvine, S.J.C.; Beattie, N.S.; Zoppi, G. A combined Na and Cl treatment to promote grain growth in MOCVD grown CdTe thin films. J. Alloy. Compd. 2017, 699, 969–975. [Google Scholar] [CrossRef]
- Teloeken, A.C.; Lamb, D.A.; Dunlop, T.O.; Irvine, S.J.C. Effect of bending test on the performance of CdTe solar cells on flexible ultra-thin glass produced by MOCVD. Sol. Energy Mater. Sol. Cells 2020, 211, 110552. [Google Scholar] [CrossRef]
- Kartopu, G.; Oklobia, O.; Turkay, D.; Diercks, D.R.; Gorman, B.P.; Barrioz, V.; Campbell, S.; Major, J.D.; Al Turkestani, M.K.; Yerci, S.; et al. Study of thin film poly-crystalline CdTe solar cells presenting high acceptor concentrations achieved by in-situ arsenic doping. Sol. Energy Mater. Sol. Cells 2019, 194, 259–267. [Google Scholar] [CrossRef]
- Lamb, D.A.; Irvine, S.J.C.; Clayton, A.J.; Kartopu, G.; Barrioz, V.; Hodgson, S.D.; Baker, M.A.; Grilli, R.; Hall, J.; Underwood, C.I.; et al. Characterization of MOCVD thin-film CdTe photovoltaics on space-qualified cover glass. IEEE J. Photovolt. 2016, 6, 557–561. [Google Scholar] [CrossRef] [Green Version]
- Kartopu, G.; Barrioz, V.; Monir, S.; Lamb, D.A.; Irvine, S.J.C. CdTe thin film solar cells produced using a chamberless inline process via metalorganic chemical vapour deposition. Thin Solid Films 2015, 578, 93–97. [Google Scholar] [CrossRef]
- Monir, S.; Kartopu, G.; Barrioz, V.; Lamb, D.; Irvine, S.J.C.; Yang, X.; Vagapov, Y. Thin CdTe layers deposited by a chamberless inline process using MOCVD, simulation and experiment. Appl. Sci. 2020, 10, 1734. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.G.; Wu, Y.Y.; Huang, X.B.; Barrioz, V.; Irvine, S.J.C. Numerical simulation of the deposition process and the epitaxial growth of cadmium telluride thin film in a MOCVD reactor. Comput. Therm. Sci. Int. J. 2013, 5, 177–188. [Google Scholar] [CrossRef]
- Sung, H.G.; Jeong, K.; Heo, J. Performance characteristics of a pintle nozzle using the conformal sliding mesh technique. Aerosp. Sci. Technol. 2017, 61, 85–94. [Google Scholar] [CrossRef]
- Haringa, C.; Vandewijer, R.; Mudde, R.F. Inter-compartment interaction in multi-impeller mixing. Part II. Experiments, sliding mesh and large Eddy simulations. Chem. Eng. Res. Des. 2018, 136, 886–899. [Google Scholar] [CrossRef] [Green Version]
- Houzeaux, G.; Cajas, J.C.; Discacciati, M.; Eguzkitza, B.; Gargallo-Peiró, A.; Rivero, M.; Vázquez, M. Domain decomposition methods for domain composition purpose: Chimera, overset, gluing and sliding mesh methods. Arch. Comput. Methods Eng. 2017, 24, 1033–1070. [Google Scholar] [CrossRef] [Green Version]
- Barth, T.; Herbin, R.; Ohlberger, M. Finite Volume Methods: Foundation and Analysis. In Encyclopedia of Computational Mechanics, 2nd ed.; Stein, E., Borst, R., Hughes, T.J.R., Eds.; John Wiley & Sons: New York, NY, USA, 2017. [Google Scholar]
- Kartopu, G.; Barrioz, V.; Irvine, S.J.C.; Clayton, A.J.; Monir, S.; Lamb, D.A. Inline atmospheric pressure metal-organic chemical vapour deposition for thin film CdTe solar cells. Thin Solid Films 2014, 558, 374–377. [Google Scholar] [CrossRef]
- Barrioz, V.; Monir, S.; Kartopu, G.; Lamb, D.A.; Brooks, W.; Siderfin, P.; Jones, S.; Clayton, A.J.; Irvine, S.J.C. MOCVD for solar cells, a transition towards a chamberless inline process. J. Cryst. Growth 2015, 414, 223–231. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Yang, X.G.; Huang, X.B.; Barrioz, V.; Monir, S.; Irvine, S.J.C.; Kartopu, G. CFD modelling of cadmium telluride (CdTe) thin film coating with inline AP-MOCVD. Appl. Mech. Mater. 2012, 217, 1265–1273. [Google Scholar] [CrossRef]
- Barrioz, V.; Kartopu, G.; Irvine, S.J.C.; Monir, S.; Yang, X.G. Material utilisation when depositing CdTe layers by inline AP-MOCVD. J. Cryst. Growth 2012, 354, 81–85. [Google Scholar] [CrossRef]

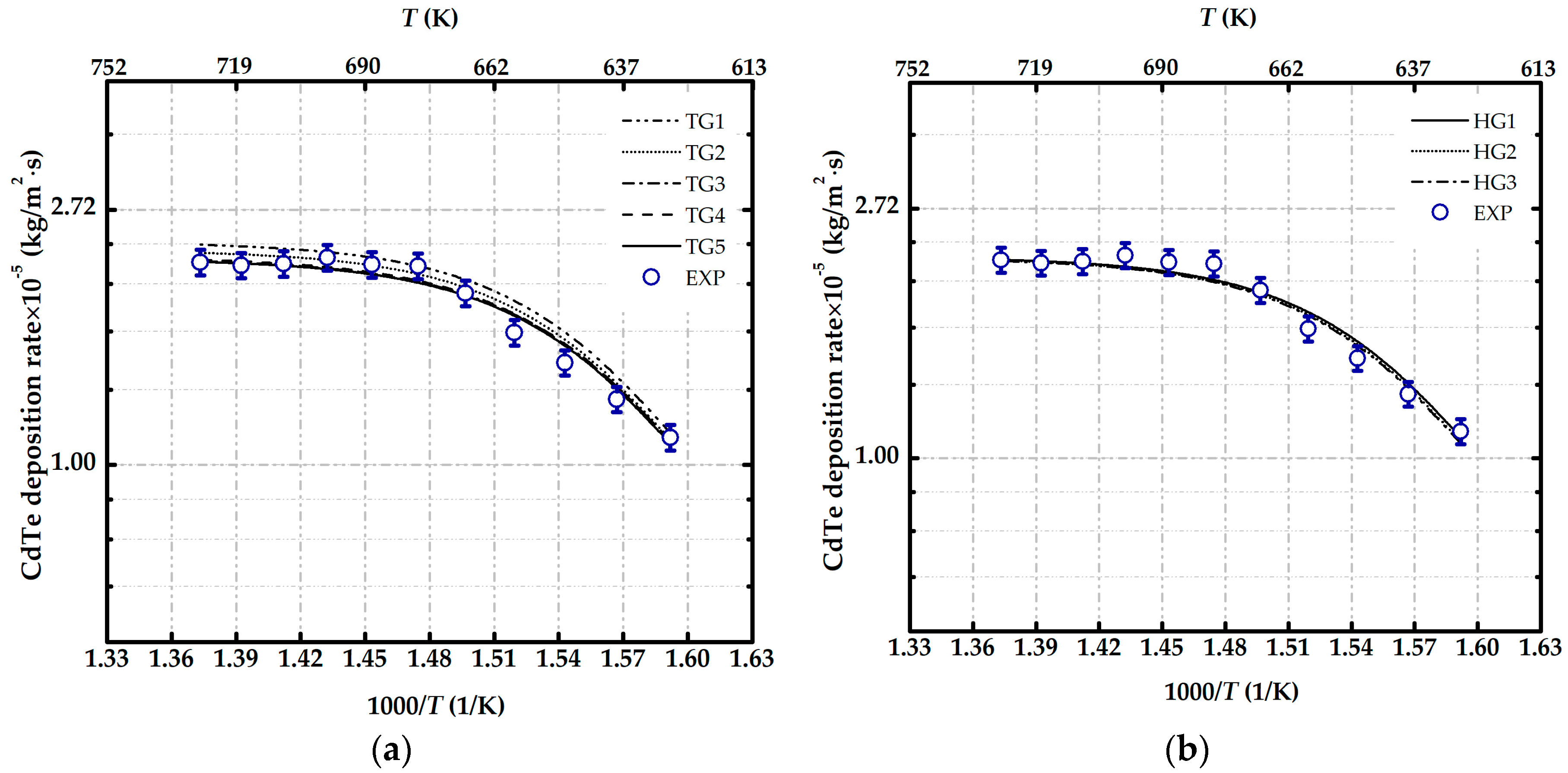




| Tetrahedral Grid | Hexahedral Grid | ||
|---|---|---|---|
| Case | Size of the Computational Mesh | Case | Size of the Computational Mesh |
| TG 1 | 59,500 | HG 1 | 17,600 |
| TG 2 | 114,600 | HG 2 | 173,400 |
| TG 3 | 268,000 | HG 3 | 746,600 |
| TG 4 | 444,200 | – | – |
| TG 5 | 2,823,700 | – | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wu, Y.; Yang, X.; Huang, C. Numerical Analysis of an Inline Metal-Organic Chemical Vapour Deposition Process Based on Sliding-Mesh Modelling. Coatings 2020, 10, 1198. https://doi.org/10.3390/coatings10121198
Zhou X, Wu Y, Yang X, Huang C. Numerical Analysis of an Inline Metal-Organic Chemical Vapour Deposition Process Based on Sliding-Mesh Modelling. Coatings. 2020; 10(12):1198. https://doi.org/10.3390/coatings10121198
Chicago/Turabian StyleZhou, Xiaosong, Yiyi Wu, Xiaogang Yang, and Chaowen Huang. 2020. "Numerical Analysis of an Inline Metal-Organic Chemical Vapour Deposition Process Based on Sliding-Mesh Modelling" Coatings 10, no. 12: 1198. https://doi.org/10.3390/coatings10121198
APA StyleZhou, X., Wu, Y., Yang, X., & Huang, C. (2020). Numerical Analysis of an Inline Metal-Organic Chemical Vapour Deposition Process Based on Sliding-Mesh Modelling. Coatings, 10(12), 1198. https://doi.org/10.3390/coatings10121198




