Mechanical Behavior and Damage of Zinc Coating for Hot Dip Galvanized Steel Sheet DP600
Abstract
:1. Introduction
2. Mechanical Behavior of Zinc Coating
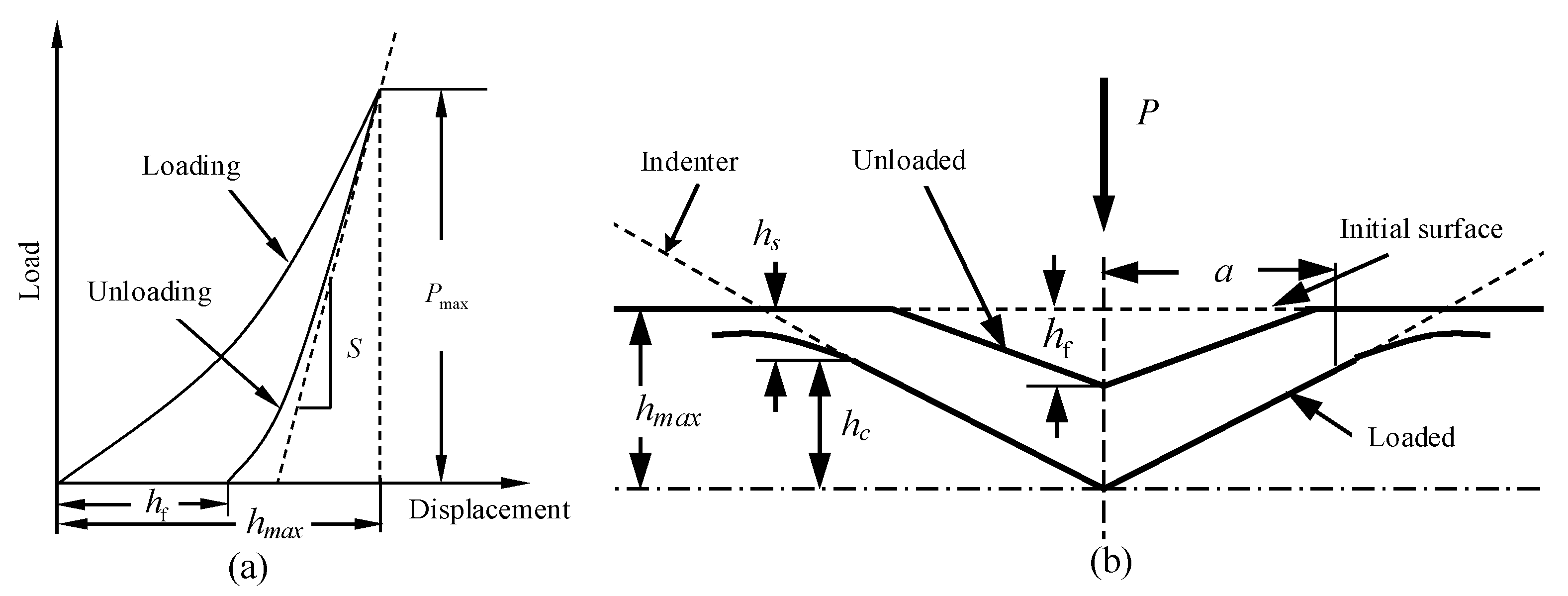
2.1. Constitutive Model of Zinc Coating
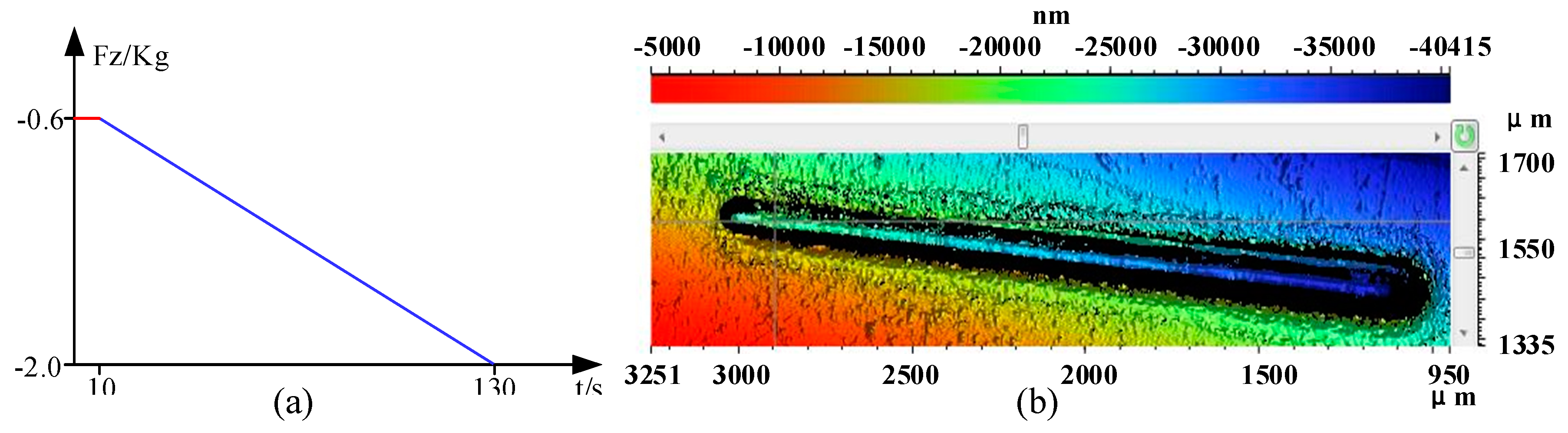
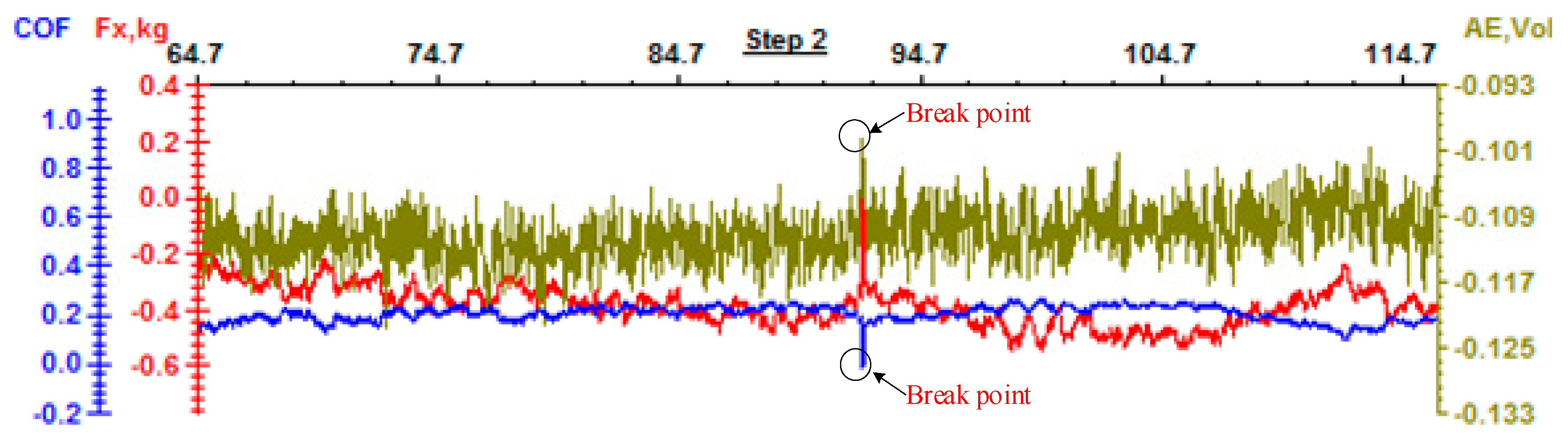
2.2. Interface Binding Energy between Zinc Coating and Substrate
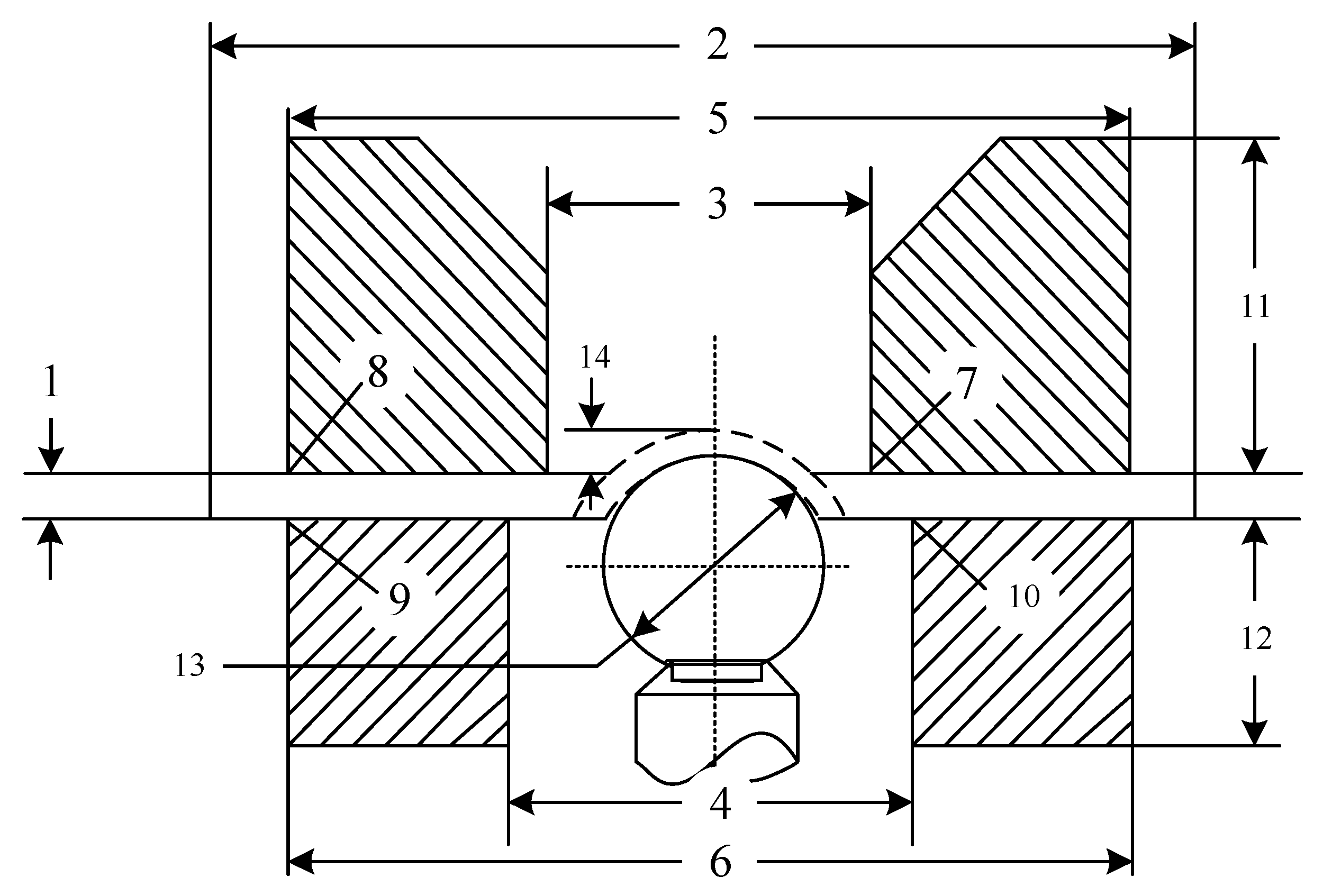
3. Hemispherical Part Drawing Experiment
4. Damage Simulations of Zinc Coating
4.1. Damage Model Based on Cohesion Element
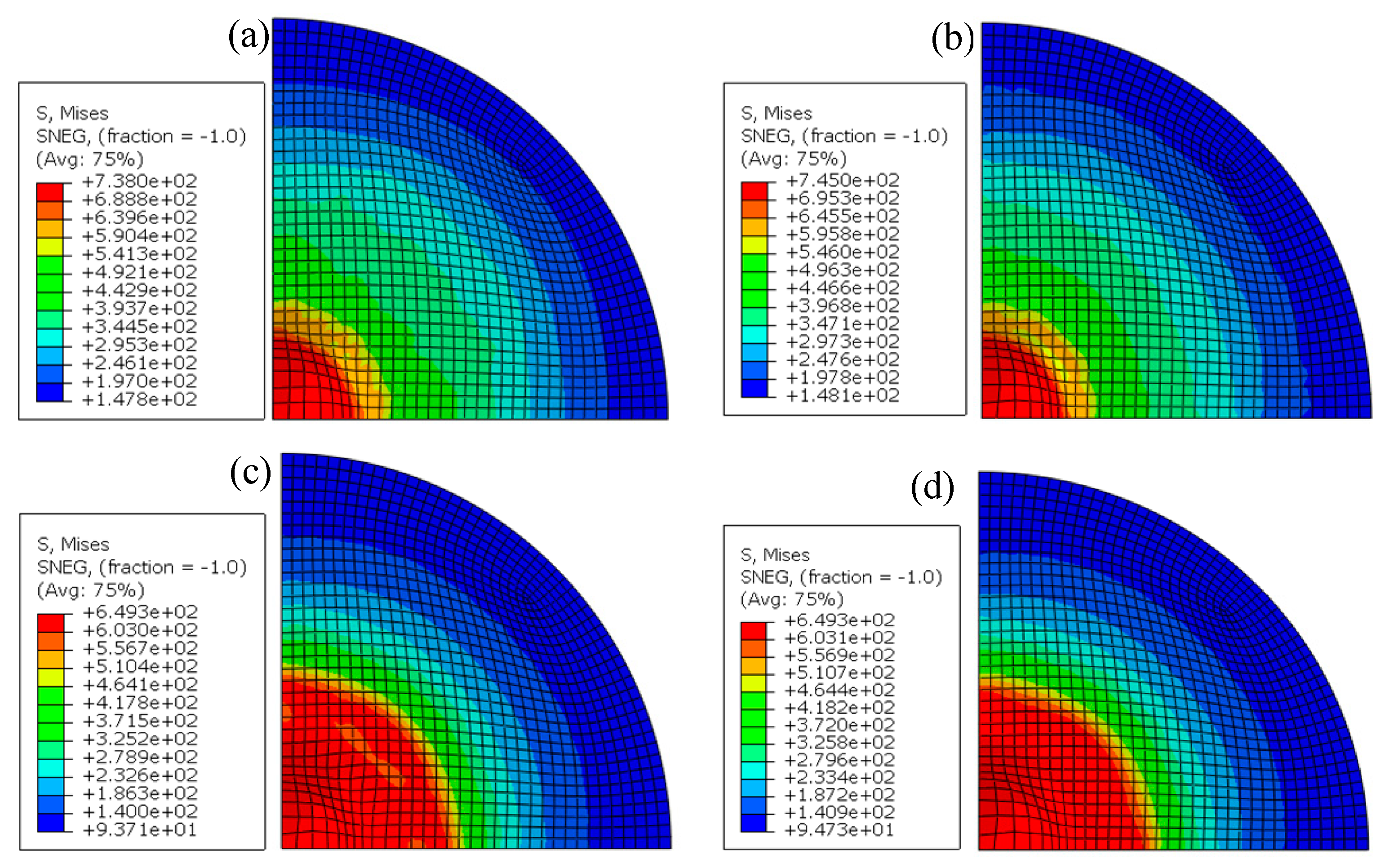
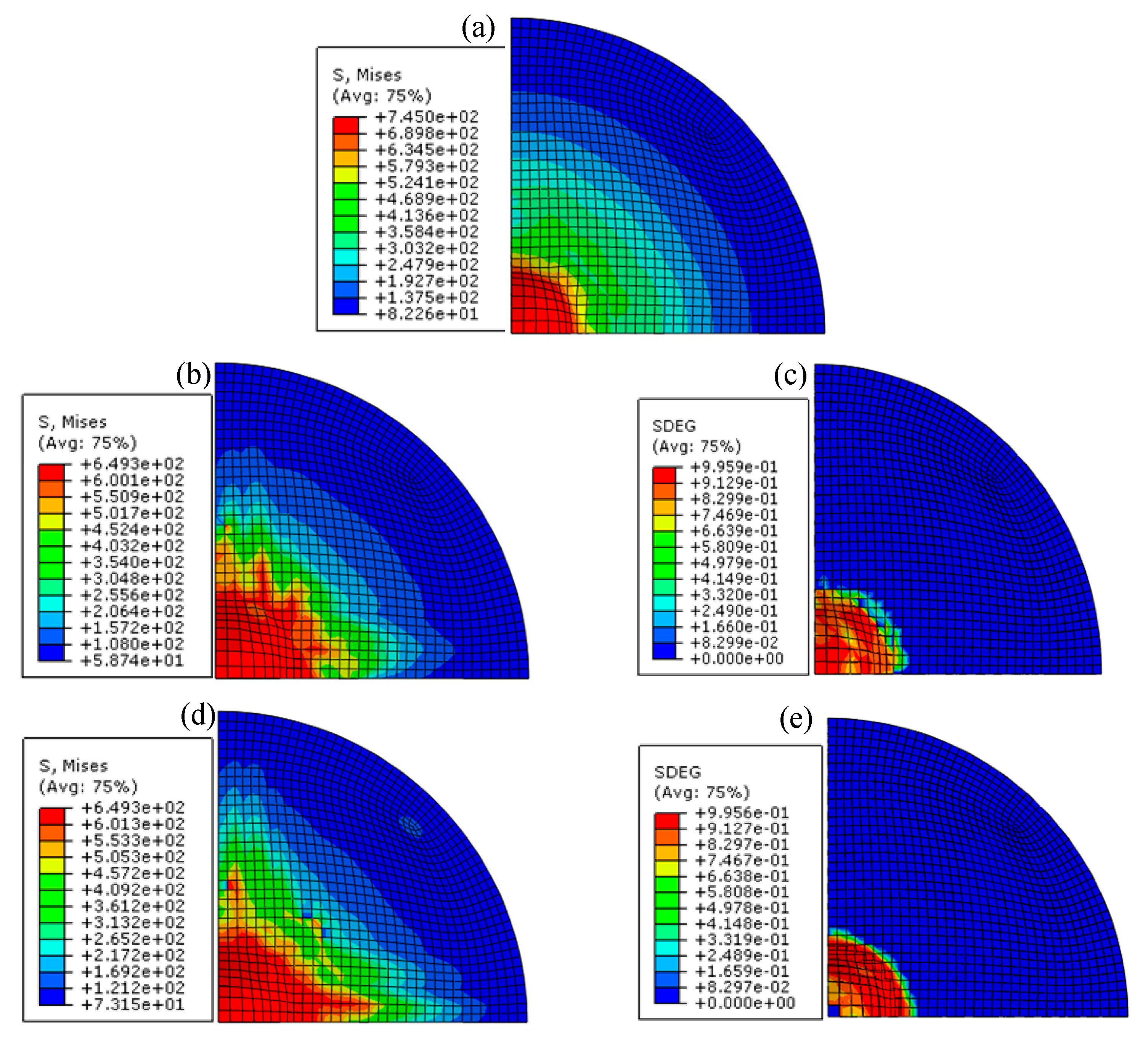
4.2. Simulation Results and Discussions
5. Conclusions
- The effect of the zinc coating on the formability of galvanized steel cannot be ignored. In this paper, we studied the zinc coating and its mechanical properties. The constitutive model of zinc coating based on Nano-indentation experiment and numerical model was proposed, and the constitutive model can accurately describe the plastic mechanical behavior of zinc coating.
- The interface binding energy is an important index to reflect the zinc coating quality, and also a critical criterion to evaluate the coating damage. Based on the nano-scratch test and Griffith’s energy theory, the interface binding strength between the coating and the substrate was obtained, which can be invoked as a criterion for the detachment between the galvanized layer and steel substrate. This provides a theoretical basis for the damage of the zinc coating in the stamping process.
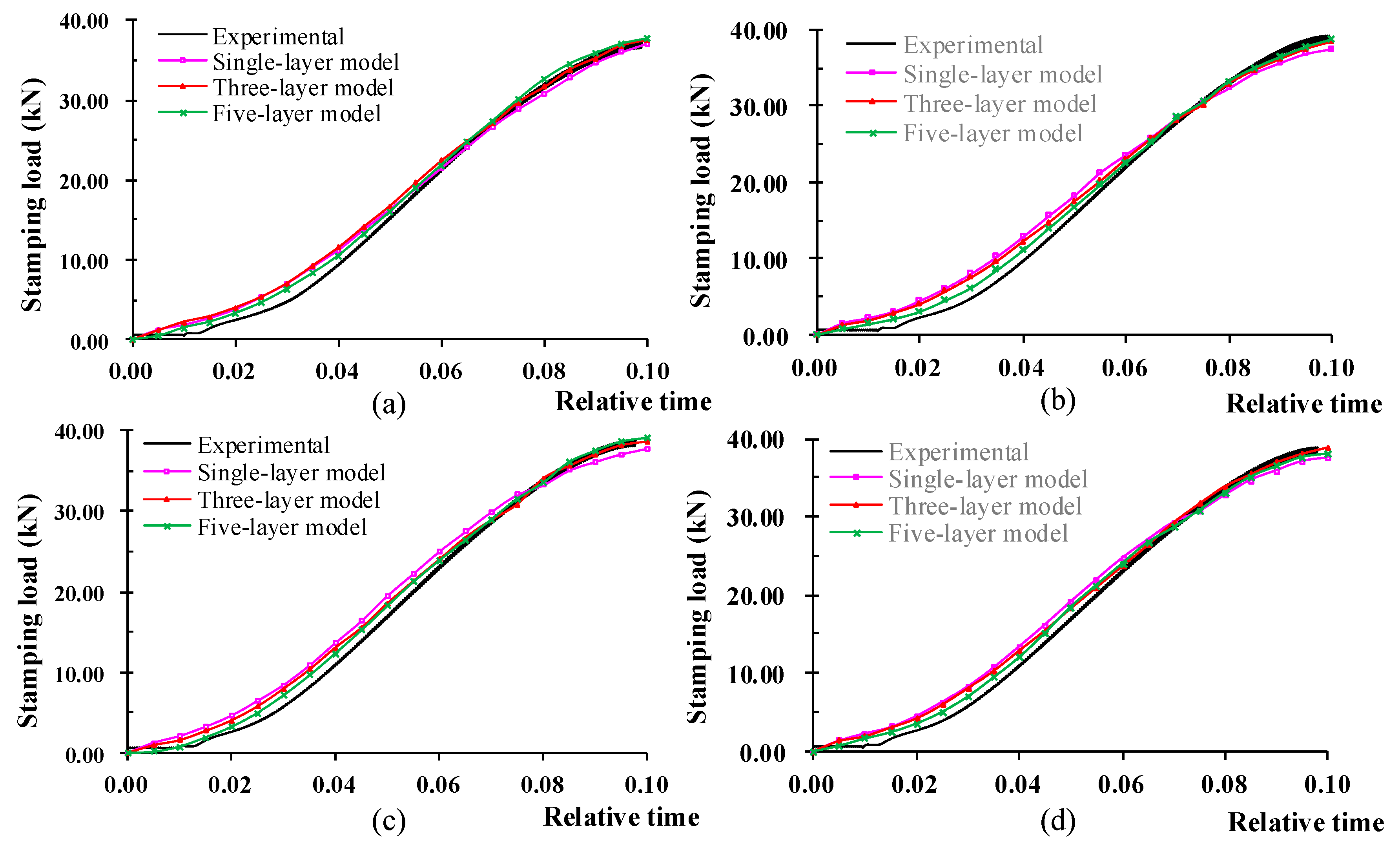
- The damage evolution of the binding between the zinc coating and the substrate was simulated by introducing a cohesive element with 0 thickness. It can simulate the detached and damage evolution of zinc coating from the substrate accurately. Compared with other multi-layer finite element models, it has improved the accuracy of the numerical simulation of stamping through the comparative analysis of the forming force history and the maximum forming force with the experimental results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anderson, D.; Winkler, S.; Bardelcik, A.; Worswick, M.J. Influence of stress triaxiality and strain rate on the failure behavior of a dual-phase DP780 steel. Mater. Des. 2014, 60, 198–207. [Google Scholar] [CrossRef]
- Shibli, S.M.A.; Meena, B.N.; Remya, R. A review on recent approaches in the field of hot dip zinc galvanizing process. Surf. Coat. Technol. 2015, 262, 210–215. [Google Scholar] [CrossRef]
- Parisot, R.; Forest, S.; Pineau, A.; Grillon, F.; Demonet, X.; Mataigne, J.M. Deformation and damage mechanisms of zinc coatings on hot-dip galvanized steel sheets: Part I. Deformation modes. Metall. Mater. Trans. A 2004, 35, 797–811. [Google Scholar] [CrossRef]
- Shen, Z.; Ding, Y.; Chen, J.; Amirkhiz, B.S.; Wen, J.Z.; Fu, L.; Gerlich, A.P. Interfacial bonding mechanism in Al/coated steel dissimilar refill friction stir spot welds. J. Mater. Sci. Technol. 2019, 35, 1027–1038. [Google Scholar] [CrossRef]
- Tokunaga, T.; Ohno, M.; Matsuura, K. Coatings on Mg alloys and their mechanical properties: A review. J. Mater. Sci. Technol. 2018, 34, 1119–1126. [Google Scholar] [CrossRef]
- Wang, X.; Wei, L.; Zhao, J.; Cheng, H.; Wang, X.; Liu, Y.; Hao, Y. Research on dynamic mechanical behavior and damage of steel structure galvanized coating. In Proceedings of the International Conference on Smart City & Systems Engineering, Changsha, China, 11–12 November 2017; pp. 244–247. [Google Scholar] [CrossRef]
- Pinger, T.; Rückriem, E.-M. Investigation on the corrosion and mechanical behavior of thin film batch galvanized thick plate components in clinch joints. Int. J. Adv. Manuf. Technol. 2015, 86, 29–36. [Google Scholar] [CrossRef]
- Cora, Ö.N.; Ağcayazı, A.; Namiki, K.; Sofuoğlu, H.; Koç, M. Die wear in stamping of advanced high strength steels-Investigations on the effects of substrate material and hard-coatings. Tribol. Int. 2012, 52, 50–60. [Google Scholar] [CrossRef]
- Wang, W.; Wang, K.; Zhao, Y.; Hua, M.; Wei, X. A study on galling initiation in friction coupling stretch bending with advanced high strength hot-dip galvanized sheet. Wear 2015, 328–329, 286–294. [Google Scholar] [CrossRef]
- Vourlias, G.; Pistofidis, N.; Stergioudis, G.; Tsipas, D. The effect of alloying elements on the crystallization behaviour and on the properties of galvanized coatings. Cryst. Res. Technol. 2004, 39, 23–29. [Google Scholar] [CrossRef]
- Zhong, N.; Zhang, K.; Li, J.; Hu, W.B. Improvement of the galvanized coating quality of high strength dual phase steels by pre-electroplating nickel layer. Steel Res. Int. 2011, 82, 180–186. [Google Scholar] [CrossRef]
- Parisot, R.; Forest, S.; Pineau, A.; Grillon, F.; Demonet, X.; Mataigne, J.M. Deformation and damage mechanisms of zinc coatings on hot-dip galvanized steel sheets: Part II. Damage modes. Metall. Mater. Trans. A 2004, 35, 813–823. [Google Scholar] [CrossRef]
- Di Cocco, V.; Iacoviello, F.; D’Agostino, L.; Natali, S. Damage micromechanisms in a hot dip galvanized steel. Procedia Struct. Integr. 2017, 3, 231–236. [Google Scholar] [CrossRef]
- Petit, E.J.; Grosbety, Y.; Aden-Ali, S.; Gilgert, J.; Azari, Z. Microstructure of the coating and mechanical properties of galvanized chromium-rich martensitic steel. Surf. Coat. Technol. 2010, 205, 2404–2411. [Google Scholar] [CrossRef]
- Yu, Z.Q.; Hou, Y.K.; Li, S.H.; Lin, Z.Q.; Zhang, W.G. Surface damage behavior of galvanized steel sheets in forming process under tension-bending. Int. J. Mod. Phys. B 2010, 24, 5877–5884. [Google Scholar] [CrossRef]
- Xu, C.; Lin, Z.Q.; Li, S.H.; Zhang, W.G. Research on shear strength of galvannealed coatings. Mater. Des. 2007, 28, 1668–1671. [Google Scholar] [CrossRef]
- Song, G.-M.; Sloof, W.G. Characterization of the failure behavior of zinc coating on dual phase steel under tensile deformation. Mat. Sci. Eng. A Struct. 2011, 528, 6432–6437. [Google Scholar] [CrossRef]
- Chang, S.-H.; Heo, Y.-M. Study on characteristics of the warm deep drawability and simulation for the galvannealed steel sheet. Adv. Sci. Lett. 2013, 19, 3697–3702. [Google Scholar] [CrossRef]
- He, Q.Z.; Hu, H.; Belouettar, S.; Guinta, G.; Yu, K.; Liu, Y.; Biscani, F.; Carrera, E.; Potier-Ferry, M. Multi-scale modelling of sandwich structures using hierarchical kinematics. Compos. Struct. 2011, 93, 2375–2383. [Google Scholar] [CrossRef]
- Behrens, B.A.; Vucetic, M.; Neumann, A.; Osiecki, T.; Grbic, N. Experimental test and FEA of a sheet metal forming process of composite material and steel foil in sandwich design using LS-DYNA. In Proceedings of the 18th International ESAFORM Conference on Material Forming, ESAFORM 2015, Graz, Austria, 15–17 April 2015; Trans Tech Publications Ltd.: Graz, Austria, 2015; pp. 439–445. [Google Scholar] [CrossRef]
- Rajabi, A.; Kadkhodayan, M.; Manoochehri, M.; Farjadfar, R. Deep-drawing of thermoplastic metal-composite structures: Experimental investigations, statistical analyses and finite element modeling. J. Mater. Process. Technol. 2015, 215, 159–170. [Google Scholar] [CrossRef]
- Shiri, S.; Naceur, H.; Roelandt, J.M. Numerical modelling of sheet metal forming and crashworthiness of laminated steel structures using multi-layered solid-shell elements. Eur. J. Comput. Mech. 2012, 21, 351–364. [Google Scholar] [CrossRef]
- Parsa, M.H.; Mohammadi, S.V.; Aghchai, A.J. Al3105/polypropylene/Al3105 laminates springback in V-die bending. Int. J. Adv. Manuf. Technol. 2014, 75, 849–860. [Google Scholar] [CrossRef]
- Parsa, M.H.; ahkami SNa Ettehad, M. Experimental and finite element study on the spring back of double curved aluminum/polypropylene/aluminum sandwich sheet. Mater. Des. 2010, 31, 4174–4183. [Google Scholar] [CrossRef]
- Li, C.; Chi, C.; Lin, P.; Zhang, H.; Liang, W. Deformation behavior and interface microstructure evolution of Al/Mg/Al multilayer composite sheets during deep drawing. Mater. Des. 2015, 77, 15–24. [Google Scholar] [CrossRef]
- Parisotab, R.; Foresta, S.; Gourguesa, A.-F.; Pineaua, A.; Mareuseb, D. Modeling the mechanical behavior of a multicrystalline zinc coating on a hot-dip galvanized steel sheet. Comp. Mater. Sci. 2000, 19, 189–204. [Google Scholar] [CrossRef]
- Ucun, İ.; Aslantas, K. Numerical simulation of orthogonal machining process using multilayer and single-layer coated tools. Int. J. Adv. Manuf. Technol. 2011, 54, 899–910. [Google Scholar] [CrossRef]
- Lee, S.; Joun, M.; Kim, D.; Lee, J. Effect of elastic-plastic behavior of coating layer on drawability and frictional characteristic of galvannealed steel sheets. J. Mech. Sci. Technol. 2016, 30, 3313–3319. [Google Scholar] [CrossRef]
- Kim, S.I.; Her, J.U.; Jang, Y.C.; Lee, Y. Experimental and finite element analysis for fracture of coating layer of galvannealed steel sheet. Trans. Nonferr. Metal. Soc. 2011, 21, s111–s116. [Google Scholar] [CrossRef]
- Bettaieb, A.B.; Tuninetti, V.; Duchene, L. Numerical simulation of T-bend of multilayer coated metal sheet using solid-shell element. In Proceedings of the 14th International Conference on Metal Forming, Metal Forming 2012, Krakow, Poland, 16–19 September 2012; Wiley-VCH Verlag: Krakow, Poland, 2012; pp. 1311–1314. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Park, H.S.; Kwon, D. An energy approach to quantification of adhesion strength from critical loads in scratch tests. Thin Solid Film. 1997, 307, 156–162. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. 1921, 221, 163–198. [Google Scholar] [CrossRef] [Green Version]










| Steel Sheet | Direction of the Sample | Yield Strength σs (MPa) | Tensile Strength σb (MPa) | Elongation δ | Normal Anisotropy r | Hardening Index n |
|---|---|---|---|---|---|---|
| Steel sheet with zinc coating | R00 | 394 | 609 | 27.1% | 1.171 | 0.168 |
| R45 | 388 | 609 | 24.8% | 0.94 | 0.176 | |
| R90 | 377 | 608 | 25.5% | 0.853 | 0.181 | |
| Steel sheet without zinc coating | R00 | 396 | 621 | 24.4% | 1.124 | 0.173 |
| R45 | 396 | 608 | 25.1% | 1.023 | 0.17 | |
| R90 | 387 | 601 | 25.3% | 0.902 | 0.175 |
| Parameter | Symbol | Dimension |
|---|---|---|
| Indentation load | [F] | LMT−2 |
| Yield strength | [σy] | L−1MT−2 |
| Hardening index | [n] | 1 |
| Elastic modulus | [Ef] | L−1MT−2 |
| Indentation depth | [h], [hf] | L |
| Critical Load (N) | Critical Friction Coefficient | Contact Radius (μm) | Elastic Modulus (GPa) Substrate/Coating | Poisson Ratio Substrate/Coating | Binding Energy (× 103 J/m2) |
|---|---|---|---|---|---|
| 15.76 | 0.202 | 21.72 | 210/135 | 0.3/0.3 | 0.2022 |
| Test Group | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 |
|---|---|---|---|---|---|---|---|---|
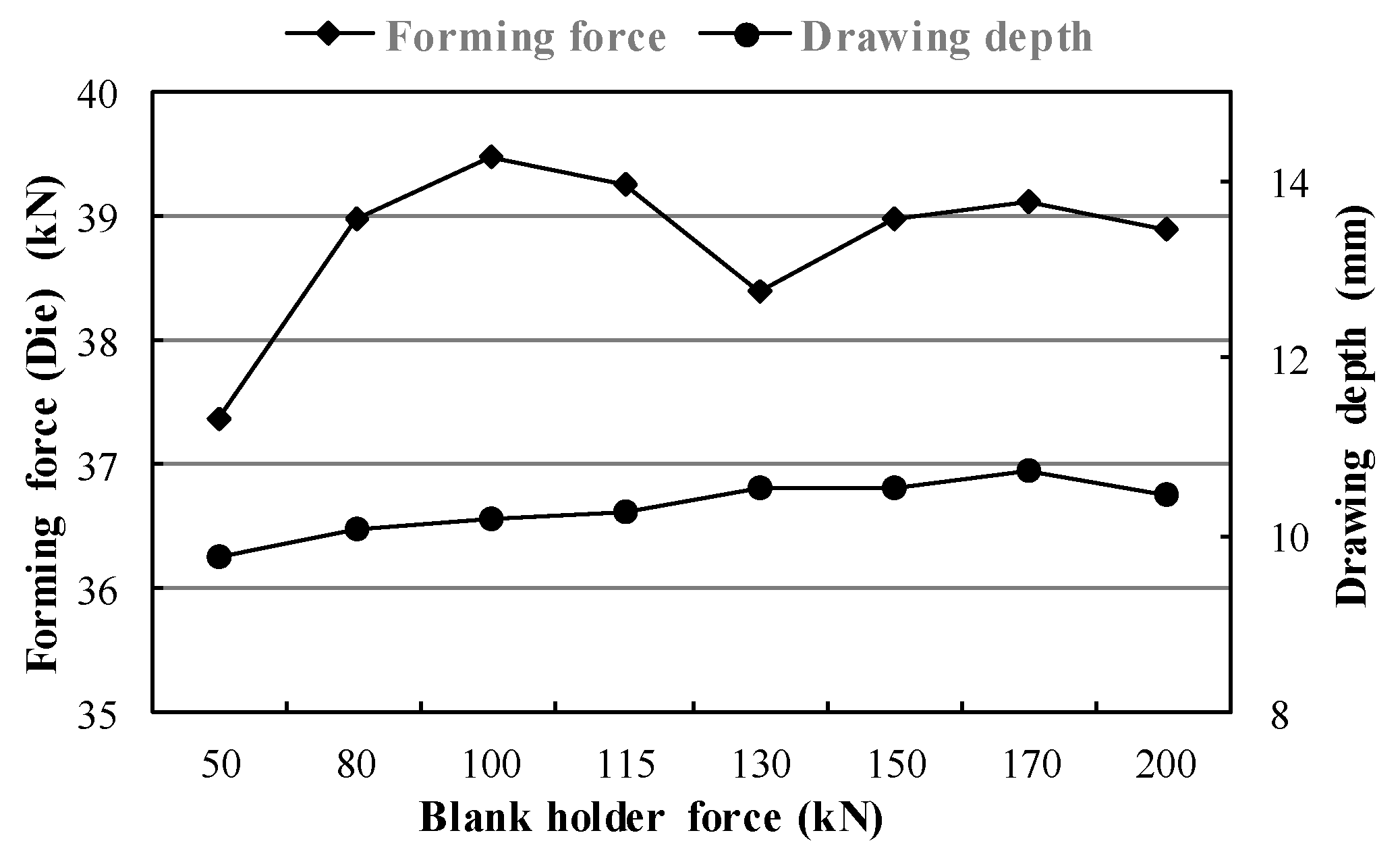
| Blank holder force/kN | 50 | 80 | 100 | 115 | 130 | 150 | 170 | 200 |
| Drawing depth/mm | 9.76 | 10.09 | 10.17 | 10.25 | 10.25 | 10.54 | 10.75 | 10.45 |
| Max. forming force/kN | 37.38 | 38.97 | 39.48 | 39.25 | 38.39 | 38.99 | 39.13 | 38.89 |
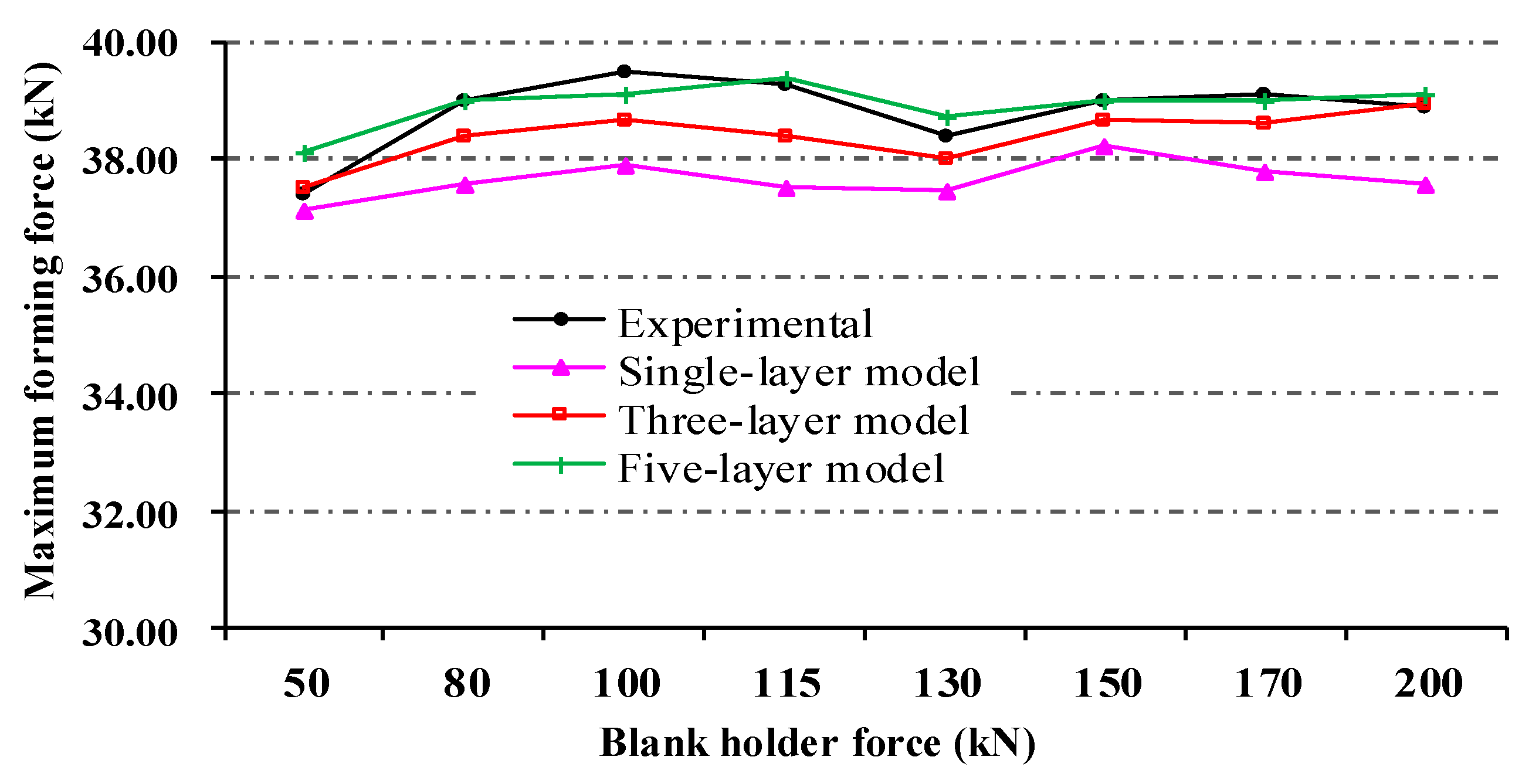
| Blank Holder Force (kN) | Experimental (kN) | Single-Layer | Three-Layers | Five-Layers | |||
|---|---|---|---|---|---|---|---|
| Simulation (kN) | Relative Deviation | Simulation (kN) | Relative Deviation | Simulation (kN) | Relative Deviation | ||
| 50 | 37.38 | 37.14 | 0.637% | 37.51 | 0.344% | 38.10 | 1.926% |
| 80 | 38.97 | 37.59 | 3.541% | 38.38 | 1.505% | 39.01 | 0.103% |
| 100 | 39.48 | 37.88 | 4.054% | 38.65 | 2.107% | 39.10 | 0.963% |
| 115 | 39.25 | 37.50 | 4.455% | 38.40 | 2.168% | 39.38 | 0.331% |
| 130 | 38.39 | 37.48 | 2.370% | 38.00 | 1.006% | 38.71 | 0.834% |
| 150 | 38.99 | 38.24 | 1.918% | 38.67 | 0.810% | 39.02 | 0.077% |
| 170 | 39.13 | 37.80 | 3.404% | 38.61 | 1.333% | 39.01 | 0.307% |
| 200 | 38.89 | 37.55 | 3.452% | 38.93 | 0.114% | 39.13 | 0.617% |
| Average deviation | 2.979% | 1.173% | 0.645% | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Long, X. Mechanical Behavior and Damage of Zinc Coating for Hot Dip Galvanized Steel Sheet DP600. Coatings 2020, 10, 202. https://doi.org/10.3390/coatings10030202
Li G, Long X. Mechanical Behavior and Damage of Zinc Coating for Hot Dip Galvanized Steel Sheet DP600. Coatings. 2020; 10(3):202. https://doi.org/10.3390/coatings10030202
Chicago/Turabian StyleLi, Gui, and Xiaoyu Long. 2020. "Mechanical Behavior and Damage of Zinc Coating for Hot Dip Galvanized Steel Sheet DP600" Coatings 10, no. 3: 202. https://doi.org/10.3390/coatings10030202




