Radiation and Magnetic Field Impacts on Time-Dependent Mixed Convection Flow and Heat Transmission of Maxwellian Fluid Past A Stretching Sheet
Abstract
:1. Introduction
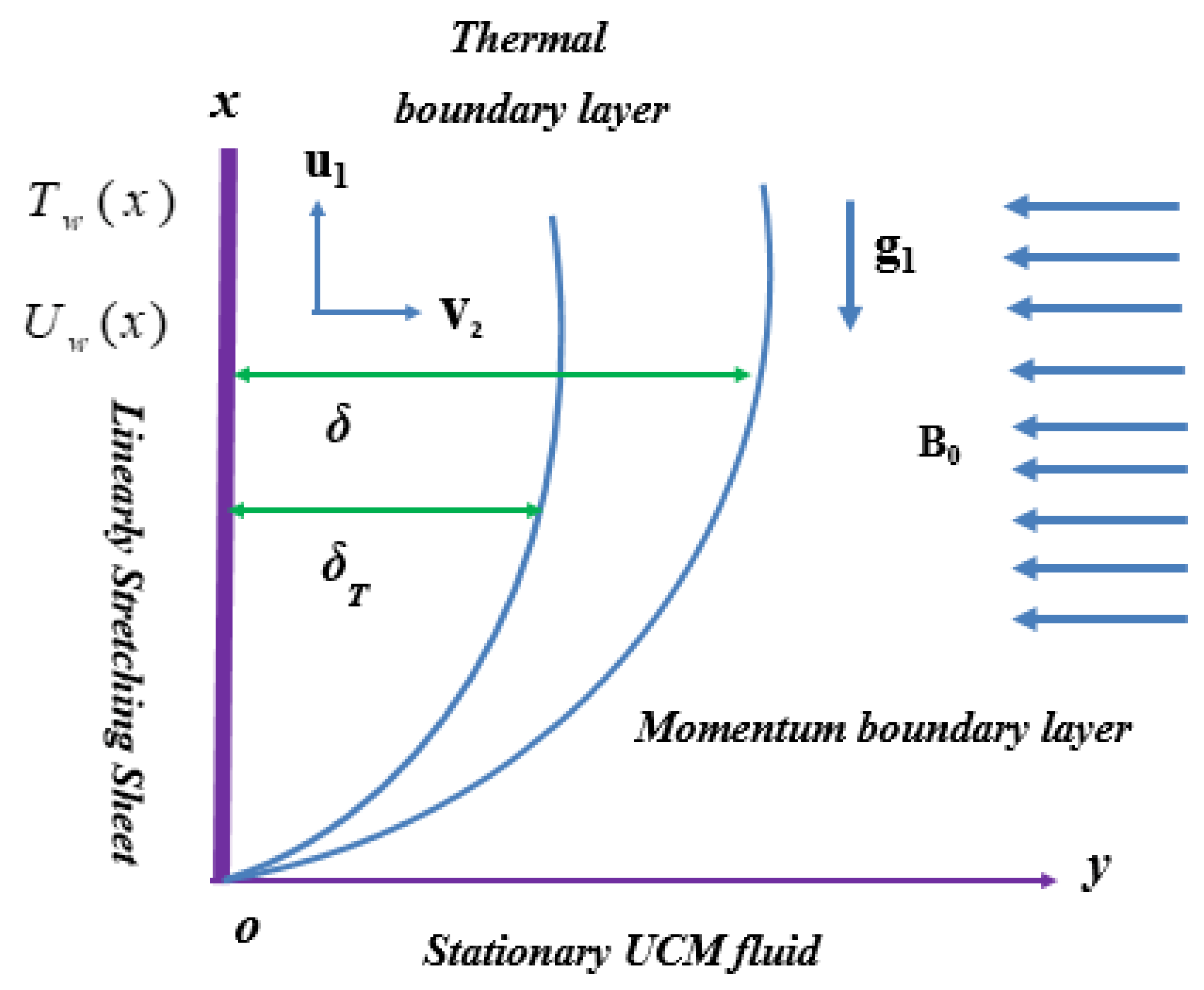
2. Problem Development
3. Exact Solution
3.1. Initial Steady Flow
3.2. Final Unsteady State Flow
4. Implicit Finite Difference Method (IFDM)
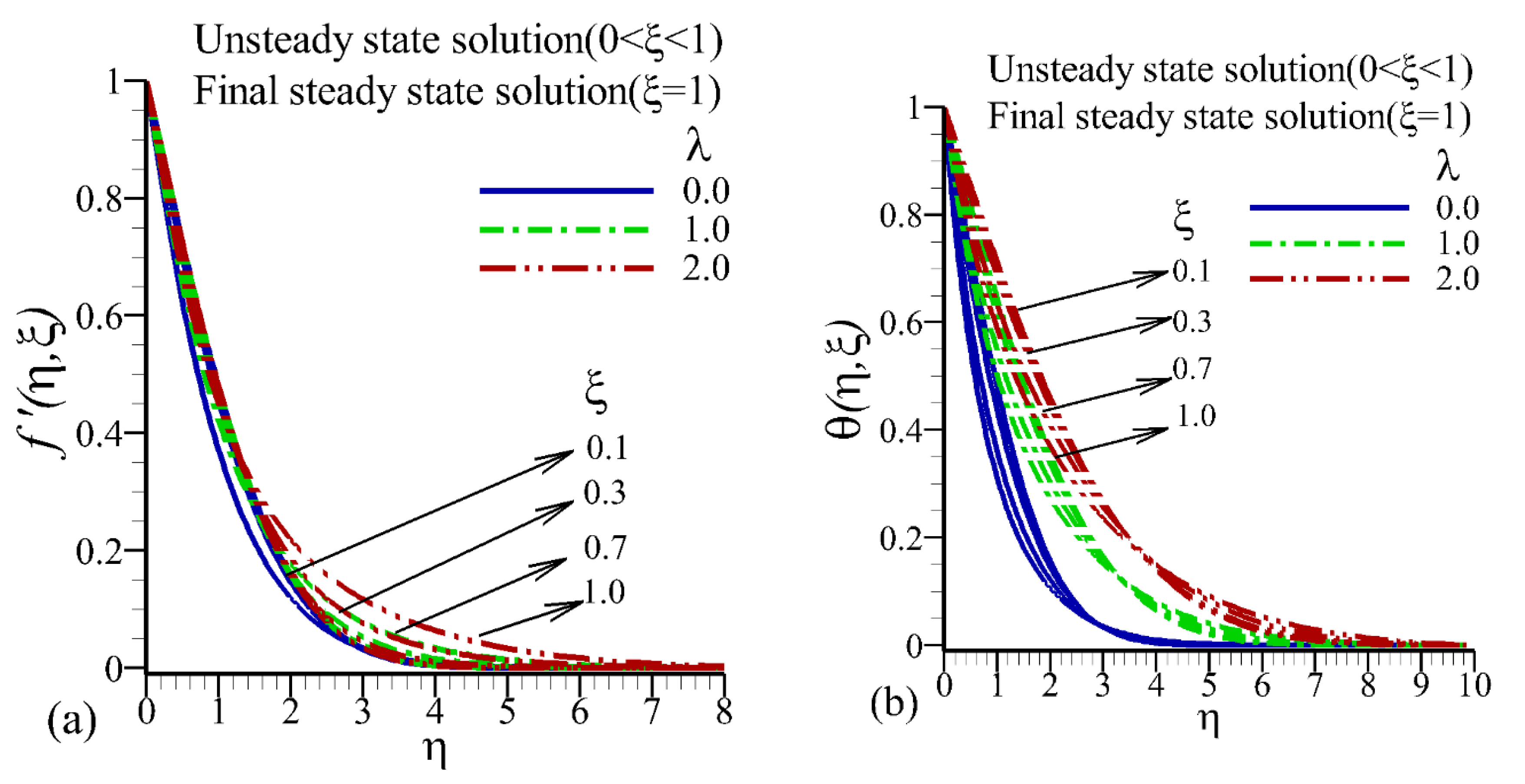
5. Numerical Results and Discussions
6. Concluding Remarks
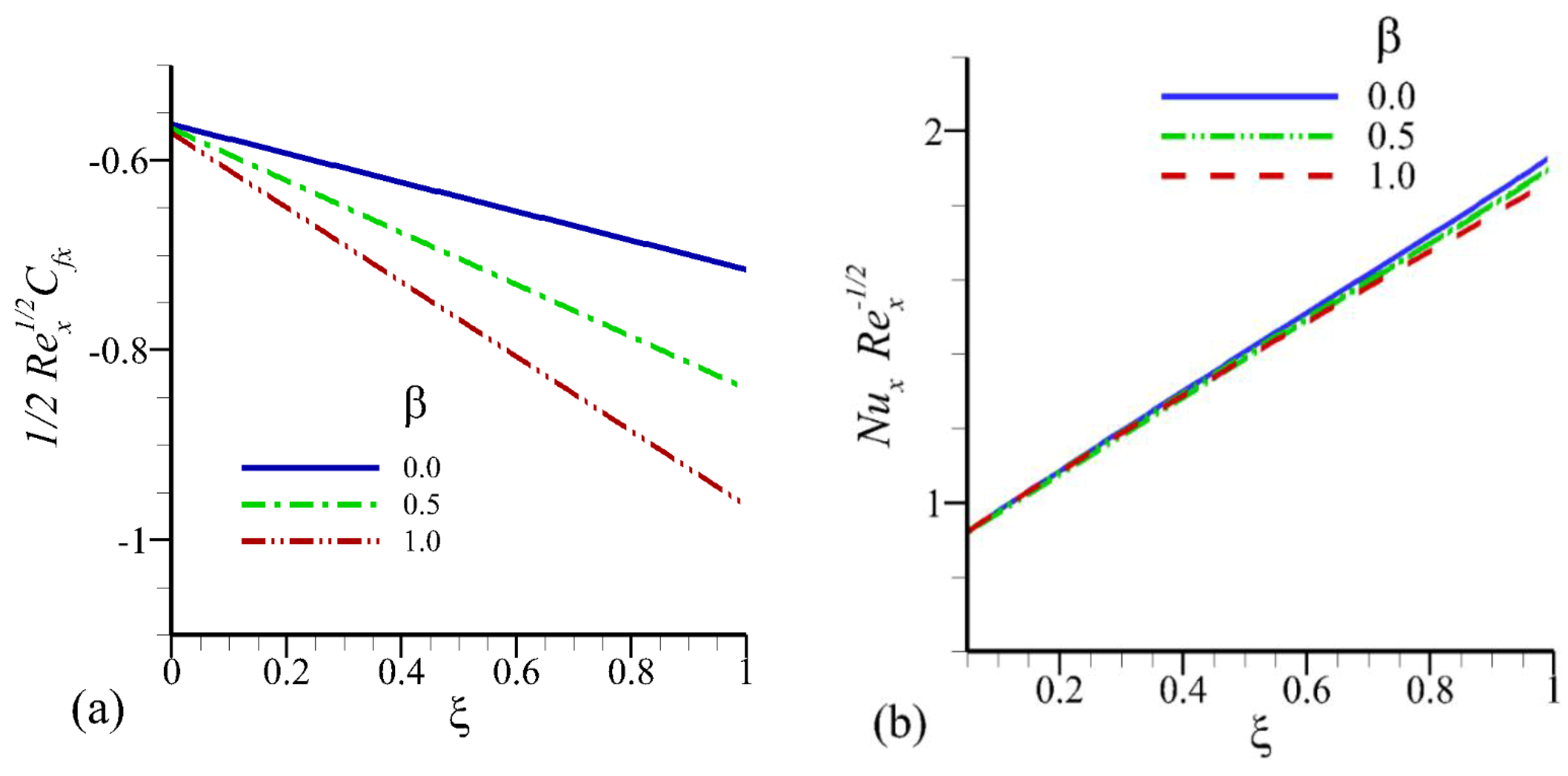
- A decline in skin friction and the heat transfer rate was noted with a rise in values of the relaxation time parameter.
- It was depicted that skin friction decreased with rising values of mixed convection parameter and , while the heat transmission rate showed the totally opposite behavior.
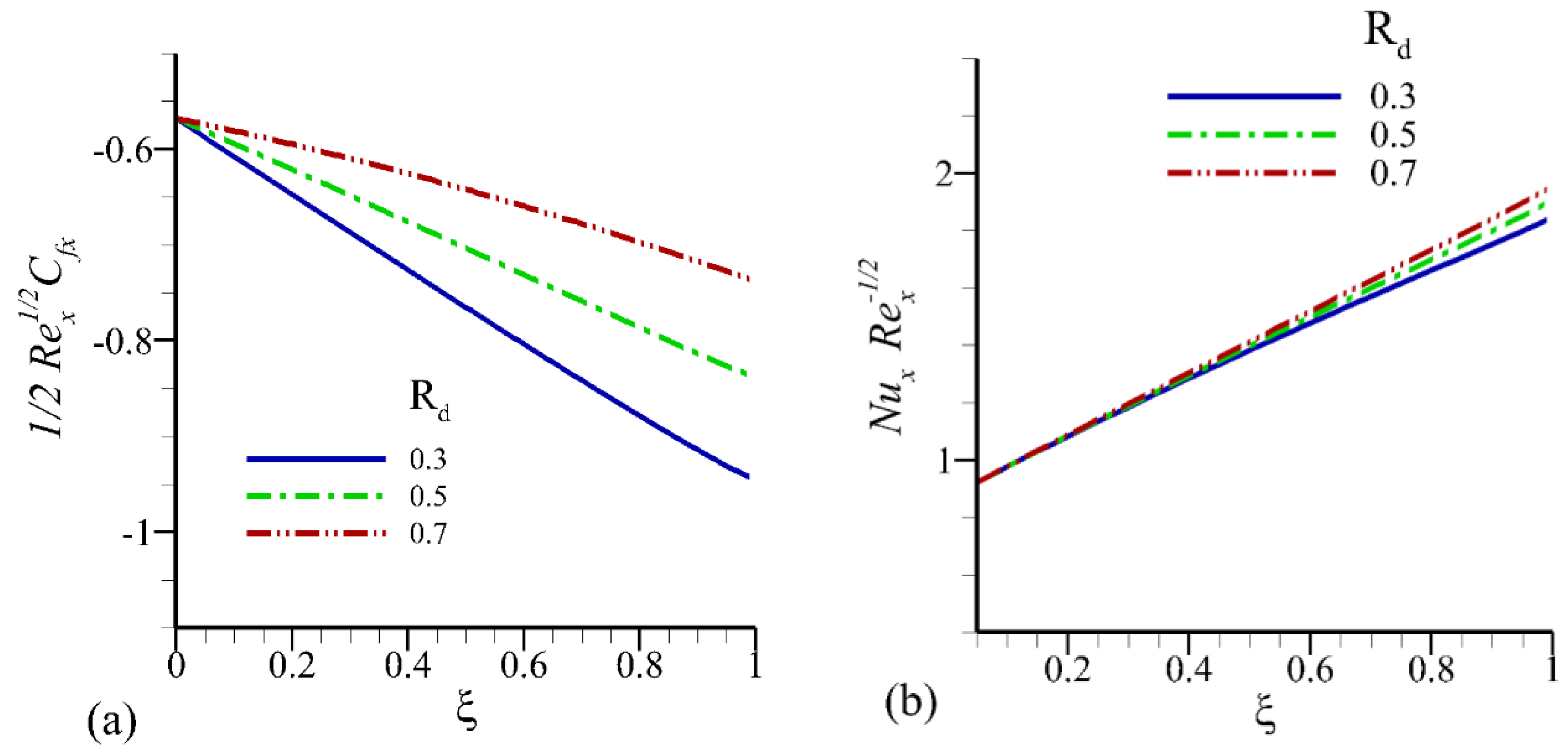
- The rise in radiation parameter reduced the local skin friction coefficient and led to enhance the heat transfer rate at the surface.
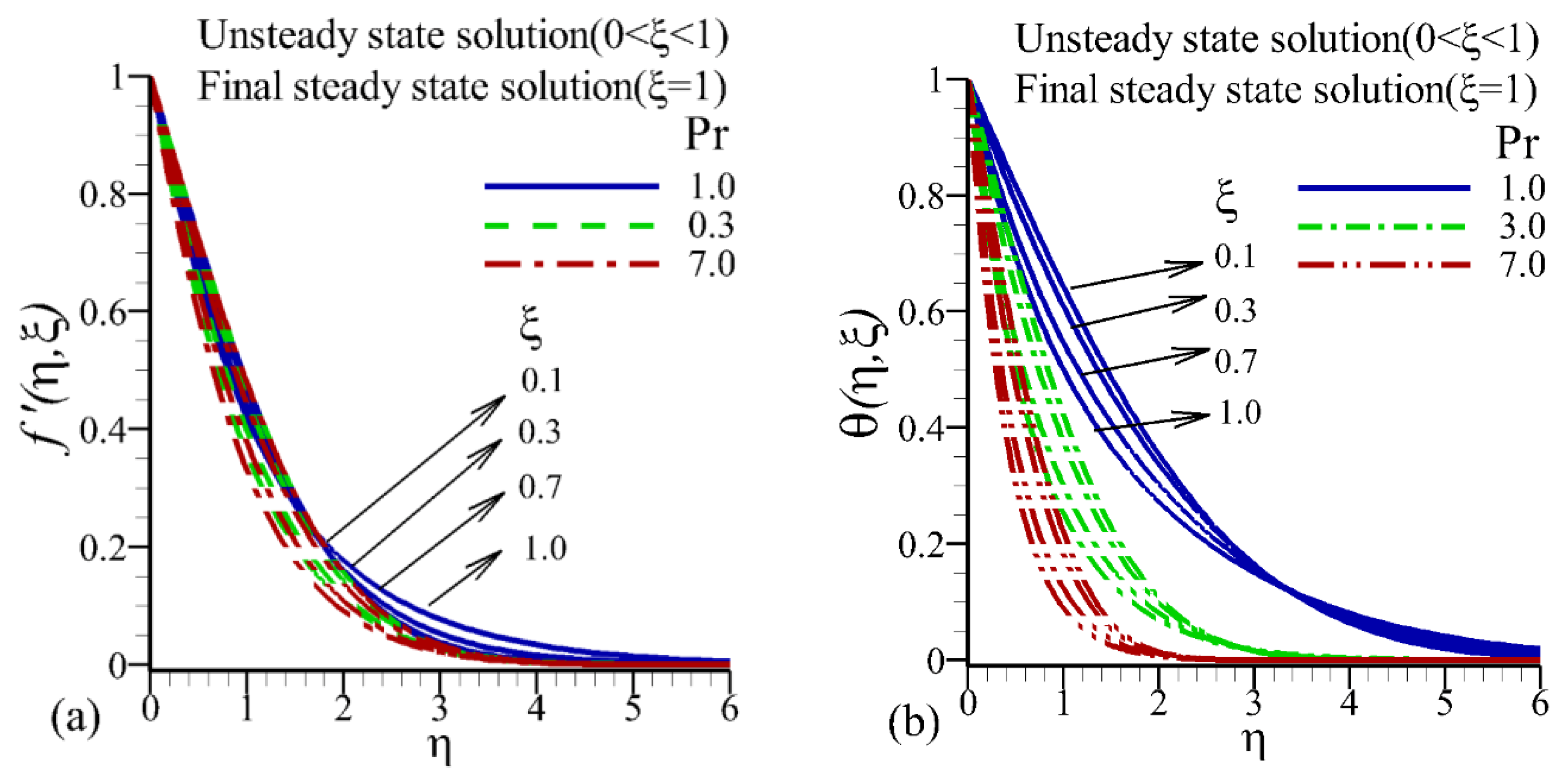
- It was noticed that higher values of the Prandtl number reduced the temperature and thermal boundary layer thickness rapidly.
- A rise in velocity and decline in heat transfer rate were witnessed with lower values.
- The magnetic field parameter turned down the local skin friction.
- The thermal diffusion rate could be controlled by varying the Prandtl number.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Prandtl number | Magnetic field | ||
| Radiative heat flux | t | Time | |
| Skin friction coefficient | Radiation parameter | ||
| Local Nusselt number | T | Temperature | |
| Rex | Local Reynolds number | Re | Reynold number |
| Specific heat capacity | M | Magnetic field parameter | |
| Local Grashof number | Kinematic viscosity |
Greek Symbols
| Relaxation time parameter | Stefan–Boltzmann constant | ||
| Fluid density | Stream function | ||
| Thermal diffusivity | Wall shear stress | ||
| Mean absorption coefficient | Mixed convection parameter |
References
- Ishak, A.; Nazar, R.; Pop, I. Hydro magnetic Flow and Heat Transfer Adjacent to a Stretching Vertical Sheet. Heat Mass Transf. 2008, 44, 921–927. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary layer behavior on continuous solid surfaces. II: The boundary layer on a continuous flat surface. AICHE J. 1961, 7, 221–225. [Google Scholar] [CrossRef]
- Crane, L.J. Flow Past a Stretching Plate. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Erickson, L.E.; Fan, L.T.; Fox, V.G. Heat and mass transfer on a moving continuous flat plate with suction or injection. Ind. Eng. Chem. Res. Fund. 1966, 5, 19–25. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Grubka, J.; Bobba, K.M. Heat transfer characteristics of a continuous stretching surface with variable temperature. ASME J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Chen, C.K.; Char, M.I. Heat transfer of a continuous stretching surface with suction and injection. J. Math. Anal. Appl. 1988, 135, 568–580. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.E. Heat transfer characteristics of a continuous stretching surface. Heat Mass transf. 1994, 29, 227–234. [Google Scholar] [CrossRef]
- Chen, C.H. Laminar mixed convection adjacent to vertical continuous stretching sheets. Heat Mass transf. 1998, 33, 471–476. [Google Scholar] [CrossRef]
- Wang, C.Y. Analysis of viscous flow due to stretching sheet with surface slip and suction. Nonlinear Anal. RWA 2009, 10, 375–380. [Google Scholar] [CrossRef]
- Andersson, H.I.; Bech, K.H.; Dandapat, B.S. Magneto hydrodynamic Flow of a Power Law Fluid over a Stretching Sheet. Int. J. Non Linear Mech. 1992, 27, 929–936. [Google Scholar] [CrossRef]
- Hassanien, I.A. Flow and Heat Transfer on a Continuous Flat Surface Moving in a Parallel Free Stream of Power-Law Fluid. Appl. Model. 1996, 20, 779–784. [Google Scholar] [CrossRef]
- Sadeghy, K.; Sharifi, M. Local Similarity Solution for the Flow of a ‘Second-Grade’ Viscoelastic Fluid above a Moving Plate. Int. J. Non Linear Mech. 2004, 39, 1265–1273. [Google Scholar] [CrossRef]
- Serdar, B.; SalihDokuz, M. Three-Dimensional Stagnation Point Flow of a Second Grade Fluid Towards a Moving Plate. Int. J. Eng. Sci. 2006, 44, 49–58. [Google Scholar]
- Haroun, M.H. Effect of Deborah Number and Phase Difference on Peristaltic Transport of a Third-Order Fluid in an Asymmetric Channel. Commun. Nonlinear Sci. Numer. Simul. 2007, 12, 1464–1480. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Zeb, A.; Ghori, Q.K.; Benharbit, A.M. Homotopy Perturbation Method for Heat Transfer Flow of a Third Grade Fluid between Parallel Plates. Chaos Solitons Fractals 2008, 36, 182–192. [Google Scholar] [CrossRef]
- Sajid, M.; Ahmad, I.; Hayat, T.; Ayub, M. Unsteady Flow and Heat Transfer of a Second Grade Fluid over a Stretching Sheet. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 96–108. [Google Scholar] [CrossRef]
- Heyhat, M.M.; Khabazi, N. Non-Isothermal Flow of Maxwell Fluids above Fixed Flat Plates under the Influence of a Transverse Magnetic Field. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2010, 225, 909–916. [Google Scholar] [CrossRef]
- Kayvan, S.; Hajibeygi, H.; Taghavi, S.-M. Stagnation-point flow of upper-convected Maxwell fluids. Int. J. Non Linear Mech. 2006, 41, 1242–1247. [Google Scholar]
- Aliakbar, V.; Alizadeh-Pahlavan, A.; Sadeghy, K. The influence of thermal radiation on MHD flow of Maxwellian fluids above stretching sheets. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 779–794. [Google Scholar] [CrossRef]
- Alizadeh-Pahlavan, A.; Sadeghy, K. On the use of homotopy analysis method for solving unsteady MHD flow of Maxwellian fluids above impulsively stretching sheets. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1355–1365. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Sajid, M. Series solution for the upper-convected Maxwell fluid over a porous stretching plate. Phys. Lett. A 2006, 358, 396–403. [Google Scholar] [CrossRef]
- Abel, M.S.; Tawade, J.V.; Nandeppanavar, M.M. MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica 2012, 47, 385–393. [Google Scholar]
- Cess, R.D. The interaction of thermal radiation with free convection heat and mass transfer. Int. J. Heat Mass Transf. 1966, 9, 1269–1277. [Google Scholar] [CrossRef]
- Hossain, M.A.; Takhar, H.S. Radiation effect on mixed convection along a vertical plate with uniform surface temperature. Heat Mass Transf. 1996, 31, 243–248. [Google Scholar] [CrossRef]
- Cheng, E.H.; Özişik, M.N. Radiation with free convection in an absorbing, emitting and scattering medium. Int. J. Heat Mass Transf. 1972, 15, 1243–1252. [Google Scholar] [CrossRef]
- Raptis, A. Radiation and free convection flow through a porous medium. Int. J. Commun. Heat Mass Transf. 1998, 25, 289–295. [Google Scholar] [CrossRef]
- Hossain, M.A.; Alim, M.A.; Rees, D.A.S. The effect of radiation on free convection from a porous vertical plate. Int. J. Heat Mass Transf. 1999, 42, 181–191. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Pop, I.; Asghar, S. Effects of radiation and magnetic field on the mixed convection stagnation-point flow over a vertical stretching sheet in a porous medium. Int. J. Heat Mass Transf. 2010, 53, 466–474. [Google Scholar] [CrossRef]
- Duwairi, H.M.; Duwairi, R.M. Thermal radiation effects on MHD-Rayleigh flow with constant surface heat flux. Heat Mass Transf. 2004, 41, 51–57. [Google Scholar] [CrossRef]
- Gorla, R.S.R. Radiative effect on conjugate forced convection and conductive heat transfer in a circular pin. Int. J. Heat Fluid Flow 1988, 9, 49–51. [Google Scholar] [CrossRef]
- Pop, S.R.; Grosan, T.; Pop, I. Radiation effects on the flow near the stagnation point of a stretching sheet. Tech. Mech. 2004, 25, 100–106. [Google Scholar]
- Al-Odat, M.Q.; Damseh, R.A.; Al-Azab, T.A. Thermal boundary layer on an exponentially stretching continuous surface in the presence of magnetic field effect. Int. J. Appl. Mech. Eng. 2006, 11, 289–299. [Google Scholar]
- Sajid, M.; Hayat, T. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int. Commun. Heat Mass Transf. 2008, 35, 347–356. [Google Scholar] [CrossRef]
- Prasad, V.R.; Reddy, N.B.; Muthucumaraswamy, R. Radiation and mass transfer effects on two-dimensional flow past an impulsively started infinite vertical plate. Int. J. Therm. Sci. 2007, 46, 1251–1258. [Google Scholar] [CrossRef]
- Andersson, H.I.; Aarseth, J.B.; Dandapat, B.S. Heat Transfer in a Liquid Film on an Unsteady Stretching Surface. Int. J. Heat Mass Transf. 2000, 43, 69–74. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A.; Bazid, M.A.A. Heat Transfer over an Unsteady Stretching Surface. Heat Mass Transf. 2004, 41, 1–4. [Google Scholar] [CrossRef]
- Sharidan, S.; Mahmood, T.; Pop, I. Similarity Solutions for the Unsteady Boundary Layer Flow and Heat Transfer due to a Stretching Sheet. Int. J. Appl. Mech. Eng. 2006, 11, 647–654. [Google Scholar]
- Ali, M.E.; Magyari, E. Unsteady Fluid and Heat Flow Induced by a Submerged Stretching Surface While Its Steady Motion is Slowed Down Gradually. Int. J. Heat Mass Transf. 2007, 50, 188–195. [Google Scholar] [CrossRef]
- Dandapat, B.S.; Santra, B.; Vajravelu, K. The Effects of Variable Fluid Properties and Thermo-capillarity on the Flow of a Thin Film on an Unsteady Stretching Sheet. Int. J. Heat Mass Transf. 2007, 50, 991–996. [Google Scholar] [CrossRef]
- Tsai, R.; Huang, K.H.; Huang, J.S. Flow and Heat Transfer over an Unsteady Stretching Surface with a Non-Uniform Heat Source. Int. Commun. Heat Mass Transf. 2008, 35, 1340–1343. [Google Scholar] [CrossRef]
- Liu, I.C.; Andersson, H.I. Heat Transfer in a Liquid Film on an Unsteady Stretching Sheet. Int. J. Therm. Sci. 2008, 47, 766–772. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Effect of Thermal Radiation on Unsteady Mixed Convection Flow and Heat Transfer over a Porous Stretching Surface in Porous Medium. Int. J. Heat Mass Transf. 2009, 52, 3261–3265. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Effects of Slip on Unsteady Mixed Convective Flow and Heat Transfer Past a Stretching Surface. Chin. Phys. Lett. 2010, 27, 124401. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Heat Transfer Analysis for Unsteady MHD Flow Past a Non-Isothermal Stretching Surface. Nucl. Eng. Des. 2011, 241, 4835–4839. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Heat Transfer Analysis for Unsteady Flow of a Maxwell Fluid over a Stretching Surface in the Presence of a Heat Source/Sink. Chin. Phys. Lett. 2012, 29, 054703. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Aly, A.M.; Mansour, M.A. Similarity Solution for Unsteady Heat and Mass Transfer from a Stretching Surface Embedded in a Porous Medium with Suction/Injection and Chemical Reaction Effects. Chem. Eng. Commun. 2010, 197, 846–858. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C. Slip Effects on an Unsteady Boundary Layer Stagnation-Point Flow and Heat Transfer Towards a Stretching Sheet. Chin. Phys. Lett. 2011, 28, 094702. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Tariq, M. Finite element simulation of multiple slip effects on MHD unsteady Maxwell nanofluid flow over a permeable stretching sheet with radiation and thermo-diffusion in the presence of chemical reaction. Processes 2019, 7, 628. [Google Scholar] [CrossRef] [Green Version]
- Na, T.Y. (Ed.) Computational Methods in Engineering Boundary Value Problems; Academic Press: New York, NY, USA, 1980. [Google Scholar]





| Sadeghy et al. [19] | Subhas et al. [23] | Present Results | Subhas et al. [21] | Present Results | |
|---|---|---|---|---|---|
| 0.0 | −1.0000000 | −0.999962 | −0.999962 | −1.095445 | −1.095151 |
| 0.2 | −1.0549000 | −1.051948 | −1.052001 | −1.188270 | −1.188321 |
| 0.4 | −1.1008400 | −1.101850 | −1.101843 | −1.275878 | −1.275888 |
| 0.6 | −1.0015016 | −1.150163 | −1.150133 | −1.358733 | −1.358771 |
| 0.8 | −1.1987200 | −1.196692 | −1.196634 | −1.437369 | −1.437357 |
| 1.2 | − | −1.285257 | −1.285269 | −1.512280 | −1.512280 |
| 1.6 | − | −1.368641 | −1.368630 | −1.095445 | −1.095445 |
| 2.0 | − | −1.447617 | −1.447654 | −1.188270 | −1.188119 |
| 0.0 | −0.56784 | 0.86725 |
| 0.1 | −0.59342 | 0.97241 |
| 0.2 | −0.61735 | 1.06797 |
| 0.3 | −0.64177 | 1.16383 |
| 0.4 | −0.66621 | 1.25733 |
| 0.5 | −0.69096 | 1.35039 |
| 0.6 | −0.71573 | 1.44164 |
| 0.7 | −0.74067 | 1.53248 |
| 0.8 | −0.76554 | 1.62206 |
| 0.9 | −0.79034 | 1.71184 |
| 1.0 | −0.81459 | 1.80201 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haider, S.; Syed Muhammad, I.; Li, Y.-Z.; Faraz; Saeed Butt, A. Radiation and Magnetic Field Impacts on Time-Dependent Mixed Convection Flow and Heat Transmission of Maxwellian Fluid Past A Stretching Sheet. Coatings 2020, 10, 208. https://doi.org/10.3390/coatings10030208
Haider S, Syed Muhammad I, Li Y-Z, Faraz, Saeed Butt A. Radiation and Magnetic Field Impacts on Time-Dependent Mixed Convection Flow and Heat Transmission of Maxwellian Fluid Past A Stretching Sheet. Coatings. 2020; 10(3):208. https://doi.org/10.3390/coatings10030208
Chicago/Turabian StyleHaider, Sajjad, Imran Syed Muhammad, Yun-Zhang Li, Faraz, and Adnan Saeed Butt. 2020. "Radiation and Magnetic Field Impacts on Time-Dependent Mixed Convection Flow and Heat Transmission of Maxwellian Fluid Past A Stretching Sheet" Coatings 10, no. 3: 208. https://doi.org/10.3390/coatings10030208
APA StyleHaider, S., Syed Muhammad, I., Li, Y.-Z., Faraz, & Saeed Butt, A. (2020). Radiation and Magnetic Field Impacts on Time-Dependent Mixed Convection Flow and Heat Transmission of Maxwellian Fluid Past A Stretching Sheet. Coatings, 10(3), 208. https://doi.org/10.3390/coatings10030208




