Investigation of Interfacial Free Energy of Three-Phase Contact on a Glass Sphere in Case of Cationic-Anionic Surfactant Aqueous Mixtures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Surface Tension Measurements
2.2.2. Contact Angle Measurements
3. Calculating Interface Free Energies—Discussion
- Berthelot made the assumption where Wsl is adhesion work and Wss, Wll are cohesion works of the corresponding phases [34].
- Antonoff attempted to determine γs by proposed formula [35]:
- Girifalco and Good [24] modified equation of state by introducing the parameter Φ from the most general thermodynamic considerations, characterizing the interfacial interactions.
- Other methods:
4. Results and Discussion
5. Conclusions
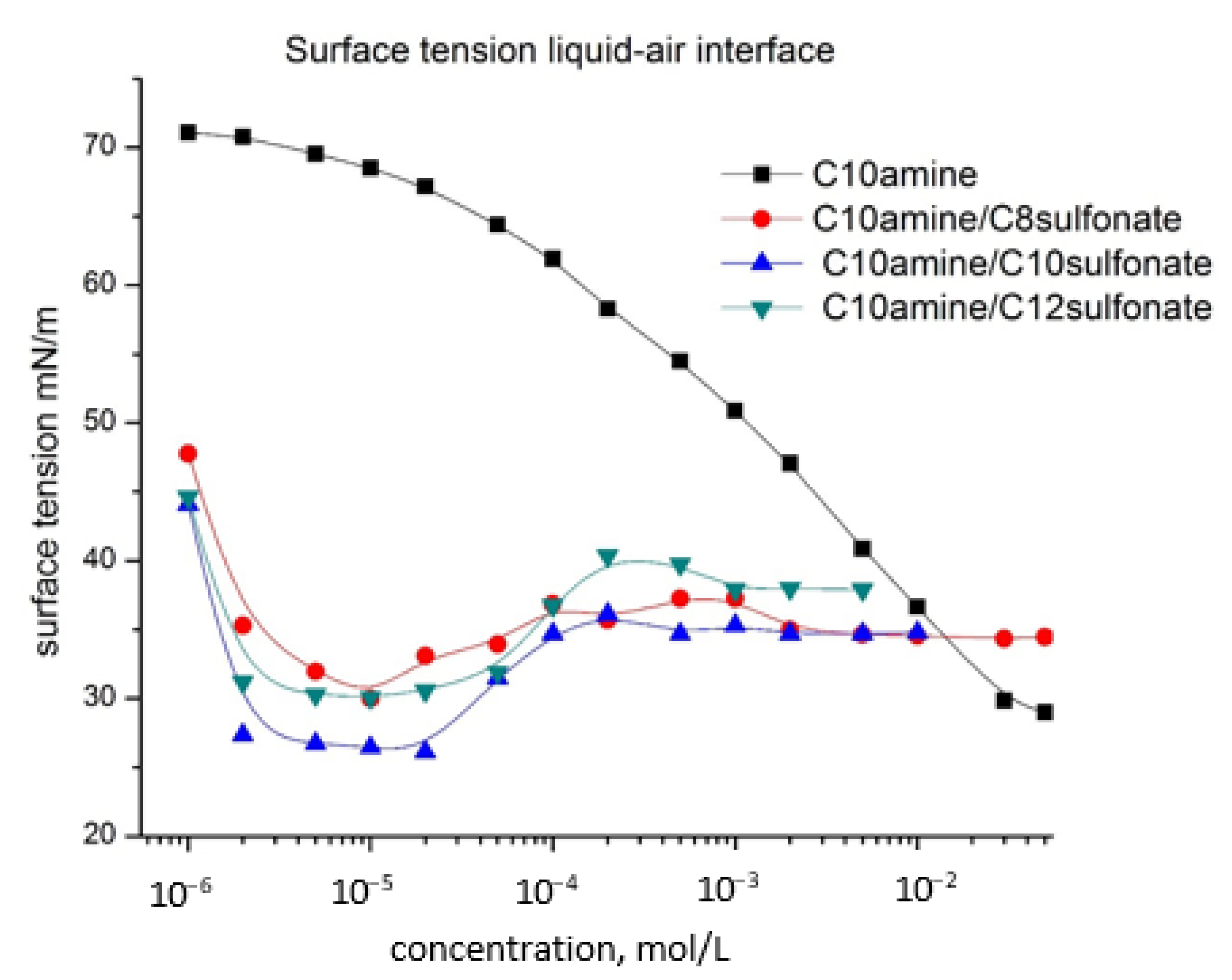
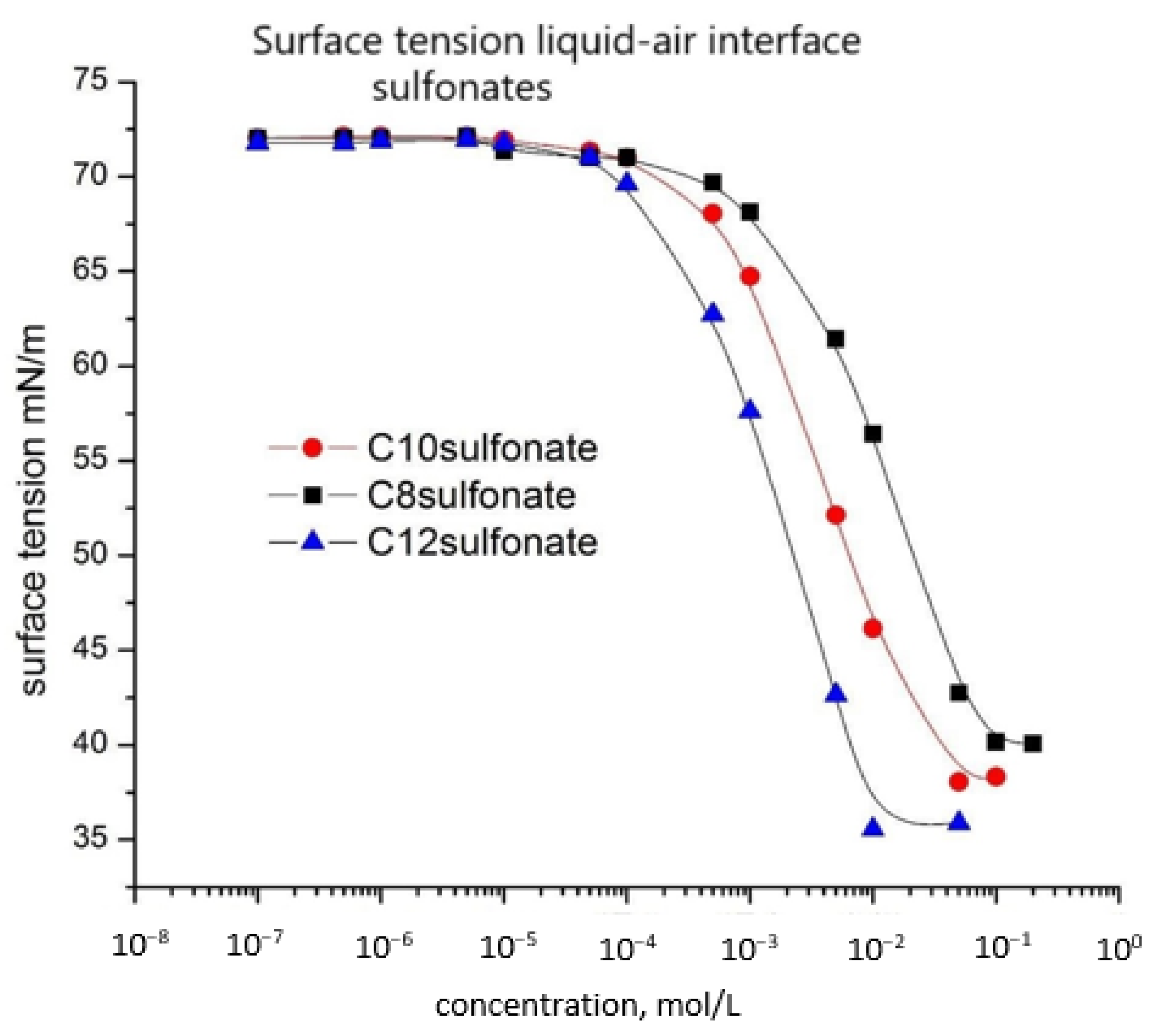
- The surface tension values of aqueous solutions of cationic surfactant, anionic surfactants, and anionic/cationic surfactant mixtures are measured. The surface tension decreases upon the increase of the concentration of each one of the surfactants. The length of the hydrocarbon chain determined the hydrophobicity of the surfactant molecule. When cationic and anionic surfactants are mixed a synergistic effect of additional lowering of the surface tension emerges. The effect is the strongest when the lengths of the hydrocarbon tails of the cationic and anionic surfactants are equal. This is explained with the formation of precipitation complexes, whose hydrophobicity is maximal when the hydrocarbon chains of the two types of surfactants are equal—C10amine/C10sulphonate form the most surface-active complexes, followed by C10amine/C8sulphonate and finally C10amine/C12sulphopnate;
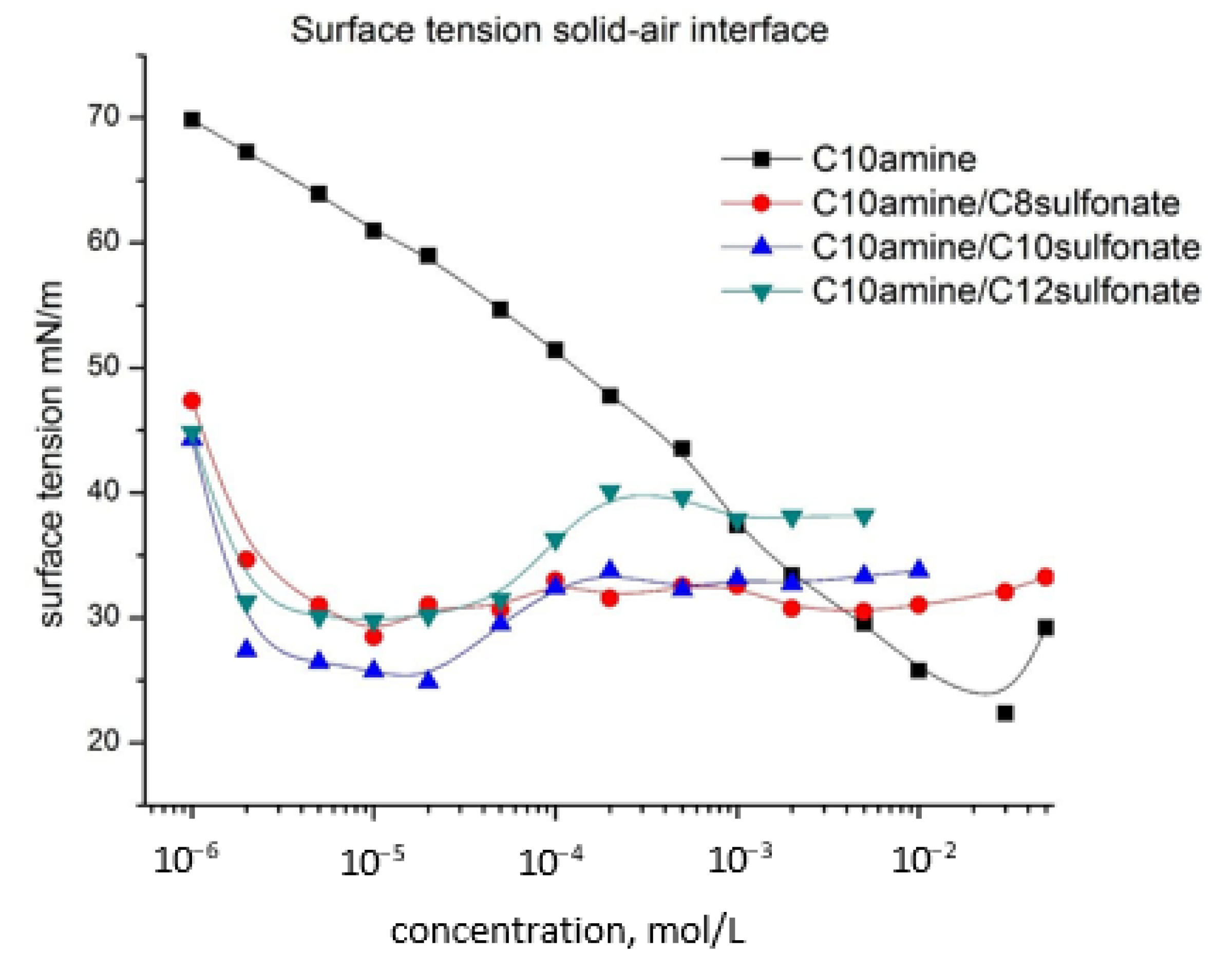
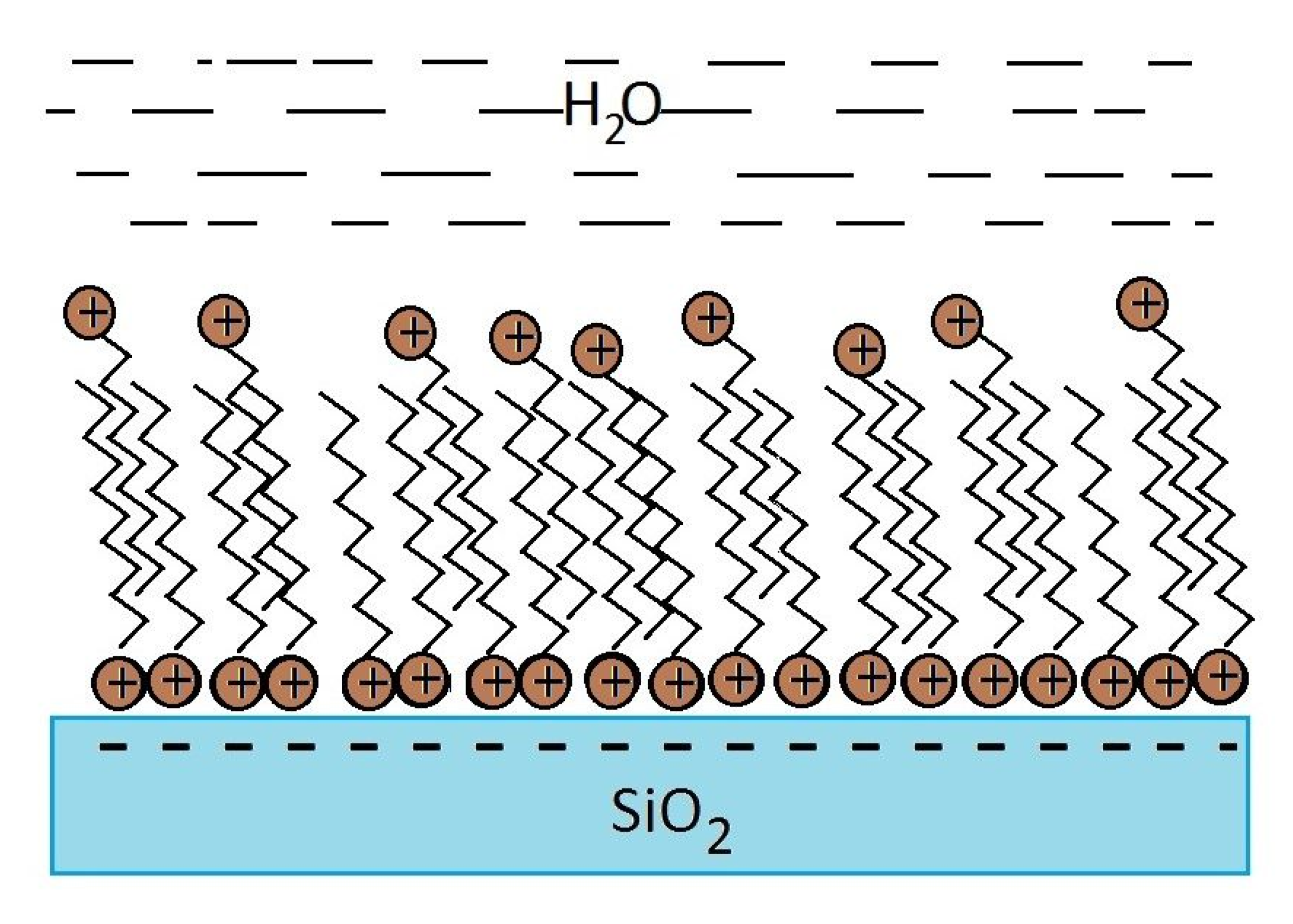
- The silica particles increase their hydrophobicity with the increase of the surfactant concentration in both cases—the cationic surfactant only and cationic/anionic surfactant mixtures until reaching maximum, after which the silica particles becomes more hydrophilic with the increase of the surfactant concentration. This dependence is the strongest in the case of cationic surfactant and weakens with the mixture in the order of C10amine/C8sulphonate, C10amine/C10sulphonate, and C10amine/C12sulphopnate. The optimal concentration of the maxima of θ for each one of the cases shifts toward the smaller concentrations in the order of C10amine/C8sulphonate, C10amine/C10sulphonate, and C10amine/C12sulphopnate, and their maximal value of θ decreases in the same order;
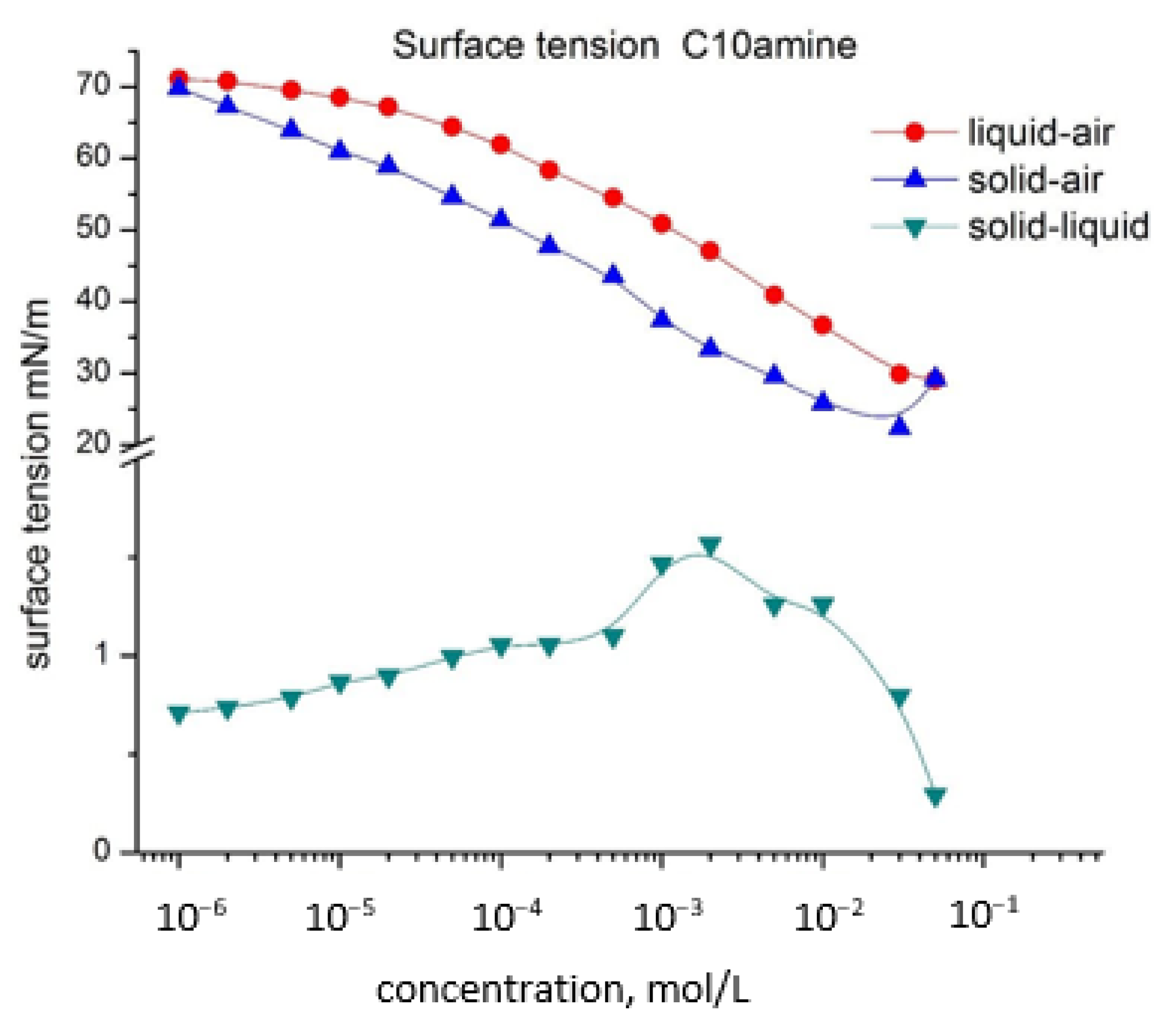
- Surface tensions of solid–air and solid–liquid phase surfaces are calculated for different surfactant concentrations by the method proposed by L.A. Girifalco and R.J. Good [24]. In the opinion of the authors Girifalco and Good, the possible mistakenness of the contribution of the adsorption layer in the parameter Φ does not exceed 5%;
- Calculated surface tension of solid–air interface vs. concentration for C10 amine and mixed systems are close to those for the liquid–air surface, but are slightly lower. In the case of mixed systems, the graph has a specific structure similar to that of liquid–air surface dependence. Here again a synergistic effect is observed—the lowest surface tension values for the C10 amine/C10sulfonate system. At the same time, the values of the solid–liquid phase interface are significantly lower;
- It is shown that in the whole area of concentrations the value of the work for spreading is negative. This result indicates that complete wetting does not occur. The worst are the values for C10 amine while the increase in the alkyl chain length of the sulfonates increases (algebraically) the values to positive. The best wetting is in the absence of adsorption layer (C = 0) or in a dense bi-layer.
Author Contributions
Funding
Conflicts of Interest
References
- Rosen, M.J. Surfactants and Interfacial Phenomena, 3rd ed.; Wiley: New York, NY, USA, 2004; p. 464. [Google Scholar]
- Myers, D. Surfactant Science and Technology, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Tadros, T.F. Applied Surfactants: Principles and Applications; WILEY-VCH Verlag GmbH & Co.: Weinheim, Germany, 2005. [Google Scholar]
- Kume, G.; Gallotti, M.; Nunes, G. Review on anionic/cationic surfactant mixtures. J. Surfactants Deterg. 2008, 11, 1–11. [Google Scholar] [CrossRef]
- Abe, M. Mixed Surfactant Systems, 2nd ed.; Scamehorn, J.F., Ed.; Marcel Dekker: New York, NY, USA, 2005. [Google Scholar]
- Azum, N.; Alamry, K.A.; Khan, S.B.; Rub, M.A.; Asiri, A.M.; Anwar, Y. Synergistic interaction between anionic and nonionic surfactant: Application of the mixed micelles templates for the synthesis of silver nanoparticles. Int. J. Electrochem. Sci. 2016, 11, 1852–1867. [Google Scholar]
- Olea, A.F.; Gamboa, C. Synergism in mixtures of cationic surfactant and anionic copolymers. J. Colloid Interface Sci. 2003, 257, 321–326. [Google Scholar] [CrossRef]
- Azum, N.; Rub, M.A.; Asiri, A.M. Micellization and interfacial behavior of binary and ternary mixtures in aqueous medium. J. Mol. Liq. 2016, 216, 94–98. [Google Scholar] [CrossRef]
- Rub, M.A.; Azum, N.; Kumar, D.; Khan, F.; Asiri, A.M. Clouding phenomenon of amphiphilic drug promazine hydrochloride solutions: Influence of pharmaceutical excipients. J. Ind. Eng. Chem. 2015, 21, 1119–1126. [Google Scholar] [CrossRef]
- Bergström, M.; Pedersen, J.S.; Schurtenberger, P.; Egelhaa, S.U. Small-angle neutron scattering (SANS) study of vesicles and lamellar sheets formed from mixtures of an anionic and a cationic surfactant. J. Phys. Chem. B 1999, 103, 9888–9897. [Google Scholar] [CrossRef]
- Liu, W.G.; Wei, D.Z.; Wang, B.Y.; Fang, P.; Wang, X.H.; Cui, B.Y. A new collector used for flotation of oxide minerals. Trans. Nonferrous Met. Soc. China 2009, 19, 1326–1330. [Google Scholar] [CrossRef]
- Hanumantha Rao, K.; Forssberg, K.S.E. Mixed collector systems in flotation. Int. J. Miner. Process. 1997, 51, 67–79. [Google Scholar] [CrossRef]
- Hanumantha, K.; Rao, K.S.; Forssberg, E. Solution Chemistry of Mixed Cationic/Anionic Collectors and Flotation Separation of Feldspar from Quartz. In Proceedings of the XVIII IMPC, Sydney, Australia, 23–28 May 1993; pp. 837–844. [Google Scholar]
- Hanumantha, K.; Rao, J.M.; Cases, O.; Baress, K.S.; Forssberg, E. Flotation, electrokinetic and FT-IR studies of mixed anionic/cationic collectors in muscovite-biotite system. In Mineral Processing: Recent Advances and Future Trends; Mehrotra, S.P., Shekhar, R., Eds.; Allied Publ. Ltd.: New Delhi, India, 1995. [Google Scholar]
- Patist, A.; Devi, S.; Shah, D.O. Importance of 1:3 Molecular ratio on the interfacial properties of mixed surfactant systems. Langmuir 1999, 15, 7403–7405. [Google Scholar] [CrossRef]
- Patist, A.; Oh, S.G.; Shiao, S.V.; Ling, T.F.; Lee, K.H.; Sharma, M.K.; Devi, S.; Shah, D.O. Unity in Diversity in Interfacial Phenomena. In Emulsions, Foams and Thin Films; Mittal, K.L., Kumar, P., Eds.; Marsel Dekker Inc.: New York, NY, USA, 2000; pp. 31–59. [Google Scholar]
- Shiao, S.Y.; Chhabra, V.; Patist, A.; Free, M.L.; Huibers, P.D.T.; Gregory, A.; Patel, S.; Shah, D.O. Chain length compatibility effects in mixed surfactant systems for technological applications. Adv. Colloid Interface Sci. 1998, 74, 1–29. [Google Scholar] [CrossRef]
- Patist, A.; Chhabra, V.; Pagidipati, R.; Shah, R.; Shah, D.O. Effect of chain length compatibility on micellar stability in sodium dodecyl sulfate/alkyltrimethylammonium bromide solutions. Langmuir 1997, 13, 432–434. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Schulze, H.J. Colloidal Science of Flotation; Marcel Dekker: New York, NY, USA, 2003; p. 840. [Google Scholar]
- Binks, B.P. Modern Aspects of Emulsion Science; The Royal Society of Chemistry: Cambridge, UK, 1998. [Google Scholar]
- Exerowa, D.; Kruglyakov, P.M. Foam and Foam Films: Theory, Experiment, Application; Marcel Dekker: New York, NY, USA, 1997; p. 796. [Google Scholar]
- Mendoza, A.J.; Guzmán, E.; Martínez-Pedrero, F.; Ritacco, H.; Rubio, R.G.; Ortega, F.; Starov, V.M.; Miller, R. Particle laden fluid interfaces: Dynamics and interfacial rheology. Adv. Colloid Interface Sci. 2014, 206, 303–319. [Google Scholar] [CrossRef] [PubMed]
- Khristov, K.; Petkova, H.; Alexandrova, L.; Nedyalkov, M.; Platikanov, D.; Exerowa, D.; Beetge, J. Foam, emulsion and wetting films stabilized by polyoxyalkylated diethylenetriamine (DETA) polymeric surfactants. Adv. Colloid Interface Sci. 2011, 168, 105–113. [Google Scholar] [CrossRef] [PubMed]
- Girifalco, L.A.; Good, R.J. A theory for the estimation of surface and interfacial energies. I. Derivation and application to interfacial tension. J. Phys. Chem. 1957, 61, 904–909. [Google Scholar] [CrossRef]
- Lecomte Du Noüy, P. An interfacial tensiometer for universal use. J. Gen. Physiol. 1925, 7, 625–632. [Google Scholar] [CrossRef]
- Rosen, M.J.; Sulthana, S.B. The interaction of alkylglycosides with other surfactants. J. Colloid Interface Sci. 2001, 239, 528–534. [Google Scholar] [CrossRef]
- Mingins, J.; Scheludko, A. Attachment of spherical particles to the surface of a pendant drop and the tension of the wetting perimeter. J. Chem. Soc. Farad. Trans. 1 Phys. Chem. Cond. Phases 1979, 75, 1–6. [Google Scholar] [CrossRef]
- Young, T. An essay on the “Cohesion of Fluids”. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar]
- Bangham, D.H. The gibbs adsorption equation and adsorption on solids. Trans. Farad. Soc. 1937, 33, 805–811. [Google Scholar] [CrossRef]
- Bangham, D.H.; Razouk, R.I. Adsorption and the wettability of solid surfaces. Trans. Farad. Soc. 1937, 33, 1459–1463. [Google Scholar] [CrossRef]
- Venzmer, J.; Wilkowski, S.P. Trisiloxane Surfactants—Mechanisms of Spreading and Wetting; Auner, N., Weis, J., Eds.; Wiley Online Library: Weinheim, Germany, 2005; pp. 140–151. [Google Scholar]
- Venzmer, J. Superspreading—20years of physicochemical research. Curr. Opin. Colloid Interface Sci. 2011, 16, 335–343. [Google Scholar] [CrossRef]
- Wang, X.; Chen, L.; Bonaccurso, E.; Venzmer, J. Dynamic wetting of hydrophobic polymers by aqueous surfactant and superspreader solutions. Langmuir 2013, 29, 14855–14864. [Google Scholar] [CrossRef] [PubMed]
- Kwok, D.Y.; Neumann, A.W. Contact angle measurement and contact angle interpretation. Adv. Colloid Interface Sci. 1999, 81, 167–249. [Google Scholar] [CrossRef]
- Antonoff, G.N. Sur La Tension Superficielle Des Solutions Dans La Zone Critique. J. Chim. Phys. 1907, 5, 364–371. [Google Scholar] [CrossRef]
- Dredgier, O.N.; Neumann, A.W.; Sell, P.J. Über die grenzflächenenergetische Zustandsfunktion II. Kolloid Z. Z. Polym. 1965, 204, 102–112. [Google Scholar] [CrossRef]
- Neumann, A.W.; Good, R.J.; Hope, C.J.; Sejpal, M. An equation-of-state approach to determine surface tensions of low-energy solids from contact angles. JCIS 1974, 49, 291–304. [Google Scholar] [CrossRef]
- Li, D.; Neumann, A.W. A reformulation of the equation of state for interfacial tensions. JCIS 1990, 137, 304–307. [Google Scholar] [CrossRef]
- Li, D.; Neumann, A.W. Equation of state for interfacial tensions of solid-liquid systems. Adv. Colloid Interface Sci. 1992, 39, 299–345. [Google Scholar] [CrossRef]
- Neumann, A.W.; Spelt, J.K. Applied Surface Thermodynamics; Marcel Dekker: New York, NY, USA, 1996. [Google Scholar]
- Kwok, D.Y.; Lam, C.N.C.; Li, A.; Zhu, K.; Wu, R.; Neumann, A.W. Low-rate dynamic contact angles on polystyrene and the determination of solid surface tensions. Polym. Eng. Sci. 1998, 38, 1675–1684. [Google Scholar] [CrossRef]
- Kwok, D.Y.; Wu, R.; Li, A.; Neumann, A.W. Contact angle measurements and interpretation: Wetting behavior and solid surface tensions for poly (alkyl methacrylate) polymers. J. Adhes. Sci. Technol. 2000, 14, 719–743. [Google Scholar] [CrossRef]
- Fowkes, F.M. Attractive forces at interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- Fowkes, F.M. Donor-acceptor interactions at interfaces. J. Adhes. 1972, 4, 155–159. [Google Scholar] [CrossRef]
- Fowkes, F.M. Calculation of work of adhesion by pair potential suummation. J. Colloid Interface Sci. 1968, 28, 493–505. [Google Scholar] [CrossRef]
- Owens, D.K.; Wendt, R.C. Estimation of the surface free energy of polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- Wu, S. Calculation of interfacial tension in polymer system. J. Polym. Sci. C 1971, 34, 19–30. [Google Scholar] [CrossRef]
- Wu, S. Polar and nonpolar interactions in adhesion. J. Adhes. 1973, 5, 39–55. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Good, R.J.; Chaudhury, M.K. The role of van der Waals forces and hydrogen bonds in “hydrophobic interactions” between biopolymers and low energy surfaces. JCIS 1986, 111, 378–390. [Google Scholar] [CrossRef]
- van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Interfacial Lifshitz—Van der Waals and Polar Interactions in Macroscopic Systems. Chem. Rev. 1988, 88, 927–941. [Google Scholar] [CrossRef]
- Fox, H.W.; Zisman, W.A. The spreading of liquids on low-energy surfaces. II. Modified tetrafluoroethylene polymers. JCIS 1952, 7, 109–121. [Google Scholar] [CrossRef]
- Fox, H.W.; Zisman, W.A. The spreading of liquids on low-energy surfaces. III. Hydrocarbon surfaces. JCIS 1952, 7, 428–442. [Google Scholar] [CrossRef]
- Chibowski, E.; Ontiveros-Ortega, A.; Perea-Carpio, R. On the interpretation of contact angle hysteresis. J. Adhes. Sci. Technol. 2002, 16, 1367–1404. [Google Scholar] [CrossRef]
- Chibowski, E. Surface free energy of a solid from contact angle hysteresis. Adv. Colloid Interface Sci. 2003, 103, 149–172. [Google Scholar] [CrossRef]
- Alexandrova, L.; Rao, K.H.; Forsberg, K.S.E.; Grigorov, L.; Pugh, R.J. Three-phase contact parameters measurements for silica-mixed cationic-anionic surfactant systems. Coll. Surf. A 2009, 348, 228–233. [Google Scholar] [CrossRef]
- Alexandrova, L.; Hanumantha Rao, K.; Forsberg, K.S.E.; Grigorov, L.; Pugh, R.J. The influence of mixed cationic-anionic surfactants on the three-phase contact parameters in silica-solution systems. Coll. Surf. A 2011, 373, 145–151. [Google Scholar] [CrossRef]
- Alexandrova, L.; Tsekov, R. Kinetics of air/vesicle-suspension/quartz three-phase contact. Coll. Surf. A 1998, 131, 295–301. [Google Scholar] [CrossRef]
- Brasher, L.L.; Kaler, E.W. A small-angle neutron scattering (SANS) contrast variation investigation of aggregate composition in catanionic surfactant mixtures. Langmuir 1996, 12, 6270–6276. [Google Scholar] [CrossRef]
- Filipovic-Vincekovic, N.; Skrtic, O.; Tomasic, V. Interactions in dodecylammonium chloride/dodecyl sulfate systems. Ber. Bunsenges. Phys. Chem. 1991, 95, 1646–1651. [Google Scholar] [CrossRef]
- Skrtic, O.; Babic-Ivancic, V.; Bujan, M.; Tusek-Boiic, L.; Filipovic Vincekovic, N. On the formation of catanionic surfactant precipitate. Ber. Bunsenges. Phys. Chem. 1993, 97, 121–127. [Google Scholar] [CrossRef]
- Bujan, M.; Vdović, N.; Filipović-Vinceković, N. Phase transitions in cationic and anionic surfactant mixtures. Coll. Surf. A 1996, 118, 121–126. [Google Scholar] [CrossRef]
- Guzmán, E.; Ritacco, H.; Ortega, F.; Svitova, T.; Radke, C.J.; Rubio, R.G. Adsorption kinetics and mechanical properties of Ultrathin polyelectrolyte multilayers: Liquid-supported versus solid-supported films. J. Phys. Chem. B 2009, 113, 7128–7137. [Google Scholar] [CrossRef]
- Xiao, J.X.; Bao, Y.X. An unusual variation of surface tension with concentration of mixed cationic-anionic surfactants. Chin. J. Chem. 2001, 19, 73–75. [Google Scholar] [CrossRef]
- Herrington, K.L.; Kaler, E.W.; Miller, D.D.; Zasadzinski, J.A.; Chiruvolu, S. Phase behavior of aqueous mixtures of dodecyltrimethylammonium bromide (DTAB) and sodium dodecyl sulfate (SDS). J. Phys. Chem. 1993, 97, 13792–13802. [Google Scholar] [CrossRef]
- Góralczyk, D.; Hac, K.; Wydro, P.S. Surface properties of the binary mixed systems of alkylpyridinium halides and sodium alkylsulfonates. Coll. Surf. A 2003, 220, 55–60. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexandrova, L.A.; Grigorov, L.S.; Grozev, N.A.; Karakashev, S.I. Investigation of Interfacial Free Energy of Three-Phase Contact on a Glass Sphere in Case of Cationic-Anionic Surfactant Aqueous Mixtures. Coatings 2020, 10, 573. https://doi.org/10.3390/coatings10060573
Alexandrova LA, Grigorov LS, Grozev NA, Karakashev SI. Investigation of Interfacial Free Energy of Three-Phase Contact on a Glass Sphere in Case of Cationic-Anionic Surfactant Aqueous Mixtures. Coatings. 2020; 10(6):573. https://doi.org/10.3390/coatings10060573
Chicago/Turabian StyleAlexandrova, Lidia A., Ljudmil S. Grigorov, Nikolay A. Grozev, and Stoyan I. Karakashev. 2020. "Investigation of Interfacial Free Energy of Three-Phase Contact on a Glass Sphere in Case of Cationic-Anionic Surfactant Aqueous Mixtures" Coatings 10, no. 6: 573. https://doi.org/10.3390/coatings10060573
APA StyleAlexandrova, L. A., Grigorov, L. S., Grozev, N. A., & Karakashev, S. I. (2020). Investigation of Interfacial Free Energy of Three-Phase Contact on a Glass Sphere in Case of Cationic-Anionic Surfactant Aqueous Mixtures. Coatings, 10(6), 573. https://doi.org/10.3390/coatings10060573





