Abstract
A procedure based on approximate solutions of three-dimensional equations of wave propagation is utilized for calculating Bechmann’s number for the harmonic overtones of thickness-shear modes in the rotated Y-cut quartz crystal plates. Bechmann’s number is used for the optimization and improvement of electrodes to yield superior performance in the design of quartz crystal resonators. Originally, Bechmann’s number is found through practical experiences, and analytical results were provided afterward to enable optimal design of novel resonator structures. The outcomes in this study are from a simplified theoretical prediction and they are consistent with known empirical results, making it is possible to design optimal quartz crystal resonators for cases without adequate experimental data for a higher frequency and smaller size.
1. Introduction
Pure thickness-shear waves without couplings to other modes in a plate have displacement in parallel to the middle plane and surfaces of the plate and perpendicular to the direction of wave propagation. At long wavelengths, the frequencies of thickness-shear waves are approximately proportional to the number of nodes of displacement across the thickness of the plate; i.e., the waves exist in a series of harmonic overtones. Each harmonic overtone has a cut-off frequency of , below which the wavenumber is imaginary so the wave is nonpropagating. In the portion of a plate coated with electrodes, the cut-off frequency is lowered slightly to due to the extra mass and increased thickness equivalently. Consequently, there is a noticeable frequency gap between and , resulting in real and imaginary wavenumbers in different regions, which make waves propagate in the plated portion but not in the unplated portion. This is the unique functioning principle of quartz crystal resonators in preserving the energy input through electrodes. Under such circumstances, now let us consider that only the central portion of the plate is coated with symmetric electrodes in Figure 1, across which the driving voltage has a frequency between and as the functioning frequency of the resonator. As can be expected intuitively from the basic principle of a quartz crystal resonator, the plate portion between the electrodes excites the propagating thickness-shear wave, but the corresponding wave at the same frequency, in the remaining part of the plate, or the unplated portion, decays exponentially in the propagating direction, thus showing in a total reflection phenomenon so that thickness-shear vibrational energy is significantly trapped in the region under the electrodes. For a electrode that are long enough, many anharmonic overtone modes can have frequencies less than and be completely trapped under the electrodes. If the electrode is small enough, the wavelength of the first anharmonic overtone mode will be so short that the mode and all the higher modes are greater than in frequencies, and only the fundamental mode can be trapped. This will reduce the energy conversion between wave modes and make the energy dissipation very too small to disturb superior performance. To realize this situation, the critical length of the electrode is the wavelength of a thickness-shear wave in the electroded portion of the plate, at the cut-off frequency of the thickness-shear wave in the unplated portion of the plate, which is larger. The ratio of this critical wavelength to the thickness of the plate is Bechmann’s number to be used for the optimal design of quartz crystal resonators [1,2]. At such a frequency, the thickness-shear waves will propagate under the electrode but not in the unplated regions, satisfying the functioning condition of a resonator. With such a structural configuration, the performance of the resonator will be more sensitive to the driving voltage, implying the optimal design and precision feature in applications. Such a requirement has been studied theoretically with plate equations [1,2,3] for both thickness-twist and thickness-shear wave modes. Curran and Koneval [4,5] have carried out a series of experiments and obtained empirical results with vital applications in resonator development and improvement. Their formula and related constants from empirical studies for the Bechmann’s number are compared with approximate predictions from a simple analysis in this paper. Although the concept of Bechmann’s number was invented for the optimization of quartz crystal resonators with specific definitions and narrow applications, it has also been used in the characterization of other types of resonators and sensors [6,7]. In today’s design process of quartz crystal resonators, analytical tools such as finite element method have been widely used for structural validation and optimization, but it is conceivable that a simple index such as Bechmann’s number can simplify the choices of design parameters, which are increasing with complicated models nowadays.
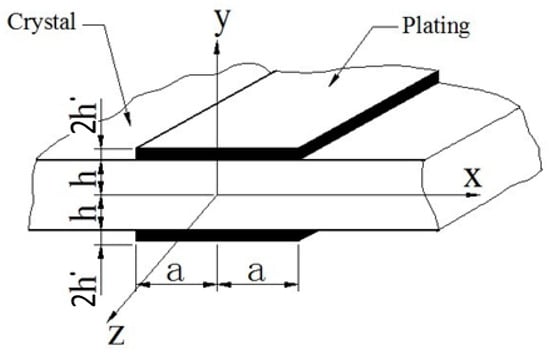
Figure 1.
The portion of plated electrodes in an infinite quartz crystal plate.
2. Vibration Equations of Quartz Crystal Plates and Approximation
The quartz crystal plate refers to to rectangular coordinate axes x, y, and z, with the faces at a diagonal axis of elastic symmetry of the quartz crystal, as shown in Figure 1. Without including the consideration of the piezoelectric effect, the stress–strain relationships for the rotated Y-cut of quartz crystal under deformation are [2]
where are elastic constants, and stresses and strains are related to the displacements with [2]
Furthermore, the stresses must satisfy the equations of motion of wave propagation
The equations of the linear theory of elasticity of anisotropic materials are constituted by the 15 Equations in (1)–(3). This is for the simplified analysis of the quartz crystal plates without considering the piezoelectric effect due to the weak coupling of mechanical and electrical quantities in the above equations. In certain circumstances, like the infinite plates, solutions for thickness-shear vibrations can be obtained for plates without and with electrode coatings through a simple but accurate approximation in one dimension fashion as the required simplification.
The thickness-shear modes in a plate that are to be considered have the general form of [2]
with only one displacement component, is vibration frequency and is time, respectively. Then, with the exponential time factor omitted, with the displacement in (4), strain components in (2) are
As a result, stress components with strain components in (5) are
Consequently, we now have the three equations of motion in the thickness-shear displacement as
The main interest in this study is the displacement of thickness-shear vibration mode, where the displacement is an even function in x and an odd function in y. The simple reason for even is because the modes will include the lowest anharmonic series, this is currently the only interest for resonator optimization; odd in y is because vibration modes which are even in y does not contribute to the electric current through the plate if the piezoelectricity is included from the device functioning point of view. With this consideration, the appropriate form of displacement amplitude function U in (14) has to be
where and are two wavenumbers related to and , respectively. Upon substituting (8) into (7), we find that
For the portion of plate without electrode coating, the boundary condition on the board surface is [2]
Here, we have neglected the displacement U variation with x. For (6) and (8), approximately satisfy the first two of (10) and the third if
where m is the order of the harmonic overtones of vibrations. Hence, (9) becomes [2]
This is the simplified dispersion relation of thickness-shear waves in an unplated, infinite, plate of rotated Y-cut of quartz crystal based on one displacement component. At the frequencies, say , are proportional to the odd integers m, implying the overtones that of an infinite plate are harmonic. For the given m, the wavenumbers are real for and imaginary for . Therefore, a given harmonic overtone is a nonpropagating wave with frequency below and a propagating wave above .
3. Plates with Electrode Coatings
If there is a thin electrode film on both sides of the quartz crystal plate as a conductive coating, as shown in Figure 1, we take the deformation in (8) as
with different amplitude, wavenumbers, and frequency from (8). By following the same procedure above, then (7) takes the form
where is the frequency of vibration of the coated plate. Again, as before, the solution must satisfy the first two boundary conditions in (10). Instead of using the third condition of (10), we calculate the inertia of the electrodes into accounting by setting [2]
where indicates the density of the electrode material and 2 indicates the thickness of each electrode. Clearly, the electrodes are now considered as tractions on the surfaces. Substituting (13) into the last Equation of (6), then substituting the result into (15), we obtain the frequency equation as [2]
where
The dimensionless frequency indicates the ratio of the frequencies of vibration of the coated plate to the cut-off frequency of the lowest mode of the unplated plate, and R indicates the ratio of the mass per unit area of both electrodes to the mass per unit area of the plate. Now, solve (14) for according to and , we have [2]
The implified dispersion relation for thickness-shear waves in an infinite, a rotated Y-cut quartz crystal plate coated with electrodes, is given by (18) and (16). Since mass ratio R is usually quite small in comparison with unity, and the dispersion curves are similar to those for the unplated plate, however, the frequencies are slightly lower because the mass loading and thickness increase through the presence of electrodes. Such changes are needed and important in the resonator functioning. The computation of the dispersion curve can be simplified by replacing [2]
The roots, as expected, are in the vicinity of multiples of . With the substitution of (19), then frequency Equation (16) becomes
For , the cut-off frequencies around are found, and from (18)–(20) with , then the frequency solutions to be approximately
whereas the cut-off frequencies of the unplated plate are given by the same formula that R set to zero. In other words, (21) is the resonant frequency for a plate with and without coatings and it is exact if there is no coating, or R = 0. A simimar procedure with three-dimensional equations and three displacement components was presented by Haines [3] in Mindlin’s approach [1,2]. More details on the analysis of the effects of electrodes for the optimal performance of quartz crystal resonators can be found in more papers with a close relationship to the approximation and formulation in this study [8,9,10].
4. Bechamann’s Number of a Resonator
Now, we consider a plate coated with a pair of identical electrode strips, covering the both faces of the plate symmetrically and parallel to the width direction, or the z axis. As explained by earlier authors [1,2,3,4,5], Bechmann’s number is a ratio, to the thickness of the plate, of the wavelength in the electrode portion at the cut-off frequency of the unelectroded portion of the plate. This definition includes neglecting the subtle difference between the distributions of displacements in the two waves, across the thickness of the plate. The wavelength of the plated portion of the plate is , then the cut-off frequency of the mth harmonic of the unplated plate is m times the cut-off frequency of the first mode, and the plate thickness is 2h. Hence, Bechmann’s number for the thickness-shear waves is [1,2,3]
To calculate for a given order m of harmonic overtone and calculate a given mass ratio R for the essential structural properties of the structure, we can insert the m and R which we chosen into (19) and (18), with given in the denominator of (22). For AT-cut quartz crystal plates, the elastic constants needed in the calculation are, in units of GPa
A simple, approximate, and clear explicit formula for BTT may be obtained as follows. Becase the first root of (20) is approximately for the small mR, from (19),
Inserting this in (18), with , and the result in (22), we have
This is to be compared with the Curran and Koneval’s empirical formula [3] for BTT which, in the notation of this paper, is
where M indicates an empirical constant assigned a value of 2.8 when m = 1. Now, for small mR, we have, from (21)
Hence, Curran and Koneval’s constant of M is [2]
For the AT-cut of quartz crystal, constants in (28) and (23) give M = 2.45. There is a slight difference due to approximations made in the boundary conditions or the neglect of mode couplings. We can compare this with the similar results of Mindlin and Lee [1], M = 2.75, which considered the coupling of flexural vibrations. For the harmonic overtones: m = 3, M = 2.4; m = 5, M = 2.6, we find that our result is very close to the empirical data by Curran and Koneval [4] for higher-order modes. The above results are listed in Table 1 for a better comparison.

Table 1.
Comparisons of Bechmann’s Numbers from Different Authors.
5. Conclusions
By approximating the thickness-shear vibrations of quartz crystal plates with and without coatings of electrodes by a simple displacement function, analytical solutions of vibration frequency and wavelengths are obtained from the ideal structure for the specific mode. By comparing the analytical results of Bechmann’s number with empirical results, a good agreement has been observed for higher-order harmonic modes. It demonstrated that, through an approximate procedure with simple assumptions, Bechmann’s number for the optimal determination of electrodes or the rotated Y-cut quartz crystal resonators is determined and verified. This showed that the theoretical solutions of the optimal electrode configuration are accurate and a similar procedure should also be applicable to other material types to obtain useful results. Since the design of a quartz crystal resonator is an iterative process in a relationship with blank electrodes, mounting, packaging, and more importantly, the manufacturing process, an optimal selection of initial design will be essential in the fast completion of the product development cycle. A theoretical prediction of key design parameters through analytical procedure is always desirable in providing digital support enhancement to many of the analog and empirical procedures. It is natural to apply the same procedure to other resonator types for possible optimal solutions to improving the design and development process.
Author Contributions
The authors have fully participated in and contributed to the research work of this paper thorough conceptualization, formulation, calculation, data analysis, validation, and the final writing and revision. The concept of this analytical approach was from J.W. and Y.C. worked on the derivation of equations at the guidance of J.W. and H.Z. worked on the data analysis and final completion of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported in part by the National Natural Science Foundation of China (Grant Nos. 11672142, 11772349, and 11972354) and the K.C. Wong Magna Fund of Ningbo University. Additional support is from the Technology Innovation 2025 Program (Grant No. 2019B10122) of the Municipality of Ningbo.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mindlin, R.; Lee, P. Thickness-shear and flexural vibrations of partially plated, crystal plates. Int. J. Solids Struct. 1966, 2, 125–139. [Google Scholar] [CrossRef]
- Mindlin, R.D. Bechmann’s number for harmonic overtones of thickness/twist vibrations of rotated-Y-cut quartz plates. J. Acoust. Soc. Am. 1967, 41, 96–973. [Google Scholar] [CrossRef]
- Haines, D.W. Bechmann’s number for harmonic overtones of thickness-shear vibrations of rotated-Y-cut quartz plates. Int. J. Solids Struct. 1969, 5, 11–15. [Google Scholar] [CrossRef]
- Curran, D.R.; Koneval, D.J. Factors in the design of VHF filter crystals. In Proceedings of the 19th Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 20–22 April 1965; pp. 213–268. [Google Scholar]
- Curran, D.R.; Koneval, D.J. Energy trapping and the design of single and multi-electrode filter crystals. In Proceedings of the 18th Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 4–6 May 1964; pp. 93–119. [Google Scholar]
- Quinn, J.J. Electromagnetic generation of acoustic waves and the surfaceimpedance of metals. Phys. Lett. A 1967, 25A, 522–523. [Google Scholar] [CrossRef]
- Burdess, B.J.; Hu, Z.X.; Grigg, H.T.; Dale, C.; Hedley, J.; Fu, C.; Spoors, J.; O’Meara, N.; Keegana, K. Experimental verification of a quasi-trapped degenerate modemagnetic acoustic resonator. Sens. Actuators A 2018, 269, 238–248. [Google Scholar]
- Horton, W.H.; Smythe, R.C. Theory of thickness-shear vibrators, with extensions and applications to VHF acoustically-coupled-resonator filters. In Proceedings of the 21st Annual Symposium on Frequency Control, Fort Monmouth, NJ, USA, 24–26 April 1967; pp. 160–178. [Google Scholar]
- Wang, J.; Shen, L.-J. Exact thickness-shear resonance frequency of electroded piezoelectric crystal plates. J. Zhejiang Univ. A 2005, 6, 980–985. [Google Scholar]
- Yang, J.; Chen, Z.; Hu, H.; Jiashi, Y.; Ziguang, C.; Hongping, H. Electrically forced vibration of a thickness-twist mode piezoelectric resonator with non-uniform electrodes. Acta Mech. Solida Sin. 2007, 20, 266–274. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).