Top Coating Anti-Erosion Performance Analysis in Wind Turbine Blades Depending on Relative Acoustic Impedance. Part 1: Modelling Approach
Abstract
1. Introduction
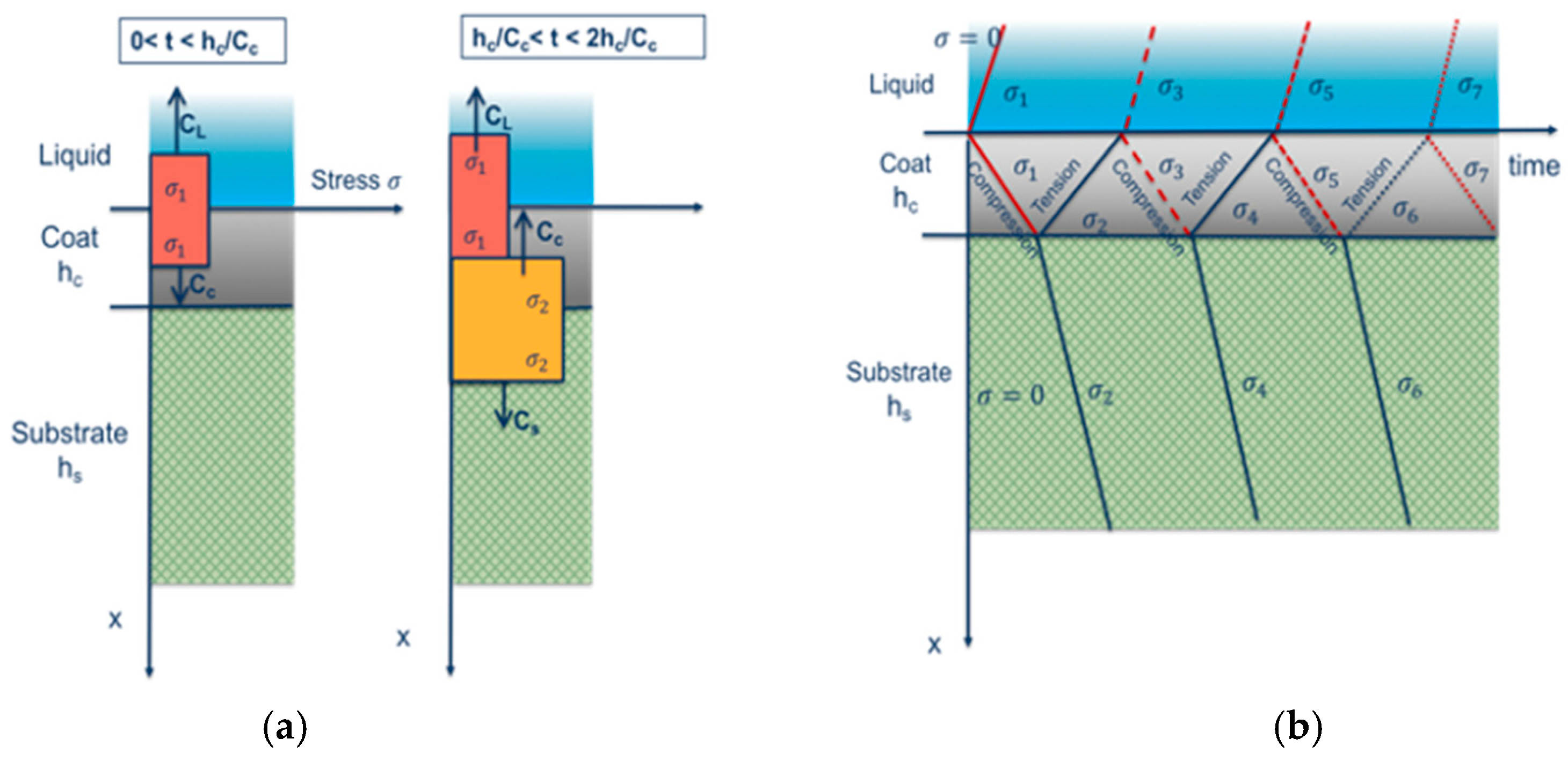
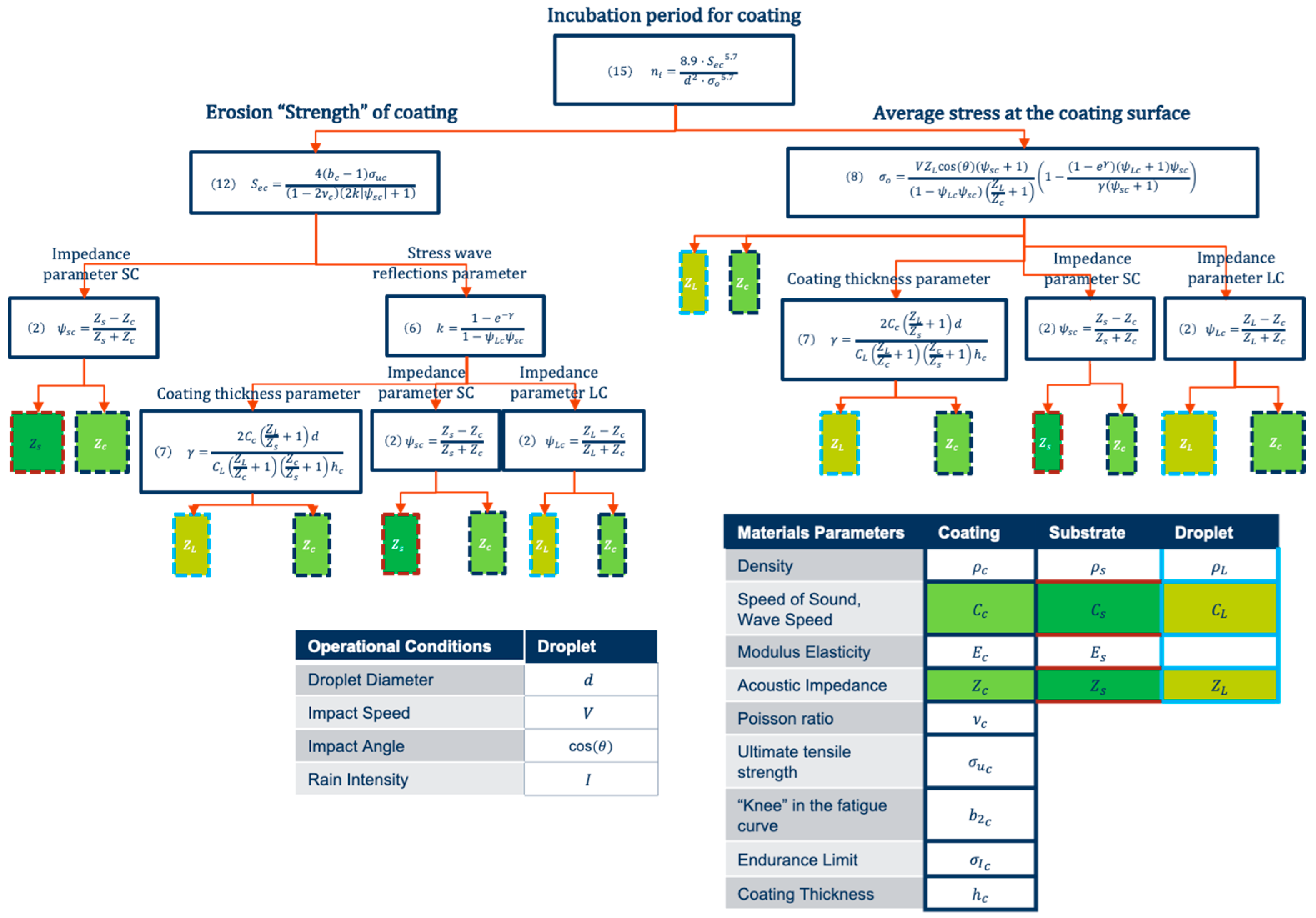
2. Wear Erosion Lifetime Prediction Modelling from Fundamental Material Properties. A Review of Springer Model
3. Single Droplet Impact Modelling Considering Viscoelastic Material Characterization
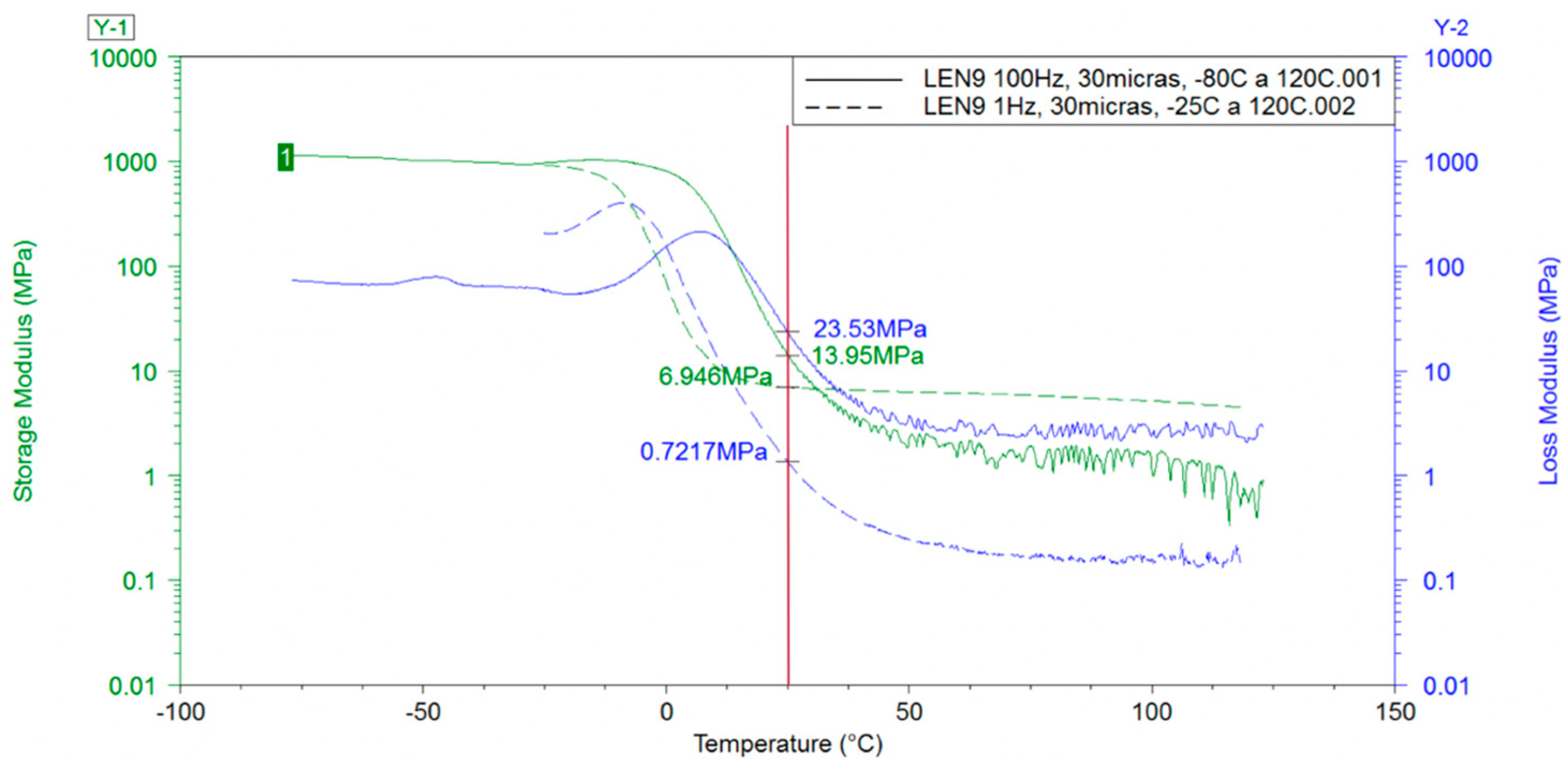
3.1. Thin Coatings mechAnical Properties at High-Strain-Rates
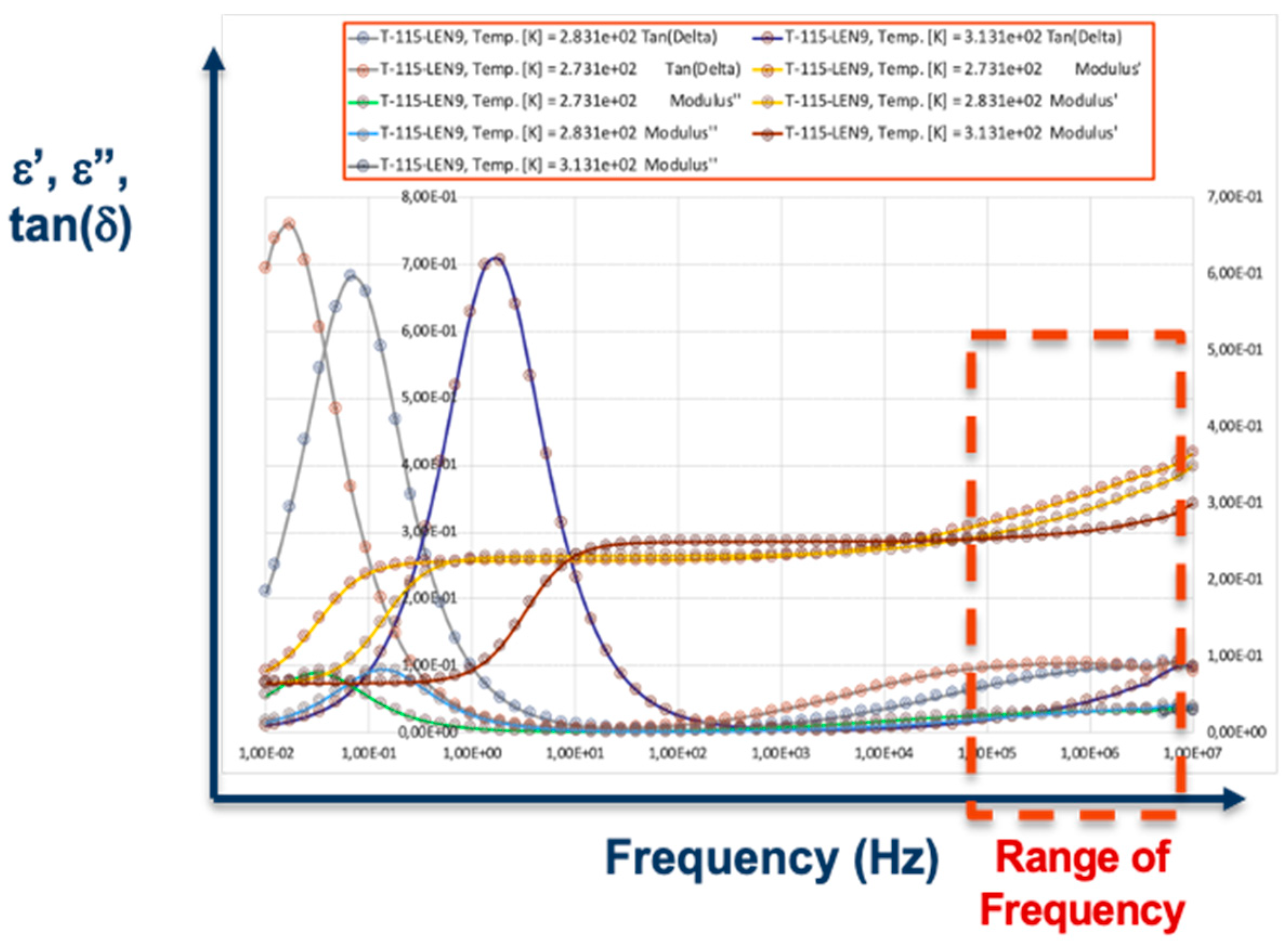
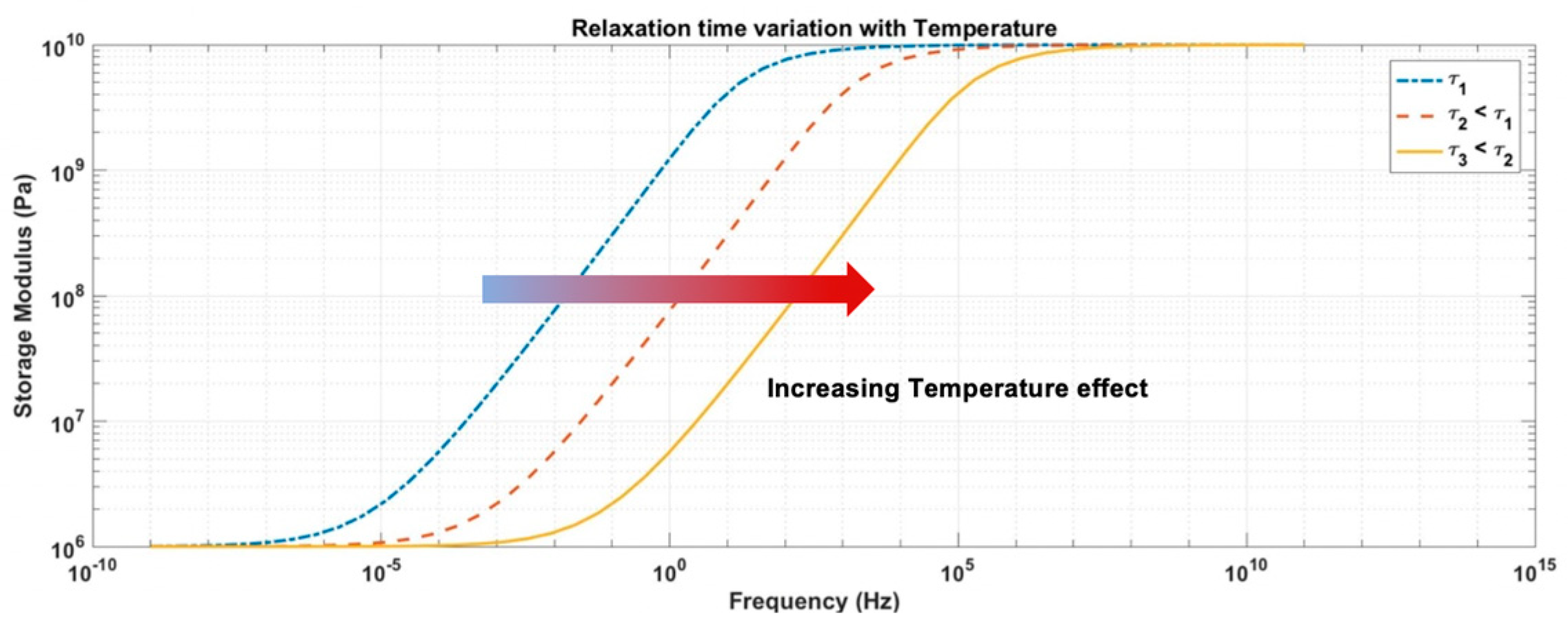
3.2. Stress-Strain Frequency Range Analysis during Droplet Impingement
- Including appropriate coating material models that allow us to observe the viscoelastic behaviour (with consideration for high transient strain rate deformation, and variable stiffness and damping with frequency) and not as a pure elastic event. Water droplet properties are incorporated and assumed constant in this work, but more complex material models could also be included in the developed modelling. Moreover, density variations for coating and water due temperature are also circumvented and are assumed constant during the impact event.
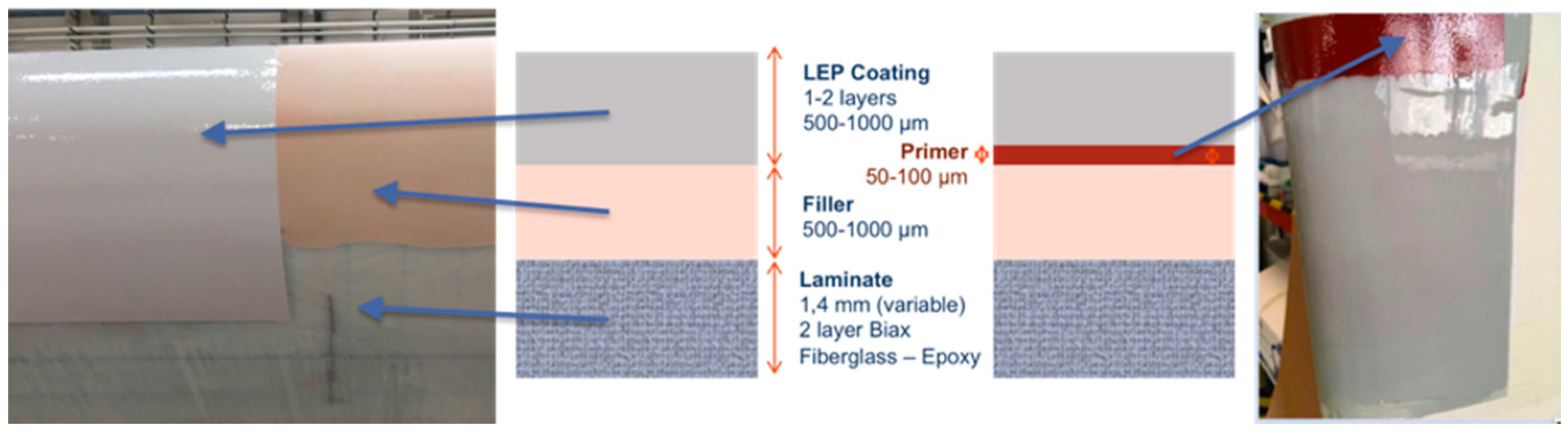
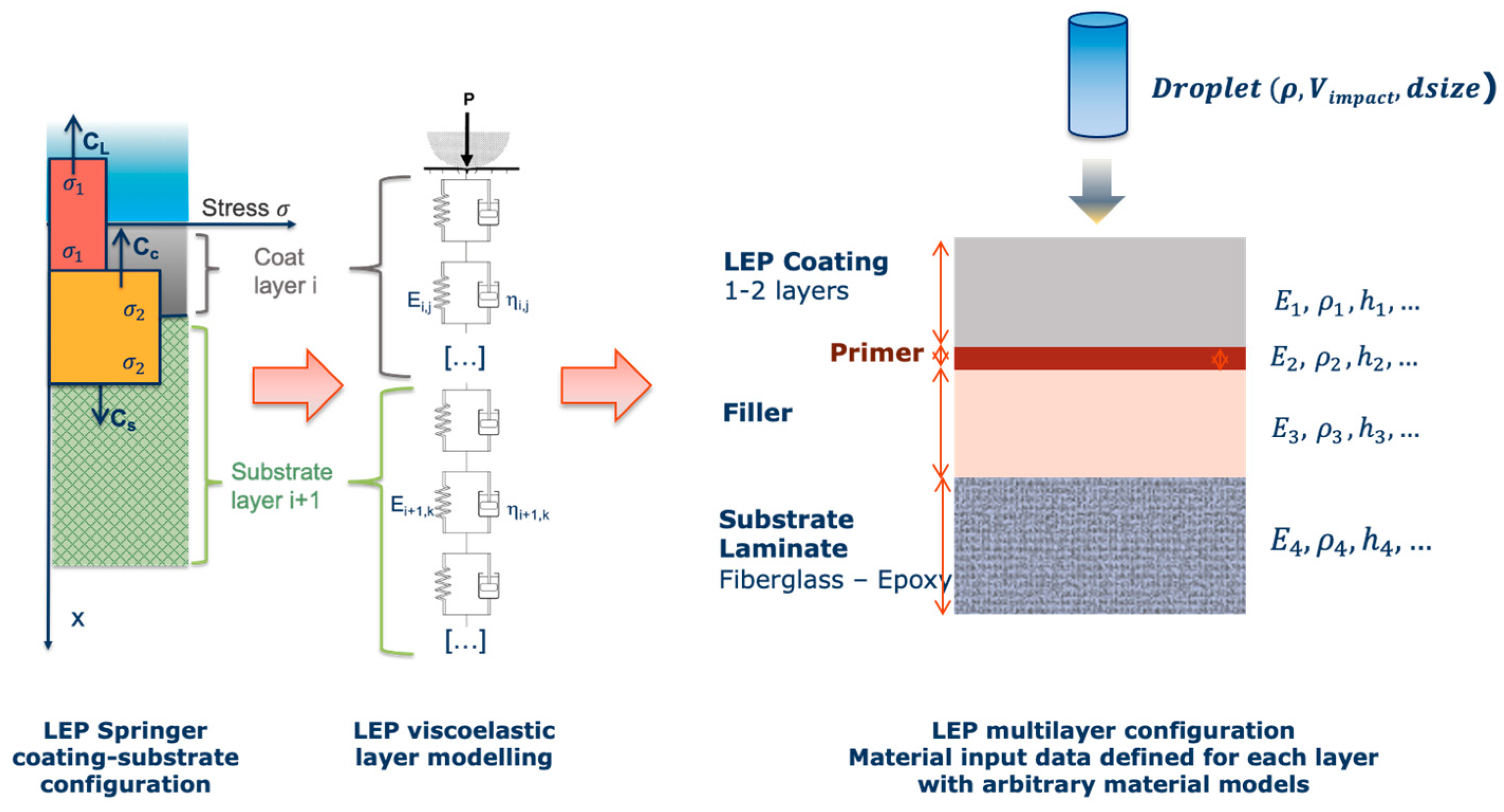
- Springer model undertakes a two layered structure with the substrate thickness assumed semi-infinite. We will treat the LEP system as a multilayer configuration so We will be able to observe additional wave reflections on the interfaces that affect also the surface coating. The algorithm considers water as an additional layer to allow stress wave reflections at liquid-coating interface. The initial impact conditions consider the coating as a dry surface, nevertheless, the water could also be considered as an additional thin layer from previous droplet impact but it is neglected in this work to avoid complex liquid-coating contact modelling following Springer assumptions simplification.
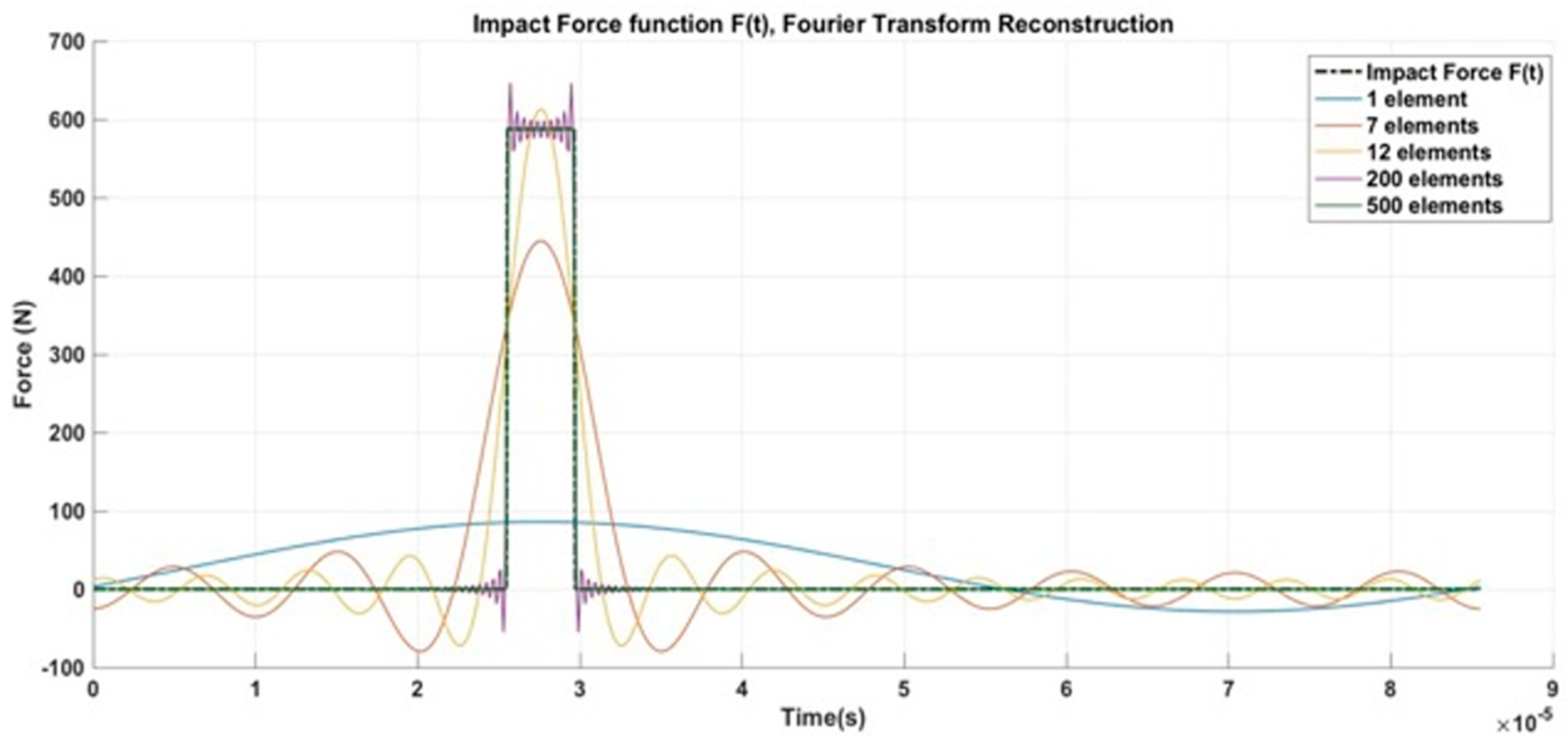
- 1D formulation examines the impact of a liquid droplet treating the problem only as tensile-compression event. This simplification is applicable since shear stresses and shear material characterization are out of the scope of the fatigue analysis case involved.
- Pure elastic model, where A is the impact area defined by the droplet size and E is the elastic modulus
- Kelvin-Voight (KV) viscoelastic model, where is the viscosity,and considering appropriate estimation of the viscosity attenuation observed in as:
3.3. Influence of Coating-Substrate Thickness Variations
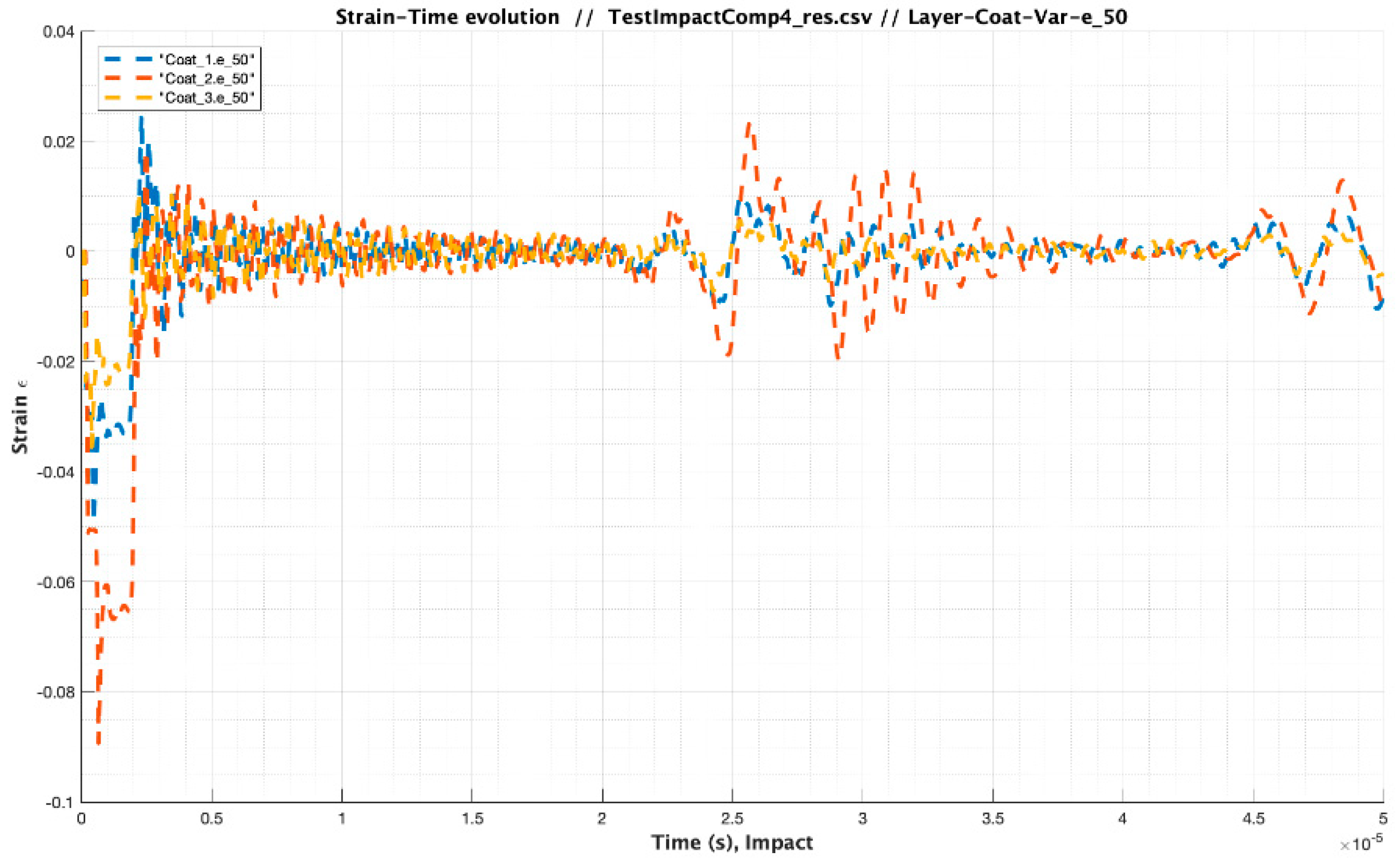
3.4. Influence of Coating Viscoelastic Property Variations
3.5. Influence of Droplet Size Variations
3.6. Influence of Droplet Impact Velocity Variations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cortés, E.; Sánchez, F.; O’Carroll, A.; Madramany, B.; Hardiman, M.; Young, T.M. On the material characterization of wind turbine blade coatings: Effect of the interphase adhesion on rain erosion performance. Materials 2017, 10, 1146. [Google Scholar] [CrossRef]
- Tobin, E.F.; Young, T.M.; Raps, D.; Rohr, O. Comparison of liquid impingement results from whirling arm and water-jet erosion test facilities. Wear 2011, 271, 2625–2631. [Google Scholar] [CrossRef]
- Gohardani, O. Impact of erosion testing aspects on current and future flight conditions. Prog. Aerosp. Sci. 2011, 47, 280–303. [Google Scholar] [CrossRef]
- Adler, W.F. Waterdrop impact modeling. Wear 1995, 186, 341–351. [Google Scholar] [CrossRef]
- Fang, J.; Owens, R.G.; Tacher, L.; Parriaux, A. A numerical study of the sph method for simulating transient viscoelastic free surface flows. J. Nonnewton. Fluid Mech. 2006, 139, 68–84. [Google Scholar] [CrossRef]
- Verma, A.S.; Castro, S.G.P.; Jiang, Z.; Teuwen, J.J.E. Numerical investigation of rain droplet impact on offshore wind turbine blades under different rainfall conditions: A parametric study. Compos. Struct. 2020, 241, 112096. [Google Scholar] [CrossRef]
- Yonemoto, Y.; Kunugi, T. Universality of Droplet Impingement: Low-to-high viscosities and surface tensions. Coatings 2018, 8, 409. [Google Scholar] [CrossRef]
- Keegan, M.H.; Nash, D.H.; Stack, M.M. On erosion issues associated with the leading edge of wind turbine blades. J. Phys. D Appl. Phys. 2013, 46, 383001. [Google Scholar] [CrossRef]
- Doagou-Rad, S.; Mishnaevsky, L.; Bech, J.I. Leading edge erosion of wind turbine blades: Multiaxial critical plane fatigue model of coating degradation under random liquid impacts. Wind Energy 2020, 1, 1–15. [Google Scholar] [CrossRef]
- Mishnaevsky, L.; Fæster, S.; Mikkelsen, L.P.; Kusano, Y.; Bech, J.I. Micromechanisms of leading edge erosion of wind turbine blades: X-ray tomography analysis and computational studies. Wind Energy 2020, 23, 547–562. [Google Scholar] [CrossRef]
- Mishnaevsky, L., Jr.; Sütterlin, J. Micromechanical model of surface erosion of polyurethane coatings on wind turbine blades. Polym. Degrad. Stab. 2019, 166, 283–289. [Google Scholar] [CrossRef]
- Chen, J.; Geng, M.; Li, Y.; Yang, Z.; Chai, Y.; He, G. Erosion resistance and damage mechanism of TiN/ZrN nanoscale multilayer coating. Coatings 2019, 9, 64. [Google Scholar] [CrossRef]
- Springer, G.S. Erosion by Liquid Impact; John Wiley and Sons: New York, NY, USA, 1976. [Google Scholar]
- Slot, H.M.; Gelnick, E.R.M.; Rentrop, C.; van der Heide, E. Leading edge erosion of coated wind turbine blades: Review of coating life models. Renew. Energy 2015, 80, 837–848. [Google Scholar] [CrossRef]
- Eisenberg, D.; Laustsen, S.; Stege, J. Wind turbine blade coating leading edge rain erosion model: Development and validation. Wind Energy 2018, 80. [Google Scholar] [CrossRef]
- Elhadi Ibrahim, M.; Medraj, M. Water droplet erosion of wind turbine blades: Mechanics, testing, modeling and future perspectives. Materials 2020, 13, 157. [Google Scholar] [CrossRef]
- Mishnaevsky, L., Jr. Toolbox for optimizing anti-erosion protective coatings of wind turbine blades: Overview of mechanisms and technical solutions. Wind Energy 2019, 22, 1636–1653. [Google Scholar] [CrossRef]
- Arena, G.; Friedrich, K.; Ruso, P.; Padenko, E.; Acierno, D.; Filippone, G.; Wagner, J. Solid particle erosion and viscoelastic properties of thermoplastic polyurethane. eXPRESS Polym. Lett. 2015, 9, 166–176. [Google Scholar] [CrossRef]
- OPENMODELICA. Available online: https://openmodelica.org (accessed on 6 June 2020).
- Domenech, L.; Garcia-Peñas, V.; Šakalytė, A.; Puthukara, D.; Eskil Skoglund, F.; Sánchez, F. Top coating anti-erosion performance analysis in wind turbine blades depending on relative acoustic impedance. Part 2: Material characterization and rain erosion testing evaluation. Coatings 2020, in press. [Google Scholar]
- Standard Test Method for Liquid Impingement Erosion Using Rotating Apparatus; ASTM G73-10; ASTM International: West Conshohocken, PA, USA, 2017.
- DNVGL: RP-0171. Testing of Rotor Blade Erosion Protection Systems. Recommended Practice. 2018. Available online: http://www.dnvgl.com (accessed on 1 February 2020).
- Plastics—Determination of Tensile Properties at High Strain Rates; ISO 18872:2007; ISO: Geneva, Switzerland, 2007.
- Sarva, S.S.; Deschanel, S.; Boyce, M.C.; Chen, W. Stress-strain behavior of a polyurea and a polyurethane from low to high strain rates. Polymer 2007, 48, 2208–2213. [Google Scholar] [CrossRef]
- Roland, C.M.; Twigg, J.; van Vu, Y.; Mott, P.H. High strain rate mechanical behavior of polyurea. Polymer 2007, 48, 574–578. [Google Scholar] [CrossRef]
- Fan, J.T.; Weerheijm, J.; Sluys, L.J. High-strain-rate tensile mechanical response of a polyurethane elastomeric material. Polymer 2015, 65, 72–80. [Google Scholar] [CrossRef]
- Chevalier, Y.; Vinh, J.T. Mechanics of Viscoelastic Materials and Wave Dispersion; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Garceau, P. Characterization of Isotropic and Anisotropic Materials by Progressive Ultrasonic Waves. In Mechanics of Viscoelastic Materials and Wave Dispersion; Wiley: Hoboken, NJ, USA, 2013; pp. 513–554. [Google Scholar] [CrossRef]
- Beda, T.; Esteoule, C.; Mohamed, S.; Vinh, J.T. Viscoelastic Moduli of Materials Deduced from Harmonic Responses of Beams. In Mechanics of Viscoelastic Materials and Wave Dispersion; Wiley: Hoboken, NJ, USA, 2013; pp. 555–597. [Google Scholar] [CrossRef]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity; Springer: New York, NY, USA, 2010; ISBN 978-1-4899-7485-3. [Google Scholar]
- Grate, J.W.; Wenzel, S.; White, R.M. frequency-independent and frequency-dependent polymer transitions observed on flexural plate ultrasonic wave sensors. Anal. Chem. 1992, 64, 413–423. [Google Scholar] [CrossRef]
- Pascual, B.; Sánchez, F.; Doménech, L.; Cortés, E.; Ribes-Greus, A. Interconversion between dielectric and mechanical measurements of polymeric materials for wind turbine Blades. In Proceedings of the XI Congreso Nacional y II Internacional de Ingeniería Termodinámica, 11CNIT-XI-2018, Albacete, Spain, 12–28 June 2019. [Google Scholar]
- Szabo, J.P.; Keough, I.A. Method for analysis of dynamic mechanical thermal analysis data using the Havriliak-Negami model. Thermochim. Acta 2002, 392–393, 1–12. [Google Scholar] [CrossRef]
- Garcia-Bernabe, A.; Lidon-Roger, J.V.; Sanchis, M.J.; Diaz-Calleja, R.; del Castillo, L.F. Interconversion algorithm between mechanical and dielectric relaxation measurements for acetate of cis- and trans-2-phenyl-5-hydroxymethyl-1,3-dioxane. Phys. Rev. E 2015, 92, 042307. [Google Scholar] [CrossRef] [PubMed]





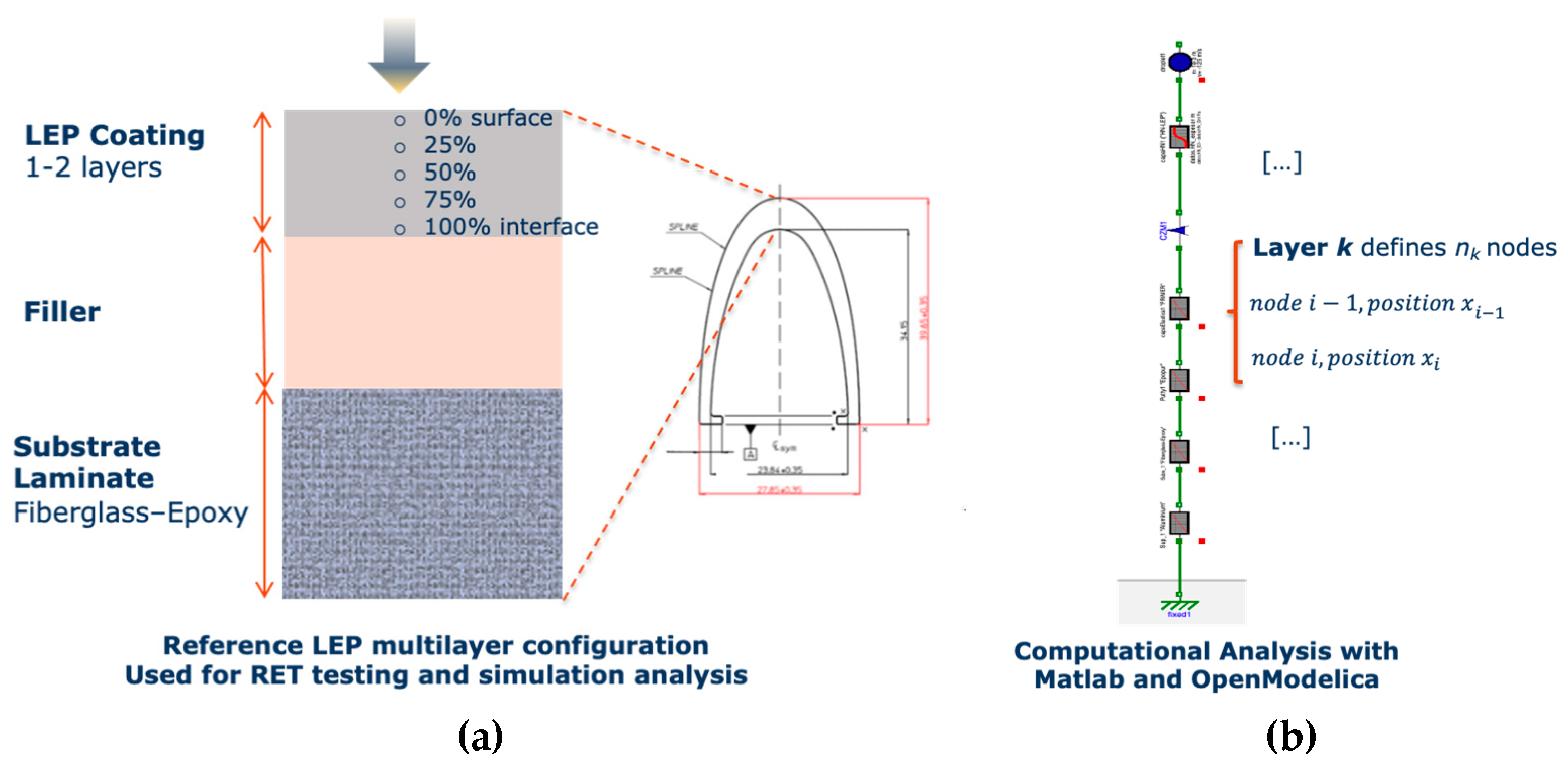


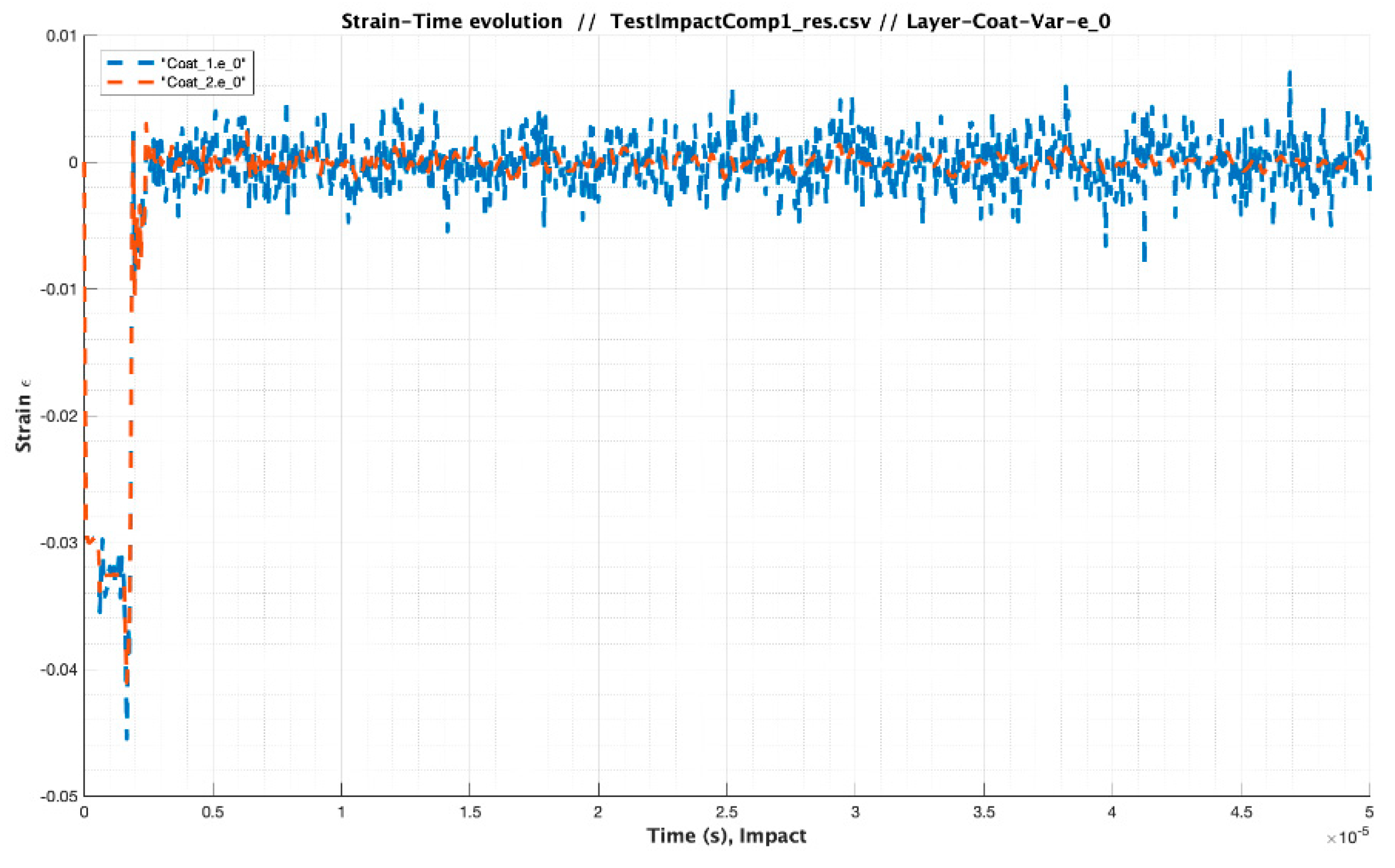
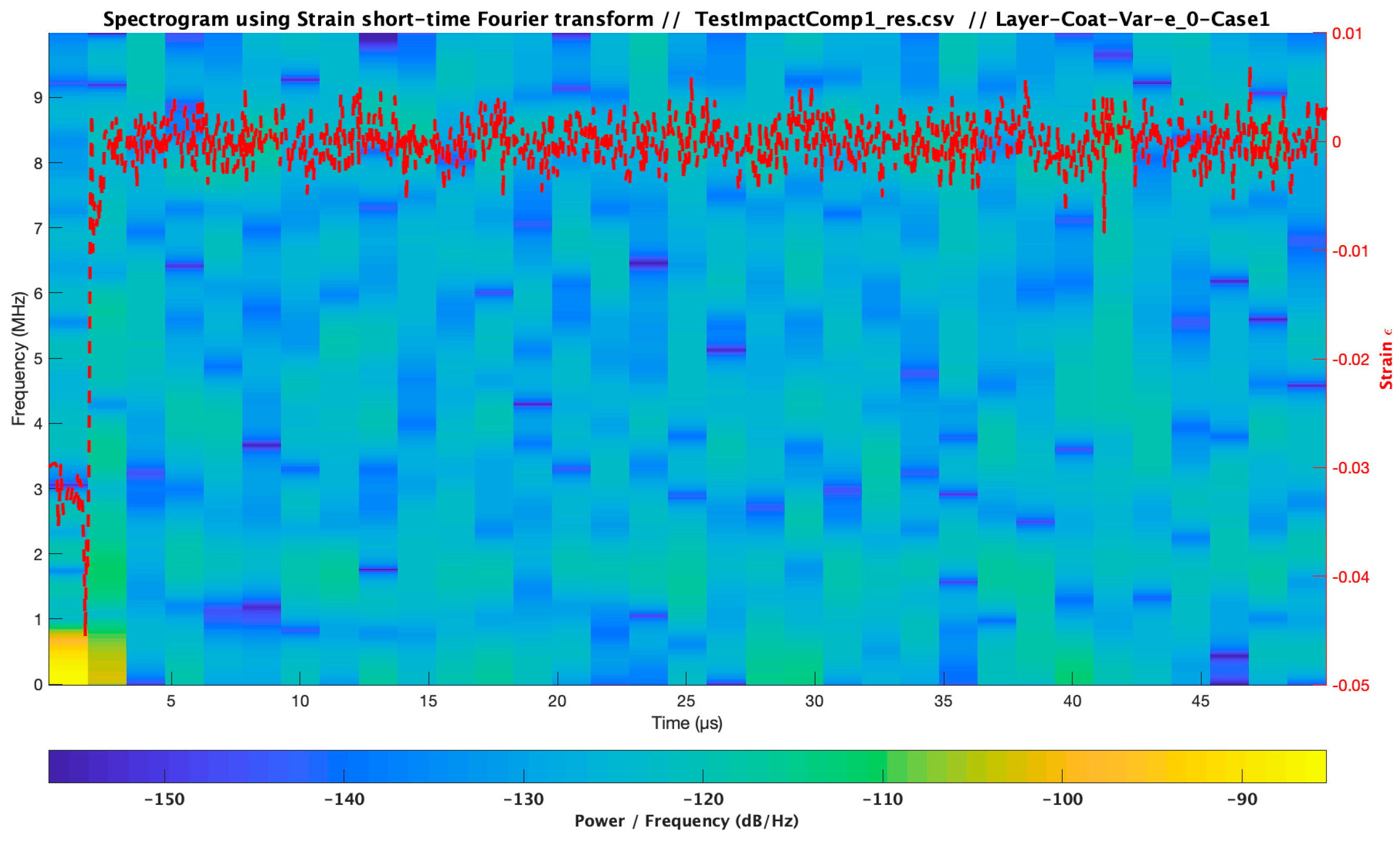
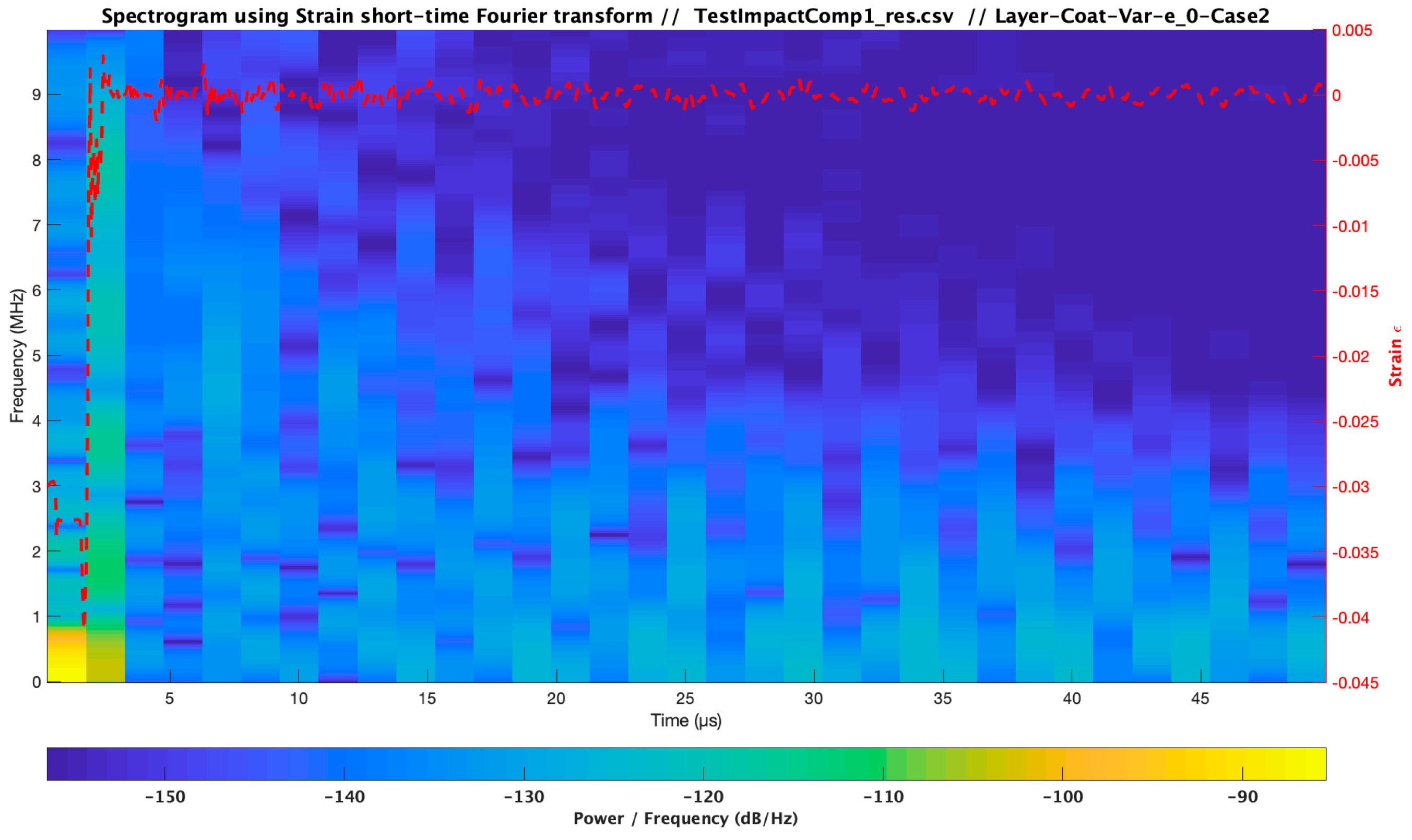
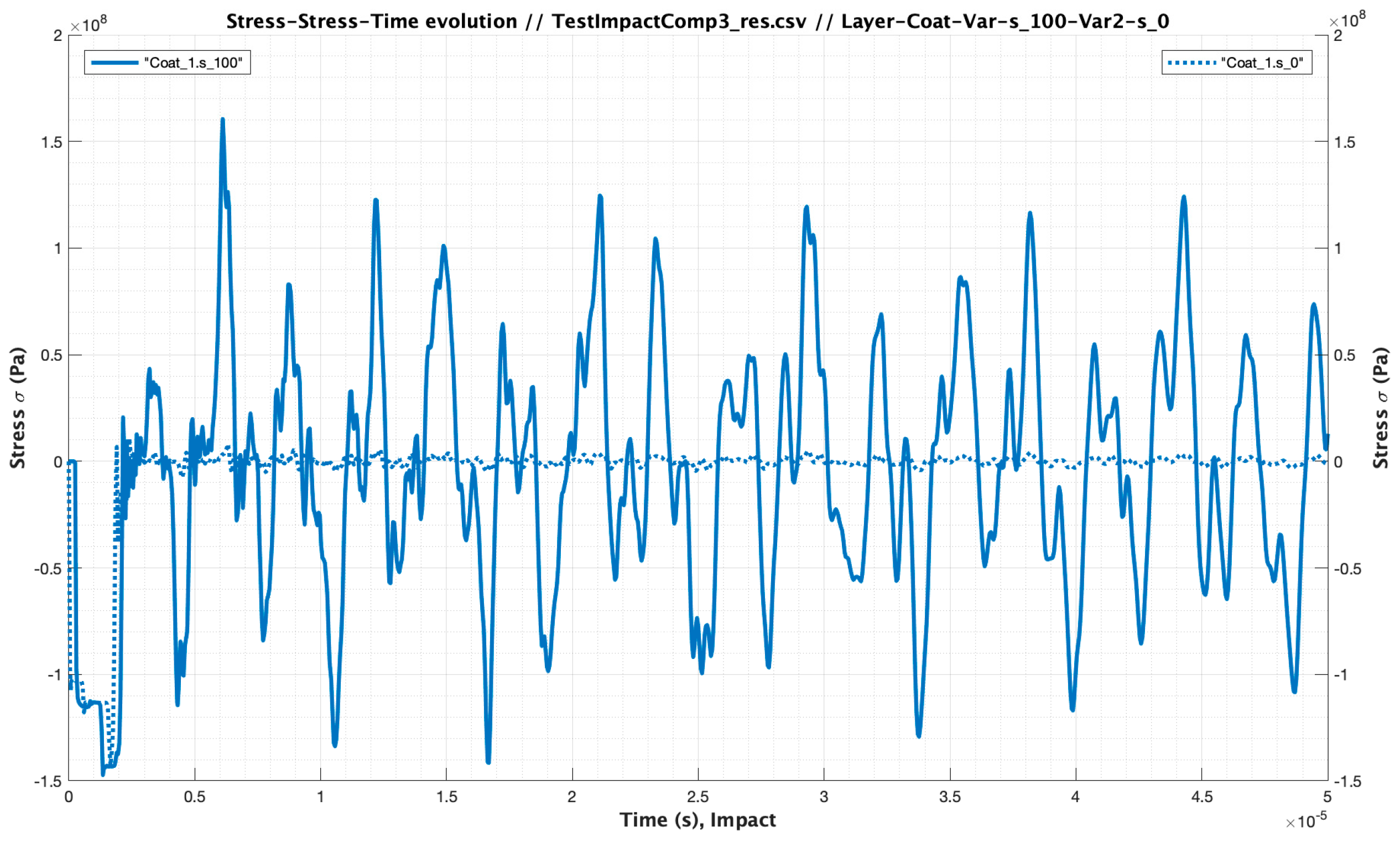
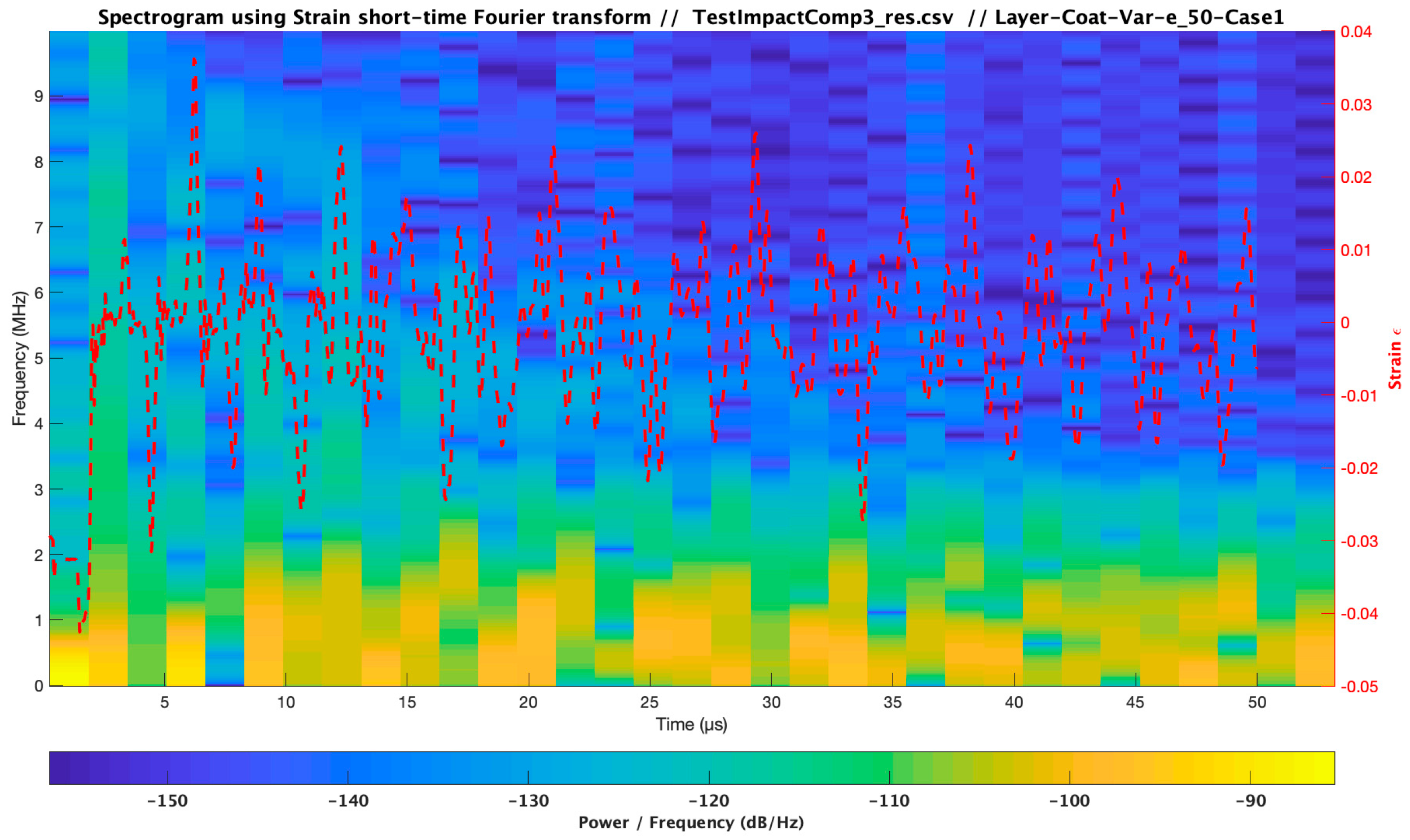

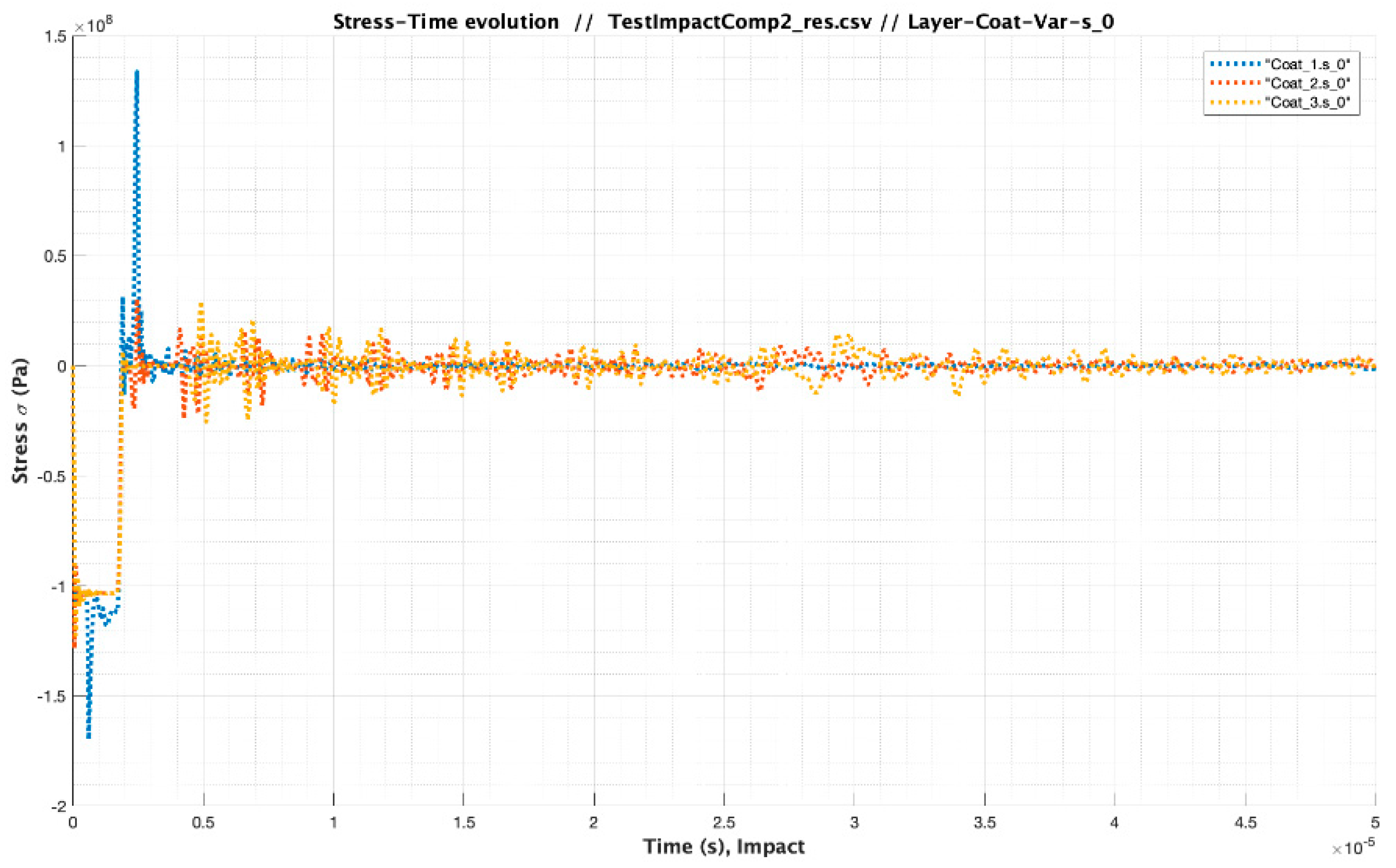
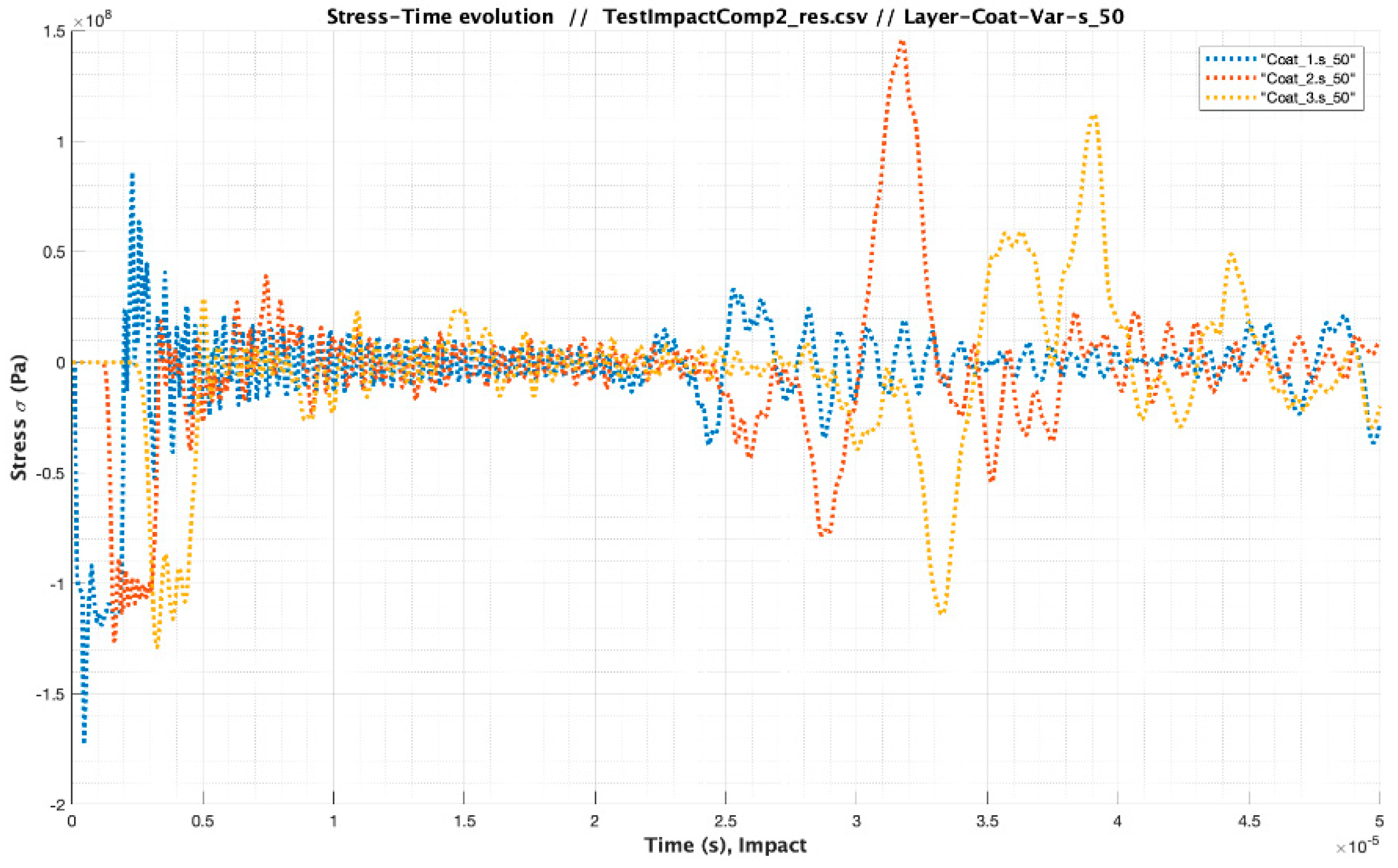
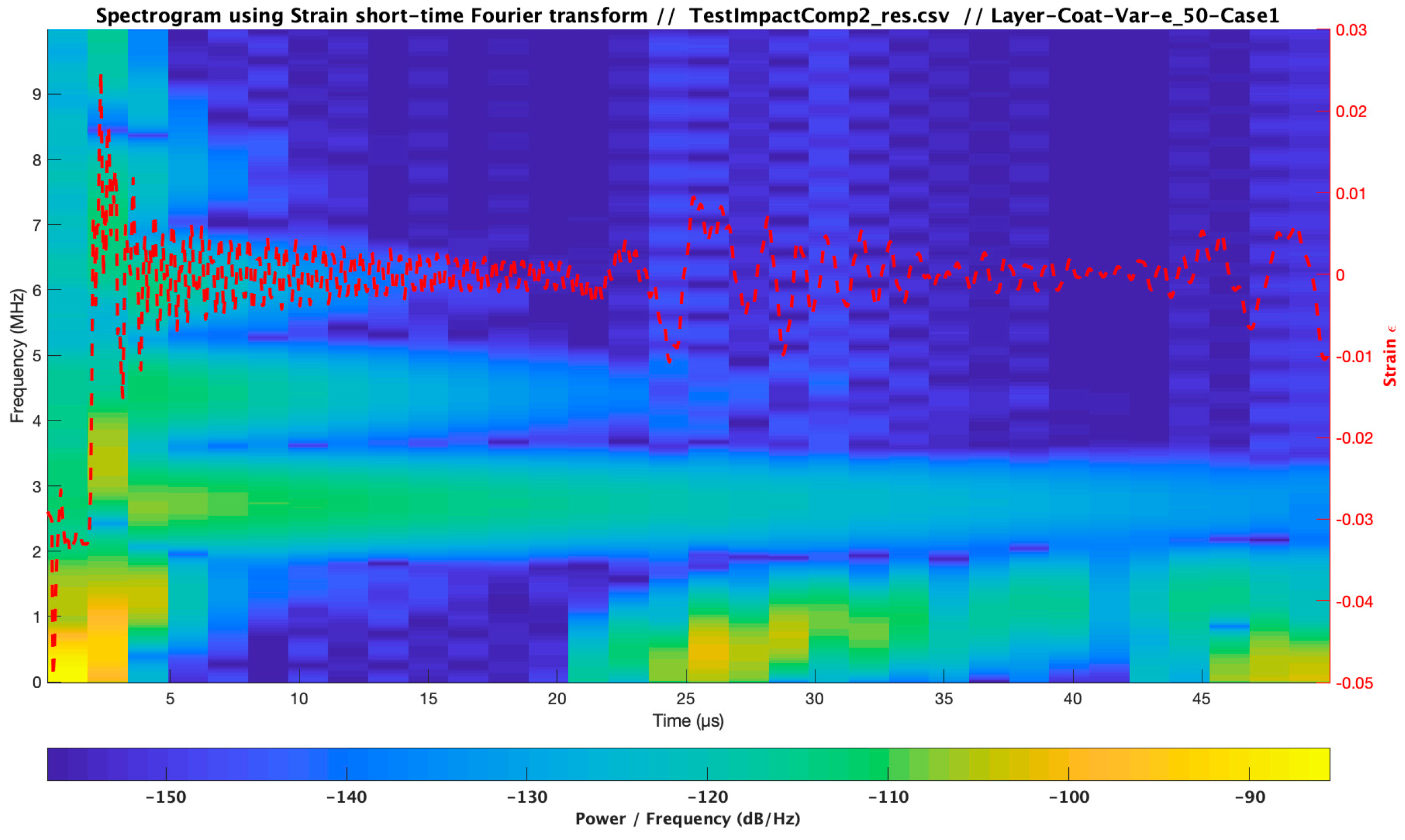
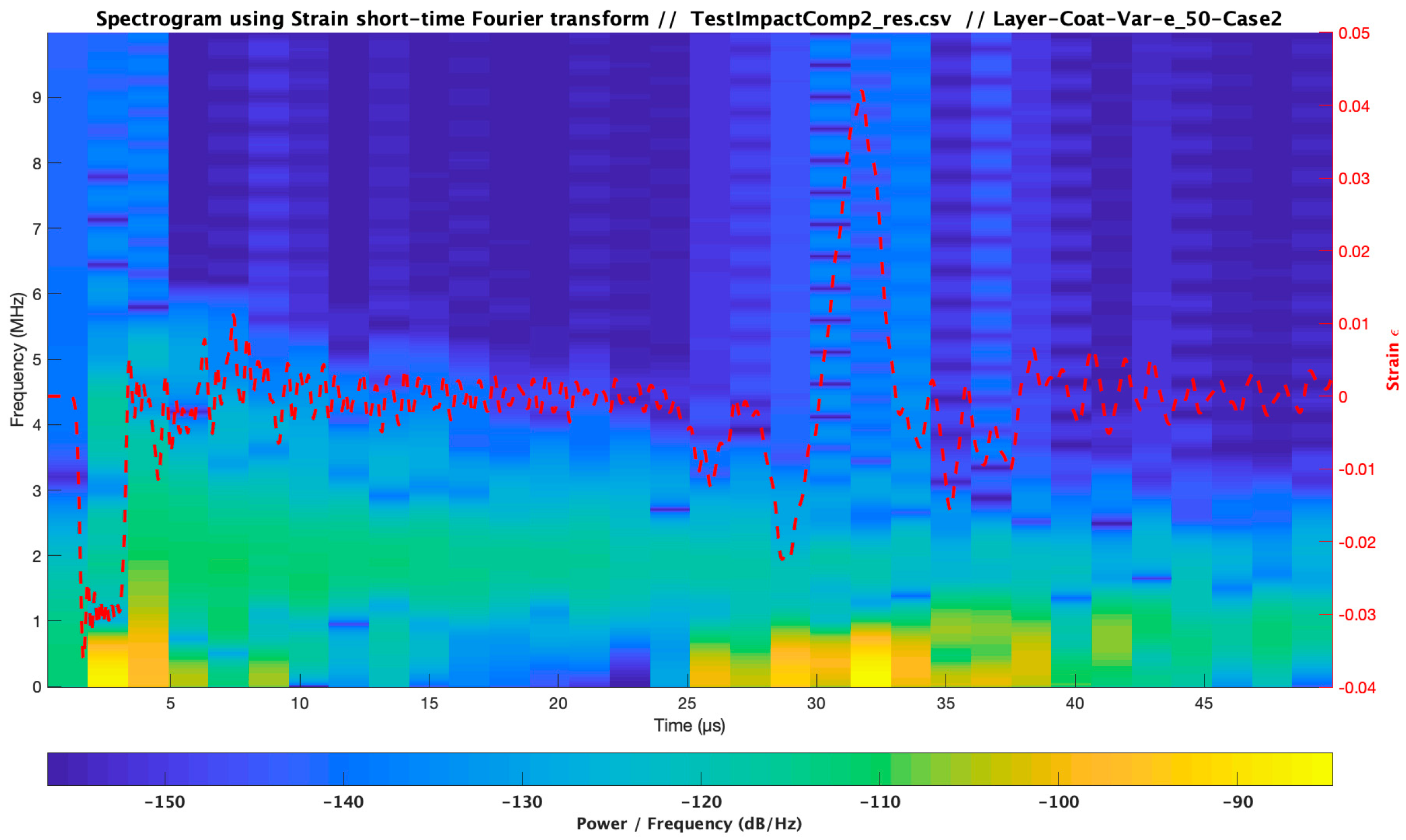
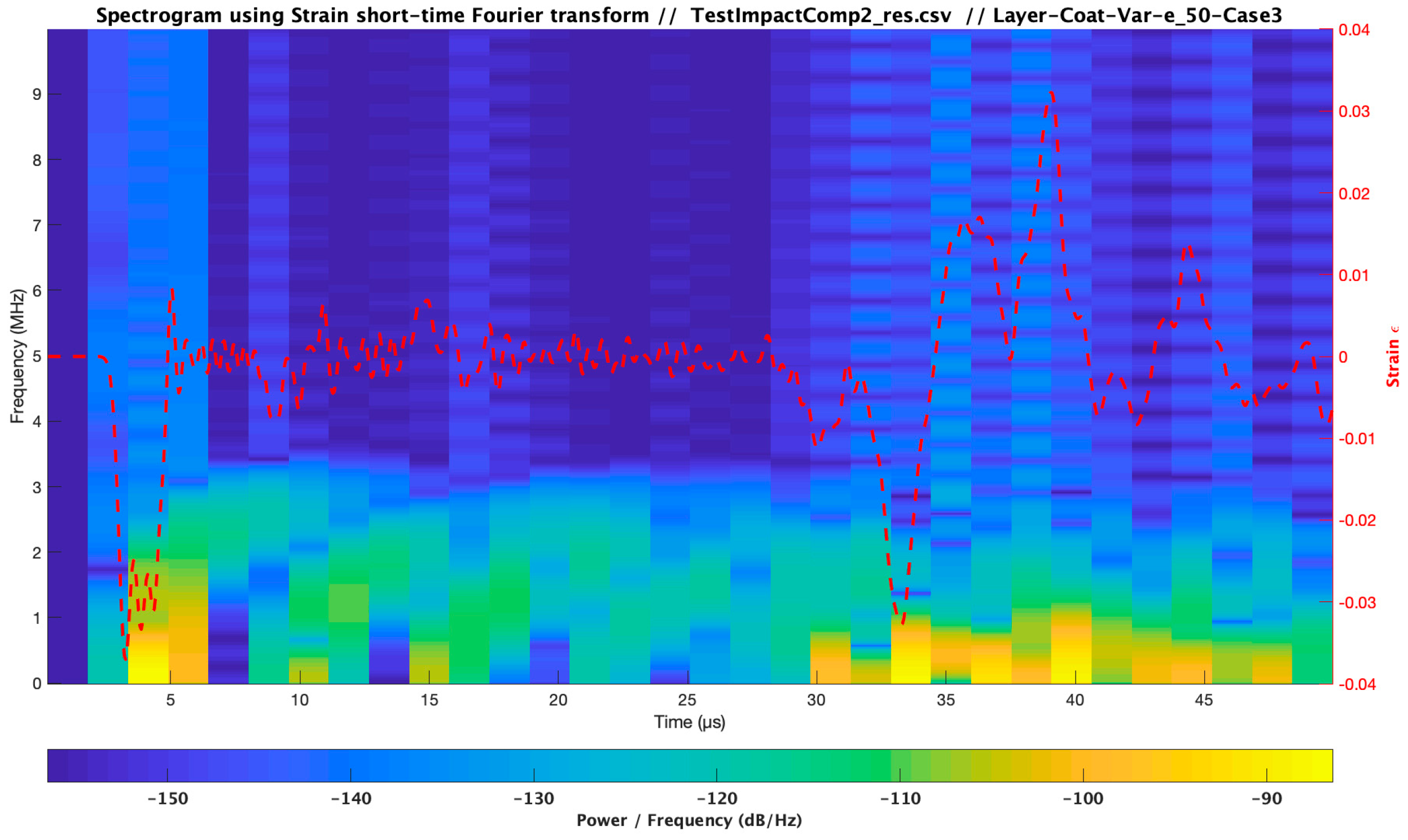
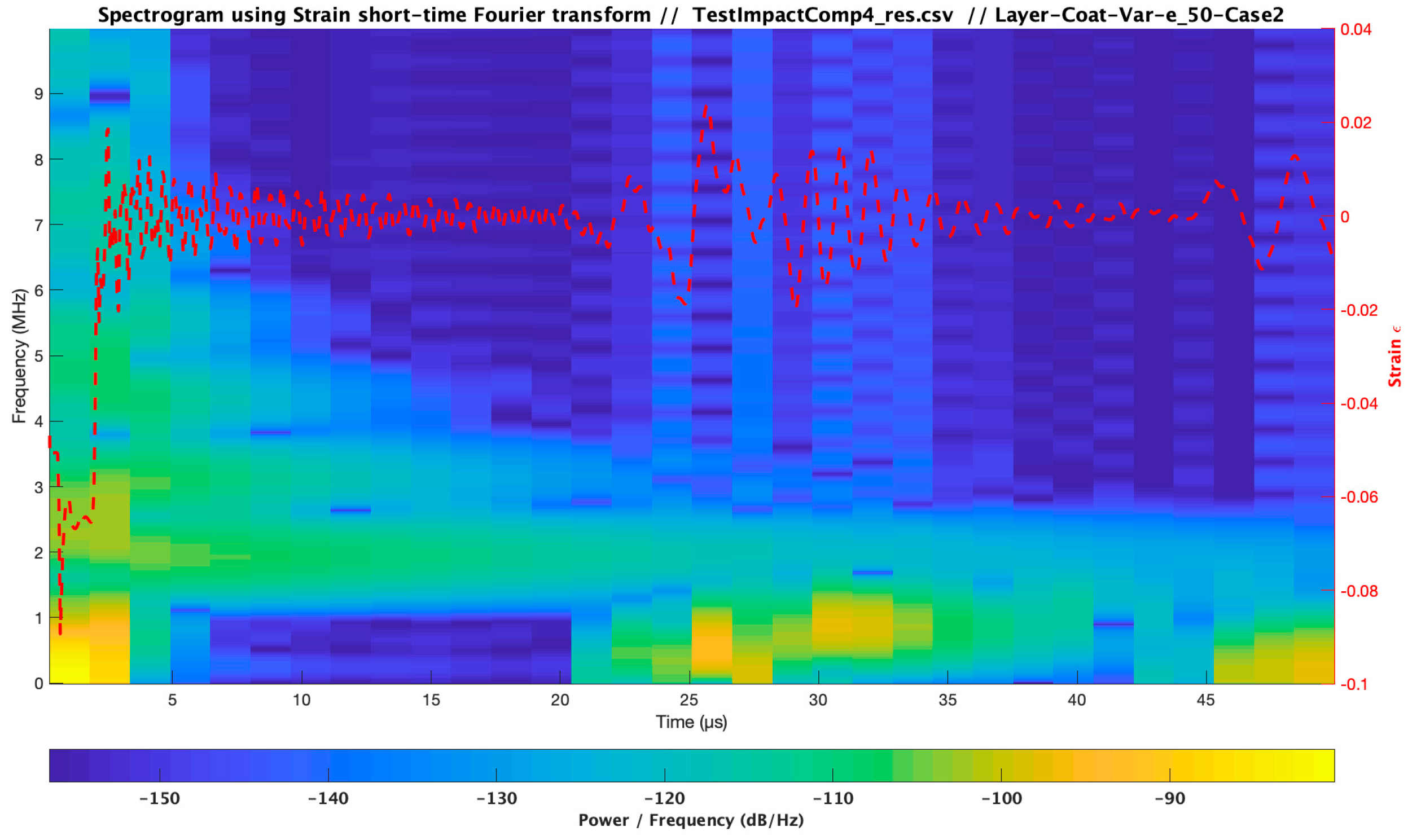
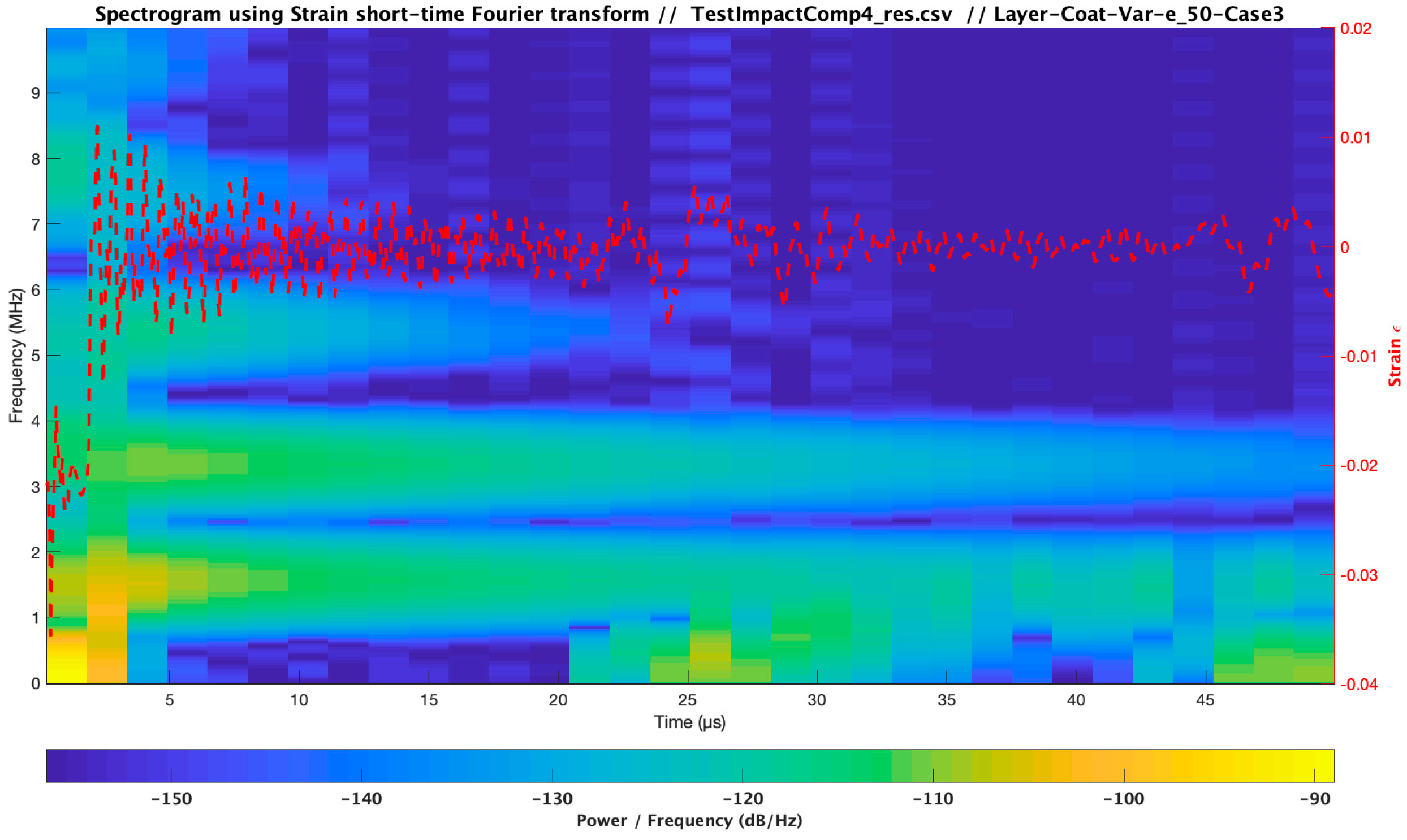
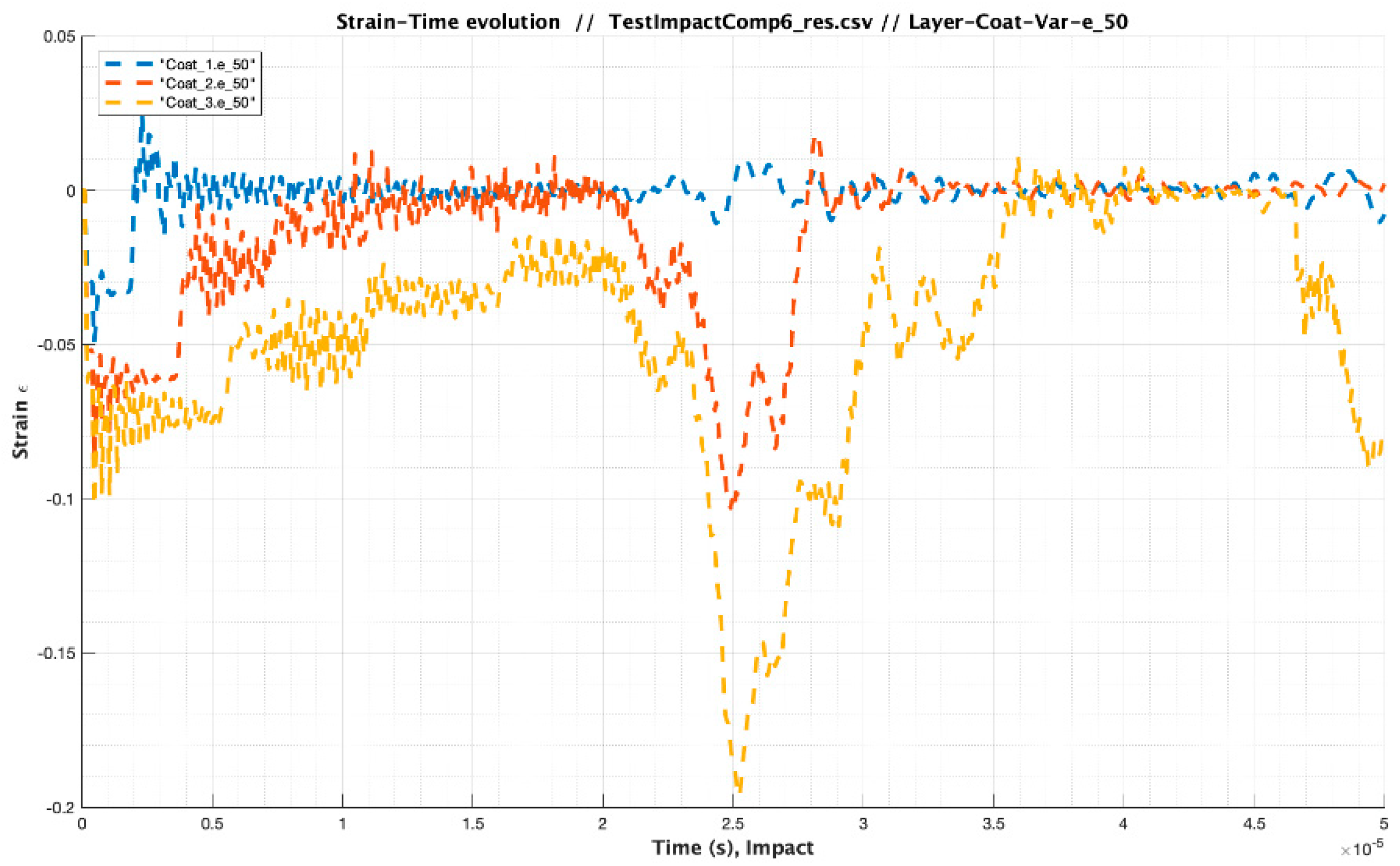
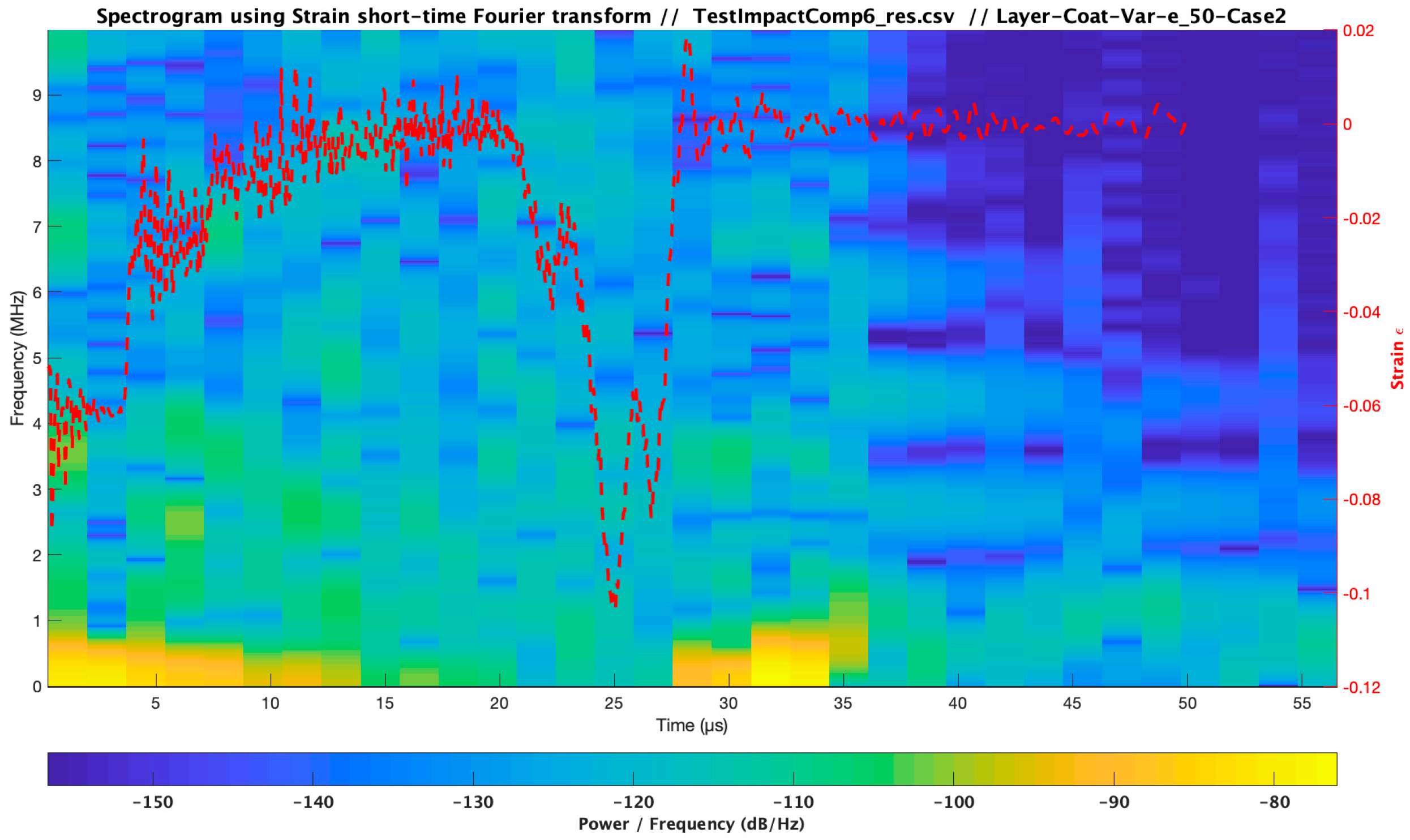
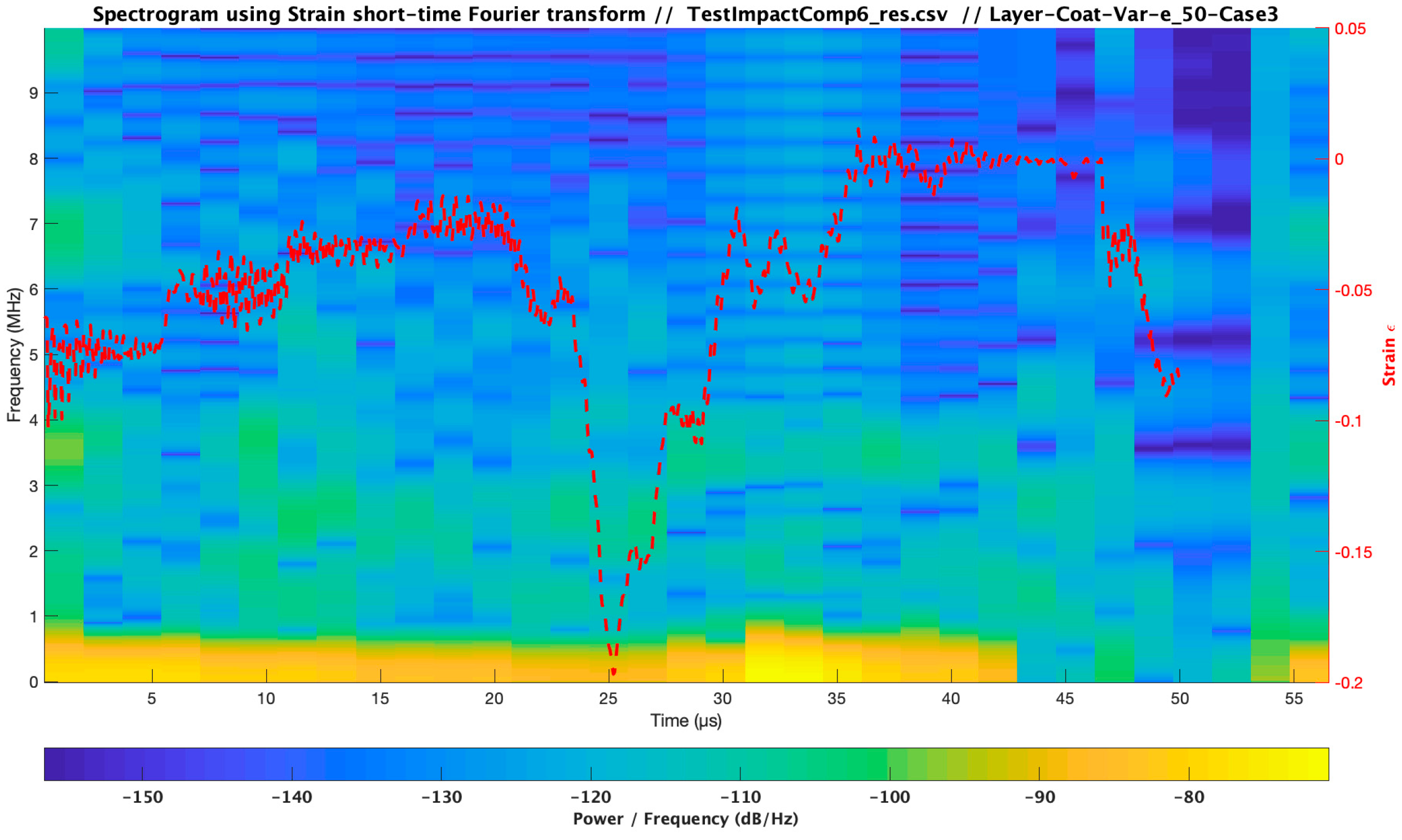
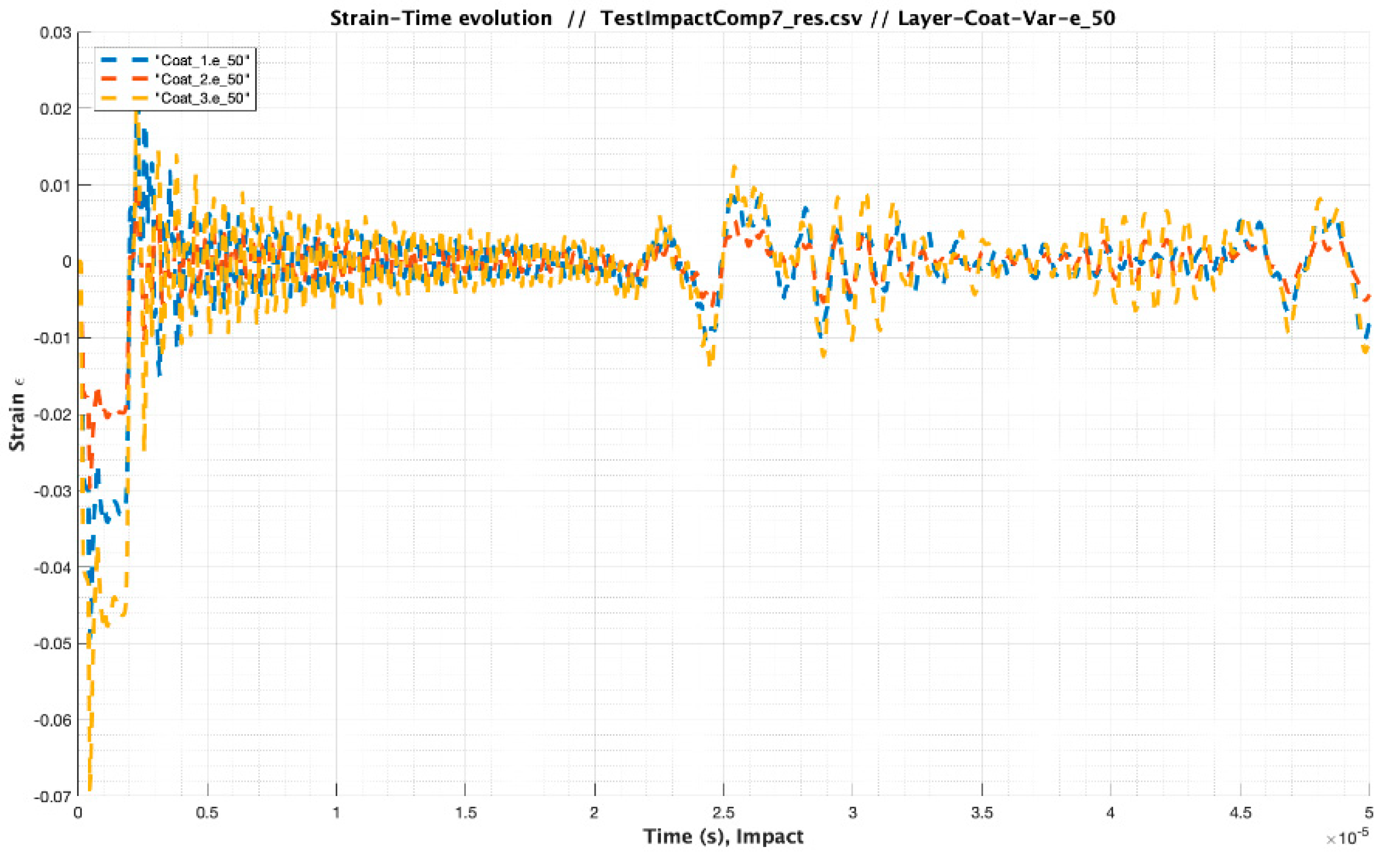
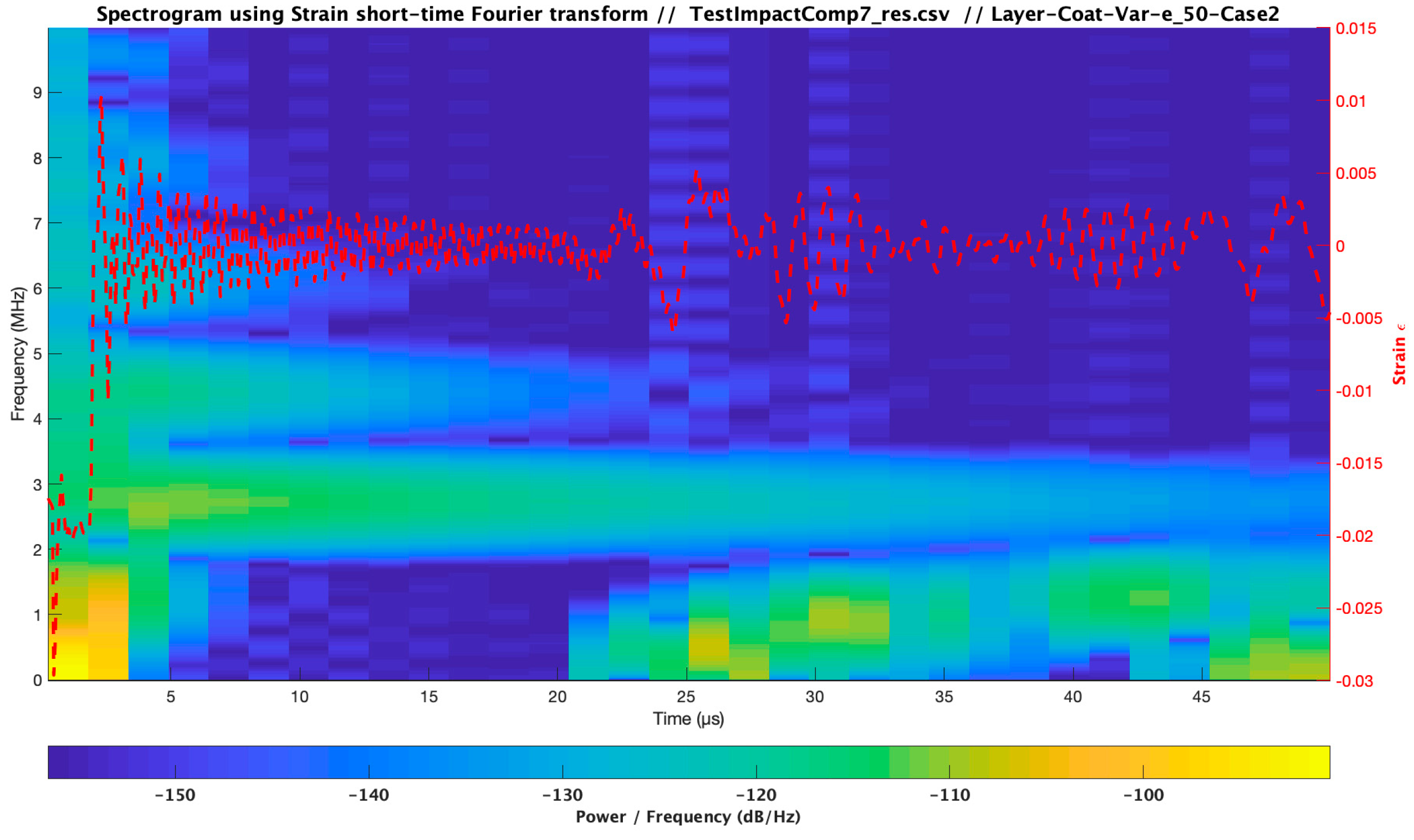
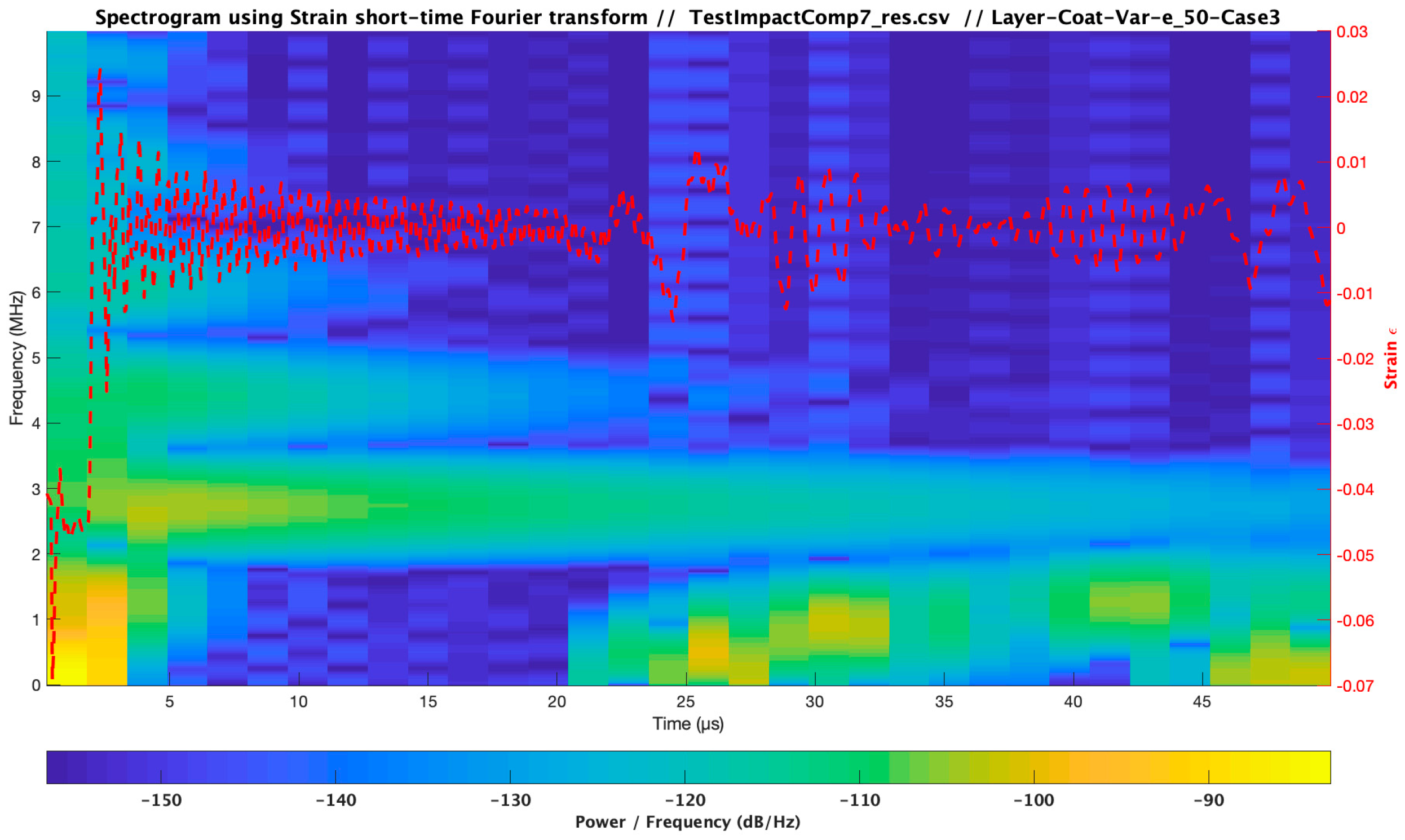
| Material | Modulus E (Pa) /Viscosity (Pa s) | Speed of Sound C (m/s) | Layer Thickness /Droplet Diameter (µm) | Impact Velocity Specimen Vcenter (m/s) |
|---|---|---|---|---|
| Water droplet | 2.19 × 109 | 1480.00 | 2000 | 121 |
| Coating LEP | 3.48 × 109/1.59 | 1733.00 | 500 | 121 |
| Filler | 4.90 × 109/3.183 | 1941.00 | 1000 | 121 |
| Substrate Laminate | 1.10 × 1010 | 2392.00 | 3400 | 121 |
| Test Impact Comparison_3 Case Analysis | Material | Modulus E (Pa) /Viscosity (Pa s) | Speed of Sound C (m/s) | Layer Thickness (µm) | Impact Velocity Specimen Vcenter (m/s) |
|---|---|---|---|---|---|
| Case 1 | Coating LEP | 3.48 × 109/1.59 | 1733.00 | 500 | 121 |
| Case 2 | 3.48 × 109/1.59 | 1733.00 | 4 × 500 | 121 |
| Test Impact Comparison_2 Case Analysis | Material | Modulus E (Pa) /Viscosity (Pa s) | Speed of Sound C (m/s) | Layer Thickness (µm) | Impact Velocity Specimen Vcenter (m/s) |
|---|---|---|---|---|---|
| Case 1 | Coating LEP | 3.48 × 109/1.59 | 1733.00 | 500 | 121 |
| Case 2 | 3.48 × 109/1.59 | 1733.00 | 10 × 500 | 121 | |
| Case 3 | 3.48 × 109/1.59 | 1733.00 | 20 × 500 | 121 | |
| Cases 1,2,3 | Filler | 4.90 × 109/3.183 | 1941.00 | 20 × 1000 | 121 |
| Test Impact Comparison_4 Case Analysis | Material | Modulus E (Pa) /Viscosity (Pa s) | Speed of Sound C (m/s) | Layer Thickness (µm) | Impact Velocity Specimen Vcenter (m/s) |
|---|---|---|---|---|---|
| Case 1 | Coating LEP | 3.48 × 109/1.59 | 1733.00 | 500 | 121 |
| Case 2 | 0.5 × 3.48 × 109/1.59 | 1733.00 | 500 | 121 | |
| Case 3 | 1.5 × 3.48 × 109/1.59 | 1733.00 | 500 | 121 | |
| Cases 1,2,3 | Filler | 4.90 × 109/3.183 | 1941.00 | 20 × 1000 | 121 |
| Test Impact Comparison_4 Case Analysis | Material | Modulus E (Pa) /Viscosity (Pa s) | Speed of Sound C (m/s) | Layer Thickness /Droplet Diameter (µm) | Impact Velocity Specimen Vcenter (m/s) |
|---|---|---|---|---|---|
| Case 1 | Water droplet | 2.19 × 109 | 1480.00 | 2000 | 121 |
| Case 2 | 2.19× 109 | 1480.00 | 2 × 2000 | 121 | |
| Case 3 | 2.19 × 109 | 1480.00 | 3 × 2000 | 121 | |
| Cases 1,2,3 | Filler | 4.90 × 109/3.183 | 1941.00 | 20 × 1000 | 121 |
| Test Impact Comparison_4 Case Analysis | Material | Modulus E (Pa) | Speed of Sound C (m/s) | Droplet Diameter (µm) | Impact Velocity Specimen Vcenter (m/s) |
|---|---|---|---|---|---|
| Case 1 | Water droplet | 2.19 × 109 | 1480.00 | 2000 | 121 |
| Case 2 | 2.19 × 109 | 1480.00 | 2000 | 0.6 × 121 | |
| Case 3 | 2.19 × 109 | 1480.00 | 2000 | 1.4 × 121 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domenech, L.; Renau, J.; Šakalytė, A.; Sánchez, F. Top Coating Anti-Erosion Performance Analysis in Wind Turbine Blades Depending on Relative Acoustic Impedance. Part 1: Modelling Approach. Coatings 2020, 10, 685. https://doi.org/10.3390/coatings10070685
Domenech L, Renau J, Šakalytė A, Sánchez F. Top Coating Anti-Erosion Performance Analysis in Wind Turbine Blades Depending on Relative Acoustic Impedance. Part 1: Modelling Approach. Coatings. 2020; 10(7):685. https://doi.org/10.3390/coatings10070685
Chicago/Turabian StyleDomenech, Luis, Jordi Renau, Asta Šakalytė, and Fernando Sánchez. 2020. "Top Coating Anti-Erosion Performance Analysis in Wind Turbine Blades Depending on Relative Acoustic Impedance. Part 1: Modelling Approach" Coatings 10, no. 7: 685. https://doi.org/10.3390/coatings10070685
APA StyleDomenech, L., Renau, J., Šakalytė, A., & Sánchez, F. (2020). Top Coating Anti-Erosion Performance Analysis in Wind Turbine Blades Depending on Relative Acoustic Impedance. Part 1: Modelling Approach. Coatings, 10(7), 685. https://doi.org/10.3390/coatings10070685






