Transient Electromagnetic Analysis of Multilayer Graphene with Dielectric Substrate Using Marching-on-in-Degree Method
Abstract
:1. Introduction
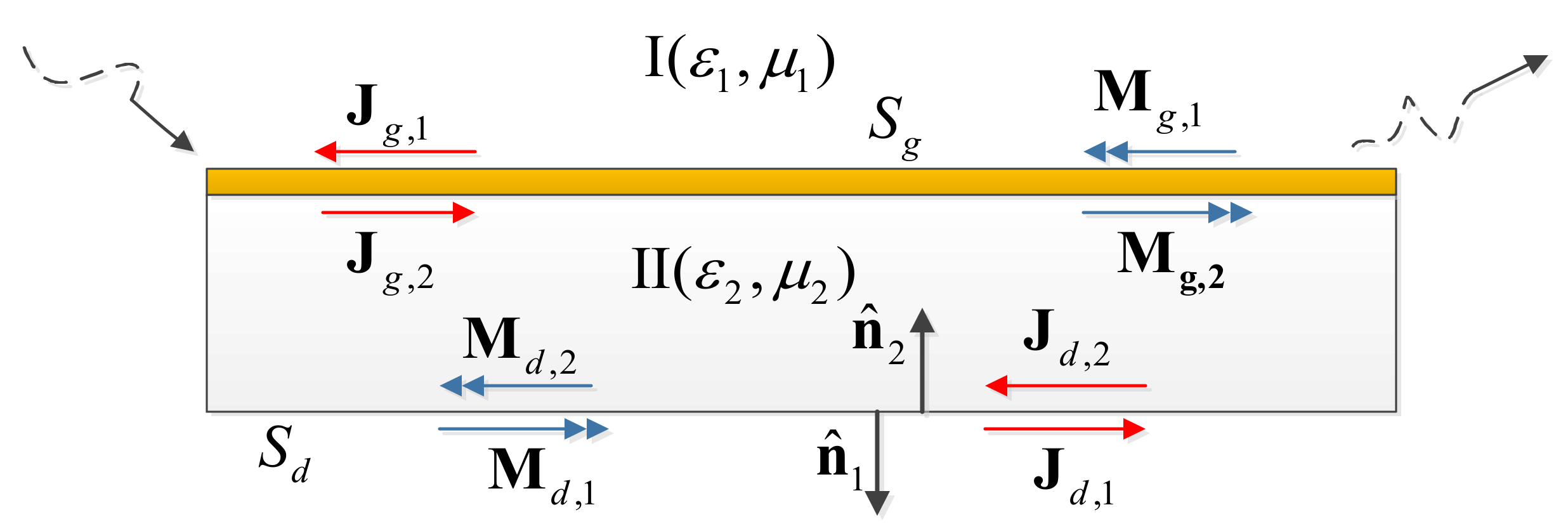
2. Formulation
2.1. Integral Equations
2.2. MOD Scheme
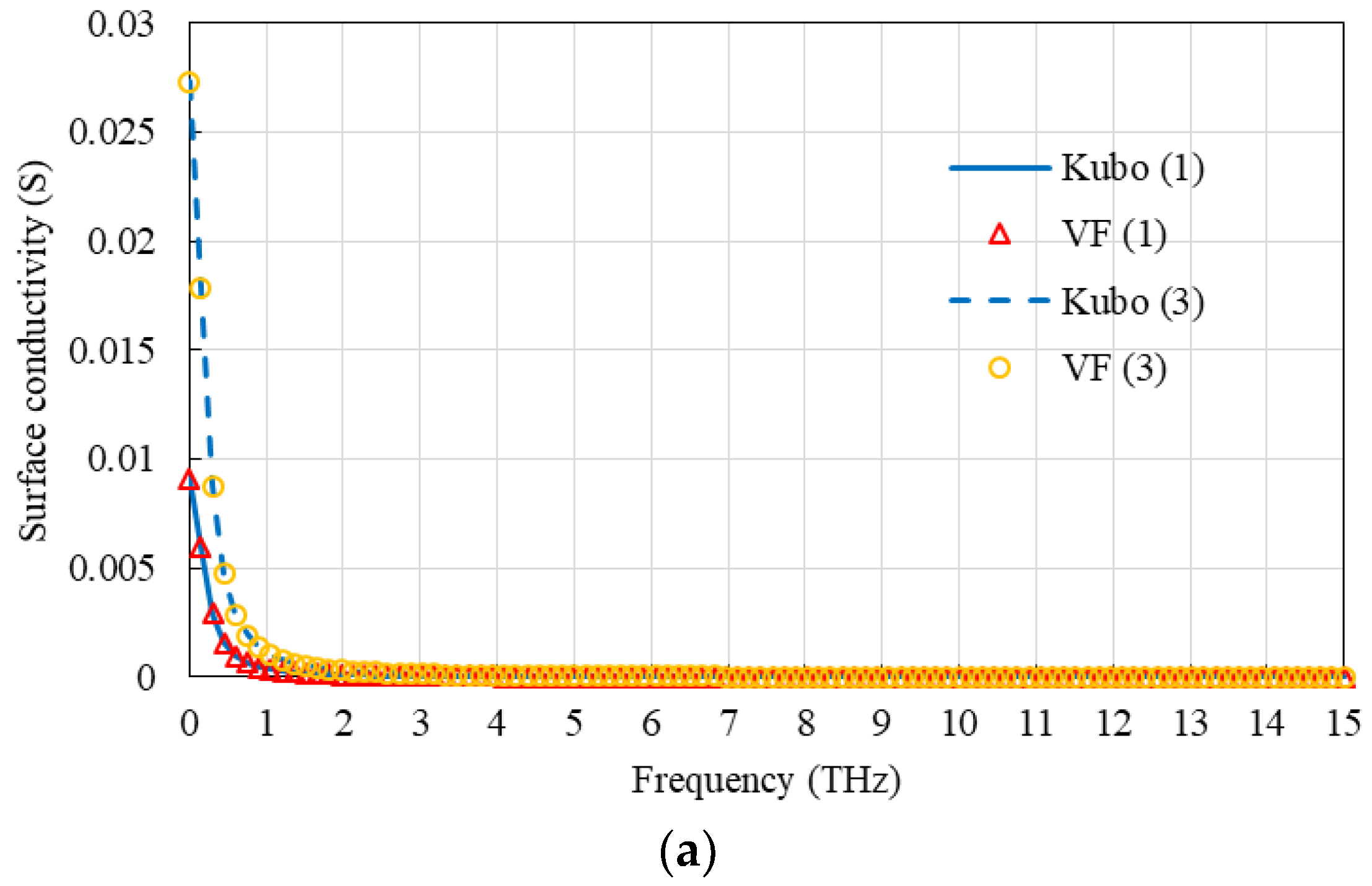
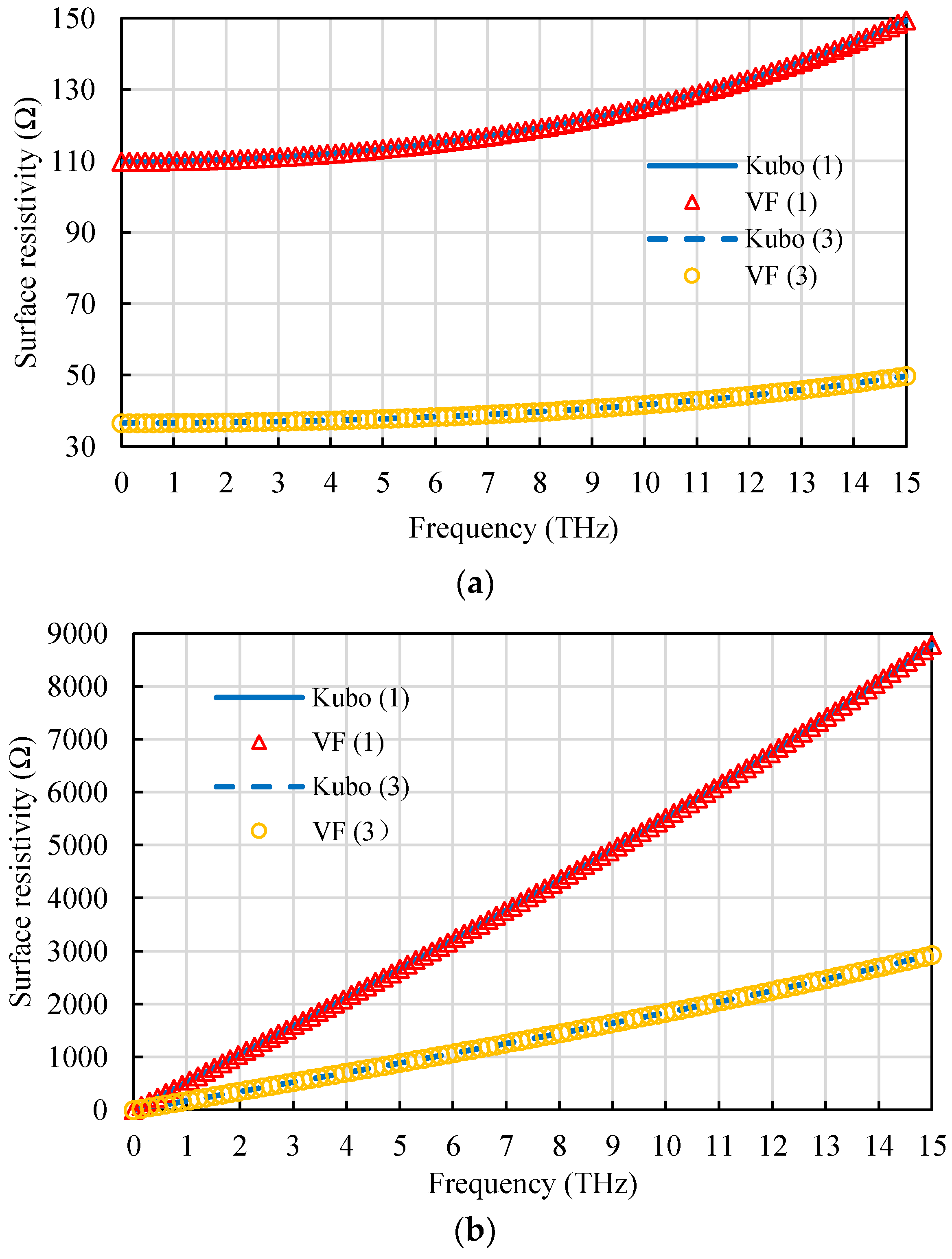
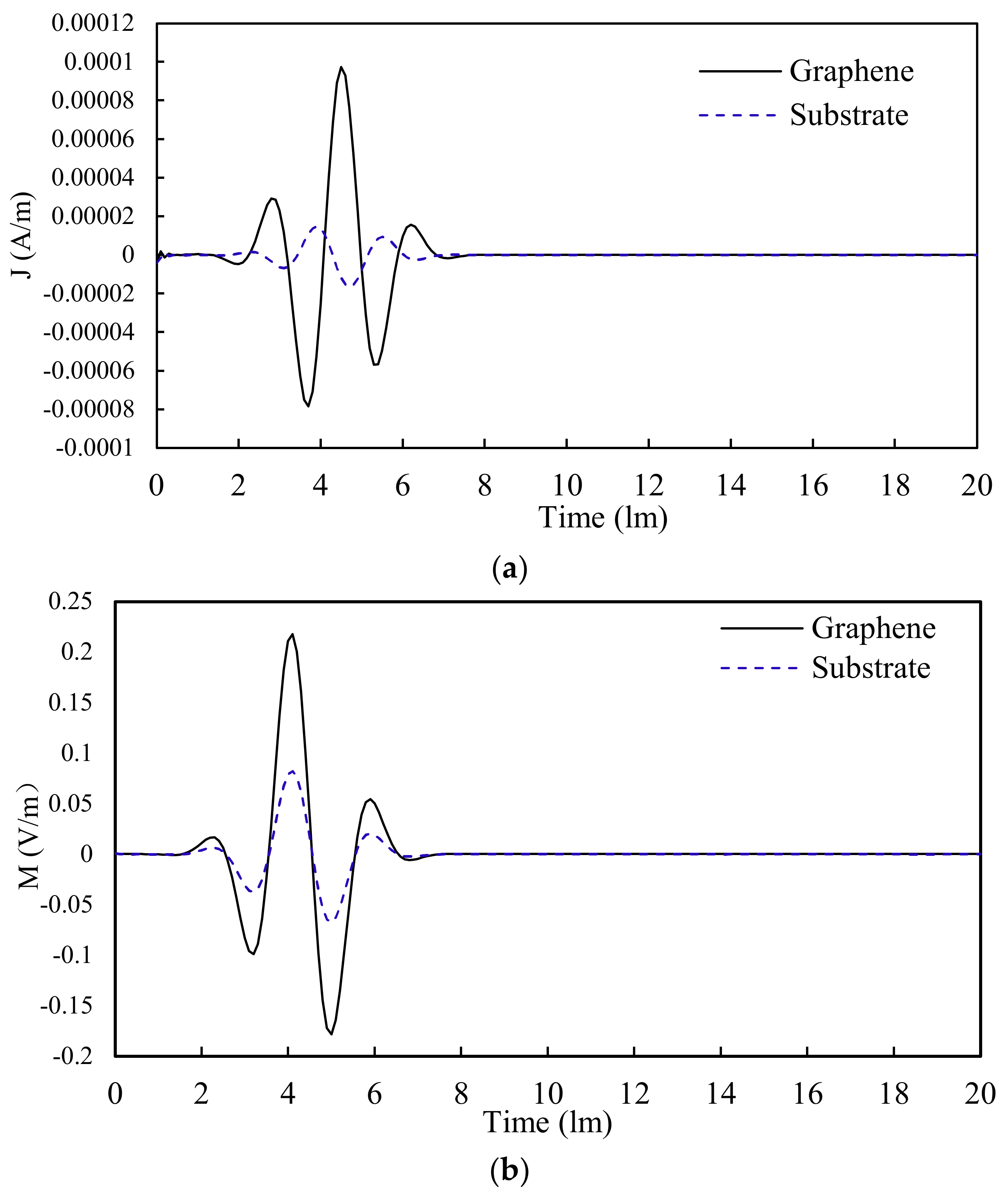
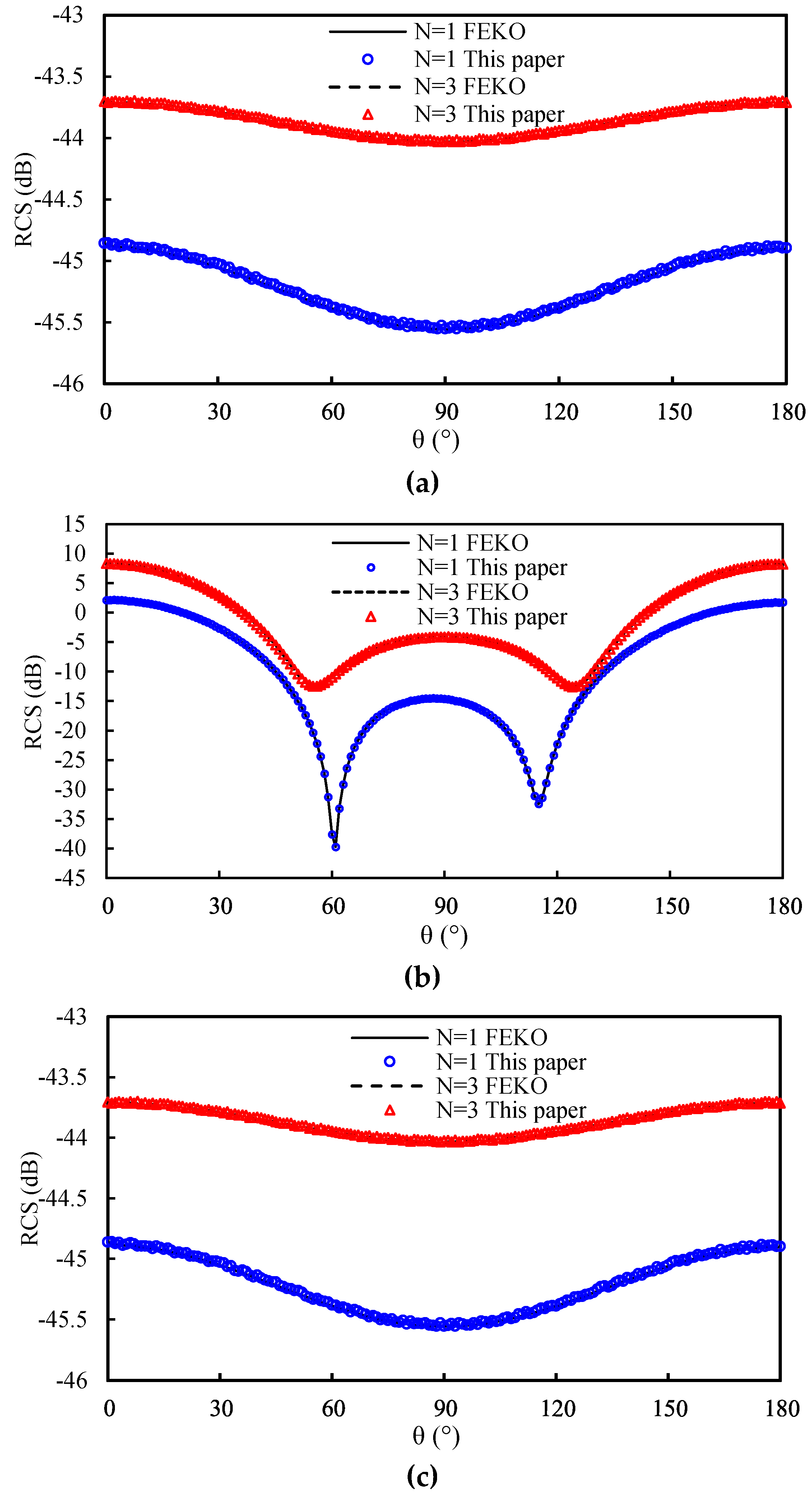
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, Y.T.; Wu, B.; Huang, B.J.; Cheng, Q. Switchable broadband terahertz absorber/reflector enabled by hybrid graphene-gold metasurface. Opt. Express 2017, 25, 7161–7169. [Google Scholar] [CrossRef] [PubMed]
- Vakil, A. Transformation Optics Using Graphene: One-Atom-Thick Optical Devices Based on Graphene. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2012. [Google Scholar]
- Tsai, H.Y.; Hsu, W.H.; Liao, Y.J. Effect of electrode coating with graphene suspension on power generation of microbial fuel cells. Coatings 2018, 8, 243. [Google Scholar] [CrossRef] [Green Version]
- Kyhl, L.; Nielsen, S.F.; Čabo, A.G.; Cassidy, A.; Miwa, J.A.; Hornekær, L. Graphene as an anti-corrosion coating layer. Faraday Discuss. 2015, 180, 495–509. [Google Scholar] [CrossRef] [PubMed]
- Tsai, P.Y.; Chen, T.E.; Lee, Y.L. Development and characterization of anticorrosion and antifriction properties for high performance polyurethane/graphene composite coatings. Coatings 2018, 8, 250. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Zhang, Y.; Wu, Q. Effect of graphene coating on the heat transfer performance of a composite anti-/deicing component. Coatings 2017, 7, 158. [Google Scholar] [CrossRef]
- Gong, F.; Li, H.; Wang, W.; Xia, D.; Liu, Q.; Papavassiliou, D.V.; Xu, Z. Recent advances in graphene-based free-standing films for thermal management: Synthesis, properties, and applications. Coatings 2018, 8, 63. [Google Scholar] [CrossRef] [Green Version]
- Hsu, A.R.; Chien, H.H.; Liao, C.Y.; Lee, C.C.; Tsai, J.H.; Hsu, C.C.; Cheng, I.; Chen, J.Z. Scan-mode atmospheric-pressure plasma jet processed reduced graphene oxides for quasi-solid-state gel-electrolyte supercapacitors. Coatings 2018, 8, 52. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.; Li, Y.; Yi, D.; Zhai, W.T.; Wei, X.C.; Zheng, W.G. Strong flexible polymer/graphene composite films with 3D saw-tooth folding for enhanced and tunable electromagnetic shielding. Carbon 2017, 113, 55–62. [Google Scholar] [CrossRef]
- Qiao, Y.C.; Wang, Y.F.; Tian, H.; Li, M.R.; Jian, J.M.; Wei, Y.H.; Tian, Y.; Wang, D.Y.; Pang, Y.; Geng, X.; et al. Multilayer graphene epidermal electronic skin. ACS Nano 2018, 12, 8839–8846. [Google Scholar] [CrossRef]
- Lin, H.; Pantoja, M.F.; Angulo, L.D.; Alvarez, J.; Martin, R.G.; Garcia, S.G. FDTD modeling of graphene devices using complex conjugate dispersion material model. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 612–614. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Ramahi, O.M. Wideband modeling of graphene using the finite-difference time-domain method. IEEE Trans. Antennas Propag. 2013, 61, 6107–6114. [Google Scholar] [CrossRef]
- Wang, D.W.; Zhao, W.S.; Gu, X.Q.; Chen, W.C.; Yin, W.Y. Wideband modeling of graphene-based structures at different temperatures using hybrid FDTD method. IEEE Trans. Nanotechnol. 2015, 14, 250–258. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.J.; Bağci, H. A resistive boundary condition enhanced DGTD scheme for the transient analysis of graphene. IEEE Trans. Antennas Propag. 2015, 63, 3065–3076. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Jiang, L.J. Modeling of magnetized graphene from microwave to THz range by DGTD with a scalar RBC and an ADE. IEEE Trans. Antennas Propag. 2015, 63, 4458–4467. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.F.; Uysal, I.E.; Li, P.; Ulku, H.A.; Bağci, H. Analysis of electromagnetic wave interactions on graphene sheets using time domain integral equations. In Proceedings of the International ACES Conference, Williamsburg, VA, USA, 22–26 March 2015. [Google Scholar]
- Shi, Y.F.; Li, P.; Uysal, I.E.; Ulku, H.A.; Bağci, H. An MOT-TDIE solver for analyzing transient fields on graphene-based devices. In Proceedings of the IEEE International Symposium Antennas Propagation (APSURSI), Fajardo, Puerto Rico, 26 June–1 July 2016. [Google Scholar]
- Wang, Q.Q.; Liu, H.Z.; Wang, Y.; Jiang, Z.N. Marching-on-in-degree time-domain integral equation solver for transient electromagnetic analysis of graphene. Coatings 2017, 7, 170. [Google Scholar] [CrossRef] [Green Version]
- Abergel, D.S.L.; Russell, A.; Fal’ko, V.I. Visibility of graphene flakes on a dielectric substrate. Appl. Phys. Lett. 2007, 91, 063125. [Google Scholar] [CrossRef] [Green Version]
- Craciun, M.F.; Russo, S.; Yamamoto, M.; Tarucha, S. Tuneable electronic properties in graphene. Nano Today 2011, 6, 42–60. [Google Scholar] [CrossRef] [Green Version]
- McCann, E.; Koshino, M. The electronic properties of bilayer graphene. Rep. Prog. Phys. 2013, 76, 056503. [Google Scholar] [CrossRef]
- Lin, I.T. Optical Properties of Graphene from the THz to the Visible Spectral Region. Master’s Thesis, University of California, Los Angeles, CA, USA, 2012. [Google Scholar]
- Du, W.; Hao, R.; Li, E.P. The study of few-layer graphene based Mach-Zehnder modulator. Opt. Commun. 2014, 323, 49–53. [Google Scholar] [CrossRef]
- Wang, Q.Q.; Shi, Y.; Liu, H.Z. Modeling of multilayer graphene at terahertz with vector fitting method. In Proceedings of the International Conference on Systems and Informatics (ICSAI), Nanjing, China, 10–12 November 2018; pp. 780–784. [Google Scholar]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Gustavsen, B. Improving the pole relocating properties of vector fitting. IEEE Trans. Power Deliv. 2006, 21, 1587–1592. [Google Scholar] [CrossRef]
- Deschrijver, D.; Gustavsen, B.; Dhaene, T. Advancements in iterative methods for rational approximation in the frequency domain. IEEE Trans. Power Deliv. 2007, 22, 1633–1642. [Google Scholar] [CrossRef]
- Pordanjani, I.R.; Xu, W. Improvement of vector fitting by using a new method for selection of starting poles. Electr. Power Syst. Res. 2014, 107, 206–212. [Google Scholar] [CrossRef]
- Jung, B.H.; Sarkar, T.K.; Chung, Y.S. Solution of time domain PMCHW formulation for transient electromagnetic scattering from arbitrarily shaped 3-D dielectric objects. Prog. Electromagn. Res. 2004, 45, 291–312. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.H.; Xia, M.Y.; Chan, C.H. Time domain integral equation approach for analysis of transient responses by metallic-dielectric composite bodies. Prog. Electromagn. Res. 2008, 87, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Mei, Z.C. Solving Time Domain Scattering and Radiation Problems in A Marching-on-in-Degree Technique for Method of Moment. Ph.D. Thesis, Syracuse University, Syracuse, NY, USA, 2014. [Google Scholar]
- Zhu, M.D.; Sarkar, T.K.; Chen, H. A stabilized marching-on-in-degree scheme for the transient solution of the electric field integral equation. IEEE Trans. Antennas Propag. 2019, 67, 3232–3240. [Google Scholar] [CrossRef]
- Zhu, M.D.; Sarkar, T.K.; Chen, H.; Wu, Y.Z. On the stability of time-domain magnetic field integral equation using Laguerre functions. IEEE Trans. Antennas Propag. 2019, 67, 3939–3947. [Google Scholar] [CrossRef]
- Chen, Q.; Lu, M.; Michielssen, E. Integral equation-based analysis of transient scattering from surfaces with an impedance boundary condition. Microw. Opt. Technol. Lett. 2004, 42, 213–220. [Google Scholar] [CrossRef]
- Shanker, B.; Lu, M.; Yuan, J.; Michielssen, E. TDIE analysis of scattering from composite bodies via exact evaluation of radiation fields. IEEE Trans. Antennas Propag. 2009, 57, 1506–1520. [Google Scholar] [CrossRef]
- Gibson, W.C. The Method of Moments in Electromagnetics, 2nd ed.; Chapman and Hall/CRC, Taylor and Francis Group: New York, NY, USA, 2014. [Google Scholar]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles, 1st ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]



| v | av′ | dv′ |
|---|---|---|
| 1 | −0.0131 × 1014 | 3.5680 × 1010 |
| 2, 3 | (–0.0132 ± j5.1838) × 1014 | 5.1373 × 1010 ± j9.1549 × 105 |
| v | av | dv |
|---|---|---|
| 1 | −1.3983 × 1015 | 1.0143 × 1017 |
| 2, 3 | (–0.0026 ± j0.2995) × 1015 | (1.2579 ± j0.0161) × 1018 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Song, Z.; Zhu, J.; Liu, H. Transient Electromagnetic Analysis of Multilayer Graphene with Dielectric Substrate Using Marching-on-in-Degree Method. Coatings 2020, 10, 718. https://doi.org/10.3390/coatings10080718
Wang Q, Song Z, Zhu J, Liu H. Transient Electromagnetic Analysis of Multilayer Graphene with Dielectric Substrate Using Marching-on-in-Degree Method. Coatings. 2020; 10(8):718. https://doi.org/10.3390/coatings10080718
Chicago/Turabian StyleWang, Quanquan, Zukun Song, Jian Zhu, and Huazhong Liu. 2020. "Transient Electromagnetic Analysis of Multilayer Graphene with Dielectric Substrate Using Marching-on-in-Degree Method" Coatings 10, no. 8: 718. https://doi.org/10.3390/coatings10080718





