Residual Stresses in Soft Magnetic FeTiB and FeZrN Films Obtained by Magnetron Deposition
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
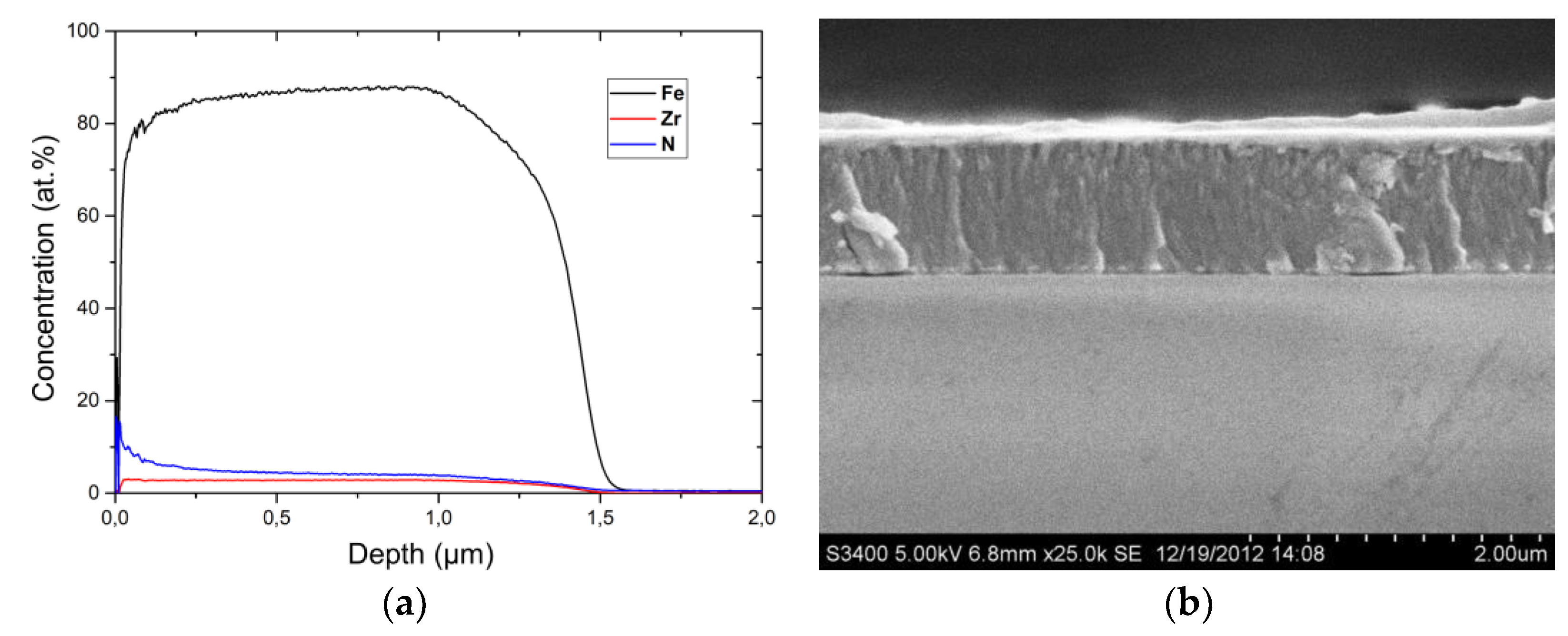
3.1. Chemical Composition of the Films
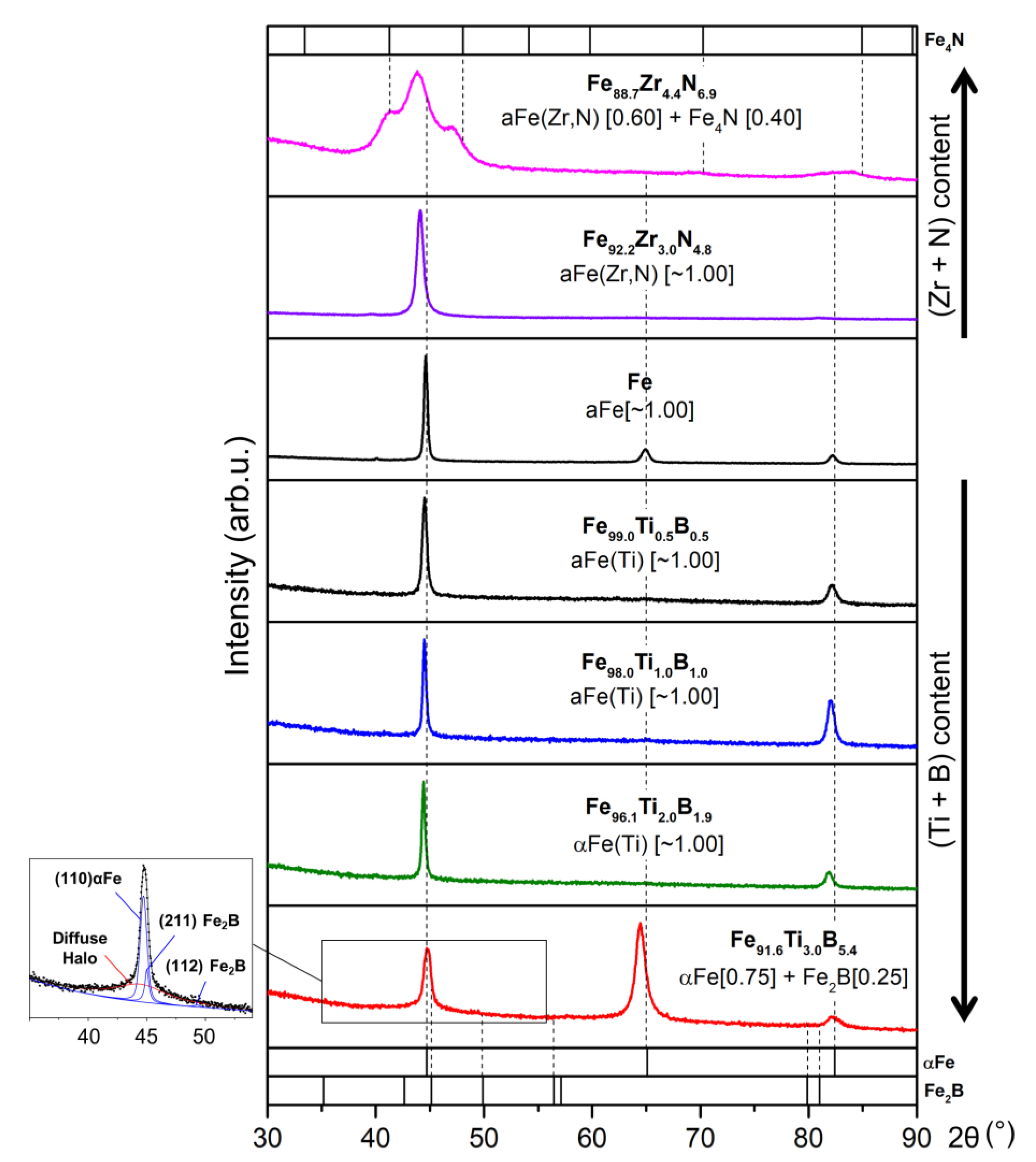
3.2. Phase Composition of the Deposited Films
3.3. Phase Composition of the Annealed Films
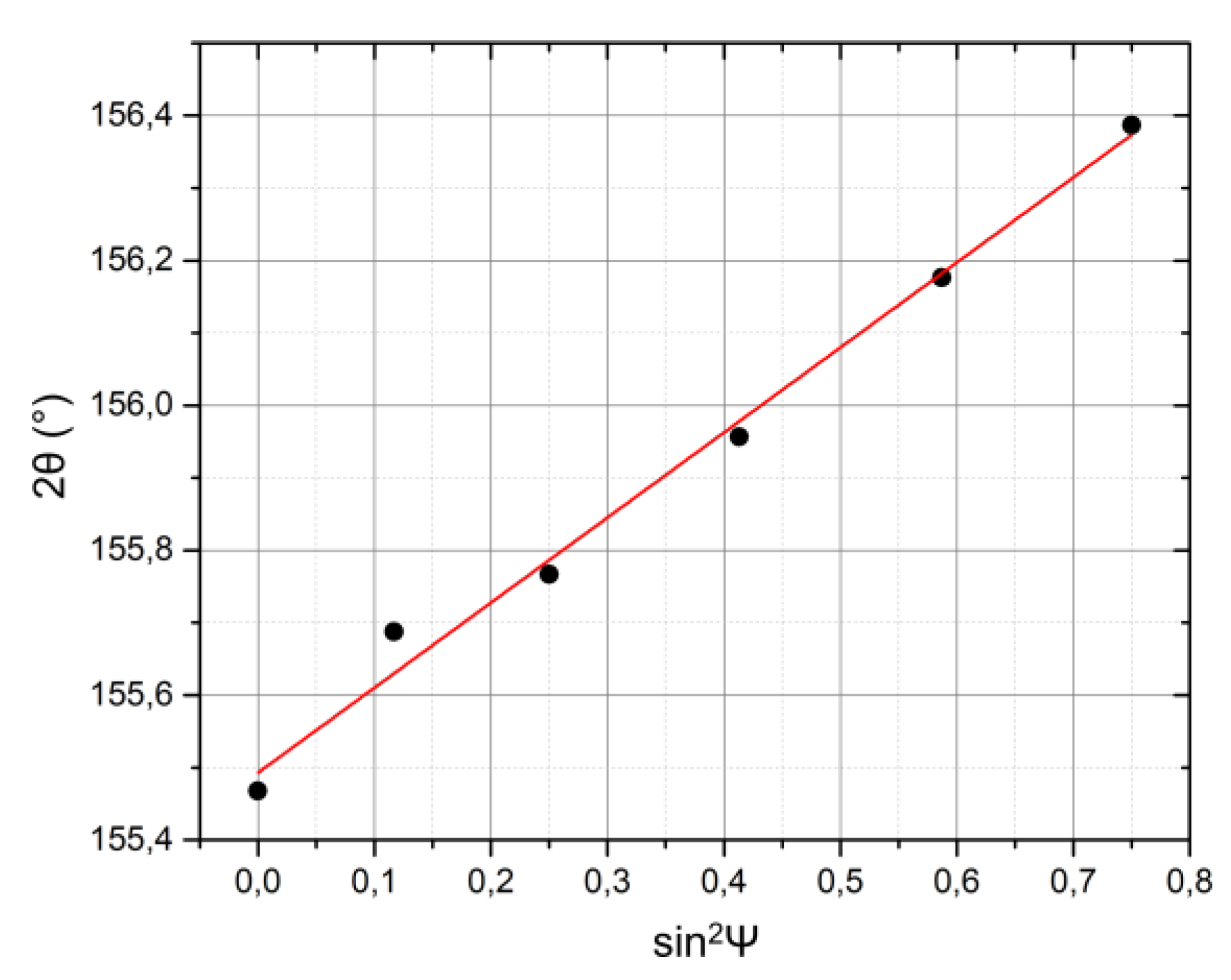
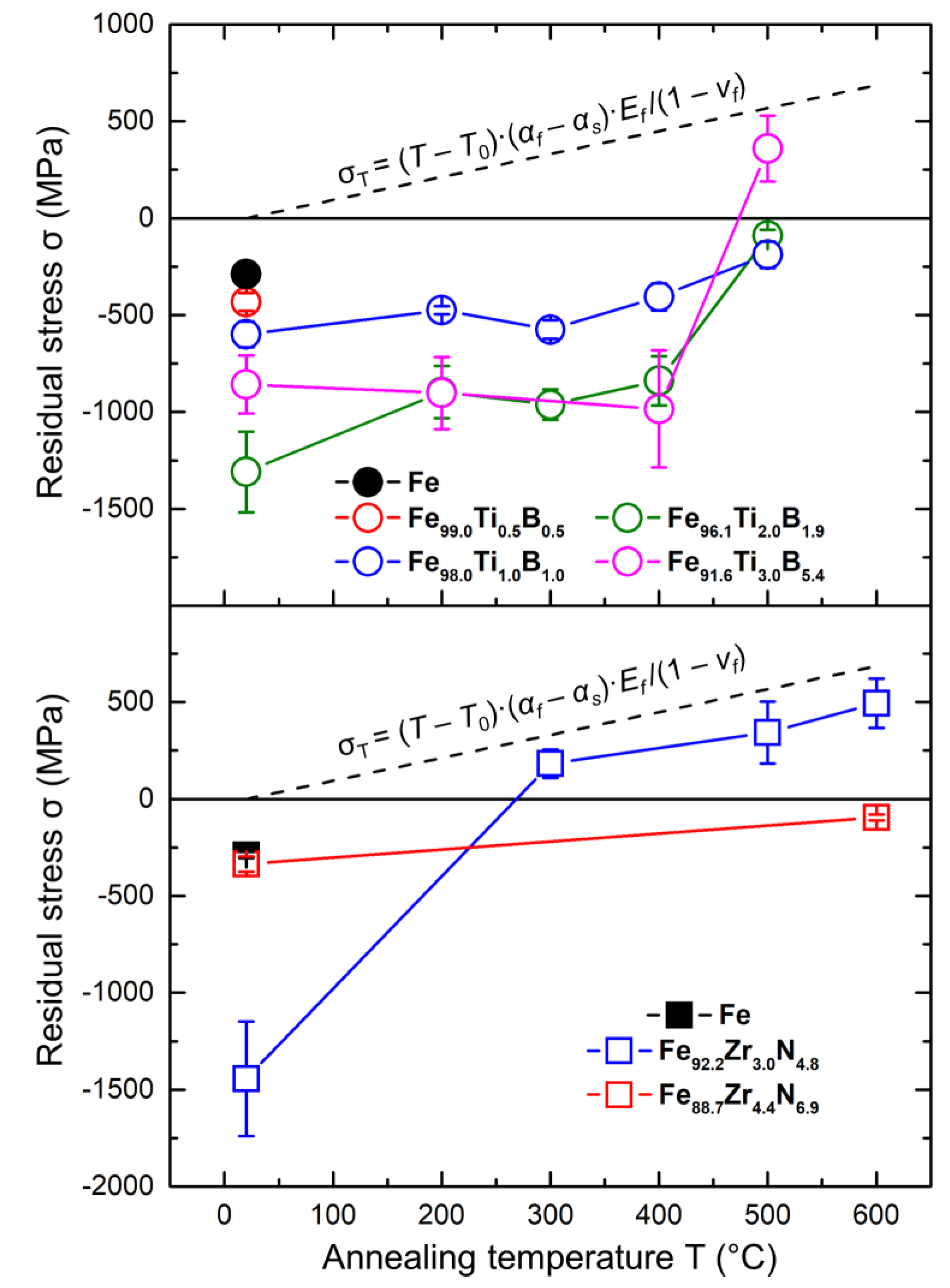
3.4. Residual Stresses in the Films
4. Conclusions
- The phase and structural states and the residual stresses of the FeTiB and FeZrN films of various compositions, which were prepared by magnetron deposition on glass substrates and subsequent 1-h annealing at temperatures of 200–600 °C, were studied by X-ray diffraction.
- Depending on the content of alloying elements, Ti and B or Zr and N, in the Fe-based films, a single-phase (bcc αFe(Ti) and αFe(Zr,N) solid solutions) or two-phase (bcc solid solution + Fe2B boride or Fe4N nitride) nanocrystalline structure are formed during deposition. The grain size varies (2–46 nm) in accordance with the chemical and phase compositions of the films. All films exhibit the high level of microstrains in grains (~0.2–0.3% for the bcc phase; ~0.4–0.7% for Fe2B and Fe4N). The structure formed upon deposition is stable during heating.
- The significant compressive stresses (up to ~1.5 GPa) are formed in all deposited films, which are associated with the formation of αFe-based supersaturated solid solutions in the films, phases with markedly different lattice parameters and unit-cell volumes, and with the high microstrains in the nanograins of the phases as well. As the annealing temperature increases, the values of the compressive stresses decrease, gradually approaching zero, and after that, compressive stresses change into tensile ones, which are related to the different thermal expansion coefficients of iron and glass.
- The heat treatment is the efficient way in order to improve the soft magnetic properties of the studied class of film materials produced by magnetron deposition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sheftel, E.N.; Harin, E.V.; Tedzhetov, V.A.; Kiryukhantsev-Korneev, P.V.; Levashov, E.A.; Perov, N.S.; Titova, A.O. Magnetic structure and magnetic properties of nanocrystalline and amorphous Fe-Zr-N films. Phys. B Condens. Matter 2016, 494, 13–19. [Google Scholar] [CrossRef]
- Sheftel, E.N.; Tedzhetov, V.A.; Harin, E.V.; Kiryukhantsev-Korneev, F.V.; Usmanova, G.S. High-induction nanocrystalline soft magnetic FeXTiYBZ films prepared by magnetron sputtering. Phys. Status Solidi C 2016, 13, 965–971. [Google Scholar] [CrossRef]
- Bunshah, R.F. Handbook of Deposition Technologies for Films and Coatings, 2nd ed.; Noyes Publications: Park Ridge, NJ, USA, 1994. [Google Scholar]
- Detor, A.J.; Hodge, A.M.; Chason, E.; Wang, Y.; Xu, H.; Conyers, M.; Nikroo, A.; Hamza, A. Stress and microstructure evolution in thick sputtered films. Acta Mater. 2009, 57, 2055–2065. [Google Scholar] [CrossRef]
- Wang, H.J.; Deng, H.A.; Chiang, S.Y.; Su, Y.F.; Chiang, K.N. Development of a process modeling for residual stress assessment of multilayer thin film structure. Thin Solid Film. 2015, 584, 146–153. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, H.; Zhang, R.; Pei, Y.; Fang, D. Measuring residual stress and its influence on properties of porous ZrO2/(ZrO2+Ni) ceramics. Mater. Sci. Eng. A 2015, 622, 82–90. [Google Scholar] [CrossRef] [Green Version]
- Injeti, S.S.; Annabattula, R.K. Extending Stoney’s equation to thin, elastically anisotropic substrates and bilayer films. Thin Solid Film. 2016, 598, 252–259. [Google Scholar] [CrossRef]
- Bemporad, E.; Brisotto, M.; Depero, L.E.; Gelfi, M.; Korsunsky, A.M.; Lunt, A.J.G.; Sebastiani, M. A critical comparison between XRD and FIB residual stress measurement techniques in thin films. Thin Solid Film. 2014, 572, 224–231. [Google Scholar] [CrossRef]
- Sheftel’, E.N.; Tedzhetov, V.A.; Kiryukhantsev-Korneev, F.V.; Harin, E.V.; Usmanova, G.S.; Zhigalina, O.M. Investigation of the Processes of the Formation of a Nonequilibrium Phase-Structural State in FeTiB Films Obtained by Magnetron Sputtering. Russ. J. Non-Ferr. Met. 2020, 61, 753–761. (in press). [Google Scholar] [CrossRef]
- Shelekhov, E.V.; Sviridova, T.A. Programs for X-ray analysis of polycrystals. Metal Sci. Heat Treat. 2000, 42, 309–313. [Google Scholar] [CrossRef]
- Noyan, I.C.; Cohen, J.B. Residual Stress: Measurement by Diffraction and Interpretation; Springer-Verlag: New York, NY, USA, 1987. [Google Scholar]
- Hanabusa, T.; Suzuki, K.; Akita, K. Standard Method for X-ray Study; The Society of Materials Science: Kyoto, Japan, 2005. [Google Scholar]
- Carneiro, J.O.; Teixeira, V.; Azevedo, S. Residual Stresses in Thin Films Evaluated by Different Experimental Techniques. In Encyclopedia of Thermal Stresses, 1st ed.; Hetnarski, R.B., Ed.; Springer: Amsterdam, The Netherlands, 2014; Volume 1, pp. 4222–4231. [Google Scholar] [CrossRef]
- Zeman, H.; Musil, J.; Vlček, J.; Mayrhofer, P.H.; Mitterer, C. Thermal annealing of sputtered Al-Si-Cu-N films. Vacuum 2003, 72, 21–28. [Google Scholar] [CrossRef]
- Sheftel, E.N.; Ivanov, A.N.; Usmanova, G.S. X-ray diffraction study of the evolution of phase and structural state and macroscopic stress during annealing of soft magnetic Fe95-xZr5Nx films prepared by ion-plasma deposition. Crystallogr. Rep. 2014, 59, 266–275. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Kirby, R.K.; Taylor, R.E.; Desai, P.D. Thermal Expansion–Metallic Elements and Alloys. In Thermophysical Properties of Matter—The TPRC Data Series; IFI/Plenum Press: New York, NY, USA, 1975; Volume 12. [Google Scholar]
- Touloukian, Y.S.; Kirby, R.K.; Taylor, R.E.; Lee, T.R. Thermal Expansion–Nonmetallic Solids. In Thermophysical Properties of Matter–the TPRC Data Series; IFI/Plenum Press: New York, NY, USA, 1977; Volume 13. [Google Scholar]
| Film | Tann, °C | νi Phase | a/c, Å | D, nm | ε, % |
|---|---|---|---|---|---|
| Fe | As-dep. | ~1.00 αFe | 2.872 | 45.6 | 0.268 |
| Fe99.0Ti0.5B0.5 | As-sput. | ~1.00 αFe(Ti) | 2.879 | 24.4 | 0.247 |
| - | 200 | ~1.00 αFe(Ti) | 2.877 | 24.7 | 0.248 |
| - | 300 | ~1.00 αFe(Ti) | 2.874 | 26.1 | 0.256 |
| - | 400 | ~1.00 αFe | 2.866 | 31.2 | 0.264 |
| - | 500 | ~1.00 αFe | 2.866 | 32.4 | 0.250 |
| Fe98.0Ti1.0B1.0 | As-sput. | ~1.00 αFe(Ti) | 2.879 | 35.5 | 0.237 |
| - | 200 | ~1.00 αFe(Ti) | 2.880 | 35.9 | 0.247 |
| - | 300 | ~1.00 αFe(Ti) | 2.876 | 38.2 | 0.242 |
| - | 400 | ~1.00 αFe(Ti) | 2.879 | 36.4 | 0.230 |
| - | 500 | ~1.00 αFe(Ti) | 2.875 | 34.3 | 0.279 |
| Fe96.1Ti2.0B1.9 | As-sput. | ~1.00 αFe(Ti) | 2.885 | 34.1 | 0.205 |
| - | 200 | ~1.00 αFe(Ti) | 2.883 | 38.5 | 0.229 |
| - | 300 | ~1.00 αFe(Ti) | 2.879 | 30.7 | 0.187 |
| - | 400 | ~1.00 αFe(Ti) | 2.878 | 27.4 | 0.216 |
| - | 500 | ~1.00 αFe(Ti) | 2.871 | 34.5 | 0.239 |
| Fe91.6Ti3.0B5.4 | As-sput. | 0.75 αFe 0.25 Fe2B | 2.890 – | 8.2 22.7 | 0.160 0.399 |
| - | 200 | 0.69 αFe 0.31 Fe2B | 2.890 – | 8.4 – | 0.365 – |
| - | 300 | 0.76 αFe 0.24 Fe2B | 2.892 – | 8.3 – | 0.177 – |
| - | 400 | 0.72 αFe 0.28 Fe2B | 2.889 – | 8.4 – | 0.127 – |
| - | 500 | 0.80 αFe 0.20 Fe2B | 2.874 5.114/4.229 | 8.3 44.7 | 0.203 0.331 |
| Fe92.2Zr3.0N4.8 | As-sput. | ~1.00 αFe(Zr,N) | 2.904 | 13.6 | 0.247 |
| - | 300 | ~1.00 αFe(Zr,N) | 2.900 | 14.0 | 0.301 |
| - | 400 | ~1.00 αFe(Zr,N) | 2.898 | 14.8 | 0.270 |
| - | 500 | ~1.00 αFe(Zr,N) | 2.883 | 18.4 | 0.300 |
| - | 600 | ~1.00 αFe(Zr,N) | 2.877 | 21.4 | 0.302 |
| Fe88.7Zr4.4N6.9 | As-sput. | 0.58 αFe(Zr,N) 0.42 Fe4N | 2.887 3.818 | 2.0 5.5 | 0.066 0.745 |
| - | 400 | 0.61 αFe(Zr,N) 0.39 Fe4N | 2.887 3.821 | 2.0 6.7 | 0.093 0.635 |
| - | 500 | 0.51 αFe(Zr,N) 0.49 Fe4N | 2.872 3.793 | 2.9 8.2 | 0.131 0.482 |
| - | 600 | 0.28 αFe(Zr,N) 0.57 Fe3N 0.15 ZrO2 | 2.864 – 5.087 | 14.6 3.4 3.7 | 0.038 0.164 0.379 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tedzhetov, V.A.; Sheftel, E.N.; Harin, E.V.; Kiryukhantsev-Korneev, P.V. Residual Stresses in Soft Magnetic FeTiB and FeZrN Films Obtained by Magnetron Deposition. Coatings 2021, 11, 34. https://doi.org/10.3390/coatings11010034
Tedzhetov VA, Sheftel EN, Harin EV, Kiryukhantsev-Korneev PV. Residual Stresses in Soft Magnetic FeTiB and FeZrN Films Obtained by Magnetron Deposition. Coatings. 2021; 11(1):34. https://doi.org/10.3390/coatings11010034
Chicago/Turabian StyleTedzhetov, Valentin A., Elena N. Sheftel, Eugene V. Harin, and Philipp V. Kiryukhantsev-Korneev. 2021. "Residual Stresses in Soft Magnetic FeTiB and FeZrN Films Obtained by Magnetron Deposition" Coatings 11, no. 1: 34. https://doi.org/10.3390/coatings11010034
APA StyleTedzhetov, V. A., Sheftel, E. N., Harin, E. V., & Kiryukhantsev-Korneev, P. V. (2021). Residual Stresses in Soft Magnetic FeTiB and FeZrN Films Obtained by Magnetron Deposition. Coatings, 11(1), 34. https://doi.org/10.3390/coatings11010034







