Homogeneity Assessment of Asphalt Concrete Base in Terms of a Three-Dimensional Air-Launched Ground Penetrating Radar
Abstract
:1. Introduction
2. Principle of Three-Dimensional GPR
2.1. 3D GPR Antenna
2.2. Step-Frequency
3. Test Methods
3.1. GPR Data Acquisition and Processing
3.2. Three Calculation Methods of Dielectric Constants
3.2.1. The Coring Method
3.2.2. The Reflection Amplitudes Method
3.2.3. Common-Mid-Point (CMP) Method of 3D GPR
3.3. Calculation Methods of Thickness
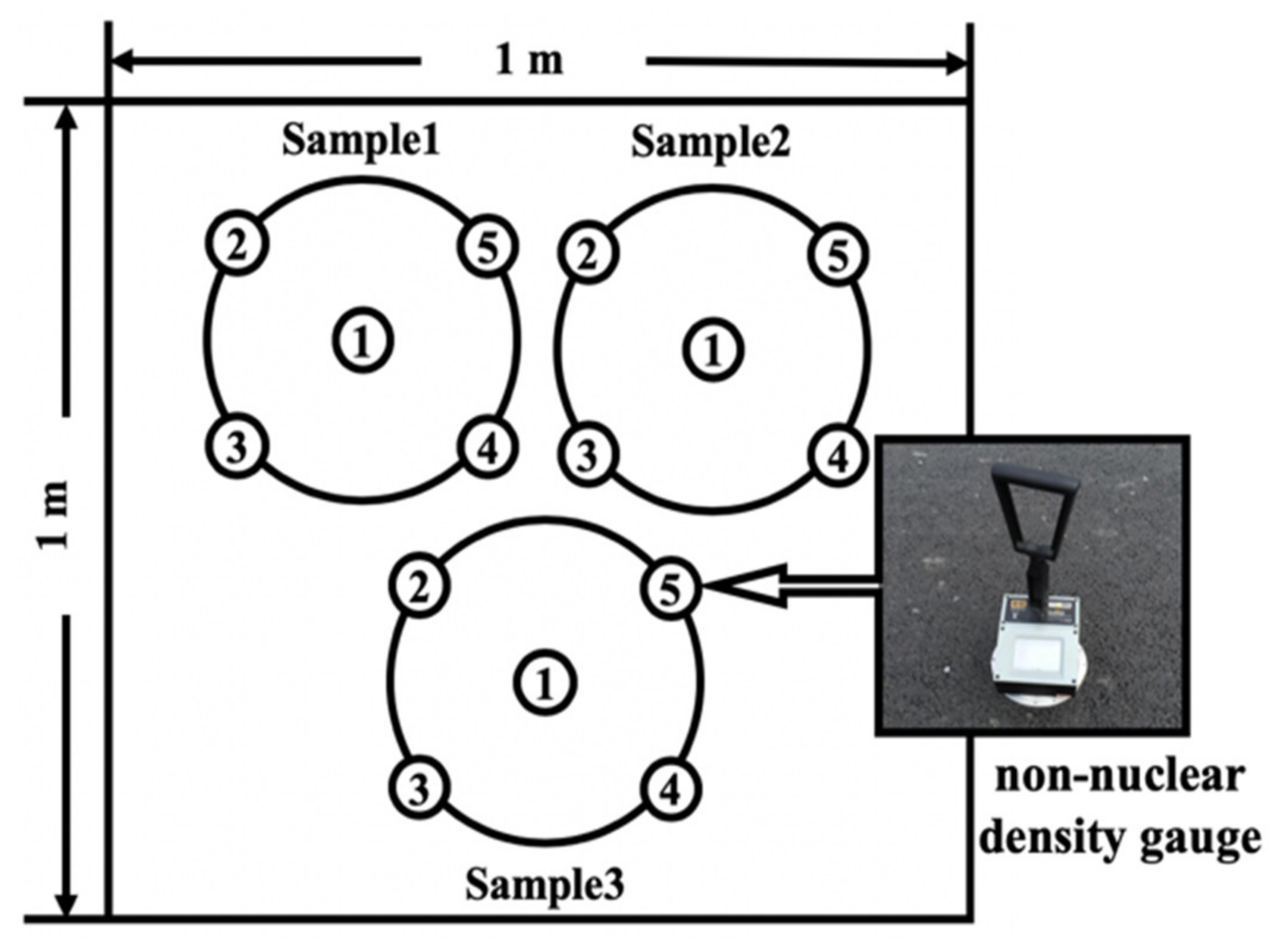
3.4. Calculation Methods of Density
3.5. Calibration Method of Actual Density
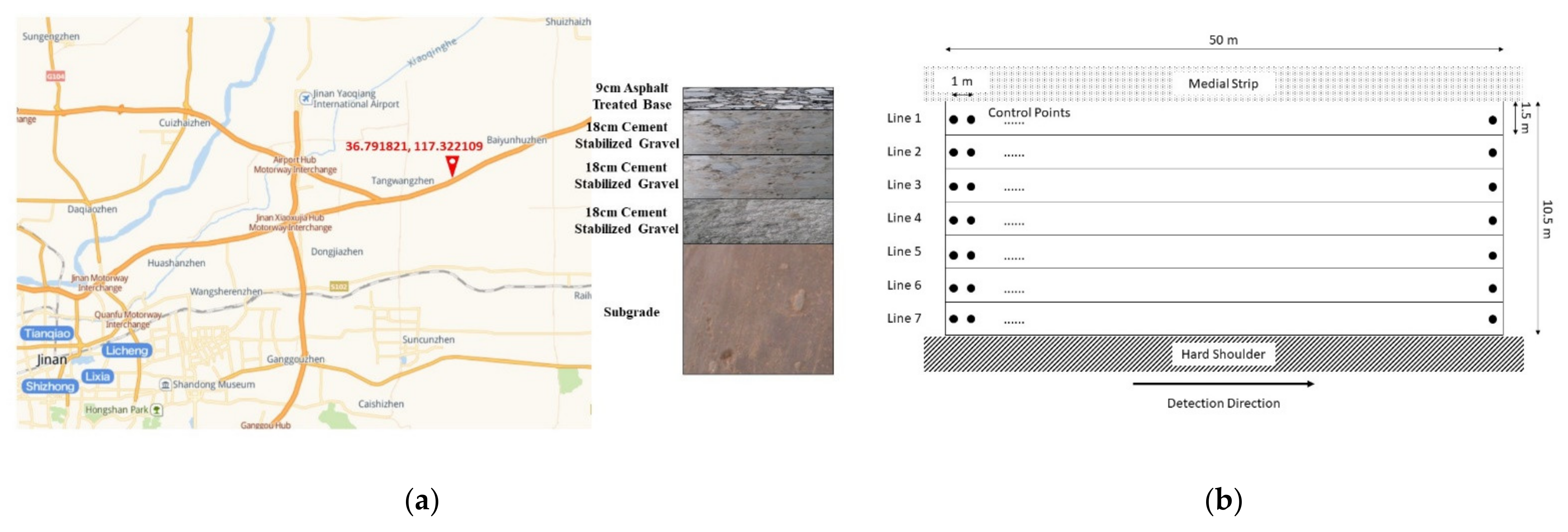
3.6. Field Test in a Newly Constructed Pavement
4. Results and Discussion
4.1. Comparison of the Dielectric Constants Estimated by Different Methods
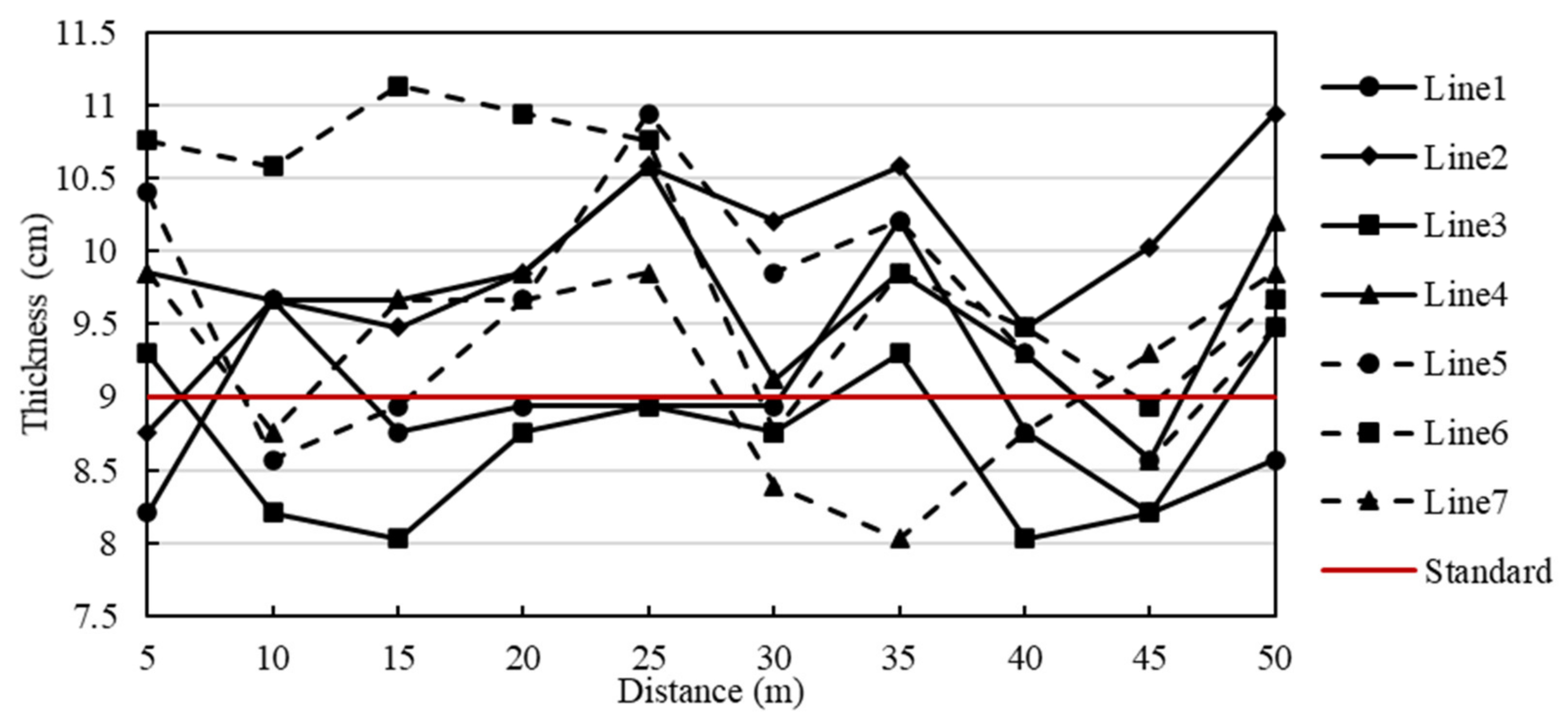
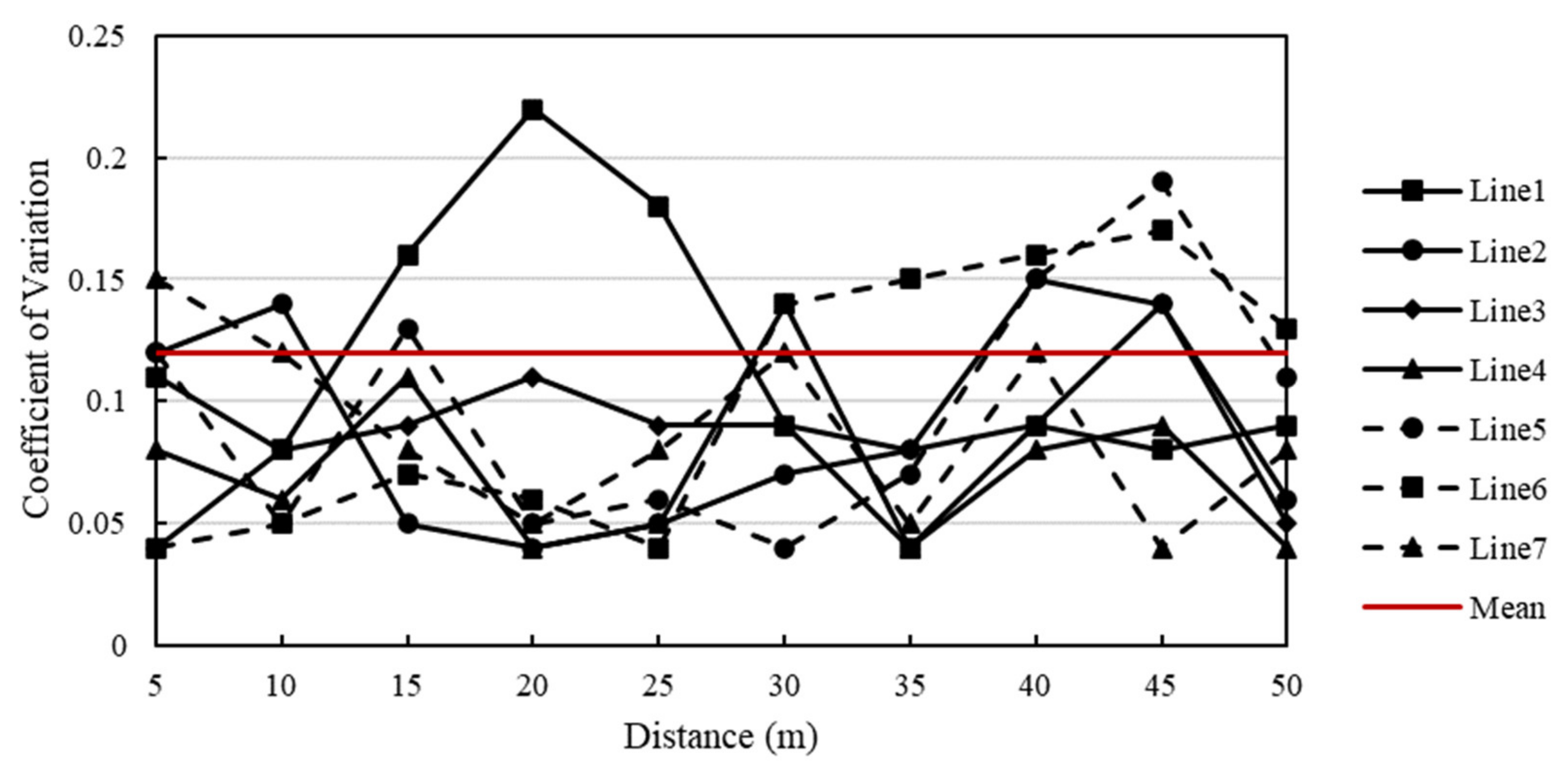
4.2. Assessment of Thickness Homogeneity
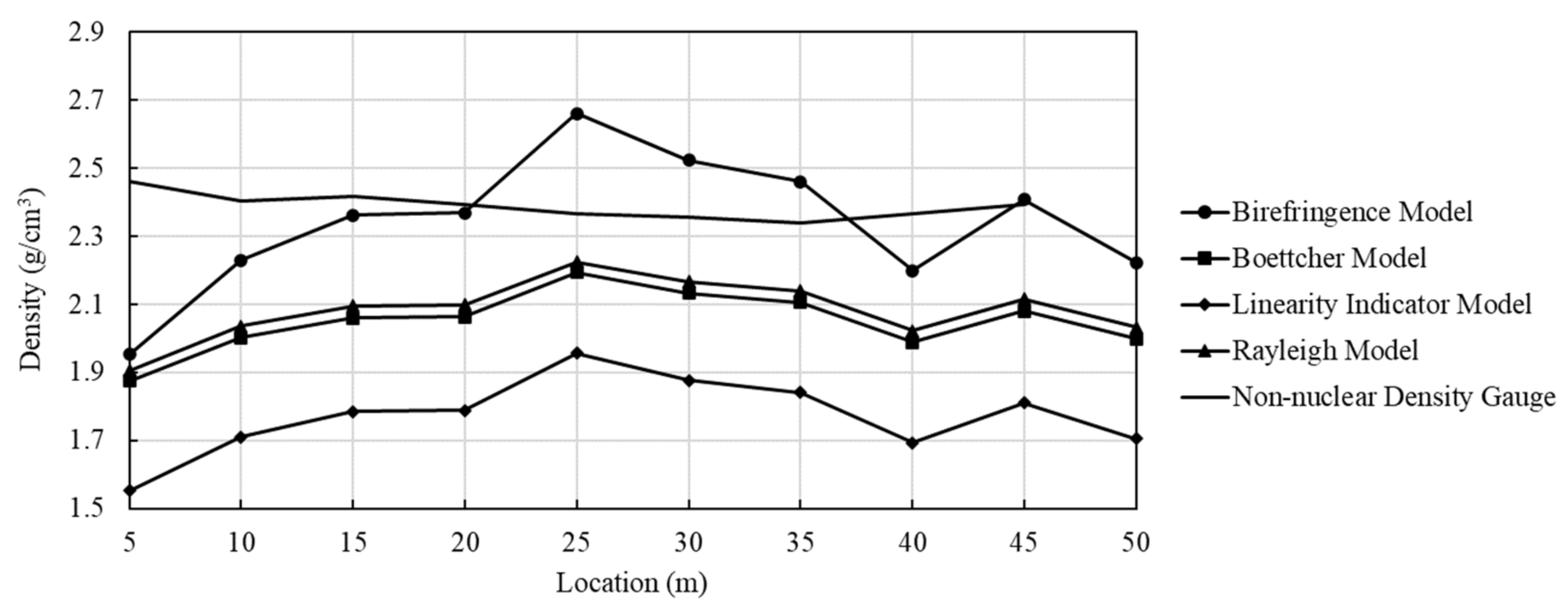
4.3. Assessment of Density Homogeneity
5. Conclusions
- (1)
- The Common Mid-Point Method, using the air-launched bowknot monopole antennae matrix, had a satisfactory performance in determination of the dielectric constant of the asphalt concrete base and presented an error of 1%, when compared with the calculated dielectric constant from cores. The results indicated potential of the Common Mid-Point Method to be adopted for providing reliable estimation results on the dielectric constant of an asphalt concrete layer and obtaining accurate calculated thickness.
- (2)
- In terms of GPR and the Common Mid-Point Method, thickness homogeneity assessment on the tested filed found that the thickness of an asphalt concrete base showed the thin area to be close to the edge of the pavement and the middle section of the asphalt concrete base.
- (3)
- Among the Birefringence, Boettcher, Linearity indicator, and Rayleigh models, the Rayleigh model was suggested to predict density, and the predicted density exhibited a good correlation coefficient with the measured density. The results of the Rayleigh model presented an average correction factor of 1.15, when compared to the density from the non-nuclear density gauge.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, S.Q.; Zhao, S.; Al-Qadi, I. Continuous real-time monitoring of flexible pavement layer density and thickness using ground penetrating radar. NDT E Int. 2018, 100, 48–54. [Google Scholar] [CrossRef]
- Zhao, S.; Al-Qadi, I. Development of regularization methods on simulated ground-penetrating radar signals to predict thin asphalt overlay thickness. Signal Process. 2017, 132, 261–271. [Google Scholar] [CrossRef]
- Leng, Z.; Al-Qadi, I.; Shangguan, P.C.; Son, S. Field application of Ground-Penetrating Radar for measurement of asphalt mixture density case study of Illinois Route 72 overlay. Transp. Res. Rec. J. Transp. Res. Board 2012, 2304, 133–141. [Google Scholar] [CrossRef]
- Al-Qadi, I.; Lahouar, S. Measuring layer thicknesses with GPR-theory to practice. Constr. Build. Mater. 2005, 19, 763–772. [Google Scholar] [CrossRef]
- Loizos, A.; Plati, C. Accuracy of pavement thicknesses estimation using different ground penetrating radar analysis approaches. NDT E Int. 2007, 40, 147–157. [Google Scholar] [CrossRef]
- Aleksey, K.; Aleksandra, V.; Evgeniy, V.T.; Anderson, N.L.; Sneed, L.H. Utilization of air-launched ground penetrating radar (GPR) for pavement condition assessment. Constr. Build. Mater. 2017, 141, 130–139. [Google Scholar]
- Wallace, W.L.; Xavier, D.; Peter, A. A review of Ground Penetrating Radar application in civil engineering: A 30-year journey from Locating and Testing to Imaging and Diagnosis. NDT E Int. 2018, 96, 58–78. [Google Scholar]
- Mezgeen, R.; Vega, P.; Mercedes, S.; Jorge, C.; Pais, F.; Caio, S. An experimental and numerical approach to combine Ground Penetrating Radar and computational modelling for the identification of early cracking in cement concrete pavements. NDT E Int. 2020, 115, 102293. [Google Scholar]
- Mercedes, S.; Susana, L.; Belen, R.; Henrique, L. Non-destructive testing for the analysis of moisture in the masonry arch bridge of Lubians (Spain). Struct. Control Health Monit. 2013, 20, 1366–1376. [Google Scholar]
- Saarenketo, T.; Scullion, T. Road evaluation with ground penetrating radar. J. App. Geophys. 2000, 43, 119–138. [Google Scholar] [CrossRef]
- Al-Qadi, I.; Leng, Z.; Lahouar, S.; Baek, J. In-place hot-mix asphalt density estimation using ground-penetrating radar. Transp. Res. Rec. J. Transp. Res. Board 2010, 2152, 19–27. [Google Scholar] [CrossRef] [Green Version]
- Shangguan, P.C.; Al-Qadi, I.; Coenen, A.; Zhao, S. Algorithm development for the application of ground-penetrating radar on asphalt pavement compaction monitoring. Int. J. Pavement Eng. 2016, 17, 189–200. [Google Scholar] [CrossRef]
- Zhao, S.; Shangguan, P.C.; Al-Qadi, I. Application of regularized deconvolution technique for predicting pavement thin layer thicknesses from ground penetrating radar data. NDT E Int. 2015, 73, 1–7. [Google Scholar] [CrossRef]
- Zhao, S.; Al-Qadi, I. Development of an analytic approach utilizing the extended common midpoint method to estimate asphalt pavement thickness with 3-D ground-penetrating radar. NDT E Int. 2016, 78, 29–36. [Google Scholar] [CrossRef]
- Plati, C.; Loizos, A. Using ground-penetrating radar for assessing the structural needs of asphalt pavement. Nondestr. Test. Eval. 2012, 27, 273–284. [Google Scholar] [CrossRef]
- Maser, K.R.; Scullion, T. Automated pavement subsurface profiling using radar: Case studies of four experimental field sites. Transp. Res. Rec. J. Transp. Res. Board 1992, 1344, 148–154. [Google Scholar]
- Poikajarvi, J.; Peisa, K.; Herronen, T.; Aursand, P.O.; Maijala, P.; Narbro, A. GPR in road investigations-equipment tests and quality assurance of new asphalt pavement. Nondestr. Test. Eval. 2012, 27, 293–303. [Google Scholar] [CrossRef]
- Goel, A.; Das, A. Nondestructive testing of asphalt pavements for structural condition evaluation: A state of the art. Nondestr. Test. Eval. 2008, 23, 121–140. [Google Scholar] [CrossRef]
- Spagnolini, U. Permittivity measurements of multilayered media with monostatic pulse radar. IEEE Trans. Geosci. Remote 1997, 35, 454–463. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Al-Qadi, I. Algorithm development for real-time thin asphalt concrete overlay compaction monitoring using ground-penetrating radar. NDT E Int. 2019, 104, 114–123. [Google Scholar] [CrossRef]
- Plati, C.; Georgouli, K.; Cliatt, B.; Loizos, A. Incorporation of GPR data into genetic algorithms for assessing recycled pavements. Constr. Build. Mater. 2017, 154, 1263–1271. [Google Scholar] [CrossRef]
- Eskelinen, P.; Pellinen, T. Comparison of different radar technologies and frequencies for road pavement evaluation. Constr. Build. Mater. 2018, 164, 888–898. [Google Scholar] [CrossRef]
- Tosti, F.; Ciampoli, L.B.; D’Amico, F.; Alani, A.M.; Benedetto, A. An experimental-based model for the assessment of the mechanical properties of road pavements using ground-penetrating radar. Constr. Build. Mater. 2018, 165, 966–974. [Google Scholar] [CrossRef]
- Araujo, S.; Beaucamp, B.; Delbreilh, L.; Dargent, É.; Fauchard, C. Compactness/density assessment of newly-paved highway containing recycled asphalt pavement by means of non-nuclear method. Constr. Build. Mater. 2017, 154, 1151–1163. [Google Scholar] [CrossRef]
- Yao, K.; Chen, Q.; Xiao, H.; Liu, Y.; Lee, F.H. Small-strain shear modulus of cement-treated marine clay. J. Mater. Civ. Eng. 2020, 32, 04020114. [Google Scholar] [CrossRef]
- Marecos, V.; Fontul, S.; Solla, M.; de Lurdes Antunes, M. Evaluation of the feasibility of Common Mid-Point approach for air-coupled GPR applied to road pavement assessment. Measurement 2018, 128, 295–305. [Google Scholar] [CrossRef]
- Hu, J.H.; Vennapusa, P.; White, D.J.; Beresnev, I. Pavement thickness and stabilized foundation layer assessment using ground-coupled GPR. Nondestr. Test. Eval. 2016, 31, 267–287. [Google Scholar] [CrossRef]
- Marecos, V.; Fontul, S.; Antunes, M.; Solla, M. Evaluation of a highway pavement using non-destructive tests Falling Weight Deflectometer and Ground Penetrating Radar. Constr. Build. Mater. 2017, 154, 1164–1172. [Google Scholar] [CrossRef]
- Dong, Z.H.; Ye, S.B.; Gao, Y.Z.; Fang, G.; Zhang, X.; Xue, Z.; Zhang, T. Rapid detection methods for asphalt pavement thicknesses and defects by a vehicle-mounted Ground Penetrating Radar (GPR) system. Sensors 2016, 16, 2067. [Google Scholar] [CrossRef] [Green Version]
- Kassem, E.; Chowdhury, A.; Scullion, T.; Masad, E. Application of ground-penetrating radar in measuring the density of asphalt pavements and its relationship to mechanical properties. Int. J. Pavement Eng. 2016, 17, 503–516. [Google Scholar] [CrossRef]





| Parameters | Minimum Frequency | Maximum Frequency | Frequency Step | Dwell Time | Sampling Time | Sampling Distance |
|---|---|---|---|---|---|---|
| Value | 60 MHz | 2980 MHz | 20 MHz | 3.0 µs | 25 ns | 20.4 mm |
| Test Content | Density (g/cm3) | ||
|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | |
| Test Point 1 | 2.34 | 2.39 | 2.34 |
| Test Point 2 | 2.37 | 2.41 | 2.44 |
| Test Point 3 | 2.29 | 2.50 | 2.43 |
| Test Point 4 | 2.37 | 2.51 | 2.54 |
| Test Point 5 | 2.50 | 2.44 | 2.42 |
| Mean of Test Points | 2.37 | 2.45 | 2.44 |
| Coring Sample | 2.35 | 2.36 | 2.35 |
| Sample | Dielectric Constant | Error | |||
|---|---|---|---|---|---|
| Coring Method | Reflection Amplitudes Method | Common Mid-Point Method | (εRAM − εCore)/ εCore | (εCMP − εCore)/ εCore | |
| 1 | 4.94 | 2.56 | 5.06 | −48% | 2% |
| 2 | 5.67 | 2.66 | 5.48 | −53% | −3% |
| 3 | 4.75 | 3.45 | 4.84 | −27% | 2% |
| 4 | 4.55 | 6.73 | 4.85 | 48% | 7% |
| 5 | 4.81 | 4.40 | 4.83 | −9% | 0% |
| Average Value | 4.94 | 3.96 | 5.01 | −20% | 1% |
| Standard Deviation | 0.38 | 1.53 | 0.25 | - | - |
| Coefficient of Variation | 0.08 | 0.39 | 0.05 | - | - |
| Test Contents | Sample 1 | Sample 2 | Sample 3 |
|---|---|---|---|
| Coring Thickness | 11.2 cm | 9.2 cm | 10.6 cm |
| Calculated Thickness | 12.0 cm | 10.0 cm | 12.0 cm |
| Coring/Calculated | 0.933 | 0.920 | 0.883 |
| Correction Factor | Mean = 0.912 | ||
| Test Contents | Thickness (cm) | ||||||
|---|---|---|---|---|---|---|---|
| Line 1 | Line 2 | Line 3 | Line 4 | Line 5 | Line 6 | Line 7 | |
| Mean | 8.92 | 9.96 | 8.7 | 9.67 | 9.59 | 10.09 | 9.21 |
| Standard Deviation | 1.15 | 1.02 | 0.93 | 0.87 | 1.18 | 1.27 | 1.03 |
| Coefficient of Variation | 0.13 | 0.10 | 0.11 | 0.09 | 0.12 | 0.13 | 0.11 |
| All Area Mean | 9.45 | ||||||
| All Area Standard Deviation | 1.17 | ||||||
| All Area Coefficient of Variation | 0.12 | ||||||
| Location | Dielectric Constant | Birefringence Model | Boettcher Model | Linearity Indicator Model | Rayleigh Model |
|---|---|---|---|---|---|
| Bulk Density (g/cm3) | |||||
| 5 m | 4.54 | 1.95 | 1.88 | 1.55 | 1.91 |
| 10 m | 4.90 | 2.23 | 2.00 | 1.71 | 2.04 |
| 15 m | 5.07 | 2.36 | 2.06 | 1.79 | 2.10 |
| 20 m | 5.08 | 2.37 | 2.06 | 1.79 | 2.10 |
| 25 m | 5.46 | 2.66 | 2.19 | 1.96 | 2.23 |
| 30 m | 5.28 | 2.52 | 2.13 | 1.88 | 2.17 |
| 35 m | 5.20 | 2.46 | 2.11 | 1.84 | 2.14 |
| 40 m | 4.86 | 2.20 | 1.99 | 1.69 | 2.02 |
| 45 m | 5.13 | 2.41 | 2.08 | 1.81 | 2.12 |
| 50 m | 4.89 | 2.22 | 2.00 | 1.71 | 2.03 |
| Prediction Model | Birefringence Model | Boettcher Model | Linearity Indicator Model | Rayleigh Model |
|---|---|---|---|---|
| Correlation Coefficient | −0.712 | −0.714 | −0.713 | −0.719 |
| Location | Rayleigh Model | Non-Nuclear Density Gauge | Correction Factor (G Non-Nuclear/G Rayleigh) | Mean |
|---|---|---|---|---|
| 5 m | 1.91 | 2.46 | 1.29 | 1.15 |
| 10 m | 2.04 | 2.41 | 1.18 | |
| 15 m | 2.10 | 2.42 | 1.15 | |
| 20 m | 2.10 | 2.39 | 1.14 | |
| 25 m | 2.22 | 2.37 | 1.06 | |
| 30 m | 2.17 | 2.36 | 1.09 | |
| 35 m | 2.14 | 2.34 | 1.09 | |
| 40 m | 2.02 | 2.37 | 1.17 | |
| 45 m | 2.12 | 2.39 | 1.13 | |
| 50 m | 2.03 | 2.39 | 1.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Han, W.; Chen, L.; Zhang, Z.; Xue, Z.; Wei, J.; Yan, X.; Hu, G. Homogeneity Assessment of Asphalt Concrete Base in Terms of a Three-Dimensional Air-Launched Ground Penetrating Radar. Coatings 2021, 11, 1398. https://doi.org/10.3390/coatings11111398
Zhang X, Han W, Chen L, Zhang Z, Xue Z, Wei J, Yan X, Hu G. Homogeneity Assessment of Asphalt Concrete Base in Terms of a Three-Dimensional Air-Launched Ground Penetrating Radar. Coatings. 2021; 11(11):1398. https://doi.org/10.3390/coatings11111398
Chicago/Turabian StyleZhang, Xiaomeng, Wenyang Han, Luchuan Chen, Zhengchao Zhang, Zhichao Xue, Jincheng Wei, Xiangpeng Yan, and Guiling Hu. 2021. "Homogeneity Assessment of Asphalt Concrete Base in Terms of a Three-Dimensional Air-Launched Ground Penetrating Radar" Coatings 11, no. 11: 1398. https://doi.org/10.3390/coatings11111398






