Topology Optimization of Hard-Coating Thin Plate for Maximizing Modal Loss Factors
Abstract
:1. Introduction
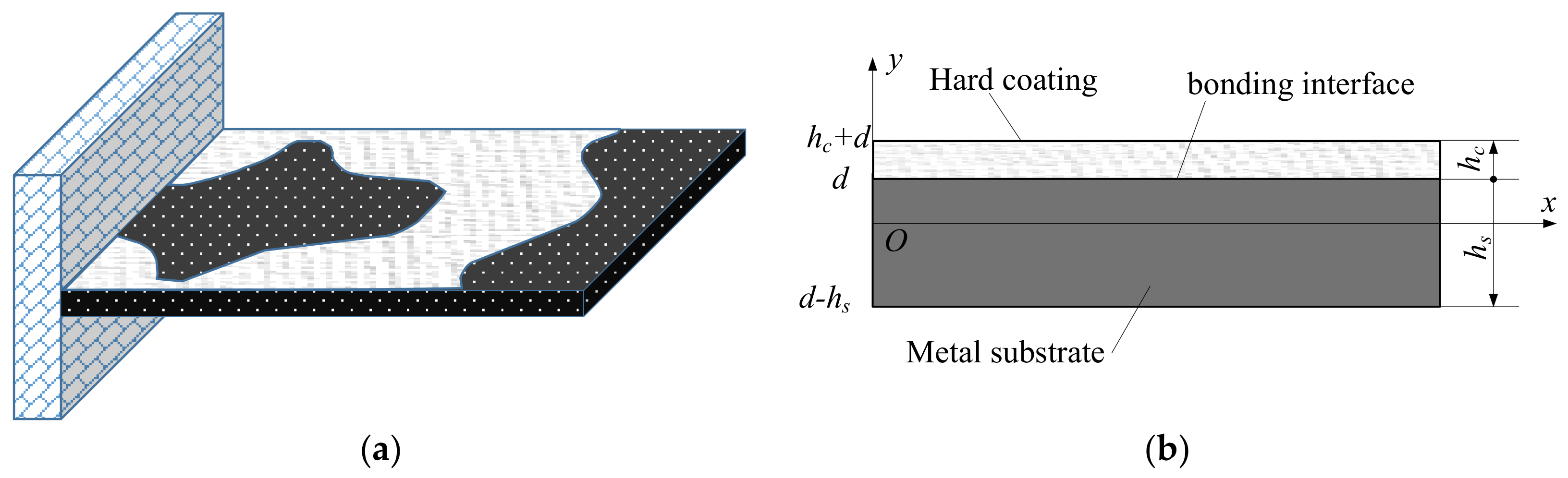
2. Analytic Model
2.1. Dynamic Model
- each layer of material meets the basic assumptions of material mechanics, and the structural deformation is small deformation
- the base and hard coating meet the Kichhoff thin plate theory hypothesis
- ignore the shear deformation of base and hard coating
- ignore the moment of inertia of each layer of material
- The results show that the transverse displacement of the same coordinate position of each layer in Z direction is equal
- the bonding of materials in each layer is firm, and there is no relative sliding between layers.
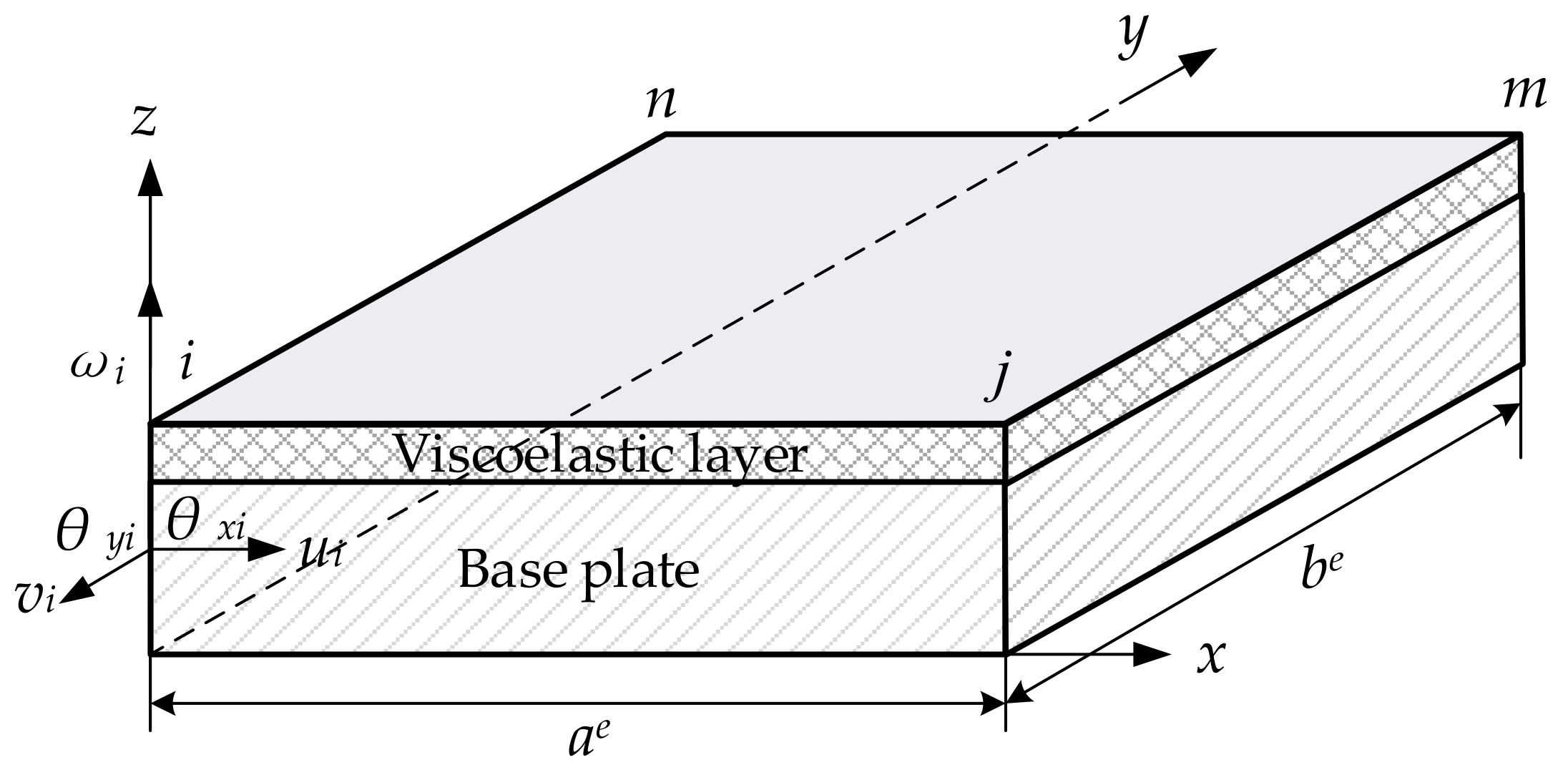
2.2. Damping Model
3. Topology Optimization of the Hard Coating
3.1. Optimization Model
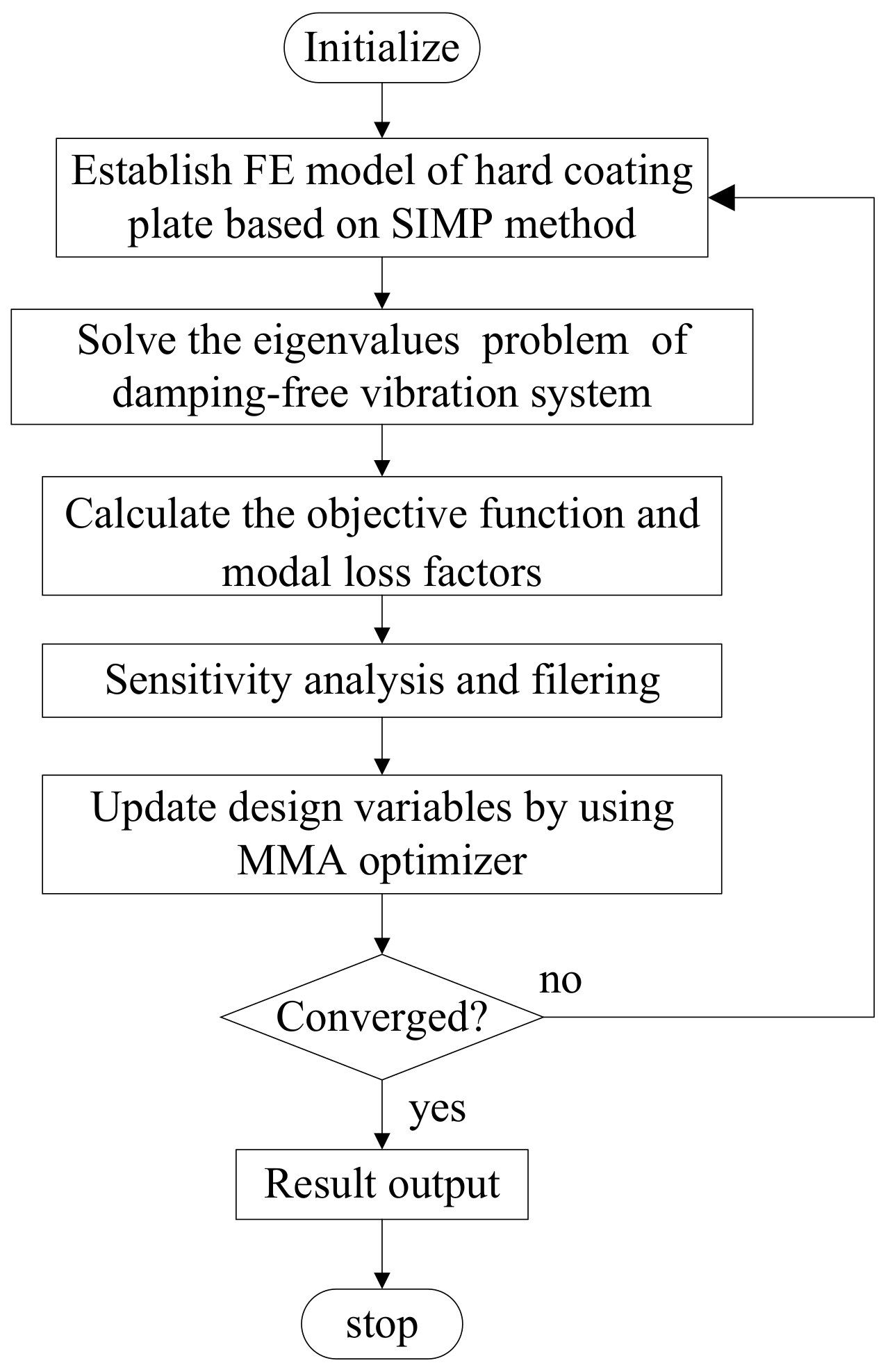
3.2. Optimization Procedure
- Define volume constraint fraction, initialize design variables and set the corresponding parameters.
- Reassemble the mass matrix and stiffness matrix of the hard coating structure according to the value of design variables and SIMP material interpolation model.
- Carry out the modal analysis of the hard coating structure and calculate the objective function value.
- Analysis and filter the sensitivities of objective function to prevent checkerboard patterns in the design.
- Update the design variables using the MMA algorithm.
- Check whether the result converges, and if so, end the iteration. If it does not converge, the iteration is repeated.
- Output design variables and object values and display the topological distribution geometry of hard coating materials.
4. Numerical Verification
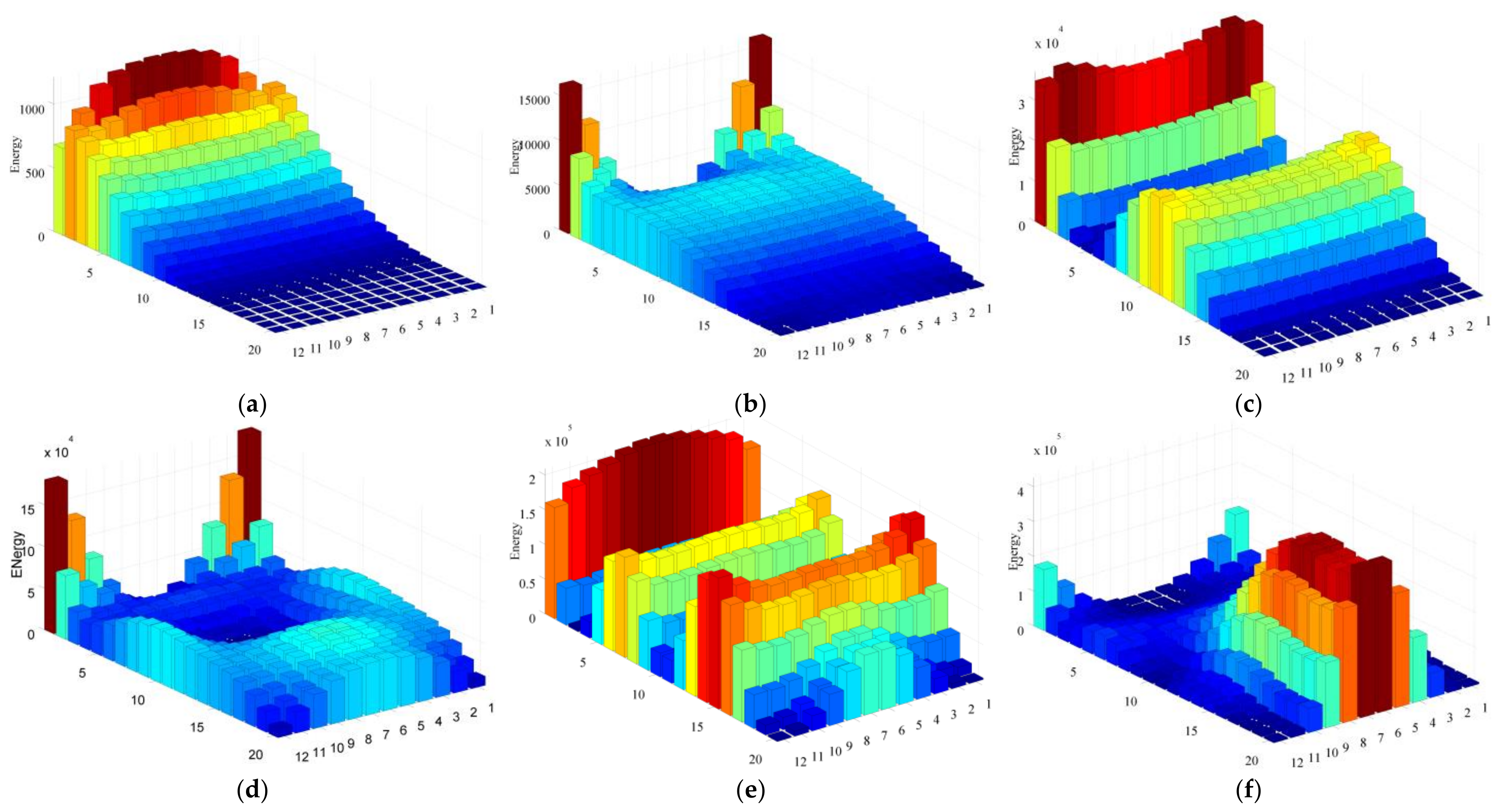
4.1. Modal Strain Energy Distribution
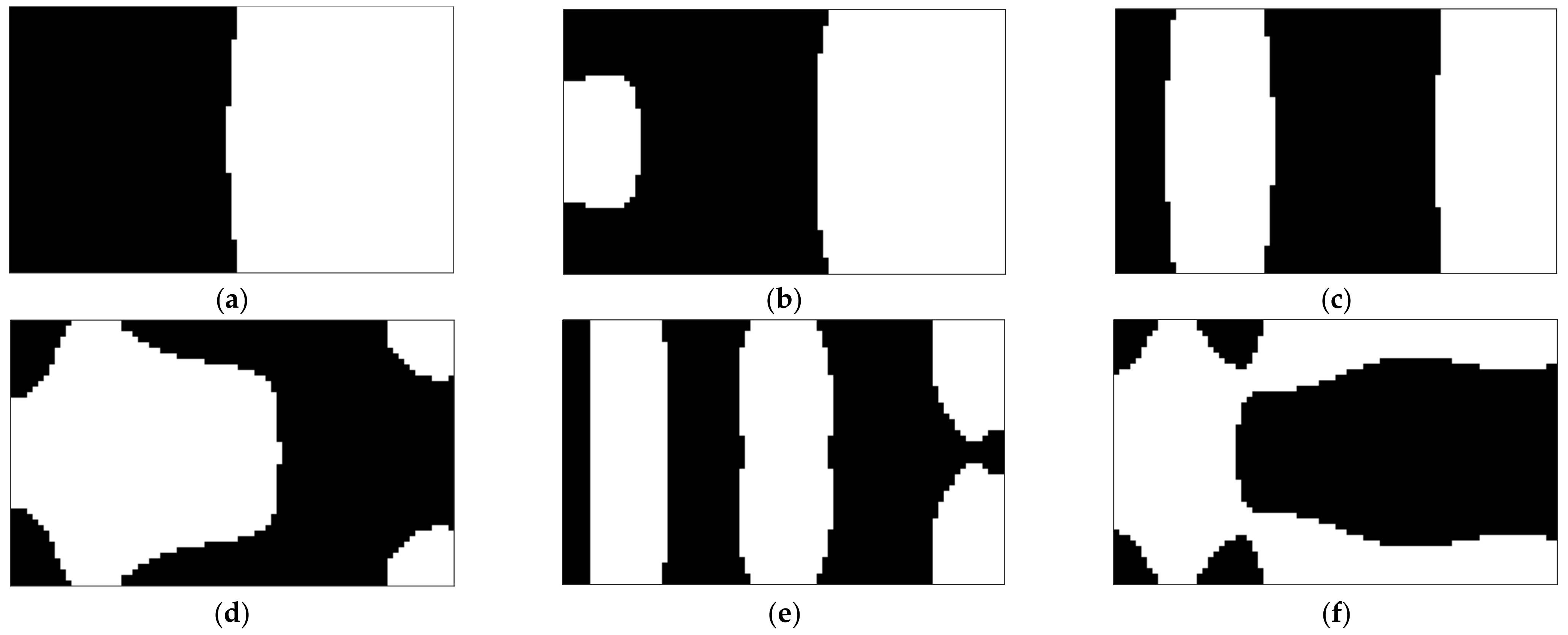
4.2. Damping Optimization for a Single Mode
4.3. Damping Optimization for a Multiple Mode
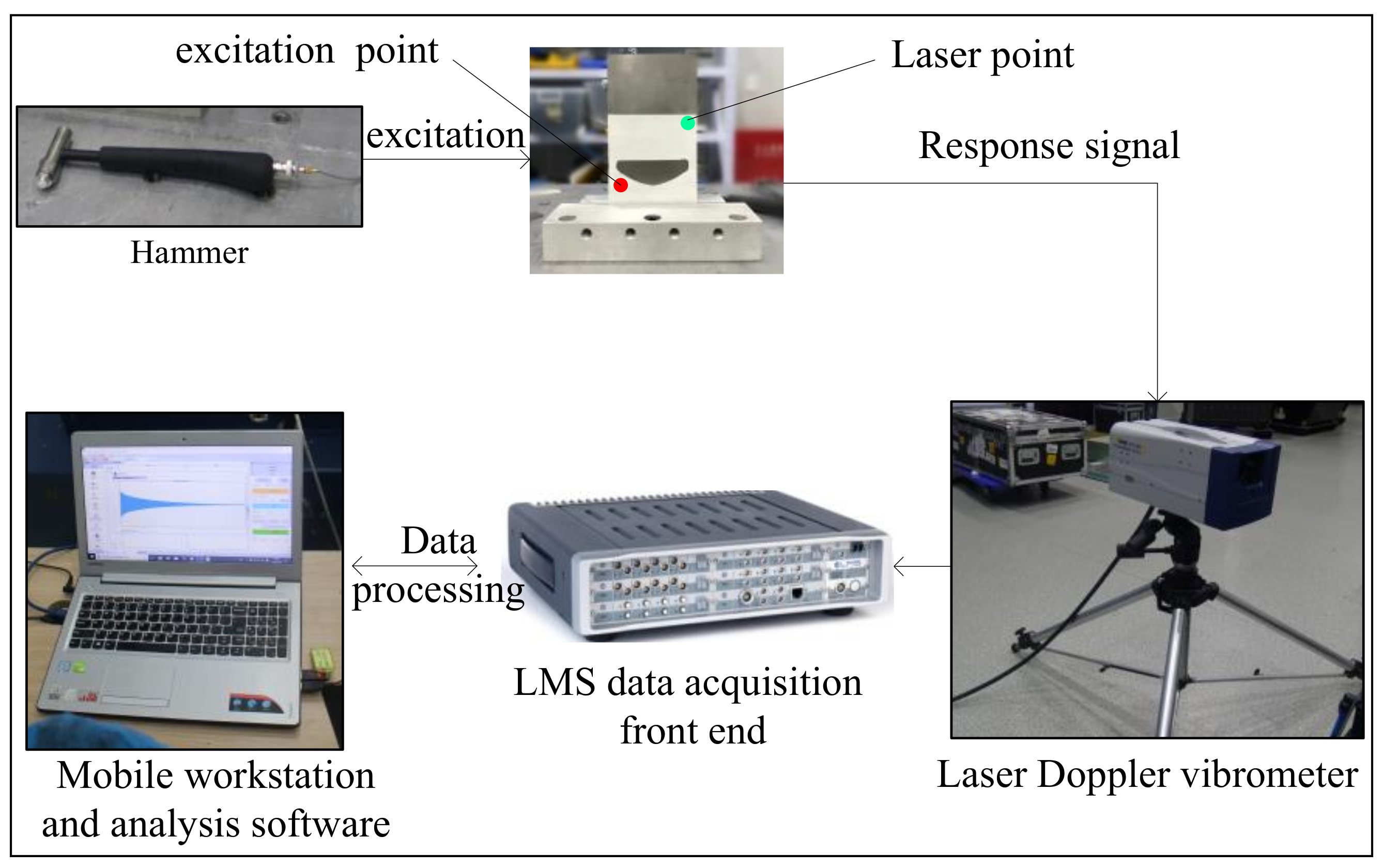
5. Experimental Verification
- the hard coated cantilever plate is fixed on the shaking table with a fixture
- the excitation signal is generated by hammering the surface of the composite plate
- the vibration acceleration response of the composite plate is measured with a laser vibrometer
- the response signal collected by the LMS data acquisition mobile front end is transmitted to the mobile workstation, and the analysis software processes the response signal and outputs the results.
6. Conclusions
- Through the topology optimization results of multi single mode, it can be seen that the hard coating damping materials are mainly distributed in the region with high modal strain energy, which is consistent with the traditional empirical method. Compared with full coverage, local coverage can not only effectively suppress vibration, but also save materials. And, the less the coating material, the smaller the change of the matrix structure itself.
- The topology optimization of hard coated thin plate with multiple mode loss factors can effectively suppress the vibration in a certain frequency band. In practical engineering, the vibration environment of the thin walled structure is often the combined action of various vibration loads in a certain frequency band, which shows that the method proposed in this paper has practical significance.
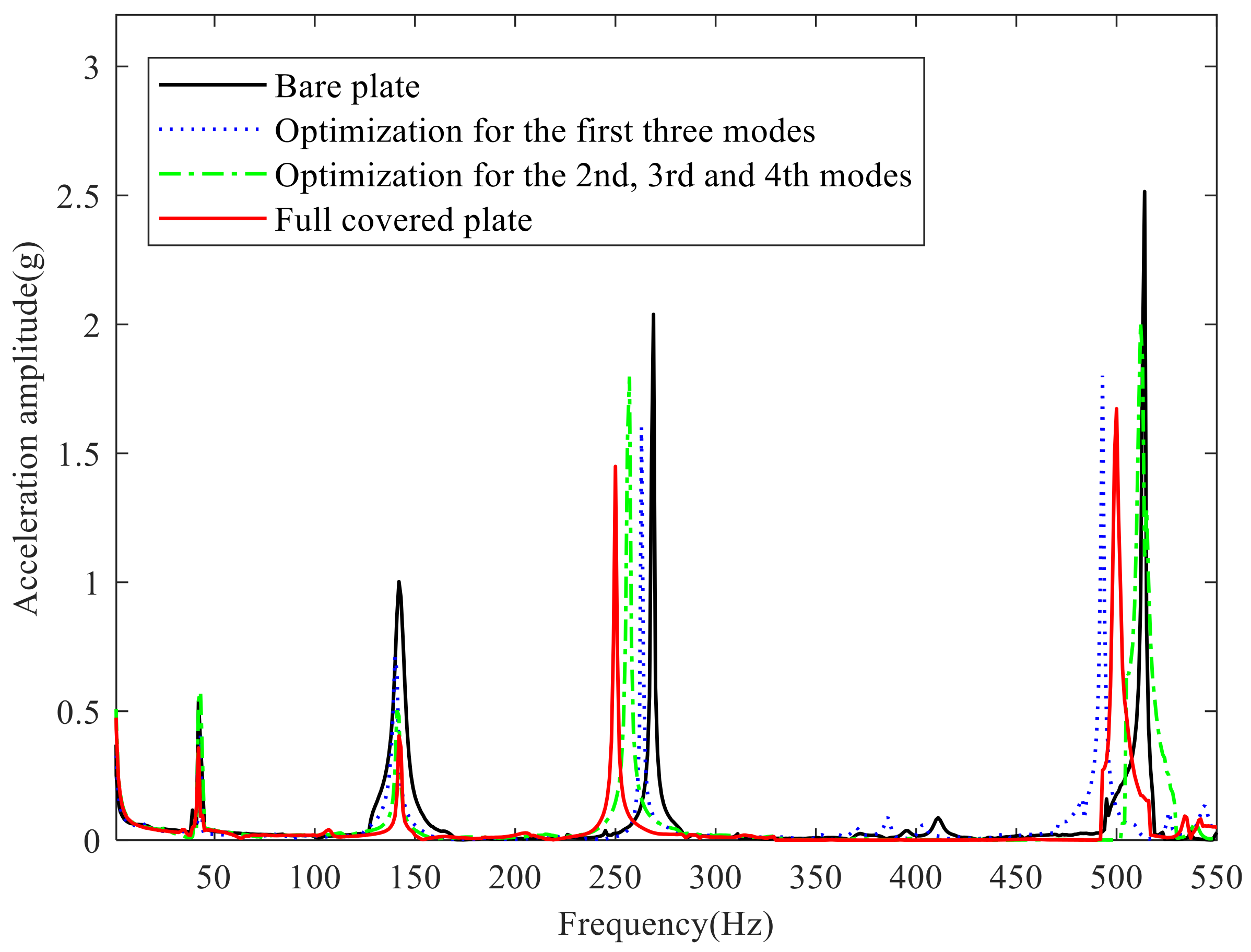
- The objective function converges to the optimal value stably, the optimization result is clear, there is no checkerboard phenomenon, and it is easy to reconstruct and process. The experimental results are consistent with the simulation results. The above results show that the method is effective and practical.
- The experimental results show that the proposed topology optimization design method can effectively suppress the vibration in a certain frequency band, which proves the correctness of the proposed method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ivancic, F.; Palazotto, A. Experimental considerations for determining the damping coefficients of hard coatings. J. Aerosp. Eng. 2005, 18, 8–17. [Google Scholar] [CrossRef]
- Gregori, G.; Lì, L.; Nychka, J.A.; Clarke, D.R. Vibration damping of superalloys and thermal barrier coatings at high-temperatures. Mat. Sci. Eng. A Struct. 2007, 466, 256–264. [Google Scholar] [CrossRef]
- Casadei, B.K.; Clarke, D.R. Finite element study of multi-modal vibration damping for thermal barrier coating applications. Comp. Mater. Sci. 2013, 79, 908–917. [Google Scholar] [CrossRef]
- Sun, W.; Li, H.; Han, Q.K. Identification of mechanical parameters of hard-coating materials with strain-dependence. J. Mech. Sci. Technol. 2014, 28, 81–92. [Google Scholar] [CrossRef]
- Wei, S.; Liu, X.; Jiang, J. Vibration analysis of hard-coating laminated plate considering strain-dependent characteristic. J. Low Freq. Noise Vib. Act. Control 2018, 37, 1–12. [Google Scholar]
- Sun, W.; Liu, R.; Fan, Y. Analytical modeling and damping optimization for a thin plate partially covered with hard coating. Arch. Appl. Mech. 2018, 88, 897–912. [Google Scholar] [CrossRef]
- Wei, S.; Rong, L. Damping optimization of hard-coating thin plate by the modified modal strain energy method. Coatings 2017, 7, 32. [Google Scholar]
- Ansari, M.; Shoja-Razavi, R.; Barekat, M.; Man, H.C. High-temperature oxidation behavior of laser-aided additively manufactured NiCrAlY coating. Corros. Sci. 2017, 118, 168–177. [Google Scholar] [CrossRef]
- Feng, G.; Wei, S. Vibration characteristics and damping analysis of the blisk-deposited hard coating using the Rayleigh-Ritz method. Coatings 2017, 7, 108. [Google Scholar]
- Li, H.; Sun, W.; Zhu, M.; Xue, P. Experimental study on the influence on vibration characteristics of thin cylindrical shell with hard coating under cantilever boundary condition. Shock. Vib. 2017, 2017, 1–23. [Google Scholar] [CrossRef]
- Du, G.; Tan, Z.; Li, G.; Ba, D.; Liu, K. Damping properties of arc ion plating NiCrAlY coating with vacuum annealing. Coatings 2018, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhou, Z.; Sun, H.; Sun, W.; Wen, B. Theoretical study on the influence of hard coating on vibration characteristics of fiber-reinforced composite thin shell. Coatings 2018, 8, 87. [Google Scholar] [CrossRef] [Green Version]
- Stefano, A.; Giuseppe, C.; Angelo, C. Experimental evaluation and modeling of the damping properties of multi-layer coated composites. Coatings 2018, 8, 53. [Google Scholar]
- Tassini, N.; Patsias, S.; Lambrinou, K. Ceramic coatings: A phenomenological modeling for damping behavior related to microstructural features. Mat. Sci. Eng. A Struct. 2006, 442, 509–513. [Google Scholar] [CrossRef]
- Torvik, P.J. A Slip Damping model for plasma sprayed ceramics. J. Appl. Mech. 2009, 76, 1089–1094. [Google Scholar] [CrossRef]
- Al-Rub, R.; Palazotto, A.N. Micromechanical theoretical and computational modeling of energy dissipation due to nonlinear vibration of hard ceramic coatings with microstructural recursive faults. Int. J. Solids. Struct. 2010, 47, 2131–2142. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.X.; Han, Q.K.; Jin, Z.H.; Qu, T. Solution of natural characteristics of a hard-coating plate based on Lindstedt–Poincaré perturbation method and its valedictions by FEM and measurement. Nonlinear Dynam. 2015, 81, 1207–1218. [Google Scholar] [CrossRef]
- Hui, L.; Liu, Y.; Wei, S. Analysis of nonlinear vibration of hard coating thin plate by finite element iteration method. Shock. Vib. 2014, 2014, 941709. [Google Scholar]
- Chen, Y.; Zhai, J.; Han, Q. Vibration and damping analysis of the bladed disk with damping hard coating on blades. Aerosp. Sci. Technol. 2016, 58, 248–257. [Google Scholar] [CrossRef]
- Lumsdaine, A. Topology optimization of constrained damping layer treatments. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 17–22 November 2002; Volume 36258, pp. 149–156. [Google Scholar]
- Lumsdaine, A.; Pai, R. Design of constrained layer damping topologies. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Washington, DC, USA, 15–21 November 2003; Volume 37076, pp. 219–227. [Google Scholar]
- Chen, Y.C.; Huang, S.C. An optimal placement of CLD treatment for vibration suppression of plates. Int. J. Mech. Sci. 2002, 44, 1801–1821. [Google Scholar] [CrossRef]
- Hou, S.W.; Jiao, Y.H.; Chen, Z.B. Optimum layout of passive constrained layer damping treatment using genetic algorithms. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Vancouver, BC, Canada, 12–18 November 2010; Volume 44502, pp. 371–376. [Google Scholar]
- Zheng, H.; Cai, C.; Pau, G.S.H.; Liu, G.R. Minimizing vibration response of cylindrical shells through layout optimization of passive constrained layer damping treatments. J. Sound. Vib. 2005, 279, 739–756. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Sigmund, O. On the usefulness of non-gradient approaches in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 589–596. [Google Scholar] [CrossRef]
- Ling, Z.; Ronglu, X.; Yi, W.; El-Sabbagh, A. Topology optimization of constrained layer damping on plates using Method of Moving Asymptote (MMA) approach. Shock Vib. 2011, 18, 221–244. [Google Scholar] [CrossRef]
- Fang, Z.P.; Zheng, L. Topology optimization for minimizing the resonant response of plates with constrained layer damping treatment. Shock. Vib. 2015, 2015, 376854. [Google Scholar] [CrossRef]
- Zheng, W.; Lei, Y.; Li, S.; Huang, Q. Topology optimization of passive constrained layer damping with partial coverage on plate. Shock. Vib. 2013, 20, 199–211. [Google Scholar] [CrossRef]
- Nazir, A.; Jeng, J.Y. A high-speed additive manufacturing approach for achieving high printing speed and accuracy. J. Mech. Eng. Sci. 2019, 234, 1–9. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Meth. Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef] [Green Version]

| Lamina | Length (m) | Width (m) | Thickness (mm) | Young’s Modulus | Loss Factor (Gpa) | Poisson Ratio | Density (kg/m3) |
|---|---|---|---|---|---|---|---|
| Base plate | 0.2 | 0.12 | 2 | 110 | 0.0008 | 0.3 | 4420 |
| coating | 0.2 | 0.12 | 0.02 | 50 | 0.02 | 0.3 | 2600 |
| Orders | Nature Frequency/Hz |
|---|---|
| 1 | 41.48 |
| 2 | 152.81 |
| 3 | 258.13 |
| 4 | 508.49 |
| 5 | 714.45 |
| 6 | 809.60 |
| Order | Fully Covered | Partially Covered | Difference (%) |
|---|---|---|---|
| 1 | 0.0031 | 0.0029 | 6.45 |
| 2 | 0.0031 | 0.0025 | 19.35 |
| 3 | 0.0031 | 0.0027 | 12.90 |
| 4 | 0.0031 | 0.0024 | 22.58 |
| 5 | 0.0031 | 0.0025 | 19.35 |
| 6 | 0.0031 | 0.0028 | 9.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Chen, R.; Guo, S.; Fu, J. Topology Optimization of Hard-Coating Thin Plate for Maximizing Modal Loss Factors. Coatings 2021, 11, 774. https://doi.org/10.3390/coatings11070774
Luo H, Chen R, Guo S, Fu J. Topology Optimization of Hard-Coating Thin Plate for Maximizing Modal Loss Factors. Coatings. 2021; 11(7):774. https://doi.org/10.3390/coatings11070774
Chicago/Turabian StyleLuo, Haitao, Rong Chen, Siwei Guo, and Jia Fu. 2021. "Topology Optimization of Hard-Coating Thin Plate for Maximizing Modal Loss Factors" Coatings 11, no. 7: 774. https://doi.org/10.3390/coatings11070774
APA StyleLuo, H., Chen, R., Guo, S., & Fu, J. (2021). Topology Optimization of Hard-Coating Thin Plate for Maximizing Modal Loss Factors. Coatings, 11(7), 774. https://doi.org/10.3390/coatings11070774








