A Numerical Investigation on the Combined Effects of MoSe2 Interface Layer and Graded Bandgap Absorber in CIGS Thin Film Solar Cells
Abstract
:1. Introduction
- Bandgap values at the front, middle and back of the absorber layer, depending on the composition of Ga;
- Position of the notch, where composition of Ga is minimum.
2. Methodology–Device Architecture and Simulation
3. Results and Discussion
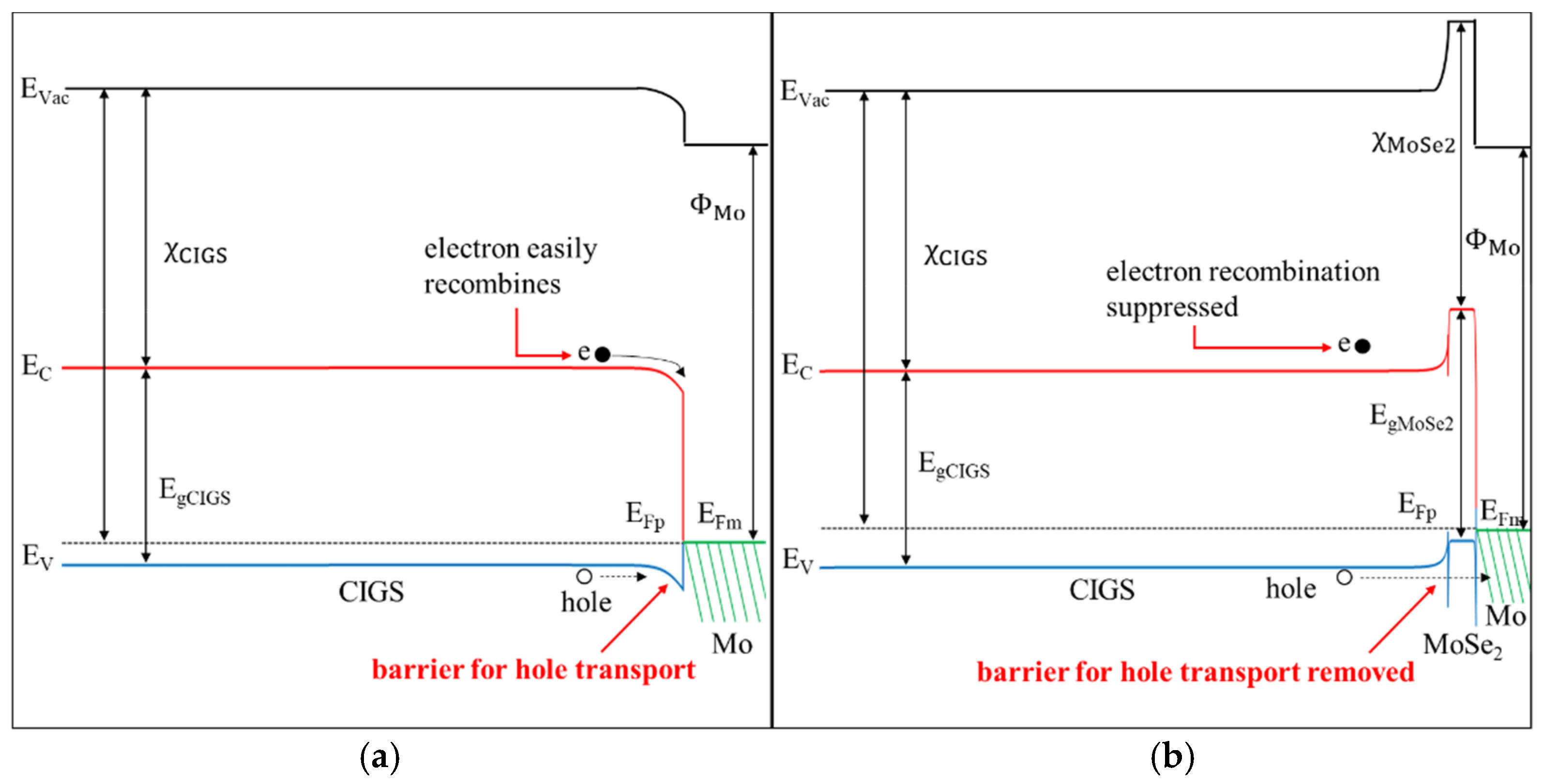
3.1. Study of MoSe2 Interfacial Layer in CIGS Thin Film Solar Cell Structure
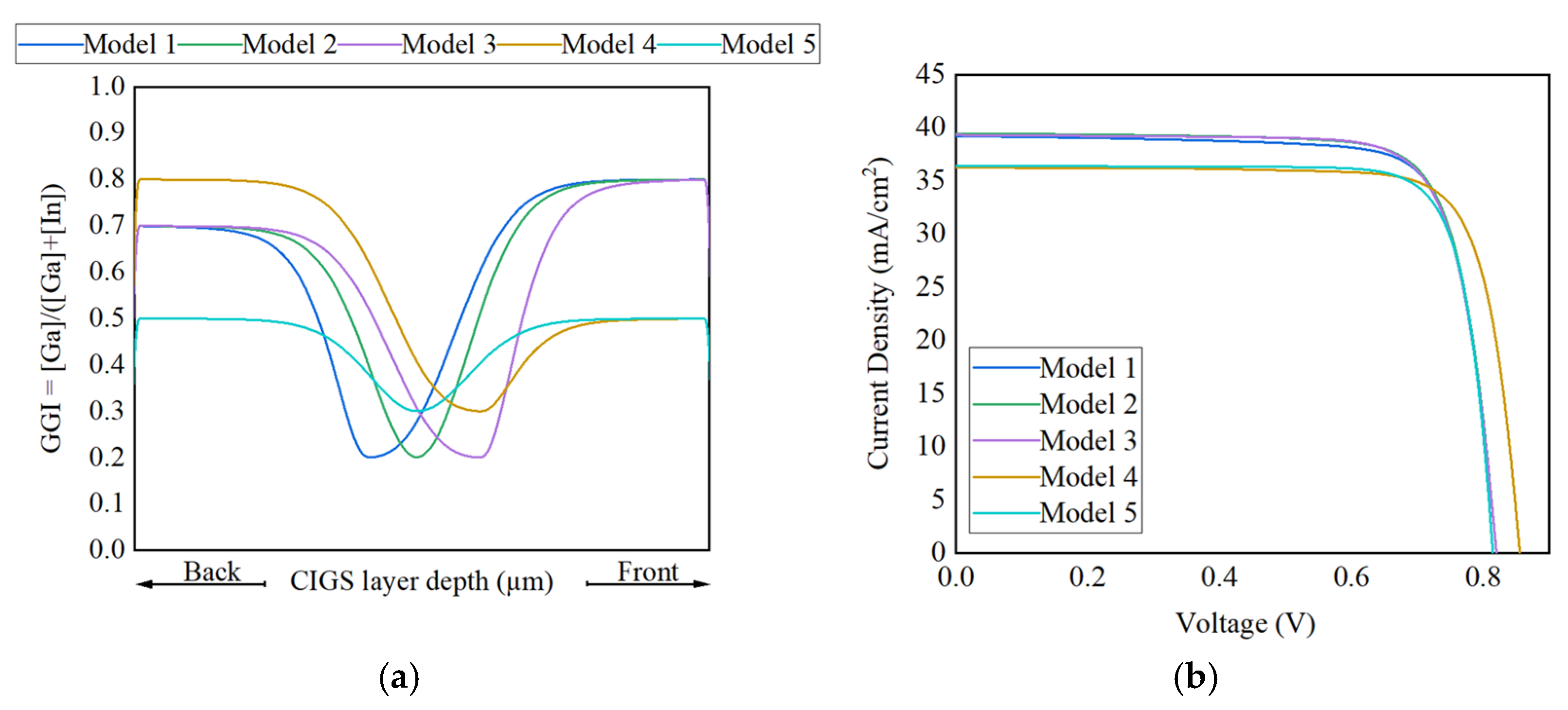
3.2. Study of Absorber Layer Bandgap Grading in CIGS Solar Cell Structure
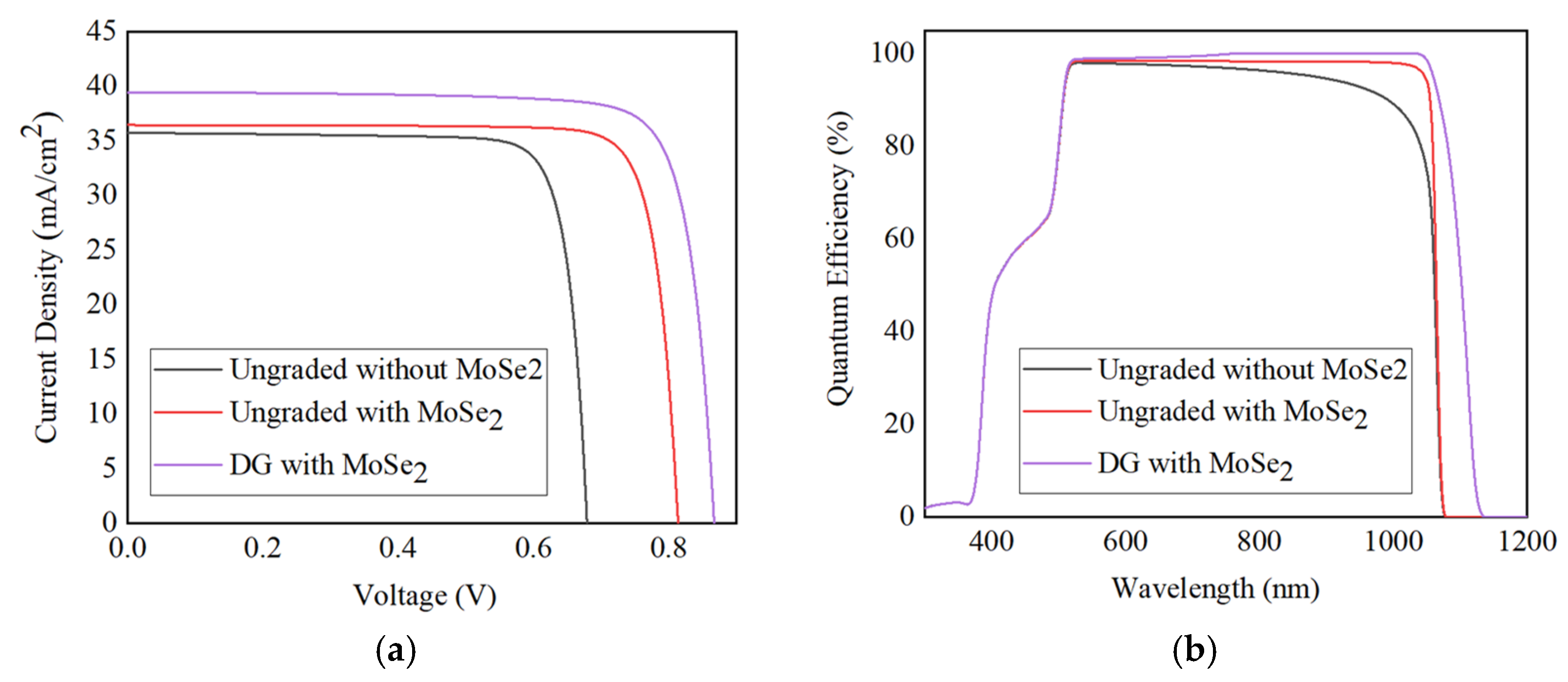
3.3. Optimizing Bandgap Energy of MoSe2 Layer for Compatibility with Double Graded (DG) Bandgap Profile of CIGS Absorber Layer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Material | ZnO | CdS | CIGS | MoSe2 |
|---|---|---|---|---|
| Defect type | Donor | Donor | Acceptor | Acceptor |
| Energy level (eV) | 1.65 | 1.2 | 0.6 | 0.7 |
| (cm2) | 1.0 × 10−15 | 1.0 × 10−17 | 5.3 × 10−13 | 5.3 × 10−13 |
| (cm2) | 1.0 × 10−12 | 9.8 × 10−13 | 1.0 × 10−18 | 1.0 × 10−18 |
| (cm−3) | 1.0 × 1016 | 1.0 × 1018 | 1.0 × 1014 | 1.0 × 1014 |
| Parameter | Back Contact | Front Contact |
|---|---|---|
| (eV) | 0.6348 | Flat band |
| (cm/s) | 1.0 × 107 | 1.0 × 107 |
| (cm/s) | 1.0 × 107 | 1.0 × 107 |
| Reflectivity | NA | 0.02 |
| Parameter | Definition |
|---|---|
| Dielectric permittivity | |
| Mobility of electron/holes | |
| Acceptor/donor concentration | |
| Bandgap energy | |
| Effective density of states in the conduction/valence band | |
| Electron affinity | |
| Capture cross section of electron/holes | |
| Defect concentration | |
| Barrier height | |
| Surface recombination velocity of electron/holes |
References
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Ho-Baillie, A.W.Y. Solar cell efficiency tables (Version 55). Prog. Photovolt. Res. Appl. 2020, 28, 3–15. [Google Scholar] [CrossRef]
- Siebentritt, S. What limits the efficiency of chalcopyrite solar cells? Sol. Energy Mater. Sol. Cells 2011, 95, 1471–1476. [Google Scholar] [CrossRef]
- Kohara, N.; Nishiwaki, S.; Hashimoto, Y.; Negami, T.; Wada, T. Electrical properties of the Cu(In,Ga)Se2/ MoSe2/Mo structure. Sol. Energy Mater. Sol. Cells 2001, 67, 209–215. [Google Scholar] [CrossRef]
- Nishiwaki, S.; Kohara, N.; Negami, T.; Nishitani, M.; Wada, T. Characterization of Cu(In,Ga)Se2/Mo Interface in CIGS Solar Cells. MRS Proc. 1997, 485, 139. [Google Scholar] [CrossRef]
- Klinkert, T.; Theys, B.; Patriarche, G.; Jubault, M.; Donsanti, F.; Guillemoles, J.F.; Lincot, D. New insights into the Mo/Cu(In,Ga)Se2 interface in thin film solar cells: Formation and properties of the MoSe2 interfacial layer. J. Chem. Phys. 2016, 145, 154702. [Google Scholar] [CrossRef]
- Wada, T.; Kohara, N.; Nishiwaki, S.; Negami, T. Characterization of the Cu(In,Ga)Se2/Mo interface in CIGS solar cells. Thin Solid Films 2001, 387, 118–122. [Google Scholar] [CrossRef]
- Neugebohrn, N.; Hammer, M.S.; Neerken, J.; Parisi, J.; Riedel, I. Analysis of the back contact properties of Cu(In,Ga)Se2solar cells employing the thermionic emission model. Thin Solid Films 2015, 582, 332–335. [Google Scholar] [CrossRef]
- Wei, S.-H.; Zunger, A. Effects of Ga addition to CuInSe2 on its electronic, structural, and defect properties. Appl. Phys. Lett. 1998, 72, 3199–3201. [Google Scholar] [CrossRef] [Green Version]
- Cai, C.-H.; Chen, R.-Z.; Chan, T.-S.; Lu, Y.-R.; Huang, W.-C.; Yen, C.-C.; Zhao, K.; Lo, Y.-C.; Lai, C.-H. Interplay between potassium doping and bandgap profiling in selenized Cu(In,Ga)Se 2 solar cells: A functional CuGa: KF surface precursor layer. Nano Energy 2018, 47, 393–400. [Google Scholar] [CrossRef]
- Morales-Acevedo, A. A simple model of graded band-gap CuInGaSe2 solar cells. Energy Procedia 2010, 2, 169–176. [Google Scholar] [CrossRef] [Green Version]
- Gloeckler, M.; Sites, J.R. Band-gap grading in Cu(In,Ga)Se2solar cells. J. Phys. Chem. Solids 2005, 66, 1891–1894. [Google Scholar] [CrossRef]
- Saadat, M.; Moradi, M.; Zahedifar, M. CIGS absorber layer with double grading Ga profile for highly efficient solar cells. Superlattices Microstruct. 2016, 92, 303–307. [Google Scholar] [CrossRef]
- Zheng, X.; Li, W.; Aberle, A.G.; Venkataraj, S. Efficiency enhancement of ultra-thin Cu(In,Ga)Se 2 solar cells: Optimizing the absorber bandgap profile by numerical device simulations. Curr. Appl. Phys. 2016, 16, 1334–1341. [Google Scholar] [CrossRef]
- Aissani, H.; Helmaoui, A.; Moughli, H. Numerical Modeling of Graded Band-Gap CIGS Solar Celle for High Efficiency. Int. J. Appl. Eng. Res. 2017, 12, 227–232. [Google Scholar]
- Song, J.; Li, S.S.; Huang, C.H.; Crisalle, O.D.; Anderson, T.J. Device modeling and simulation of the performance of Cu(In1-x,Gax)Se2solar cells. Solid State Electron. 2004, 48, 73–79. [Google Scholar] [CrossRef]
- Huang, C.H. Effects of Ga content on Cu(In,Ga)Se2 solar cells studied by numerical modeling. J. Phys. Chem. Solids 2008, 69, 330–334. [Google Scholar] [CrossRef]
- Amin, N.; Chelvanathan, P.; Hossain, M.I.; Sopian, K. Numerical modelling of ultra thin Cu(In,Ga)Se2solar cells. Energy Procedia 2012, 15, 291–298. [Google Scholar] [CrossRef] [Green Version]
- Kuo, S.-Y.; Hsieh, M.-Y.; Hsieh, D.-H.; Kuo, H.-C.; Chen, C.-H.; Lai, F.-I. Device Modeling of the Performance of Cu(In,Ga)Se2 Solar Cells with V-Shaped Bandgap Profiles. Int. J. Photoenergy 2014, 2014, 186579. [Google Scholar] [CrossRef]
- Lundberg, O.; Edoff, M.; Stolt, L. The effect of Ga-grading in CIGS thin film solar cells. Thin Solid Films 2005, 480, 520–525. [Google Scholar] [CrossRef]
- Park, J.; Shin, M. Numerical Optimization of Gradient Bandgap Structure for CIGS Solar Cell with ZnS Buffer Layer Using Technology Computer-Aided Design Simulation. Energies 2018, 11, 1785. [Google Scholar] [CrossRef] [Green Version]
- Belghachi, A.; Limam, N. Effect of the absorber layer band-gap on CIGS solar cell. Chin. J. Phys. 2017, 55, 1127–1134. [Google Scholar] [CrossRef]
- Khoshsirat, N.; Md Yunus, N.A.; Hamidon, M.N.; Shafie, S.; Amin, N. Analysis of absorber layer properties effect on CIGS solar cell performance using SCAPS. Optik 2015, 126, 681–686. [Google Scholar] [CrossRef]
- Burgelman, M.; Verschraegen, J.; Minnaert, B.; Marlein, J. Numerical simulation of thin film solar cells: Practical exercises with SCAPS. In Proceedings of the International Workshop on Numerical Modelling of Thin Film Solar Cells (NUMOS), Gent, Belgium, 28–30 March 2007. [Google Scholar]
- Jackson, P.; Hariskos, D.; Wuerz, R.; Kiowski, O.; Bauer, A.; Friedlmeier, T.M.; Powalla, M. Properties of Cu(In,Ga)Se2solar cells with new record efficiencies up to 21.7%. Phys. Status Solidi-Rapid Res. Lett. 2015, 9, 28–31. [Google Scholar] [CrossRef]
- Gloeckler, M.; Fahrenbruch, A.L.; Sites, J.R. Numerical modeling of CIGS and CdTe solar cells: Setting the baseline. In Proceedings of the 3rd World Conference onPhotovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; Volume 1, pp. 491–494. [Google Scholar]
- Minemoto, T.; Matsui, T.; Takakura, H.; Hamakawa, Y.; Negami, T.; Hashimoto, Y.; Uenoyama, T.; Kitagawa, M. Theoretical analysis of the eff ect of conduction band of set of window/CIS layers on performance of CIS solar cells using device simulation. Sol. Energy Mater. Sol. Cells 2001, 67, 83–88. [Google Scholar] [CrossRef]
- Ikball Ahamed, E.M.K.; Matin, M.A.; Amin, N. Modeling and simulation of highly efficient ultra-thin CIGS solar cell with MoSe2 tunnel. In Proceedings of the 4th International Conference on Advances in Electrical Engineering, ICAEE 2017, Dhaka, Bangladesh, 28–30 September 2017; pp. 681–685. [Google Scholar]
- Burgelman, M.; Marlein, J. Analysis of graded band gap solar cells with SCAPS. In Proceedings of the 23rd European Photovoltaic Solar Energy Conference, Valencia, Spain, 1–5 September 2008; pp. 2151–2155. [Google Scholar]
- Thompson, A.G.; Woolley, J.C. Energy-gap variation in mixed III–V alloys. Can. J. Phys. 1967, 45, 255–261. [Google Scholar] [CrossRef]
- Dejene, F.B.; Alberts, V. Structural and optical properties of homogeneous Cu(In,Ga)Se2 thin films prepared by thermal reaction of InSe/Cu/GaSe alloys with elemental Se vapour. J. Phys. D Appl. Phys. 2005, 38, 22. [Google Scholar] [CrossRef]
- Paulson, P.D.; Birkmire, R.W.; Shafarman, W.N. Optical characterization of CuIn1-xGaxSe2 alloy thin films by spectroscopic ellipsometry. J. Appl. Phys. 2003, 94, 879–888. [Google Scholar] [CrossRef]
- Parisi, A.; Pernice, R.; Rocca, V.; Curcio, L.; Stivala, S.; Cino, A.C.; Cipriani, G.; Di Dio, V.; Ricco Galluzzo, G.; Miceli, R.; et al. Graded carrier concentration absorber profile for high efficiency CIGS solar cells. Int. J. Photoenergy 2015, 2015, 410549. [Google Scholar] [CrossRef]
- Zarabar, F.I.; Zuhdi, A.W.M.; Bahrudin, M.S.; Abdullah, S.F.; Hasani, A.H. Numerical modelling of graded bandgap CIGS solar cell for performance improvement. In Proceedings of the 2019 Electron Devices Technology and Manufacturing Conference, EDTM 2019, Marina Bay Sands, Singapore, 13–15 March 2019. [Google Scholar]
- Severino, N.; Bednar, N.; Adamovic, N. Guidelines for Optimization of the Absorber Layer Energy Gap for High Efficiency Cu(In,Ga)Se 2 Solar Cells. J. Mater. Sci. Chem. Eng. 2018, 6, 147–162. [Google Scholar] [CrossRef] [Green Version]
- Lorbada, R.V.; Walter, T.; Marrón, D.F.; Muecke, D.; Lavrenko, T.; Salomon, O.; Schaeffler, R. Phototransistor behavior in CIGS solar cells and the effect of the back contact barrier. Energies 2020, 13, 4753. [Google Scholar] [CrossRef]
- Alzoubi, T.; Moustafa, M. Simulation analysis of functional MoSe2 layer for ultra-thin Cu(In,Ga)Se2 solar cells architecture. Mod. Phys. Lett. B 2020, 34, 2050065. [Google Scholar] [CrossRef]
- Zhu, X.; Zhou, Z.; Wang, Y.; Zhang, L.; Li, A.; Huang, F. Determining factor of MoSe2 formation in Cu(In,Ga)Se2 solar Cells. Sol. Energy Mater. Sol. Cells 2012, 101, 57–61. [Google Scholar] [CrossRef]
- Gao, S.; Jiang, Z.; Wu, L.; Ao, J.; Zeng, Y.; Sun, Y.; Zhang, Y. Interfaces of high-efficiency kesterite Cu2 ZnSnS(e)4 thin film solar cells. Chinese Phys. B 2018, 27, 018803. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Lin, S.; Li, W.; Cheng, S.; Zhang, Y.; Liu, Y.; Liu, W. Review on Alkali Element Doping in Cu(In,Ga)Se2Thin Films and Solar Cells. Engineering 2017, 3, 452–459. [Google Scholar] [CrossRef]
- Ott, T.; Walter, T.; Unold, T. Phototransistor effects in Cu(In,Ga)Se2 solar cells. Thin Solid Films 2013, 535, 275–278. [Google Scholar] [CrossRef]
- Ott, T.; Schönberger, F.; Walter, T.; Hariskos, D.; Kiowski, O.; Salomon, O.; Schäffler, R. Verification of phototransistor model for Cu(In,Ga)Se2solar cells. Thin Solid Films 2015, 582, 392–396. [Google Scholar] [CrossRef]
- Anderson, R.L. Germanium-Gallium Arsenide Heterojunctions [Letter to the Editor]. IBM J. Res. Dev. 1960, 4, 283–287. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; Wiley: Hoboken, NJ, USA, 2007; ISBN 978-0-471-14323-9. [Google Scholar]
- Hossain, E.S.; Chelvanathan, P.; Shahahmadi, S.A.; Sopian, K.; Bais, B.; Amin, N. Performance assessment of Cu2SnS3 (CTS) based thin film solar cells by AMPS-1D. Curr. Appl. Phys. 2018, 18, 79–89. [Google Scholar] [CrossRef]
- Ferdaous, M.T.; Shahahmadi, S.A.; Chelvanathan, P.; Akhtaruzzaman, M.; Alharbi, F.H.; Sopian, K.; Tiong, S.K.; Amin, N. Elucidating the role of interfacial MoS 2 layer in Cu 2 ZnSnS 4 thin film solar cells by numerical analysis. Sol. Energy 2019, 178, 162–172. [Google Scholar] [CrossRef]
- Dullweber, T.; Rau, U.; Contreras, M.A.; Noufi, R.; Schock, H.W. Photogeneration and carrier recombination in graded gap Cu(In, Ga)Se2 solar cells. IEEE Trans. Electron. Devices 2000, 47, 2249–2254. [Google Scholar] [CrossRef]
- Wang, Y.; Muryobayashi, T.; Nakada, K.; Li, Z.; Yamada, A. Correlation between carrier recombination and valence band offset effect of graded Cu(In,Ga)Se2 solar cells. Sol. Energy Mater. Sol. Cells 2019, 201, 110070. [Google Scholar] [CrossRef]
- Song, T.; Kanevce, A.; Sites, J.R. Emitter/absorber interface of CdTe solar cells. J. Appl. Phys. 2016, 119, 233104. [Google Scholar] [CrossRef]
- Paul, S.; Grover, S.; Repins, I.L.; Keyes, B.M.; Contreras, M.A.; Ramanathan, K.; Noufi, R.; Zhao, Z.; Liao, F.; Li, J.V. Analysis of Back-Contact Interface Recombination in Thin-Film Solar Cells. IEEE J. Photovolt. 2018, 8, 871–878. [Google Scholar] [CrossRef]
- Paul, S.; Lopez, R.; Mia, M.D.; Swartz, C.H.; Li, J.V. A Simulation Study on Radiative Recombination Analysis in CIGS Solar Cell. In Proceedings of the 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017. [Google Scholar]
- Li, J.V.; Grover, S.; Contreras, M.A.; Ramanathan, K.; Kuciauskas, D.; Noufi, R. A recombination analysis of Cu(In,Ga)Se2 solar cells with low and high Ga compositions. Sol. Energy Mater. Sol. Cells 2014, 124, 143–149. [Google Scholar] [CrossRef]








| Layer | Window | Buffer | Absorber | Interface |
|---|---|---|---|---|
| Material | ZnO | CdS | CIGS | MoSe2 |
| Thickness (μm) | 0.15 | 0.05 | 2.5 | 0.01–0.1 |
| 9 | 9 | 13.6 | 7.29 | |
| (cm2 V−1 s−1) | 100 | 100 | 100 | 25 |
| (cm2 V−1 s−1) | 25 | 25 | 25 | 100 |
| (cm−3) | 0 | 0 | 2.0 × 1016 | 1.0 × 1014–1.0 × 1020 |
| (cm−3) | 1.0 × 1018 | 1.0 × 1017 | 0 | 0 |
| (eV) | 3.3 | 2.4 | 1.011–1.676 (1 Ga-dep) | 1.0–1.5 |
| (cm−3) | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1018 |
| (cm−3) | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1019 |
| χ (eV) | 4.00 | 4.00 | 4.350–3.685 (1 Ga-dep) | 3.5–4.5 |
| Grading Profile | Grading Parameters | Variation |
|---|---|---|
| Double grading (DG) | Back/front composition (GGI) | 0–1 |
| (notch position) | 0 m–2.5 m | |
| (lowest composition) | 0–1 |
| 1.0 × 1014 | 1.0 × 1015 | 1.0 × 1016 | 1.0 × 1017 | 1.0 × 1018 | 1.0 × 1019 | 1.0 × 1020 | ||
|---|---|---|---|---|---|---|---|---|
| MoSe2/Mo | 4.9872 | 5.0467 | 5.1062 | 5.1658 | 5.2253 | 5.2848 | 5.3443 | |
| MoSe2/Mo | 0.0372 | 0.0967 | 0.1562 | 0.2158 | 0.2753 | 0.3348 | 0.3943 | |
| Band Diagram Parameters (eV) | |||||||
|---|---|---|---|---|---|---|---|
| 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | ||
| MoSe2/Mo | 4.8848 | 4.9848 | 5.0848 | 5.1848 | 5.2848 | 5.3848 | |
| MoSe2/Mo | −0.0652 | 0.0348 | 0.1348 | 0.2348 | 0.3348 | 0.4348 | |
| MoSe2/Mo | 1.05 | 1.05 | 1.05 | 1.05 | 1.05 | 1.05 | |
| MoSe2/Mo | −0.05 | 0.05 | 0.15 | 0.25 | 0.35 | 0.45 | |
| CIGS/MoSe2 | −0.04 | −0.04 | −0.04 | −0.04 | −0.04 | −0.04 | |
| CIGS/MoSe2 | −0.16 | −0.06 | 0.04 | 0.14 | 0.24 | 0.34 | |
| CIGS/MoSe2 | 0.00065 | 0.10065 | 0.20065 | 0.30065 | 0.40065 | 0.50065 | |
| Performance Parameter | Proposed Cell (CIGS without MoSe2) | Proposed Cell (CIGS with Optimized MoSe2) | Reference Cell [24] |
|---|---|---|---|
| JSC (mA/cm2) | 35.75 | 36.44 | 36.60 |
| VOC (V) | 0.681 | 0.815 | 0.746 |
| FF (%) | 82.88 | 78.46 | 79.30 |
| PCE (%) | 20.19 | 23.30 | 21.70 |
| Grading Profile | Grading Parameters | Optimum Values Found |
|---|---|---|
| Back grading (BG) | Back composition (GGI) | 0.7 |
| (lowest composition) | 0.3 | |
| Front grading (FG) | Front composition (GGI) | 0.8 |
| (lowest composition) | 0.3 |
| Ga Profiles | Solar Cell Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| Front:Back (GGI) | (eV) | (GGI) | 1 2.5– (μm) | VOC (V) | JSC (mA/cm2) | FF (%) | PCE (%) | |
| Model 1 (DG) | 0.8:0.7 | 1.50:1.43 | 0.2 | 2.00 | 0.820 | 39.20 | 78.36 | 25.18 |
| Model 2 (DG) | 0.8:0.7 | 1.50:1.43 | 0.2 | 1.25 | 0.820 | 39.45 | 78.47 | 25.37 |
| Model 3 (DG) | 0.8:0.7 | 1.50:1.43 | 0.2 | 0.25 | 0.820 | 39.31 | 78.41 | 25.26 |
| Model 4 (DG) | 0.5:0.8 | 1.28:1.50 | 0.3 | 0.25 | 0.856 | 36.24 | 80.07 | 24.83 |
| Model 5 (DG) | 0.5:0.5 | 1.28:1.28 | 0.3 | 1.25 | 0.815 | 36.40 | 81.53 | 24.19 |
| Ungraded bandgap cell | 0.3:0.3 | 1.20:1.20 | NA | NA | 0.815 | 36.44 | 78.46 | 23.30 |
| CIGS Bandgap (eV) | MoSe2 Bandgap | 1 (eV) | 2 (eV) | 3 (eV) | Solar Cell Parameters | |||
|---|---|---|---|---|---|---|---|---|
| VOC (V) | JSC (mA/cm2) | FF (%) | PCE (%) | |||||
| 1.50:1.43 | 1.0 | −0.07 | −0.36 | −0.1993 | 0.939 | 39.44 | 80.94 | 29.97 |
| 1.1 | −0.07 | −0.26 | −0.0993 | 1.166 | 39.47 | 68.35 | 31.46 | |
| 1.2 | −0.07 | −0.16 | 0.0007 | 1.055 | 39.47 | 75.09 | 30.97 | |
| 1.3 | −0.07 | −0.06 | 0.1007 | 0.868 | 39.45 | 81.89 | 28.06 | |
| 1.4 | −0.07 | 0.04 | 0.2007 | 0.820 | 39.45 | 78.47 | 25.37 | |
| Performance Parameter | Baseline Cell (Ungraded Bandgap without MoSe2) | Proposed Cell (Ungraded Bandgap with Optimized MoSe2) | Proposed Cell (DG Bandgap with Optimized MoSe2) |
|---|---|---|---|
| JSC (mA/cm2) | 35.75 | 36.44 | 39.45 |
| VOC (V) | 0.681 | 0.815 | 0.868 |
| FF (%) | 82.88 | 78.46 | 81.89 |
| PCE (%) | 20.19 | 23.30 | 28.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Za’abar, F.I.; Yusoff, Y.; Mohamed, H.; Abdullah, S.F.; Mahmood Zuhdi, A.W.; Amin, N.; Chelvanathan, P.; Bahrudin, M.S.; Rahman, K.S.; Samsudin, N.A.; et al. A Numerical Investigation on the Combined Effects of MoSe2 Interface Layer and Graded Bandgap Absorber in CIGS Thin Film Solar Cells. Coatings 2021, 11, 930. https://doi.org/10.3390/coatings11080930
Za’abar FI, Yusoff Y, Mohamed H, Abdullah SF, Mahmood Zuhdi AW, Amin N, Chelvanathan P, Bahrudin MS, Rahman KS, Samsudin NA, et al. A Numerical Investigation on the Combined Effects of MoSe2 Interface Layer and Graded Bandgap Absorber in CIGS Thin Film Solar Cells. Coatings. 2021; 11(8):930. https://doi.org/10.3390/coatings11080930
Chicago/Turabian StyleZa’abar, Fazliyana Izzati, Yulisa Yusoff, Hassan Mohamed, Siti Fazlili Abdullah, Ahmad Wafi Mahmood Zuhdi, Nowshad Amin, Puvaneswaran Chelvanathan, Mohd. Shaparuddin Bahrudin, Kazi Sajedur Rahman, Nurul Asma Samsudin, and et al. 2021. "A Numerical Investigation on the Combined Effects of MoSe2 Interface Layer and Graded Bandgap Absorber in CIGS Thin Film Solar Cells" Coatings 11, no. 8: 930. https://doi.org/10.3390/coatings11080930
APA StyleZa’abar, F. I., Yusoff, Y., Mohamed, H., Abdullah, S. F., Mahmood Zuhdi, A. W., Amin, N., Chelvanathan, P., Bahrudin, M. S., Rahman, K. S., Samsudin, N. A., & Wan Abdullah, W. S. (2021). A Numerical Investigation on the Combined Effects of MoSe2 Interface Layer and Graded Bandgap Absorber in CIGS Thin Film Solar Cells. Coatings, 11(8), 930. https://doi.org/10.3390/coatings11080930









