Development of a Mechanistic Method to Obtain Load Position Strain in Instrumented Pavement
Abstract
:1. Introduction
2. Proposal of the Mechanistic Method to Obtain Load Position Strain
2.1. Preliminaries
2.2. Mechanistic Method to Obtain Load Position Strain
3. Verification of Proposed Method in the Field
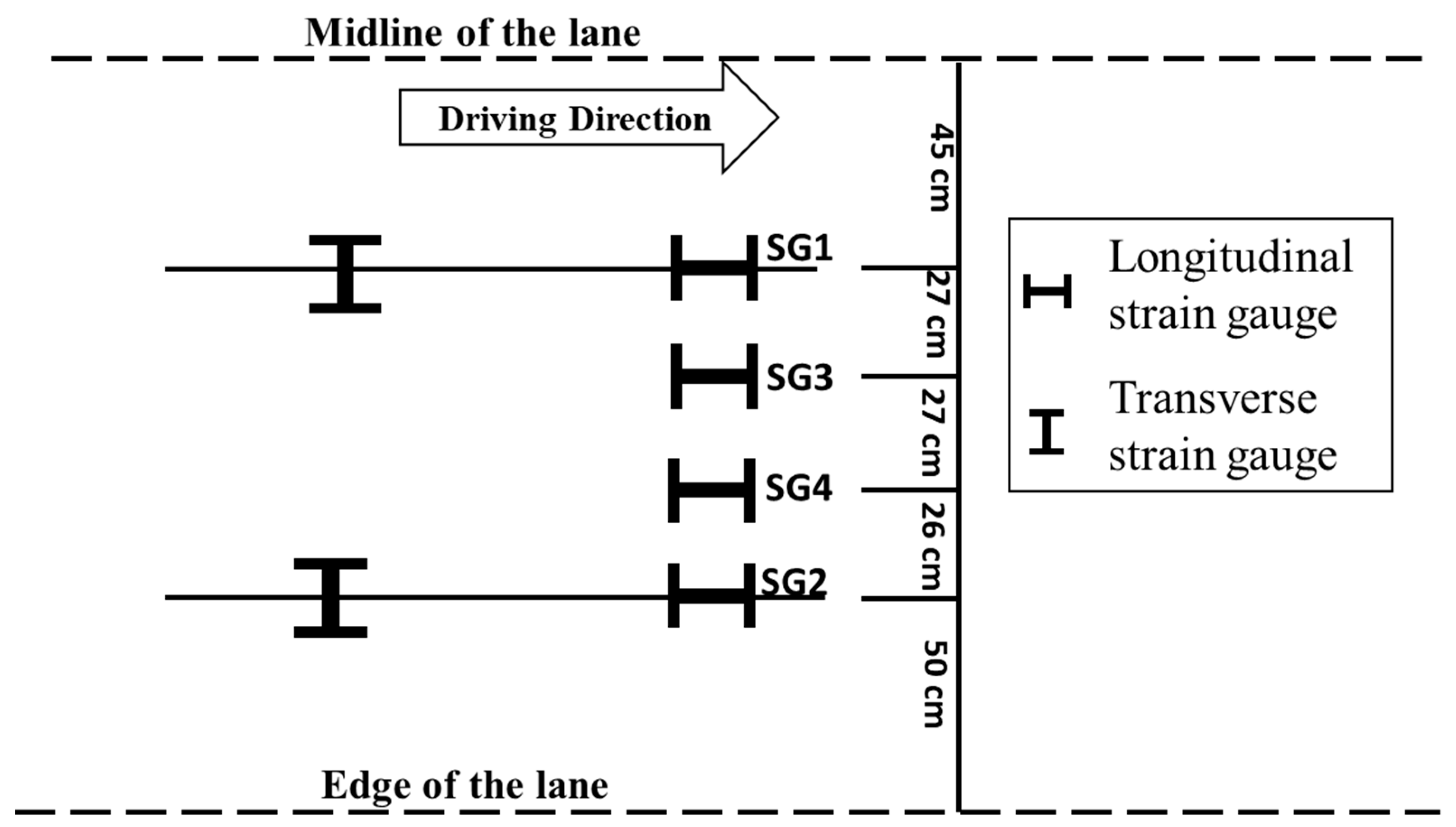
3.1. Test Plan
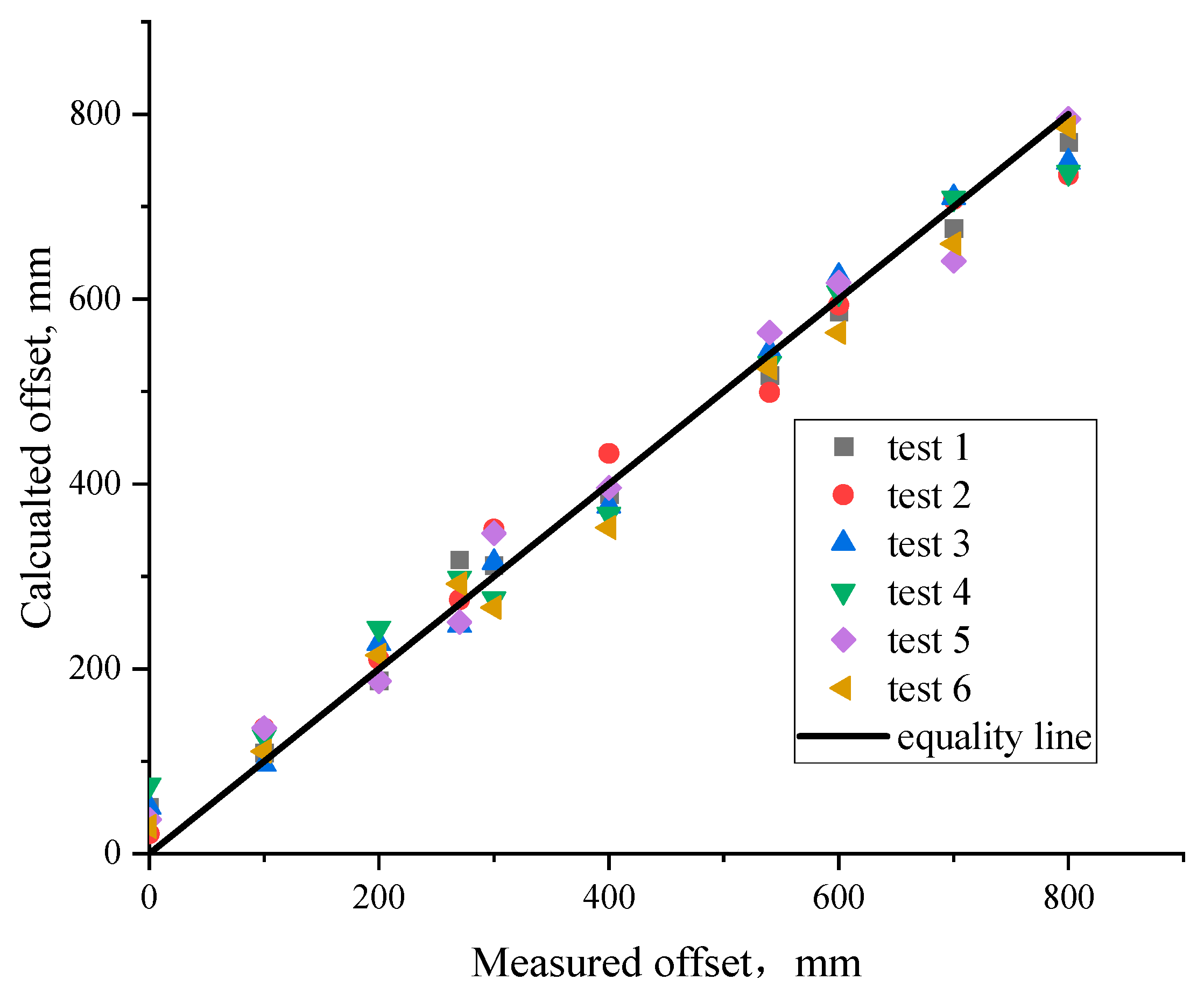
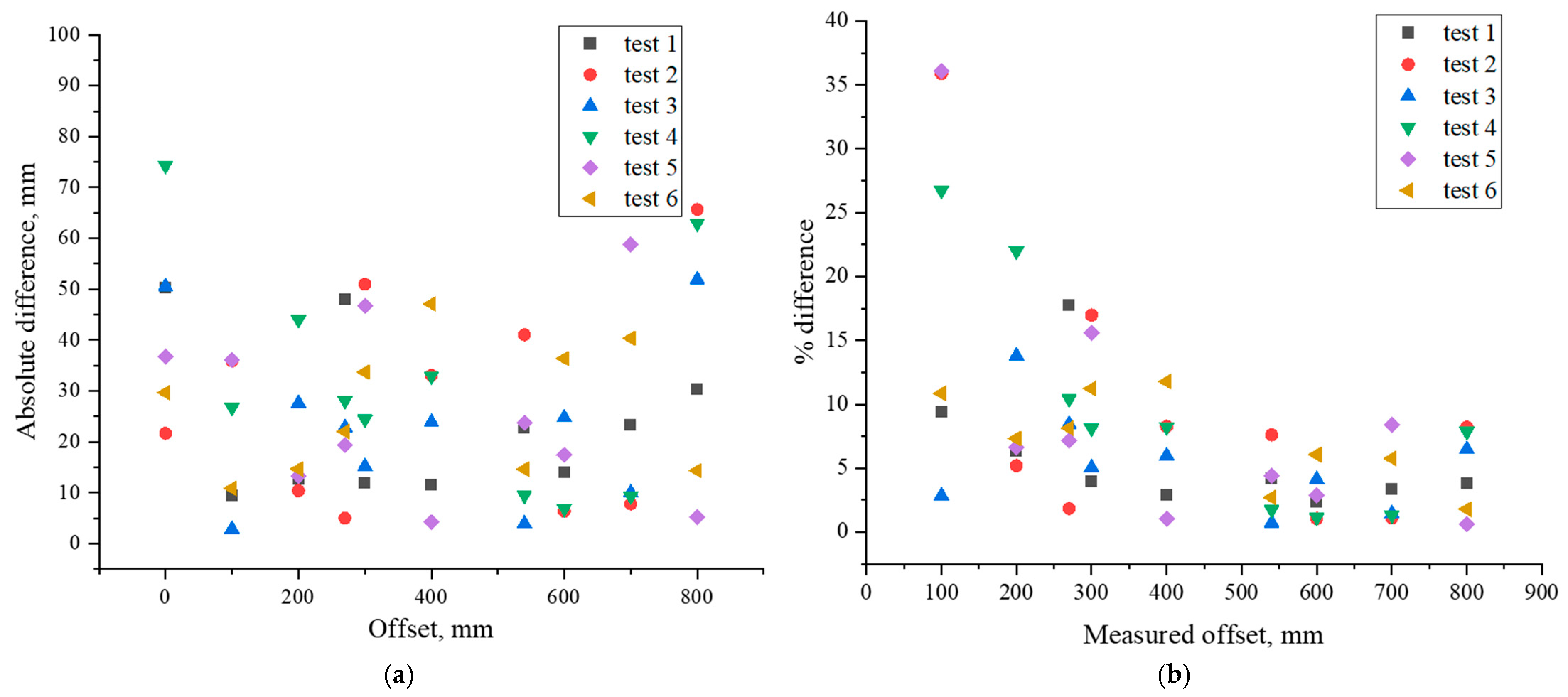
3.2. Offset Verification
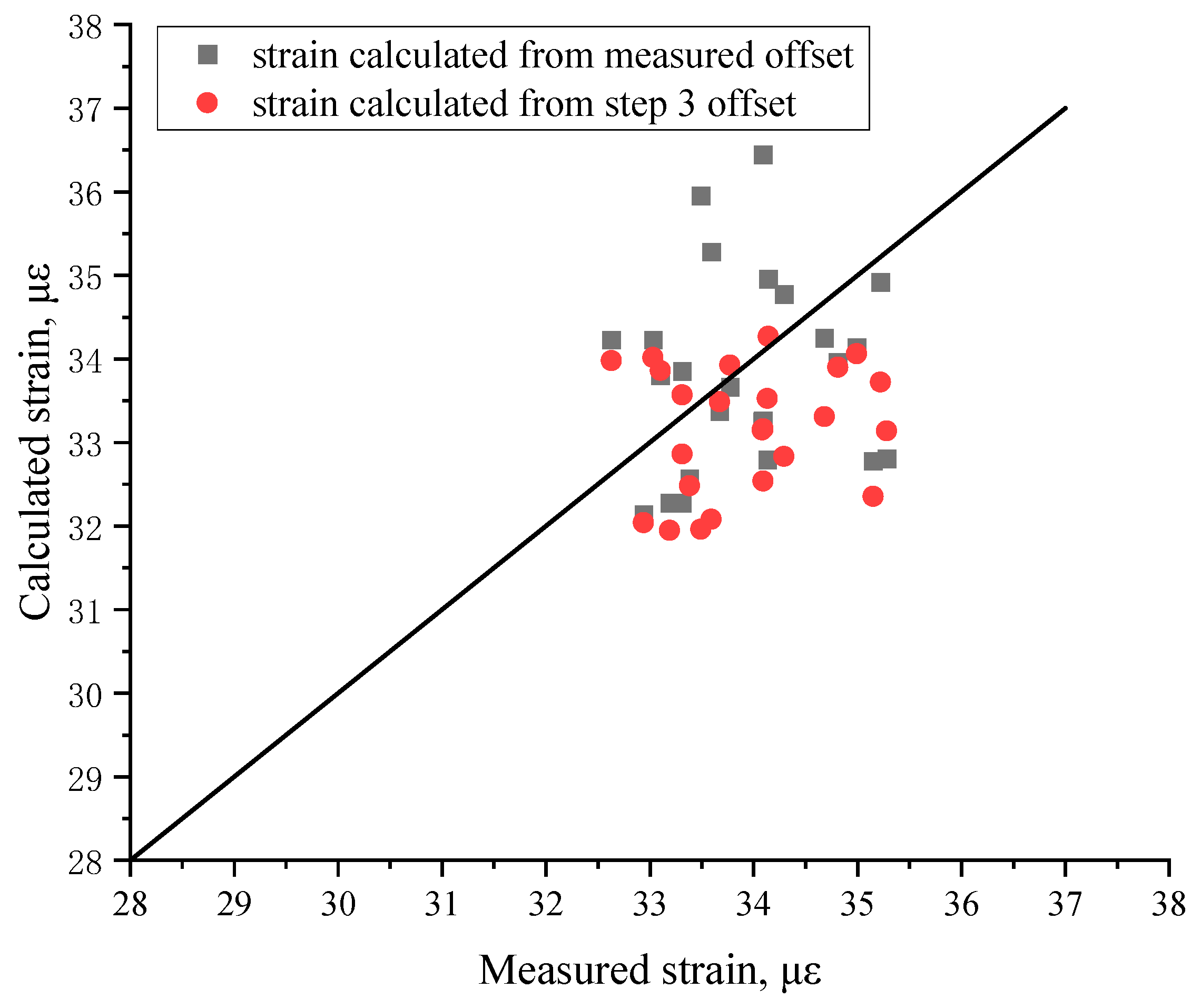
3.3. Load Position Strain Verification
4. Application of the Proposed Method
5. Discussion
6. Conclusions
- The proposed method was based on the elastic multilayer theory and correlated the theoretical strain with the measured strain by a second-order polynomial model. It allows the calculation of the load position stain without installation of lateral position system in instrumented pavement.
- In the proposed method, it was recommended that at least two gauges should be installed into the pavement with the lateral space 80 cm at least to cover the wheel wander range.
- The result of the verification shows that the ranges of the differences between the measured strains and those calculated from the offset were 0.5–2.5 με for the absolute difference and 0.5–16% for the %difference. The one-way analysis of variance showed there is no significant difference between the measured and calculated from the proposed method.
- The result of the application shows that load position strain calculated from proposed method has a good correlation with temperature which means this method maintains a good consistency with the results of verification.
- Due to the limited validation and application data, the applicability of this method in other pavement structures needs to be further verified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Timm, D.H.; Priest, A.L.; McEwen, T.V. Design and Instrumentation of the Structural Pavement Experiment at the NCAT Test Track. Report No. 04-01; National Center for Asphalt Technology, Auburn University: Auburn, AL, USA, 2004. [Google Scholar]
- Selvaraj, S.I. Review on the Use of Instrumented Pavement Test Data in Validating Flexible Pavement Mechanistic Load Response Models. In Proceedings of the 8th International Conference on Traffic and Transportation Studies, Changsha, China, 1–3 August 2012. [Google Scholar]
- Al-Qadi, I.L.; Loulizi, A.; Elseifi, M.; Lahouar, S. The Virginia Smart Road: The impact of pavement instrumentation on understanding pavement performance. J. Assoc. Asph. Paving Technol. 2004, 73, 427–465. [Google Scholar]
- Nur, H.E.I.; Singh, D.; Musharraf, Z.P.E. Dynamic Modulus-based Field Rut Prediction Model from an Instrumented Pavement Section. Procedia-Soc. Behav. Sci. 2013, 104, 129–138. [Google Scholar]
- Asefzadeh, A.; Hashemian, L.; Bayat, A. Fatigue Life Evaluation of Pavement Embankments made with Tire Derived Aggregates. Can. J. Civ. Eng. 2018, 45, 795–802. [Google Scholar] [CrossRef]
- Solanki, P.; Zaman, M.; Muraleetharan, K.K. Field Performance Monitoring and Modeling of Instrumented Pavement on I-35 in McClain County—Construction and Instrumentation Report; School of Civil Engineering and Environmental Science, University of Oklahoma: Norman, OK, USA, 2008. [Google Scholar]
- Timm, D.H.; Priest, A.L. Wheel Wander at the NCAT Test Track (No. 05–02); National Center for Asphalt Technology: Auburn, AL, USA, 2005. [Google Scholar]
- Shafiee, M.H.; Nassiri, S.; Eng, P.; Bayat, A. Field investigation of the effect of operational speed and lateral wheel wander on flexible pavement mechanistic responses. In Proceedings of the Transportation 2014: Past, Present, Future—2014 Conference and Exhibition of the Transportation Association of Canada, Montreal, QC, Canada, 28 September–October 2014. [Google Scholar]
- Chen, F.; Song, M.; Ma, X.; Zhu, X. Assess the impacts of different auftonomous trucks’ lateral control modes on asphalt pavement performance. Transp. Res. Part C. Emerg. Technol. 2019, 103, 17–29. [Google Scholar] [CrossRef]
- Noorvand, H.; Karnati, G.; Underwood, B.S. Autonomous vehicles: Assessment of the implications of truck positioning on flexible pavement performance and design. Transp. Res. Rec. 2017, 2640, 21–28. [Google Scholar] [CrossRef]
- Willis, J.R.; Timm, D.H. Repeatability of Asphalt Strain Measurements Under Full-Scale Dynamic Loading. J. Transp. Res. Board 2008, 2087, 40–48. [Google Scholar] [CrossRef]
- Timm, D.H.; Robbins, M.M.; Willis, J.R.; Tran, N.; Taylor, A.J. Field and Laboratory Study of High-Polymer Mixtures at the NCAT Test Track Interim Report; National Center for Asphalt Technology: Auburn, AL, USA, 2012. [Google Scholar]
- Burnham, T.R.; Tewfik, A.; Srirangarajan, S. Development of a Computer Program for Selecting Peak Dynamic Sensor Responses from Pavement Testing; Minnesota Department of Transportation: Saint Paul, MN, USA, 2007.
- Benekohal, R.F.; Hall, K.T.; Miller, H.W. Effect of lane widening on lateral distribution of truck wheels. Transp. Res. Rec. 1990, 1286, 57–66. [Google Scholar]
- Buiter, R.; Cortenraad, W.M.; Van Eck, A.C.; Van Rij, H. Effects of Transverse Distribution of Heavy Vehicles on Thickness Design of Full-Depth Asphalt Pavements. Transp. Res. Rec. 1989, 1227, 66–74. [Google Scholar]
- Bruno, S.; Del Serrone, G.; Di Mascio, P.; Loprencipe, G.; Ricci, E.; Moretti, L. Technical Proposal for Monitoring Thermal and Mechanical Stresses of a Runway Pavement. Sensors 2021, 21, 6797. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Han, W.; Ma, S.; Hu, G. Enhanced Processing of Low Signal-to-Noise-Ratio Dynamic Signals from Pavement Testing. Measurement 2021, 182, 109697. [Google Scholar] [CrossRef]
- Mazumder, M.; Kim, H.; Lee, S.J. Perpetual Pavement: Future Pavement Network. J. Adv. Constr. Mater. 2015, 19, 1. [Google Scholar]
- Van Cauwelaert, F.J.; Lequeux, D. Computer Programs for the Determination of stresses and Displacements in four Layered Structures; Water Experiment Station, U.S. Army Corps of Engineers: Vicksburg, MS, USA, 1986.
- Yang, Y.; Wei, J.; Lin, W.; Timm, D.; Huber, G. Binzhou Perpetual Pavement Test Road Dynamic Response of Pavement Under Very Heavy Loads. Int. J. Road Mater. Pavement Des. 2009, 10, 151–166. [Google Scholar] [CrossRef]
- Yang, Y.S.; Wang, L.; Wei, J.C.; Ma, S.J. Typical Pavement Structure Dynamic Response Data Collection and Analysis under Heavy Vehicle Loading. J. Highw. Transp. Res. Dev. 2010, 27, 10–16. [Google Scholar]





| Dynamic Strain, με | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test Number | 1 | 2 | 3 | 4 | 5 | 6 | |||||||
| Strain Gauge | SG1 | SG2 | SG1 | SG2 | SG1 | SG2 | SG1 | SG2 | SG1 | SG2 | SG1 | SG2 | |
| Offset, mm | 0 | 34.09 | 21.69 | 34.81 | 21.29 | 34.08 | 21.69 | 32.94 | 21.64 | 33.38 | 20.85 | 34.99 | 21.64 |
| 100 | 34.20 | 23.52 | 33.91 | 24.12 | 34.36 | 23.26 | 32.74 | 23.02 | 34.52 | 24.56 | 35.21 | 24.26 | |
| 200 | 34.06 | 25.83 | 33.92 | 26.47 | 33.66 | 26.83 | 32.52 | 26.45 | 33.95 | 25.73 | 32.48 | 25.48 | |
| 270 | 32.07 | 28.57 | 33.59 | 28.38 | 34.01 | 27.77 | 32.60 | 28.34 | 34.01 | 27.89 | 33.45 | 28.86 | |
| 300 | 33.27 | 29.42 | 32.86 | 30.50 | 32.75 | 29.08 | 33.11 | 28.00 | 32.45 | 29.96 | 34.04 | 28.46 | |
| 400 | 32.19 | 31.31 | 31.64 | 32.56 | 31.41 | 30.08 | 32.54 | 30.81 | 30.41 | 29.85 | 32.27 | 30.02 | |
| 540 | 29.56 | 33.95 | 29.53 | 33.10 | 28.22 | 33.59 | 28.63 | 33.47 | 27.73 | 33.91 | 27.72 | 32.18 | |
| 600 | 26.43 | 33.33 | 27.01 | 34.43 | 25.86 | 34.45 | 26.59 | 34.53 | 26.37 | 34.76 | 26.67 | 32.61 | |
| 700 | 23.77 | 34.16 | 22.97 | 34.61 | 22.58 | 34.14 | 23.24 | 35.10 | 25.06 | 34.18 | 23.45 | 32.86 | |
| 800 | 20.62 | 34.29 | 21.32 | 33.49 | 20.92 | 33.59 | 21.61 | 34.09 | 19.14 | 33.19 | 20.31 | 34.68 | |
| Offset, mm | Strain Gauge | Test Number | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Load Position Strain, με | |||||||
| 0 | SG1 | 34.09 | 34.81 | 34.08 | 32.94 | 33.38 | 34.99 |
| 27 | SG3 | 33.31 | 33.10 | 32.63 | 35.28 | 33.03 | 33.77 |
| 54 | SG4 | 34.14 | 35.22 | 33.67 | 33.31 | 34.13 | 35.15 |
| 80 | SG2 | 34.29 | 33.49 | 33.59 | 34.09 | 33.19 | 34.68 |
| Pavement Structure | Materials | Thickness, cm | Modulus, MPa | Poisson’s Ratio |
|---|---|---|---|---|
| Surface course | SMA-13 | 4 | 8700 | 0.25 |
| Upper binder course | AC-20 | 8 | 9000 | 0.25 |
| Lower binder course | AC-25 | 36 | 9800 | 0.25 |
| Base course | Cement stabilized crush stones | 20 | 12,000 | 0.25 |
| Subgrade | Compacted subgrade | - | 60 | 0.4 |
| Degrees of Freedom | Sum of Squares | Mean Square | F Value | Prob > F | |
|---|---|---|---|---|---|
| Model | 1 | 79.29785 | 79.29785 | 0.00134 | 0.97084 |
| Error | 118 | 6,970,853.425 | 59,075.03 | - | - |
| Sum | 119 | 6,970,932.723 | - | - | - |
| Degrees of Freedom | Sum of Squares | Mean Square | F Value | Prob > F | |
|---|---|---|---|---|---|
| Model | 2 | 4.22862 | 2.11431 | 2.53545 | 0.08659 |
| Error | 69 | 57.53906 | 0.8339 | - | - |
| Sum | 71 | 61.76768 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Han, W.; Wei, J.; Wang, D.; Zhang, X.; Hu, W.; Chen, W. Development of a Mechanistic Method to Obtain Load Position Strain in Instrumented Pavement. Coatings 2022, 12, 14. https://doi.org/10.3390/coatings12010014
Hu G, Han W, Wei J, Wang D, Zhang X, Hu W, Chen W. Development of a Mechanistic Method to Obtain Load Position Strain in Instrumented Pavement. Coatings. 2022; 12(1):14. https://doi.org/10.3390/coatings12010014
Chicago/Turabian StyleHu, Guiling, Wenyang Han, Jincheng Wei, Deqing Wang, Xiaomeng Zhang, Wenjun Hu, and Wei Chen. 2022. "Development of a Mechanistic Method to Obtain Load Position Strain in Instrumented Pavement" Coatings 12, no. 1: 14. https://doi.org/10.3390/coatings12010014
APA StyleHu, G., Han, W., Wei, J., Wang, D., Zhang, X., Hu, W., & Chen, W. (2022). Development of a Mechanistic Method to Obtain Load Position Strain in Instrumented Pavement. Coatings, 12(1), 14. https://doi.org/10.3390/coatings12010014






