Influence of Interface Temperature on the Electric Contact Characteristics of a C-Cu Sliding System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Device
2.2. Test Conditions and Test Materials
2.3. Test Data Processing
3. Results and Discussions
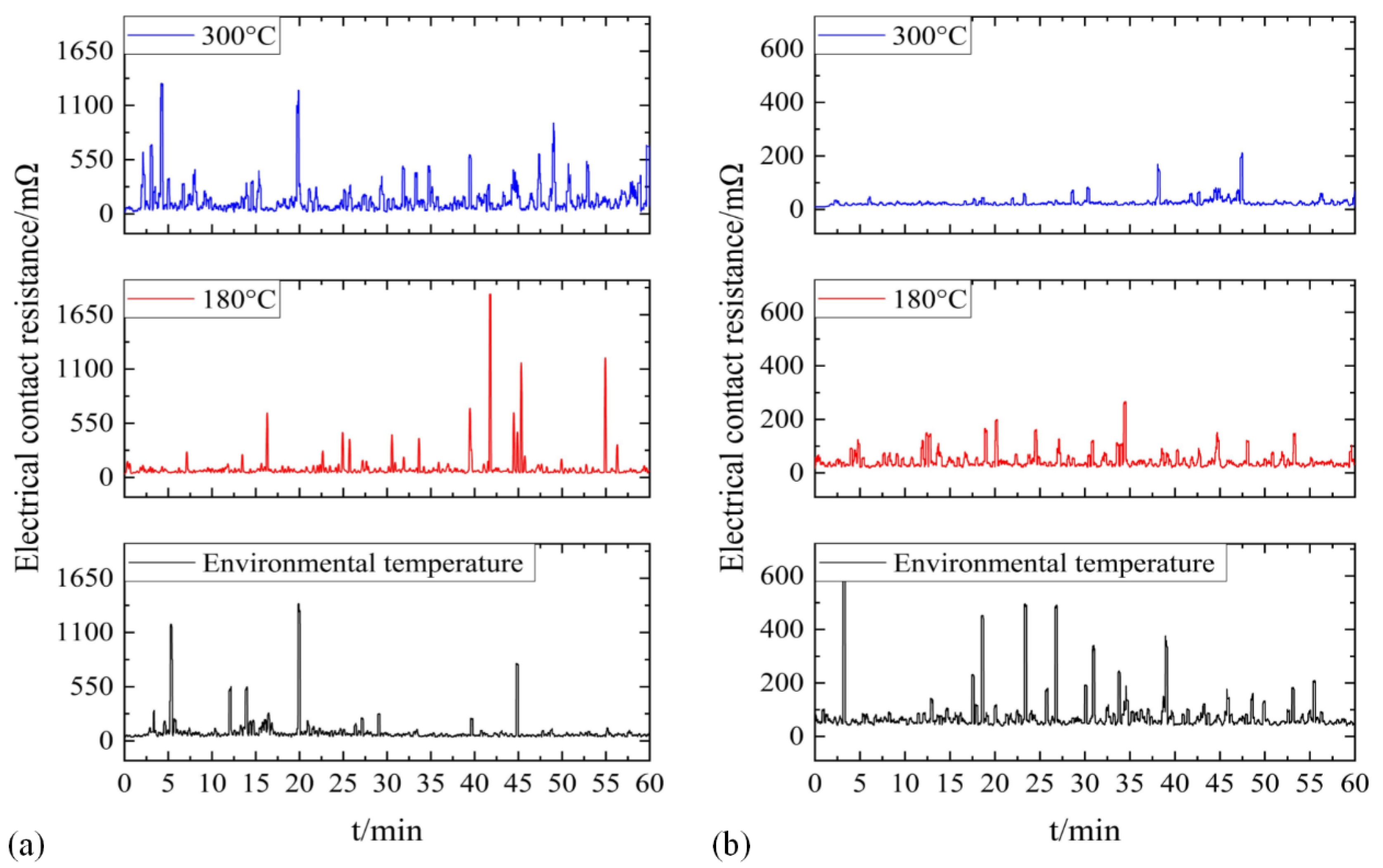
3.1. Influence of Interface Temperature on ECR under Different Current
3.2. Influence of Interface Temperature on Arc Discharge under Different Current
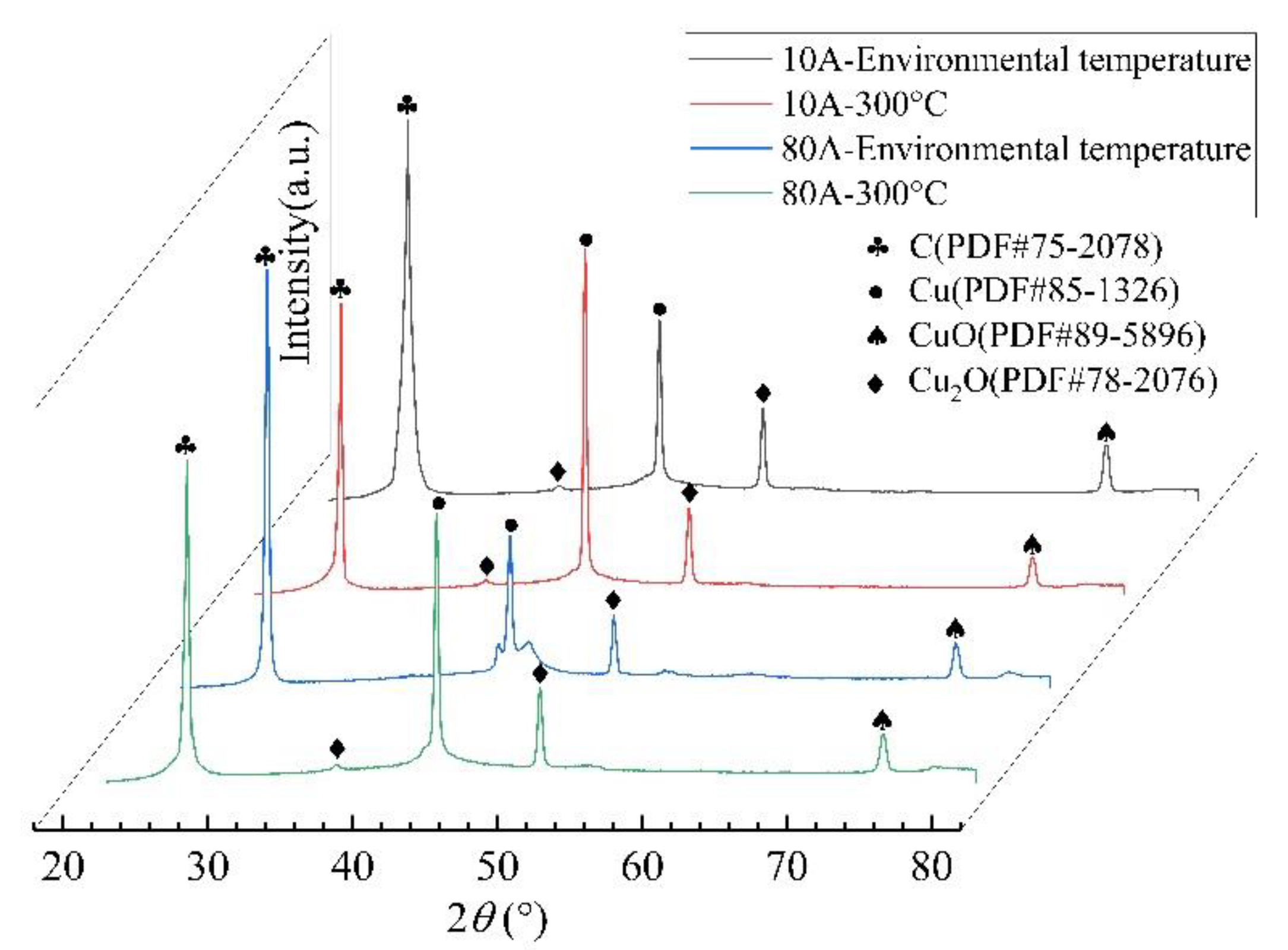
3.3. Phase Composition Analysis under Different Interface Temperature
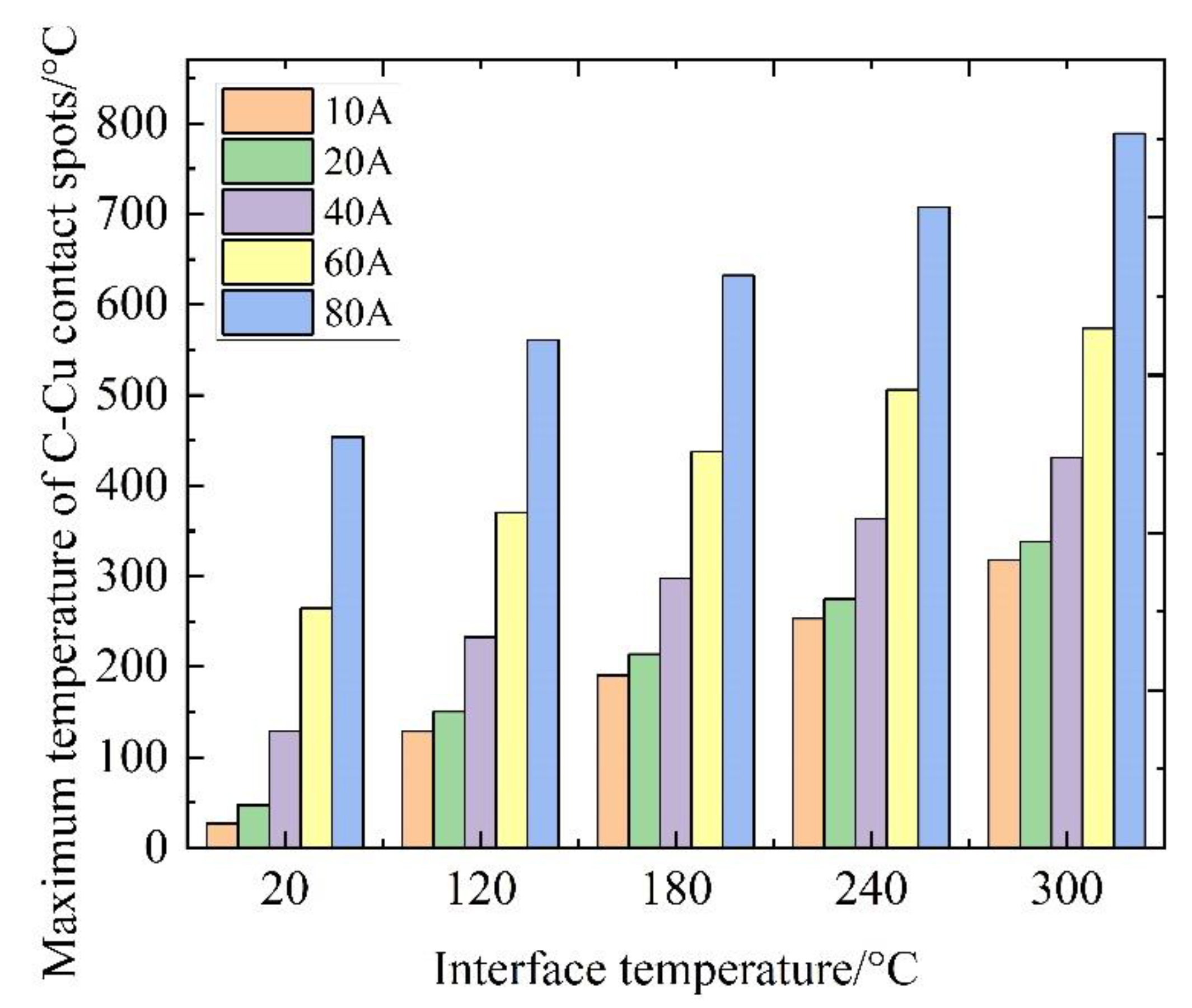
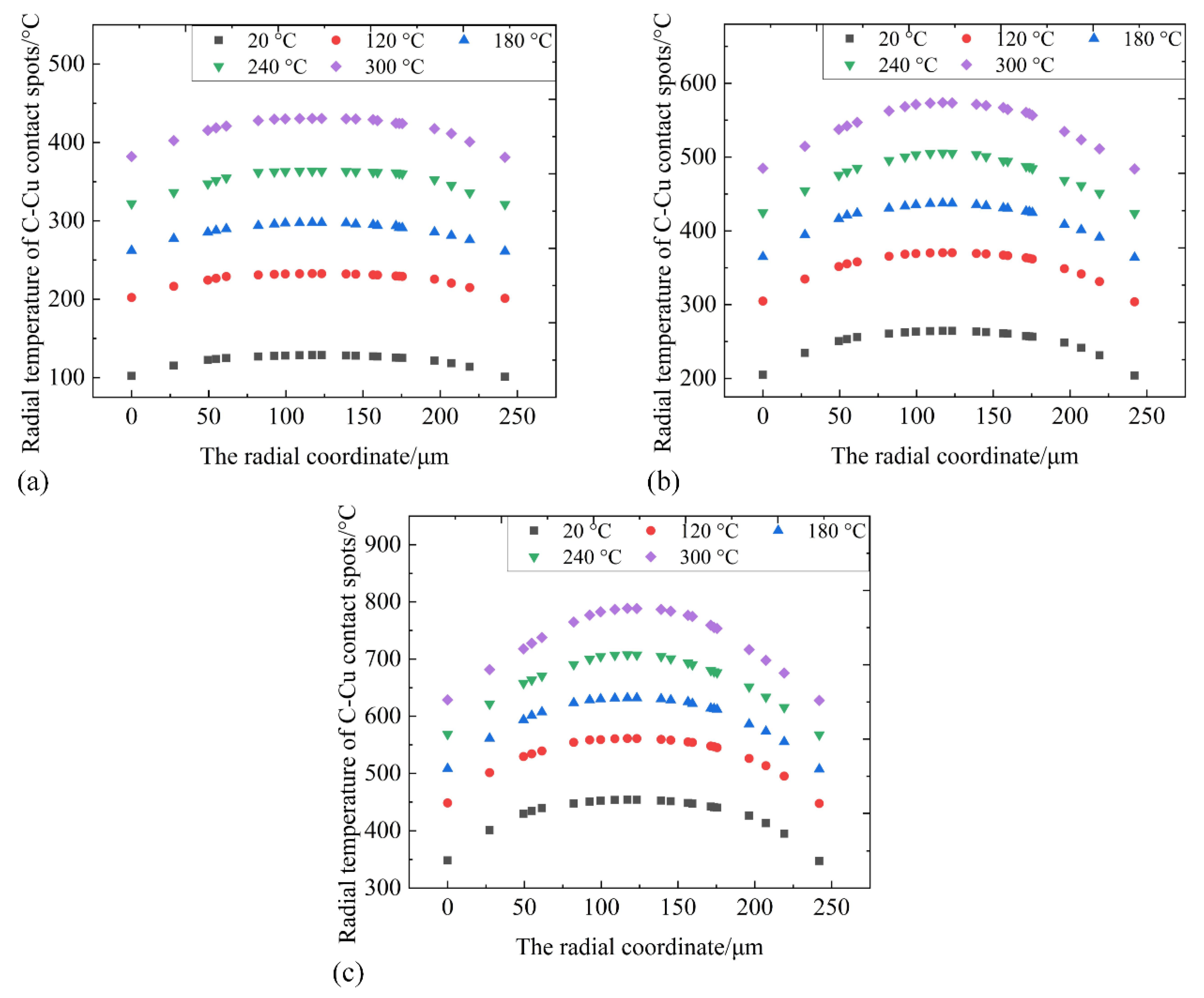
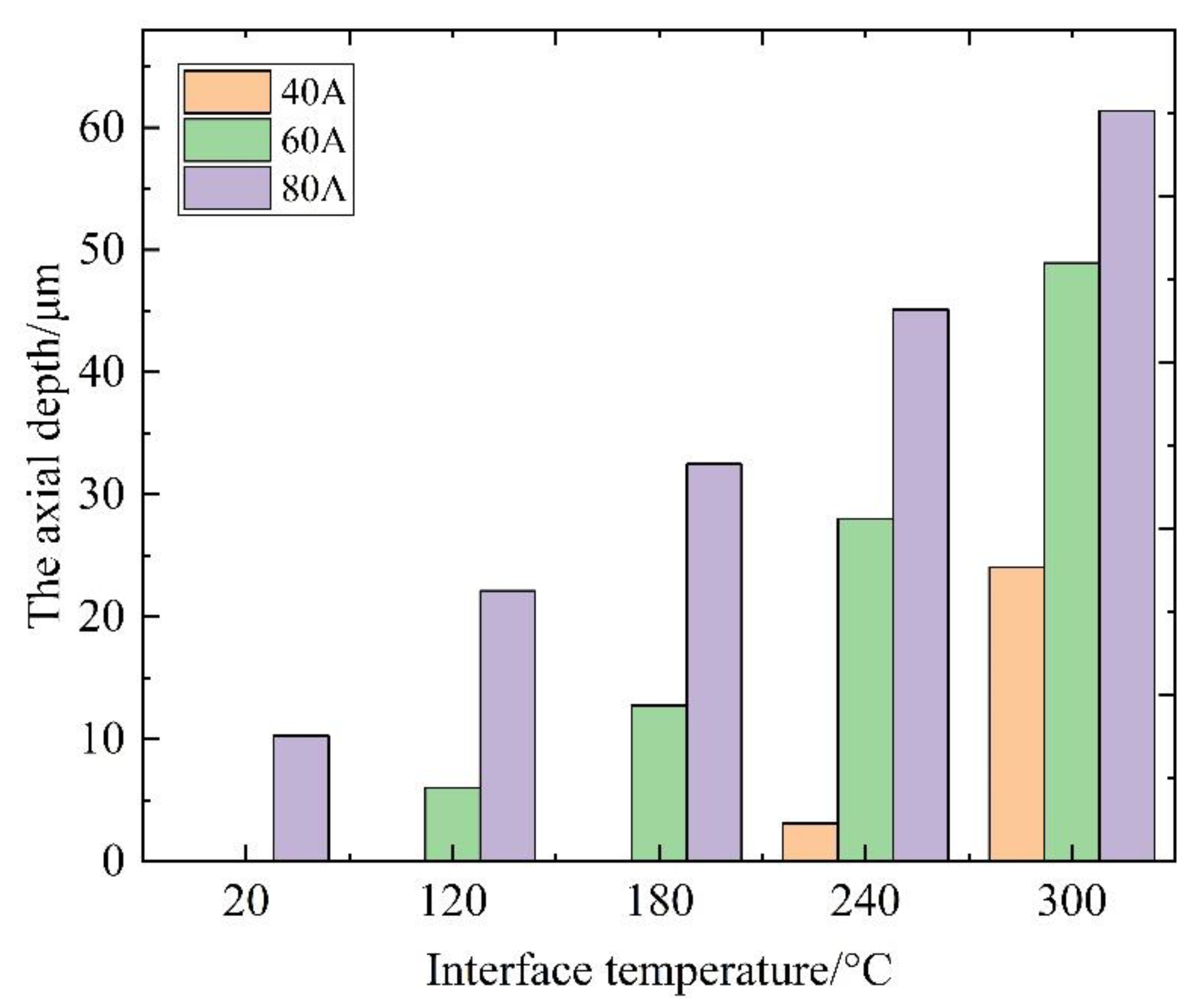
3.4. Temperature Distribution of C-Cu Contact Spot under Different Interface Temperature
3.4.1. Finite Element Model of C-Cu Contacts in Pantograph-Contact Line System
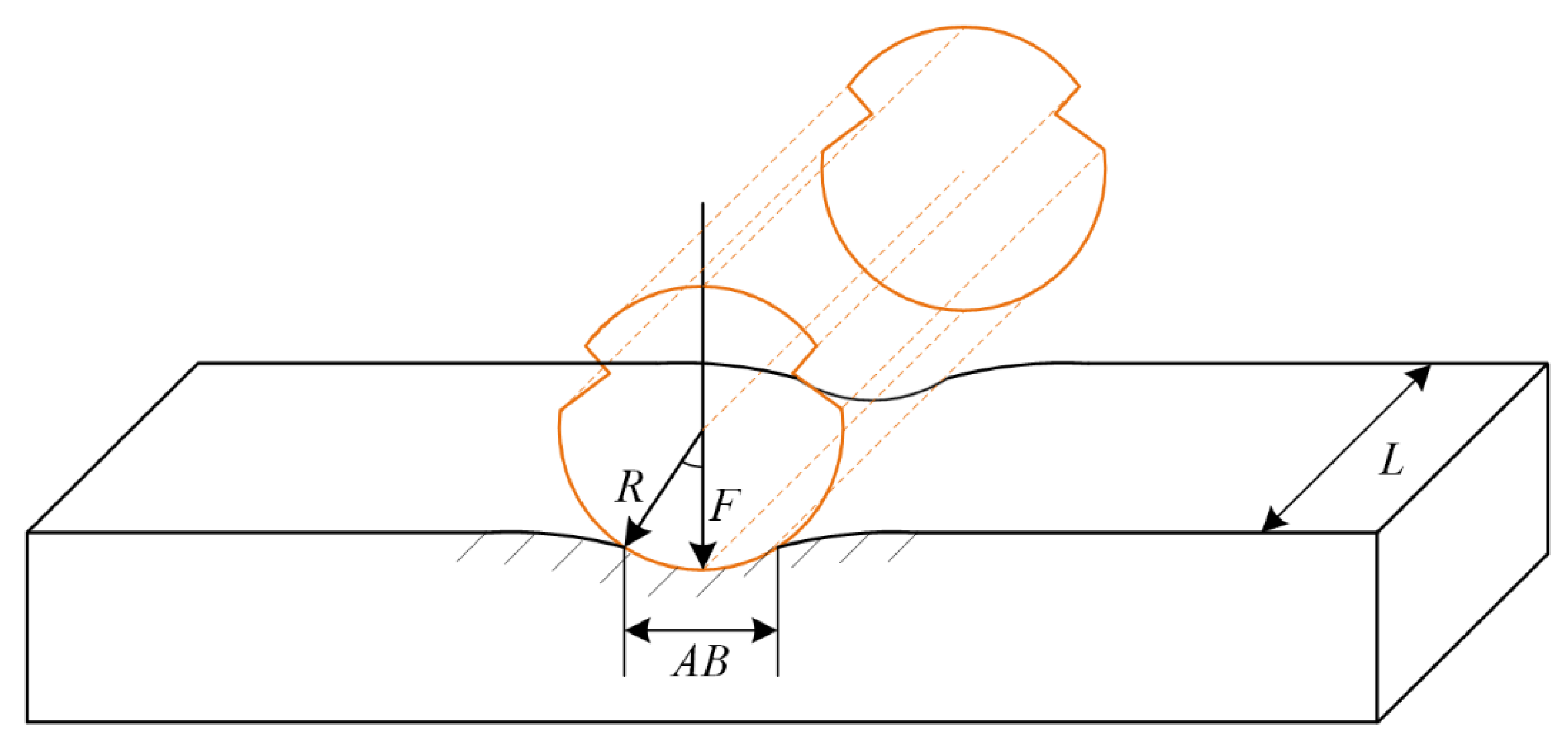
3.4.2. Analysis of the Thermal Process of the C-Cu Contact Spots in a Pantograph-Contact Line System
- (1)
- Material properties, such as density and thermal conductivity, change little within a certain temperature range, which can be ignored. In the simulation calculation, the material characteristics of carbon, copper, and their contact interface remain unchanged;
- (2)
- The friction heat and joule heat are completely absorbed by the C-Cu contact spots;
- (3)
- The distance between each contact spot is far enough, and relative to their size, so the interaction between the contact spots can be ignored;
- (4)
- The initial temperature of the carbon slider surface is set as the interface temperatures that are controlled by the external heat source in the test. The copper contact line is considered to be infinitely long, and the position that is far enough from the contact areas is set to room temperature (20 °C);
- (5)
- Only heat conduction and convection are considered in the calculation of the temperature distribution of the C-Cu contact spots, and the thermal radiation process is not considered.
3.4.3. Analysis of Temperature Distribution Characteristics of the C-Cu Contact Spots in the Pantograph-Contact Line System
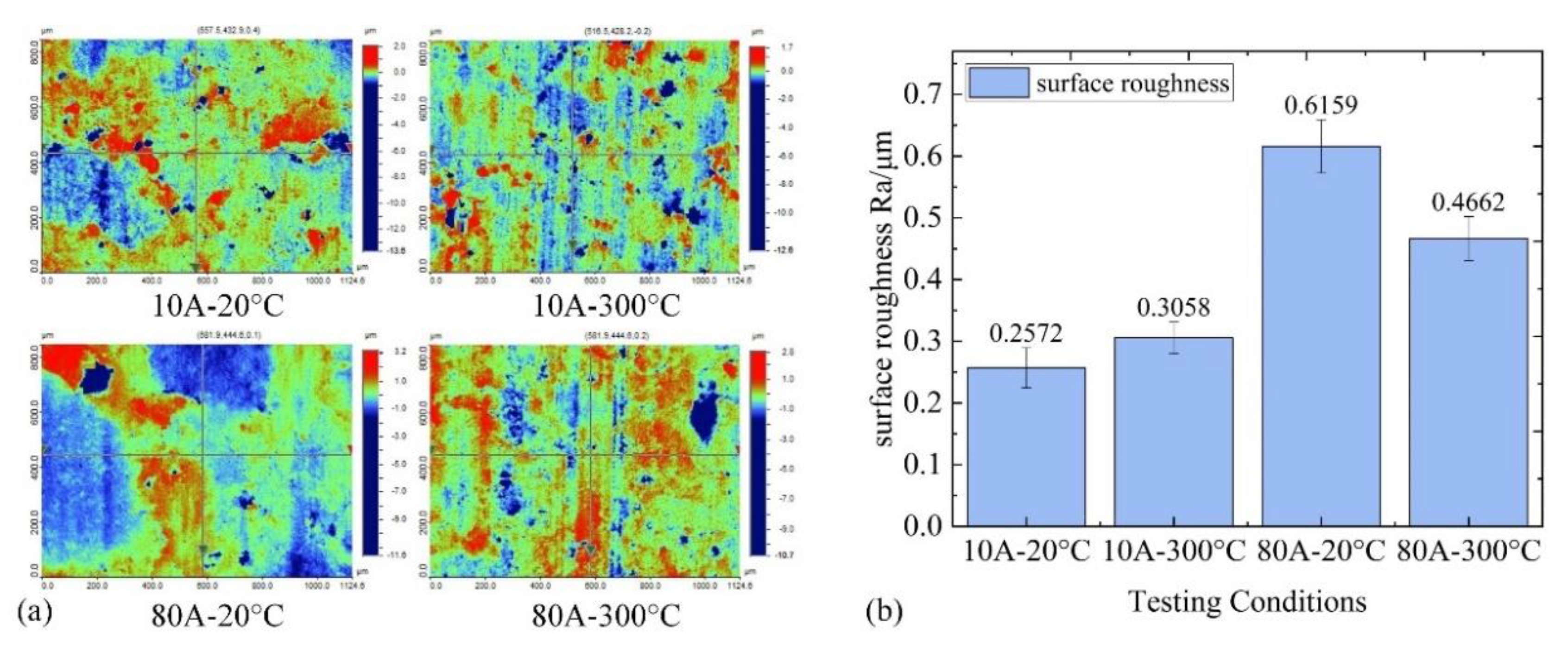
3.5. Influence of the Interface Temperature on the Surface Morphology of the Carbon Slider under Different Currents
4. Conclusions
- (1)
- When the current is ≤20 A, the AECR shows an upward trend with the rise in interface temperature; the DECR fluctuates around 75 mΩ, and the amplitude of the DECR increases. High temperature promotes the increase in copper oxide at the interface, but the temperature at the contact spots does not reach the softening temperature of the copper material. The increase in the velamen resistance is the main reason for the increase in the ECR;
- (2)
- When the current is ≥60 A, the AECR decreases with the rise in interface temperature; the DECR shifts downward, and the amplitude decreases. The temperature at the contact spots exceeds the softening temperature of the copper material. The contact spots soften, and the contraction resistance decreases. However, the rate of formation and spalling of the oxide film increases synchronously, and the velamen resistance remains constant with the rise in interface temperature. Therefore, the ECR is mainly determined by the contraction resistance;
- (3)
- When the current is ≤60 A, the single discharge energy decreases, and the discharge frequency increases with the rise in interface temperature. The reason is that the interface temperature is transmitted to the surrounding air; the thermal movement of gas molecules is intensified, and the breakdown voltage drops;
- (4)
- When the current reaches 80 A, the single discharge energy presents a V-shaped distribution with interface temperature, and the minimum point appears at 180 °C. A large amount of CO2 generated by the carbon material’s intense oxidation increases the breakdown field strength of the air around the contact interface, which is the main reason for the increase in the single discharge energy after 180 °C;
- (5)
- When the current is 10 A with rising interface temperature, the size of the discharge erosion pits decreases, the number of erosion pits increases on the carbon surface, and the surface roughness, Ra, increases by 18.9%. When the current is 80 A, the size of the erosion pits decreases significantly with the rise in interface temperature, and the surface roughness, Ra, decreases by 24.4%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, Z.; Gao, G.; Wei, W.; Yang, Z.; Xie, W.; Dong, K.; Ma, Y.; Yang, Y.; Wu, G. Characteristics of pantograph-catenary arc under low air pressure and strong airflow. High Volt. 2021, 7, 369–381. [Google Scholar] [CrossRef]
- Chen, Q.C.; Yang, Z.F.; Lin, J.H.; Wei, W.; Li, H.; Yin, G.; Liu, Y.; Li, P.; Tu, C. Scalable, low-cost, and environment-friendly preparation of high strength car-bon-matrix composites with tree-root-like structured reinforcements. Compos. Commun. 2022, 32, 101149. [Google Scholar] [CrossRef]
- Li, S.; Yang, X.; Kang, Y.; Li, Z.; Li, H. Progress on Current-Carry Friction and Wear: An Overview from Measurements to Mechanism. Coatings 2022, 12, 1345. [Google Scholar] [CrossRef]
- Gao, G.; Hao, J.; Wei, W.; Hu, H.; Zhu, G.; Wu, G. Dynamics of Pantograph–Catenary Arc During the Pantograph Lowering Process. IEEE Trans. Plasma Sci. 2016, 44, 2715–2723. [Google Scholar] [CrossRef]
- Bouchoucha, A.; Chekroud, S.; Paulmier, D. Influence of the electrical sliding speed on friction and wear processes in an electrical contact copper–stainless steel. Appl. Surf. Sci. 2004, 223, 330–342. [Google Scholar] [CrossRef]
- Yang, X.-Z.; Li, S.-B.; Cui, Y.; Kang, Y.-Q.; Li, Z.-Y.; Li, H.-W.; Dong, H. Measurement and Interpretation of the Effect of Electrical Sliding Speed on Contact Characteristics of On-Load Tap Changers. Coatings 2022, 12, 1436. [Google Scholar] [CrossRef]
- Liu, X.-L.; Li, Z.-H.; Hu, M.-J.; Zhou, C.-W.; Xiao, Q.; Yang, W.-B.; Chen, D.-Y. Research on the wear properties of carbon strips and contact wires at frigid temperatures. Wear 2021, 486–487, 204122. [Google Scholar] [CrossRef]
- Shangguan, B.; Zhang, Y.; Xing, J.; Sun, L.; Chen, Y. Comparative Study on Wear Behaviors of Metal-Impregnated Carbon Material and C/C Composite under Electrical Sliding. Tribol. Trans. 2010, 53, 933–938. [Google Scholar] [CrossRef]
- Yang, H.; Chen, G.; Gao, G.; Wu, G.; Zhang, W. Experimental research on the friction and wear properties of a contact strip of a pantograph–catenary system at the sliding speed of 350 km/h with electric current. Wear 2014, 332–333, 949–955. [Google Scholar] [CrossRef]
- Li, L.; Tian, H.; Yun, Q.; Chu, W. Study on temperature rise distribution of contact surface under cyclic load. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 235, 138–148. [Google Scholar] [CrossRef]
- Qin, W.; Jin, X.; Kirk, A.; Shipway, P.; Sun, W. Effects of surface roughness on local friction and temperature distributions in a steel-on-steel fretting contact. Tribol. Int. 2018, 120, 350–357. [Google Scholar] [CrossRef]
- Costica, N. Thermal analysis of electrical contacts from pantograph–catenary system for power supply of electric vehicles. Electr. Power Syst. Res. 2013, 96, 211–217. [Google Scholar]
- Vogler, M.; Sheppard, S. Electrical contact resistance under high hoards and elevated temperatures. Weld. J. 1993, 72, 231–298. [Google Scholar]
- Geslain, E.; Rogeon, P.; Pierre, T.; Pouvreau, C.; Cretteur, L. Coating effects on contact conditions in resistance spot weldability. J. Mater. Process. Technol. 2018, 253, 160–167. [Google Scholar] [CrossRef]
- Biele, L.; Schaaf, P.; Schmid, F. Specific Electrical Contact Resistance of Copper in Resistance Welding. Phys. Status Solidi A-Appl. Mater. Sci. 2021, 218, 2100224. [Google Scholar] [CrossRef]
- Chen, G.X.; Hu, Y.; Dong, B.J.; Yang, H.J.; Gao, G.Q.; Wu, G.N.; Zhang, W.H.; Zhou, Z.R. Experimental study on the temperature of the contact strip in sliding electric contact. Proc. Inst. Mech. Eng. Part J-J. Eng. Tribol. 2017, 231, 1268–1275. [Google Scholar] [CrossRef]
- Wang, H.; Gao, G.; Wei, W.; Yang, Z.; Yin, G.; Xie, W.; He, Z.; Ni, Z.; Yang, Y.; Wu, G. Influence of the interface temperature on the damage morphology and material transfer of C–Cu sliding contact under different current amplitudes. J. Mater. Sci. 2022, 57, 5006–5021. [Google Scholar] [CrossRef]
- Chen, G.; Yang, H.; Zhang, W.; Wang, X.; Zhang, S.; Zhou, Z. Experimental study on arc ablation occurring in a contact strip rubbing against a contact wire with electrical current. Tribol. Int. 2013, 61, 88–94. [Google Scholar] [CrossRef]
- Kaars, J.; Mayr, P.; Koppe, K. Generalized dynamic transition resistance in spot welding of aluminized 22MnB5. Mater. Des. 2016, 106, 139–145. [Google Scholar] [CrossRef]
- Le Gloannec, B.; Doyen, O.; Pouvreau, C.; Doghri, A.; Poulon-Quintin, A. Numerical simulation of resistance upset welding in rod to tube configuration with contact resistance determination. J. Mater. Process. Technol. 2016, 238, 409–422. [Google Scholar] [CrossRef]
- Biele, L.; Schaaf, P.; Schmid, F. Method for contact resistance determination of copper during fast temperature changes. J. Mater. Sci. 2020, 56, 3827–3845. [Google Scholar] [CrossRef]
- Bucca, G.; Collina, A. Electromechanical interaction between carbon-based pantograph strip and copper contact wire: A heuristic wear model. Tribol. Int. 2015, 92, 47–56. [Google Scholar] [CrossRef] [Green Version]
- Xie, W.; Wu, G.; Yang, Z.; She, P.; Wang, H.; Zuo, H.; Wei, W.; Gao, G.; Tu, C. Study on the erosion characteristics of copper-carbon electrode pairs by DC air arc. High Volt. 2021, 6, 674–683. [Google Scholar] [CrossRef]
- Dong, L.; Li, C.-X.; Chen, G.-X.; Zhong, W.; Liu, X.-Y. Simulation study on coupling temperature field under pantograph-catenary friction with electrical current. China Railw. Sci. 2014, 35, 102–106. [Google Scholar]
- Dai, L.M.; Lin, J.Z.; Ding, X.H. Effect of transient temperature rise in contact area on wear properties. China Railw. Sci. 2002, 23, 111–117. [Google Scholar]
- Young, W.; Budynas, R.; Sadegh, A. Roak’s Formulas for Stress and Strain, 8th ed.; McGraw-Hill Education Press: New York, NY, USA, 2012; pp. 93–108. [Google Scholar]
- Holm, R. Electric contact Theory and Applications, 1st ed.; Spinger Press: Berlin/Heidelberg, Germany, 1967; pp. 9–21. [Google Scholar]
- Matsumura, T.; Morooka, I.; Yokomizu, Y.; Suzuki, M. Arc Parameters in CO2-blast quenching chamber with high-pressure storage tank of different pressures. Vacuum 2006, 80, 1305–1310. [Google Scholar] [CrossRef]
- Kong, L.-R.; Zhang, S.-Y. Theoretical Explanation of the Special Temperature Dependence of Rate Constant for Oxidation of Carbon. Daxue Huaxue 2016, 31, 84–88. [Google Scholar] [CrossRef]

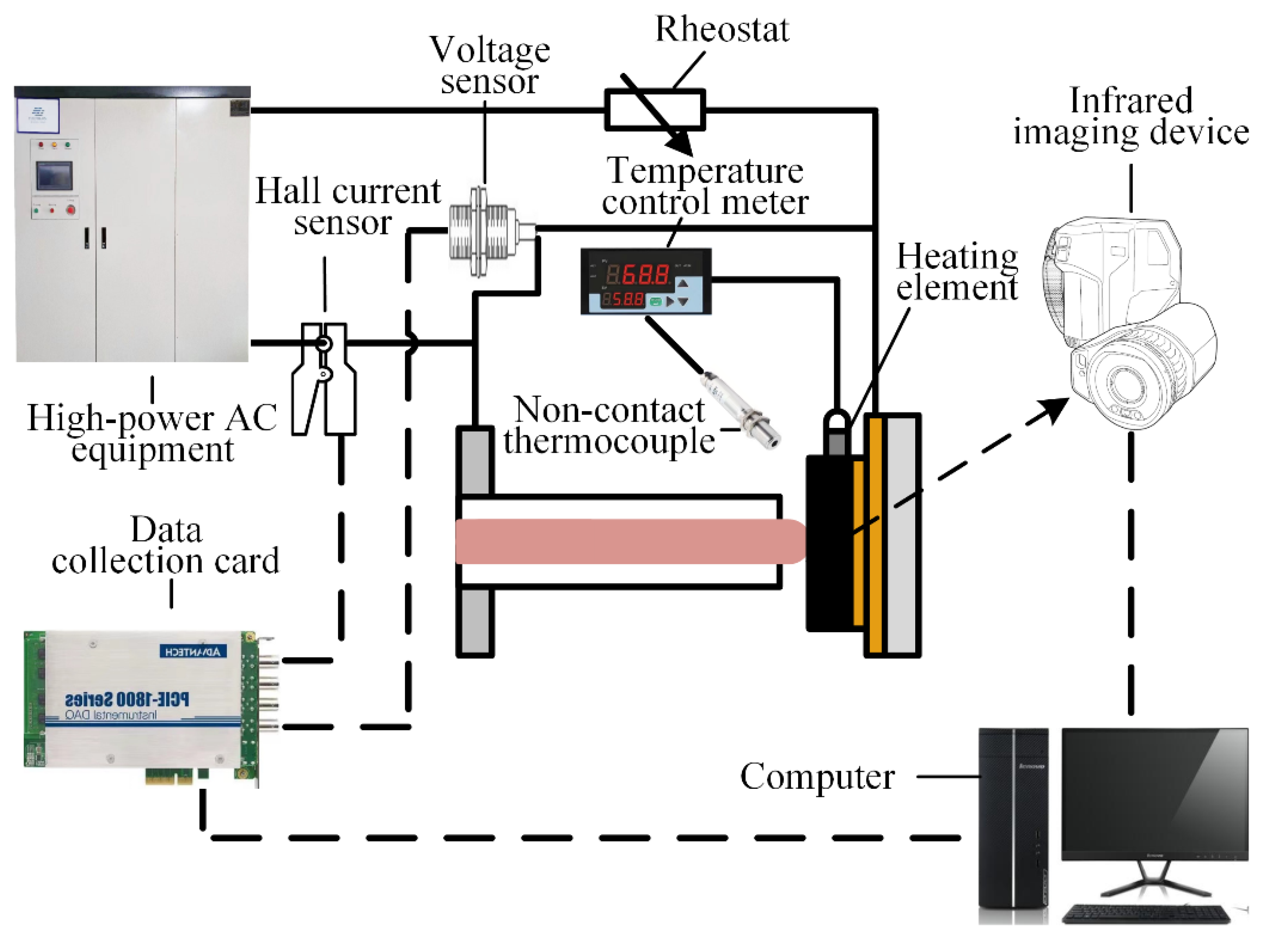



| Items | Conditions |
|---|---|
| Temperature/°C | Room temperature, 120, 180, 240, 300 |
| Sliding speed/km·h−1 | 80 |
| Normal load/N | 80 |
| Current/A | 10, 20, 40, 60, 80 |
| Sliding distance/km | 80 |
| Materials and Properties | Carbon Slider | Contact Wire |
|---|---|---|
| Element content/wt% | 99.19% C, 0.73% S, 0.08% O | 99.50% Cu, 0.50% O |
| Density/103 kg·m−3 | 1.67 | 8.9 |
| Resistivity/10−6 Ω·m | 25 | 0.018 |
| Specific heat/J·kg−1·K−1 | 769 | 380 |
| Thermal conductivity/W·m−1·K−1 | 3 | 380 |
| Hardness/107 N·m−2 | 70 | 82.6 |
| Elastic modulus/ GPa | 11.7 | 132 |
| Poisson’s ratios | 0.427 | 0.323 |
| Softening temperature/°C | — | 350 |
| Current Levels | Temperature | Chemical Compositions (wt%) | ||
|---|---|---|---|---|
| C | Cu | O | ||
| 10 A | Room temperature | 90.61 | 3.64 | 5.75 |
| 300 °C | 85.77 | 6.02 | 7.95 | |
| 80 A | Room temperature | 88.44 | 4.43 | 6.23 |
| 300 °C | 86.32 | 5.74 | 7.14 | |
| Current Levels | Temperature | Chemical Compositions (wt%) | ||
|---|---|---|---|---|
| Cu0 | Cu+ | Cu2+ | ||
| 10 A | Room temperature | 28.67 | 35.96 | 35.38 |
| 300 °C | 21.65 | 48.38 | 29.97 | |
| 80 A | Room temperature | 22.9 | 47.32 | 29.79 |
| 300 °C | 34.13 | 42.97 | 22.9 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Gao, G.; Lei, D.; Wang, Q.; Xiao, S.; Xie, Y.; Xu, Z.; Ma, Y.; Dong, K.; Chen, Q.; et al. Influence of Interface Temperature on the Electric Contact Characteristics of a C-Cu Sliding System. Coatings 2022, 12, 1713. https://doi.org/10.3390/coatings12111713
Wang H, Gao G, Lei D, Wang Q, Xiao S, Xie Y, Xu Z, Ma Y, Dong K, Chen Q, et al. Influence of Interface Temperature on the Electric Contact Characteristics of a C-Cu Sliding System. Coatings. 2022; 12(11):1713. https://doi.org/10.3390/coatings12111713
Chicago/Turabian StyleWang, Hong, Guoqiang Gao, Deng Lei, Qingsong Wang, Song Xiao, Yunlong Xie, Zhilei Xu, Yaguang Ma, Keliang Dong, Qichen Chen, and et al. 2022. "Influence of Interface Temperature on the Electric Contact Characteristics of a C-Cu Sliding System" Coatings 12, no. 11: 1713. https://doi.org/10.3390/coatings12111713
APA StyleWang, H., Gao, G., Lei, D., Wang, Q., Xiao, S., Xie, Y., Xu, Z., Ma, Y., Dong, K., Chen, Q., & Wu, G. (2022). Influence of Interface Temperature on the Electric Contact Characteristics of a C-Cu Sliding System. Coatings, 12(11), 1713. https://doi.org/10.3390/coatings12111713






