Molecular Dynamical Investigation of Lithium-Ion Adsorption on Multilayer Fullerene
Abstract
:1. Introduction
2. Simulation Method
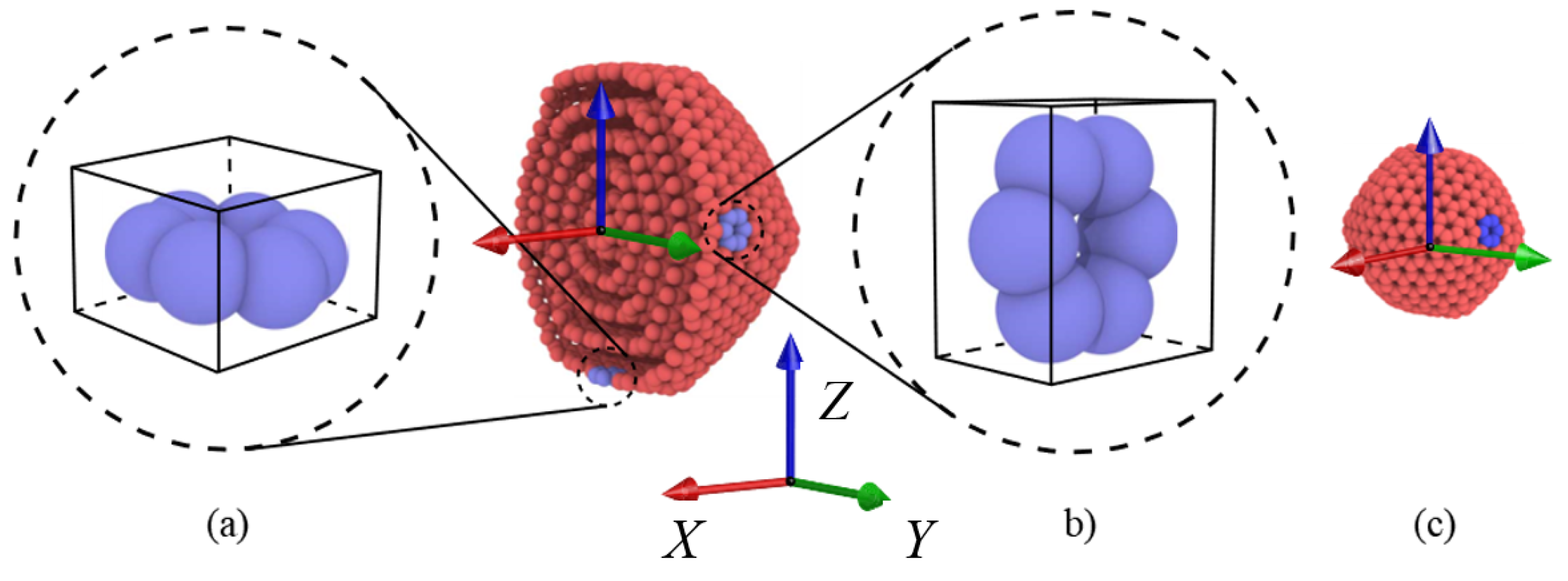
2.1. Simulation Process
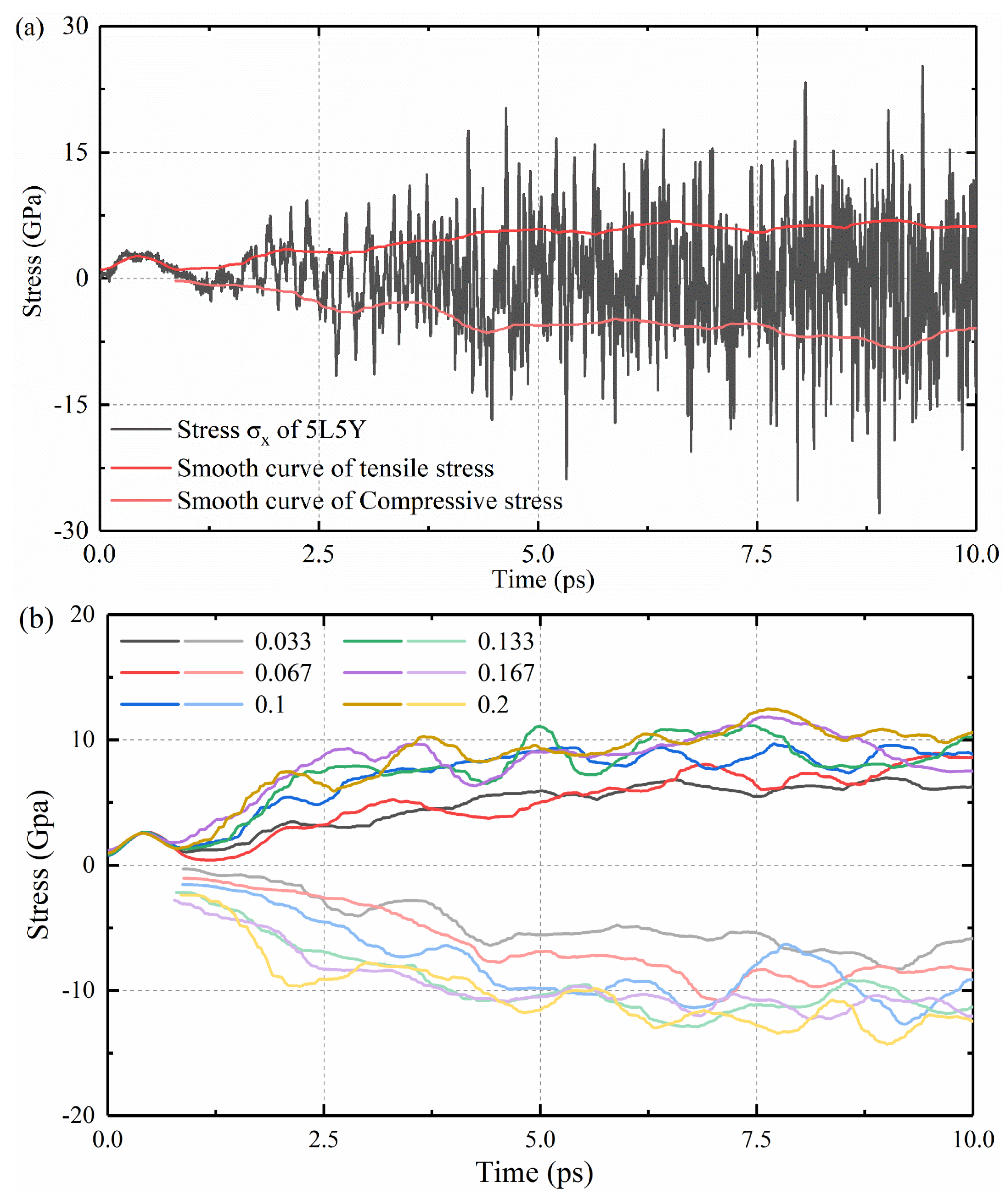
2.2. Stress Calculation
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Neto, C.; Antonio, H. The carbon new age. Mater. Today 2010, 13, 12–17. [Google Scholar] [CrossRef]
- Iijima, S. Direct observation of the tetrahedral bonding in graphitized carbon black by high resolution electron microscopy. J. Cryst. Growth 1980, 50, 675–683. [Google Scholar] [CrossRef]
- Ugarte, D. Curling and closure of graphitic networks under electron-beam irradiation. Nature 1992, 359, 707–709. [Google Scholar] [CrossRef]
- Mordkovich, V.Z.; Umnov, A.G.; Inoshita, T. Nanostructure of laser pyrolysis carbon blacks: Observation of multiwall fullerenes. Int. J. Inorg. Mater. 2000, 2, 347–353. [Google Scholar] [CrossRef]
- Ostroumova, G.; Orekhov, N.; Stegailov, V. Reactive molecular-dynamics study of onion-like carbon nanoparticle formation. Diam. Relat. Mater. 2019, 94, 14–20. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Akgöz, B. On the statics of fullerene structures. Int. J. Eng. Sci. 2019, 142, 125–144. [Google Scholar] [CrossRef]
- Gu, W.; Peters, N.; Yushin, G. Functionalized onion-like carbon, detonation nanodiamond and mesoporous carbon as cathodes in Li-ion electrochemical energy storage devices. Carbon 2013, 53, 292–301. [Google Scholar] [CrossRef]
- Wang, B.C.; Wang, H.W.; Chang, J.C.; Tso, H.C.; Chou, Y.M. More spherical large fullerenes and multi-layer fullerene cages. J. Mol. Struct. THEOCHEM 2001, 540, 171–176. [Google Scholar] [CrossRef]
- Bartelmess, J.; Giordani, S. Carbon nano-onions (multi-layer fullerenes): Chemistry and applications. Beilstein. J. Nanotechnol. 2014, 5, 1980–1998. [Google Scholar] [CrossRef] [Green Version]
- Portet, C.; Yushin, G.; Gogotsi, Y. Electrochemical performance of onion-like carbon, nanodiamonds, carbon black and multiwalled nanotubes in electrical double layer capacitors. Carbon 2007, 45, 2511–2518. [Google Scholar] [CrossRef]
- Crestani, M.G.; Puente-Lee, I.; Rendón-Vazquez, L.; Santiago, P.; del Rio, F.; Morales-Morales, D.; García, J.J. The catalytic reduction of carbon dioxide to carbon onion particles by platinum catalysts. Carbon 2005, 43, 2621–2624. [Google Scholar] [CrossRef]
- Porada, S.; Borchardt, L.; Oschatz, M.; Bryjak, M.; Atchison, J.S.; Keesman, K.J.; Kaskel, S.; Biesheuvel, P.M.; Presser, V. Direct prediction of the desalination performance of porous carbon electrodes for capacitive deionization. Energy Environ. Sci. 2013, 6, 3700. [Google Scholar] [CrossRef] [Green Version]
- Pech, D.; Brunet, M.; Durou, H.; Huang, P.; Mochalin, V.; Gogotsi, Y.; Taberna, P.-L.; Simon, P. Ultrahigh-power micrometre-sized supercapacitors based on onion-like carbon. Nat. Nanotechnol. 2010, 5, 651–654. [Google Scholar] [CrossRef] [Green Version]
- Jäckel, N.; Weingarth, D.; Zeiger, M.; Aslan, M.; Grobelsek, I.; Presser, V. Comparison of onion-like carbon and carbon blacks as conductive additives for carbon supercapacitors in organic electrolytes. J. Power Sources 2014, 272, 1122–1133. [Google Scholar] [CrossRef]
- McDonough, J.K.; Gogotsi, Y. Onion-like carbon: Synthesis and electrochemical applications. Interface Mag. 2013, 22, 61–66. [Google Scholar] [CrossRef]
- Plonska-Brzezinska, M.E.; Echegoyen, L. Carbon nano-onions for supercapacitor electrodes: Recent developments and applications. J. Mater. Chem. A 2013, 1, 13703. [Google Scholar] [CrossRef]
- Tang, W.; Wu, J.; Wang, X.; Xia, X.; Tu, J. Integrated carbon nanospheres arrays as anode materials for boosted sodium ion storage. Green Energy Environ. 2018, 3, 50–55. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open visualization tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Ganesh, P.; Kim, J.; Park, C.; Yoon, M.; Reboredo, F.A.; Kent, P.R.C. Binding and diffusion of lithium in graphite: Quantum monte carlo benchmarks and validation of van der Waals density functional methods. J. Chem. Theory Comput. 2014, 10, 5318–5323. [Google Scholar] [CrossRef]
- Kühne, M.; Börrnert, F.; Fecher, S.; Ghorbani-Asl, M.; Biskupek, J.; Samuelis, D.; Krasheninnikov, A.; Kaiser, U.; Smet, J.H. Reversible superdense ordering of lithium between two graphene sheets. Nature 2018, 564, 234–239. [Google Scholar] [CrossRef] [PubMed]
- McNutt, N.W.; Rios, O.; Maroulas, V.; Keffer, D.J. Interfacial Li-ion localization in hierarchical carbon anodes. Carbon 2017, 111, 828–834. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, H. The C-Li (Carbon-Lithium) system. Bull. Alloy Phase Diagr. 1989, 10, 69–72. [Google Scholar] [CrossRef]
- Shi, H.; Barker, J.; Saïdi, M.Y.; Koksbang, R.; Morris, L. Graphite structure and lithium intercalation. J. Power Sources 1997, 68, 291–295. [Google Scholar] [CrossRef]
- Shimizu, A.; Tachikawa, H. The dynamics on migrations of Li+ ion and Li atom at 700 K around the circumference of graphite cluster model: A direct molecular dynamics study. Chem. Phys. Lett. 2001, 339, 110–116. [Google Scholar] [CrossRef]
- Kganyago, K.R.; Ngoepe, P.E. Structural and electronic properties of lithium intercalated graphite. Phys. Rev. B 2003, 68, 205111. [Google Scholar] [CrossRef]
- Zhang, R. Growth mechanism of Ni-graphene composite coating on mild steel: A combined experimental and molecular dynamics study. Int. J. Electrochem. Sci. 2022, 17, 220939. [Google Scholar] [CrossRef]
- Chakraborti, N.; Das, S.; Jayakanth, R.; Pekoz, R.; Erkoç, Ş. Genetic algorithms applied to Li+ ions contained in carbon nanotubes: An investigation using particle swarm optimization and differential evolution along with molecular dynamics. Mater. Manuf. Processes 2007, 22, 562–569. [Google Scholar] [CrossRef]
- Ailenei, A.-E.; Beu, T.A. Ion transport through gated carbon nanotubes: Molecular dynamics simulations using polarizable water. J. Mol. Struct. 2021, 1245, 131022. [Google Scholar] [CrossRef]
- Kang, J.W.; Hwang, H.J. A Bucky shuttle three-terminal switching device: Classical molecular dynamics study. Phys. E Low-Dimens. Syst. Nanostructures 2004, 23, 36–44. [Google Scholar] [CrossRef]
- Kang, J.W.; Hwang, H.J. Model schematics of a nanoelectronic device based on multi-endo-fullerenes electromigration. Phys. E Low-Dimens. Syst. Nanostructures 2005, 27, 245–252. [Google Scholar] [CrossRef]
- Piątek, A.; Dawid, A.; Gburski, Z. The properties of endohedral potassium ion fullerene cluster: MD simulation. J. Mol. Struct. 2008, 887, 144–147. [Google Scholar] [CrossRef]
- Chen, L.; Wang, X.; Kumar, S. Thermal transport in fullerene derivatives using molecular dynamics simulations. Sci. Rep. 2015, 5, 12763. [Google Scholar] [CrossRef] [Green Version]
- Hu, D.; Hu, J.; Jiang, H.; Xu, J. A highly effective energy mitigation system combining carbon nanotube and buckyballs. Eur. Phys. J. Spec. Top. 2018, 227, 155–166. [Google Scholar] [CrossRef]
- Silveira, J.F.; Pagnussati, R.A.; Kleinpaul, J.; Paupitz, R.; Muniz, A.R. Nanoporous carbon superstructures based on covalent bonding of porous fullerenes. Carbon 2018, 130, 424–432. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Zeng, Q.; Yu, A. Interaction forces between carbon nanospheres: A molecular dynamics simulation study. Chem. Eng. Sci. 2015, 121, 23–31. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Song, M.K.; Hong, S.D.; No, K.T. The structure of lithium intercalated graphite using an effective atomic charge of lithium. J. Electrochem. Soc. 2001, 148, A1159. [Google Scholar] [CrossRef]
- Frankland, S. The stress–strain behavior of polymer–nanotube composites from molecular dynamics simulation. Compos. Sci. Technol. 2003, 63, 1655–1661. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Hodak, M.; Lee, R.S. Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B 2000, 62, 13104–13110. [Google Scholar] [CrossRef]
- Li, X.; Song, W.; Smedskjaer, M.M.; Mauro, J.C.; Bauchy, M. Quantifying the internal stress in over-constrained glasses by molecular dynamics simulations. J. Non-Cryst. Solids X 2019, 1, 100013. [Google Scholar] [CrossRef]
- Liu, B.; Qiu, X. How to compute the atomic stress objectively? J. Comput. Theor. Nanosci. 2009, 6, 1081–1089. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Komvopoulos, K. A stress analysis method for molecular dynamics systems. Int. J. Solids Struct. 2020, 193–194, 98–105. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| 0.1050 | |
| 0.0250 | |
| 3.8510 | |
| 2.4510 |
| Number | Ratio | Concentration (atoms/nm3) |
|---|---|---|
| 50 | 0.033 | 0.46 |
| 100 | 0.067 | 0.92 |
| 150 | 0.1 | 1.38 |
| 200 | 0.133 | 1.85 |
| 250 | 0.167 | 2.31 |
| 300 | 0.2 | 2.77 |
| Concentration (atoms/nm3) | Group 5L5Y | Group 5L5(-Z) | ||||
|---|---|---|---|---|---|---|
| 0.033 | 6.24715 | 1.66906 | 6.42387 | 6.36227 | 6.28345 | 0.72257 |
| 0.067 | 7.70491 | 3.90405 | 8.48047 | 8.00011 | 7.94726 | 0.88737 |
| 0.1 | 9.59082 | 3.173 | 9.7935 | 9.45388 | 9.92849 | 1.15529 |
| 0.133 | 10.77693 | 3.87023 | 10.47897 | 10.89653 | 11.02246 | 2.29164 |
| 0.167 | 11.07554 | 3.34023 | 11.52931 | 11.12232 | 11.36959 | 2.67114 |
| 0.2 | 11.77553 | 3.87955 | 11.87052 | 11.37549 | 12.07888 | 3.01447 |
| Concentration (atom/nm3) | Group 5L5Y | Group 5L5(-Z) | ||||
|---|---|---|---|---|---|---|
| 0.033 | 7.76728 | 1.63038 | 8.43773 | 8.11088 | 7.8469 | 0.9264 |
| 0.067 | 9.82621 | 3.51548 | 9.987 | 10.20131 | 10.47156 | 2.31871 |
| 0.1 | 12.75335 | 3.67027 | 13.49606 | 12.81874 | 12.90796 | 3.47614 |
| 0.133 | 14.15314 | 4.42892 | 14.05658 | 13.77621 | 14.353 | 4.56613 |
| 0.167 | 14.7284 | 4.11106 | 15.18183 | 14.79008 | 15.66053 | 4.48393 |
| 0.2 | 14.47299 | 4.65719 | 14.29492 | 14.68558 | 14.63591 | 4.79911 |
| Velocity | Group 5L5Y | Group 5L5(-Z) | ||||
|---|---|---|---|---|---|---|
| 10 | 9.61928 | 3.20742 | 10.29145 | 9.41925 | 9.61151 | 1.90242 |
| 20 | 11.78373 | 3.88003 | 11.87032 | 11.37543 | 12.07914 | 3.01467 |
| 30 | 13.44391 | 4.34859 | 14.09353 | 13.96878 | 14.06485 | 3.8023 |
| 40 | 14.47299 | 4.65719 | 14.29492 | 14.68558 | 14.63591 | 4.79911 |
| - | |||
|---|---|---|---|
| Group 5L5Y | 11.77553 | 3.87934 | 11.87005 |
| Group 3L3Y | 16.67001 | 5.09723 | 15.54763 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Guan, J.; Chen, H.; Li, M.; Hua, Z.; Niu, F.; Zhang, Y. Molecular Dynamical Investigation of Lithium-Ion Adsorption on Multilayer Fullerene. Coatings 2022, 12, 1824. https://doi.org/10.3390/coatings12121824
Lu J, Guan J, Chen H, Li M, Hua Z, Niu F, Zhang Y. Molecular Dynamical Investigation of Lithium-Ion Adsorption on Multilayer Fullerene. Coatings. 2022; 12(12):1824. https://doi.org/10.3390/coatings12121824
Chicago/Turabian StyleLu, Jinbin, Jie Guan, Hao Chen, Minghua Li, Zhongwei Hua, Fuzhou Niu, and Yang Zhang. 2022. "Molecular Dynamical Investigation of Lithium-Ion Adsorption on Multilayer Fullerene" Coatings 12, no. 12: 1824. https://doi.org/10.3390/coatings12121824
APA StyleLu, J., Guan, J., Chen, H., Li, M., Hua, Z., Niu, F., & Zhang, Y. (2022). Molecular Dynamical Investigation of Lithium-Ion Adsorption on Multilayer Fullerene. Coatings, 12(12), 1824. https://doi.org/10.3390/coatings12121824








