Splitting an Impacting Droplet by a Superhydrophobic Wire

Abstract

Splitting a droplet into several segments is of great significance in many applications such as the detection of tiny liquid samples, whereas the surface tension tends to hold liquid to remain as one drop, causing difficulty in separating the droplet into pieces. In this work, a method is proposed to split an impacting droplet with a relatively high velocity or Weber number into two halves by a superhydrophobic wire. The effects of the wire wettability and the impact velocity of the droplet on the splitting phenomena and the efficacy to an anti-icing application are investigated. Compared to a hydrophilic wire, a superhydrophobic wire splits an impacting droplet at a relatively high speed of the Weber number greater than 3.1 and inhibits ice accretion at the temperature as low as −20 °C. The results suggest that a superhydrophobic wire can be utilized in the droplet manipulation and anti-icing applications such as power lines in high latitude areas.

1. Introduction

Manipulation of a droplet has a wide range of engineering applications, such as microfluidics [1], heat transfer [2], water collection [3,4], inkjet printing [5], and clinical blood tests [6]. A series of approaches have been proposed to control the motion of droplets, such as bioinspired self-driven conical tips [7,8], electrowetting on the dielectric device [9], vibratory microfluidics [10], as well as modifications of surface wettability [11]. When a droplet lies on a superhydrophobic surface with micro/nano-sized structures of low surface energy, it beads up due to surface tension and rolls down even at a tiny tilted angle [12]. Moreover, an impacting droplet upon the superhydrophobic surfaces rebounds off the surface. The high mobility of droplets on the superhydrophobic surfaces enables the wide engineering applications including self-cleaning [13,14], anti-icing [15,16,17,18,19,20,21], and condensation enhancement [8,22,23]. However, it is difficult for the superhydrophobic surfaces to trap and split a droplet without external assistance.

Single droplet splitting is vital for the highly efficient clinical detection [24], precious inkjet printing [25], open-air microfluidic devices [26], and interfacial heat transfer [27], whereas finding an efficient and quick method of separating a drop with little assistance from tools is still challenging. Recently, superhydrophobic surfaces have been shown to be a resourceful way to control wettability and manipulation of droplet motions. Superhydrophobic surfaces are composed of low surface energy materials whose surfaces are typically featured with micro- or nanoscale roughness, or structures that can trap air at contact with aqueous liquid [28,29]. The stable air sandwiched between the liquid and the superhydrophobic surface enables a high mobility of a droplet on the surface. A highly hydrophobic knife was shown to successfully cut a stationary droplet without the generation of satellite droplets [30,31]. It was also shown that a moving droplet guided by a superhydrophobic trap could be cut into halves by a stationary superhydrophobic knife [32]. For an impacting droplet on a superhydrophobic surface, the contact time of the droplet on the superhydrophobic surface scales with the droplet size, $t_c\approx 2.2\sqrt{\rho R^3/\gamma }$ where ρ, R, and γ are the density of fluid, the radius of a droplet, and the surface tension of the droplet, respectively [33]. It suggests that the contact time of a droplet on a superhydrophobic substrate can be reduced by reducing the droplet size. Since the heat transfer from a droplet to a substrate relies on the contact time, the superhydrophobic surface with properly designed surface patterns to reduce the contact time can help avoid or delay the icing of the impacting droplet at subfreezing temperature. Bird et al. successfully reduced the contact time of an impacting droplet by using a rib structure on a superhydrophobic substrate to split the droplet into two [18]. By introducing superhydrophobic stripes on a hydrophilic substrate, an impacting droplet could also be split into several segments by properly designing the number and position of the superhydrophobic stripes [34]. One of the applications where such splitting phenomena with a reduced contact time of an impacting droplet at low temperature can benefit is the anti-icing of power lines. Although such anti-icing efficacy was demonstrated on flat substrates, the demonstration for cylindrical wires resembling power lines has not been made yet.

In this paper, we propose a new method to split a moving droplet with a superhydrophobic wire of stainless steel. We experimentally show that a droplet can be cut into halves when it impacts a superhydrophobic wire at a relatively high speed, whereas it keeps its integrity when hitting a hydrophilic wire of stainless steel. We support the experimental results with theoretical modelling that suggests that there should exist a critical Weber number (We, a dimensionless number representing the relative importance of the fluid’s inertia compared to its surface tension) to allow the splitting behaviour. Due to the reduced contact time and area on the superhydrophobic surface compared to a hydrophilic one, we also show that the superhydrophobic wire can significantly inhibit ice accretion in a cold environment as low as −20 °C for the anti-icing application.

2. Experimental Section

2.1. Hydrophobization of Stainless-Steel Wire

The experiments were performed for the two different wetting conditions of the stainless-steel wire, including both the hydrophilic and superhydrophobic ones. The bare stainless-steel wire of a diameter of d = 0.5 mm (Fe26395-1 kg, Sino Science and Technology Co., Ltd., Ji’nan, Shandong, China) was employed as a hydrophilic wire as received. For the preparation of a superhydrophobic wire, the bare stainless-steel wire was spray-coated with a customized superhydrophobic coating solution [35]. For the superhydrophobic coating solution, hydrophobic SiO₂ nanoparticles with a diameter of ~100 nm (Aerosil RX300, Essen, Germany) and a binder of methylphenyl silicone resin (SR355S, Momentive Performance Materials, Leverkusen, Germany) were pre-mixed in acetone for 10 min in an ultrasonic cleaner. Then, the solution was spray-coated on the stainless-steel wire by a spray gun and dried in the air for 2 h. Before the spray-coating, the bare stainless-steel wire was cleaned by deionized water, ethanol, and acetone for 2 min in an ultrasonic cleaner.

Since the wire diameter is too small (only 0.5 mm) to measure the apparent contact angle of a sessile droplet, the wettability of the coating was checked with a flat substrate of the same stainless-steel material (Sino Science and Technology Co., Ltd. ST38620). Figure 1a shows the apparent contact angle of a sessile droplet of water on the bare flat stainless-steel surface. The advancing and receding contact angles on the stainless-steel substrate were also measured to be 80° and 25°, respectively. In contrast, Figure 1b shows the apparent contact angle of a sessile droplet of water on the superhydrophobic-coated stainless-steel surface. The advancing and receding contact angles of a water droplet measured on the superhydrophobic-coated stainless-steel substrate were 168° and 164°, respectively, confirming the superhydrophobicity [35]. Figure 1c shows the morphology of the superhydrophobic coating applied on the stainless-steel substrate. Figure 1d,e show the micrographs of the bare stainless-steel wire and the superhydrophobic-coated wire, respectively. Whereas the apparent contact angle of a sessile droplet of water could not be measured directly on the surfaces of wires, their advancing and receding contact angles of the impacting droplet were estimated from the images captured during the experiment.

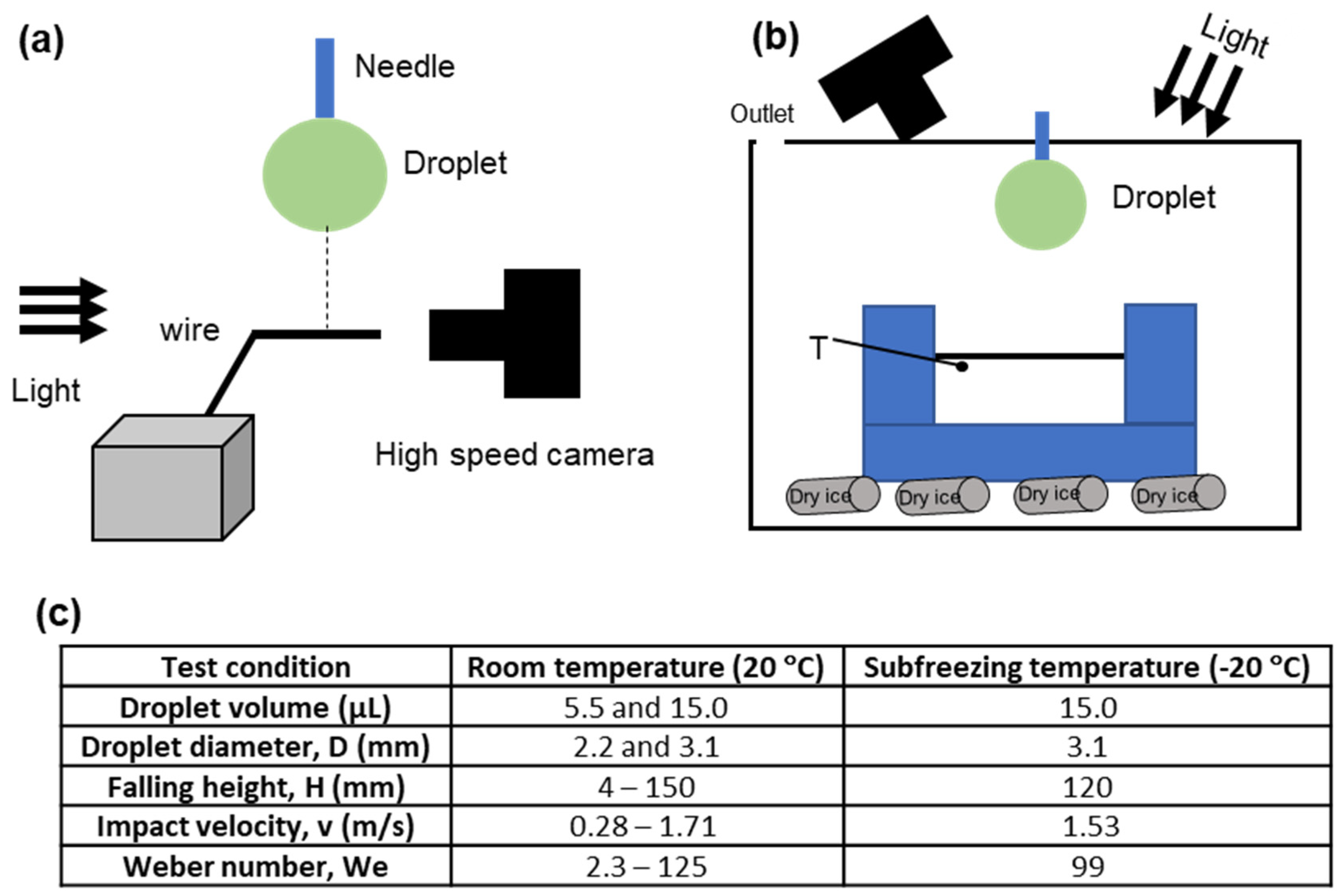
2.2. Experimental Setup for Tests at Room Temperature

The droplet splitting process at the impact to the wires at room temperature was observed in the experimental setup shown in Figure 2a. A droplet at room temperature was released by a stainless-steel needle. Droplets of two different volumes, 5.5 and 15 μL, were tested. The diameter of the droplet (D) is 2.3 and 3.1 mm, respectively, estimated by assuming the droplet being spherical. The droplet volume was estimated by measuring the droplet mass with the known density of water being 998 kg/m³. The mass of a droplet was calculated by averaging the total mass of 100 droplets released from a needle. It was repeated 10 times with each time for 100 droplets to estimate the standard deviation. The standard deviation of the droplet mass was less than 0.88%, which corresponds to the standard deviation of the droplet diameter less than 0.28%. The relatively large droplet sizes compared to that of a wire were used so that the sizable difference can allow the splitting of the impacting droplet. The wire was fixed by a clip right below the needle. The falling position of the droplet was adjusted to be coincident with the centre of the stainless-steel wire before tests. The falling height (H) of the droplet ranged from 4 to 150 mm to vary the impacting speed of the droplet. The corresponding impact velocity (v) of the droplet should be in the range of v = 0.3–1.7 m/s based on the theoretical prediction by $v=\sqrt{2gH}$. For the given droplet size and velocity, the Weber number (We = ρDv²/γ, where ρ, D, and γ represent the water density, droplet diameter, and the surface tension of water in air, respectively) covers the two-orders of magnitude ranging from 2.3 to 150. The test conditions of the droplet are summarized in Figure 1c. After the release from the needle, the droplet impacts upon the wire, and the impacting process is captured by a high-speed camera (MotionXtra NX-4, IDT Corporation, Pasadena, USA) at 4000 fps.

2.3. Experimental Setup for Tests at Subfreezing Temperature

The icing accretion process on the wires (d = 0.5 mm) was tested in the experimental setup shown in Figure 2b. The experiments were performed in an insulation box of the size of 150 × 150 × 150 mm³. Protected by the insulation box, an aluminium box of 50 × 50 × 50 mm³ was placed on top of an aluminium plate which was cooled by a 10-mm thick layer of dry ice as low as −20 °C. The insulating box has a small outlet on top to evacuate CO₂ gas from the dry ice and to avoid the increase in pressure inside. The evaporated CO₂ is dry so that the relative humidity (HR) inside the box remains low to avoid frosting. The prepared wire was fixed on both sides of the aluminium box. A T-typed thermocouple was placed 10 mm away from the wire to measure the temperature before and during the tests. To observe the freezing process for a long duration, a digital CCD camera (Koolertron, 5 MP) was used at a rate of 24 fps. Only the relatively large size of a droplet (15 μL, D = 3.1 mm) was tested to identify the ice accretion process more clearly, released by the needle at a room temperature and impacted upon the cooled wire every 1 min. Limited by the size of the needle, the releasing height of the droplet was fixed to be 120 mm, which had the velocity and We number of the impacting droplet to the wire correspond to be 1.5 m/s and 99, respectively. The test conditions are also summarized in Figure 1c.

3. Results & Discussion

3.1. Effect of the Wire Wettability on Droplet Splitting Behaviors

The wettability of the wire affects the splitting behaviors of the impacting droplet significantly. When a droplet of 5.5 µL impacts a hydrophilic wire at v = 0.44 m/s (We = ρDv²/γ = 6.2, where ρ, D, and γ represent the water density, droplet diameter, and the surface tension of water in air, respectively) as shown in Figure 3a (see also Video S1 in the Supporting Information), the droplet lets the wire pass through its body, and two advancing heads merge behind the wire. The arrows in Figure 3b indicate the tangent direction of the water–air interface at the contact line. When the droplet moves downward, the three-phase contact lines of the droplet on the wire move forward to the bottom of the wire due to the hydrophilicity with the advancing contact angle similar to the one on the flat substrate (i.e., ~80°). As a result, the contact lines of the two advancing heads merge during the impacting process. The hydrophilicity of the stainless-steel wire enables the recombination of the droplet after splitting, and, hence, the integrity of the droplet after the impact. Moreover, the hydrophilic wire has a high adhesion force to water molecules so that a tiny satellite droplet is generated and stays on the hydrophilic wire after the impact, as marked in Figure 3a.

When a droplet impacts the superhydrophobic wire with the same velocity and We number, the droplet splits into two halves, as shown in Figure 4a (see also Video S2 in the Supporting Information). During the impacting process, the contact angles of the advancing heads of the droplet on the superhydrophobic wire are close to the advancing contact angle of superhydrophobic coatings, i.e., 168°. Opposite to the one on the hydrophilic wire, the surface tension at the three-phase contact line hinders the advancing process of the contact line on the superhydrophobic wire with the high advancing contact angle, as marked by the arrows in Figure 4b. It avoids the two advancing heads from merging during the impacting process. Instead, the inertia of the two advancing heads makes them keep moving downward to split the droplet into two halves with no noticeable satellite droplets left on the wire.

3.2. Threshold for the Droplet Splitting

When a droplet was split into two smaller ones, the surface area increased by $\sqrt[3]{2}$, and the surface energy of the system increased at the same time. In other words, the kinetic energy is converted to the increase in the surface energy during the splitting process. For the splitting behavior to happen, there should be enough kinetic energy of the impacting droplet.

For a droplet with a diameter of D, the surface energy of the droplet in the air is $E_{\mathrm{s}}=\pi D^2\gamma$ with the unit of Joule, where γ is the surface tension of water in air. The kinetic energy of the droplet before the impact is

$$E_{\mathrm{d}}=\frac{1}{12}\pi \rho D^3{v}^2$$

(1)

with the unit of Joule where ρ and v represent the liquid density and the droplet velocity. Assuming the droplet is split into two spherical droplets with an equal volume, the increment of the surface energy after splitting is

$$\Delta E_{\mathrm{s}}=\pi D^2\gamma (\sqrt[3]{2}-1)$$

(2)

with the unit of Joule. For the splitting behavior to happen, $E_{\mathrm{d}}>\Delta E_{\mathrm{s}}$, which can be reduced to

$$\frac{\rho D{v}^2}{\gamma }>12(\sqrt[3]{2}-1)\approx 3.1$$

(3)

It should be noted that the dimensionless number $\frac{\rho D{v}^2}{\gamma }$ is the Weber number (We), representing the relative ratio of the fluid’s inertia compared to its surface tension. Equation (3) shows that for the droplet splitting behavior to happen, the Weber number (We) should be greater than the critical value of 3.1.

Splitting behaviors on the superhydrophobic wire were tested for varying Weber numbers by controlling the droplet velocity or size. As shown in Figure 5 (see also Video S3 in the Supporting Information), our experimental results agree well with the theoretical expectation. When We < 3.1, as shown in Figure 5a, the droplet was distorted during the early period of the impact and then rebounded off the superhydrophobic wire without breaking into two. Once We > 3.1, the kinetic energy is high enough to split the droplet into two, as shown in Figure 5b.

3.3. Anti-Icing of the Superhydrophobic Wire

When a droplet impacted a superhydrophobic wire at We > 3.1 with the splitting, the contact time of the droplet on the wire was ~12 ms as shown in Figure 4, whereas it took ~26 ms for the impacting droplet to leave the hydrophilic wire as shown in Figure 3. Both the contact time and contact area between the droplet and the superhydrophobic wire were reduced compared to those on the hydrophilic wire, which can help reduce the heat transfer rate between the droplet and surface. Such effects can be beneficial for the anti-icing applications such as for power lines.

Figure 6 shows the freezing process of an impacting droplet of 15 μL at 1.5 m/s (We = 94) upon the hydrophilic wire at −20 °C. When the droplet of a room temperature impacts upon the hydrophilic wire at the subfreezing temperature, a part of the droplet leaves behind and adheres to the hydrophilic wire as shown in the second image (i.e., 40 ms) in Figure 6. The remaining water on the wire gradually freezes as shown in the third image (i.e., 240 ms) in Figure 6. When droplets continuously impact upon the hydrophilic wire one after another every minute, the accumulation of ice on the wire gets greater as shown in the last image in Figure 6.

For comparison, Figure 7 shows the freezing process of an impacting droplet upon the superhydrophobic wire under the same experimental condition as the one shown in Figure 6. On the superhydrophobic wire at the subfreezing temperature, no water or ice on the wire was noticed until the impact by the 9th droplet, as droplets become split into two, as shown in the second image in Figure 7. At the impact of the 10th droplet, as shown in the third image in Figure 7, a tiny ice particulate started to be noticed on the wire. After the onset of the ice particulate, the ice accretion becomes more severe on the initial flaw at the wire, although the following impacting droplets still become split. Compared to the one on the hydrophilic wire, the accumulated ice on the superhydrophobic wire was shaped to be spherical and grew locally (i.e., only on the top impact region). Although the superhydrophobic coating cannot completely prevent the onset and accumulation of ice on the wire, it delays the ice accumulation and reduces the size and area of ice accumulation. The results show that the superhydrophobic wire can be icephobic due to the splitting phenomena with the much-reduced contact time and area between the impacting droplet and wire surface. Such superhydrophobic wires can be of great significance in the anti-icing application for power lines in cold regions.

4. Conclusions

The impacting processes of a droplet of a room temperature upon hydrophilic and superhydrophobic wires at both room and subfreezing temperatures have been investigated and compared. Compared to the hydrophilic wire, the superhydrophobic wire allows the split of the impacting droplet into two small ones with a significantly reduced contact time and area on the wire at the relatively high We number. Agreeing with the theoretical expectation, the critical We number for the splitting phenomena is around 3.1. The splitting phenomena with the reduced contact time and area of the impacting droplet on the superhydrophobic wire can be leveraged for anti-icing effects so that the superhydrophobic wire delays the onset of ice buildups on the wire at subfreezing temperature and minimizes the size and area for ice accretion. The finding is of significance for not only droplet manipulation but also anti-icing applications of superhydrophobic wires. For example, if power lines are treated to be superhydrophobic, it is expected that ice accretion can be inhibited significantly due to the unique splitting behaviors with the much-reduced contact time and area of the impacting droplet.