Electron Beam Sintering of Composite Al2O3-ZrO2 Ceramics in the Forevacuum Pressure Range
Abstract
:1. Introduction
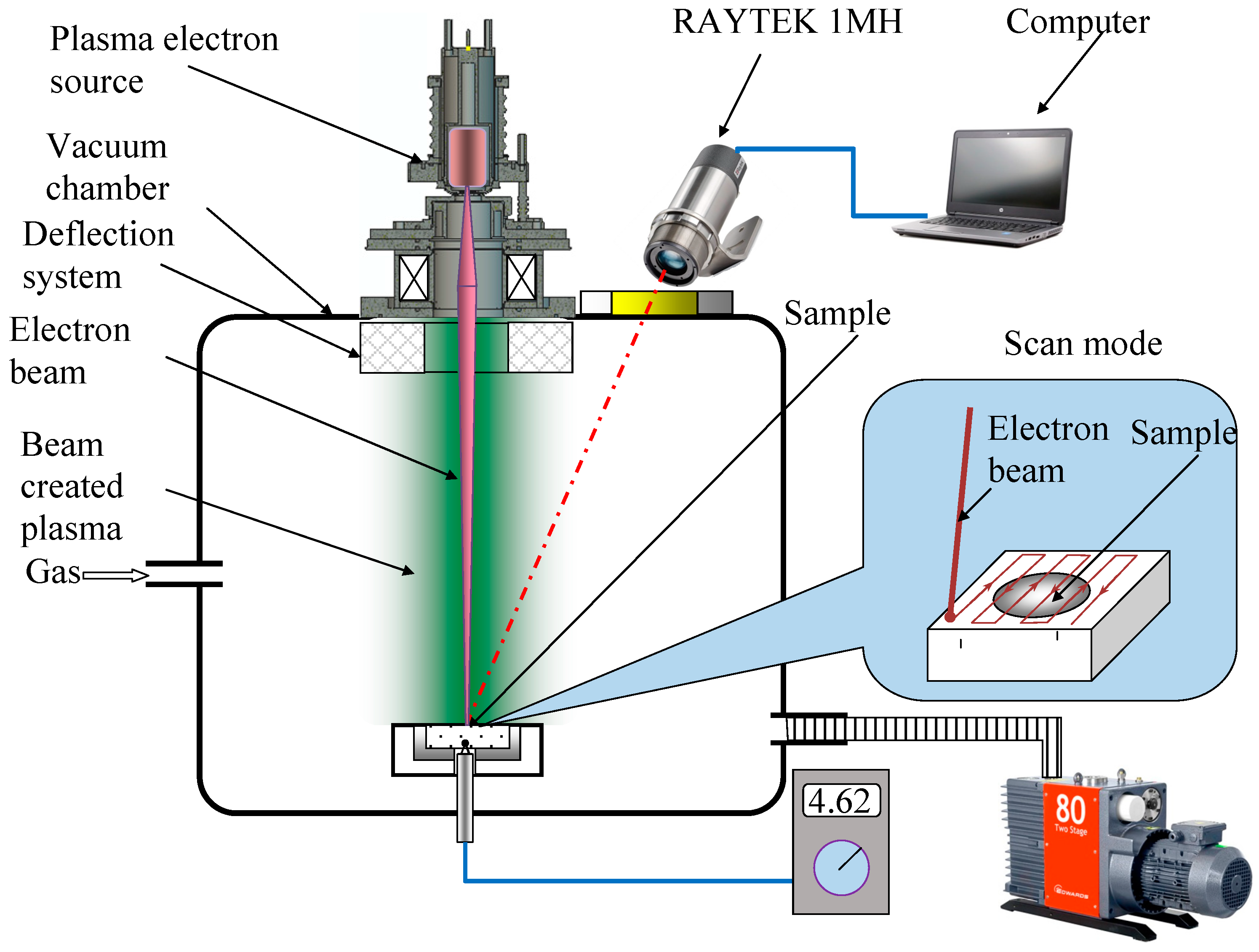
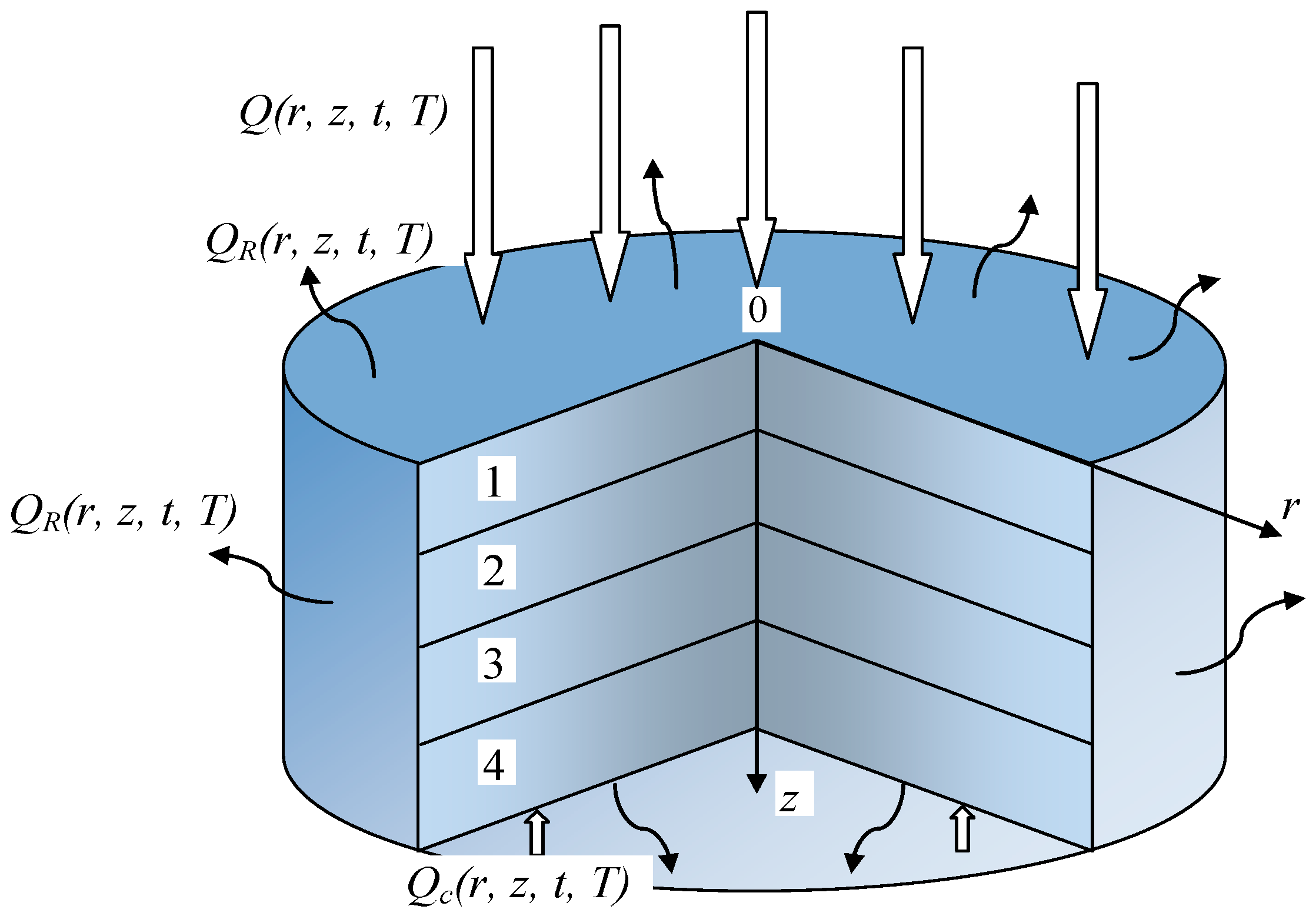
2. Materials and Methods
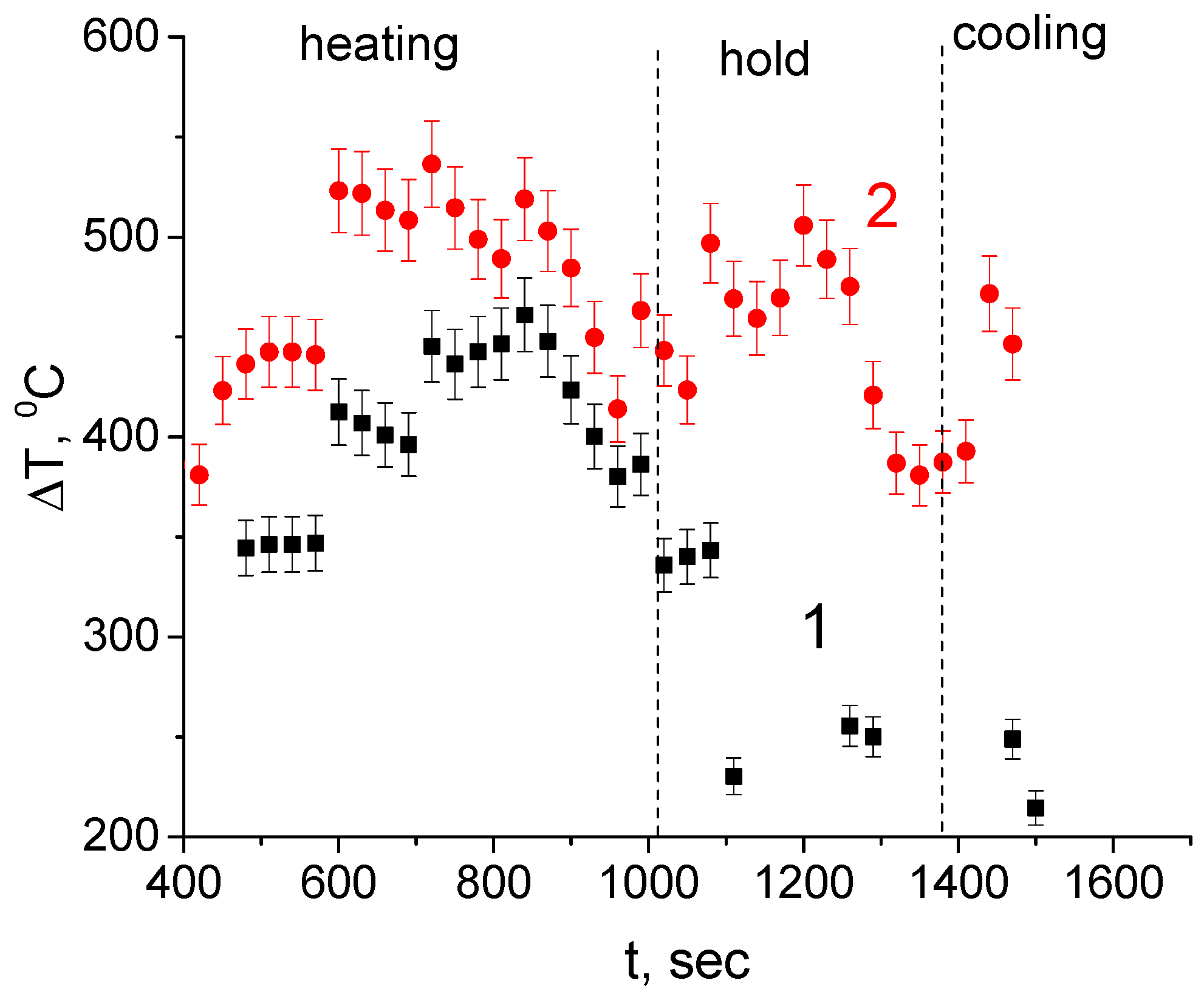
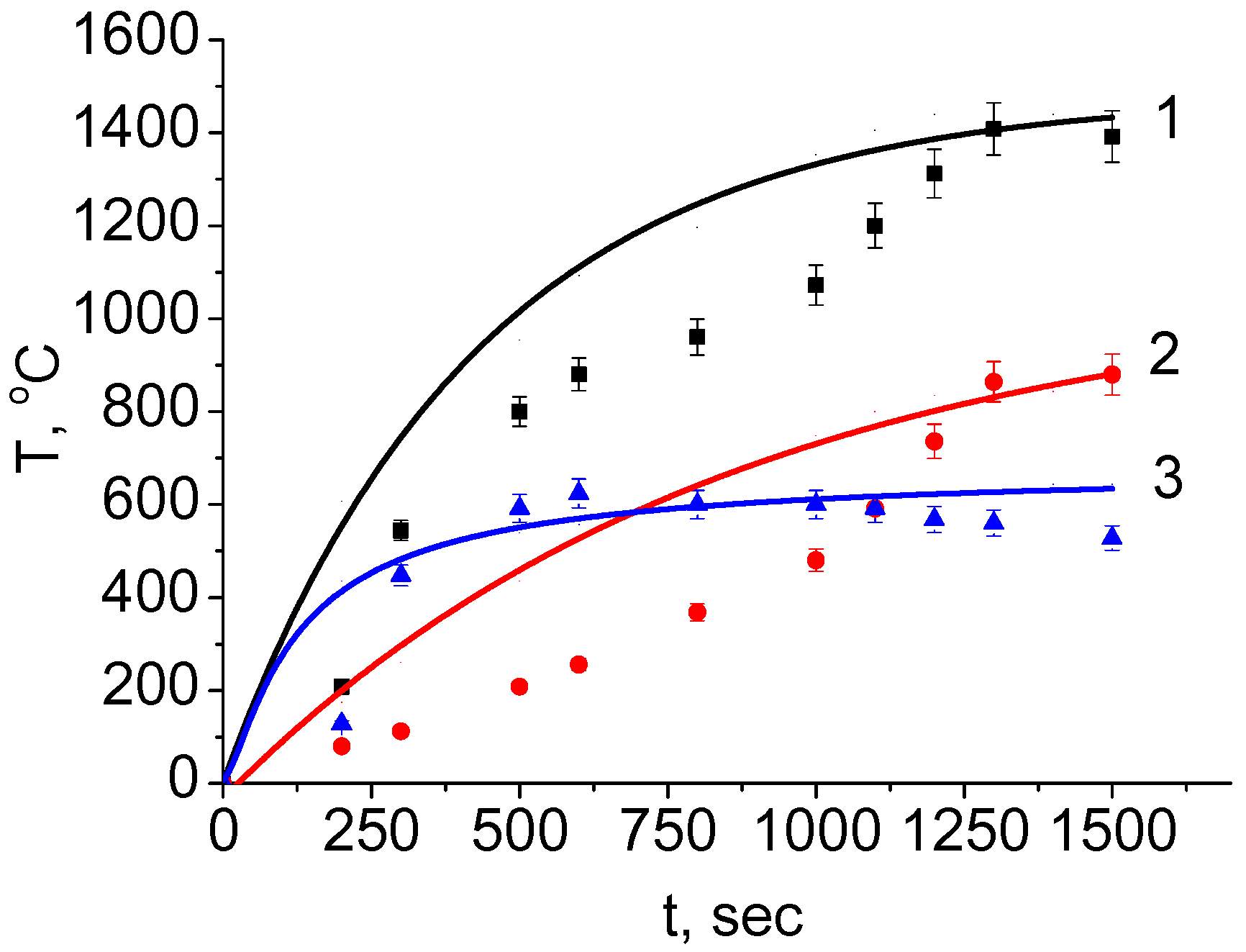
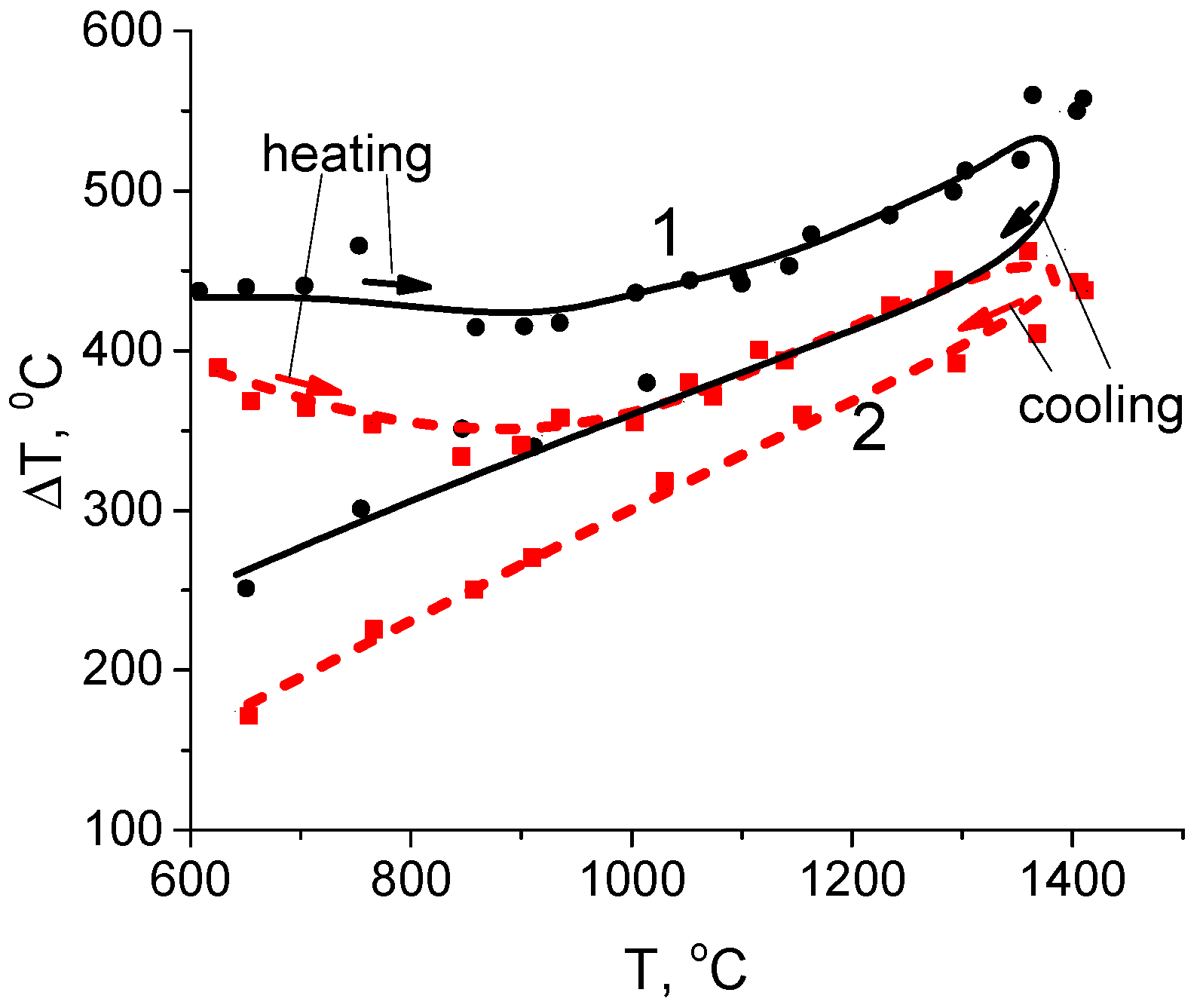
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shin, Y.-S.; Rhee, Y.-W.; Kang, S.-J.L. Experimental Evaluation of Toughening Mechanisms in Alumina-Zirconia Composites. J. Am. Ceram. Soc. 2004, 82, 1229–1232. [Google Scholar] [CrossRef]
- Pfeifer, S.; Demirci, P.; Duran, R.; Stolpmann, H.; Renfftlen, A.; Nemrava, S.; Niewa, R.; Clauß, B.; Buchmeiser, M.R. Synthesis of zirconia toughened alumina (ZTA) fibers for high performance materials. J. Eur. Ceram. Soc. 2016, 36, 725–731. [Google Scholar] [CrossRef]
- Korobenkov, M.V.; Kulkov, S.N. Structure and properties of ZTA composites for joint replacement. AIP Conf. Proc. 2017, 1882, 020035. [Google Scholar]
- Chuankrerkkul, N.; Somton, K.; Wonglom, T.; Dateraksa, K. Physical and Mechanical Properties of Zirconia Toughened Alumina (ZTA) Composites Fabricated by Powder Injection Moulding. Chiang Mai J. Sci. 2016, 43, 375–380. [Google Scholar]
- Exare, C.; Kiat, J.-M.; Guiblin, N.; Porcher, F.; Petricek, V. Structural evolution of ZTA composites during synthesis and processing. J. Eur. Ceram. Soc. 2015, 35, 1273–1283. [Google Scholar] [CrossRef]
- Chen, J.; Xie, Z.; Zeng, W.; Wu, W. Toughening mechanisms of ZTA ceramics at cryogenic temperature (77 K). Ceram. Int. 2017, 43, 3970–3974. [Google Scholar] [CrossRef]
- Naga, S.M.; Awaad, M.; Bondioli, F.; Fino, P.; Hassan, A.M. Thermal diffusivity of ZTA composites with different YSZ quantity. J. Alloys Compd. 2017, 695, 1859–1862. [Google Scholar] [CrossRef]
- Olhero, S.; Ganesh, I.; Torres, P.; Alves, F.; Ferreira, J.M.F. Aqueous colloidal processing of ZTA composites. J. Am. Ceram. Soc. 2009, 92, 9–16. [Google Scholar] [CrossRef]
- Sapuan, S.M. Composite Materials: Concurrent Engineering Approach; Butterworth-Heinemann: Oxford, UK, 2017; pp. 57–93. [Google Scholar]
- Maitra, S.; Roy, J. Nanoceramic matrix composites. In Advances in Ceramic Matrix Composites; Elsevier: Amsterdam, The Netherlands, 2018; pp. 27–48. [Google Scholar]
- Kopeliovich, D. Advances in manufacture of ceramic matrix composites by infiltration techniques. In Advances in Ceramic Matrix Composites; Elsevier: Amsterdam, The Netherlands, 2018; pp. 93–119. [Google Scholar]
- Pfeiffer, S.; Florio, K.; Puccio, D.; Grasso, M.; Colosimo, B.M.; Aneziris, C.G.; Graule, T. Direct laser additive manufacturing of high performance oxide ceramics: A state-of-the-art review. J. Eur. Ceram. Soc. 2021, 41, 6087–6114. [Google Scholar] [CrossRef]
- Vailes, J.; Hagedorn, Y.-C.; Wilhelm, M.; Konrad, W. Additive manufacturing of ZrO2-Al2O3 ceramic components by selective laser melting. Rapid Prototyp. J. 2013, 19, 51–57. [Google Scholar]
- Pulgarín, H.L.C.; Albano, M.P. Sintering and Microstrusture of Al2O3 and Al2O3-ZrO2 Ceramics. Procedia Mater. Sci. 2015, 8, 180–189. [Google Scholar] [CrossRef] [Green Version]
- Daguano, J.K.M.F.; Santos, C.; Souza, R.C.; Balestra, R.M.; Strecker, K.; Elias, C.N. Properties of ZrO2–Al2O3 composite as a function of isothermal holding time. Int. J. Refract. Met. Hard Mater. 2007, 25, 374–379. [Google Scholar] [CrossRef]
- Maca, K.; Pouchly, V.; Shen, Z. Two-step sintering and spark plasma sintering of Al2O3, ZrO2 and SrTiO3 ceramics. Integr. Ferroelectr. 2008, 99, 114–124. [Google Scholar] [CrossRef]
- Lee, B.T.; Hiraga, K.; Shindo, D.; Nishiyama, A. Microstructure of pressureless-sintered Al2O3-24 vol% ZrO2 composite studied by high-resolution electron microscopy. J. Mater. Sci. 1994, 29, 959–964. [Google Scholar] [CrossRef]
- Liu, X.; Zou, B.; Xing, H.; Huang, C. The preparation of ZrO2-Al2O3 composite ceramic by SLA-3D printing and sintering processing. Ceram. Int. 2020, 46, 937–944. [Google Scholar] [CrossRef]
- Hu, K.; Li, X.; Qu, S.; Li, Y. Effect of Heating Rate on Densification and Grain Growth During Spark Plasma Sintering of 93W-5.6Ni-1.4Fe Heavy Alloys. Met. Mater. Trans. A 2013, 44, 4323–4336. [Google Scholar] [CrossRef]
- Bakeev, I.Y.; Klimov, A.; Oks, E.M.; Zenin, A. Generation of high-power-density electron beams by a forevacuum-pressure plasma-cathode electron source. Plasma Sources Sci. Technol. 2018, 27, 075002. [Google Scholar] [CrossRef]
- Burdovitsin, V.A.; Goreev, A.K.; Klimov, A.; Zenin, A.A.; Oks, E. Expansion of the working range of forevacuum plasma electron sources toward higher pressures. Tech. Phys. 2012, 57, 1101–1105. [Google Scholar] [CrossRef]
- Burdovitsin, V.A.; Klimov, A.S.; Oks, E.M. On the possibility of electron-beam processing of dielectrics using a forevacuum plasma electron source. Tech. Phys. Lett. 2009, 35, 511–513. [Google Scholar] [CrossRef]
- Klimov, A.S.; Bakeev, I.Y.; Zenin, A.A. Influence of electron-beam processing mode on the sintering of alumina ceramics. IOP Conf. Ser. Mater. Sci. Eng. 2019, 597, 012070. [Google Scholar] [CrossRef] [Green Version]
- Klimov, A.S.; Bakeev, I.Y.; Oks, E.M.; Zenin, A.A.; Dvilis, E.S. Electron beam sintering of ceramics for additive manufacturing. Vacuum 2019, 169, 108933. [Google Scholar] [CrossRef]
- Klimov, A.S.; Zenin, A.A.; Bakeev, I.Y.; Oks, E.M. Formation of Gradient Metalloceramic Materials Using Electron-Beam Irradiation in the Forevacuum. Russ. Phys. J. 2019, 62, 1–7. [Google Scholar] [CrossRef]
- Alper, A.M. Science of Ceramics; Stewart, G.H., Ed.; Academic Press: London, UK, 1967; Volume 3, p. 339. [Google Scholar]
- Korolev, A.; Knyazev, A.V.; Gavrilov, I.R. X-ray diffraction and calorimetric studies of powder nanocrystalline systems based on ZrO2(Y) and Al2O3 with second insoluble component. Phys. Solid State 2012, 54, 267–272. [Google Scholar] [CrossRef]
- Subbarao, E.C.; Maiti, H.S.; Srivastava, K.K. Martensitic transformation in zirconia. Acta Metall. 1972, 20, 1281–1289. [Google Scholar] [CrossRef]
- Nettleship, L.; Stevens, R. Tetragonal zirconia polycrystals (TZP). A review. Int. J. High Technol. Ceram. 1987, 3, 1–32. [Google Scholar] [CrossRef]
- Hannink, R.H.J.; Kelly, P.M.; Muddle, B.C. Transformation toughening in zirconia-containing ceramics. J. Amer. Ceram. Soc. 2000, 83, 461–487. [Google Scholar] [CrossRef]
- Piconi, C. Advances in Ceramic Biomaterials Ceramics for Joint Replacement; Woodhead Publishing: Amsterdam, The Netherlands, 2017; pp. 129–179. [Google Scholar] [CrossRef]



| Material | Density, kg/m3 | Specific Heat, J/(kg⋅K) | Heat Conductivity Coefficient, W/(m⋅K) |
|---|---|---|---|
| 100% ZrO2 | 5800 | 549 | 1.8 |
| 70% ZrO2, 30% Al2O3 | 5248 | 650 | 7 |
| 30% ZrO2, 70% Al2O3 | 4515 | 782 | 15 |
| 100% Al2O3 | 3960 | 883 | 20 |
| Layer No. | Composition, Mass% | Sample of the First Type | Sample of the Second Type |
|---|---|---|---|
| Thickness h, mm | |||
| 1 | 100% ZrO2 | 0.75 | 0.4 |
| 2 | 70% ZrO2, 30% Al2O3 | 0.75 | 0.6 |
| 3 | 30% ZrO2, 70% Al2O3 | 0.75 | 0.8 |
| 4 | 100% Al2O3 | 0.75 | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimov, A.; Bakeev, I.; Oks, E.; Zenin, A. Electron Beam Sintering of Composite Al2O3-ZrO2 Ceramics in the Forevacuum Pressure Range. Coatings 2022, 12, 278. https://doi.org/10.3390/coatings12020278
Klimov A, Bakeev I, Oks E, Zenin A. Electron Beam Sintering of Composite Al2O3-ZrO2 Ceramics in the Forevacuum Pressure Range. Coatings. 2022; 12(2):278. https://doi.org/10.3390/coatings12020278
Chicago/Turabian StyleKlimov, Aleksandr, Ilya Bakeev, Efim Oks, and Aleksey Zenin. 2022. "Electron Beam Sintering of Composite Al2O3-ZrO2 Ceramics in the Forevacuum Pressure Range" Coatings 12, no. 2: 278. https://doi.org/10.3390/coatings12020278
APA StyleKlimov, A., Bakeev, I., Oks, E., & Zenin, A. (2022). Electron Beam Sintering of Composite Al2O3-ZrO2 Ceramics in the Forevacuum Pressure Range. Coatings, 12(2), 278. https://doi.org/10.3390/coatings12020278






