Simulation of Epitaxial Film–Substrate Interaction Potential
Abstract
:1. Introduction
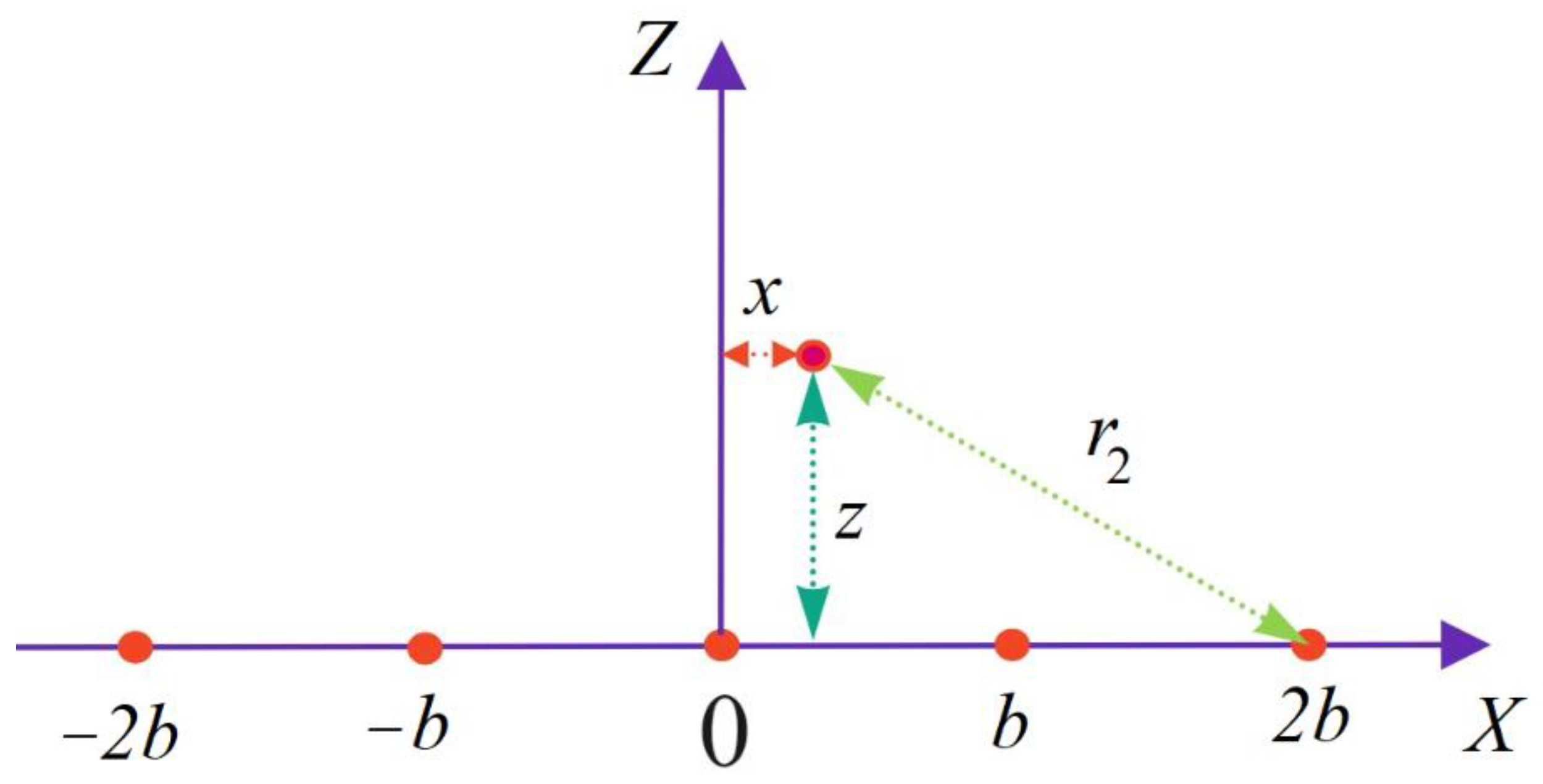
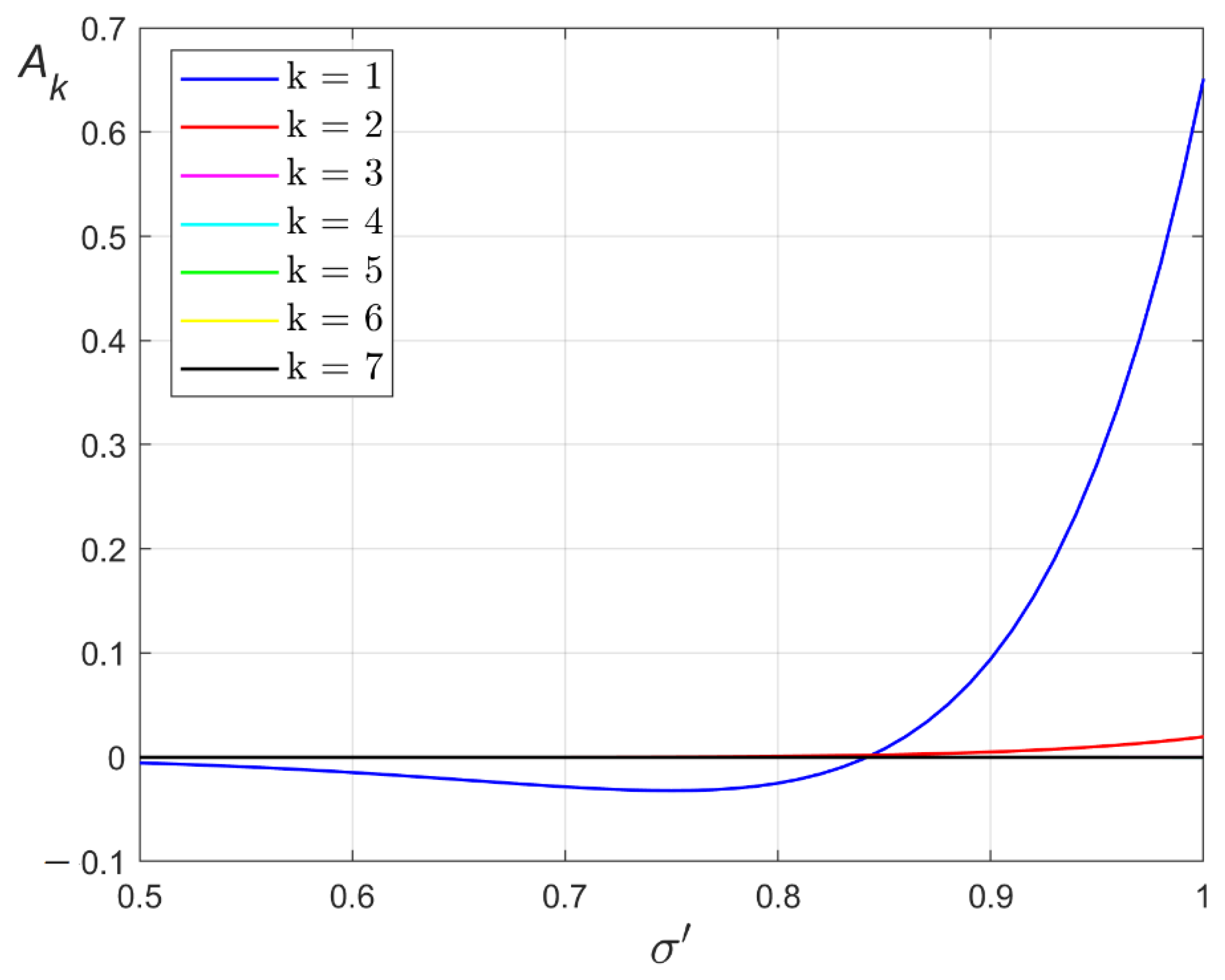
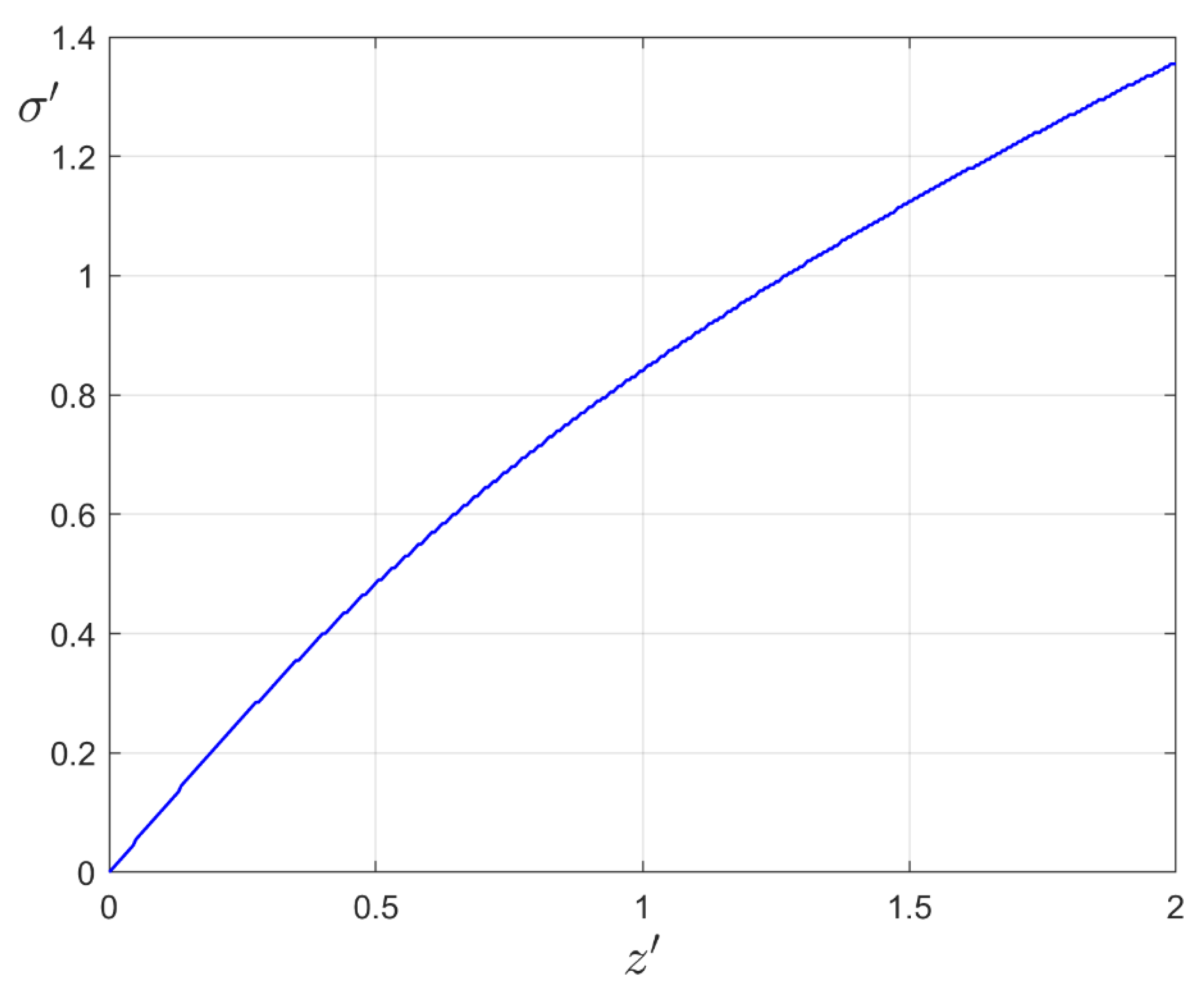
2. Substrate Potential Modeling
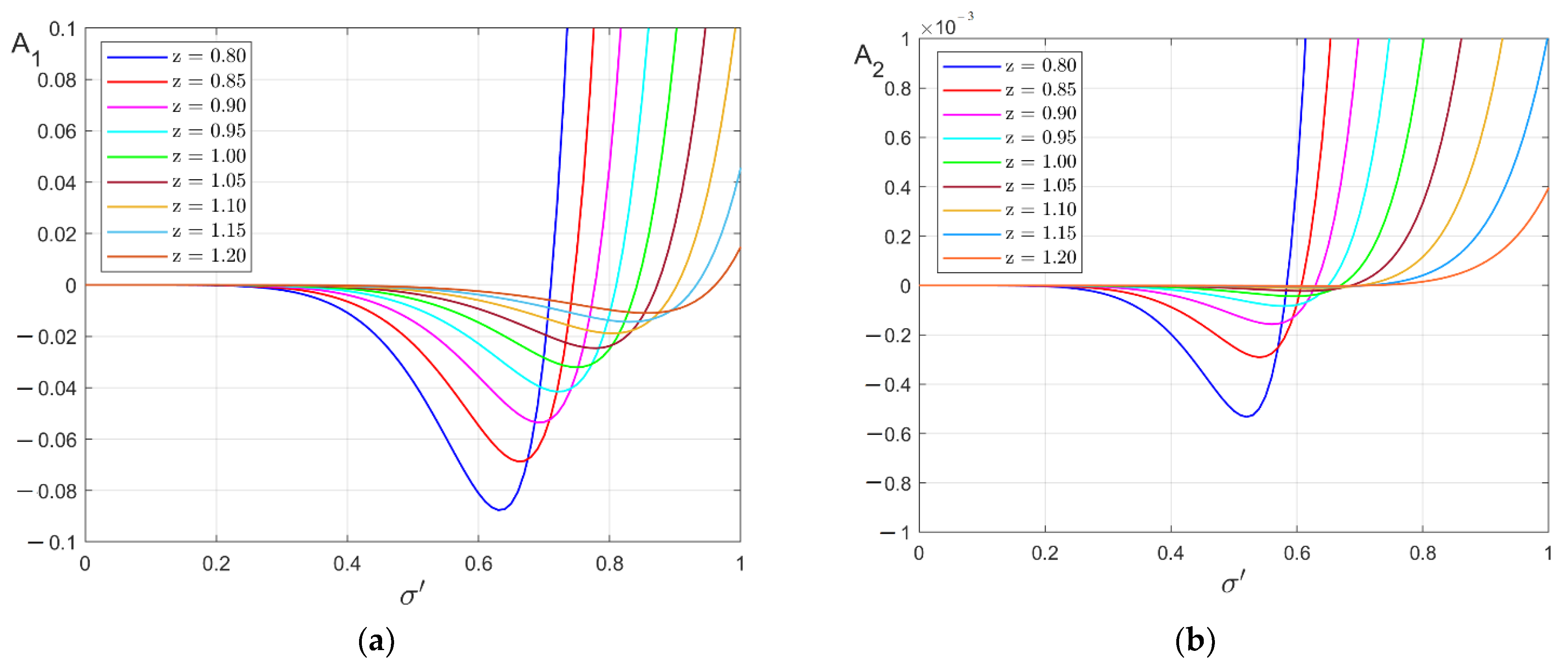
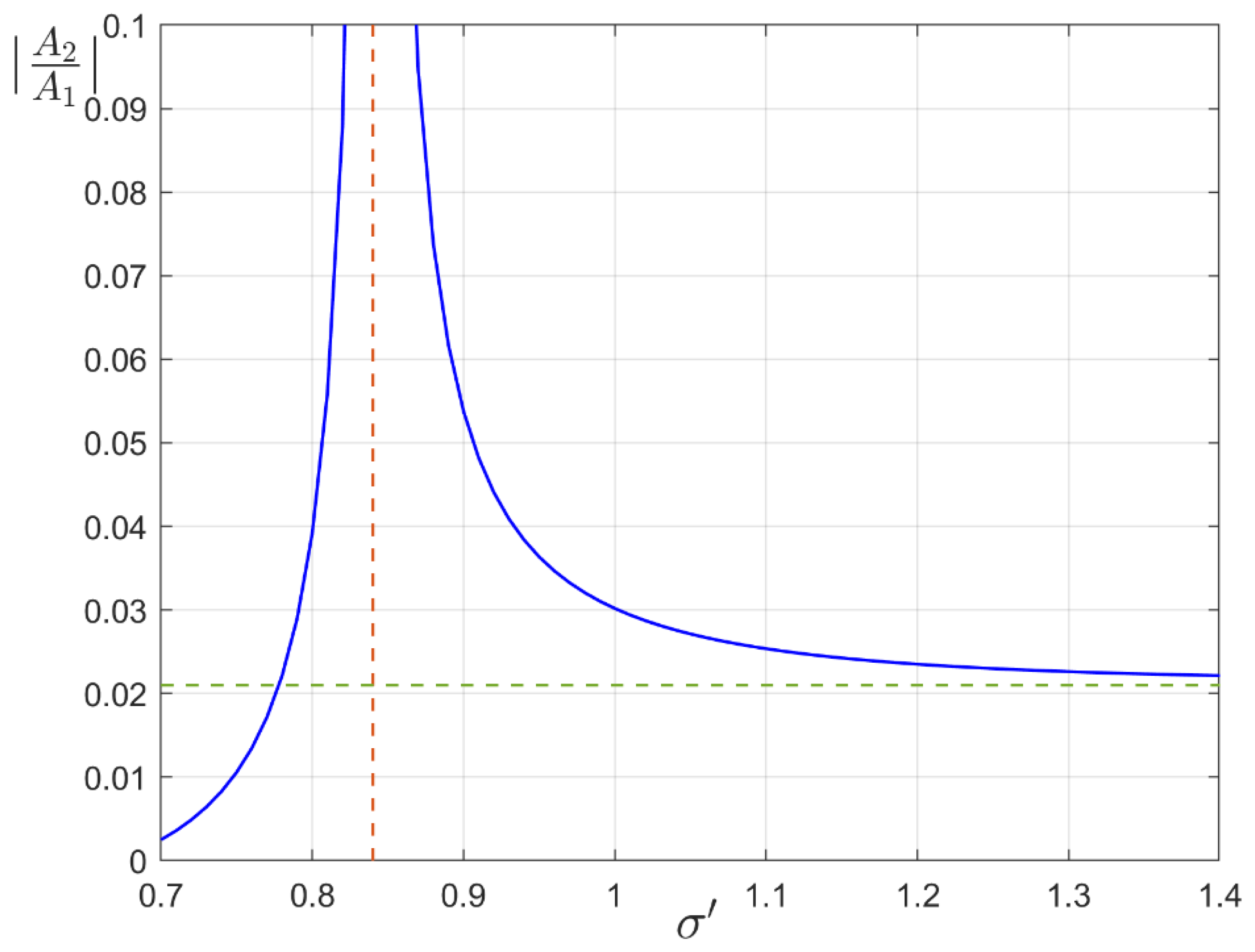
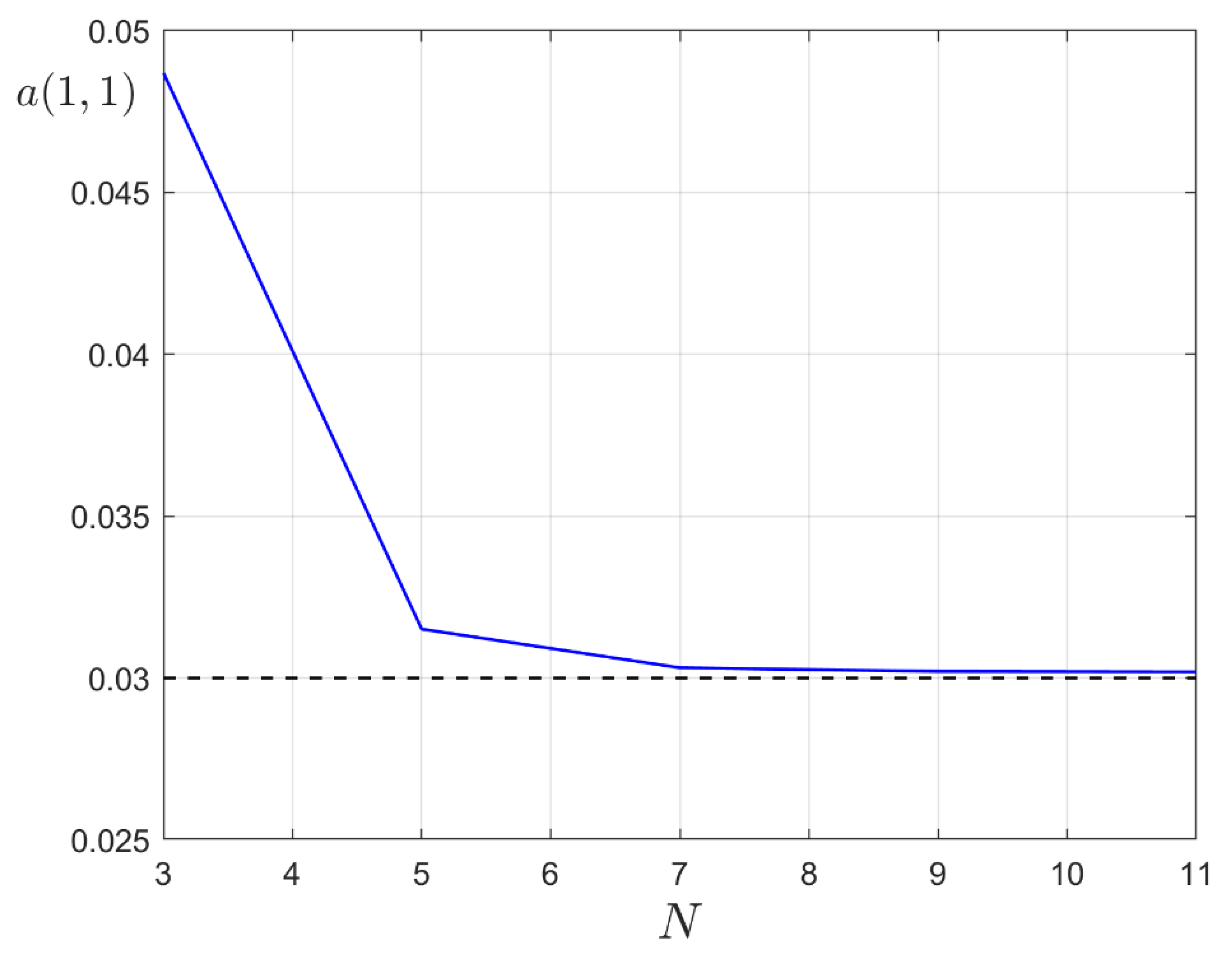
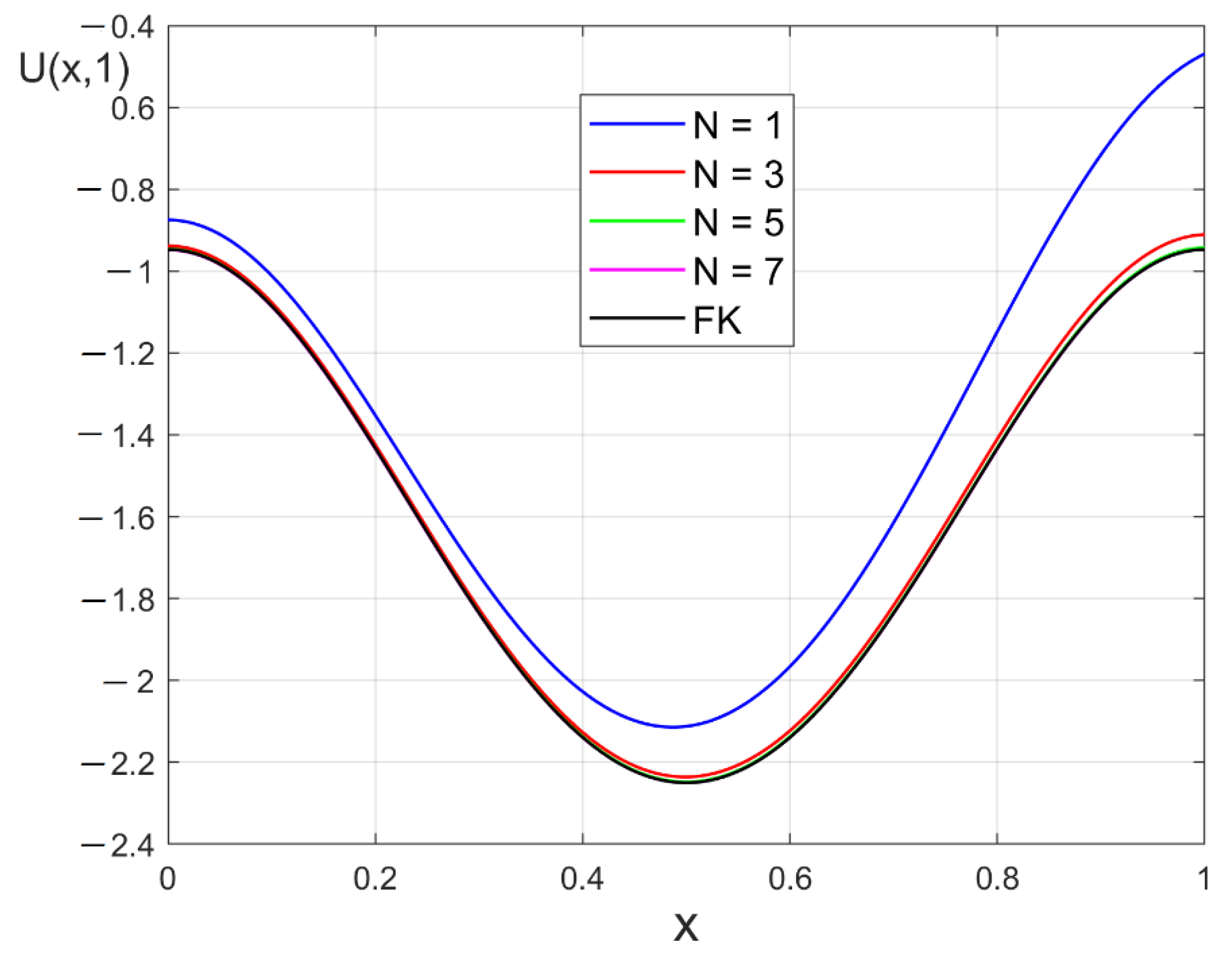
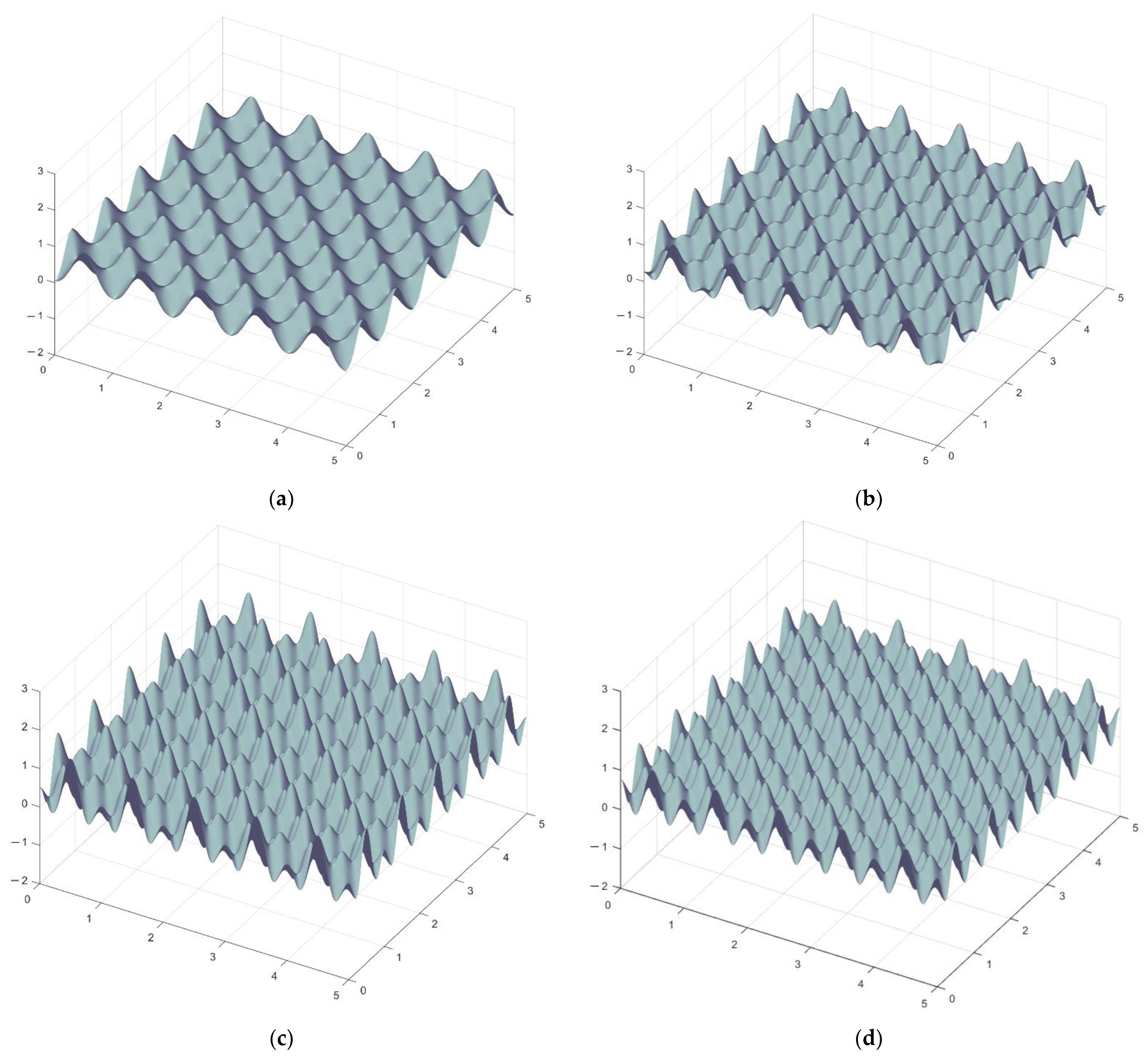
3. Ground State of Monoatomic Film
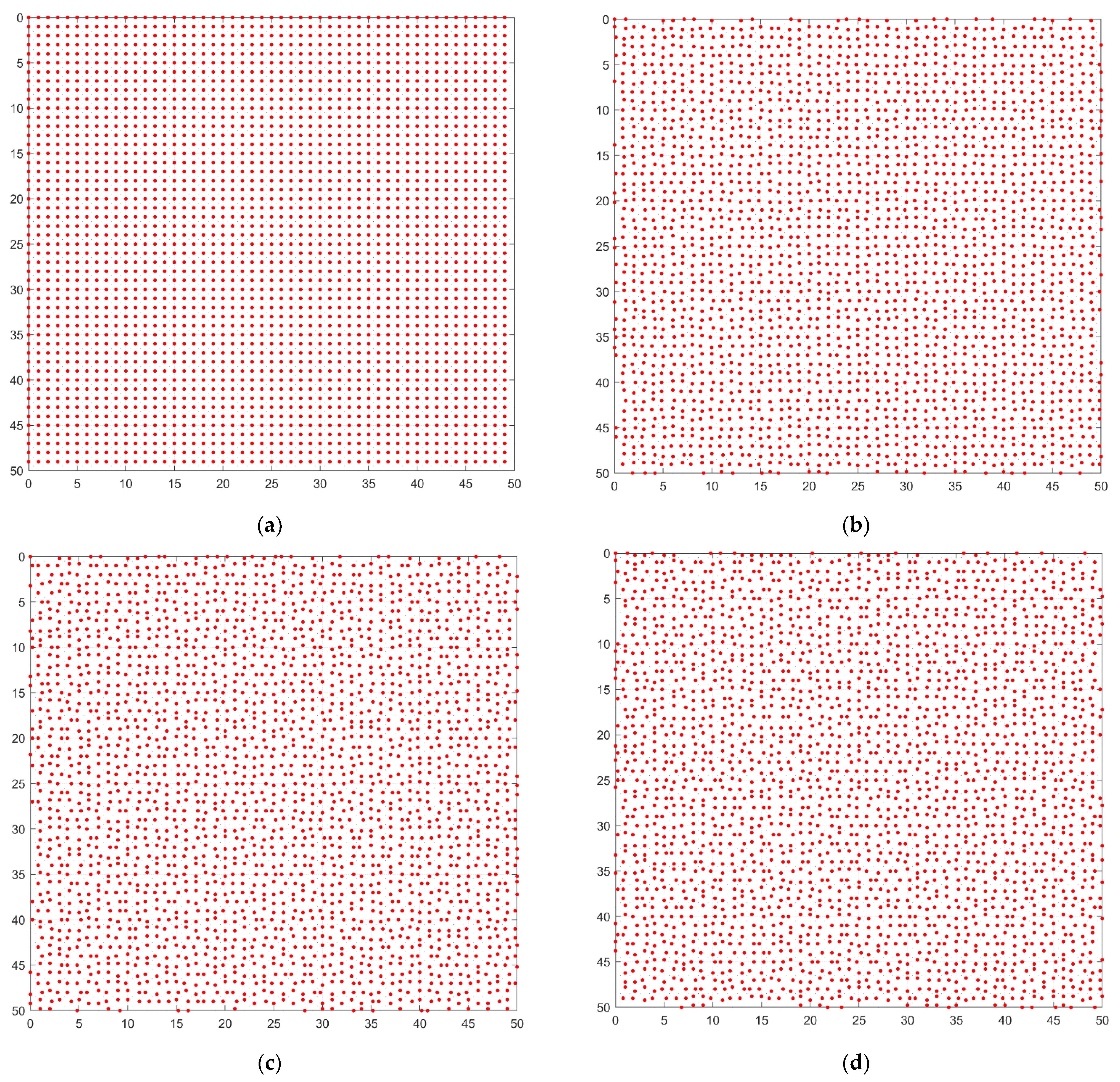
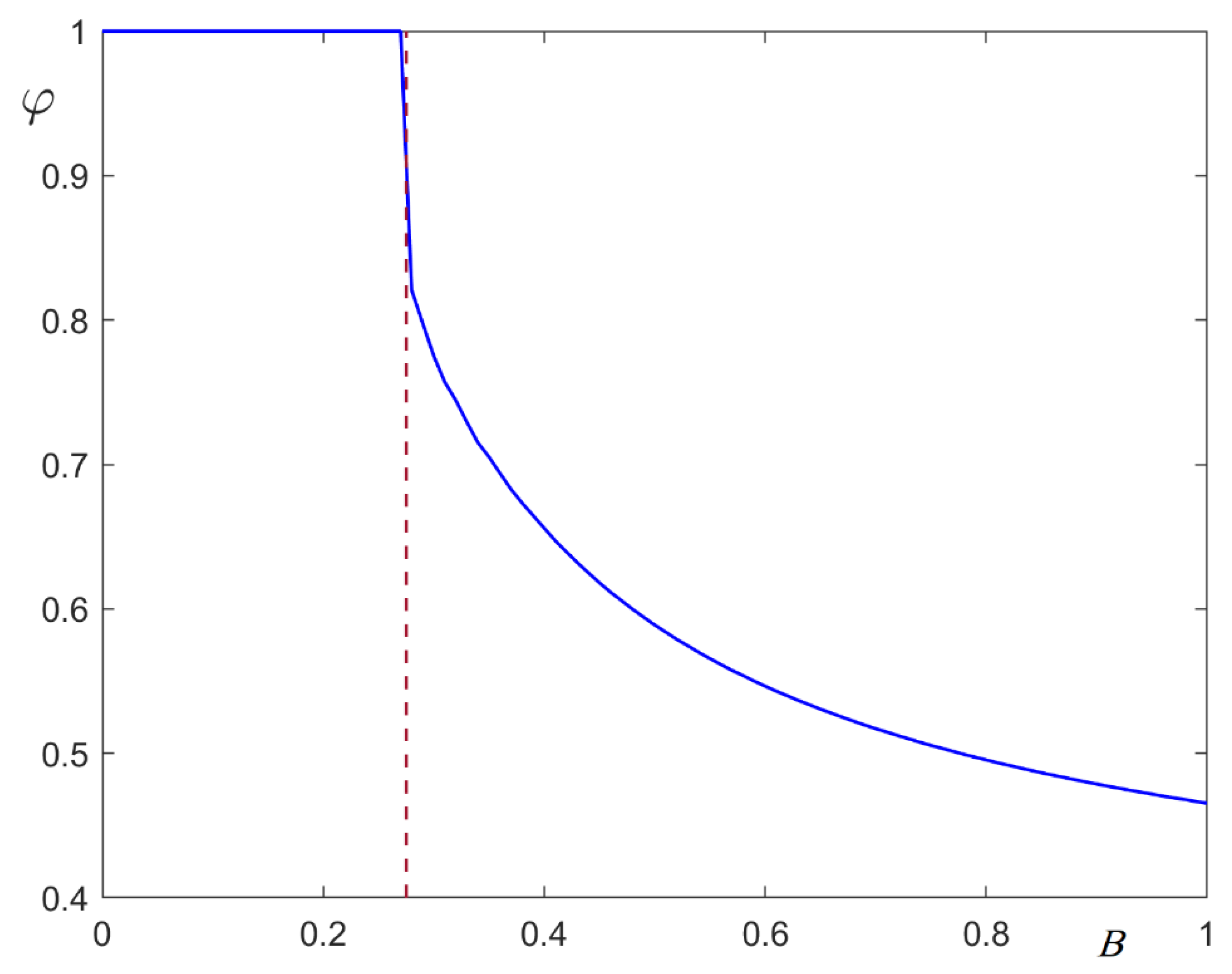
4. Structural Phase Transition
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhabrev, V.A.; Margolin, V.I.; Tupik, V.A.; Su, C.T. Simulating the aggregation of nanoparticles on a substrate surface upon vacuum deposition. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2015, 9, 877–879. [Google Scholar] [CrossRef]
- Aguirre, N.F.; Mateo, D.; Mitrushchenkov, A.O.; Pi, M.; de Lara-Castells, M.P. Helium mediated deposition: Modeling the He−TiO2(110)-(1×1) interaction potential and application to the collision of a helium droplet from density functional calculations. J. Chem. Phys. 2012, 136, 124703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frenkel, Y.; Kontorova, T. On the theory of plastic deformation and twinning. Acad. Sci. USSR J. Phys. 1939, 1, 137–149. [Google Scholar]
- Yuan, X.-P.; Zheng, Z.-G. Ground-state transition in a two-dimensional Frenkel-Kontorova model. Chin. Phys. Lett. 2011, 28, 100507. [Google Scholar] [CrossRef]
- Savin, A.V.; Zubova, E.A.; Manevitch, L.I. Survival condition for low-frequency quasi-one-dimensional breathers in a two-dimensional strongly anisotropic crystal. Phys. Rev. B 2005, 71, 224303. [Google Scholar] [CrossRef]
- Babushkin, A.Y.; Abkaryan, A.K.; Dobronets, B.S.; Krasikov, V.S.; Filonov, A.N. The ground state of the Frenkel–Kontorova model. Phys. Solid State 2016, 58, 1834–1845. [Google Scholar] [CrossRef]
- Vainchtein, A.; Cuevas-Maraver, J.; Kevrekidis, P.G.; Xu, H. Stability of traveling waves in a driven Frenkel–Kontorova model. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105236. [Google Scholar] [CrossRef] [Green Version]
- Quapp, W.; Bofill, J.M. Description of zero field steps on the potential energy surface of a Frenkel-Kontorova model for annular Josephson junction arrays. Eur. Phys. J. B 2021, 94, 105. [Google Scholar] [CrossRef]
- Tekić, J.; Botha, A.E.; Mali, P.; Shukrinov, Y.M. Inertial effects in the dc+ac driven underdamped Frenkel-Kontorova model: Subharmonic steps, chaos, and hysteresis. Phys. Rev. E 2019, 99, 022206. [Google Scholar] [CrossRef]
- Byckov, I.V.; Belim, S.V.; Maltsev, I.V.; Shavrov, V.G. Phase transition and magnetoelectric effect in 2D ferromagnetic films on a ferroelectric substrate. Coatings 2021, 11, 1325. [Google Scholar] [CrossRef]
- Belim, S.V. Investigation of phase transitions in ferromagnetic nanofilms on a non-magnetic substrate by computer simulation. Materials 2022, 15, 2390. [Google Scholar] [CrossRef]
- Belim, S.V.; Bychkov, I.V.; Maltsev, I.; Kuzmin, D.A.; Shavrov, V.G. Tuning of 2D magnets Curie temperature via substrate. J. Magn. Magn. Mater. 2022, 541, 168553. [Google Scholar] [CrossRef]
- Remoissenet, M.; Peyrard, M. Soliton dynamics in new models with parametrized periodic double-well and asymmetric substrate potentials. Phys. Rev. B 1984, 29, 3153. [Google Scholar] [CrossRef]
- Djuidjé Kenmoé, G.; Kofané, T. Frictional stick-slip dynamics in a nonsinusoidal Remoissenet-Peyrard potential. Eur. Phys. J. B 2007, 55, 347–354. [Google Scholar] [CrossRef]
- Yang, S.; Yu, S.; Cho, M. Influence of mold and substrate material combinations on nanoimprint lithography process: MD simulation approach. Appl. Surf. Sci. 2014, 301, 189–198. [Google Scholar] [CrossRef]
- Akbarzadeh, H.; Yaghoubi, H.; Salemi, S. Investigation of thermal behavior of graphite-supported Ag nanoclusters of different sizes using molecular dynamics simulations. Fluid Phase Equilibria 2014, 365, 68–73. [Google Scholar] [CrossRef]
- Kornich, G.V.; Betz, G.; Zaporojtchenko, V.; Pugina, K.V.; Faupel, F. Molecular dynamics simulations of interactions of Ar and Xe ions with surface Cu clusters at low impact energies. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2005, 228, 41–45. [Google Scholar] [CrossRef]
- Rojas, M.I. Off lattice Monte Carlo simulation study for different metal adlayers onto (111) substrates. Surf. Sci. 2004, 569, 76–88. [Google Scholar] [CrossRef]
- Hwang, S.F.; Li, Y.H.; Hong, Z.H. Molecular dynamic simulation for Co cluster deposition on Si substrate. Adv. Mater. Res. 2012, 560–561, 1138–1145. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Ringhofer, C.; Vasileska, D. Parameter-free effective potential method for use in particle-based device simulations. IEEE Trans. Nanotechnol. 2005, 4, 465–471. [Google Scholar] [CrossRef]
- Claassens, C.H.; Terblans, J.J.; Hoffman, M.J.H.; Swart, H.C. Kinetic Monte Carlo simulation of monolayer gold film growth on a graphite substrate. Surf. Interface Anal. 2005, 37, 1021–1026. [Google Scholar] [CrossRef]
- Giménez, M.C.; Ramirez-Pastor, A.J.; Leiva, E.P.M. Monte Carlo simulation of metal deposition on foreign substrates. Surf. Sci. 2006, 600, 4741–4751. [Google Scholar]
- Fu, T.; Peng, X.; Feng, C.; Zhao, Y.; Wang, Z. MD simulation of growth of Pd on Cu (111) and Cu on Pd (111) substrates. Appl. Surf. Sci. 2015, 356, 651–658. [Google Scholar]
- Hong, Z.-H.; Hwang, S.-F.; Fang, T.-H. The deposition of Fe or Co clusters on Cu substrate by molecular dynamic simulation. Surf. Sci. 2011, 605, 46–53. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the determination of molecular fields. II. From the equation of state of a gas. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1924, 106, 463–477. [Google Scholar]
- Pyykkö, P.; Atsumi, M. Molecular single-bond covalent radii for elements 1–118. Chem. Eur. J. 2008, 15, 186–197. [Google Scholar] [CrossRef]
- Morse, P.M. Diatomic molecules according to the wave mechanics. II. Vibrational levels. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991. [Google Scholar]
- Bazant, M.Z.; Kaxiras, E.; Justo, J.F. Environment-dependent interatomic potential for bulk silicon. Phys. Rev. B 1997, 56, 8542. [Google Scholar]
- Justo, J.F.; Bazant, M.Z.; Kaxiras, E.; Bulatov, V.V.; Yip, S. Interatomic potential for silicon defects and disordered phases. Phys. Rev. B 1998, 58, 2539. [Google Scholar] [CrossRef] [Green Version]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458. [Google Scholar] [CrossRef]
- Cleri, F.; Rosato, V. Tight-binding potentials for transition metals and alloys. Phys. Rev. B 1993, 48, 22. [Google Scholar] [CrossRef] [PubMed]
- Finnis, M.W.; Sinclair, J.E. A simple empirical N-body potential for transition metals. Philos. Mag. A 1984, 50, 45–55. [Google Scholar] [CrossRef]
- Todd, B.D.; Lynden-Bell, R.M. Surface and bulk properties of metals modelled with Sutton-Chen potentials. Surf. Sci. 1993, 281, 191–206. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.J.; Papaconstantopoulos, D.A. Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys. Rev. B 1999, 59, 3393. [Google Scholar] [CrossRef] [Green Version]
- Sutton, A.P.; Chen, J. Long-range Finnis–Sinclair potentials. Philos. Mag. Lett. 1990, 61, 139–146. [Google Scholar] [CrossRef]
- Wang, X.F.; Gu, D.; Xiao, T.; Xu, X.F.; He, Y.; Huang, C.Z.; Zhang, Z.L.; Li, T.L.; Zhu, W.L.; Lai, T.S. Effect of substrate on phase-change characteristics of GeSb thin films and its potential application in three-level electrical storage. AIP Adv. 2019, 9, 015105. [Google Scholar] [CrossRef] [Green Version]
- Prainetr, N.; Voraud, A.; Thaowonkaew, S.; Horprathum, M.; Muthitamongkol, P.; Seetawan, T. Effect of substrates on thermoelectric properties of Ag–Sb–Te thin films within the temperature annealing. Phys. B Condens. Matter 2020, 582, 411977. [Google Scholar] [CrossRef]
- Lu, Y.; Li, H.; Yang, G. Varied longitudinal microstructure of μc-Si:H films by tuning substrate temperature. Surf. Eng. 2015, 31, 763–769. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, T.; Yu, L.; Shen, F.; Wang, J.; Cui, K. Improving oxidation resistance of TZM alloy by deposited Si–MoSi2 composite coating with high silicon concentration. Ceram. Int. 2022, 48, 20895–20904. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, L.; Fu, T.; Wang, J.; Shen, F.; Cui, K. Microstructure evolution and growth mechanism of Si-MoSi2 composite coatings on TZM (Mo-0.5Ti-0.1Zr-0.02 °C) alloy. J. Alloys Compd. 2022, 894, 162403. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, K.; Fu, T.; Wang, J.; Shen, F.; Zhang, X.; Yu, L. Formation of MoSi2 and Si/MoSi2 coatings on TZM (Mo–0.5Ti–0.1Zr–0.02C) alloy by hot dip silicon-plating method. Ceram. Int. 2021, 47, 23053–23065. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belim, S.V.; Tikhomirov, I.V.; Bychkov, I.V. Simulation of Epitaxial Film–Substrate Interaction Potential. Coatings 2022, 12, 853. https://doi.org/10.3390/coatings12060853
Belim SV, Tikhomirov IV, Bychkov IV. Simulation of Epitaxial Film–Substrate Interaction Potential. Coatings. 2022; 12(6):853. https://doi.org/10.3390/coatings12060853
Chicago/Turabian StyleBelim, Sergey V., Ilya V. Tikhomirov, and Igor V. Bychkov. 2022. "Simulation of Epitaxial Film–Substrate Interaction Potential" Coatings 12, no. 6: 853. https://doi.org/10.3390/coatings12060853





