Design, Optimization and Cutting Performance Evaluation of an Internal Spray Cooling Turning Tool
Abstract
:1. Introduction
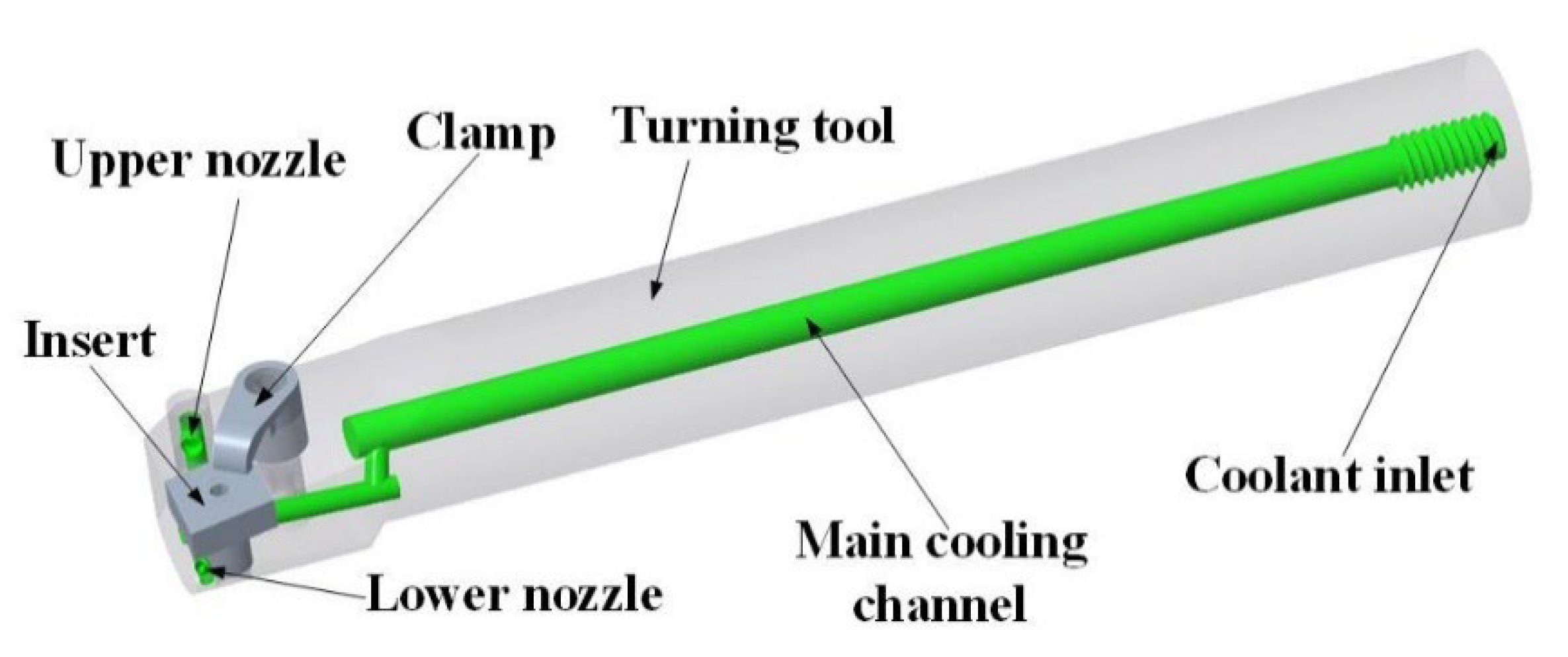
2. Cooling Structure Design of the Internal Spray Cooling Turning Tool
3. Structure Optimization of Internal Spray Cooling Turning Tool
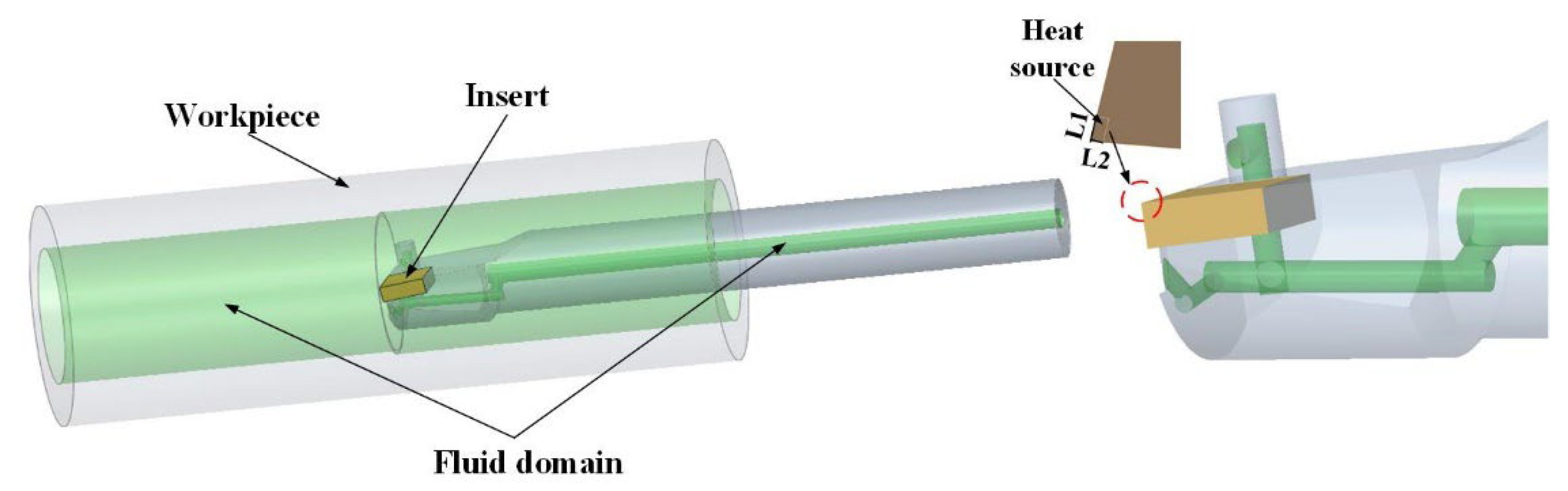
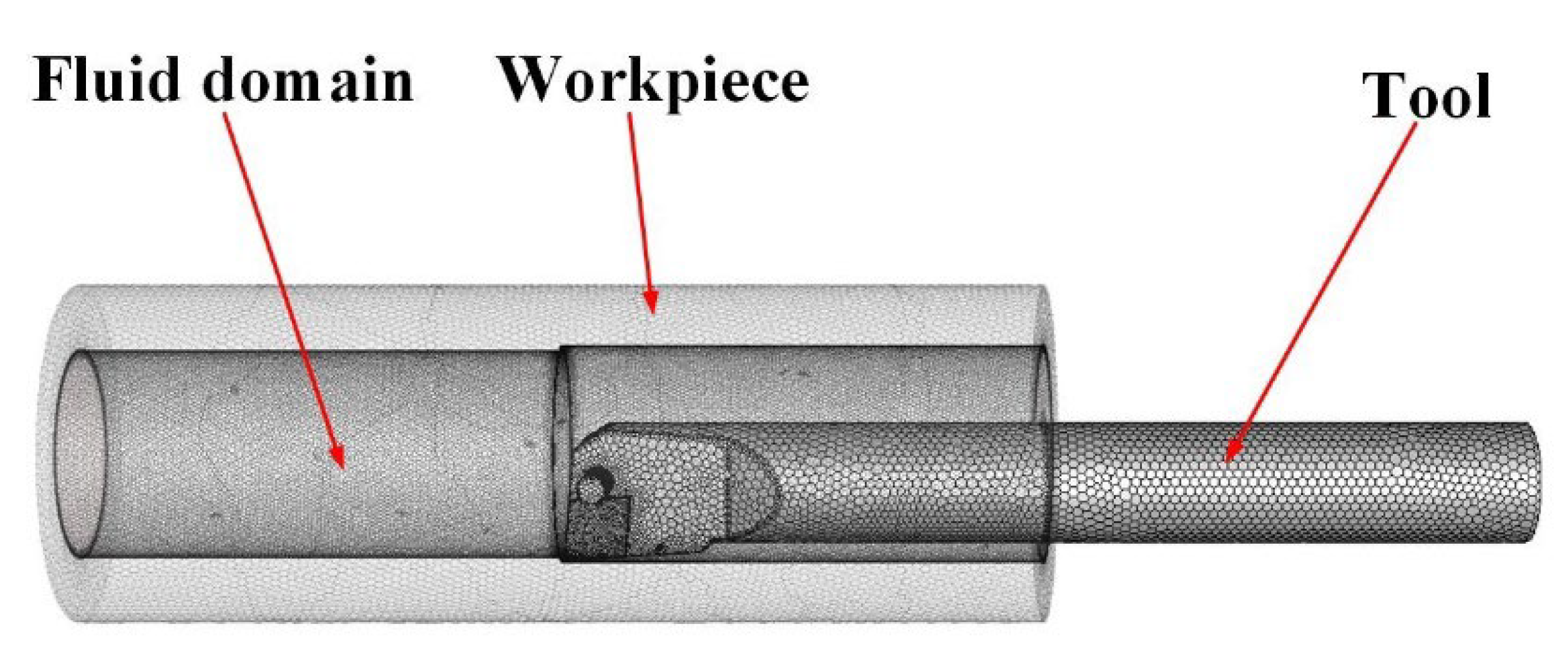
3.1. Establishment of Simulation Model
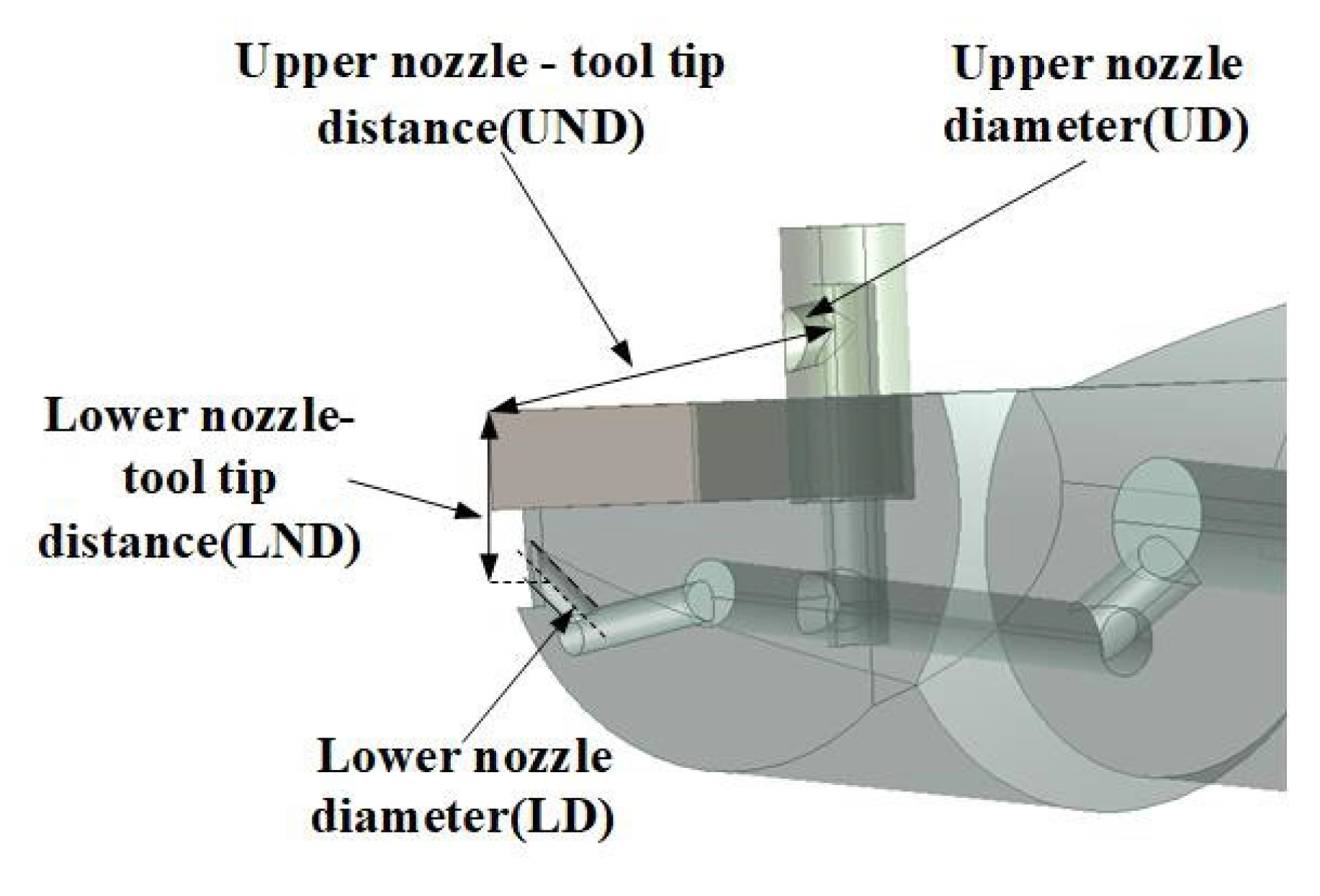
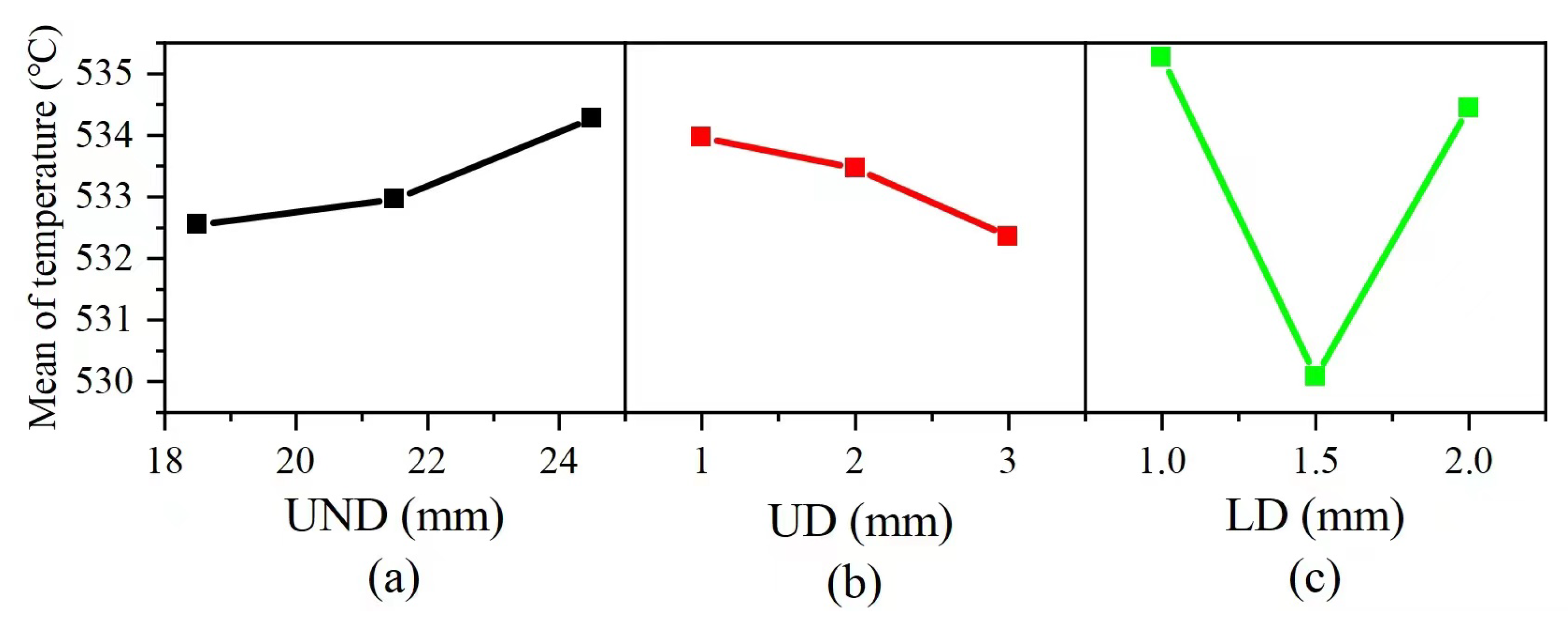
3.2. Optimization of Tool Cooling Structure Parameters
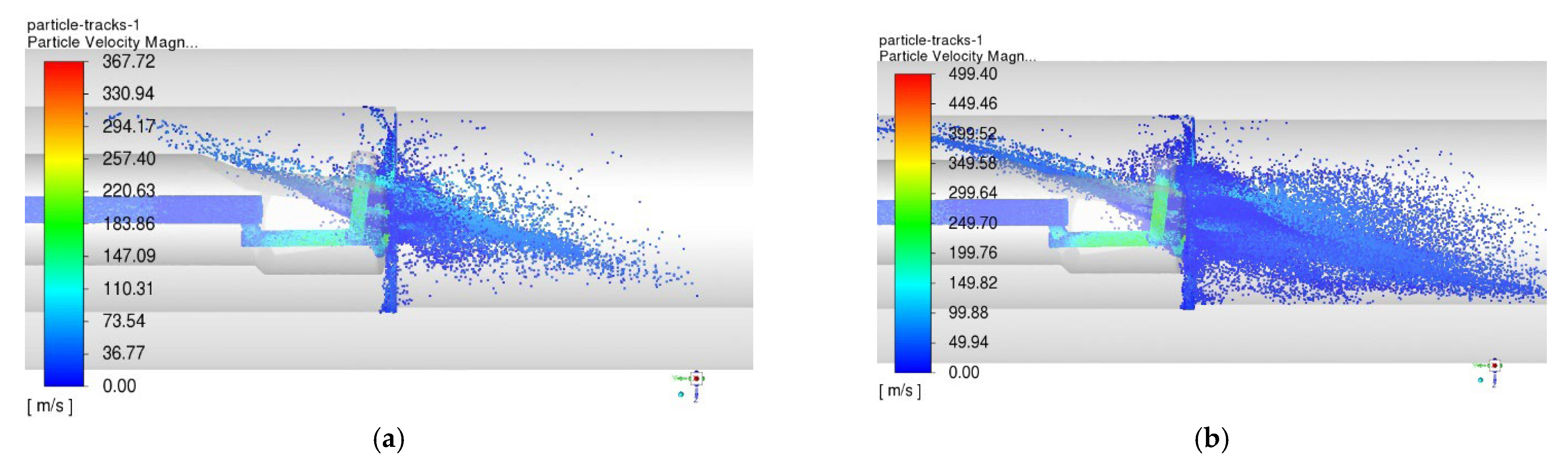
3.3. Simulation Results Analysis
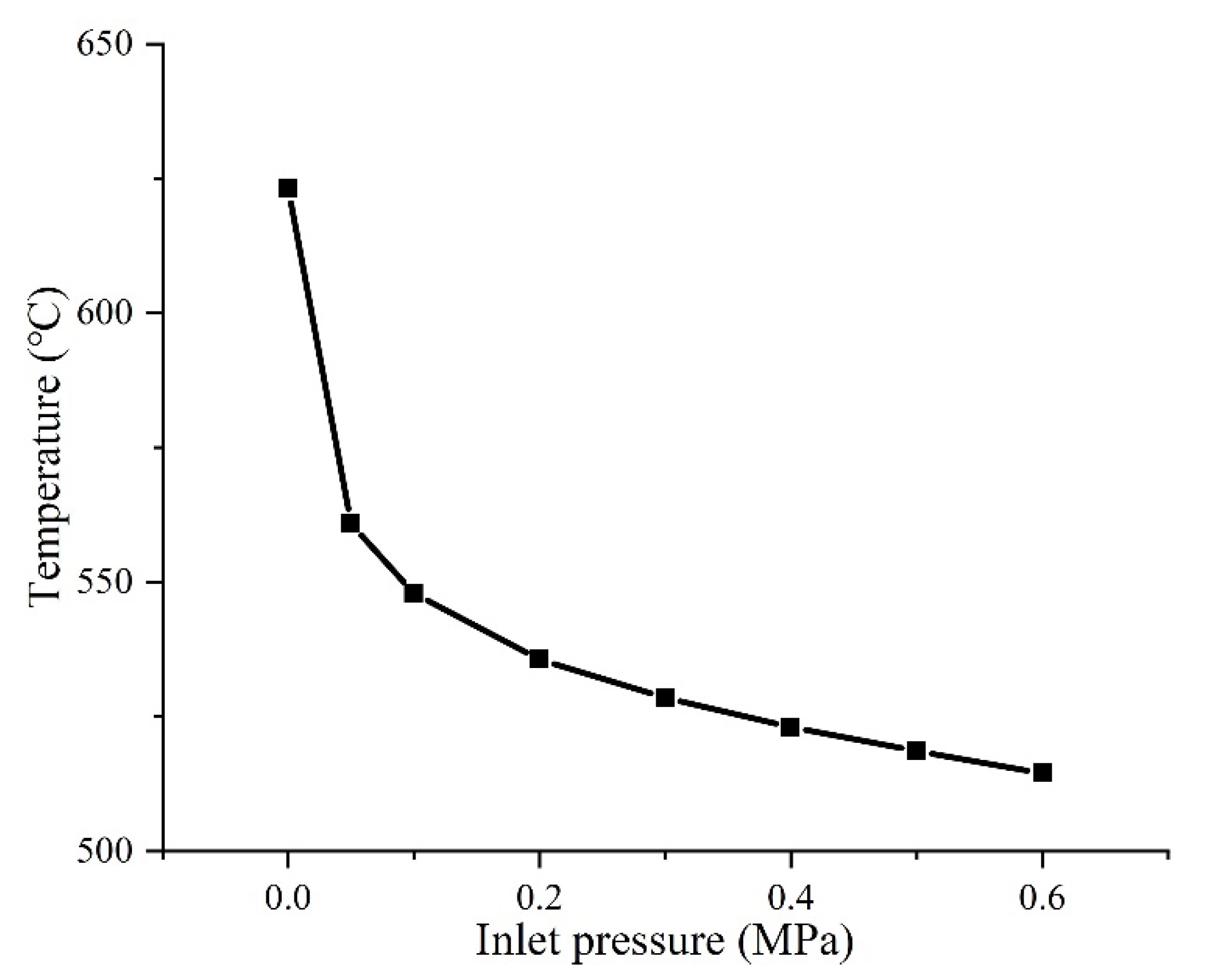
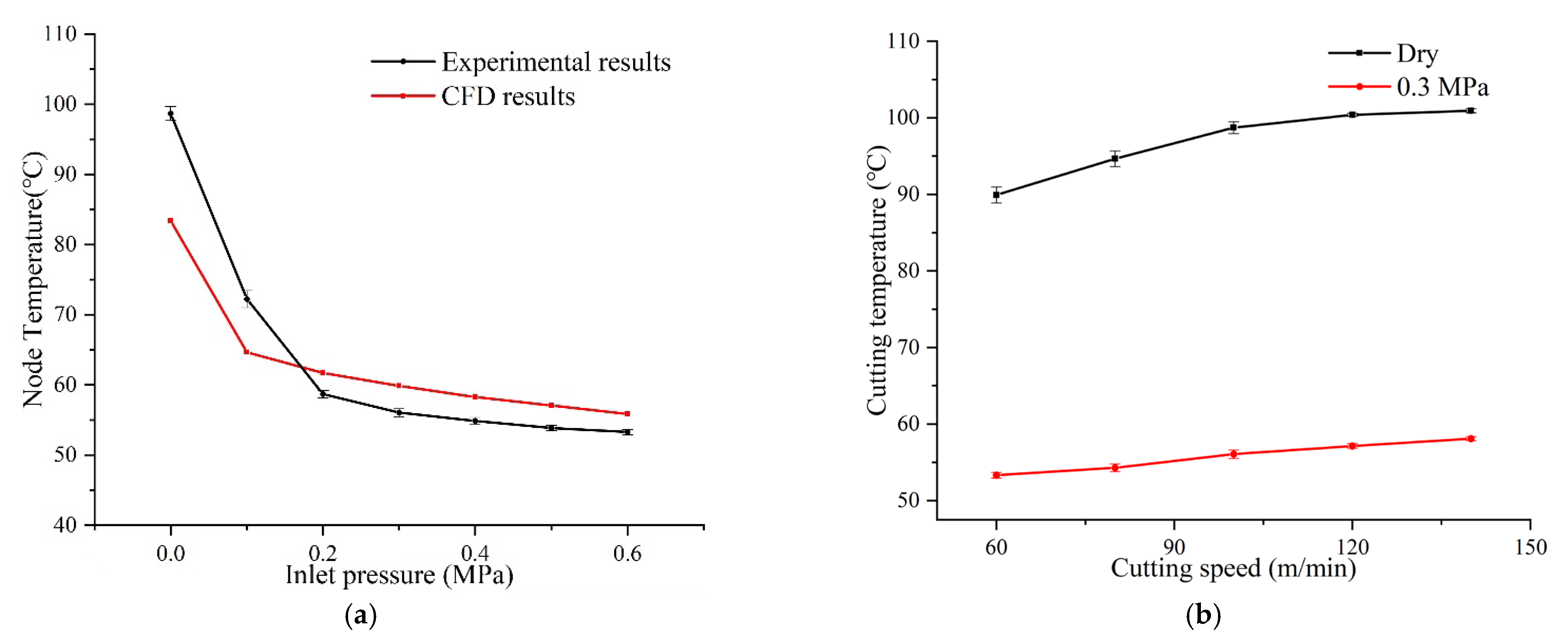
3.4. Influence of Inlet Pressure on Cooling Performance
4. Tool Preparation and Cutting Experiments
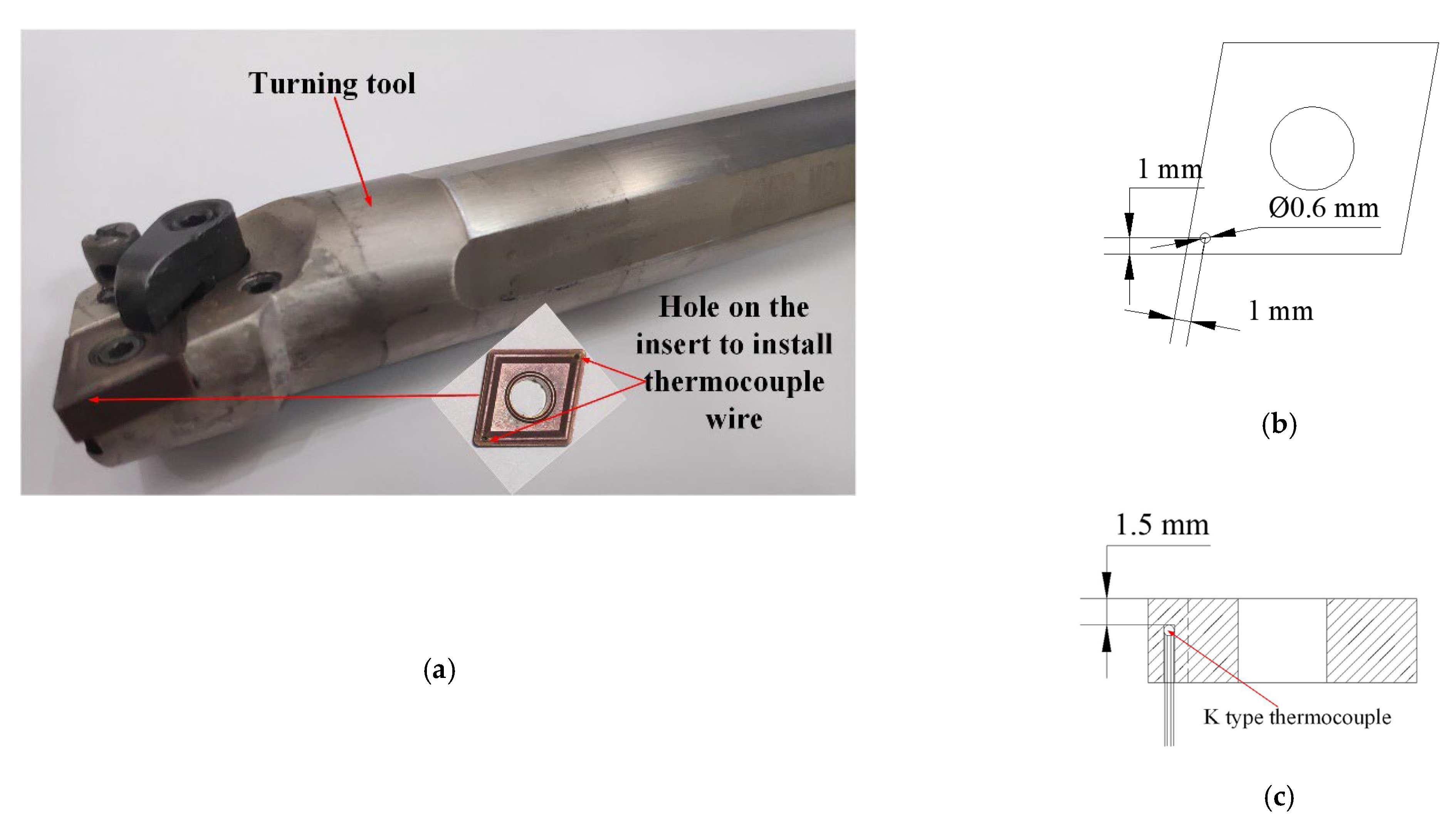
4.1. Tool Manufacturing
4.2. Experimental Conditions and Settings
4.3. Results and Discussion
4.3.1. Cutting Temperature
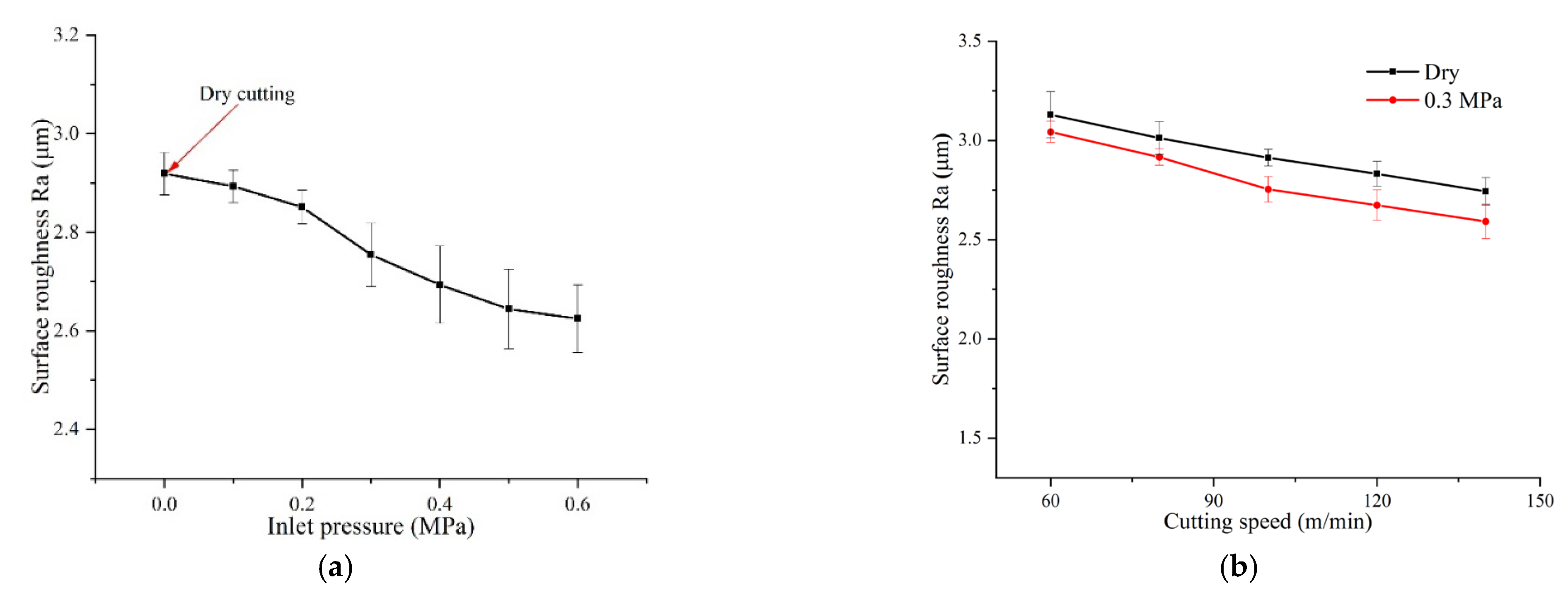
4.3.2. Surface Roughness
4.3.3. Chip Morphology
5. Conclusions
- The structure parameters with the best cooling performance were determined, namely the diameter of upper nozzle is 3 mm, the diameter of lower nozzle is 1.5 mm, and the distance between upper nozzle and tool tip is 18.5 mm.
- With the increase in spray pressure, the velocity of air and droplets, and the convective heat transfer increase. The temperature decreases rapidly yet then mildly with the increasing inlet pressure due to the gradual saturation of the convective heat transfer. The internal turning experiments demonstrate that compared to the dry cutting, the cutting temperature with the internal spray cooling can be reduced by 41–44% with the inlet pressure of 0.3 MPa.
- The workpiece surface quality can be significantly improved under the spray cooling condition with larger tool inlet pressure. The internal spray cooling method can reduce the surface roughness of the workpiece by 0.1μm–0.25 μm compared to that of the dry cutting condition. Particularly, the roughness of the inner surface of the workpiece can be reduced by 9.93% with the tool inlet pressure of 0.6 MPa.
- The increasing tool inlet pressure and cutting speed can efficiently decrease the chip length, and furthermore facilitate the chip removal to improve the cutting performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suyama, D.I.; Diniz, A.E.; Pederiva, R. Tool vibration in internal turning of hardened steel using cBN tool. Int. J. Adv. Manuf. Technol. 2017, 88, 2485–2495. [Google Scholar] [CrossRef]
- Basovich, S.; Arogeti, S. Identification and robust control for regenerative chatter in internal turning with simultaneous compensation of machining error. Mech. Syst. Signal Process. 2021, 149, 107208. [Google Scholar] [CrossRef]
- Longbottom, J.M.; Lanham, J.D. Cutting temperature measurement while machining—A review. Aircr. Eng. Aerosp. Technol. 2005, 77, 122–130. [Google Scholar] [CrossRef]
- Ezugwu, E.O.; Wang, Z.M. Titanium alloys and their machinability—A review. J. Mater. Process. Technol. 1997, 68, 262–274. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process—Part II: Temperature rise distribution due to frictional heat source at the tool–chip interface. Int. J. Mech. Sci. 2001, 43, 57–88. [Google Scholar] [CrossRef]
- Debnath, S.; Reddy, M.M.; Yi, Q.S. Environmental friendly cutting fluids and cooling techniques in machining: A review. J. Clean. Prod. 2014, 83, 33–47. [Google Scholar] [CrossRef]
- Sharif, M.N.; Pervaiz, S.; Deiab, I. Potential of alternative lubrication strategies for metal cutting processes: A review. Int. J. Adv. Manuf. Technol. 2017, 89, 2447–2479. [Google Scholar] [CrossRef]
- Shokrani, A.; Dhokia, V.; Newman, S.T. Energy conscious cryogenic machining of Ti-6Al-4V titanium alloy. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 1690–1706. [Google Scholar] [CrossRef]
- Chiou, R.Y.; Lu, L.; Chen JS, J.; North, M.T. Investigation of dry machining with embedded heat pipe cooling by finite element analysis and experiments. Int. J. Adv. Manuf. Technol. 2007, 31, 905–914. [Google Scholar] [CrossRef]
- Minton, T.; Ghani, S.; Sammler, F.; Bateman, R.; Fürstmann, P.; Roeder, M. Temperature of internally-cooled diamond-coated tools for dry-cutting titanium. Int. J. Mach. Tools Manuf. 2013, 75, 27–35. [Google Scholar] [CrossRef]
- Meena, A.; Mansori, M.E. Study of dry and minimum quantity lubrication drilling of novel austempered ductile iron (ADI) for automotive applications. Wear 2011, 271, 2412–2416. [Google Scholar] [CrossRef]
- Pereira, O.; Rodriguez, A.; Fernandez-Abia, A.I.; Barreiro, J.; Lopez de Lacalle, L.N. Cryogenic and minimum quantity lubrication for an eco-efficiency turning of AISI 304. J. Clean. Prod. 2016, 139, 440–449. [Google Scholar] [CrossRef]
- Li, B.D.; Rui, Z.Y. Friction and wear behaviours of YG8 sliding against austempered ductile iron under dry, chilled air and minimal quantity lubrication conditions. Adv. Mech. Eng. 2019, 11, 1687814019847064. [Google Scholar] [CrossRef]
- Das, A.; Padhan, S.; Das, S.R.; Alsoufi, M.S.; Ibrahim AM, M.; Elsheikh, A. Performance assessment and chip morphology evaluation of austenitic stainless steel under sustainable machining conditions. Metals 2021, 11, 1931. [Google Scholar] [CrossRef]
- Zeilmann, R.P.; Weingaertner, W.L. Analysis of temperature during drilling of Ti6Al4V with minimal quantity of lubricant. J. Mater. Process. Technol. 2006, 179, 124–127. [Google Scholar] [CrossRef]
- Jessy, K.; Dinakaran, D.; Seshagiri Rao, V. Influence of different cooling methods on drill temperature in drilling GFRP. Int. J. Adv. Manuf. Technol. 2015, 76, 609–621. [Google Scholar] [CrossRef]
- Li, Y.; Wu, W. Investigation of drilling machinability of compacted graphite iron under dry and minimum quantity lubrication (MQL). Metals 2019, 9, 1095. [Google Scholar] [CrossRef]
- Qin, X.D.; Liu, W.T.; Li, S.T.; Tong, W.; Ji, X.L.; Meng, F.J.; Liu, J.H.; Zhao, E.H. A comparative study between internal spray cooling and conventional external cooling in drilling of Inconel 718. Int. J. Adv. Manuf. Technol. 2019, 104, 4581–4592. [Google Scholar] [CrossRef]
- Shu, S.R.; Zhang, Y.; He, Y.Y.; Zhang, H. Design of a novel turning tool cooled by combining circulating internal cooling with spray cooling for green cutting. J. Adv. Mech. Des. Syst. Manuf. 2021, 15, JAMDSM0003. [Google Scholar] [CrossRef]
- Gan, Y.Q.; Wang, Y.Q.; Liu, K.; Wang, S.Q.; Yu, Q.B.; Che, C.; Liu, H.B. The development and experimental research of a cryogenic internal cooling turning tool. J. Clean. Prod. 2021, 319, 128787. [Google Scholar] [CrossRef]
- Obikawa, T.; Asano, Y.; Kamata, Y. Computer fluid dynamics analysis for efficient spraying of oil mist in finish-turning of Inconel 718. Int. J. Mach. Tools Manuf. 2009, 49, 971–978. [Google Scholar] [CrossRef]
- Duchosal, A.; Serra, R.; Leroy, R. Numerical study of the inner canalization geometry optimization in a milling tool used in micro quantity lubrication. Mech. Ind. 2014, 15, 435–442. [Google Scholar] [CrossRef]
- Zhang, C.L.; Zhang, S.; Yan, X.F.; Zhang, Q. Effects of internal cooling channel structures on cutting forces and tool life in side milling of H13 steel under cryogenic minimum quantity lubrication condition. Int. J. Adv. Manuf. Technol. 2016, 83, 975–984. [Google Scholar] [CrossRef]
- Peng, R.T.; Jiang, H.J.; Tang, X.Z.; Huang, X.F.; Xu, Y.; Hu, Y.B. Design and performance of an internal-cooling turning tool with micro-channel structures. J. Manuf. Process. 2019, 45, 690–701. [Google Scholar] [CrossRef]
- Zaman, P.B.; Dhar, N.R. Design and evaluation of an embedded double jet nozzle for MQL delivery intending machinability improvement in turning operation. J. Manuf. Process. 2019, 44, 179–196. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, G.; Aggarwal, V. Analysis and optimization of nozzle distance during turning of EN-31 steel using minimum quantity lubrication. Mater. Today Proc. 2021, 49, 1360–1366. [Google Scholar] [CrossRef]
- Liu, J.Y.; Han, R.D.; Zhang, L. Study on the effect of jet flow parameters with water vapor as coolants and lubricants in green cutting. Ind. Lubr. Tribol. 2007, 59, 278–284. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Dhar, N.R.; Kamruzzaman, M.; Ahmed, M. Effect of minimum quantity lubrication (MQL) on tool wear and surface roughness in turning AISI-4340 steel. J. Mater. Process. Technol. 2006, 172, 299–304. [Google Scholar] [CrossRef]
- Yang, H.; Wang, R.; Guo, Z.; Lin, R.; Wei, S.; Weng, J. Cutting performance of multicomponent AlTiZrN-coated cemented Carbide (YG8) tools during milling of high-chromium cast iron. Coatings 2022, 12, 686. [Google Scholar] [CrossRef]





| Variable | Value | Variable | Value |
|---|---|---|---|
| Density of insert (kg/m3) | 14,900 | Heat flux on contact area (W/mm2) | 40 |
| Thermal conductivity of insert (W/m∙K) | 52.3 | initial temperature (°C) | 20 |
| Specific heat of insert (J/kg∙K) | 302 | Specific heat of water (J/kg·K) | 4182 |
| Density of toolholder (kg/m3) | 7850 | Viscosity of water (kg/m·s) | 0.001 |
| Thermal conductivity of toolholder (W/m∙K) | 16.3 | Density of water (kg/m3) | 998.2 |
| Specific heat of toolholder (J/kg∙K) | 502 | Thermal conductivity of water (W/m·K) | 0.6 |
| Tool-chip contact area (L1 mm × L2 mm) | 1 × 0.5 | Inlet pressure of spray cooling (MPa) | 0.3 |
| Parameters | Levels | |||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| A | UND (mm) | 18.5 | 21.5 | 24.5 |
| B | UD (mm) | 1 | 2 | 3 |
| C | LD (mm) | 1 | 1.5 | 2 |
| No. | Upper Nozzle–Tool Tip Distance (A) /mm | Upper Nozzle Diameter (B) /mm | Lower Nozzle Diameter (C) /mm | Maximum Temperature/°C |
|---|---|---|---|---|
| 1 | 18.5 | 1 | 1 | 536.19 |
| 2 | 18.5 | 2 | 1.5 | 529.99 |
| 3 | 18.5 | 3 | 2 | 531.47 |
| 4 | 21.5 | 1 | 1.5 | 529.14 |
| 5 | 21.5 | 2 | 2 | 535.29 |
| 6 | 21.5 | 3 | 1 | 534.47 |
| 7 | 24.5 | 1 | 2 | 536.58 |
| 8 | 24.5 | 2 | 1 | 535.12 |
| 9 | 24.5 | 3 | 1.5 | 531.14 |
| K1 | 532.55 | 533.97 | 535.26 | Ki is the average value of maximum temperature at each factor level; R is the value of range |
| K2 | 532.96 | 533.47 | 530.09 | |
| K3 | 534.28 | 532.36 | 534.44 | |
| R | 1.73 | 1.61 | 5.17 |
| Parameter | Value |
|---|---|
| Cutting speed (m/min) | 60, 80, 100, 120, 140 |
| Feed rate (mm/r) | 0.1 |
| Depth of cut (mm) | 0.5 |
| Cooling conditions | 0.1–0.6 MPa/dry cutting |
| Coolant flow rate (mL/h) | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Shu, S.; Li, H.; Chen, X. Design, Optimization and Cutting Performance Evaluation of an Internal Spray Cooling Turning Tool. Coatings 2022, 12, 1141. https://doi.org/10.3390/coatings12081141
Liu L, Shu S, Li H, Chen X. Design, Optimization and Cutting Performance Evaluation of an Internal Spray Cooling Turning Tool. Coatings. 2022; 12(8):1141. https://doi.org/10.3390/coatings12081141
Chicago/Turabian StyleLiu, Leping, Shengrong Shu, Huimin Li, and Xuan Chen. 2022. "Design, Optimization and Cutting Performance Evaluation of an Internal Spray Cooling Turning Tool" Coatings 12, no. 8: 1141. https://doi.org/10.3390/coatings12081141






