Low and Anisotropic Tensile Strength and Thermal Conductivity in the Single-Layer Fullerene Network Predicted by Machine-Learning Interatomic Potentials
Abstract
:1. Introduction
2. Computational Methods
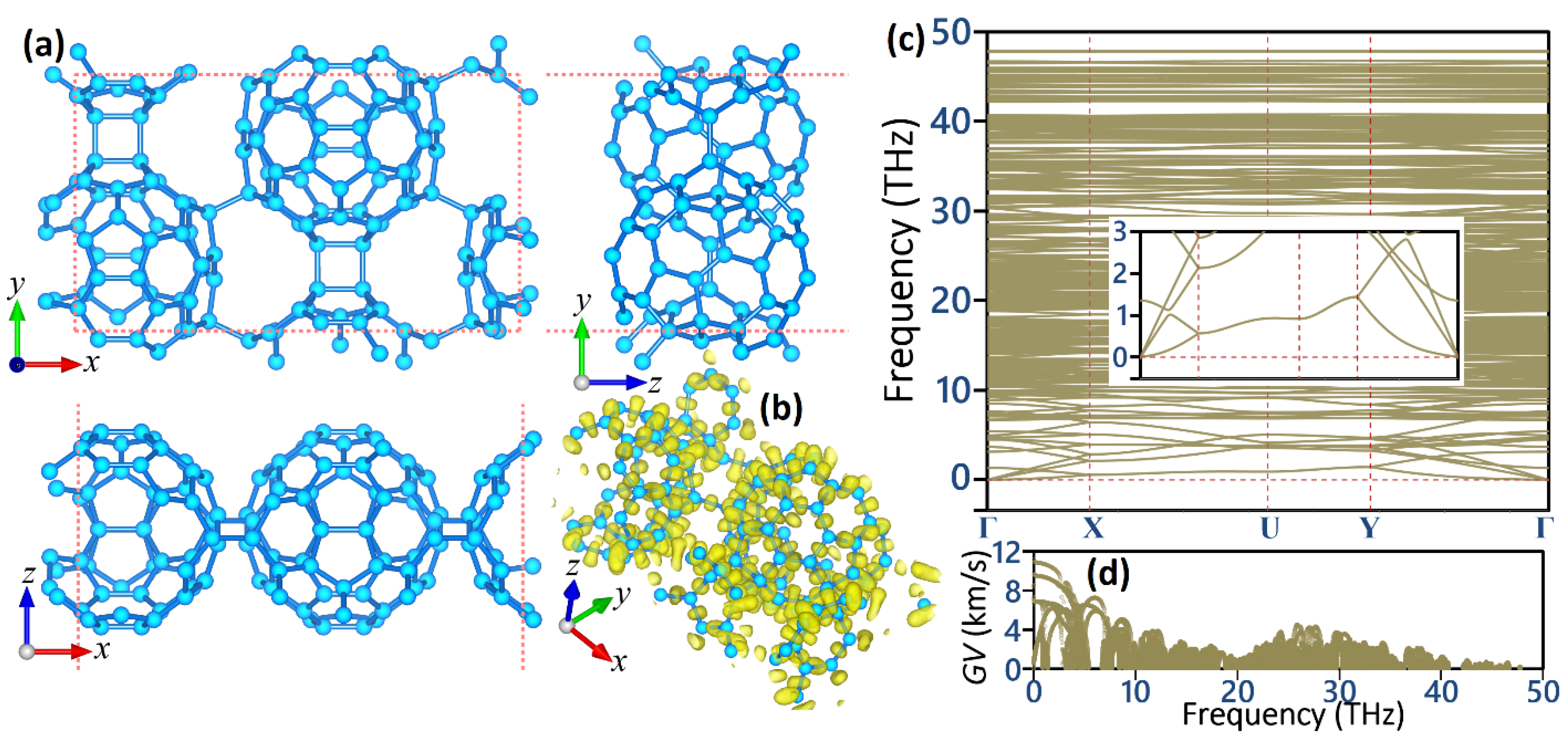
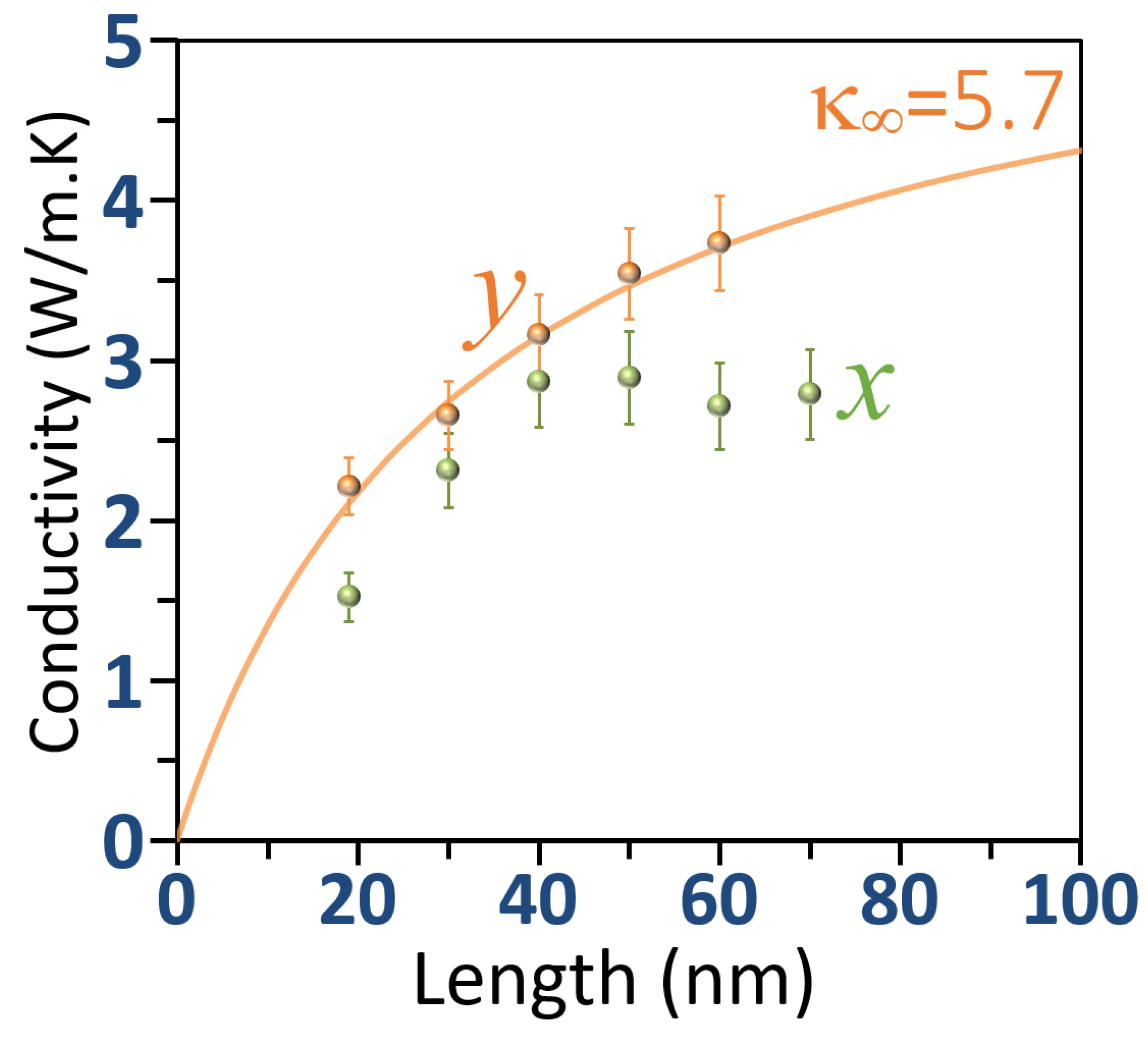
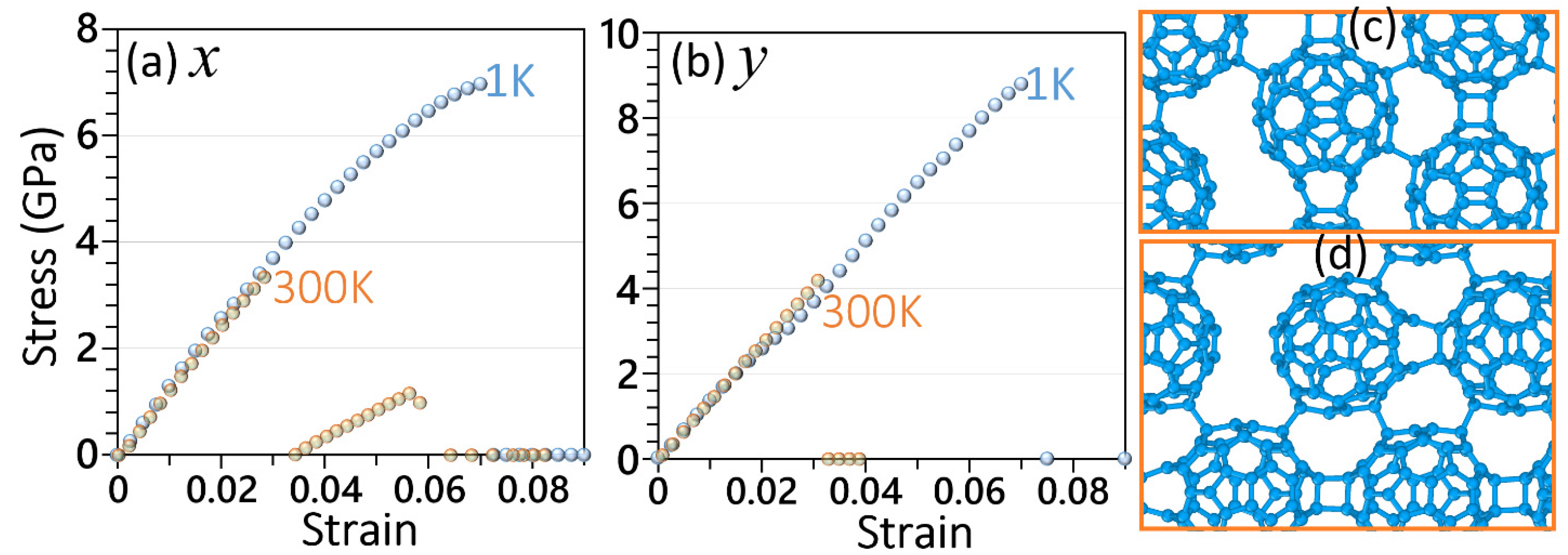
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The Rise of Graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K.; Guinea, F. The Electronic Properties of Graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Ghosh, S.; Calizo, I.; Teweldebrhan, D.; Pokatilov, E.P.; Nika, D.L.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Extremely High Thermal Conductivity of Graphene: Prospects for Thermal Management Applications in Nanoelectronic Circuits. Appl. Phys. Lett. 2008, 92, 151911. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, X.F.; Zhang, X.; Zhu, Q.; Dong, H.; Zhao, M.; Oganov, A.R. Phagraphene: A Low-Energy Graphene Allotrope Composed of 5-6-7 Carbon Rings with Distorted Dirac Cones. Nano Lett. 2015, 15, 6182–6186. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Yan, L.; Tripp, M.W.; Krejčí, O.; Dimosthenous, S.; Kachel, S.R.; Chen, M.; Foster, A.S.; Koert, U.; Liljeroth, P.; et al. Biphenylene Network: A Nonbenzenoid Carbon Allotrope. Science 2021, 372, 852–856. [Google Scholar] [CrossRef] [PubMed]
- Bakharev, P.V.; Huang, M.; Saxena, M.; Lee, S.W.; Joo, S.H.; Park, S.O.; Dong, J.; Camacho-Mojica, D.C.; Jin, S.; Kwon, Y.; et al. Chemically Induced Transformation of Chemical Vapour Deposition Grown Bilayer Graphene into Fluorinated Single-Layer Diamond. Nat. Nanotechnol. 2020, 15, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-Graphene: A New Carbon Allotrope. Proc. Natl. Acad. Sci. USA 2015, 8, 2372–2377. [Google Scholar] [CrossRef]
- Raeisi, M.; Mortazavi, B.; Podryabinkin, E.V.; Shojaei, F.; Zhuang, X.; Shapeev, A.V. High Thermal Conductivity in Semiconducting Janus and Non-Janus Diamanes. Carbon 2020, 167, 51–61. [Google Scholar] [CrossRef]
- Hatam-Lee, S.M.; Rajabpour, A.; Volz, S. Thermal Conductivity of Graphene Polymorphs and Compounds: From C3N to Graphdiyne Lattices. Carbon 2020, 161, 816–826. [Google Scholar] [CrossRef]
- Pereira, C.L.F. Investigating Mechanical Properties and Thermal Conductivity of 2D Carbon-Based Materials by Computational Experiments. Comput. Mater. Sci. 2021, 196, 110493. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shojaei, F.; Zhuang, X.; Pereira, L.F.C. First-Principles Investigation of Electronic, Optical, Mechanical and Heat Transport Properties of Pentadiamond: A Comparison with Diamond. Carbon Trends 2021, 3, 100036. [Google Scholar] [CrossRef]
- Tromer, R.M.; Ribeiro, L.A.; Galvão, D.S. A DFT Study of the Electronic, Optical, and Mechanical Properties of a Recently Synthesized Monolayer Fullerene Network. Chem. Phys. Lett. 2022, 804, 139925. [Google Scholar] [CrossRef]
- Arabha, S.; Aghbolagh, Z.S.; Ghorbani, K.; Hatam-Lee, M.; Rajabpour, A. Recent Advances in Lattice Thermal Conductivity Calculation Using Machine-Learning Interatomic Potentials. J. Appl. Phys. 2021, 130, 210903. [Google Scholar] [CrossRef]
- Arabha, S.; Rajabpour, A. Thermo-Mechanical Properties of Nitrogenated Holey Graphene (C2N): A Comparison of Machine-Learning-Based and Classical Interatomic Potentials. Int. J. Heat Mass Transf. 2021, 178, 121589. [Google Scholar] [CrossRef]
- Javvaji, B.; Mortazavi, B.; Zhuang, X.; Rabczuk, T. Exploring Tensile Piezoelectricity and Bending Flexoelectricity of Diamane Monolayers by Machine Learning. Carbon 2021, 185, 558–567. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Shapeev, A.V. Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials. Multiscale Model. Simul. 2016, 14, 1153–1173. [Google Scholar] [CrossRef]
- Novikov, I.; Gubaev, K.; Podryabinkin, A.S.E. The MLIP Package: Moment Tensor Potentials with MPI and Active Learning. Mach. Learn. Sci. Technol. 2021, 2, 025002. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Shojaei, F.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. A First-Principles and Machine-Learning Investigation on the Electronic, Photocatalytic, Mechanical and Heat Conduction Properties of Nanoporous C5N Monolayers. Nanoscale 2022, 14, 4324–4333. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shojaei, F.; Shapeev, A.V.; Zhuang, X. A Combined First-Principles and Machine-Learning Investigation on the Stability, Electronic, Optical, and Mechanical Properties of Novel C6N7-Based Nanoporous Carbon Nitrides. Carbon 2022, 194, 230–239. [Google Scholar] [CrossRef]
- Podryabinkin, E.V.; Shapeev, A.V. Active Learning of Linearly Parametrized Interatomic Potentials. Comput. Mater. Sci. 2017, 140, 171–180. [Google Scholar] [CrossRef]
- Mortazavi, B.; Novikov, I.S.; Podryabinkin, E.V.; Roche, S.; Rabczuk, T.; Shapeev, A.V.; Zhuang, X. Exploring Phononic Properties of Two-Dimensional Materials Using Machine Learning Interatomic Potentials. Appl. Mater. Today 2020, 20, 100685. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mortazavi, B. Ultrahigh Thermal Conductivity and Strength in Direct-Gap Semiconducting Graphene-like BC6N: A First-Principles and Classical Investigation. Carbon 2021, 182, 373–383. [Google Scholar] [CrossRef]
- Mortazavi, B.; Silani, M.; Podryabinkin, E.V.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. First-Principles Multiscale Modeling of Mechanical Properties in Graphene/Borophene Heterostructures Empowered by Machine-Learning Interatomic Potentials. Adv. Mater. 2021, 33, 2102807. [Google Scholar] [CrossRef] [PubMed]
- Silvi, B.; Savin, A. Classification of Chemical-Bonds Based on Topological Analysis of Electron Localization Functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Mortazavi, B.; Podryabinkin, E.V.; Roche, S.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. Machine-Learning Interatomic Potentials Enable First-Principles Multiscale Modeling of Lattice Thermal Conductivity in Graphene/Borophene Heterostructures. Mater. Horiz. 2020, 7, 2359–2367. [Google Scholar] [CrossRef]
- Mortazavi, B.; Novikov, I.S.; Shapeev, A.V. A Machine-Learning-Based Investigation on the Mechanical/Failure Response and Thermal Conductivity of Semiconducting BC2N Monolayers. Carbon 2022, 188, 431–441. [Google Scholar] [CrossRef]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of Atomic-Level Simulation Methods for Computing Thermal Conductivity. Phys. Rev. B 2002, 65, 144306. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mortazavi, B.; Zhuang, X. Low and Anisotropic Tensile Strength and Thermal Conductivity in the Single-Layer Fullerene Network Predicted by Machine-Learning Interatomic Potentials. Coatings 2022, 12, 1171. https://doi.org/10.3390/coatings12081171
Mortazavi B, Zhuang X. Low and Anisotropic Tensile Strength and Thermal Conductivity in the Single-Layer Fullerene Network Predicted by Machine-Learning Interatomic Potentials. Coatings. 2022; 12(8):1171. https://doi.org/10.3390/coatings12081171
Chicago/Turabian StyleMortazavi, Bohayra, and Xiaoying Zhuang. 2022. "Low and Anisotropic Tensile Strength and Thermal Conductivity in the Single-Layer Fullerene Network Predicted by Machine-Learning Interatomic Potentials" Coatings 12, no. 8: 1171. https://doi.org/10.3390/coatings12081171
APA StyleMortazavi, B., & Zhuang, X. (2022). Low and Anisotropic Tensile Strength and Thermal Conductivity in the Single-Layer Fullerene Network Predicted by Machine-Learning Interatomic Potentials. Coatings, 12(8), 1171. https://doi.org/10.3390/coatings12081171







