Experimental Characterization of a Foil Journal Bearing Structure with an Anti-Friction Polymer Coating
Abstract
:1. Introduction
2. Materials and Methods
2.1. Object of Investigation
2.2. Description of the Test Rig
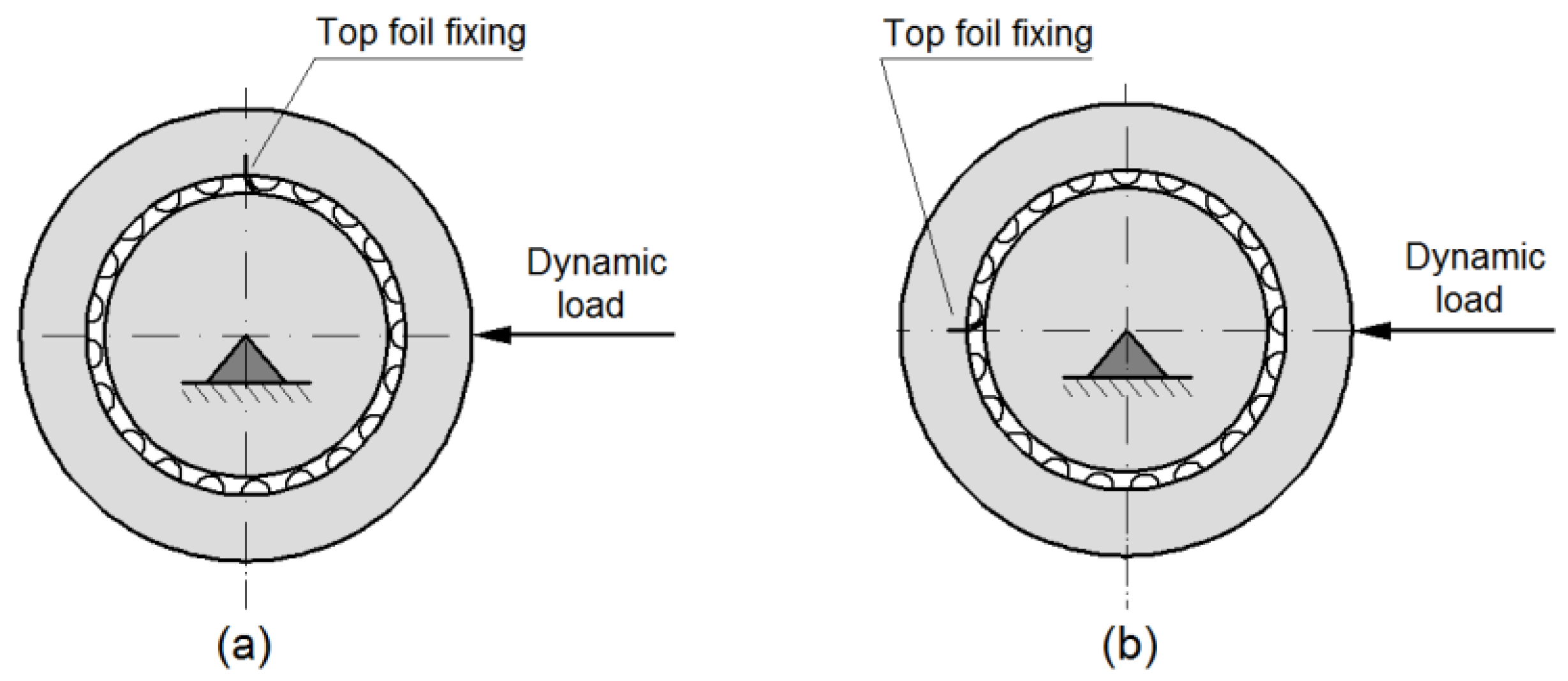
2.3. Experimental Procedure
3. Results and Discussion
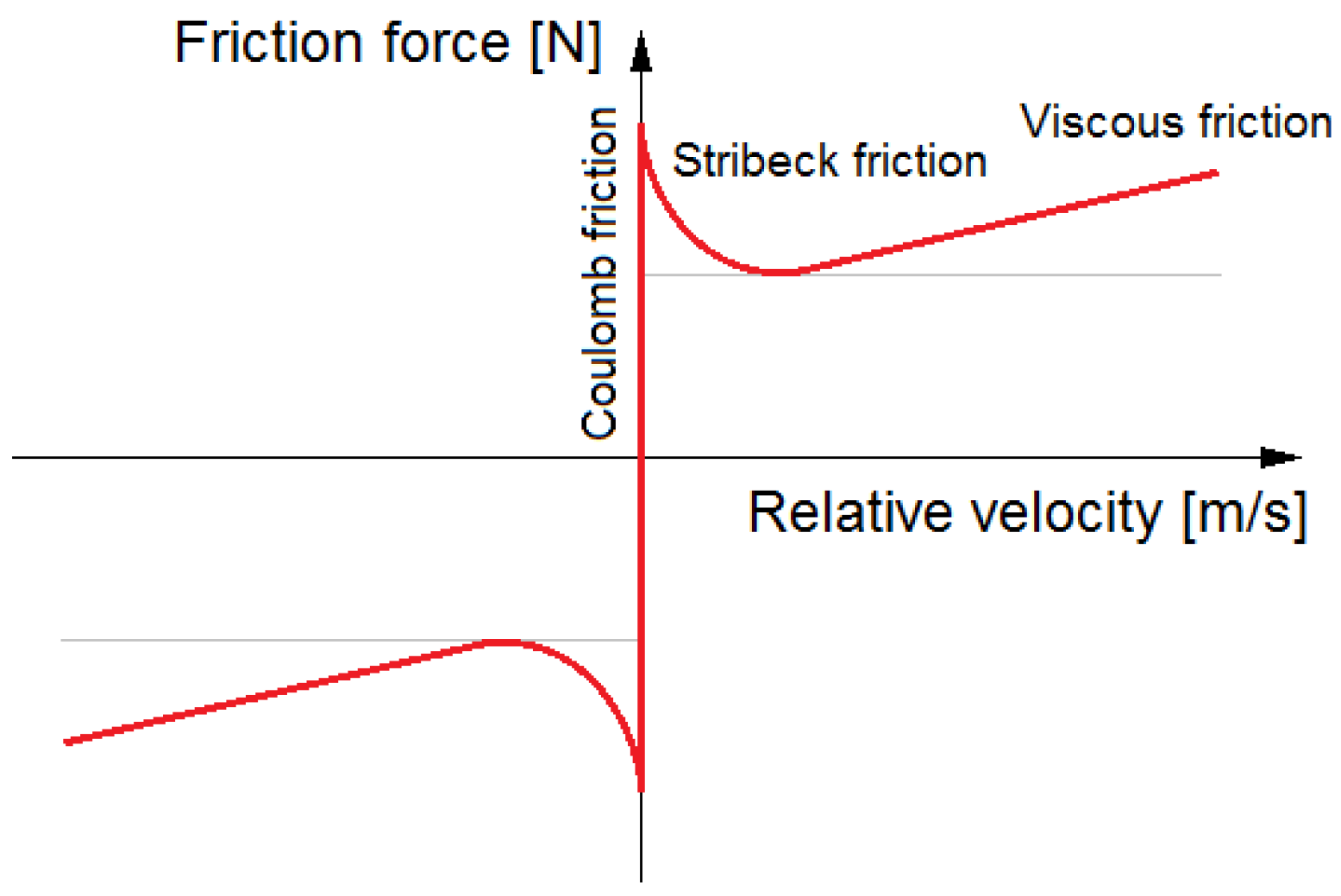
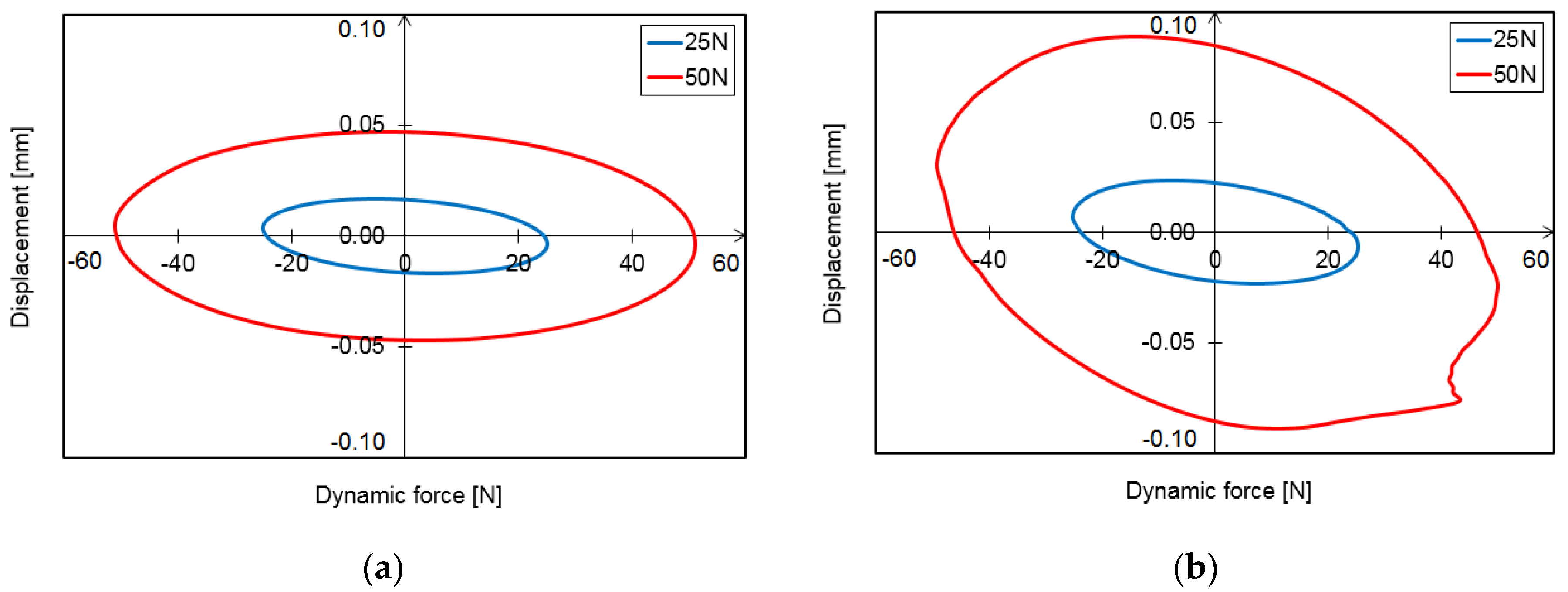
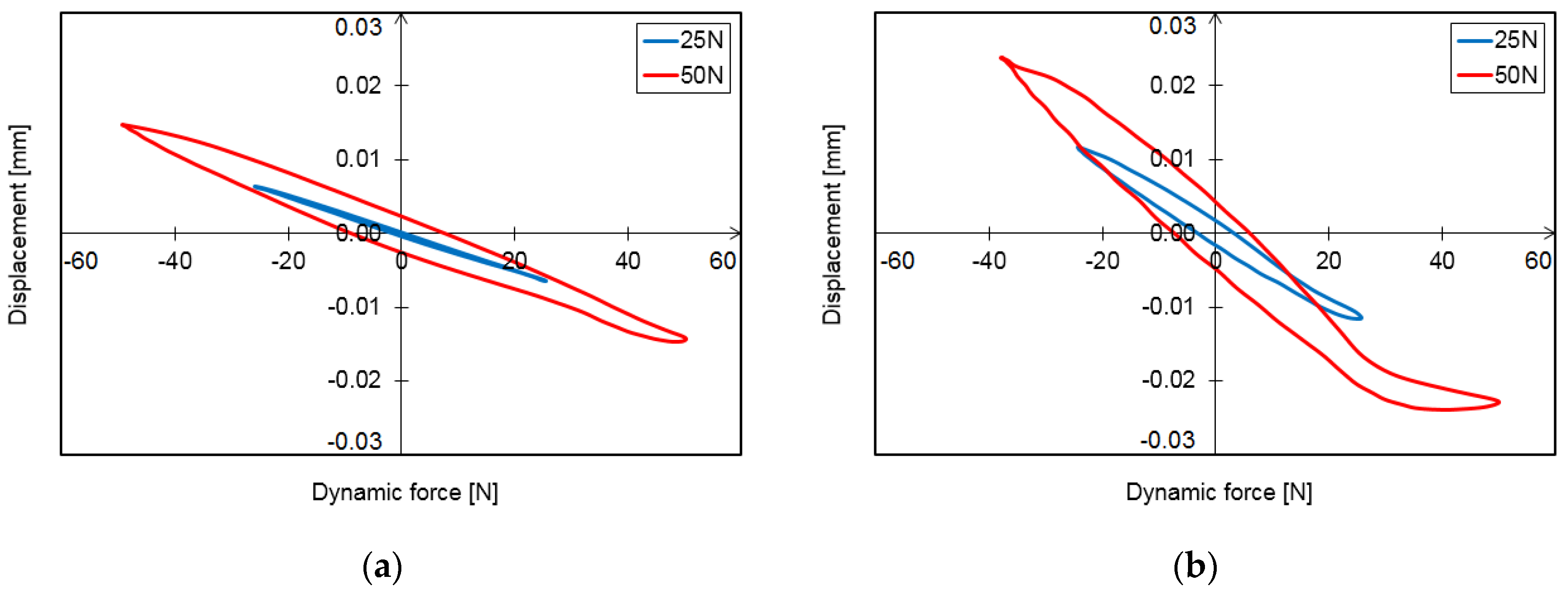
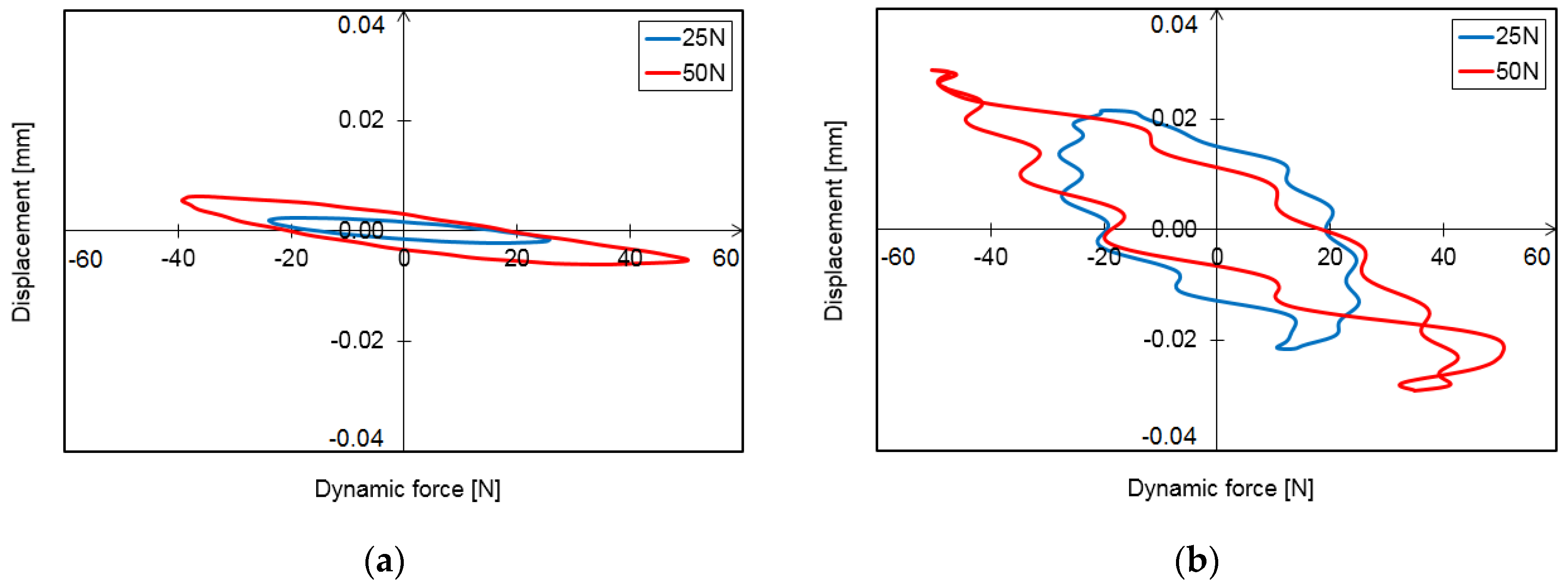
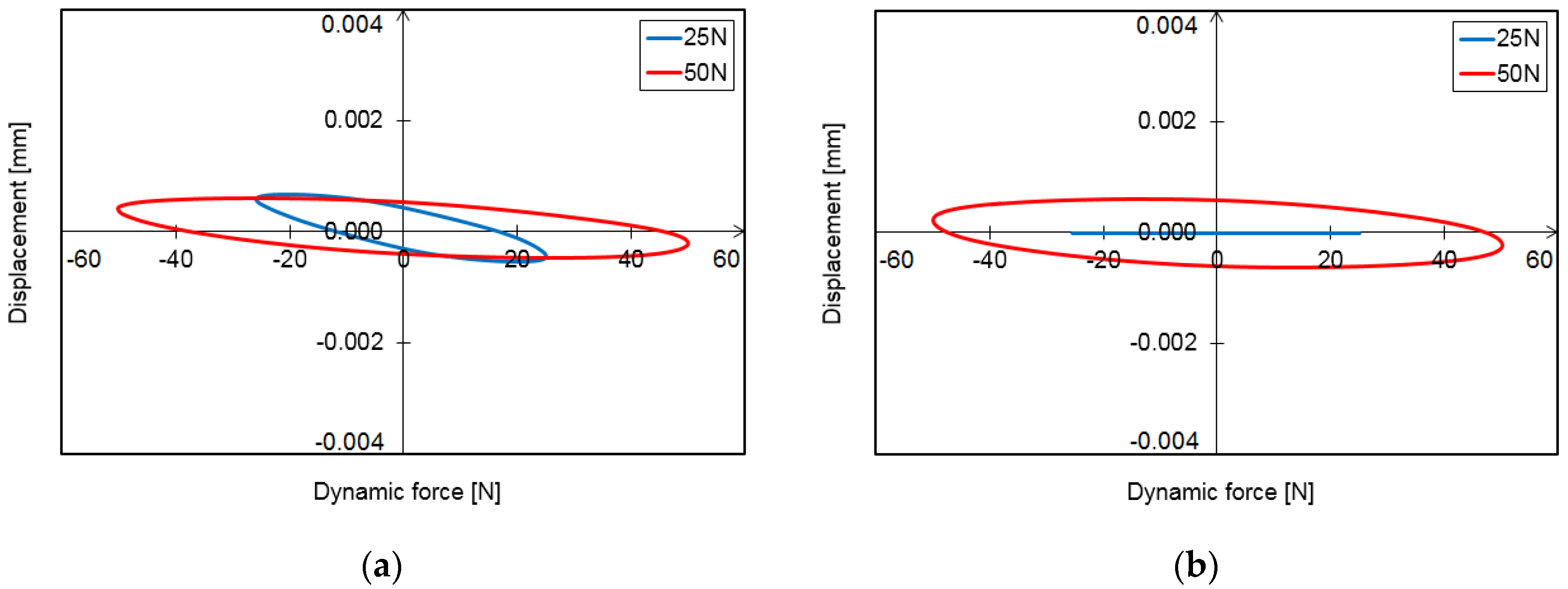
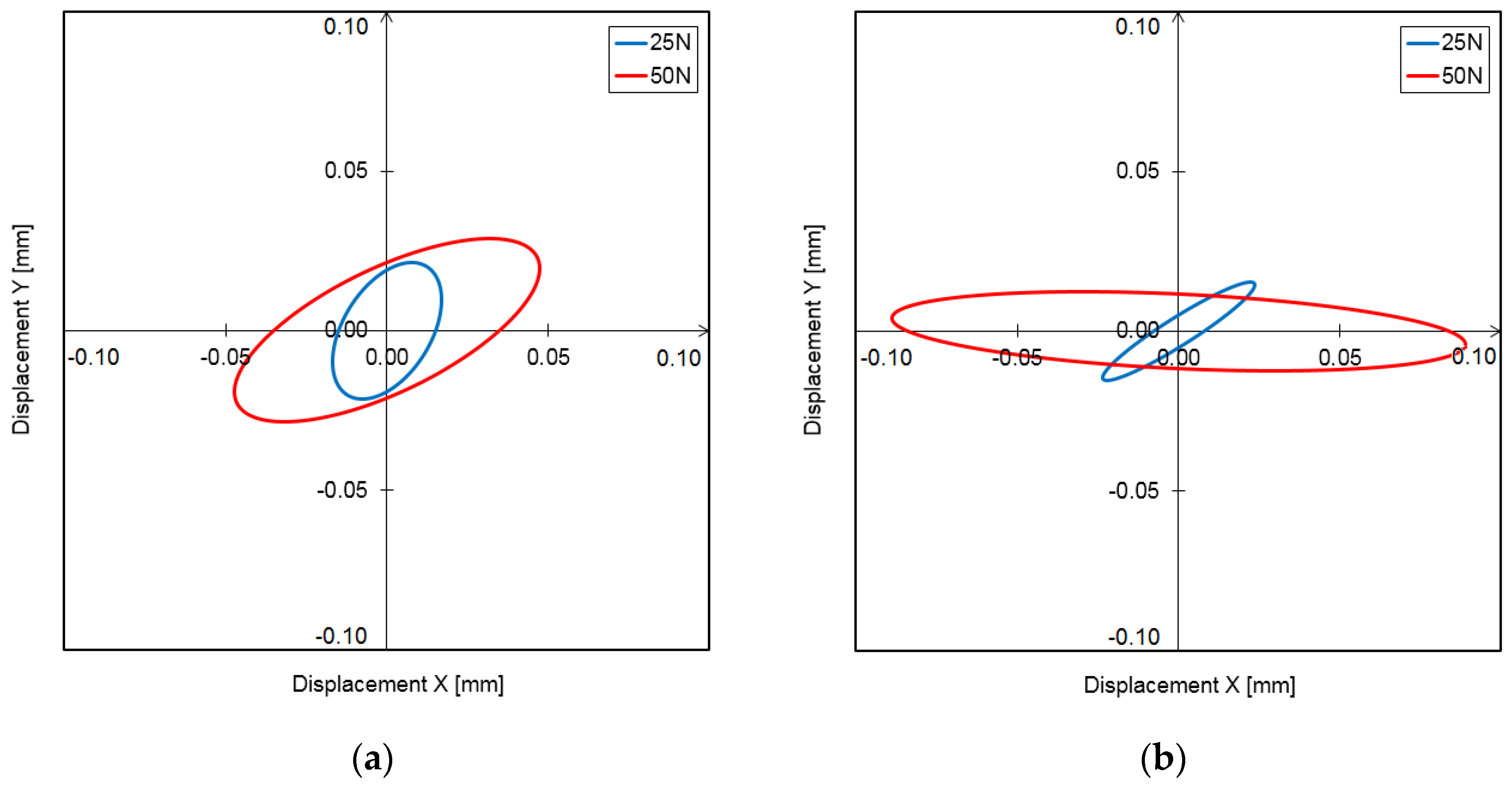
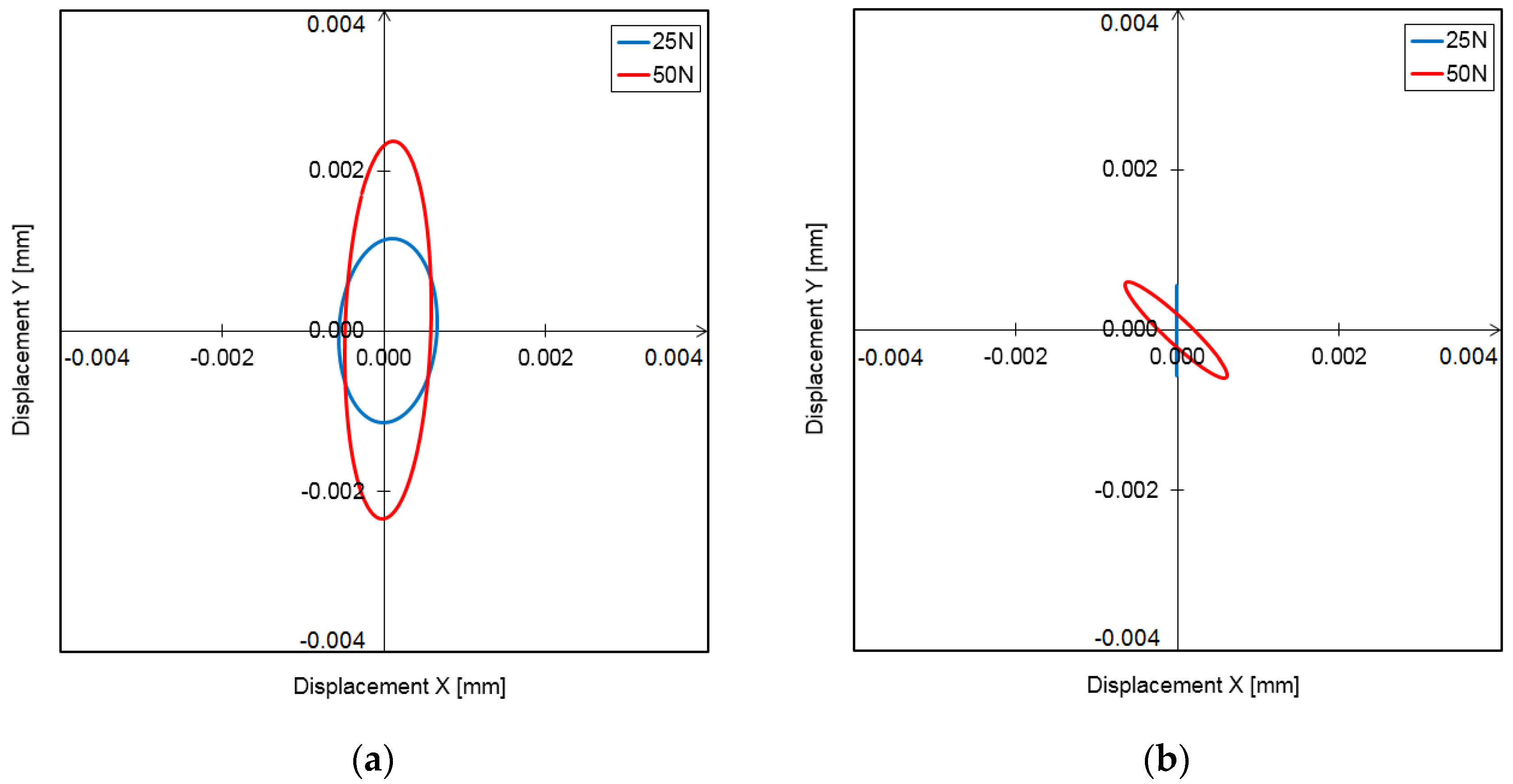
3.1. Hysteresis Loops
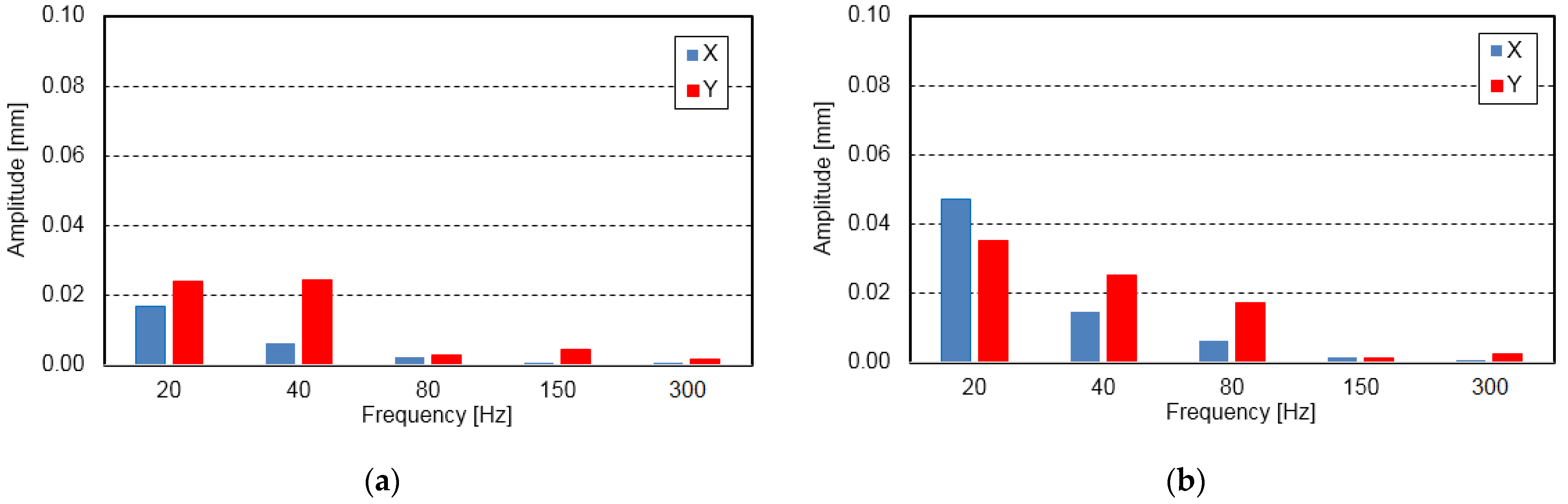
3.2. Vibration Trajectories
4. Conclusions
- Hysteresis loops have a very wide range of applications when it comes to analyzing the dynamic properties of a foil bearing structure. They can be used to evaluate the vibration damping capacity of the system. However, based on the study carried out, it is important to note that in the bump-type foil bearing structure, apart from the displacements that take place in the direction of the acting load, there are also displacements that occur in the perpendicular direction. These are due to the bearing design and the strong mechanical interactions that occur between the flexible components with complex geometries. Under certain load conditions, the displacements in the direction perpendicular to the direction of the acting force may be even greater than in the main direction, so they will also have a significant impact on the energy dissipation in such a system. Since the foil bearing structure has a high degree of anisotropy in terms of stiffness and damping, this must be taken into account when determining their stiffness and damping coefficients. This is a new finding that may change the approach used to determine the dynamic characteristics of a foil bearing structure. The sleeve displacements in the two directions must therefore be taken into account, both in the case of experimental methods and in the modeling and numerical analysis.
- It is important to note that the experimental studies discussed in this article concern a bump-type foil bearing with a specific design and materials, and an individually selected assembly preload. The results obtained may be adequate for a certain group of similar foil bearings, but should not be extended to all foil bearings. Since foil bearings are an evolving technology, and various modifications and improvements are being made all the time, which often have a very large impact on their characteristics, the authors of this article recommend an individual approach to each new design.
- The results of the study show that the anti-friction material used (polytetrafluoroethylene-based material with the trade designation AS20), with which one side of the top foil was coated, fulfilled its purpose perfectly. The run-in process of the foil bearing with such a coating was very fast, and a temporary increase in the temperature of the top foil was followed by its stabilization at a very low level. After being run-in, the bearing exhibited low friction torque, and the protective coating was not damaged at all. After the target tests were carried out, during which the bearing structure was subjected to dynamic loads, the anti-friction coating was not damaged. The bearing was still suitable both for further dynamic tests and high-speed operations. The materials used in the tested bearing show great potential for use in real conditions.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, L.L.; Guenat, E.; Schiffmann, J. A Review of grooved dynamic gas bearings. Appl. Mech. Rev. 2020, 72, 010802. [Google Scholar] [CrossRef]
- Samanta, P.; Hirani, H. On the evolution of passive magnetic bearings. J. Tribol. 2022, 144, 040801. [Google Scholar] [CrossRef]
- Supreeth, D.K.; Bekinal, S.I.; Chandranna, S.R.; Doddamani, M. A review of superconducting magnetic bearings and their application. IEEE Trans. Appl. Supercond. 2022, 32, 3800215. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Sharma, A.; Upadhyay, N.; Kankar, P.K.; Amamath, M. Nonlinear dynamic investigations on rolling element bearings: A review. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Samanta, P.; Murmu, N.C.; Khonsari, M.M. The evolution of foil bearing technology. Tribol. Int. 2019, 135, 305–323. [Google Scholar] [CrossRef]
- Walton, J.F.; Hesmat, H. Application of foil bearings to turbomachinery including vertical operation. J. Eng. Gas Turbines Power 2002, 124, 1032–1041. [Google Scholar] [CrossRef]
- Hoffmann, H.; Pronobis, T.; Liebich, R. Stability analysis of pressurized gas foil bearings for high speed applications. In Proceedings of the 11th International Conference on Turbochargers and Turbocharging, London, UK, 13–14 May 2014. [Google Scholar]
- De Santiago, O.; San Andres, L. Parametric study of bump foil gas bearings for industrial applications. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 445–456. [Google Scholar]
- Kumar, J.; Khamari, D.S.; Behera, S.K.; Sahoo, R.K. A review of thermohydrodynamic aspects of gas foil bearings. Proc. Inst. Mech. Eng. Part J.-J. Eng. Tribol. 2022, 236, 1466–1490. [Google Scholar] [CrossRef]
- Kozancki, Z.; Tkacz, E.; Lagodzinski, J.; Miazga, K. Oil-free bearings for hermetic high-speed turbomachinery. J. Vib. Eng. Technol. 2014, 2, 351–360. [Google Scholar]
- Brenkacz, L.; Zywica, G.; Bogulicz, M. Selection of the oil-free bearing system for a 30 kW ORC microturbine. J. Vibroeng. 2019, 21, 318–330. [Google Scholar] [CrossRef]
- Kicinski, J. The dynamics of microturbines lubricated using unconventional agents. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 369–377. [Google Scholar] [CrossRef]
- Sim, K.; Lee, Y.B.; Kim, T.H. Rotordynamic analysis of an oil-free turbocharger supported on lobed gas foil bearings-predictions versus test data. Tribol. Trans. 2014, 57, 1086–1095. [Google Scholar] [CrossRef]
- San Andres, L.; Ryu, K.; Diemer, P. Prediction of gas thrust foil bearing performance for oil-free automotive turbochargers. J. Eng. Gas Turbines Power 2015, 137, 032502. [Google Scholar] [CrossRef]
- Mutra, R.R.; Srinivas, J.; Rzadkowski, R. An optimal parameter identification approach in foil bearing supported high-speed turbocharger rotor system. Arch. Appl. Mech. 2021, 91, 1557–1575. [Google Scholar] [CrossRef]
- Dellacorte, C.; Lukaszewicz, V.; Valco, M.J.; Radil, K.C.; Heshmat, H. Performance and durability of high temperature foil air bearings for oil-free turbomachinery. Tribol. Trans. 2000, 43, 774–780. [Google Scholar] [CrossRef]
- Li, H.; Geng, H.P.; Lin, H.; Feng, S. The influence of material selection and pre-deformation on the performance of foil bearing. Mechanika 2020, 26, 265–270. [Google Scholar] [CrossRef]
- Laskowski, J.A.; DellaCorte, C. Friction and wear characteristics of candidate foil bearing materials from 25 °C to 800 °C. Lubr. Eng. 1996, 52, 605–616. [Google Scholar]
- Baginski, P.; Zywica, G. Experimental study of various low-friction coatings for high-temperature gas foil bearings under cold-start conditions. J. Eng. Gas Turbines Power 2022, 144, 081007. [Google Scholar] [CrossRef]
- Dellacorte, C. Tribological composition optimization of chromium-carbide-based solid lubricant coatings for foil gas bearings at temperatures to 650 °C. Surf. Coat. Technol. 1998, 36, 87–97. [Google Scholar] [CrossRef]
- Dellacorte, C.; Fellenstein, J.A.; Benoy, P.A. Evaluation of advanced solid lubricant coatings for foil air bearings operating at 25° and 500 °C. Tribol. Trans. 2008, 42, 338–342. [Google Scholar] [CrossRef]
- Zhua, S.; Chenga, J.; Qiaoa, Z.; Yanga, J. High temperature solid-lubricating materials: A review. Tribol. Int. 2019, 133, 206–223. [Google Scholar] [CrossRef]
- Heshmat, H.; Hryniewicz, P.; Walton, J.F., II; Willis, J.P.; Jahanmir, S.; DellaCorte, C. Low-friction wear-resistant coatings for high-temperature foil bearings. Tribol. Int. 2005, 38, 1059–1075. [Google Scholar] [CrossRef]
- Radil, K.; DellaCorte, C. The performance of PS400 subjected to sliding contact at temperatures from 260 to 927 °C. Tribol. Trans. 2017, 60, 957–964. [Google Scholar] [CrossRef]
- Khoele, K.; Ama, O.M.; Ray, S.S.; Popoola, A.P.; Desai, D.; Delport, D.J. Tribocorrosion behavior of bare and nanocoated foils used on high-speed air-foil bearings. Int. J. Adv. Manuf. Technol. 2022, 120, 3225–3235. [Google Scholar] [CrossRef]
- Kouediatouka, A.N.; Ma, Q.; Liu, Q.; Mawignon, F.J.; Rafique, F.; Dong, G. Design methodology and application of surface texture: A review. Coatings 2022, 12, 1015. [Google Scholar] [CrossRef]
- Feng, K.; Liu, Y.; Zhao, X.; Liu, W. Experimental evaluation of the structure characterization of a novel hybrid bump-metal mesh foil bearing. ASME J. Tribol. 2016, 138, 021702. [Google Scholar] [CrossRef]
- Hoffmann, R.; Liebich, R. Experimental and numerical analysis of the dynamic behaviour of a foil bearing structure affected by metal shims. Tribol. Int. 2017, 115, 378–388. [Google Scholar] [CrossRef]
- Feng, K.; Liu, W.; Yu, R.; Zhang, Z. Analysis and experimental study on a novel gas foil bearing with nested compression springs. Tribol. Int. 2017, 107, 65–76. [Google Scholar] [CrossRef]
- Martowicz, A.; Roemer, J.; Kantor, S.; Zdziebko, P.; Zywica, G.; Baginski, P. Gas Foil Bearing Technology Enhanced with Smart Materials. Appl. Sci. 2021, 11, 2757. [Google Scholar] [CrossRef]
- Wang, Y.P.; Kim, D. Experimental identification of force coefficients of large hybrid air foil bearings. ASME J. Eng. Gas Turbines Power 2014, 136, 032503. [Google Scholar] [CrossRef]
- Hou, Y.; Zheng, Y.; Chen, S.; Liu, X.; Lai, T. The numerical study of static and dynamic characteristics of multi-layer protuberant foil bearing. J. Adv. Mech. Des. Syst. Manuf. 2015, 9, JAMDSM0058. [Google Scholar] [CrossRef]
- Baginski, P.; Zywica, G.; Lubieniecki, M.; Roamer, J. The effect of cooling the foil bearing on dynamics of the rotor-bearings system. J. Vibroeng. 2018, 20, 843–857. [Google Scholar] [CrossRef] [Green Version]
- Martowicz, A.; Roamer, J.; Lubieniecki, M.; Zywica, G.; Baginski, P. Experimental and numerical study on the thermal control strategy for a gas foil bearing enhanced with thermoelectric modules. Mech. Syst. Signal Process. 2020, 138, 106581. [Google Scholar] [CrossRef]
- DellaCorte, C. Oil-free shaft support system rotordynamics: Past, present and future challenges and opportunities. Mech. Syst. Signal Process. 2012, 29, 67–76. [Google Scholar] [CrossRef]
- Guenat, E.; Schiffmann, J. Performance potential of gas foil thrust bearings enhanced with spiral grooves. Tribol. Int. 2019, 131, 438–445. [Google Scholar] [CrossRef]
- Park, J.; Sim, K. A feasibility study of controllable gas foil bearings with piezoelectric materials via rotordynamic model predictions. In Proceedings of the Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Kim, T.H.; San Andres, L. Limits for high-speed operation of gas foil bearings. ASME J. Tribol. 2006, 128, 670–673. [Google Scholar] [CrossRef]
- Bonello, P.; Bin Hassan, M.F. An experimental and theoretical analysis of a foil-air bearing rotor system. J. Sound Vib. 2018, 413, 395–420. [Google Scholar] [CrossRef]
- Gu, Y.; Lan, X.; Ren, G.; Zhou, M. An efficient three-dimensional foil structure model for bump-type gas foil bearings considering friction. Friction 2020, 9, 1450–1463. [Google Scholar] [CrossRef]
- Qin, K.; Jacobs, P.A.; Keep, J.A.; Li, D.; Jahn, I.H. A fluid-structure-thermal model for bump-type foil thrust bearings. Tribol. Int. 2018, 121, 481–491. [Google Scholar] [CrossRef]
- San Andres, L.; Kim, T.H. Thermohydrodynamic analysis of bump type gas foil bearings: A model anchored to test data. ASME J. Eng. Gas Turbines Power 2010, 132, 042504. [Google Scholar] [CrossRef]
- Iordanoffa, I.; Bou Saidb, B.; Mezianneb, A.; Berthierb, Y. Effect of internal friction in the dynamic behaviour of aerodynamic foil bearings. Tribol. Int. 2008, 41, 387–395. [Google Scholar] [CrossRef]
- Matute, J.A.; Ruiz, R.; Diaz, S.E. A view to the energy dissipation mechanism of a gas foil bearing’s structure due to dry friction. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; p. GT2012-68926. [Google Scholar]
- Zywica, G.; Baginski, P.; Bogulicz, M. Experimental and numerical evaluation of the damping properties of a foil bearing structure taking into account the static and kinetic dry friction. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 7. [Google Scholar] [CrossRef]
- Khan, Z.A.; Chacko, V.; Nazir, H. A review of friction models in interacting joints for durability design. Friction 2017, 5, 1–22. [Google Scholar] [CrossRef]
- Le Lez, S.; Arghir, M.; Frene, J. Static and dynamic characterization of a bump-type foil bearing structure. ASME J. Tribol. 2007, 129, 75–83. [Google Scholar] [CrossRef]
- Rubio, D.; Andres, S.L. Structural stiffness, dry friction coefficient, and equivalent viscous damping in a bump-type foil gas bearing. ASME J. Eng. Gas Turbines Power 2007, 129, 494–502. [Google Scholar] [CrossRef]
- Swanson, E.E. Bump foil damping using a simplified model. ASME J. Tribol. 2006, 128, 542–550. [Google Scholar] [CrossRef]
- Sim, K.; Park, J. Performance measurements of gas bearings with high damping structures of polymer and bump foil via electric motor driving tests and 1-DOF shaker dynamic loading tests. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016; p. GT2016-57345. [Google Scholar] [CrossRef]
- Zywica, G.; Baginski, P.; Andrearczyk, A. A new method of manufacturing a foil bearing using tools made by the rapid prototyping technology. CIRP J. Manuf. Sci. Technol. 2020, 31, 514–524. [Google Scholar] [CrossRef]
- Kim, T.H.; Breedlove, A.W.; San Andres, L. Characterization of a foil bearing structure at increasing temperatures: Static load and dynamic force performance. J. Tribol. 2009, 131, 041703. [Google Scholar] [CrossRef]
- Zywica, G.; Baginski, P.; Bogulicz, M.; Martowicz, A.; Roemer, J.; Kantor, S. Numerical identification of the dynamic characteristics of a nonlinear foil bearing structure: Effect of the excitation force amplitude and the assembly preload. J. Sound Vib. 2022, 520, 116663. [Google Scholar] [CrossRef]
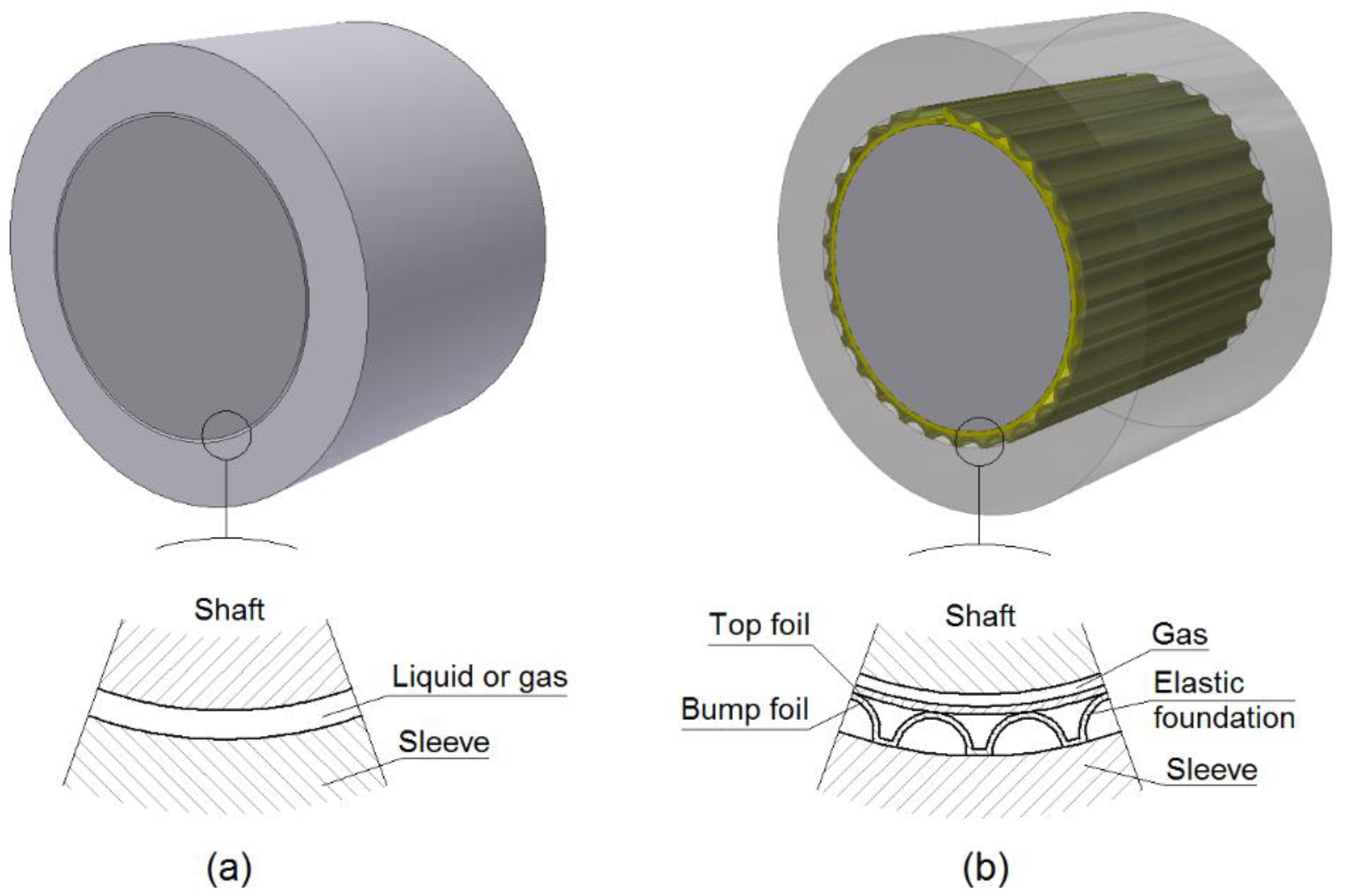

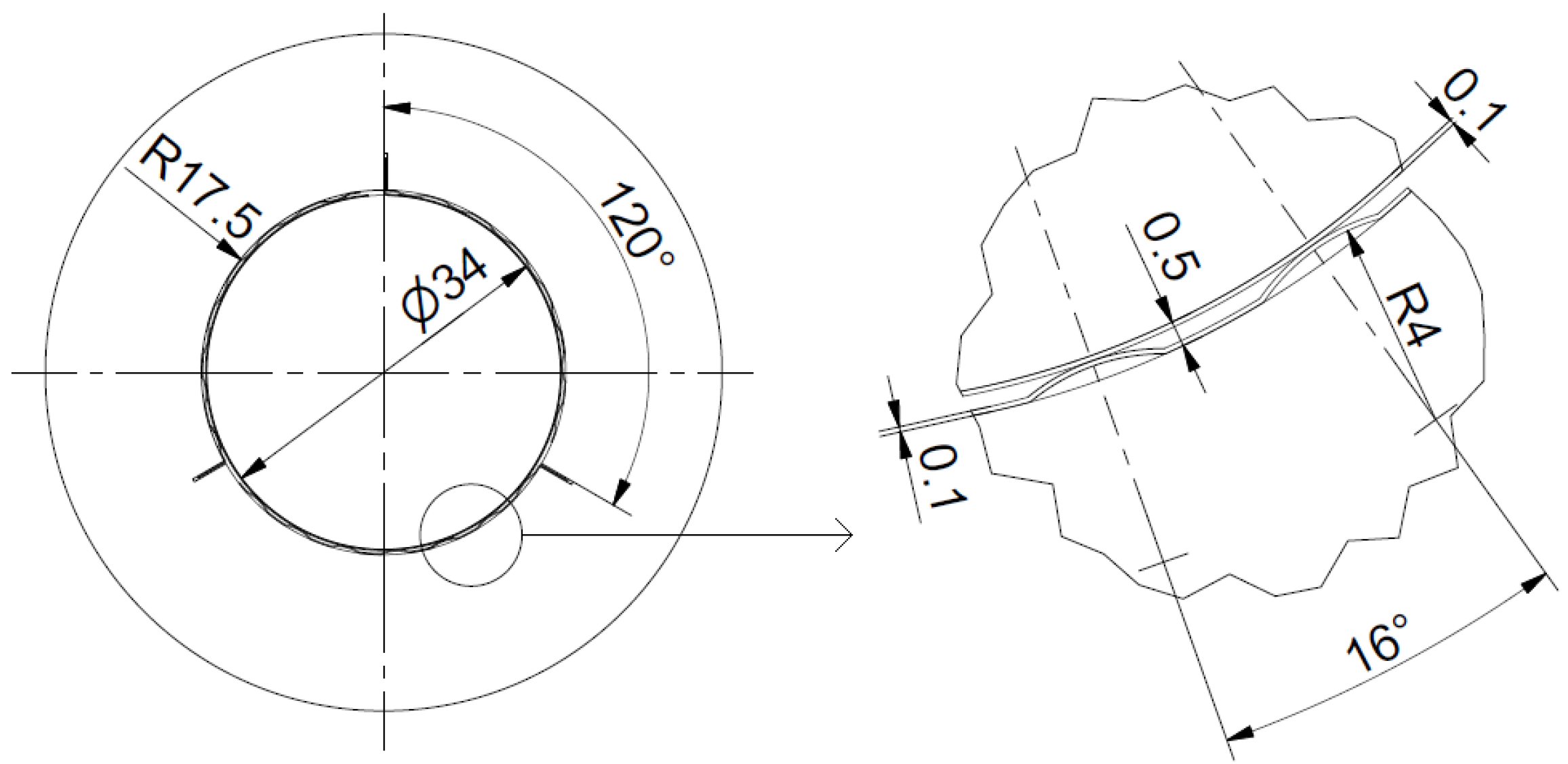






| Parameter | Value |
|---|---|
| Journal diameter | 34 mm |
| Sleeve inner diameter | 35 mm |
| Bearing length | 40 mm |
| Bearing mass | 930 g |
| Number of top foils | 1 |
| Number of bump foils | 3 |
| Top foil thickness | 0.115 mm |
| Bump foil thickness | 0.1 mm |
| Number of bumps of a single bump foil | 7 |
| Bump radius (inner) | 4 mm |
| Bump height | 0.3 mm |
| Angle between bumps | 16° |
| Journal material | steel (1.7225) |
| Journal coating (0.25 mm thick) | Cr2O3 |
| Top/bump foil material | Inconel 625 |
| Top foil coating (10–15 µm thick) | AS20 (PTFE based) |
| Sleeve material | bronze (CuSn10P) |
| Frequency [Hz] | Configuration (a) | Configuration (b) | ||
|---|---|---|---|---|
| Force [N] | ||||
| 20 | 25 | 50 | 25 | 50 |
| 40 | 25 | 50 | 25 | 50 |
| 80 | 25 | 50 | 25 | 50 |
| 150 | 25 | 50 | 25 | 50 |
| 300 | 25 | 50 | 25 | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żywica, G.; Bagiński, P.; Roemer, J.; Zdziebko, P.; Martowicz, A.; Kaczmarczyk, T.Z. Experimental Characterization of a Foil Journal Bearing Structure with an Anti-Friction Polymer Coating. Coatings 2022, 12, 1252. https://doi.org/10.3390/coatings12091252
Żywica G, Bagiński P, Roemer J, Zdziebko P, Martowicz A, Kaczmarczyk TZ. Experimental Characterization of a Foil Journal Bearing Structure with an Anti-Friction Polymer Coating. Coatings. 2022; 12(9):1252. https://doi.org/10.3390/coatings12091252
Chicago/Turabian StyleŻywica, Grzegorz, Paweł Bagiński, Jakub Roemer, Paweł Zdziebko, Adam Martowicz, and Tomasz Zygmunt Kaczmarczyk. 2022. "Experimental Characterization of a Foil Journal Bearing Structure with an Anti-Friction Polymer Coating" Coatings 12, no. 9: 1252. https://doi.org/10.3390/coatings12091252
APA StyleŻywica, G., Bagiński, P., Roemer, J., Zdziebko, P., Martowicz, A., & Kaczmarczyk, T. Z. (2022). Experimental Characterization of a Foil Journal Bearing Structure with an Anti-Friction Polymer Coating. Coatings, 12(9), 1252. https://doi.org/10.3390/coatings12091252









