Single-Layer MoS2: A Two-Dimensional Material with Negative Poisson’s Ratio
Abstract
:1. Introduction
2. Computational Methods
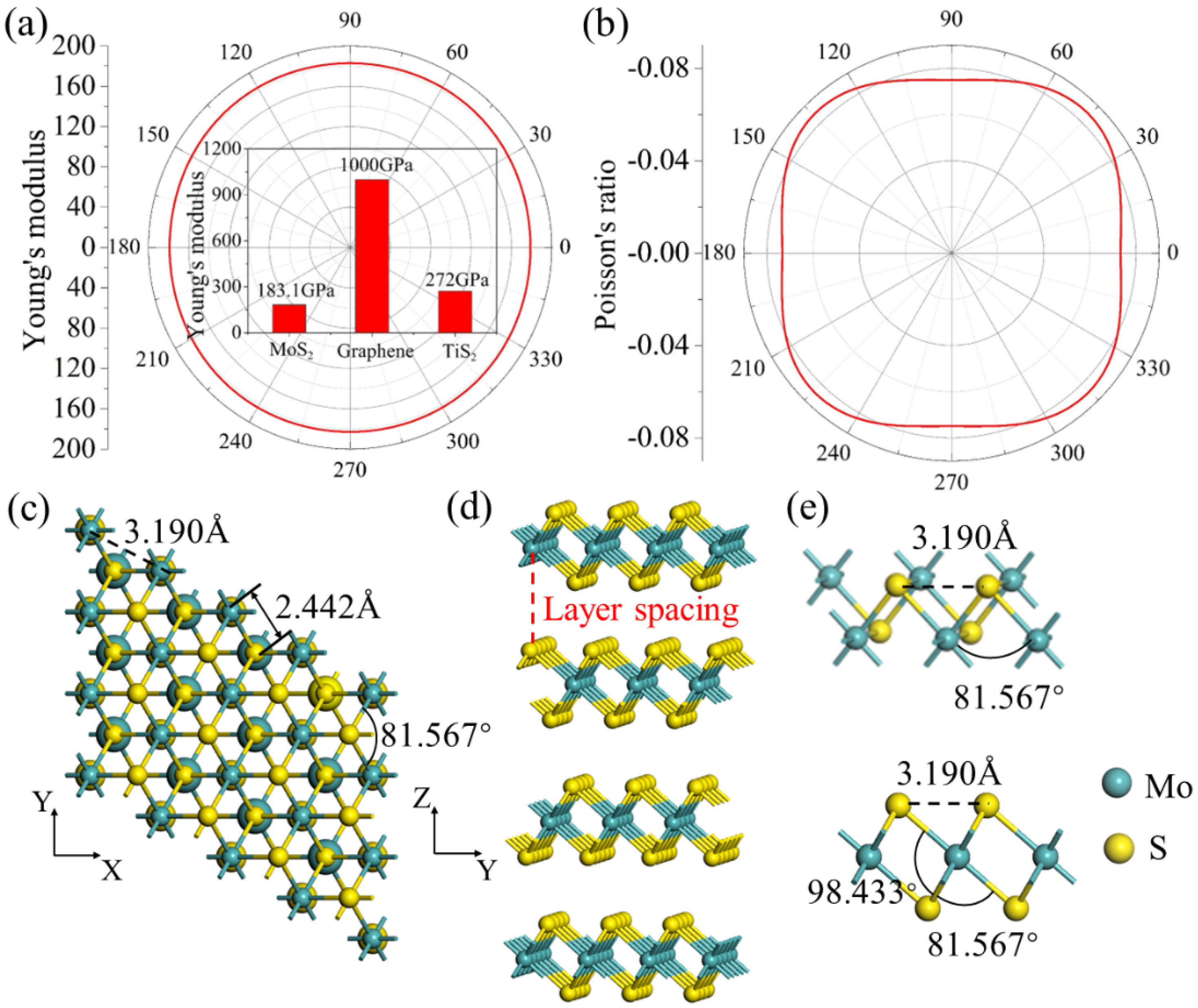
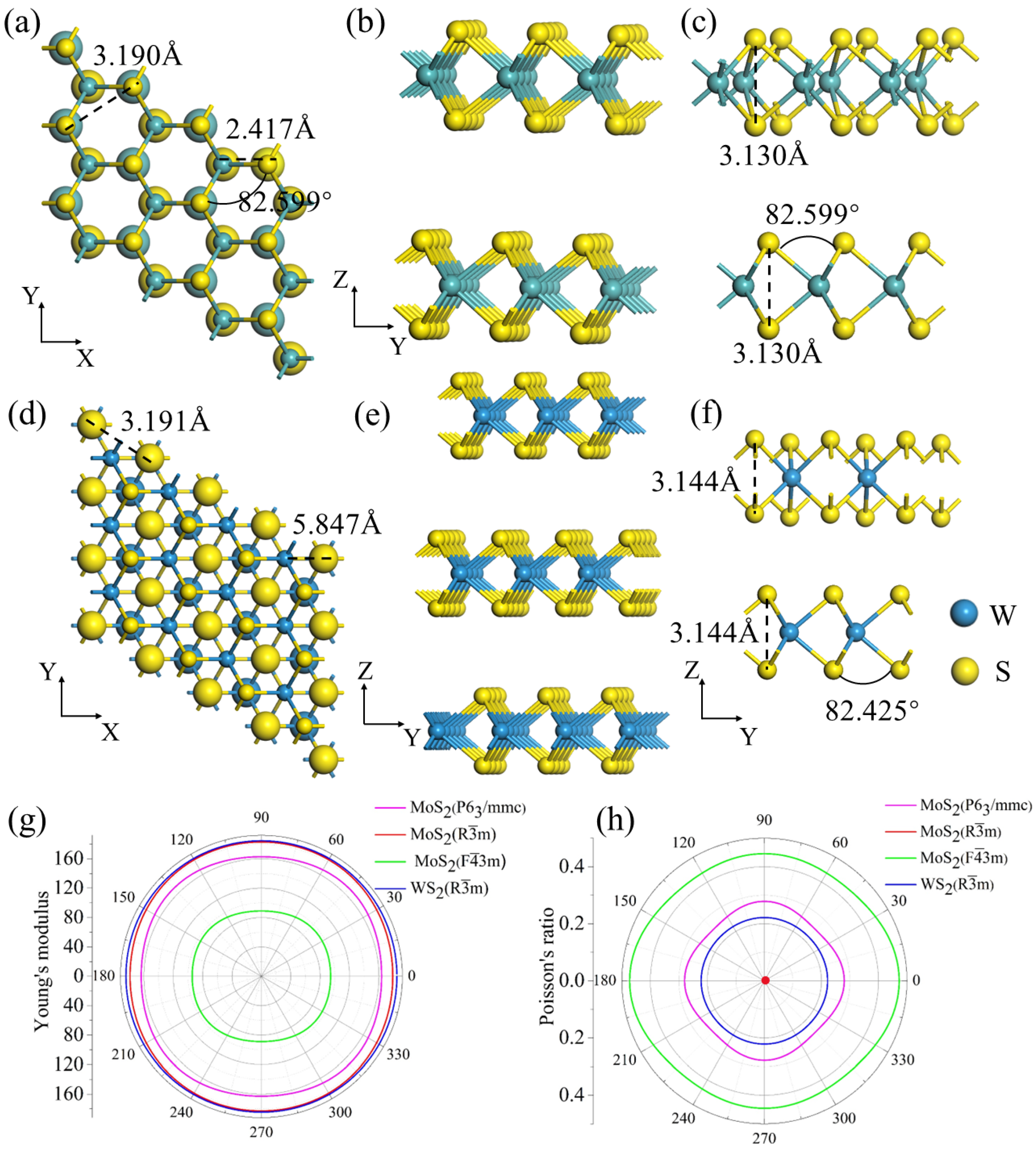
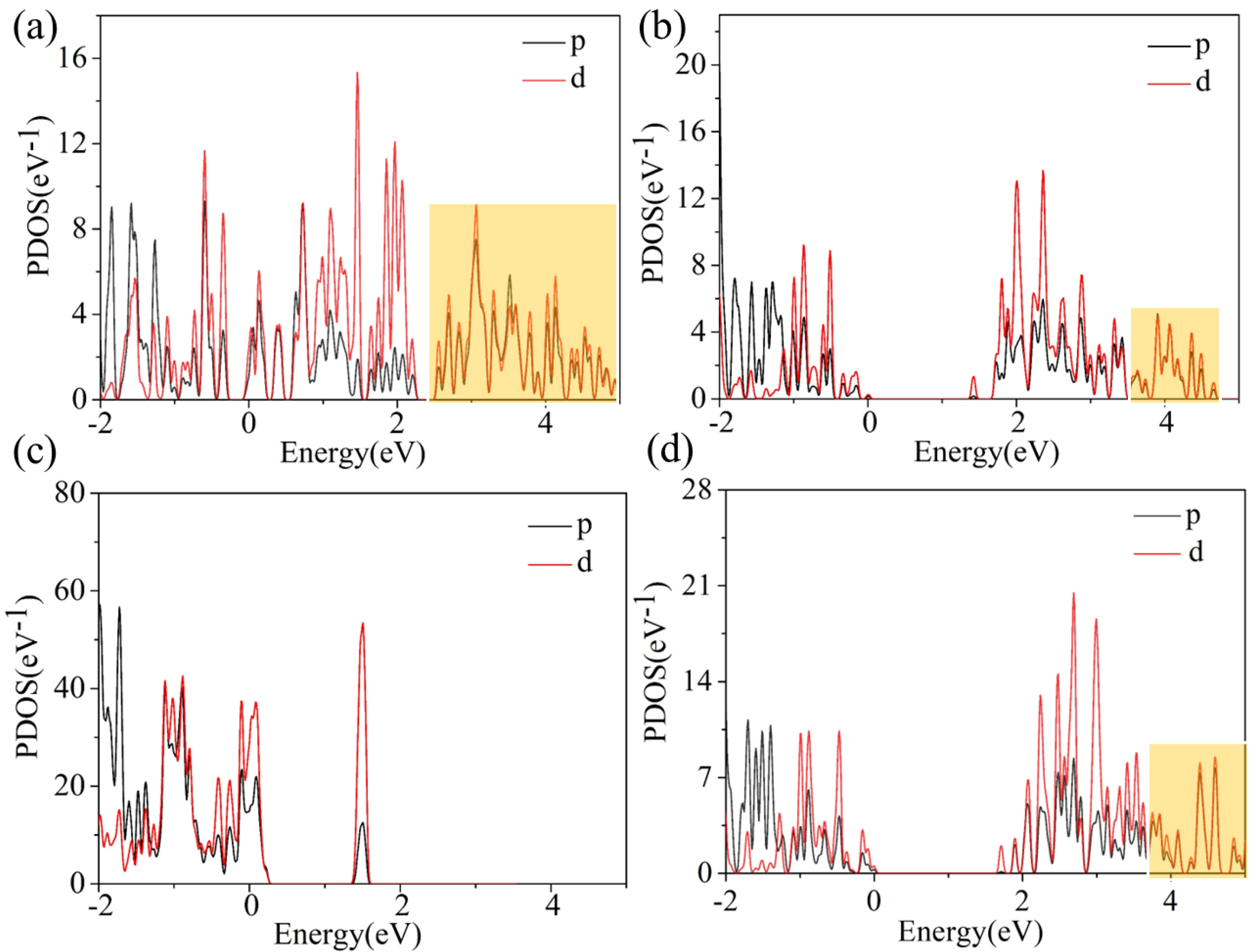
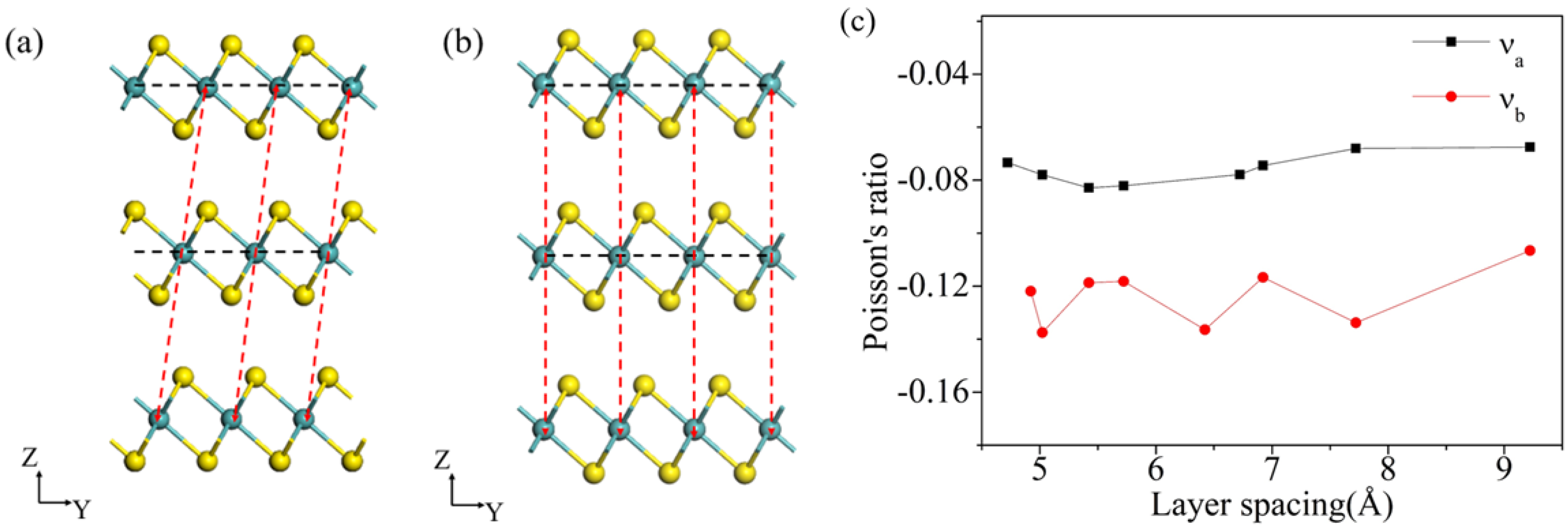
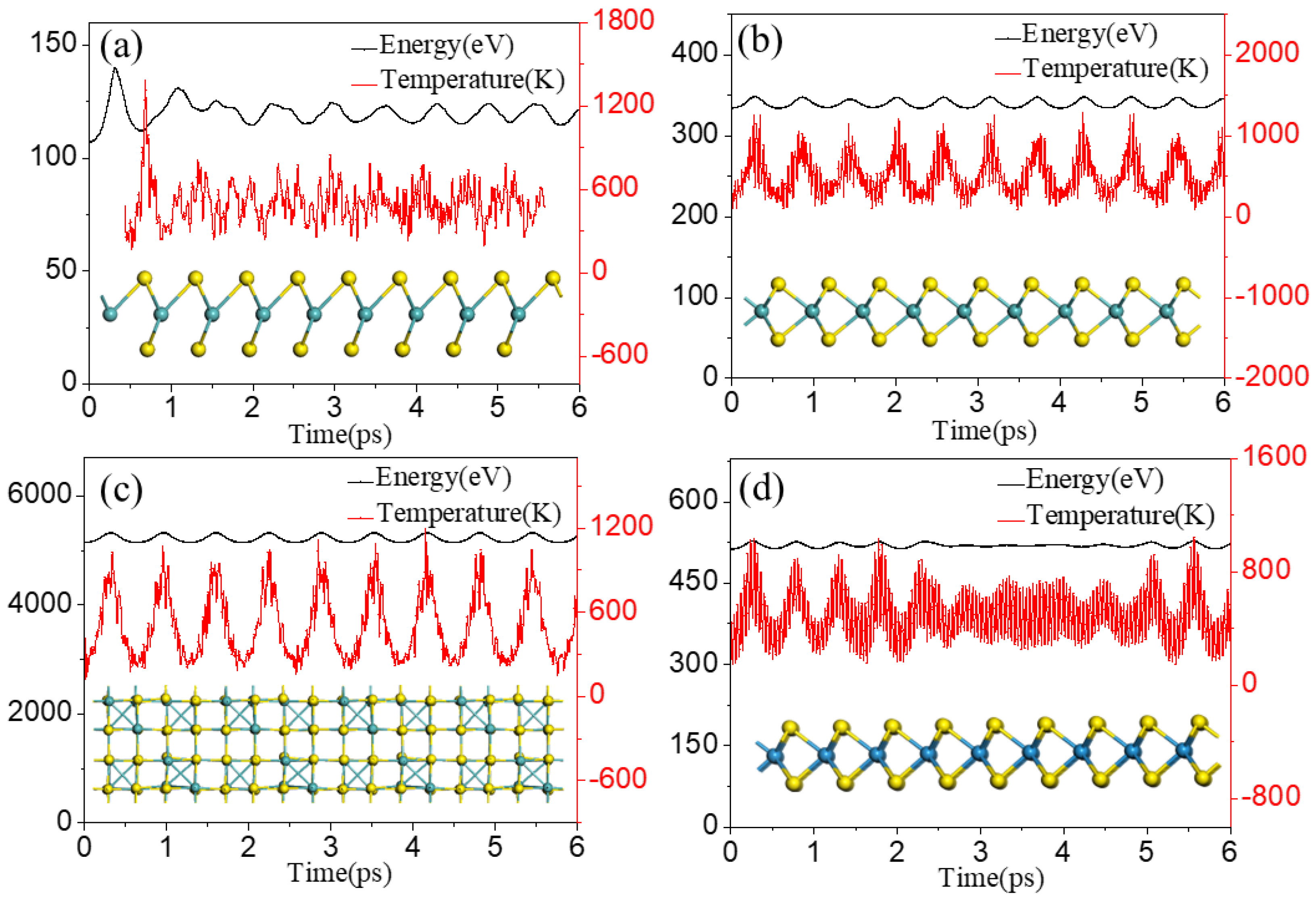
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, C.; Zhou, J.; Wu, H.; Deng, K.; Jena, P.; Kan, E. Quantum anomalous Hall effect in ferromagnetic transition metal halides. Phys. Rev. B 2017, 95, 45113. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Qin, G.; Zhang, F. Effects of Internal Relaxation of Biaxial Strain on Structural and Electronic Properties of In0.5Al0.5N Thin Film. Coatings 2022, 12, 598. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Yuan, R.; Zhou, Y.; Fan, X.; Lu, Q. Negative-Poisson-Ratio polyimide aerogel fabricated by tridirectional freezing for High- and Low-Temperature and Impact-Resistant applications. Chem. Eng. J. 2022, 433, 134404. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.; Shi, W.; Xie, B.; Yang, M. Review on auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Ting, T.C.T.; Chen, T. Poisson’s ratio for anisotropic elastic materials can have no bounds. Q. J. Mech. Appl. 2005, 58, 73–82. [Google Scholar] [CrossRef]
- Hu, H.; Silberschmidt, V. A composite material with Poisson’s ratio tunable from positive to negative values: An experimental and numerical study. J. Mater. Sci. 2013, 48, 8493–8500. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Dong, X.; Li, N.; Ren, J. Novel Two-Dimensional Silicon Dioxide with in-Plane Negative Poisson’s Ratio. Nano Lett. 2017, 17, 772–777. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaminakis, N.T.; Stavroulakis, G.E. Topology optimization for compliant mechanisms, using evolutionary-hybrid algorithms and application to the design of auxetic materials. Compos. Part B 2012, 43, 2655–2668. [Google Scholar] [CrossRef]
- Blackburn, S.; Wilson, D.L. Shaping ceramics by plastic processing. J. Eur. Ceram. Soc. 2008, 7, 1341–1351. [Google Scholar] [CrossRef]
- Lipsett, A.W.; Beltzer, A.I. Reexamination of dynamic problems of elasticity for negative Poisson’s ratio. J. Acoust. Soc. Am. 1988, 84, 2179. [Google Scholar] [CrossRef]
- Lakes, R.; Elms, K. Indentability of Conventional and Negative Poisson’s Ratio Foams. J. Compos. Mater. 1993, 27, 1193. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Gao, L.; Zhou, W.; Wang, Y.; Lu, Y. Novel 2D metamaterials with negative Poisson’s ratio and negative thermal expansion. Extrem. Mech. Lett. 2019, 30, 100498. [Google Scholar] [CrossRef]
- Demir, H.; Cosgun, A.E. The Effect on Energy Efficiency of Yttria-Stabilized Zirconia on Brass, Copper and Hardened Steel Nozzle in Additive Manufacturing. Coatings 2022, 12, 690. [Google Scholar] [CrossRef]
- Khomenko, V.; Butenko, O.; Chernysh, O.; Barsukov, V.; Suchea, M.P.; Koudoumas, E. Electromagnetic Shielding of Composite Films Based on Graphite, Graphitized Carbon Black and Iron-Oxide. Coatings 2022, 12, 665. [Google Scholar] [CrossRef]
- Buet, E.; Braun, J.; Sauder, C. Influence of Texture and Thickness of Pyrocarbon Coatings as Interphase on the Mechanical Behavior of Specific 2.5D SiC/SiC Composites Reinforced with Hi-Nicalon S Fibers. Coatings 2022, 12, 573. [Google Scholar] [CrossRef]
- Jiang, J.; Park, H.S. Negative Poisson’s ratio in single-layer black phosphorus. Nat. Commun. 2014, 5, 4727. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, F.; Li, Y.; Chen, Z. Semi-metallic Be5C2 monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson’s ratio. Nat. Commun. 2016, 7, 11488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.C.; Qin, G.; Fang, W.Z.; Cui, H.J.; Zheng, Q.R.; Yan, Q.B.; Su, G. Tinselenidene: A Two-dimensional Auxetic Material with Ultralow Lattice Thermal Conductivity and Ultrahigh Hole Mobility. Sci. Rep. 2016, 6, 19830. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Zhuo, Z.; Kou, L.; Du, A.; Tretiak, S. Computational Dissection of Two-Dimensional Rectangular Titanium Mononitride TiN: Auxetics and Promises for Photocatalysis. Nano Lett. 2017, 17, 4466–4472. [Google Scholar] [CrossRef]
- Qin, G.; Yan, Q.B.; Qin, Z.; Yue, S.Y.; Cui, H.J.; Zheng, Q.R.; Su, G. Hinge-like Structure Induced Unusual Properties of Black Phosphorus and New Strategies to Improve the Thermoelectric Performance. Sci. Rep. 2015, 4, 6946. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Li, X.; Li, P.; Yang, J. δ-Phosphorene: A Two-Dimensional Material with a Highly Negative Poisson’s Ratio. Nanoscale 2017, 9, 850–855. [Google Scholar] [CrossRef]
- Meng, L.B.; Ni, S.; Zhang, Y.J.; Li, B.; Zhou, X.W.; Wu, W.D. Two-Dimensional Zigzag-Shaped Cd2C Monolayer with a Desirable Bandgap and High Carrier Mobility. J. Mater. Chem. C 2018, 6, 9175–9180. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, Y.; Zhou, M.; Zhang, J.; Zhou, X.; Ni, S.; Wu, W. Unique Zigzag-Shaped Buckling Zn2C Monolayer with Strain-Tunable Band Gap and Negative Poisson Ratio. Inorg. Chem. 2018, 57, 1958–1963. [Google Scholar] [CrossRef]
- Peng, R.; Ma, Y.; He, Z.; Huang, B.; Kou, L.; Dai, Y. Single-Layer Ag2S: A Two-Dimensional Bidirectional Auxetic Semiconductor. Nano Lett. 2019, 19, 1227–1233. [Google Scholar] [CrossRef]
- Miró, P.; Audiffred, M.; Heine, T. An atlas of two-dimensional materials. Chem. Soc. Rev. 2014, 43, 6537–6554. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Marconcini, P.; Hossian, M.S.; Qiu, W.; Evans, R.; Macucci, M.; Skafidas, E. A tight binding and k.p study of monolayer stanene. Sci. Rep. 2017, 7, 12069. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Y.; Yan, J.; Gong, X.; Tang, X.; Xu, X.; Meng, T.; Bu, F.; Cai, D.; Zhang, Z.; Nie, G.; et al. All-in-one asymmetric micro-supercapacitor with Negative Poisson’s ratio structure based on versatile electrospun nanofibers. Chem. Eng. J. 2022, 433, 133580. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Yan, Q.; Ruzsinszky, A. Negative Poisson’s ratio in 1T-type crystalline two-dimensional transition metal dichalcogenides. Nat. Commun. 2017, 8, 15224. [Google Scholar] [CrossRef] [Green Version]
- Hung, N.T.; Nugraha, A.; Saito, R. Two-dimensional MoS2 electromechanical actuators. J. Phys. D Appl. Phys. 2018, 51, 75306. [Google Scholar] [CrossRef] [Green Version]
- Esteban-Puyuelo, R.; Sarma, D.D.; Sanyal, B. Complexity of mixed allotropes of MoS2 unraveled by first-principles theory. Phys. Rev. B 2020, 102, 165412. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.I.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 27117. [Google Scholar] [CrossRef]
- Fan, Y.; Xie, D.; Ma, D.; Jing, F.; Matthews, D.T.A.; Ganesan, R.; Leng, Y. Evaluation of the Crystal Structure and Mechanical Properties of Cu Doped TiN Films. Coatings 2022, 12, 652. [Google Scholar] [CrossRef]
- Jacobsen, E.; Lyons, R. The sliding DFT. IEEE Signal Process. Mag. 2003, 20, 74–80. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Chen, W.; Zhao, X.; Su, H.; Chen, Z. Anisotropic Electronic Characteristics, Adsorption, and Stability of Low-Index BiVO4 Surfaces for Photoelectrochemical Applications. ACS Appl. Mater. Interfaces 2018, 10, 5475–5484. [Google Scholar] [CrossRef] [PubMed]
- Cadelano, E.; Palla, P.L.; Giordano, S.; Colombo, L. Elastic Properties of Hydrogenated Graphene. Phys. Rev. B 2010, 82, 235414. [Google Scholar] [CrossRef] [Green Version]
- Andrew, R.C.; Mapasha, R.E.; Ukpong, A.M.; Chetty, N. Mechanical properties of graphene and boronitrene. Phys. Rev. B 2012, 85, 125428. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Chen, C. Structure-strength relations of distinct MoN phases from first-principles calculations. Phys. Rev. Mater. 2020, 4, 44002. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Xie, L.; Liang, Y.; Hong, G.; Dai, H. MoS2 Nanoparticles Grown on Graphene: An Advanced Catalyst for the Hydrogen Evolution Reaction. J. Am. Chem. Soc. 2011, 19, 7296–7299. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Lorenz, T.; Teich, D.; Joswig, J.; Seifert, G. Theoretical Study of the Mechanical Behavior of Individual TiS2 and MoS2 Nanotubes. J. Phys. Chem. C 2012, 21, 11714–11721. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372–2377. [Google Scholar] [CrossRef] [Green Version]
- Xiao, W.; Xiao, G.; Rong, Q.; Wang, L. Theoretical discovery of novel two-dimensional VA-N binary compounds with auxiticity. Phys. Chem. Chem. Phys. 2018, 20, 22027–22037. [Google Scholar] [CrossRef] [PubMed]
- Kou, L.; Ma, Y.; Tang, C.; Sun, Z.; Du, A.; Chen, C. Auxetic and Ferroelastic Borophane: A Novel 2D Material with Negative Poisson’s Ratio and Switchable Dirac Transport Channels. Nano Lett. 2016, 16, 7910–7914. [Google Scholar] [CrossRef]
- Jong, M.D.; Chen, W.; Angsten, T.; Jain, A.; Notestine, R.; Gamst, A.; Sluiter, M.; Ande, C.K.; Zwaag, S.V.D.; Plata, J.; et al. Charting the complete elastic properties of inorganic crystalline compounds. Sci. Data 2015, 2, 150009. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Niu, M.; Fu, J.; Xi, Z.; Lei, M.; Quhe, R. Negative Poisson’s ratio in puckered two-dimensional materials. Phys. Rev. Mater. 2019, 3, 54002. [Google Scholar] [CrossRef]
- Jin, W.; Sun, W.; Kuang, X.; Lu, C.; Kou, L. Negative Poisson Ratio in Two-Dimensional Tungsten Nitride: Synergistic Effect from Electronic and Structural Properties. J. Phys. Chem. Lett. 2020, 11, 9643–9648. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Cao, X.; Tan, Y.; Wang, Y.; Hu, J.; Li, B.; Chen, Z. Single-Layer MoS2: A Two-Dimensional Material with Negative Poisson’s Ratio. Coatings 2023, 13, 283. https://doi.org/10.3390/coatings13020283
Zhu Y, Cao X, Tan Y, Wang Y, Hu J, Li B, Chen Z. Single-Layer MoS2: A Two-Dimensional Material with Negative Poisson’s Ratio. Coatings. 2023; 13(2):283. https://doi.org/10.3390/coatings13020283
Chicago/Turabian StyleZhu, Yucheng, Xiaofei Cao, Yuan Tan, Yao Wang, Jun Hu, Baotong Li, and Zhong Chen. 2023. "Single-Layer MoS2: A Two-Dimensional Material with Negative Poisson’s Ratio" Coatings 13, no. 2: 283. https://doi.org/10.3390/coatings13020283
APA StyleZhu, Y., Cao, X., Tan, Y., Wang, Y., Hu, J., Li, B., & Chen, Z. (2023). Single-Layer MoS2: A Two-Dimensional Material with Negative Poisson’s Ratio. Coatings, 13(2), 283. https://doi.org/10.3390/coatings13020283