Monocrystalline Nickel Nanogrinding Subsurface Deformation-Layer Depth Study Based on Orthogonal Tests
Abstract
:1. Introduction
2. Model and Simulation Conditions
3. Results and Analysis
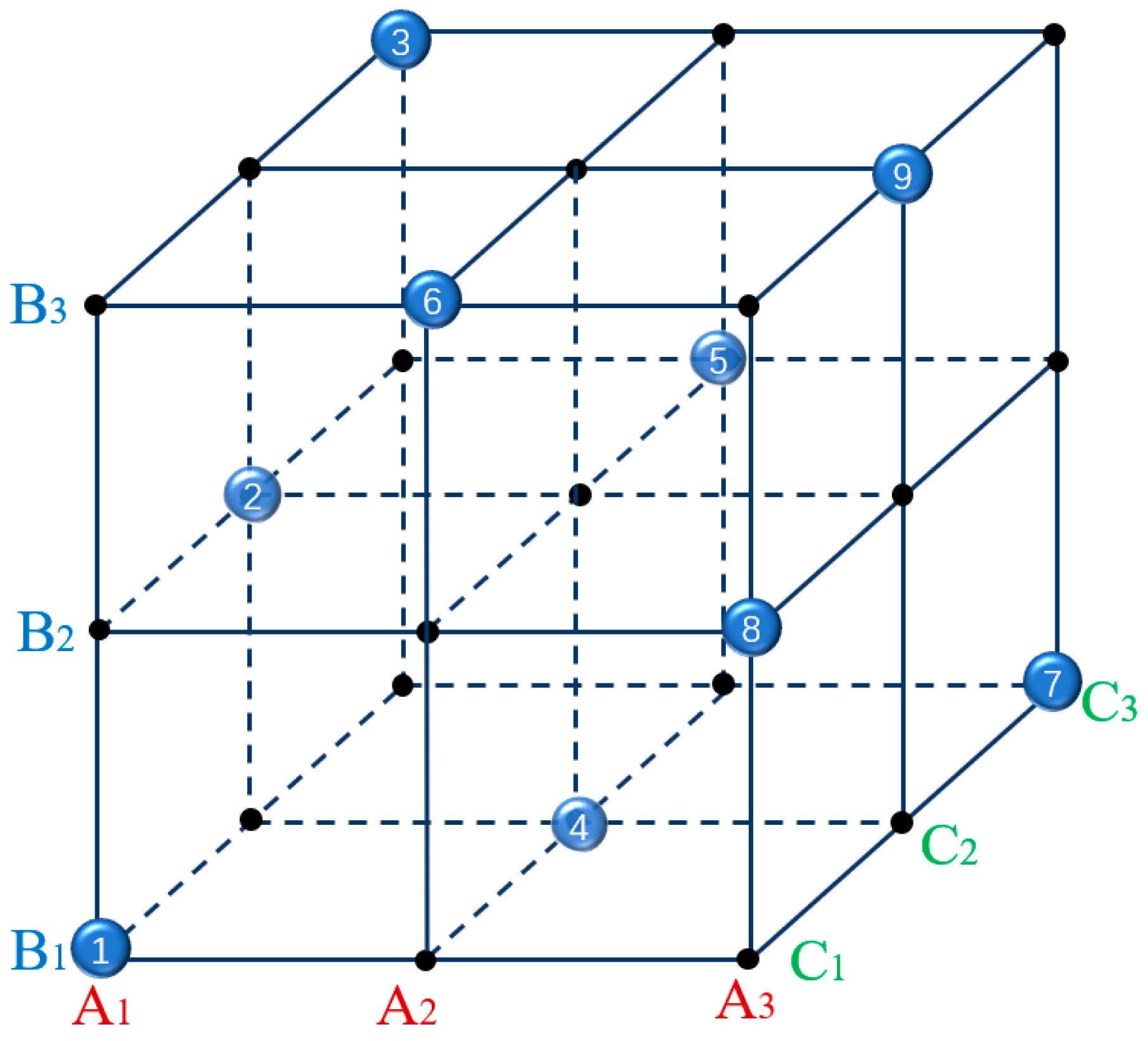
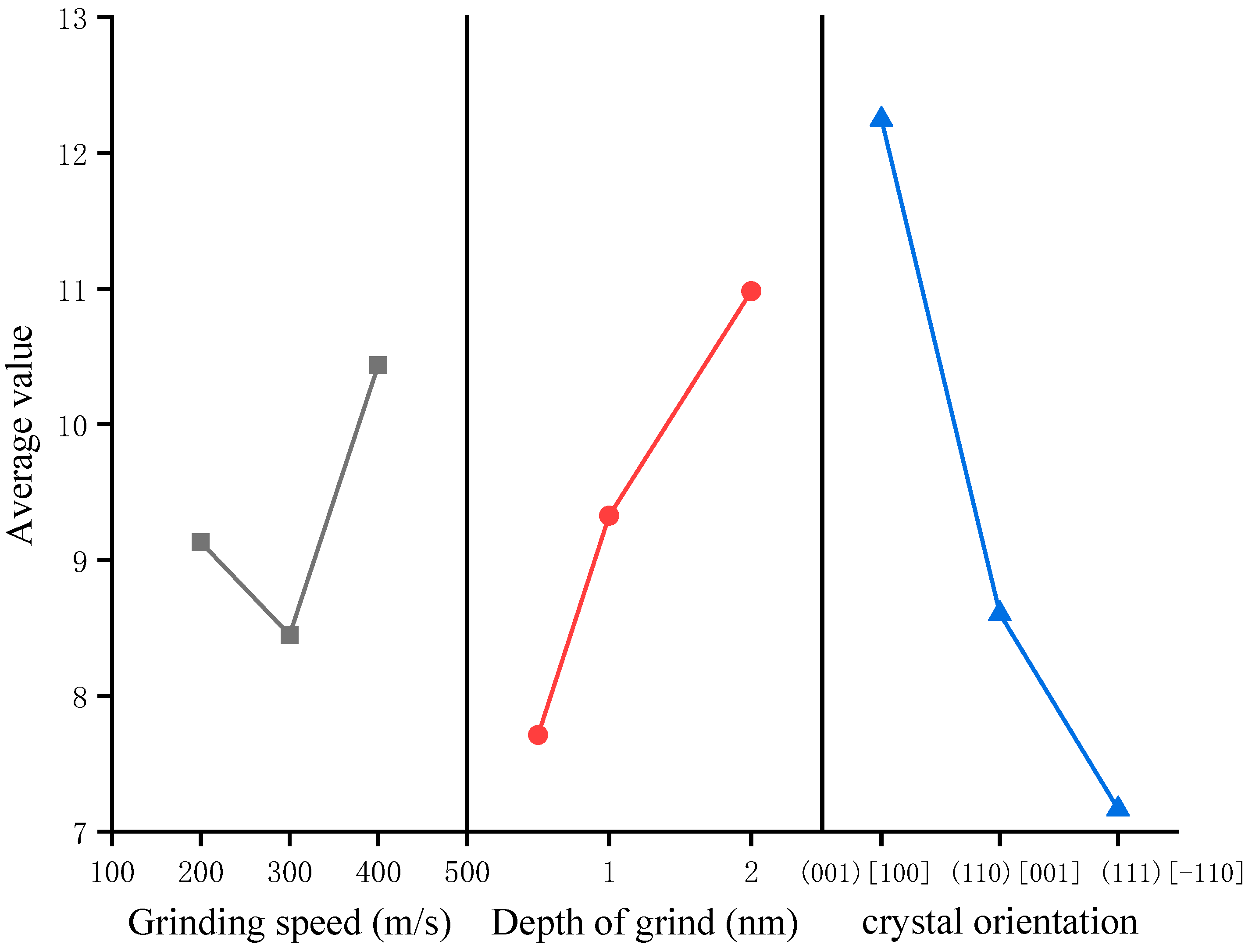
3.1. Orthogonal Calculation Results
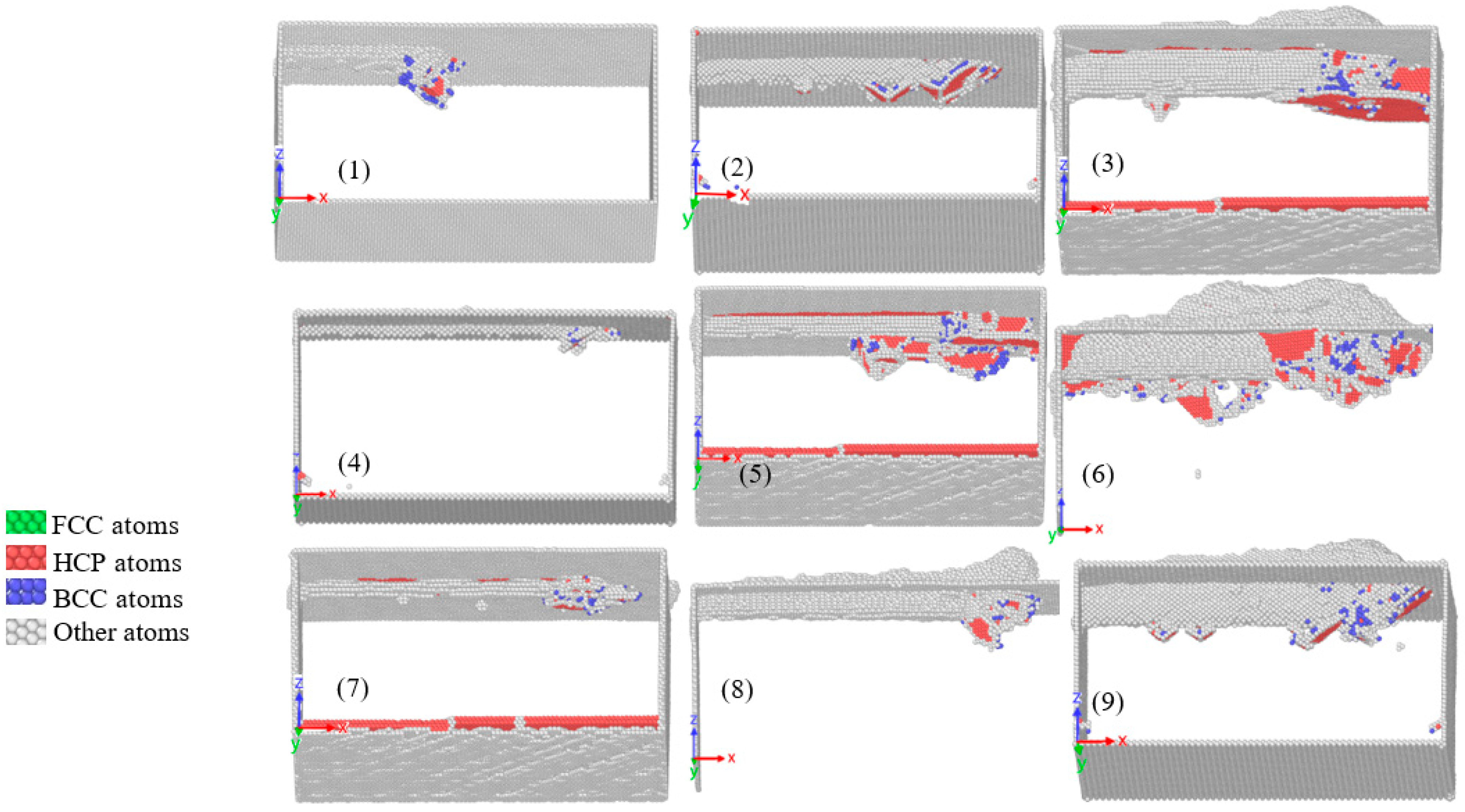
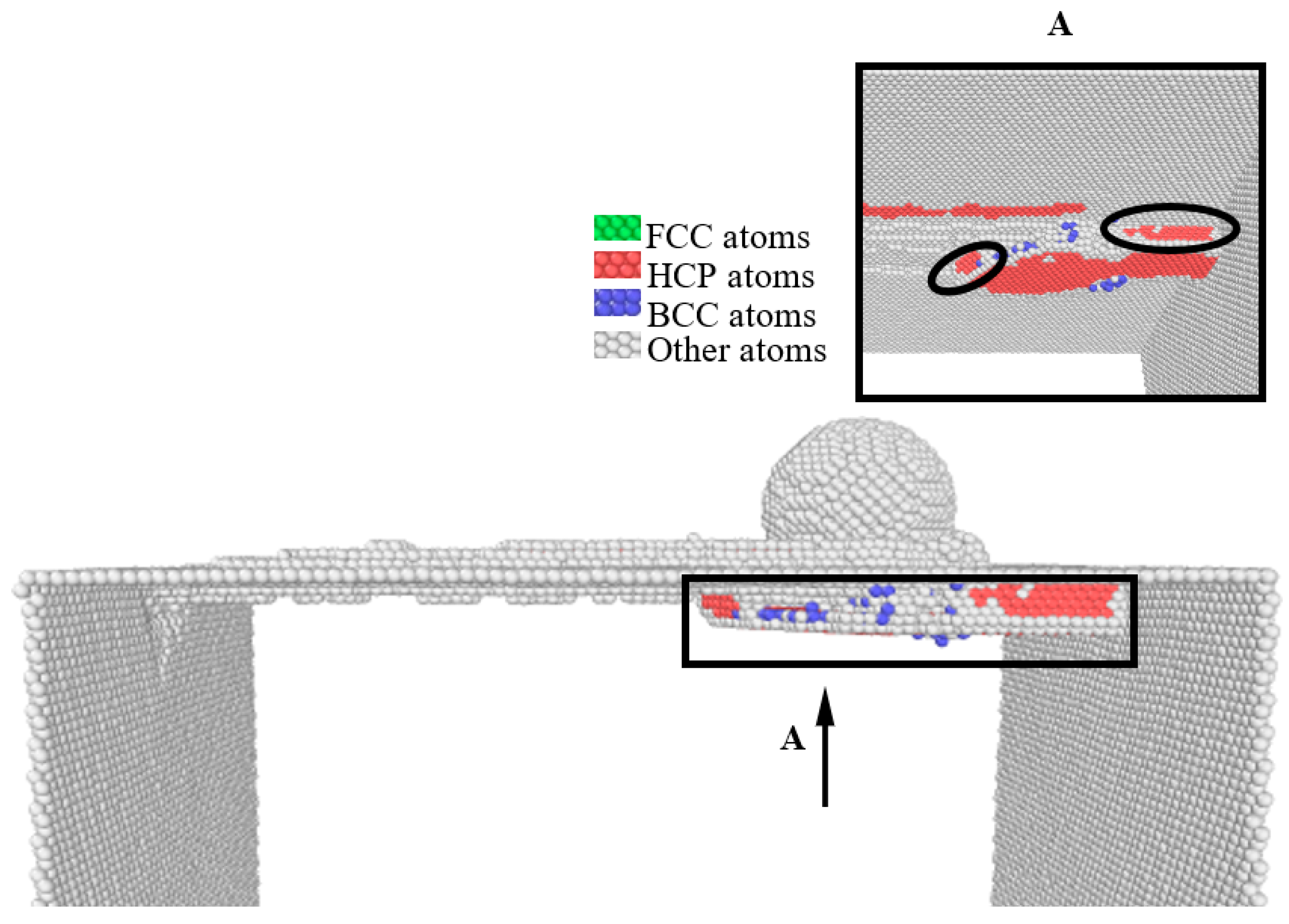
3.2. Subsurface Defects
3.3. Optimal Combination Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, Q.; Gong, Y.; Zhou, Y.; Wen, X. Experimental study of micro-milling mechanism and surface quality of a nickel-based single crystal superalloy. J. Mech. Sci. Technol. 2017, 31, 171–180. [Google Scholar] [CrossRef]
- Wu, Y.; Xiang, J.; Yang, C.; Lu, W.; Lieber, C.M. Single-crystal metallic nanowires and metal/semiconductor nanowire heterostructures. Nature 2004, 430, 61. [Google Scholar] [CrossRef]
- Li, Z.; Yan, Y.; Wang, J.; Geng, Y. Molecular dynamics study on tip-based nanomachining: A review. Nanoscale Res. Lett. 2020, 15, 1–12. [Google Scholar] [CrossRef]
- Herrer, L.; Martín, S.; Cea, P. Nanofabrication techniques in large-area molecular electronic devices. Appl. Sci. 2020, 10, 6064. [Google Scholar] [CrossRef]
- Kim, M.; Kim, M.K. Four-dimensional nanofabrication for next-generation optical devices. J. Korean Phys. Soc. 2022, 81, 516–524. [Google Scholar] [CrossRef]
- Liu, B. Research on Nanometer Cutting Mechanism Based on Scanning Electron Microscope; Tianjin University: Tianjin, China, 2015. [Google Scholar]
- Meng, B.; Yuan, D.; Zheng, J.; Qiu, P.; Xu, S. Tip-based nanomanufacturing process of single crystal SiC: Ductile deformation mechanism and process optimization. Appl. Surf. Sci. 2020, 500, 144039. [Google Scholar] [CrossRef]
- Yan, Y.; Li, Z.; Jia, J.; Wang, J.; Geng, Y. Molecular dynamics simulation of the combination effect of the tip inclination and scratching direction on nanomachining of single crystal silicon. Comput. Mater. Sci. 2021, 186, 110014. [Google Scholar] [CrossRef]
- Eder, S.J.; Leroch, S.; Grützmacher, P.G.; Spenger, T.; Heckes, H. A multiscale simulation approach to grinding ferrous surfaces for process optimization. Int. J. Mech. Sci. 2021, 194, 106186. [Google Scholar] [CrossRef]
- Eder, S.J.; Rodríguez Ripoll, M.; Cihak-Bayr, U.; Dini, D.; Gachot, C. Unraveling and mapping the mechanisms for near-surface microstructure evolution in CuNi alloys under sliding. ACS Appl. Mater. Interfaces 2020, 12, 32197–32208. [Google Scholar] [CrossRef]
- Eder, S.J.; Grützmacher, P.G.; Rodríguez Ripoll, M.; Dini, D.; Gachot, C. Effect of temperature on the deformation behavior of copper nickel alloys under sliding. Materials 2020, 14, 60. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, L.; Yang, S. On the deformation mechanism of 6H-SiC under the nanogrinding of multiple abrasive grains. Tribol. Int. 2023, 179, 108119. [Google Scholar] [CrossRef]
- Karkalos, N.E.; Markopoulos, A.P. Determination of the efficiency of hot nano-grinding of mono-crystalline fcc metals using molecular dynamics method. Micromachines 2022, 13, 415. [Google Scholar] [CrossRef]
- Markopoulos, A.P.; Karkalos, N.E.; Papazoglou, E.L. Meshless methods for the simulation of machining and micro-machining: A review. Arch. Comput. Methods Eng. 2019, 27, 831–853. [Google Scholar] [CrossRef]
- Xu, F.; Fang, F.; Zhang, X. Study on surface generation in nano-cutting by large-scale molecular dynamics simulation. Int. J. Adv. Manuf. Technol. 2019, 104, 4325–4329. [Google Scholar] [CrossRef]
- Wang, J.; Fang, F.; Li, L. Cutting of graphite at atomic and close-to-atomic scale using flexible enhanced molecular dynamics. Nanomanufacturing Metrol. 2022, 5, 240–249. [Google Scholar] [CrossRef]
- Dai, L.; Chen, G.; Shan, Z. Study on ultra-high speed nano-grinding of monocrystalline copper with V-shaped diamond abrasive grains based on molecular dynamics method. Diam. Relat. Mater. 2021, 111, 108224. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, X.; Chen, J. Surface deformation, phase transition and dislocation mechanisms of single crystalline 6H-SiC in oblique nano-cutting. Appl. Surf. Sci. 2022, 588, 152944. [Google Scholar] [CrossRef]
- Zhao, P.; Zhao, B.; Pan, J.; Wu, J. Nano-grinding process of single-crystal silicon using molecular dynamics simulation: Nano-grinding parameters effect. Mater. Sci. Semicond. Process. 2022, 143, 106531. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Markopoulos, A.P.; Savvopoulos, I.K.; Karkalos, N.E.; Manolakos, D.E. Molecular dynamics modeling of a single diamond abrasive grain in grinding. Front. Mech. Eng. 2015, 10, 168–175. [Google Scholar] [CrossRef]
- Eder, S.J.; Cihak-Bayr, U.; Bianchi, D.; Feldbauer, G.; Betz, G. Thermostat influence on the structural development and material removal during abrasion of nanocrystalline ferrite. ACS Appl. Mater. Interfaces 2017, 9, 13713–13725. [Google Scholar] [CrossRef] [PubMed]
- Shiari, B.; Miller, R.E.; Klug, D.D. Multiscale simulation of material removal processes at the nanoscale. J. Mech. Phys. Solids 2007, 55, 2384–2405. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.J.; Papaconstantopoulos, D.A. Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys. Rev. B 1999, 59, 3393. [Google Scholar] [CrossRef]
- Lin, Z.; Huang, J.; Jeng, Y. 3D nano-scale cutting model for nickel material. Mater. Process. Technol. 2007, 192–193, 27–36. [Google Scholar] [CrossRef]
- Ren, J.; Hao, M.; Lv, M.; Wang, S.; Zhu, B. Molecular dynamics research on ultra-high-speed grinding mechanism of monocrystalline nickel. Appl. Surf. Sci. 2018, 455, 629–634. [Google Scholar] [CrossRef]
- Zhang, J. Research on the Formation Mechanism of Surface Layer of Crystalline Copper Nanomachined Based on Molecular Dynamics; Harbin Institute of Technology: Harbin, China, 2011. [Google Scholar]
- Zhang, J.J.; Sun, T.; Yan, Y.D.; Liang, Y.C.; Dong, S. Molecular dynamics simulation of subsurface deformed layers in AFM-based nanometric cutting process. Appl. Surf. Sci. 2008, 254, 4774–4779. [Google Scholar] [CrossRef]
- Ren, J.; Liang, G.X.; Lv, M. Effect of different crystal orientations on the surface integrity during nanogrinding of monocrystalline nickel. Model. Simul. Mater. Sci. Eng. 2019, 27, 075007. [Google Scholar] [CrossRef]
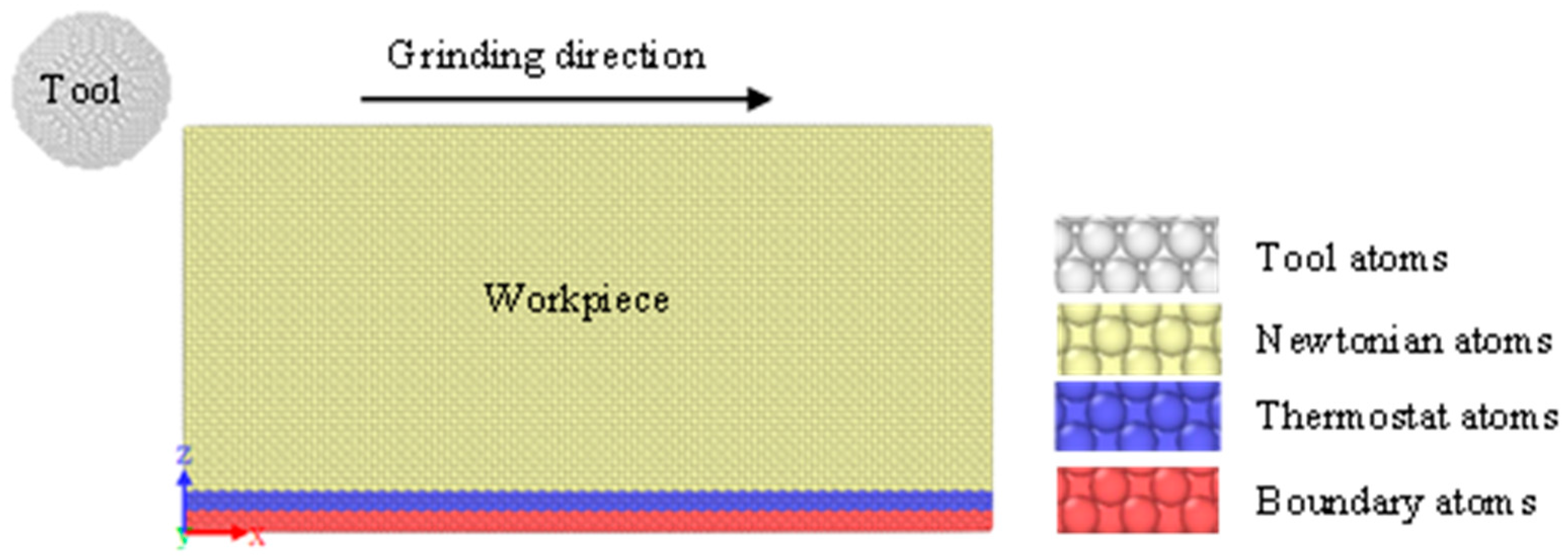
| Configuration | MD Simulation Conditions | |
|---|---|---|
| Potential used | Ni-Ni:EAM [25], Ni-C:Morse [26] | |
| Grinding grain dimension, r/nm | 2 | |
| Workpiece dimension | 21.2 nm × 21.2 nm × 10.6 nm | |
| Numbers of atoms in various crystal orientation workpieces | Crystal set-up | No. of atoms |
| (110)[001] | 437,155 | |
| (111)[10] | 440,530 | |
| (001)[100] | 446,551 | |
| Grinding speed, v/m/s | 200/300/400 | |
| Depth of grind, H/nm | 0.5/1/2 | |
| Time step, t/fs | 1 | |
| Initial temperature, T/K | 293 | |
| Level | Factor | |||
|---|---|---|---|---|
| Grinding Speed, v/m/s A | Depth of Grind, H/nm B | Crystal Orientation C | Blank Column D | |
| 1 | 200 | 0.5 | (001)[100] | |
| 2 | 300 | 1.0 | (110)[001] | |
| 3 | 400 | 2.0 | (111)[10] | |
| Test Group | Grinding Speed, v/(m/s) A | Grinding Depth, H/nm B | Crystal Orientation C | Blank Column D | Deformation Depth, S/Å |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 9.58040 |
| 2 | 1 | 2 | 2 | 2 | 9.14992 |
| 3 | 1 | 3 | 3 | 3 | 8.66310 |
| 4 | 2 | 1 | 2 | 3 | 6.15190 |
| 5 | 2 | 2 | 3 | 1 | 5.43415 |
| 6 | 2 | 3 | 1 | 2 | 13.76130 |
| 7 | 3 | 1 | 3 | 2 | 7.40060 |
| 8 | 3 | 2 | 1 | 3 | 13.39560 |
| 9 | 3 | 3 | 2 | 1 | 10.51295 |
| average value 1 | 9.131 | 7.711 | 12.246 | 8.509 | |
| average value 2 | 8.449 | 9.327 | 8.605 | 10.104 | |
| average value 3 | 10.436 | 10.979 | 7.166 | 9.404 | |
| range | 1.987 | 3.268 | 5.080 | 1.595 |
| Factor | Deviation Sum of Squares | Degrees of Freedom | F Ratio | F Critical Value | Salience |
|---|---|---|---|---|---|
| Grinding speed | 6.118 | 2 | 1.596 | 9.000 | |
| Grinding depth | 16.022 | 2 | 4.179 | 9.000 | |
| Crystal orientation | 41.131 | 2 | 10.728 | 9.000 | * |
| Deviation | 3.83 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Lv, M. Monocrystalline Nickel Nanogrinding Subsurface Deformation-Layer Depth Study Based on Orthogonal Tests. Coatings 2023, 13, 410. https://doi.org/10.3390/coatings13020410
Ren J, Lv M. Monocrystalline Nickel Nanogrinding Subsurface Deformation-Layer Depth Study Based on Orthogonal Tests. Coatings. 2023; 13(2):410. https://doi.org/10.3390/coatings13020410
Chicago/Turabian StyleRen, Jie, and Ming Lv. 2023. "Monocrystalline Nickel Nanogrinding Subsurface Deformation-Layer Depth Study Based on Orthogonal Tests" Coatings 13, no. 2: 410. https://doi.org/10.3390/coatings13020410
APA StyleRen, J., & Lv, M. (2023). Monocrystalline Nickel Nanogrinding Subsurface Deformation-Layer Depth Study Based on Orthogonal Tests. Coatings, 13(2), 410. https://doi.org/10.3390/coatings13020410






