Mathematical Model for Early-Aged UHPFRC Compressive Strength Changes

Abstract

Compressive strength is the most important mechanical index of ultra-high performance fiber-reinforced concrete (UHPFRC). The rule of changes in compressive strength in early-aged UHPFRC is of great significance to guide concrete curing, formwork removal, and prestress stretching. Therefore, it is very necessary to study an accurate mathematical model to describe the change in compressive strength of UHPFRC at an early age. For this purpose, a new mathematical model of compressive strength age is proposed in this work for predicting the long-term strength of UHPFRC according to a few test data from early-aged UHPFRC. This new model can overcome the shortcomings of the existing models, such as the exponential model, logarithmic model, and polynomial model. The proposed model is first demonstrated by using four groups of compressive strength test data compiled from previous research studies. Subsequently, an experiment of early-aged UHPFRC compressive strength was carried out to further verify the proposed mathematical model. The mixed proportion used in the UHPFRC compressive strength test was 10.87:0.82:1 (powder:steel fiber:water), and the design strength grade was 120 MPa. Based on the UHPFRC experimental data, it was shown that the average fitting error and standard deviation of the new model were about 10%~20% of that of the logarithmic model and the polynomial model. The proposed model can precisely predict the compressive strength of UHPFRC, with a determination coefficient (R²) of 0.9974. The research results show that the average fitting error and standard deviation of this new model were significantly reduced when compared to the existing models, and the predicted compressive strength by the new model on the 60th day is the closest to the actual design strength grade of concrete. The greatest advantage of the proposed method lies in its simple formula, fast implementation, and no need for complex mathematical operations. It has been shown that the proposed model is superior to the existing models due to its higher fitting accuracy and prediction accuracy, and it can be better used to predict the later strength of UHPFRC by using only a few compressive strength test data taken at the early age stage.

1. Introduction

Concrete is widely used in bridge structure, beam, slab, column, and pile foundation engineering in building construction [1,2,3,4]. In recent years, ultra-high performance fiber reinforced concrete (UHPFRC) has become an important development direction of cement-based composites due to its ultra-high strength and excellent durability. Compressive strength is the most important mechanical parameter of UHPFRC. Yang et al. [5] found that the compressive and bending strength of the UHPFRC samples cured at 20 °C decreased by about 20% and 10% compared with the samples cured at 90 °C. Kwon et al. [6] found that the proper volume fraction of the longer fiber is essential in improving the various mechanical properties of UHPFRC, including compressive strength, strain capacity, and energy absorption capacity. Yu et al. [7] discussed the influence of UHPFRC mix design on compressive strength. They used the improved Andreasen & Andersen particle filling model to carry out the mix design to achieve the goal of a dense cement matrix. These studies revealed that curing temperature, mix ratio, and steel fiber content have an important influence on the development of the compressive strength of early-aged UHPFRC. In other words, these factors complicate the development law of UHPFRC compressive strength at an early age. The rule of changes in UHPFRC early compressive strength is of great significance to guide concrete curing, formwork removal, prestress tensioning, and later curing. In view of this, many studies have been carried out on the development law and estimation method of concrete compressive strength in the last few decades. These studies can be broadly divided into two types. The first type is the estimation methods based on multiple factors, such as the curing temperature, water-cement ratio, steel fiber content, curing time, etc. Yeh [8] studied the possibility of artificial neural network (ANN) predictions of compressive strength in high-performance concrete. It was found that the strength model based on the ANN was more accurate than the model based on regression analysis. Bui et al. [9] developed an expert system based on an ANN model and an improved firefly algorithm, which could better predict the property of high-performance concrete. Han et al. [10] studied the prediction of the compressive strength of high-performance concrete based on machine learning. By selecting the appropriate variables based on the importance of random forest measurements, the accuracy and efficiency of the proposed model prediction can be improved. Anyaoha et al. [11] adopted a new integrated computing technology-boosting smooth transition regression tree (BooST) to predict the compressive strength of high-performance concrete. The research results show that BooST is superior to other methods in prediction accuracy, with the smallest error, and is more in line with the laboratory experimental results. Hameed et al. [12] studied the ability of ANNs combined with principal component analysis (PCA) and cross-validation (CV) technology to predict the compressive strength of high-performance concrete. When compared with other models published in previous studies, the performance of the proposed model achieved the expected advantages and more stable prediction. Emad et al. [13] developed four soft computing technologies to predict the compressive strength of UHPFRC, including linear relationships, pure quadratics, M5P trees, and ANNs. The research results show that the ANN model had high prediction accuracy for the compressive strength of UHPFRC. Based on the optimized ANN model, a closed equation is proposed to quickly estimate the compressive strength of concrete. Ali et al. [14] used six models: linear regression (LR), multiple linear regression (MLR), nonlinear regression (NLR), pure quadratic (PQ), interaction (IA), and full quadratic (FQ) to predict the compressive strength of modified concrete with different nano-silica contents in different mix proportions. The research results showed that the most effective and accurate model was the FQ model. Ibrahim et al. [15] studied four models, including LR, NLR, PQ, and FQ, to evaluate the impact of recycled coarse aggregate on the long-term compressive strength of concrete under different mix proportions and different compressive strength ranges. Mohammed et al. [16] tested the effect of three water-reducing agent additives on the workability and compressive strength of concrete during the curing period of 1 to 28 days. A nonlinear M5P mathematical model is established to predict the compressive strength of concrete and to study the influence of the mix ratio on the compressive strength of concrete. Moradi et al. [17] developed a robust and time-saving method based on machine learning (ML) to predict the compressive strength of concrete with binary supplementary cementitious materials (SCMs) at different ages. It was found that the ML-based model could accurately predict the compressive strength of concrete containing any SCM at any age. Rezvan et al. [18] studied the benefits of using polyethylene terephthalate (PET) fibers as reinforcement elements in concrete by the ML method. The results showed that the content of PET fiber in concrete has a significant impact on the concrete compressive strength. Imran et al. [19] developed a new hybrid model for predicting the compressive strength of UHPFRC by using a cascaded forward neural network (CFNN) and artificial bee colony (ABC) optimization. It was found that the optimal neural network structure selected by the ABC method consists of two layers, and the developed model (CFNN-ABC) can accurately predict the compressive strength of UHPFRC. Other similar studies [20,21,22,23,24,25,26] reported the successful application of a BP neural network, probabilistic neural network, and a depth neural network in the early age strength prediction of high-strength concrete. In general, most of the first types of methods are ANN-based prediction methods. Its advantage is that it can consider the impact of various factors on compressive strength, and its limitation is that it requires a large number of test data to train the neural network.

The second type of method is to predict the later strength of concrete according to a function curve between concrete strength and age. Based on the test data from an early age, the concrete compressive strength age function equation can be obtained by data fitting, and then the concrete strength at any time can be calculated. The advantage of this kind of method is that only a few test data are needed to predict the concrete strength at any time, but the disadvantage is that only the change rule of strength with time is considered. At present, the commonly used concrete compressive strength–age curve models are the exponential model [27,28,29,30], logarithmic model [31,32], and polynomial model [33,34,35,36]. Yang et al. [27] tested the compressive strength of high-strength concrete cylinder blocks on days 1, 3, 5, 7, 10, 14, and 28. They fitted the data using the exponential model and obtained the empirical formula to predict the strength of high-strength concrete. Zhao et al. [28] examined the compressive strength of C50 concrete at different ages and generated the curve of compressive strength with age using an exponential model. Yang et al. [29] established a diachronic variation model of axial compressive strength of C60 concrete in the early aging period using the regression fitting method and combining the exponential model. Wang et al. [30] analyzed the development law of compressive strength of high-strength concrete with age. Zhao [31] discussed the development law of high-strength concrete aging strength and obtained the corresponding logarithmic fitting formula. Li et al. [32] examined the compressive strength of the C60 concrete cube on days 3, 7, 14, 28, and 60 and fitted the data using a logarithmic model to predict the later strength of concrete. Li [33] and Jin [34] developed the diachronic variation models of early-aged concrete axial-compressive strength by using a polynomial and the regression fitting method. Ling [35] analyzed the influence of concrete composition on compressive strength and established a prediction model for the compressive strength of mechanical sand concrete using a third-order nonlinear function. Jia et al. [36] examined the compressive strength of ordinary Portland concrete from the first to the 28th day and fitted the data using the cubic polynomial model to obtain the concrete compressive strength–time curve model. In general, these existing curve models may be inconsistent with the strength growth law of concrete in some aspects. For example, the strength of concrete slowly increases and tends to stabilize after 28 days of pouring. However, the polynomial model cannot conform to this rule, and the exponential model and logarithmic model cannot indicate this feature well. In addition, the strength of high-strength concrete increases rapidly in the ultra-early stage (i.e., before 7 days after pouring), which will lead to the poor fitting accuracy of the exponential model and logarithmic model at the ultra-early stage. Therefore, it is still necessary to study a new mathematical curve model to overcome the defects of the existing curve models so as to more accurately describe the change rule of UHPFRC compressive strength.

The work of this paper also belongs to the second type of method. The research significance of this work is to develop a new mathematical curve model that can accurately predict the compressive strength of UHPFRC at any time based on only a few early-age test data. For this purpose, the advantages and disadvantages of the three existing curve models are discussed first, and then a new model that can overcome the shortcomings of the existing model is proposed in Section 2. The implementation effects of the new model and the old models are compared to illustrate the feasibility and superiority of the new model by using four groups of compressive strength test data compiled from previous research studies in Section 3. Moreover, a UHPFRC early compressive strength test was carried out to further verify the proposed mathematical model in Section 4. The research results show that the average fitting error and standard deviation of the proposed model are significantly smaller than those of the existing models, and the concrete compressive strength predicted by the proposed model on the 60th day is also the closest to the design strength grade of concrete. The proposed model provides a simple and feasible way to predict the UHPFRC compressive strength with only a few early-age test data in engineering practice.

2. Compressive Strength-Time Mathematical Models

As stated before, the method of concrete strength evaluation based on a certain assumed mathematical curve is a simple and easy way in engineering practice because it only requires a few early-age test data of compressive strength. The main steps of this type of method are shown in Figure 1.

It is clear that the proper mathematical curve model is the key to determining whether such methods can be implemented successfully. This section first reviews several of the existing mathematical models of changes in concrete compressive strength with time, discusses the advantages and disadvantages of these models, and then proposes a new compressive strength–time mathematical model. Assuming that $t$ represents the age (time) after concrete pouring and $s(t)$ represents the compressive strength of concrete corresponding to the moment, $t$, the exponential model of the compressive strength-time is expressed as:

$$s(t)=x_0\cdot e^{-x_1/t}$$

(1)

In Equation (1), $x_0$ and $x_1$ denote two non-negative fitting parameters that should be obtained by curve fitting based on the strength test data of concrete at an early age. Equation (1) indicates that the advantage of the exponential model is that the function is an increasing function. $s(t)$ increases with an increase in $t$, which conforms to the law that the strength of concrete increases with its age in engineering practice. Moreover, when $t\to \infty$, $s(t)\to x_0$, which is also consistent with the law that the strength of concrete remains almost stable after 28 days. The disadvantage of the exponential model is that its definition domain lacks the point $t$ = 0. In practice, the concrete strength is 0 when $t$ = 0. It is noteworthy that the exponential model cannot contain this situation. Furthermore, the equation contains only two fitting parameters, so the accuracy of the fitting is low for data with greater dispersion.

The logarithmic model of diachronic change in compressive strength is written as:

$$s(t)=x_0+x_1\cdot \ln (t)$$

(2)

In Equation (2), $x_0$ and $x_1$ represent two fitted parameters that are obtained based on partial test data combined with curve fitting. The comparison between Equations (1) and (2) suggests that the logarithmic model can be regarded as a form of change obtained by taking logarithms on both sides of the exponential model equation. Accordingly, the advantages and disadvantages of the logarithmic model are similar to the exponential model. To be specific, a detailed advantage is that the function is an increasing function, which conforms to the law that the strength of concrete increases with its age in engineering practice. The disadvantage is that its definition domain also lacks the point of $t$ = 0, and when $t\to \infty$, the growth rate slows down but does not converge, which is not consistent with the actual growth law of concrete strength. The equation comprises only two fitted parameters, and the fitting accuracy is also low for data with greater dispersion.

Compressive strength–age polynomial model generally refers to the quadratic power function model and cubic power function model, which are expressed as follows:

$$s(t)=x_0+x_{1}t+x_2{t}^2$$

(3)

$$s(t)=x_0+x_{1}t+x_2{t}^2+x_3{t}^3$$

(4)

Equation (3) is a quadratic polynomial model, Equation (4) is a cubic polynomial model, and $x_0$, $x_1$, $x_2$, and x₃ are the fitting parameters. The advantage of the polynomial model is that the definition domain contains the point $t$ = 0, and the obtained function after fitting is an increasing function, which is more consistent with the actual strength growth law of high-strength concrete within 28 days. The equation contains three or four fitted parameters, so the fitting accuracy is higher than an exponential or logarithmic model with only two parameters. The disadvantage of the polynomial model is that when $t\to \infty$, $s(t)$ will increase rapidly, which is not consistent with the law that the strength of concrete at the later stage remains nearly unchanged in practice, so it cannot be used to predict the later strength of concrete.

In summary, it is very necessary to propose a novel mathematical model for the change of compressive strength with time to better describe the growth law of concrete compressive strength in practice. This study refers to the mathematical form of the polynomial model, maintains its advantages and overcomes its disadvantages, and proposes the following new compressive strength-time curve model:

$$s(t)=x_0+x_1\cdot (\frac{1}{t+1})+x_2\cdot {(\frac{1}{t+1})}^2$$

(5)

where $x_0$, $x_1$, and $x_2$ represent the three fitting parameters. Obviously, the novel model Equation (5) can be considered an improved form of Equation (3), and its independent variable $t$ is modified as $\frac{1}{t+1}$. The novel model shows the following advantages. (1) The definition domain contains the point $t$ = 0, and $s(t)$ = 0 can be determined when $t$ = 0 through parameter fitting, thus overcoming the disadvantage of the lack of definition domains for the exponential model and logarithmic model. (2) When $t\to \infty$, $s(t)\to x_0$, consistent with the law that the concrete strength at the later stage remains almost unchanged in practice, thus overcoming the limitation that the polynomial model does not converge when $t\to \infty$. As a result, the novel model can be adopted to predict the later strength of concrete. (3) The equation comprises three fitting parameters, and the fitting accuracy is high. The cubic term can be added to further improve the fitting accuracy if necessary, which will not be repeated here.

Next, the calculation method of the fitted parameters in the above mathematical model is expressed. The corresponding linear equations should first be established based on the compressive strength data of different ages obtained through the test to calculate the fitting parameters. With the proposed model Equation (5) as an example, the corresponding system of linear equations is written as follows:

$$y=C·x$$

(6)

$$y=\left\{\begin{array}{c}s(t_1)\\ ⋮\\ s(t_n)\end{array}\right\}$$

(7)

$$x=\left\{\begin{array}{c}{x}_0\\ x_1\\ x_2\end{array}\right\}$$

(8)

$$C=\left[\begin{array}{ccc}1& \frac{1}{t_1+1}& {(\frac{1}{t_1+1})}^2\\ ⋮& ⋮& ⋮\\ 1& \frac{1}{t_n+1}& {(\frac{1}{t_n+1})}^2\end{array}\right]$$

(9)

where $s(t_n)$ represents the compressive strength value of concrete obtained by $t_n$ time test. Obviously, the vector $y$ and the coefficient matrix $C$ are known quantities, and $x$ is the unknown fitted parameter vector. In general, the coefficient matrix of Equation (6) is a rectangular matrix with a greater number of rows than columns, i.e., the number of examined data (known quantities) is greater than the number of fitted parameters (unknowns). Equation (6) can generally be solved using the least squares method, for which both sides of Equation (6) are simultaneously multiplied by the transposed matrix $C^T$ of matrix $C$ yields:

$$C^{T}y=(C^{T}C)\cdot x$$

(10)

From Equation (10), the solution of $x$ is expressed as:

$$\widehat{x}={(C^{T}C)}^{-1}{C}^{T}y$$

(11)

The calculated $\widehat{x}$ refers to the least squares estimate of $x$.

The specific curve equation of the fitted prediction model can be obtained based on the calculated fitting parameters, and the superiority of the model can be examined in accordance with the difference between the model prediction value and the experimental test value. Therefore, the difference between the model prediction and the experimental test value is calculated as follows:

$$\left\{\delta \right\}=\left|C\cdot \widehat{x}-y\right|$$

(12)

where $\left\{\delta \right\}={({\delta }_1,\cdots ,{\delta }_n)}^T$ is called the residual vector. To be specific, ${\delta }_i$ is the residuals between the ith experimental data and the predicted value. Further calculation of the mean $\overline{\delta }$ and standard deviation $\sigma$ of the residual vector is as follows:

$$\overline{\delta }=\frac{{\delta }_1+\cdots +{\delta }_n}{n}$$

(13)

$$\sigma =\sqrt{\frac{{\displaystyle \sum _{i=1}^n{({\delta }_i-\overline{\delta })}^2}}{n}}$$

(14)

The mean $\overline{\delta }$ and standard deviation $\sigma$ of the residual vector are called the fitting mean error (absolute error) and standard deviation of error, respectively. The smaller $\overline{\delta }$ and $\sigma$, the higher the fitting accuracy of the model and the more reliable the model will be.

To check the model’s predictability, the coefficient of determination (R²) is calculated along with root mean square error (RMSE). These performance indexes are calculated to measure how close are the predicted values from the experimental ones. This helps in better evaluation of the model capabilities for compressive strength prediction. The equations for R² and RMSE are given by:

$$R^2=1-\frac{{\displaystyle \sum _{i=1}^n{(y_e-y_p)}^2}}{{\displaystyle \sum _{i=1}^n{(y_e-{\overline{y}}_e)}^2}}$$

(15)

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(y_e-y_p)}^2}}$$

(16)

where, $y_e$ = experimental value, ${\overline{y}}_e$ = mean of experimental values, $y_p$ = predicted value, and n = total number of observations.

3. Model Verification and Comparison by the Test Data Compiled from Previous Literature

Four sets of experimental data (called examples 1 to 4) from literature [28,29,36,37] are used to validate the new model, and the results are compared with the existing logarithmic model and cubic polynomial model fitting results to illustrate the advantages of the proposed model.

In example 1 (the literature [28]), the concrete cube test blocks with a side length of 150 mm were designed and fabricated according to the C50 strength grade, and the compressive strengths on days 1, 2, 3, 5, 7, 11, 14, 28, and 40 were examined under standard curing conditions, respectively, as shown in Figure 2 (expressed by symbol “o”). These data are fitted using the logarithmic model, the cubic polynomial model, and the model proposed, and the obtained fitting curves are also presented in Figure 2. The specific fitting equations for these models are expressed as follows:

$$s(t)=27.2818+8.9263\cdot \ln (t)$$

(17)

$$s(t)=26.0318+3.6070t-0.1449t^2+0.0019t^3$$

(18)

$$s(t)=58.4528-95.1937\cdot (\frac{1}{t+1})+53.3113\cdot {(\frac{1}{t+1})}^2$$

(19)

Table 1. The mean fitting errors, standard deviations, and the predicted 60th-day compressive strengths by the three models based on experimental data in example 1.

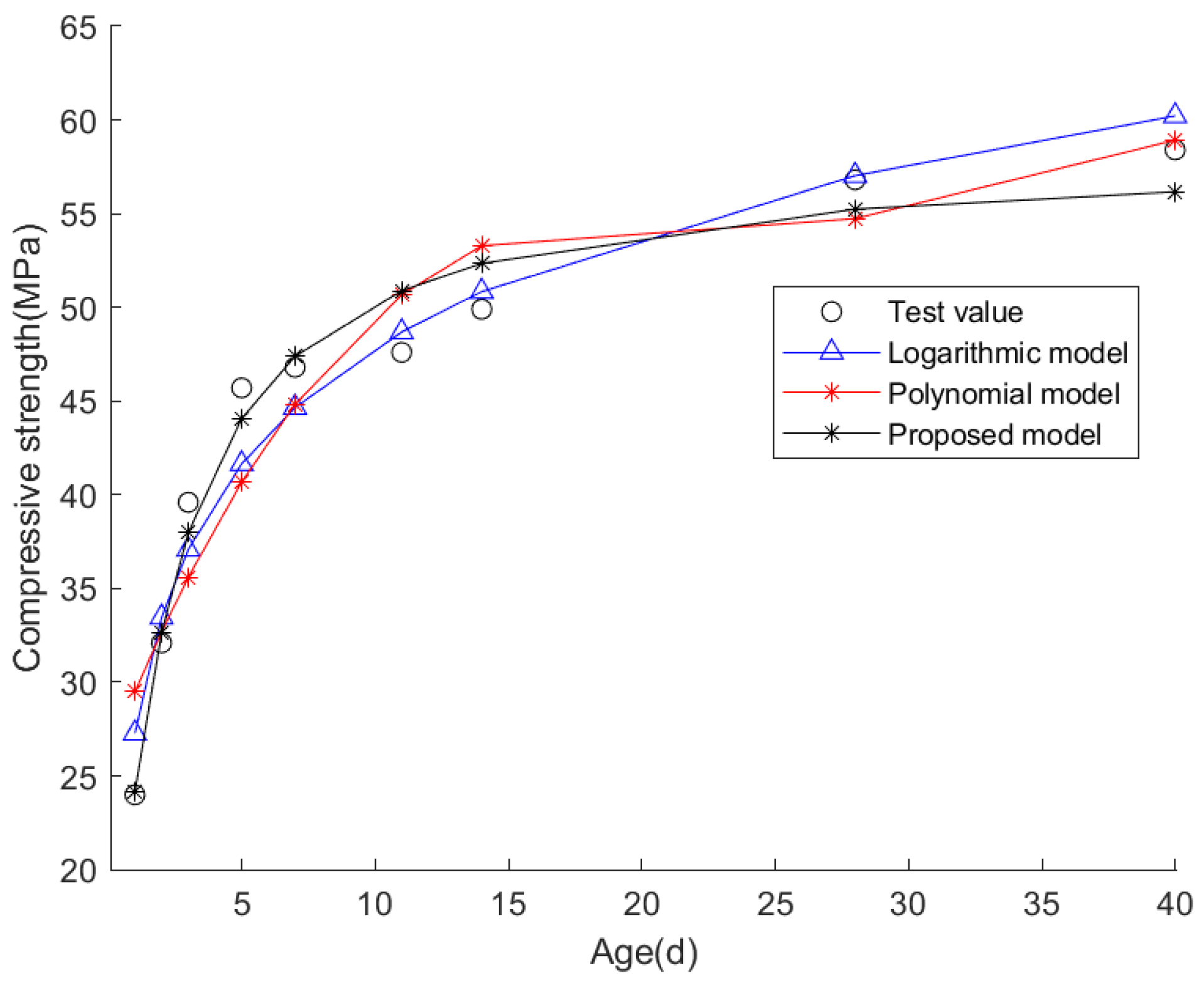
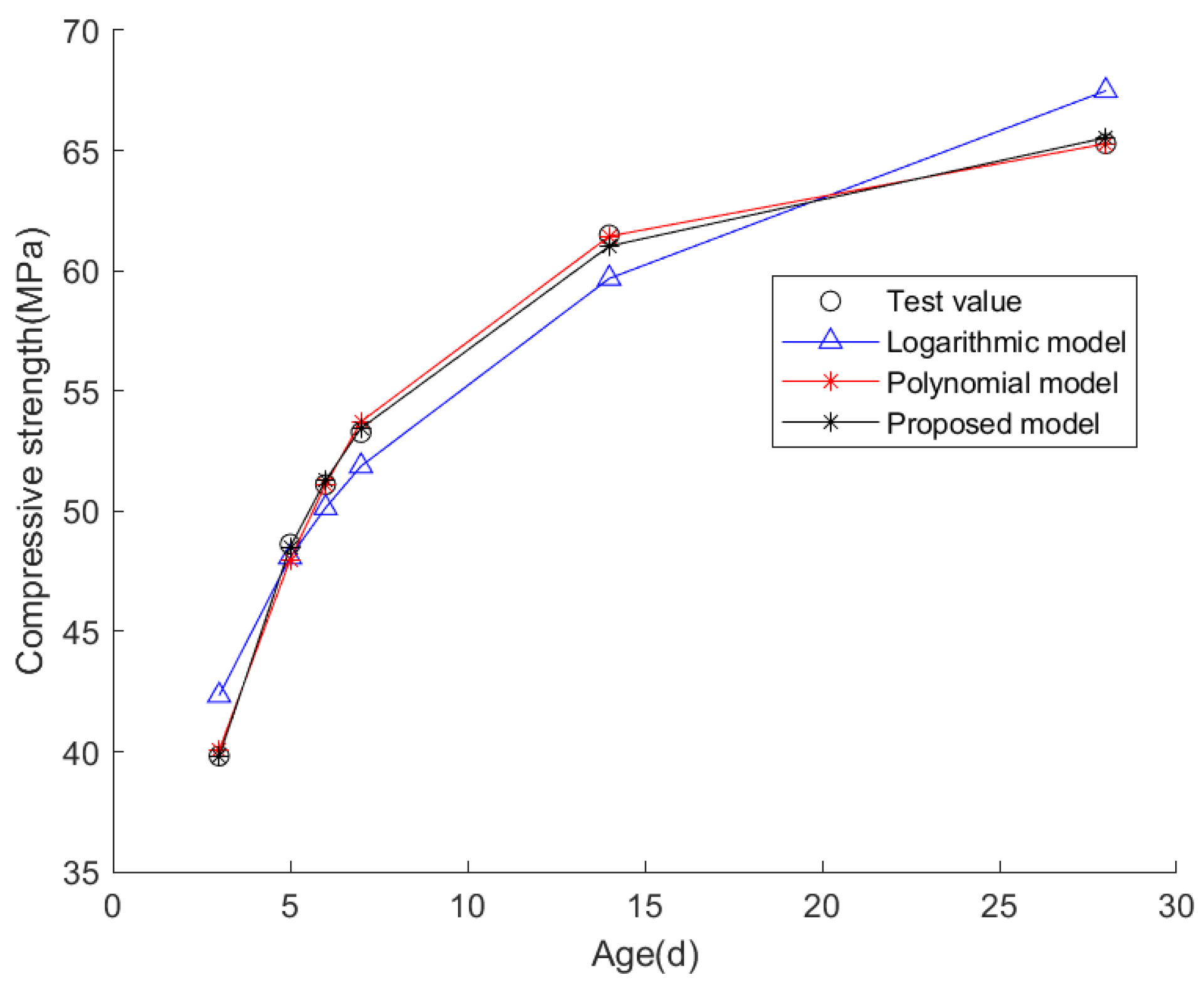
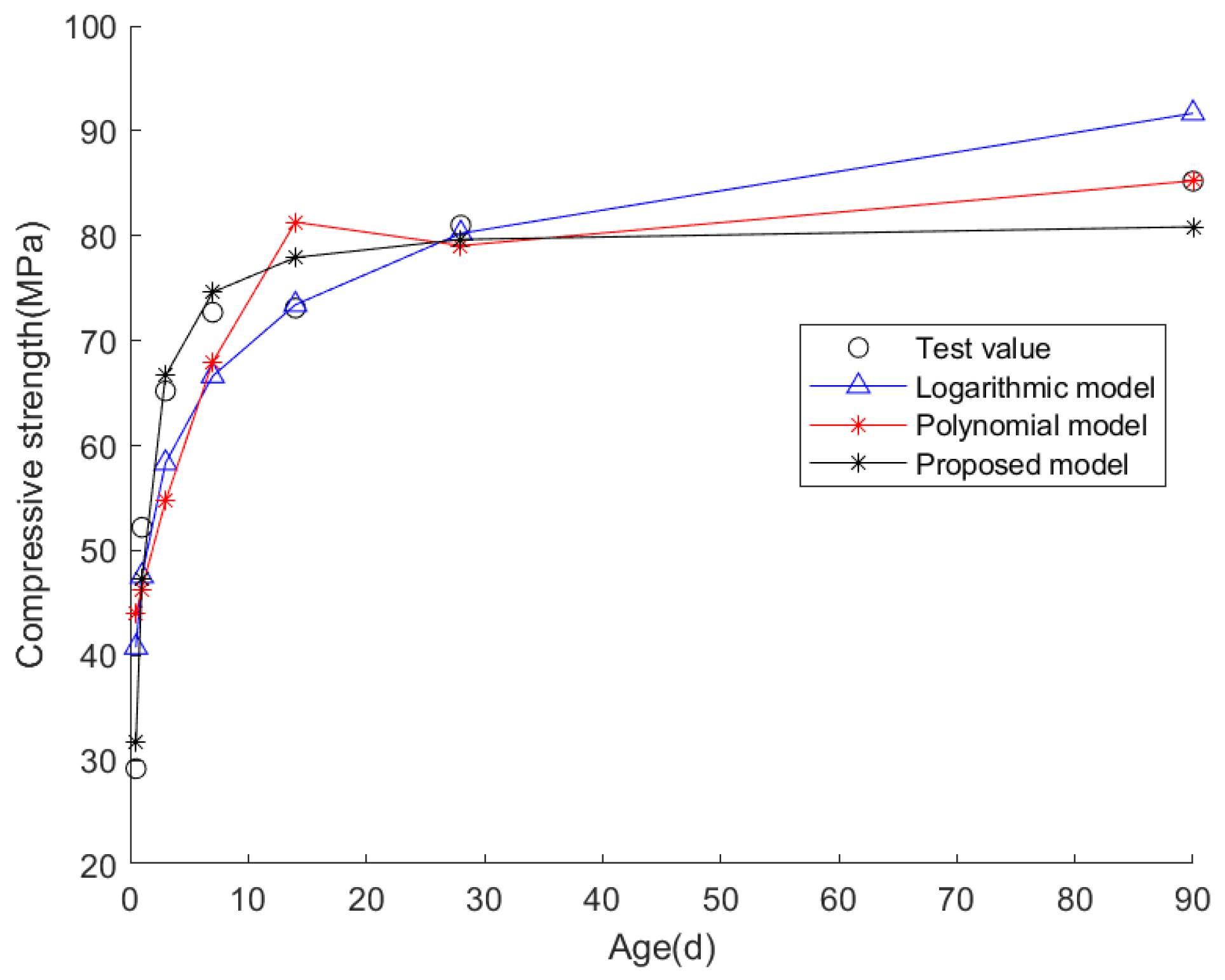
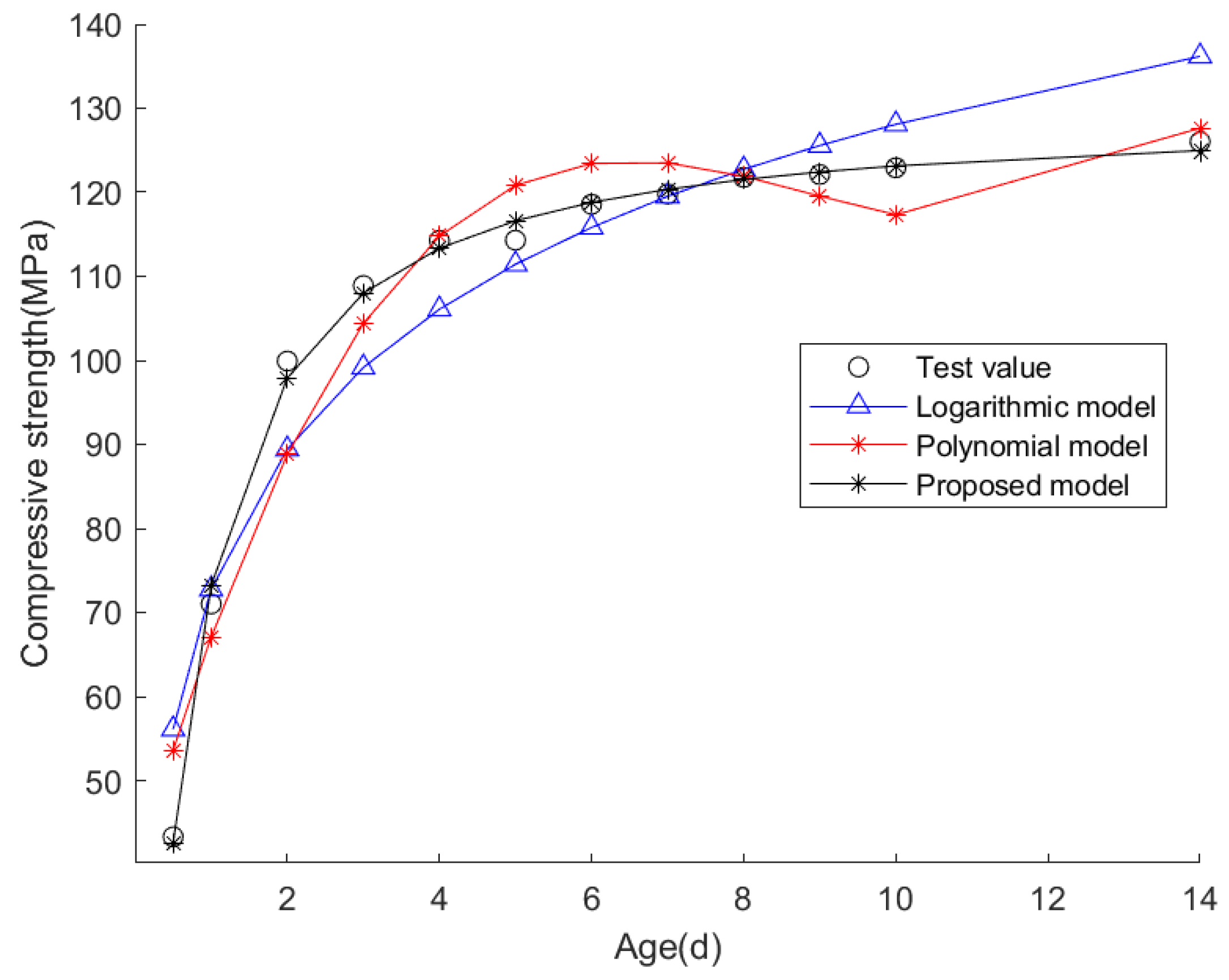
Index	Logarithmic Model	Polynomial Model	Proposed Model
Mean fitting error $\overline{\delta }$	0.1907	0.2950	0.1133
Fitted standard deviation of error $\sigma$	0.0410	0.0670	0.0194
R2	0.9541	0.8976	0.9694
RMSE	2.2453	3.3528	1.8317
Predicted day 60 compressive strength	63.83 MPa	127.39 MPa	56.91 MPa

lists the mean fitting error, standard deviation of error, R², RMSE, and the compressive strength value on day 60 predicted by these models.

It can be concluded from Table 1 that the average fitting error of the novel model is about 59% of the logarithmic model and about 38% of the polynomial model. The fitting standard deviation of the novel model is nearly 47% of the logarithmic model and about 29% of the polynomial model. The mean fitting error and mean standard deviation of the new model are significantly smaller than the logarithmic model and the cubic polynomial model. For the strength values predicted by the three models on the 60th day, only the 56.91 MPa predicted by the novel model is closest to the C50 intensity grade. It has been shown that the novel model is more accurate and reliable than the logarithmic model and the polynomial model.

In example 2 (the literature [29]), 150 mm × 150 mm × 300 mm concrete prismatic test blocks were designed and fabricated according to the C60 strength grade, and the compressive strengths on days 3, 5, 6, 7, 14, and 28 were examined, respectively, as illustrated in Figure 3 (represented by the symbol “o”). These data were fitted using the logarithmic model, the cubic polynomial model, and the model proposed, and the obtained fitting curves are presented in Figure 3. The specific fitting equations are as follows:

$$s(t)=29.9666+11.2588\cdot \ln (t)$$

(20)

$$s(t)=23.3841+6.6224t-0.3747t^2+0.0068t^3$$

(21)

$$s(t)=70.6181-151.4078\cdot (\frac{1}{t+1})+112.5353\cdot {(\frac{1}{t+1})}^2$$

(22)

The mean fitting error, standard deviations of error, R², and RMSE are shown in

Table 2. The mean fitting errors, standard deviations, and the predicted 60th-day compressive strengths by the three models based on experimental data in example 2.

Index	Logarithmic Model	Polynomial Model	Proposed Model
Mean fitting error $\overline{\delta }$	0.0847	0.0170	0.0101
Fitted standard deviation of error $\sigma$	0.0179	0.0054	0.0023
R2	0.9579	0.9984	0.9991
RMSE	1.7148	0.339	0.2442
Predicted day 60 compressive strength	76.06 MPa	550.14 MPa	68.17 MPa

. The compressive strength values on day 60 predicted by these models are also listed in Table 2.

It can be concluded from Table 2 that the average fitting error of the novel model is about 12% of the logarithmic model and about 59% of the polynomial model. The fitting standard deviation of the novel model is about 13% of the logarithmic model and about 43% of the polynomial model. The mean fitting error and mean standard deviation of the proposed model are significantly smaller than the logarithmic model and the cubic polynomial model. For the strength values predicted by the three models on the 60th day, only the 68.17 MPa predicted by the novel model is the closest to the C60 intensity grade. This shows that the novel model is more accurate and reliable than the logarithmic model and the polynomial model.

In example 3 (the literature [36]), 50 mm × 50 mm × 150 mm Portland concrete cuboid test blocks were designed, produced, and cured under standard curing conditions, and the compressive strength was examined for 1–28 days, as shown in Figure 4 (expressed by the symbol “o”). Based on the above experimental data, the fitting curves are also presented in Figure 4. The specific fitting equations are written as follows:

$$s(t)=10.2190+21.3746\cdot \ln (t)$$

(23)

$$s(t)=2.6400+10.8638t-0.5936t^2+0.0111t^3$$

(24)

$$s(t)=85.9810-273.5529\cdot (\frac{1}{t+1})+229.0393\cdot {(\frac{1}{t+1})}^2$$

(25)

The mean fitting error, standard deviation of error, R², RMSE, and the predicted compressive strength on day 60 are shown in

Table 3. The mean fitting errors, standard deviations, and the predicted 60th-day compressive strengths by the three models based on experimental data in example 3.

Index	Logarithmic Model	Polynomial Model	Proposed Model
Mean fitting error $\overline{\delta }$	1.4240	2.0567	0.6167
Fitted standard deviation of error δ	0.2581	0.3783	0.0988
R2	0.9672	0.9639	0.9623
RMSE	3.2636	3.4255	3.4973
Predicted day 60 compressive strength	97.73 MPa	917.90 MPa	81.56 MPa

.

From Table 3, it can be concluded that the average fitting error of the novel model is about 43% of the logarithmic model and about 30% of the polynomial model. The fitting standard deviation of the novel model is about 38% of the logarithmic model and about 26% of the polynomial model. For the strength values predicted by the three models on the 60th day, only the 81.56 MPa predicted by the novel model is closest to the C80 strength grade. These results show that the novel model is more accurate and reliable than the logarithmic model and the polynomial model.

In example 4 (the literature [37]), the 150 mm × 150 mm × 150 mm high-strength concrete cube test blocks were designed and fabricated according to the C80 strength grade, and the compressive strengths of days 0.5, 1, 3, 7, 14, 28, and 90 are examined respectively, as shown in Figure 5 (represented by the symbol “o”). The fitting curves obtained by the three models are also shown in Figure 5. The specific fitting equations are given as follows:

$$s(t)=47.5587+9.8023\cdot \ln (t)$$

(26)

$$s(t)=41.6676+4.8059t-0.1582t^2+0.0012t^3$$

(27)

$$s(t)=83.3955-49.5567\cdot (\frac{1}{t+1})-37.5315\cdot {(\frac{1}{t+1})}^2$$

(28)

Note that the coefficients in Equations (26)–(28) are obtained by fitting the test data, so different fitting coefficients will be obtained for the concrete test blocks with different components and water-cement ratios.

Table 4. The mean fitting errors, standard deviations, and the predicted 60th-day compressive strengths by the three models based on experimental data in example 4.

Index	Logarithmic Model	Polynomial Model	Proposed Model
Mean fitting error $\overline{\delta }$	0.4344	0.5604	0.1571
Fitted standard deviation of error $\sigma$	0.1325	0.1712	0.0314
R2	0.8738	0.7948	0.9639
RMSE	6.3454	8.0907	3.3948
Predicted day 60 compressive strength	87.69 MPa	24.89 MPa	80.57 MPa

lists the mean fitting error, standard deviation of error, R², RMSE, and the predicted compressive strength on day 60.

Similar conclusions can be drawn from Table 4 that the mean fitting error and standard deviation of the proposed model are significantly smaller than the logarithmic model and the cubic polynomial model. For the strength values predicted by the three models on the 60th day, only the 80.57 MPa predicted by the novel model is the closest to the C80 strength grade. This means that the proposed model is more reasonable and reliable than the logarithmic model and the polynomial model.

4. UHPFRC Experimental Validation

In this section, the compressive strength test of UHPFRC at a very early age is analyzed to further investigate the applicability of the proposed model. In the experiment, 36 UHPFRC cube blocks with a side length of 100 mm were designed and manufactured according to the strength level of 120 MPa. As shown in Figure 6, the main materials used in the UHPFRC include powder, steel fiber, and water. The mix proportion and basic physical parameters of the UHPFRC are listed in

Table 5. Mix proportion and basic physical parameters of UHPFRC.

Mix Proportion			Density	Initial Setting Time	Final Setting Time
Powder 2130 kg/m3	Steel fiber 160 kg/m3	Water 196 kg/m3	2488 kg/m3	$\ge$240 min	$\le$900 min

. The powder is composed of cement, silica fume, silica sand, and superplasticizer. The diameter of the steel fiber used was 0.2 mm, the length of the fibers includes 16 mm and 12 mm, and the ratio of the long fiber-to-short fiber was 1:2. Note that the main purpose of this study is to verify the applicability of the proposed curve model to the prediction of concrete compressive strength, so only one mix design was used in this experiment. More relevant experiments are needed in the future to further verify the applicability of the proposed model for predicting the early compressive strength of UHPFRC under different mix proportions and curing temperatures.

Under the standard curing conditions, the compressive strength of the test block from half a day to the 14th day was tested. The curing temperature and relative humidity were about (20 ± 2) °C and 95%, respectively. The compression strength experiment was carried out by the STYE-3000E automatic pressure tester. The loading speed was 0.6 N/mm² per second. The test process was in accordance with GB/T50081-2002 Test Methods for Mechanical Properties of Ordinary Concrete [38]. The measured compressive strengths of these cubes at different times are listed in

Table 6. The measured compressive strengths of the UHPFRC cubes (MPa).

Age (Unit: Day)	Cube 1	Cube 2	Cube 3	Mean Value
0.5	44.596	41.413	43.899	43.303
1	65.842	71.954	75.241	71.012
2	101.524	100.801	97.419	99.915
3	106.935	110.032	109.759	108.909
4	120.471	109.423	112.927	114.274
5	122.200	116.100	104.400	114.300
6	125.919	107.592	122.186	118.566
7	120.030	123.060	116.28	119.790
8	121.192	122.166	121.963	121.774
9	124.069	116.635	125.644	122.116
10	117.506	122.822	128.429	122.919
14	121.747	136.977	119.324	126.016

.

As mentioned in the previous section, based on the experimental data, the logarithmic model, the polynomial model, and the model proposed were used to fit the data, and the resulting fitting curves are shown in Figure 7. The specific fitting equations for each model are as follows:

$$s(t)=72.7723+24.0246\cdot \ln (t)$$

(29)

$$s(t)=38.3404+25.5434t-3.9534t^2+0.1489t^3$$

(30)

$$s(t)=129.3477-58.5280\cdot (\frac{1}{t+1})-107.3955\cdot {(\frac{1}{t+1})}^2$$

(31)

Note that the coefficients in Equations (29)–(31) were obtained by fitting the test data, so different fitting coefficients will be obtained for those concrete test blocks with different components and water-cement ratios. The mean fitting error, standard deviation of error, R², RMSE, and predicted compressive strength of UHPFRC on the 60th day by the three models are shown in

Table 7. The mean fitting errors, standard deviations, and the predicted 60th-day compressive strengths by the three models based on UHPFRC experimental data.

Index	Logarithmic Model	Polynomial Model	Proposed Model
Mean fitting error $\overline{\delta }$	0.3503	0.2877	0.0480
Fitted standard deviation of error $\sigma$	0.0797	0.0649	0.0095
R2	0.9130	0.9437	0.9974
RMSE	7.0595	5.6791	1.2304
Predicted day 60 compressive strength	171.13 MPa	1192 MPa	128.36 MPa

.

It can be concluded from Table 7 that the average fitting error of the new model is about 13.7% of the logarithmic model and about 16.7% of the polynomial model. The fitted standard deviation of the new model is about 11.9% of the logarithmic model and about 14.6% of the polynomial model. Obviously, the mean fitting error and mean standard deviation of the proposed new model are much smaller than the logarithmic model and the cubic polynomial model. The proposed model has the largest R² and the smallest RMSE. For the compressive strength values predicted by the three models on the 60th day, only the 128.36 MPa predicted by the new model is closest to the design intensity grade of 120 MPa. It has been shown that the new model is more accurate and reliable than the logarithmic model and the polynomial model.

5. Conclusions

In this paper, a new compressive strength–age curve model is proposed, which can accurately predict the later strength of concrete with only a few early-age test data. The proposed model was validated first by using four sets of compressive strength test data collected from previous studies. Subsequently, UHPFRC early compressive strength tests were carried out to further verify the proposed mathematical model. According to the comparative analysis of the calculation results, the following main conclusions can be drawn:

(1)

The existing compression strength–time curve models are not ideal in terms of fitting accuracy or prediction accuracy. The proposed new model can well describe the characteristics of compressive strength increases with time at the early age stage. From the comparison results, it was found that the new model is more accurate and reliable than the logarithmic model and the polynomial model;

(2)

From the UHPFRC experiment, it can be seen that the compressive strength of UHPFRC increases very rapidly at the ultra-early age stage, and the compressive strength was very close to that of the strength design grade on about the 7th day. After the 7th day, the compressive strength of UHPFRC increases slowly and gradually maintains a stable value;

(3)

Based on the UHPFRC experimental data, it has been shown that the average fitting error and standard deviation of the new model are about 10%~20% of the logarithmic model and the polynomial model. The proposed model has the largest R² of 0.9974 and the smallest RMSE of 1.2304. The 60-day compressive strength predicted by the proposed model (i.e., 128.36 MPa) is closest to the strength design grade of UHPFRC (i.e., 120 MPa).

It should be pointed out that the curing temperature, mix ratio, and steel fiber content have an important impact on the compressive strength of UHPFRC at an early age. More relevant experiments need to be carried out in the future to further verify the growth law of UHPFRC compressive strength at an early age with different components and water-cement ratios. The proposed method is a quick method to predict the compressive strength of concrete, which can be implemented using only a few early-age test data. The greatest advantage of the proposed method lies in its simple formula, fast implementation, and no need for complex mathematical operations. However, the proposed method can not consider the influence of other factors (except for age) on compressive strength, which is possible using the surrogate model or ML-based method. In the following research, a comparative study between the proposed model and the surrogate model or ML-based algorithm can be carried out to better apply it to the strength prediction of UHPFRC in engineering practice.