Linear and Nonlinear Optical Properties of PVA:SA Blend Reinforced by TiO2 Nanoparticles Prepared by Flower Extract of Aloe Vera for Optoelectronic Applications
Abstract
:1. Introduction
2. Experimental Technique
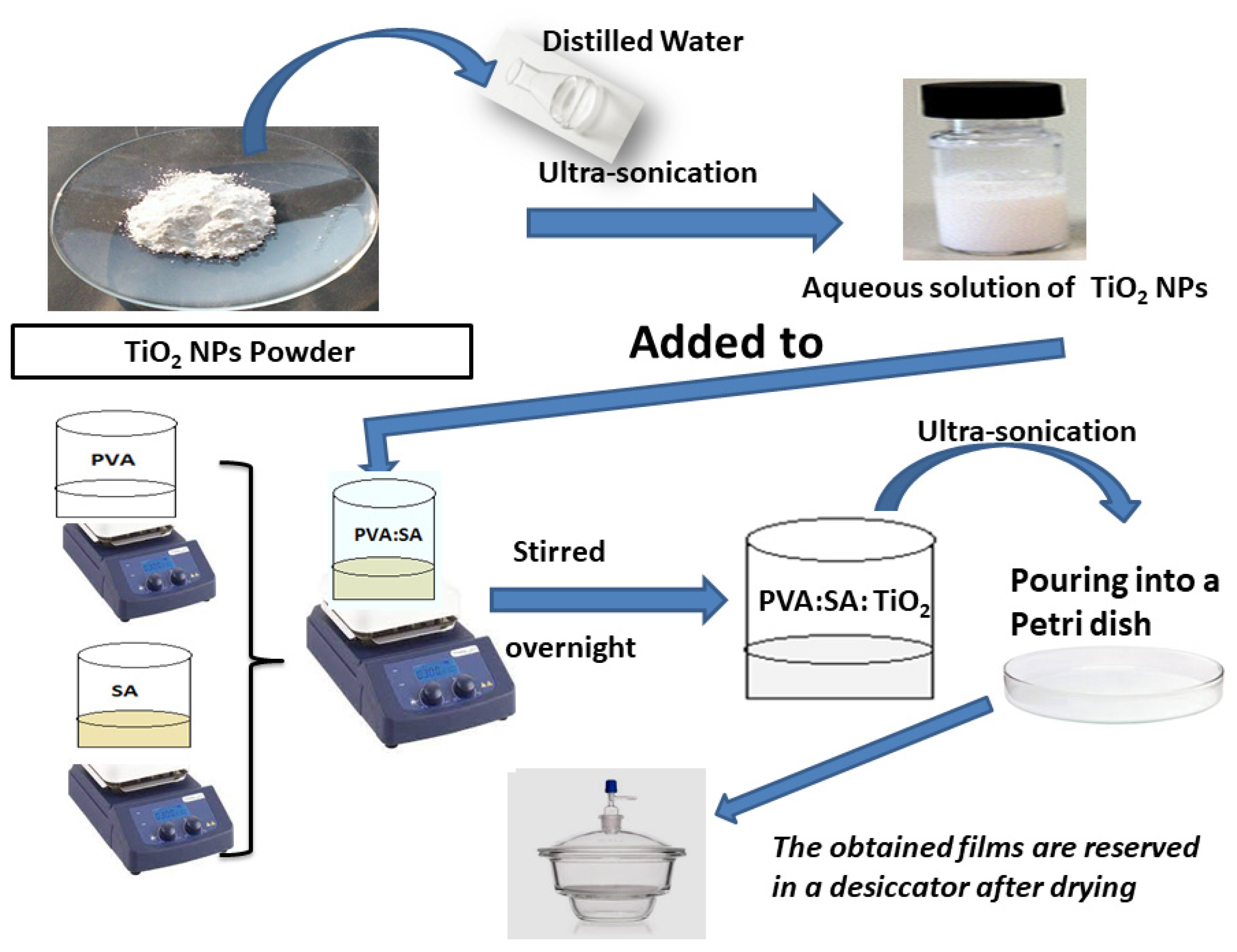
2.1. Materials and Preparation of the Samples
2.2. Absorption Measurements
2.3. X-ray Measurements
2.4. SEM and EDX Measurements
2.5. Z-Scan Analysis
3. Result and Discussion
3.1. SEM and EDX Analysis
3.2. XRD Analysis
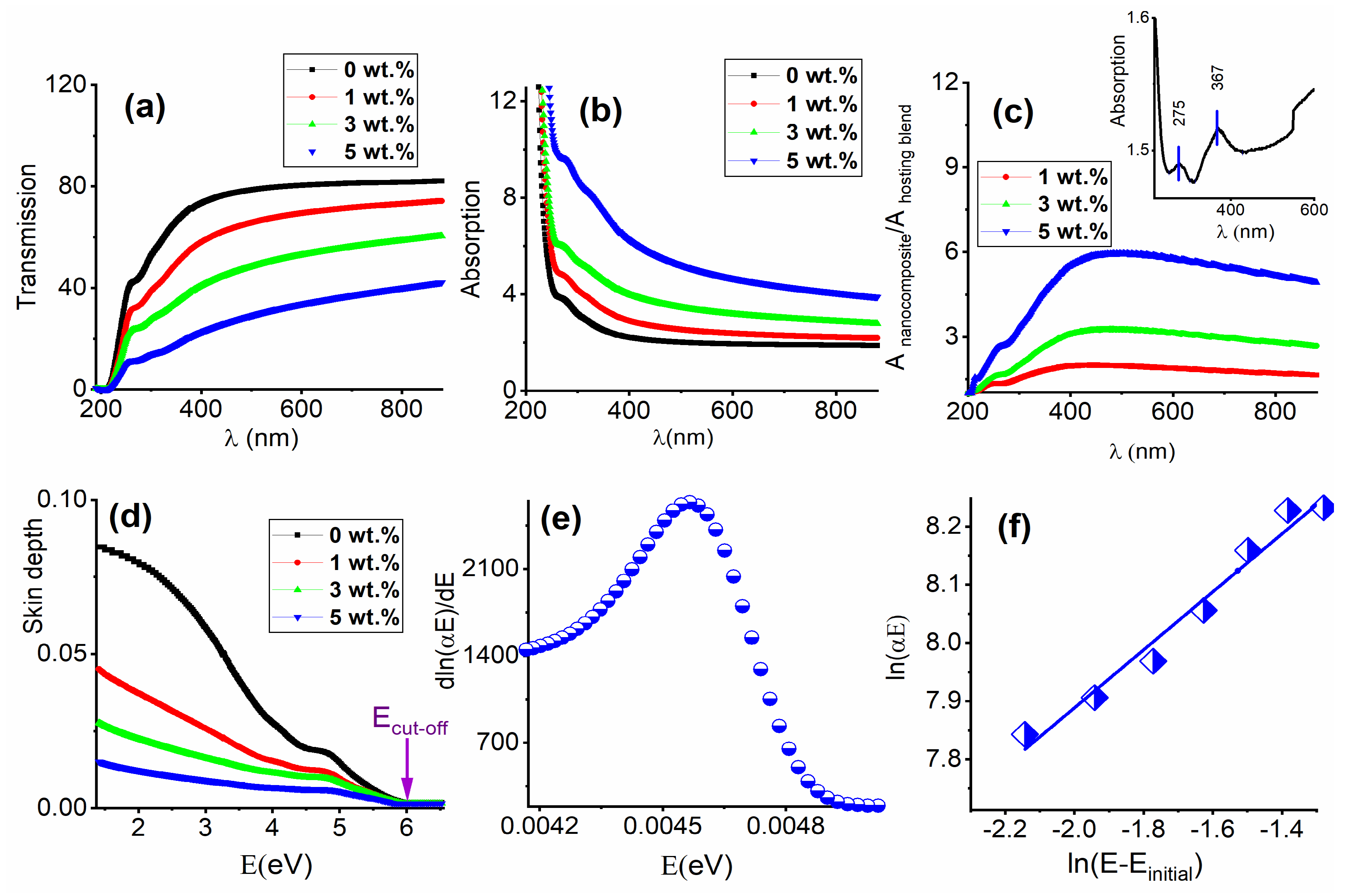
3.3. Optical Parameters Deduced from UV-Vis Spectroscopy
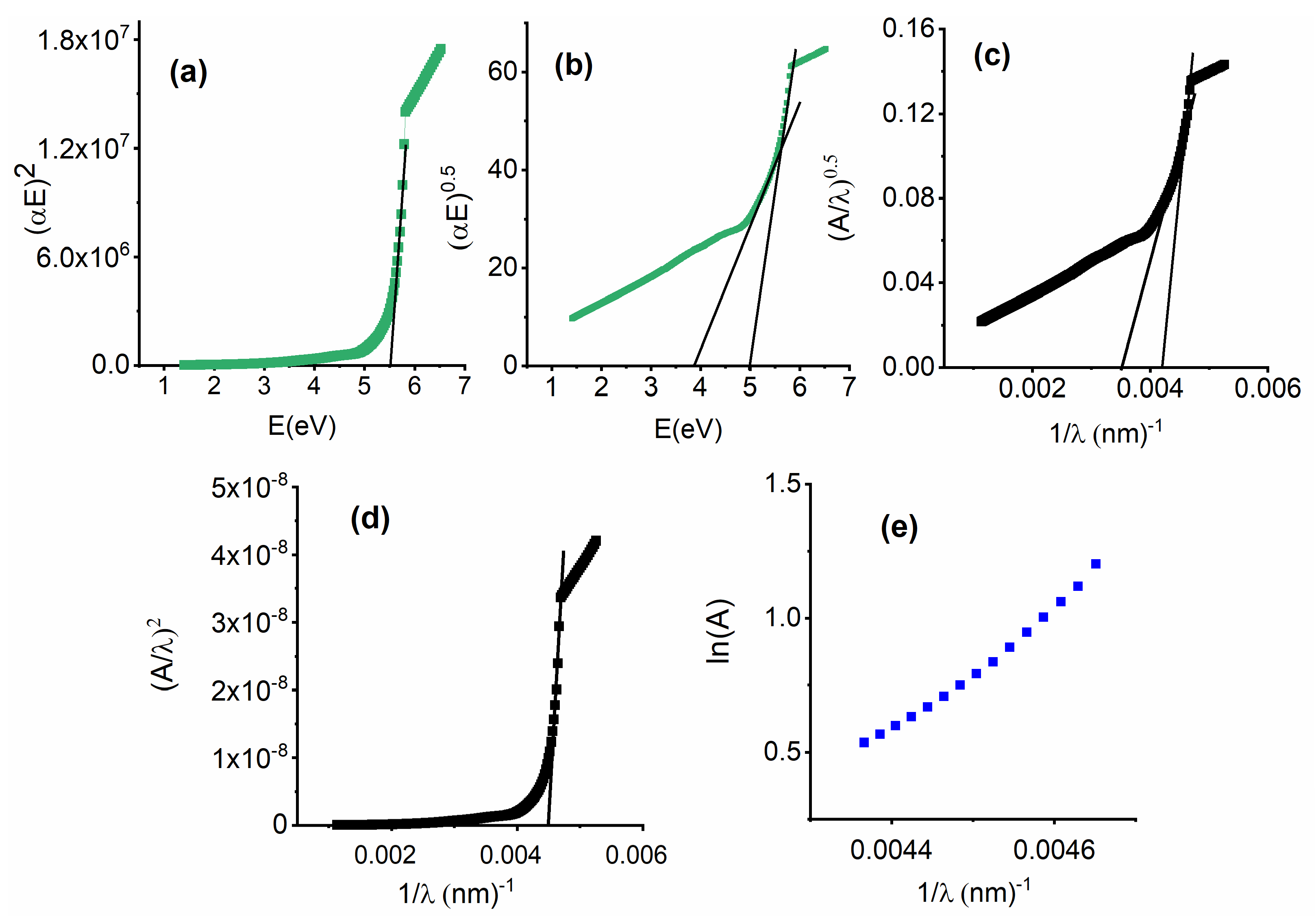
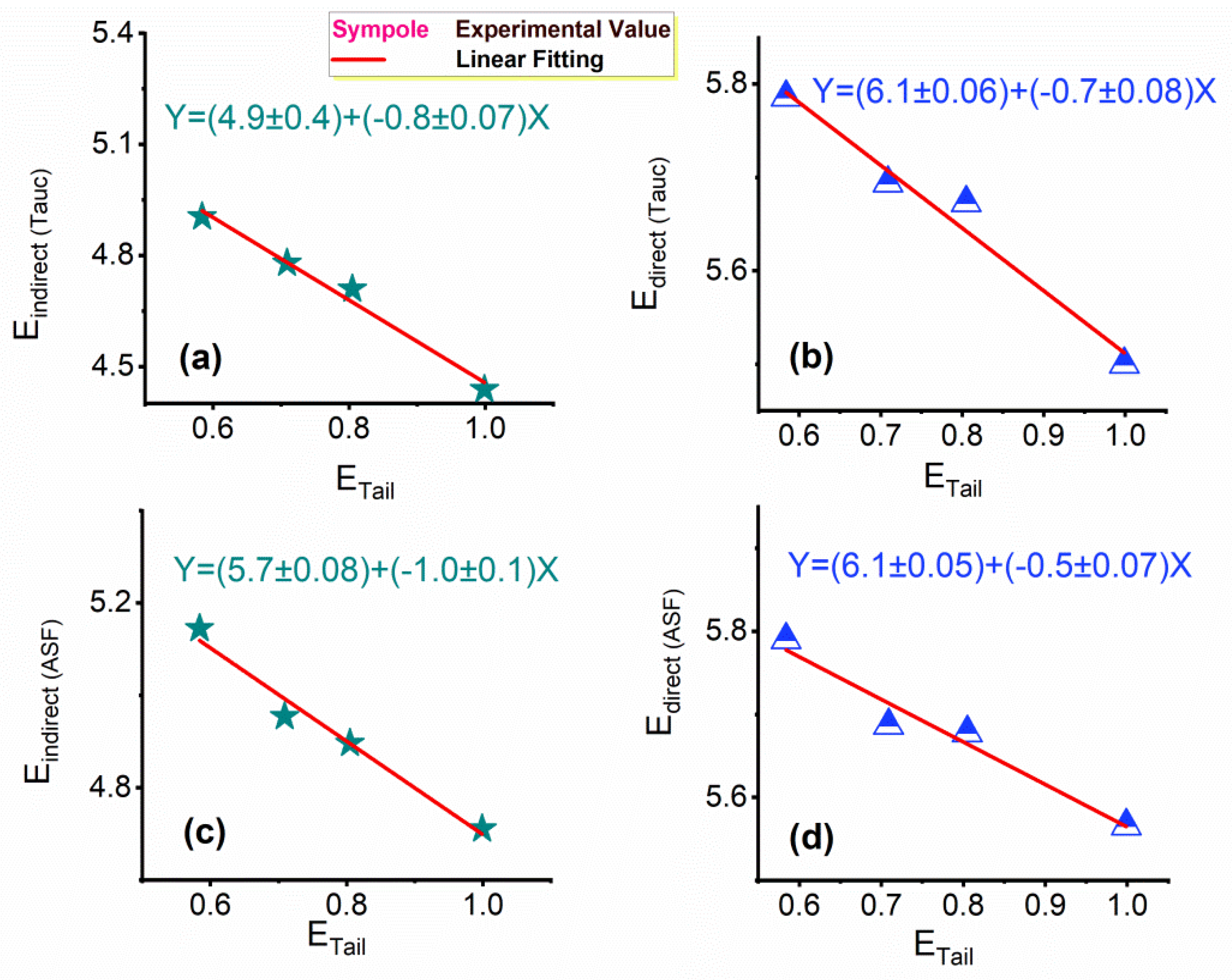
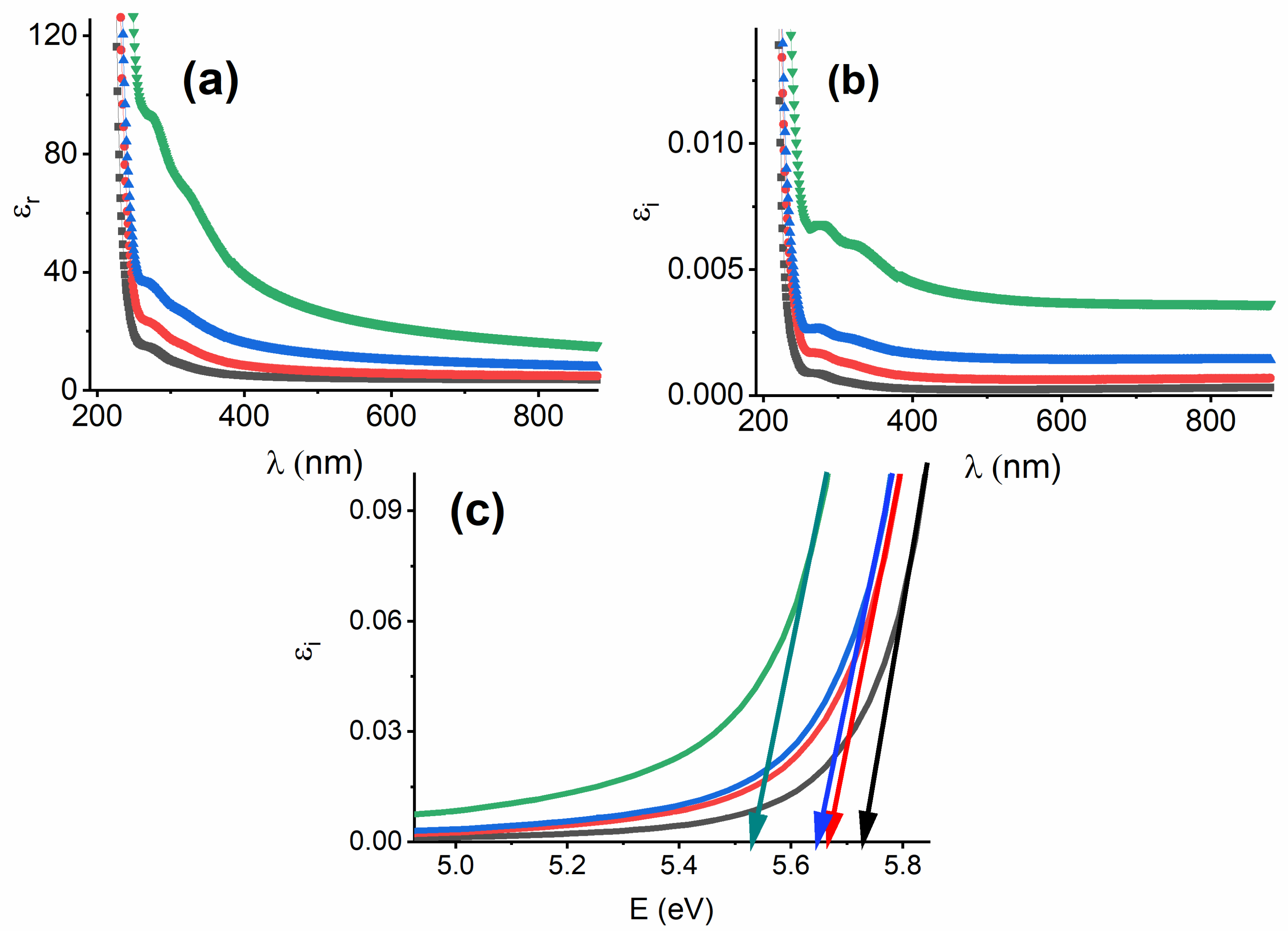
3.3.1. Interband Transitions, Urbach Energy, and the Steepness Parameter (S)
| Current Work | Previously Published Works | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Content of TiO2 (wt.%) Doped in PVA:SA 3:1 | PVA Ref [59] | SA Ref [18] | TiO2 Ref [61] | 0, 1.5, and 2.5 wt.% of TiO2 Doped in PVA Ref [60] | SA/PEO Ref [17] 30/70 wt.% | ||||
| Optical Parameter | 0 | 1 | 3 | 5 | |||||
| Einitial (eV) | 5.78 | 5.76 | 5.74 | 5.57 | |||||
| m | 0.45 ± 0.042 | 0.47 ± 0.039 | 0.45 ± 0.037 | 0.49 ± 0.037 | |||||
(eV) | 5.790 | 5.687 | 5.678 | 5.566 | |||||
(eV) | 5.145 | 4.955 | 4.897 | 4.711 | |||||
(eV) | 5.786 | 5.694 | 5.673 | 5.500 | 6.35 | 5.44 | |||
(eV) | 4.905 | 4.780 | 4.710 | 4.439 | 5.26 | 5.26 | 2.90 | 4.8, 4.2 & 3.8 | 5.05 |
| Eg estimated from plotting (εi) vs. E (eV) | 5.728 | 5.667 | 5.647 | 5.529 | |||||
(eV) | 0.584 ± 0.03 | 0.709 ± 0.028 | 0.805 ± 0.03 | 0.999 ± 0.029 | 0.23 | 0.2, 0.4 & 0.8 | |||
| S | 0.044 | 0.036 | 0.032 | 0.026 | |||||
| Ee-ph | 14.94 | 18.14 | 20.59 | 25.64 | |||||
| SMPF (%) | 27.0 | 41.8 | 58.3 | 76.4 | |||||
| SSPF (%) | 41.1 | 56.6 | 69.4 | 84.6 | |||||
3.3.2. Solar Protection Factors
Solar Material Protection Factor (SMPF)
Solar Skin Protection Factor (SSPF)
3.3.3. Refractive Index, Attenuation Coefficient, and Optical Dielectric Constants
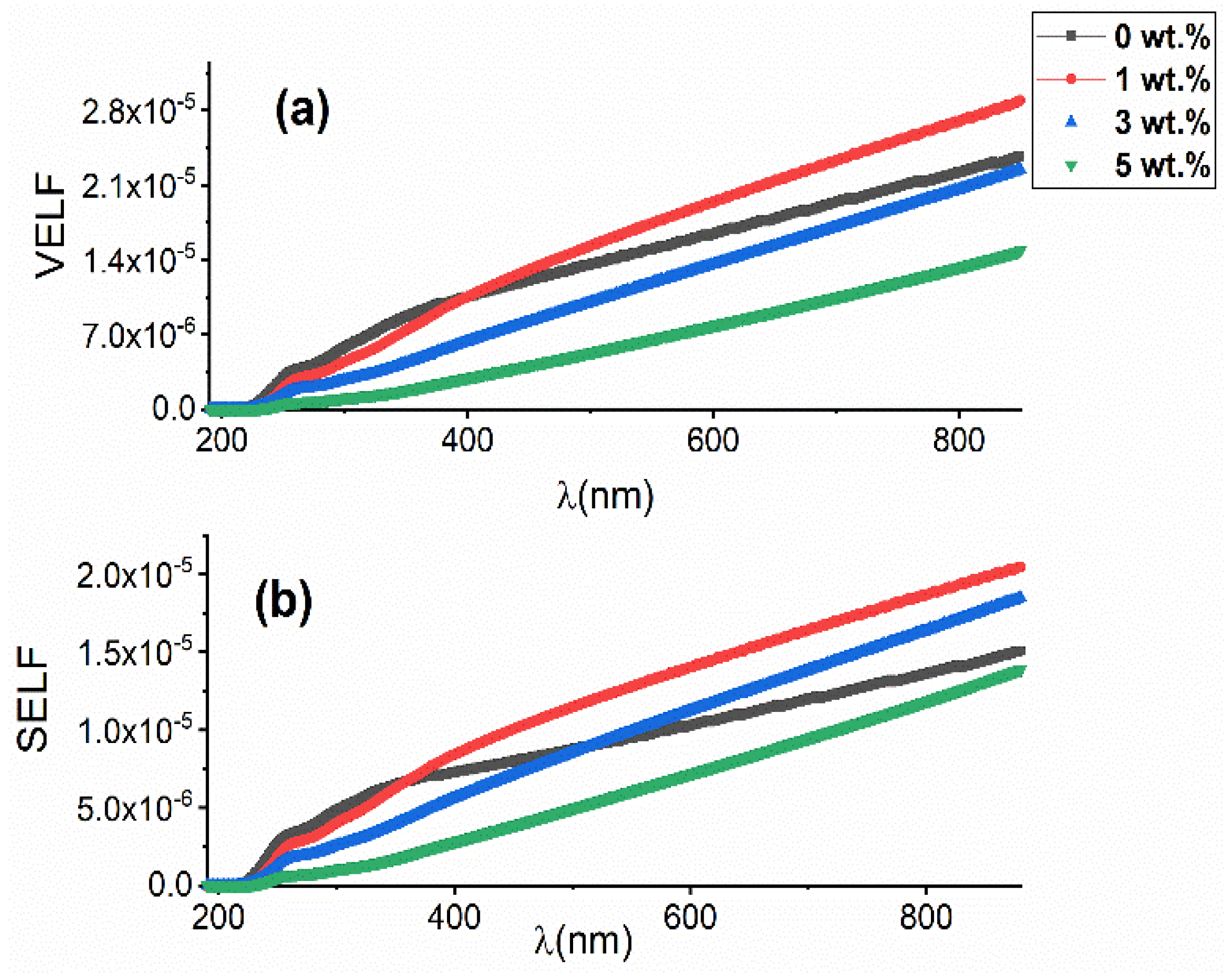
3.3.4. Volume and Surface Energy Loss Functions
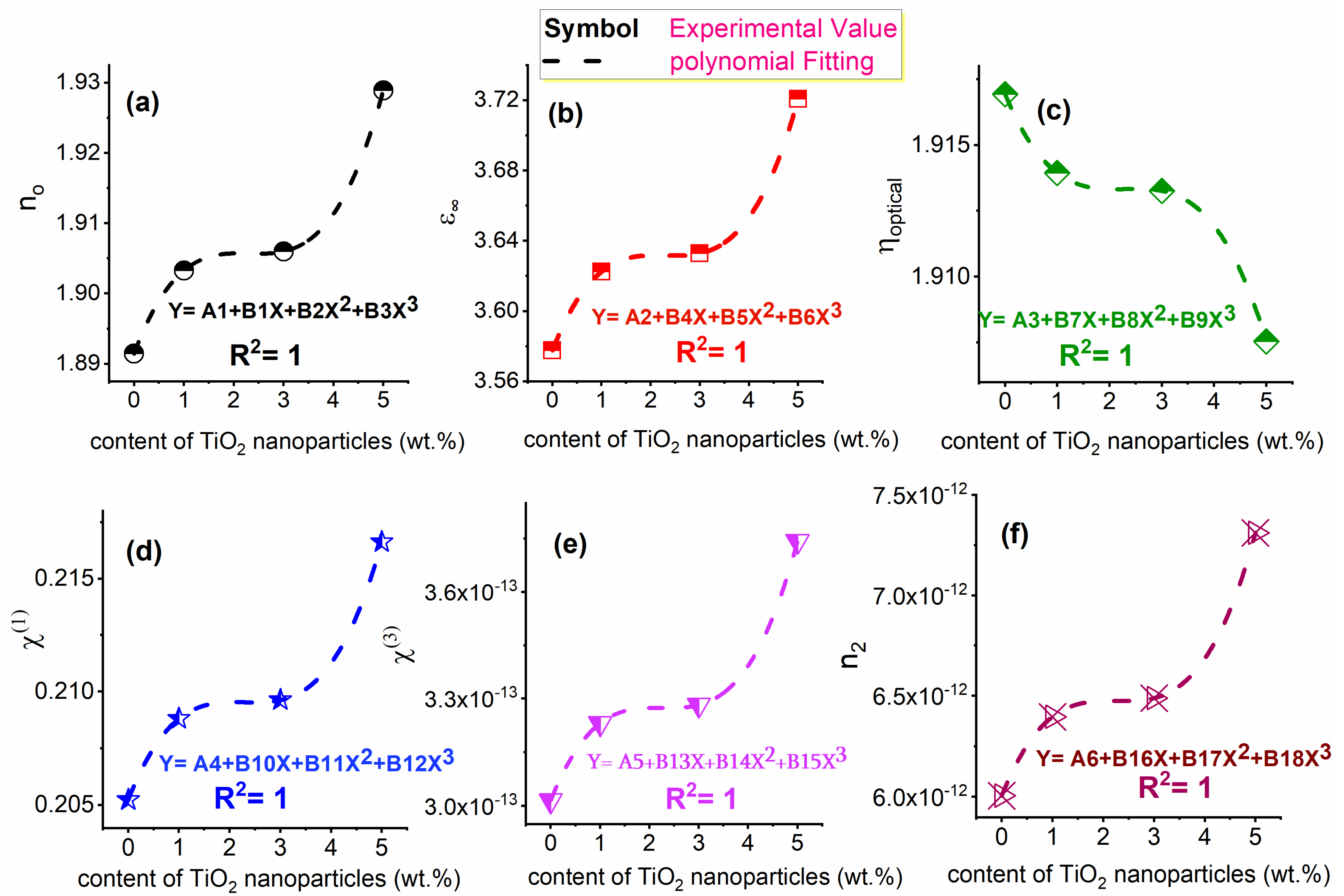
3.3.5. Linear STATIC Refractive Index (no), High-Frequency Dielectric Constant (ε∞), and Optical Electronegativity (ηopt)
3.3.6. Nonlinear Optical Parameters
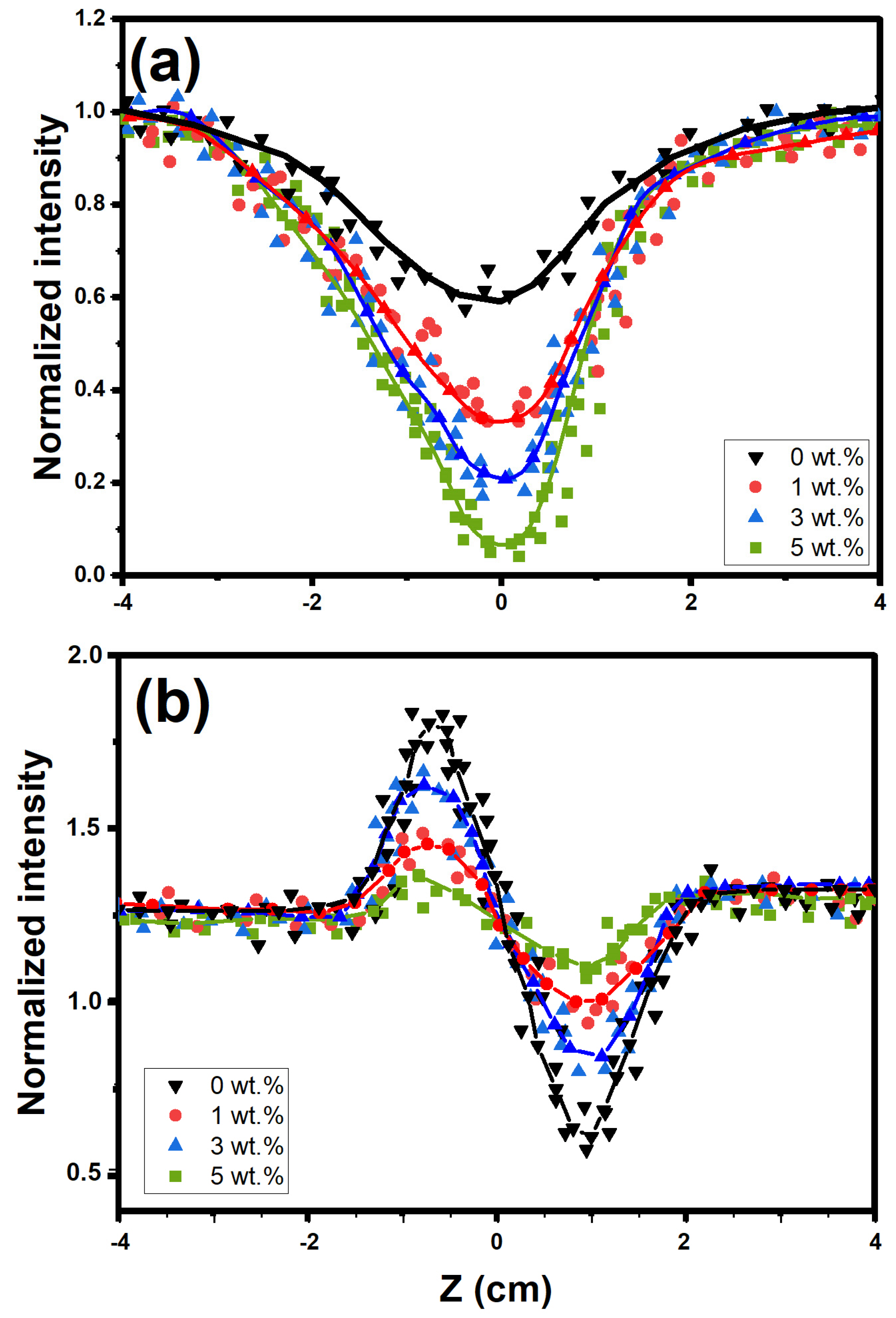
3.4. Nonlinear Optical Analysis by Z-Scan Technique
3.4.1. Investigation of Nonlinear Optical Parameters
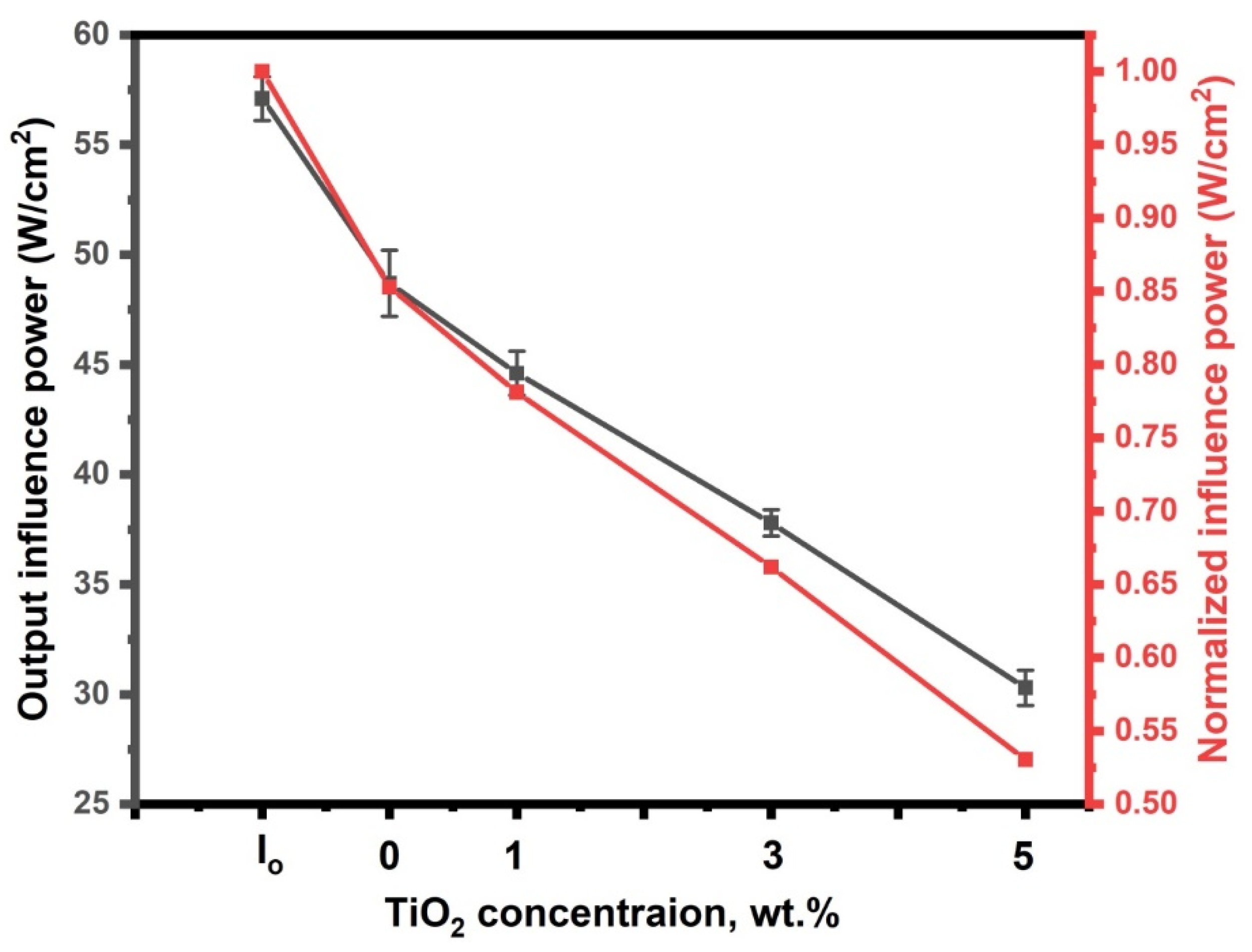
3.4.2. Optical Limiting Effectiveness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, S.A.; Hassan, Q.M.A.; Emshary, C.A.; Sultan, H.A. Characterizing optical and morphological properties of Eriochrome Black T doped polyvinyl alcohol film. Phys. Scr. 2020, 95, 095814. [Google Scholar] [CrossRef]
- Hassan, Q.M.A.; Sultan, H.A.; Al-Asad, A.S.; Kadhim, A.J.; Hussein, N.A.; Emshary, C.A. Synthesis, characterization, and study of the nonlinear optical properties of two new organic compounds. Synth. Met. 2019, 257, 116158. [Google Scholar] [CrossRef]
- Al-Asadi, A.S.; Hassan, Q.M.A.; Abdulkader, A.F.; Mohammed, M.H.; Bakr, H.; Emshary, C.A. Formation of graphene nanosheets/epoxy resin composite and study its structural. morphological and nonlinear optical properties. Opt. Mater. 2019, 89, 460–467. [Google Scholar] [CrossRef]
- Darwish, W.M.; Darwish, A.M.; Al-Ashkar, E.A. Indium(III) phthalocyanine eka-conjugated polymer as high-performance optical limiter upon nanosecond laser irradiation. High Perform. Polym. 2016, 28, 651–659. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Hassan, Q.M.A.; Abdulkader, A.F.; Bakr, H.; Emshary, C.A. Enhancement of the linear. nonlinear and optical limiting properties of epoxy resin decorated by zinc oxide nanoparticles. Phys. Scr. 2020, 95, 085503. [Google Scholar]
- Kaniyarakkal, S.; Thomas, T.; Sadagopalan, S.K.; Jayamohan, L.; Muralimanohar, R.; Vasanthakumaryamma, L. Nair vs. Synthesis. Linear and Nonlinear Optical Properties of Ag/Al2O3 Nanocomposites. Materials 2022, 15, 6322. [Google Scholar] [CrossRef] [PubMed]
- El-Metwally, E.G.; Mohammed, M.I.; Ismail, A.M. Promising naphthol green B dye doped (PVOH-PEG) composite films as a multifunctional material with engineered optical band gap. tunable dielectric properties and nonlinear J–E characteristics. Phys. Scr. 2022, 97, 065804. [Google Scholar] [CrossRef]
- Sharifi, S.; Nezhad, M.K.; Sangsefedi, S.A.; Rakhshanizadeh, F. Effect of charge and dielectric constant on linear and nonlinear optical properties of two dyes. J. Electron. Mater. 2019, 48, 4310–4323. [Google Scholar] [CrossRef]
- Abutalib, M.M.; Yahia, I.S. Selective CUT-OFF laser filters using brilliant green-doped PMMA polymeric composite films: Sensing approach. J. Mater. Sci. Mater. Electron. 2018, 29, 19798–19804. [Google Scholar] [CrossRef]
- Haripadmam, P.C.; Thanuja, T.H.; Varsha, G.S.; Beryl, C.D.; Alexander, A. Nonlinear optical absorption in PVA films doped by the novel natural dye extract from C. redflash leaves. Opt. Mater. 2021, 112, 110804. [Google Scholar] [CrossRef]
- Ali, F.M.; Kershi, R.M. Synthesis and characterization of La3+ ions incorporated (PVA/PVP) polymer composite films for optoelectronics devices. J. Mater. Sci. Mater. Electron. 2020, 31, 2557e66. [Google Scholar] [CrossRef]
- Wouters, M.; Rentrop, C.; Willemsen, P. Surface structuring and coating performance: Novel biocidefree nanocomposite coatings with anti-fouling and fouling-release properties. Prog. Org. Coat. 2010, 68, 4–11. [Google Scholar] [CrossRef]
- Shetty, B.G.; Vincent, C.; Rithin Kumar, N.B.; Rajesh, K.; Bairy, R.; Patil, P.S. Promising PVA/TiO2, CuO filled nanocomposites for electrical and third order nonlinear optical applications. Opt. Mater. 2019, 95, 109218. [Google Scholar] [CrossRef]
- D’Silva, E.D.; Ismayil, A.G.; Rao, S.V. Dopant induced modifications in the microstructure and nonlinear optical properties of 4N4MSP chalcone doped PVA films. Opt. Mater. 2020, 101, 109708. [Google Scholar] [CrossRef]
- Emshary, C.A.; Ali, I.M.; Hassan, Q.M.A.; Sultan, H.A. Linear and nonlinear optical properties of potassium dichromate in solution and solid polymer film. Phys. B Condens. Matter 2021, 613, 413014. [Google Scholar] [CrossRef]
- Kulac, M.; Aktas, C.; Tulubas, F.; Uygur, R.; Kanter, M.; Erboga, M.; Ceber, M.; Topcu, B.; Ozen, O.A. The effects of topical treatment with curcumin on burn wound healing in rats. J. Mol. Histol. 2013, 44, 83–90. [Google Scholar] [CrossRef]
- Alshehari, A.M.; Salim, E.; Oraby, A.H. Structural, optical, morphological and mechanical studies of polyethylene oxide/sodium alginate blend containing multi-walled carbon nanotubes. J. Mater. Res. Technol. 2021, 15, 5615–5622. [Google Scholar] [CrossRef]
- Omar, A.; Badry, R.; Hegazy, M.A.; Yahia, I.S.; Elhaes, H.; Zahran, H.Y.; Ibrahim, M.A.; Refaat, A. Enhancing the optical properties of chitosan, carboxymethyl cellulose, sodium alginate modified with nano metal oxide, and graphene oxide. Opt. Quantum Electron. 2022, 54, 806. [Google Scholar] [CrossRef]
- Kausar, A.; Ahmad, I.; Maaza, M.; Eisa, M.H.; Bocchetta, P. Polymer/Fullerene Nanocomposite for Optoelectronics—Moving toward Green Technology. J. Compos. Sci. 2022, 6, 393. [Google Scholar] [CrossRef]
- Kausar, A. Polymer/Nanocarbon Nanocomposite-Based Eco-friendly Textiles. In Handbook of Nanomaterials and Nanocomposites for Energy and Environmental Applications; Springer: Berlin/Heidelberg, Germany, 2021; pp. 2917–2939. [Google Scholar]
- Chandran, S.P.; Chaudhary, M.; Pasricha, R.; Ahmad, A.; Sastry, M. Synthesis of gold nanotriangles and silver nanoparticles using Aloe Vera plant extract. Biotechnol. Prog. 2006, 22, 577–583. [Google Scholar] [CrossRef]
- Tippayawat, P.; Phromviyo, N.; Boueroy, P.; Chompoosor, A. Green synthesis of silver nanoparticles in Aloe Vera plant extract prepared by a hydrothermal method and their synergistic antibacterial activity. PeerJ 2016, 4, e25892016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hanafy, M.S.; Abdel Fadeel, D.A.; Elywa, M.A.; Kelany, N.A. Green Synthesis and Characterization of TiO2 Nanoparticles Using Aloe Vera Extract at Different pH Value. Faisal Univ. (Basic Appl. Sci.) 2020, 21, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Li, L.; Yu, S.; Liu, J.; Shi, J. High performance of alginate/polyvinyl alcohol composite fifilm based on natural original melanin nanoparticles used as food thermal insulating and UV–vis block. Carbohydr. Polym. 2020, 233, 115884. [Google Scholar] [CrossRef]
- Ali, I.; Peng, C.; Lin, D.; Saroj, D.P.; Naz, I.; Khan, Z.M.; Sultan, M.; Ali, M. Encapsulated Green Magnetic Nanoparticles for the Removal of Toxic Pb2+ and Cd2+ from Water: Development. Characterization and Application. J. Environ. Manag. 2019, 234, 273–289. [Google Scholar] [CrossRef]
- Rajendran, A.; Narayanan, V.; Gnanavel, I. Study on the Analysis of Trace Elements in Aloe vera and Its Biological Importance. J. Appl. Sci. Res. 2007, 3, 1476–1478. [Google Scholar]
- Nasar, G.; Khan, M.S.; Khalil, U. Structural Study of PVA Composites with Inorganic Salts by X-ray Diffraction. J. Pak. Mater. Soc. 2009, 3, 67–70. [Google Scholar]
- Assendert, H.E.; Windle, A.H. Crystallinity in Poly (vinyl alcohol). 1. An X-Ray Diffraction Study of Atactic PVOH. Polymer 1998, 39, 4295–4302. [Google Scholar] [CrossRef]
- Aprilliza, M. Characterization and Properties of Sodium Alginate from Brown Algae Used as an Ecofriendly Superabsorbent. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Birmingham, UK, 13–15 October 2017; Volume 188, p. 012019. [Google Scholar]
- Kumar, H.; Kumar, M.; Barman, P.B.; Singh, R.R. Stable and luminescent wurtzite CdS, ZnS and CdS/ZnS core/shell quantum dots. Appl. Phys. A 2014, 117, 1249–1258. [Google Scholar] [CrossRef]
- Ali, I.M.; Al-Haddad, R.M.; Al-Rasoul, K.T. Structural and Optical Properties of Synthesized Manganese doped ZnS Quantum Dots, International innovative science. Eng. Technol. 2014, 1, 104–114. [Google Scholar]
- Ahmed, R.M.; Abd Elbary, A.M. Structural and Thermal Analysis of Carbon Nano-Particles/Polypyrrole/Poly (Ethylene–Co–Vinyl Acetate) Composites. Arab. J. Nucl. Sci. Appl. 2018, 51, 51–61. [Google Scholar] [CrossRef] [Green Version]
- John, R.; Florence, S. Optical structural and morphological studies of bean-like ZnS nanostructures by aqueous chemical method. Chalcogenide Lett. 2010, 7, 269–273. [Google Scholar]
- Stokes, A.R.; Wilson, A.J.C. The Diffraction of X Rays by Distorted Crystal Aggregates-I. Proc. Phys. Soc. 1944, 56, 174. [Google Scholar] [CrossRef]
- Soltani, N.; Dehzangi, A.; Kharazmi, A.; Saion, E.; Yunus, W.M.M.; Majlis, B.Y.; Zare, M.R.; Gharibshahi, E.; Khalilzadeh, N. Structural, Optical and Electrical Properties of Zns Nanoparticles Affecting By Organic Coating. Chalcogenide Lett. 2014, 11, 79–90. [Google Scholar]
- Rathod, S.G.; Bhajantri, R.F.; Ravindrachary, V.; Sheela, T.; Pujari, P.K.; Naik, J.; Poojary, B. Pressure sensitive dielectric properties of TiO2 doped, PVA/CN-Li nanocomposite. J. Polym. Res. 2015, 22, 6. [Google Scholar] [CrossRef]
- Purushothan, E.; Krishna, N.G. X-ray determination of crystallite sizeand effect of lattice strain on the Debye–Waller factors of Ni nano powdersusing high energy Ball Mill. Chem. Mater. Res. 2015, 7, 1–6. [Google Scholar]
- Bhargava, R.N. Doped nanocrystalline materials—Physics and applications. Luminescence 1996, 70, 85–94. [Google Scholar] [CrossRef]
- Hussein, L.I.; Abdaleem, A.H.; Darwish, M.S.A.; Mostafa, M.H.; Elsawy, M.A. Chitosan/TiO2 nanocomposites: Effect of microwave heating andsolution mixing techniques on physical properties. Egypt. J. Chem. 2020, 63, 449–460. [Google Scholar] [CrossRef]
- Rathod, P.B.; Waghuley, S.A. Synthesis and UV-Vis spectroscopic study of TiO2 nanoparticles. Int. J. Nanomanuf. 2015, 11, 185–193. [Google Scholar] [CrossRef]
- Bekele, E.T.; Gonfa, B.A.; Sabir, F.K. Use of Different Natural Products to Control Growth of Titanium Oxide Nanoparticles in Green Solvent Emulsion. Characterization, and Their Photocatalytic Application. Bioinorg. Chem. Appl. 2021, 2021, 6626313. [Google Scholar]
- Khadar, A.; Behara, D.K.; Kumar, M.K. Synthesis and characterization of controlled size TiO2 nanoparticles via green route using Aloe Vera extract. Int. J. Sci. Res. 2016, 5, 1913–1916. [Google Scholar]
- Abdelghany, A.M.; Ayaad, D.A.; Mahmoud, S.M. Antibacterial and Energy Gap Correlation of PVA/SA Biofilms Doped with Selenium Nanoparticles. Biointerface Interface Res. Appl. Chem. 2020, 10, 6236–6244. [Google Scholar]
- Ahmed, R.M.; Taha, T.A.; Ezz-Eldin, F.M. Investigation of Sm2O3 effect on opto-electrical parameters and dielectric properties of some fluorophosphate glasses. J. Mater. Sci. Mater. Electron. 2021, 32, 28919–28934. [Google Scholar] [CrossRef]
- Ahmed, R.M. Study on Different Solution-Cast Films of PMMA and PVAc. Int. J. Polym. Mater. 2008, 57, 969–978. [Google Scholar] [CrossRef]
- El-Rabaie, S.; Taha, T.A.; Higazy, A.A. Novel PbSe nanocrystals doped fluorogermanate glass matrix. Mater. Sci. Semicond. Process. 2015, 34, 88. [Google Scholar] [CrossRef]
- Tauc, J. Amorphous and Liquid Semiconductors; Plenum Press: New York, NY, USA, 1974. [Google Scholar]
- Davis, E.A.; Mott, N.F. Conduction in non-crystalline systems V. Conductivity, optical absorption and photoconductivity in amorphous semiconductors. Philos. Mag. 1970, 22, 903–922. [Google Scholar]
- Souri, D.; Shomalian, K. Bandgap determination by absorption spectrum fitting method (ASF) and structural properties of different compositions of (60-x)V2O5-40TeO2−xSb2O3 glasses. J. Non-Cryst. Solids 2009, 355, 1597–1601. [Google Scholar] [CrossRef]
- Escobar-Alarc’on, L.; Arrieta, A.; Camps, E.; Muhl, S.; Rodil, S.; Vigueras-Santiago, E. An alternative procedure for the determination of the optical band gap and thickness of amorphous carbon nitride thin films. Appl. Surf. Sci. 2007, 254, 412–415. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Process in Non-Crystalline Materials, 2nd ed.; Clarendon Press: Oxford, UK, 1979. [Google Scholar]
- Alhusiki-Alghamdi, H.M.; Alghunaim, N.S. Synthesis and Characterization of Polyethylene Oxide Incorporated with Cadmium Sulphide Nanoparticles. J. Adv. Mater. Phys. Chem. 2015, 5, 53–59. [Google Scholar] [CrossRef] [Green Version]
- Tauc, J.; Menth, A. States in the gap. J. Non-Cryst. Solids 1972, 8–10, 569–585. [Google Scholar] [CrossRef]
- Souri, D.; Mohammadi, M.; Zaliani, H. Effect of antimony on the optical and physical properties of Sb-V2O5-TeO2 glasses. Electron. Mater. Lett. 2014, 10, 1103–1108. [Google Scholar] [CrossRef]
- Fanchini, G.; Tagliaferro, A. Disorder and Urbach energy in hydrogenated amorphous carbon: A phenomenological model. Appl. Phys. Lett. 2004, 85, 730. [Google Scholar] [CrossRef]
- Ahmed, R.M. Surface and Spectroscopic Properties of CdSe/ZnS/PVC Nanocomposites, polymer composites. Polym. Compos. 2017, 38, 749–758. [Google Scholar] [CrossRef]
- Ahmed, R.M.; Atta, M.M.; Taha, E.O. Optical spectroscopy. thermal analysis, and dynamic mechanical properties of graphene nano-platelets reinforced polyvinylchloride. J. Mater. Sci. Mater. Electron. 2021, 32, 22699–22717. [Google Scholar] [CrossRef]
- O’Leary, S.K.; Zukotynski, S.; Perz, J.M. Disorder and optical absorption in amorphous silicon and amorphous germanium. J. Non-Cryst. Solids 1997, 210, 249–253. [Google Scholar] [CrossRef]
- Ahmed, R.M.; Ibrahiem, A.A.; El-Said, E.A. Enhancing the Optical Properties of Polyvinyl Alcohol by Blending It with Polyethylene Glycol. Acta Phys. Pol. A 2020, 137, 317–323. [Google Scholar] [CrossRef]
- Shehap, A.M.; Akil, D.S. Structural and optical properties of TiO2 nanoparticles/PVA for different composites thin films. Int. J. Nanoelectron. Mater. 2016, 9, 17–36. [Google Scholar]
- Chkirida, S.; Zari, N.; Achour, R.; Qaiss, A.E. Bouhfid R Effect of iron doped titanium oxide encapsulated in alginate on photocatalytic activity for the removal of dye pollutants. RSC Adv. 2020, 10, 22311. [Google Scholar] [CrossRef]
- Skettrup, T. Urbach’s rule derived from thermal fluctuations in the band-gap energy. Phys. Rev. B 1978, 18, 2622. [Google Scholar] [CrossRef] [Green Version]
- Urbach, F. The long-wavelength edge of photographic sensitivity and of the electronic absorption of solids. Phys. Rev. 1953, 92, 1324. [Google Scholar] [CrossRef]
- Karimi, M.; Rabiee, M.; Moztarzadeh, F.; Tahriri, M. Bodaghi M Retraction notice to Controlled synthesis, characterization and optical properties of CdS nanocrystalline thin films via chemical bath deposition (CBD) route. Curr. Appl. Phys. 2009, 9, 1263–1268. [Google Scholar] [CrossRef]
- Raja, V.; Sarma, A.K.; Rao, V.N. Optical properties of pure and dopedPMMA-CO-P4VPNO polymer films. Mater. Lett. 2003, 57, 4678–4683. [Google Scholar] [CrossRef]
- Al-Bataineh, Q.M.; Alsaad, A.M.; Ahmad, A.A.; Telfah, A. A novel optical model of the experimental transmission spectra of nanocomposite PVC-PS hybrid thin films doped with silica nanoparticles. Heliyon 2020, 6, e041772020. [Google Scholar] [CrossRef] [PubMed]
- Rothwarf, A.; Meakin, J.D.; Bamett, A. Polycrystalline and Amorphous Thin Films and Devices; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Jelle, B.P.; Gustavsen, A.; Nilsen, T.N.; Jacobsen, T. Solar material protection factor (SMPF) and solar skin protection factor (SSPF) for window panes and other glass structures in buildings. Sol. Energy Mater. Sol. Cells 2007, 91, 342–354. [Google Scholar] [CrossRef]
- ISO/FDIS 9050, 2003(E); Glass in Building—Determination of Light Transmittance, Solar Direct Transmittance, Total Solar Energy Transmittance, Ultraviolet Transmittance and Related Glazing Factors. ISO: Geneva, Switzerland, 2003.
- ISO 9845–1, 1992(E); Solar Energy—Reference Solar Spectral Irradiance at the Ground at Different Receiving Conditions—Part 1: Direct Normal and Hemispherical Solar Irradiance for Air Mass 1,5. ISO: Geneva, Switzerland, 1992.
- McKinlay, A.F.; Diffey, B.L. A Reference Action Spectrum for Ultraviolet Induced Erythema in Human Skin. CIE J. 1987, 6, 17–22. [Google Scholar]
- Ahmed, R.M. Optical Study on Poly (methyl methacrylate)/Poly (vinyl acetate) Blends. Int. J. Photoenergy 2009, 2009, 150389. [Google Scholar] [CrossRef]
- Abdullah, O.G.; Aziz, S.B.; Rasheed, M.A. Structural and optical characterization of PVA:KMnO4 based solid polymer electrolyte. Results Phys. 2016, 6, 1103–1108. [Google Scholar] [CrossRef] [Green Version]
- Aziz, S.B.; Hassan, A.Q.; Mohammed, S.J.; Karim, W.O.; Kadir, M.F.Z.; Tajuddin, H.A.; Chan, N.N.M.Y. Structural and Optical Characteristics of PVA:C-Dot, Composites: Tuning the Absorption of Ultra Violet (UV) Region. Nanomaterials 2019, 9, 216. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, R.M.; Ibrahiem, A.A.; El-Said, E.A. Effect of Cobalt Chloride as Filler and PVP on the Optical Properties of, P.V.A/PEG/PVP Blends. Opt. Spectrosc. 2020, 128, 642–655. [Google Scholar] [CrossRef]
- El Sayed, A.M.; El-Sayed, S.; Morsi, W.M.; Mahrous, S.; Hassen, A. Synthesis, Characterization, Optical, and Dielectric Properties of Polyvinyl Chloride/Cadmium Oxide Nanocomposite Films. Polym. Compos. 2014, 35, 1842–1851. [Google Scholar] [CrossRef]
- Moss, T.S. Relations between the refractive index and energy gap of semiconductors. Phys. Status Solidi (b) 1985, 13, 415–427. [Google Scholar] [CrossRef]
- Anani, M.; Mathieu, C.; Lebid, S.; Amar, Y.; Chama, Z.; Abid, H. Model for calculating the refractive index of a III–V semiconductor. Comput. Mater. Sci. 2008, 41, 570–575. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, J. Model for calculating the refractive index of different materials. Indian J. Pure Appl. Phys. 2010, 48, 571–574. [Google Scholar]
- Herve, P.; Vandamme, L.K.J. General Relation Between Refractive Index and Energy Gap in Semiconductors. Infrared Phys. Technol. 1994, 35, 609. [Google Scholar] [CrossRef]
- Reddy, R.R.; Ahammed, N.Y. A study on the Moss relation. Infrared Phys. Technol. 1995, 36, 825–830. [Google Scholar] [CrossRef]
- Ravindra, N.M.; Auluck, S.; Srivastva, V.K. On the Penn Gap in Semiconductors. Phys. Status Solidi (b) 1979, 93, K1551979. [Google Scholar] [CrossRef]
- Tripathy, S.K. Refractive indices of semiconductors from energy gaps. Opt. Mater. 2015, 46, 240–246. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, O.; Saber, D.R.; Taha, S.A. The Optical Characterization of Polyvinyl Alcohol: Cobalt Nitrate Solid Polymer Electrolyte Films. Adv. Mater. Lett. 2015, 6, 153. [Google Scholar] [CrossRef]
- Wise, D.L. Electrical and Optical Polymer Systems: Fundamentals: Methods, and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Suma, G.R.; Subramani, N.K.; Shilpa, K.N.; Sachhidananda, S.; Satyanarayana, S.V. Effect of Ce0.5Zr0.5O2 nano fillers on structural and optical behaviors of poly (vinyl alcohol). J. Mater. Sci. Mater. Electron. 2017, 28, 10707. [Google Scholar] [CrossRef]
- Aziz, S.B.; Abdullah, O.G.; Hussein, A.M.; Abdulwahid, R.T.; Rasheed, M.A.; Ahmed, H.M.; Abdalqadir, S.W.; Mohammed, A.R. Optical properties of pure and doped PVA: PEO based solid polymer blend electrolytes: Two methods for band gap study. J. Mater. Sci. Mater. Electron. 2017, 28, 7473–7479. [Google Scholar] [CrossRef]
- Aziz, S.B.; Abdullah, O.G.; Rasheed, M.A. A Novel polymer composite with a small optical bandgap: New approaches for photonics and optoelectronics. J. Appl. Polym. Sci. 2017, 134, 44847. [Google Scholar] [CrossRef]
- Yu, L.; Li, D.; Zhao, S.; Li, G.; Yang, K. First Principles Study on Electronic Structure and Optical Properties of Ternary Ga As: Bi Alloy. Materials 2012, 5, 2486. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Salam, A.I.; Khalid, A.; Awad, M.M.; Hussein, Y.; Ahmed, R.M. Investigating the impact of growth time of CdSe quantum dots on the structure and optical properties of its nanocomposites with SiO2 for improvement of optical devices. J. Alloys Compd. 2022, 925, 166729. [Google Scholar] [CrossRef]
- Sarkar, S.; Das, N.; Chattopadhyay, K. Optical constants. dispersion energy parameters and dielectric properties of ultra-smooth nanocrystalline BiVO4 thin films prepared by rf-magnetron sputtering. Solid. State Sci. 2014, 33, 58–66. [Google Scholar] [CrossRef]
- Dimitrov, V.; Sakka, S. Linear and nonlinear optical properties of simple oxides. II. J. Appl. Phys. 1996, 79, 1741–1745. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Senapati, S.; Alagarasan, D.; Varadharajaperumal, S.; Ganesan, R.; Naik, R. Enhancement of nonlinear optical parameters upon phase transition in new quaternary Ge20Ag10Te10Se60 films by annealing at various temperatures for optoelectronic applications. J. Alloys Compd. 2022, 927, 167000. [Google Scholar] [CrossRef]
- Duffy, J.A. Trends in energy gaps of binary compounds: An approach based upon electron transfer parameters from optical spectroscopy. J. Phys. C Solid. State Phys. 1980, 13, 2979. [Google Scholar] [CrossRef]
- Reddy, R.R.; Gopal, K.R.; Narasimhulu, K.; Reddy, L.S.S.; Kumar, K.R.; Reddy, C.V.K.; Ahmed, S.N. Correlation between optical electronegativity and refractive index of ternary chalcopyrites, semiconductors, insulators, oxides and alkali halides. Opt. Mater. 2008, 31, 209–212. [Google Scholar] [CrossRef]
- Yadav, P.; Sharma, A. Investigation of optical nonlinearities in Bi-doped Se-Te chalcogenide thin films. J. Electron. Mater. 2015, 44, 916–921. [Google Scholar] [CrossRef]
- Ticha, H.; Tichy, L. Semiempirical relation between nonlinear susceptibility (refractive index), linear refractive index and optical gap and its application to amorphous chalcogenides. J. Optoelectron. Adv. Mater. 2002, 4, 381–386. [Google Scholar]
- Mostafa, A.M.; Mwafy, E.A.; Awwad, N.S.; Ibrahium, H.A. Linear and nonlinear optical studies of Ag/Zn/ZnO nanocomposite thin film prepared by pulsed laser deposition technique. Radiat. Phys. Chem. 2021, 179, 109233. [Google Scholar] [CrossRef]
- Mostafa, A.M.; Mwafy, E.A.; Awwad, N.S.; Ibrahium, H.A. Au@Ag core/shell nanoparticles prepared by laser-assisted method for optical limiting applications. J. Mater. Sci. Mater. Electron. 2021, 32, 14728–14739. [Google Scholar] [CrossRef]
- Mostafa, A.M. The enhancement of nonlinear absorption of Zn/ZnO thin film by creation oxygen vacancies via infrared laser irradiation and coating with Ag thin film via pulsed laser deposition. J. Mol. Struct. 2021, 1226, 129407. [Google Scholar] [CrossRef]
- Mostafa, A.M. Preparation and study of nonlinear response of embedding ZnO nanoparticles in PVA thin film by pulsed laser ablation. J. Mol. Struct. 2021, 1223, 129007. [Google Scholar] [CrossRef]
- Stenzel, O.; Wilbrandt, S.; Mühlig, C.; Schröder, S. Linear and Nonlinear Absorption of Titanium Dioxide Films Produced by Plasma Ion-Assisted Electron Beam Evaporation: Modeling and Experiments. Coatings 2020, 10, 59. [Google Scholar] [CrossRef] [Green Version]
- Iliopoulos, K.; Guezguez, I.; Kerasidou, A.P.; El-Ghayoury, A.; Branzea, D.; Nita, G.; Avarvari, N.; Belmabrouk, H.; Couris, S.; Sahraoui, B. Effect of metal cation complexation on the nonlinear optical response of an electroactive bisiminopyridine ligand. Dye. Pigment. 2014, 101, 229–233. [Google Scholar] [CrossRef] [Green Version]
- Rahulan, K.M.; Padmanathan, N.; Philip, R.; Balamurugan, S.; Kanakam, C.C. Structural evaluation and nonlinear optical properties of Ni/NiO. Ni/NiCo2O4 and Co/Co3O4 nanocomposites. Appl. Surf. Sci. 2013, 282, 656–661. [Google Scholar] [CrossRef]
- Wang, J.; Sheik-Bahae, M.; Said, A.; Hagan, D.J.; Van Stryland, E.W. Time-resolved Z-scan measurements of optical nonlinearities. JOSA B 1994, 11, 1009–1017. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Hong, R.; Liu, T.; Wang, Q.; Tao, C.; Lin, H.; Zhang, D. The enhancement of nonlinear absorption of Ag thin film on laser induced defective MoOx buffer layer. Chem. Phys. Lett. 2020, 754, 137727. [Google Scholar] [CrossRef]
- Ferreira, E.; Kharisov, B.; Vázquez, A.; Méndez, E.A.; Severiano-Carrillo, I. Trejo-Durán, M. Tuning the nonlinear optical properties of Au@ Ag bimetallic nanoparticles. J. Mol. Liq. 2020, 298, 112057. [Google Scholar] [CrossRef]
- Pepe, Y.; Karatay, A.; Donar, Y.O.; Sınağ, A.; Unver, H.; Elmali, A. Tuning the energy bandgap and nonlinear absorption coefficients of CdO nanocomposite films with doping and annealing process. Opt. Mater. 2020, 103, 109880. [Google Scholar] [CrossRef]
- Alkallas, F.H.; Ahmed, H.A.; Pashameah, R.A.; Alrefaee, S.H.; Toghan, A.; Trabelsi, A.B.G.; Mostafa, A.M. Nonlinearity enhancement of Multi-walled carbon nanotube decorated with ZnO nanoparticles prepared by laser assisted method. Opt. Laser Technol. 2022, 155, 108444. [Google Scholar]
- Darwish, W.M.; Darwish, A.M.; Al-Ashkar, E.A. Synthesis and nonlinear optical properties of a novel indium phthalocyanine highly branched polymer. Polym. Adv. Technol. 2016, 26, 1014–1019. [Google Scholar] [CrossRef]
- Torres-Torres, D.; Trejo-Valdez, M.; Castañeda, L.; Torres-Torres, C.; TamayoRivera, L.; Fernández-Hernández, R.C.; Reyes-Esqueda, J.A.; Muñoz-Saldaña, J.; Rangel-Rojo, R.; Oliver, A. Inhibition of the two-photon absorption response exhibited by a bilayer TiO2 film with embedded Au nanoparticles. Opt. Express 2010, 18, 16406. [Google Scholar] [CrossRef]
- Muhammed, M.I.; Yahia, I.S.; Farid, A.S. Synthesis and characterization g-C3N4-doped PMMA polymeric nanocomposites films for electronic and optoelectronic applications. J. Appl. Polym. Sci. 2022, 139, e53064. [Google Scholar] [CrossRef]






| PVA:SA:TiO2 NPs (wt.%) | Element | Weight (%) | Atomic (%) |
|---|---|---|---|
| 0 | C | 50.5 | 58.2 |
| O | 45.5 | 39.4 | |
| Na | 4.00 | 2.41 | |
| 1 | C | 42.2 | 50.8 |
| O | 50.8 | 45.9 | |
| Na | 3.33 | 2.09 | |
| Ti | 2.31 | 0.70 | |
| 3 | C | 41.9 | 50.9 |
| O | 49.8 | 45.3 | |
| Na | 3.20 | 2.03 | |
| Ti | 3.54 | 1.08 | |
| 5 | C | 40.4 | 49.40 |
| O | 50.5 | 46.30 | |
| Na | 3.96 | 2.53 | |
| Ti | 3.69 | 1.13 |
| Content of TiO2 Doped in PVA/SA (wt.%) | 2θ (Degree) | FWHM (Degree) | d-Spacing (Å) | D (nm) | δ × 1015 (Lines/m2) | εstr. |
|---|---|---|---|---|---|---|
| 1 | 13.27 | 1.10 | 6.66 | 24.32 ± 2.2 | 1.69 | 0.041 |
| 19.51 | 2.31 | 4.55 | 0.058 | |||
| 23.28 | 9.95 | 3.81 | 0.211 | |||
| 39.99 | 13.6 | 2.25 | 0.161 | |||
| 3 | 13.13 | 0.88 | 6.73 | 27.17 ± 1.6 | 1.35 | 0.033 |
| 19.54 | 2.19 | 4.54 | 0.055 | |||
| 23.62 | 7.31 | 3.76 | 0.152 | |||
| 40.36 | 10.4 | 2.23 | 0.123 | |||
| 5 | 14.07 | 1.64 | 6.29 | 10.42 ± 1.7 | 9.21 | 0.058 |
| 19.50 | 2.37 | 4.55 | 0.060 | |||
| 22.76 | 2.13 | 3.91 | 0.045 | |||
| 25.25 | 8.03 | 3.51 | 0.156 | |||
| 40.28 | 13.6 | 2.23 | 0.161 |
| Different Concentration of TiO2 NPs in the Blend of PVA:SA | (cm−1) | (cm/W) | (cm2/W) | (esu) |
|---|---|---|---|---|
| 0 wt.% | 0.274 | 3.54 × 10−6 | 0.81 × 10−13 | 4.31 × 10−12 |
| 1 wt.% | 0.556 | 3.87 × 10−6 | 1.57 × 10−13 | 5.75 × 10−12 |
| 3 wt.% | 4.75 | 10.4 × 10−6 | 1.91 × 10−13 | 12.1 × 10−12 |
| 5 wt.% | 11.5 | 21.2 × 10−6 | 5.83 × 10−13 | 27.1 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, R.; Kelany, N.A.; Ibrahim, M.A.; Al-Senani, G.M.; Mostafa, A.M. Linear and Nonlinear Optical Properties of PVA:SA Blend Reinforced by TiO2 Nanoparticles Prepared by Flower Extract of Aloe Vera for Optoelectronic Applications. Coatings 2023, 13, 699. https://doi.org/10.3390/coatings13040699
Khalil R, Kelany NA, Ibrahim MA, Al-Senani GM, Mostafa AM. Linear and Nonlinear Optical Properties of PVA:SA Blend Reinforced by TiO2 Nanoparticles Prepared by Flower Extract of Aloe Vera for Optoelectronic Applications. Coatings. 2023; 13(4):699. https://doi.org/10.3390/coatings13040699
Chicago/Turabian StyleKhalil, Rania, Nermeen A. Kelany, Manar A. Ibrahim, Ghadah M. Al-Senani, and Ayman M. Mostafa. 2023. "Linear and Nonlinear Optical Properties of PVA:SA Blend Reinforced by TiO2 Nanoparticles Prepared by Flower Extract of Aloe Vera for Optoelectronic Applications" Coatings 13, no. 4: 699. https://doi.org/10.3390/coatings13040699
APA StyleKhalil, R., Kelany, N. A., Ibrahim, M. A., Al-Senani, G. M., & Mostafa, A. M. (2023). Linear and Nonlinear Optical Properties of PVA:SA Blend Reinforced by TiO2 Nanoparticles Prepared by Flower Extract of Aloe Vera for Optoelectronic Applications. Coatings, 13(4), 699. https://doi.org/10.3390/coatings13040699







