An Optimization Method for CNC Laser Combination Cutting of Irregular Plate Remainders

Abstract

The key research question in this study is how to cut pieces in irregular plate remainders, because there are many irregular plate leftovers created during the CNC (Computer Numerical Control) process. This will increase material utilization and allow plate leftovers to be reused. One of the issues being researched is how to arrange plate remainders on the surface of the CNC machine; this issue is known as combination layout optimization. The other issue being researched is combination cutting-path optimization of plate remainders, which aims to determine the cutting path of parts of plate remainders. A genetic algorithm based on the gravity-center NFP (No-Fit Polygon) method was applied to optimize the layout pattern, and then the geometric coordinates of a part included in one plate remainder after packing were obtained by geometric transformation with the help of a three-layer graphic data correlation model, which quickly identified the inside and outside contours of parts. A colony algorithm based on the mathematical model of cutting-path optimization was used to optimize the cutting path of the parts in the plate remainders. Finally, some simulation tests were performed to illustrate the feasibility and effectiveness of the proposed method. The results of the algorithm for packing irregular shapes for some instances show that our algorithm outperforms the other algorithms. On most instances, the average plate utilization ratio using our algorithm, after running 20 times, is improved by 1% to 9% in comparison to the best plate utilization ratio using the tree search algorithm. The best idle travel of an example achieved by the algorithm in this paper is 7632 mm after running the cutting-path optimization algorithm 20 times, while that of the traditional equivalent TSP (Traveling Salesman Problem) algorithm is 11,625 mm, which significantly demonstrates the efficiency of the algorithm.

1. Introduction

CNC (Computer Numerical Control) cutting is a type of laser processing that is computer-controlled, has a high level of cutting quality, and has been widely used in the manufacturing industry. The optimization of cutting path is of great significance because the cutting path apparently affects cutting time and efficiency.

Cutting-path optimization has been studied from various perspectives in many types of literature [1,2,3], but the majority of these studies focus on the scenario of cutting parts without a hole packed in a rectangular raw material, which slightly contradicts actual production because parts with a hole are also common. Furthermore, there is always a plate remainder after cutting in a rectangular raw material, which is frequently uneven. In large-scale sheet-metal-manufacturing enterprises, the accumulation of a high number of plate remainders during the long-term production process is unavoidable. The reuse of these plate remainders is important for enhancing material usage and lowering production costs, which is also the focus of this paper’s major research.

Assuming that there are some parts (both with and without holes) that need to be cut and there are many plate remainders with different sizes and shapes that can be reused, we first match the parts and the plate remainders while taking the utilization rate of the plate remainders into consideration. Then, we adjust plate remainders on the CNC machine surface to obtain the layout pattern because most plate remainders are small, and finally, we calculate the optimal cutting path of parts in the plate remainders.

There are three sub-problems: How should the parts be arranged in the plate remainders? How should the plate remainders be packed on the surface of the CNC machine? How do you find the optimal cutting path? Packing the parts in the plate remainders is a classical two-dimensional layout optimization problem that has been researched for many years, with detailed studies available in [4,5,6]. Since we assumed that the parts to be cut have already been packed in plate remainders, the first sub-problem is not discussed in this study. The two sub-problems to be studied are combination layout optimization and the combination cutting-path optimization of plate remainders.

We have reason to anticipate that the cutting path will be rather short if the plate remainders are tightly packed together. Though preventing overlapping is a challenge because of the uneven shape of the plate remainders that must be packed, the combination layout optimization of plate remainders is still a two-dimensional layout optimization problem. Another challenge is obtaining the geometric coordinates of a part included in one plate residual after packing, as the plate remaining can move and spin on the CNC machine surface at any angle, other than merely 90 degrees, in a typical two-dimensional layout problem. In this study, a genetic algorithm based on the gravity-center NFP (No-Fit Polygon) method is applied to optimize the layout pattern, and then the geometric coordinates of a part included in one plate remainder after packing are derived by geometric transformation.

Cutting-path optimization aims to minimize the idle travel of the cutting path. The colony algorithm is used to determine the cutting sequence of the parts to be cut after obtaining the layout pattern of the plate remainders, and then the mathematical model of cutting-path optimization is employed to compute the idle travel of the cutting path. Experiments are conducted on several different cases to evaluate the performance of the method suggested in this study. The results signify that the method is effective in solving CNC laser combination cutting of irregular plate remainders.

The main contributions of this paper include two aspects. First, the combination layout optimization method uses a genetic algorithm to pack the irregular remainders with varying sizes and the three-layer graphic data correlation model to obtain the coordinates of each part to be cut belonging to the corresponding remainder. Second, the optimal cutting path is achieved by an ant colony algorithm, which reduces the idle travel of the laser head.

The remainder of this paper is organized as follows. In Section 2, we review the related literature. We describe the problem of combination cutting of plate remainders in Section 3. Section 4 and Section 5 provide descriptions of the combination layout optimization and the combination cutting-path optimization of plate remainders, respectively. To demonstrate the suggested strategy, simulated experiments are provided in Section 6. Section 7 summarizes the conclusions and discussion of further research.

2. Literature Review

The cutting path of the plate remainders is a complex problem that is influenced by the quality of the layout of the plate remainders, the cutting sequence of the parts to be cut, and the cutting constraint rules, among other factors.

There are numerous algorithms for handling two-dimensional layout optimization problems; most address how to pack rectangles in a rectangular strip [7,8]. Research on packing layouts of irregular shapes is also available, but there is not much of it. Albano A et al. [9] and Jose F et al. [10] constructed a tree search algorithm and a TOPOS algorithm for the two-dimensional irregular-pieces layout optimization problem, respectively. Meta-heuristic algorithms are often used to solve the layout optimization problem; although they are not always superior at finding the global optimal solution, they are less vulnerable to becoming trapped in a local optimum. The most popular techniques are genetic algorithms [11,12] and simulated annealing algorithms [13,14].

Many intelligent algorithms [15] have tackled the cutting-path optimization problem, including genetic algorithms [16,17,18], simulated annealing algorithms [1,19,20], ant colony algorithms [21,22,23], and mixed meta-heuristic algorithms [24].

Xu et al. [25] proposed a method to optimize and smooth the cutting direction to minimize the total-motion energy consumption of the entire cutting path, which was searched by using the Dijkstra shortest-path algorithm. Wang et al. [26] optimized the cutting parameters and the path of the tool to promote the surface quality within a given processing time by optimizing the feed speed, the path spacing, and the movement distance in the feed direction simultaneously. Sui et al. [27] proposed a novel method for generation and optimization of the milling tool path. Dewil et al. [15] analyzed in depth the relevant solution methods for different cutting-path optimization problems. Abdullah et al. [21] used an improved ant colony algorithm to optimize the path of the milling tool, reducing the processing time in the milling process. Eapen et al. [28] proposed the MASTRI algorithm to calculate cutting paths by considering matching, spanning trees, and triangulation. Tian et al. [22] used an ant colony optimization algorithm to generate optimal tool motion paths and reduce non-cutting idle travel time. Kiani et al. [29] used an ant colony optimization algorithm to minimize processing time for parts with many geometric pits. Ghaiebi et al. [30] and Liu et al. [31] used an ant colony optimization algorithm to optimize the process planning sequence in drilling operations, maximizing production efficiency. Medina-Rodríguez et al. [32] and Montiel-Ross et al. [33] proposed a parallel ACO algorithm that could obtain the optimal sequence of G commands for drilling printed circuit boards. When optimizing the drill sequence of the holes, the tool stroke could be shortened. Abbas et al. [34] proposed the improved ACO algorithm to optimize the optimal tool path for products with many concentric circular holes. Manber et al. [35] studied graph theory and applied it to minimize the cost of perforation to cut thick metal plates. Zhong et al. [36] proposed an improved hybrid genetic algorithm. Han et al. [20] and Dewi et al. [37] solved the cutting-path problem using an improved simulated annealing algorithm and a micro-genetic algorithm, respectively. Kim et al. [38] proposed a micro-genetic algorithm that could achieve near-optimal solutions and greatly improve computational time and solution. Lee et al. [39] proposed that the perforation position could be set at any position on the contour line segment and then adopted a two-step genetic algorithm to minimize the non-cutting motion of the cutting head. Jin M et al. [40] solved the guillotine cutting problem in several stocks with different regular shapes.

The majority of the aforementioned literature focused on cutting parts in a rectangular plate, whereas there were only a small number of related studies on the layout and cutting optimization methods for plate remainders with regular shapes, which do not directly apply to the scenario of combination cutting of parts in irregular plate remainders. In order to address major issues with the reuse of plate remnants, this work primarily examined the combination cutting layout and path optimization method for irregular plate remainders.

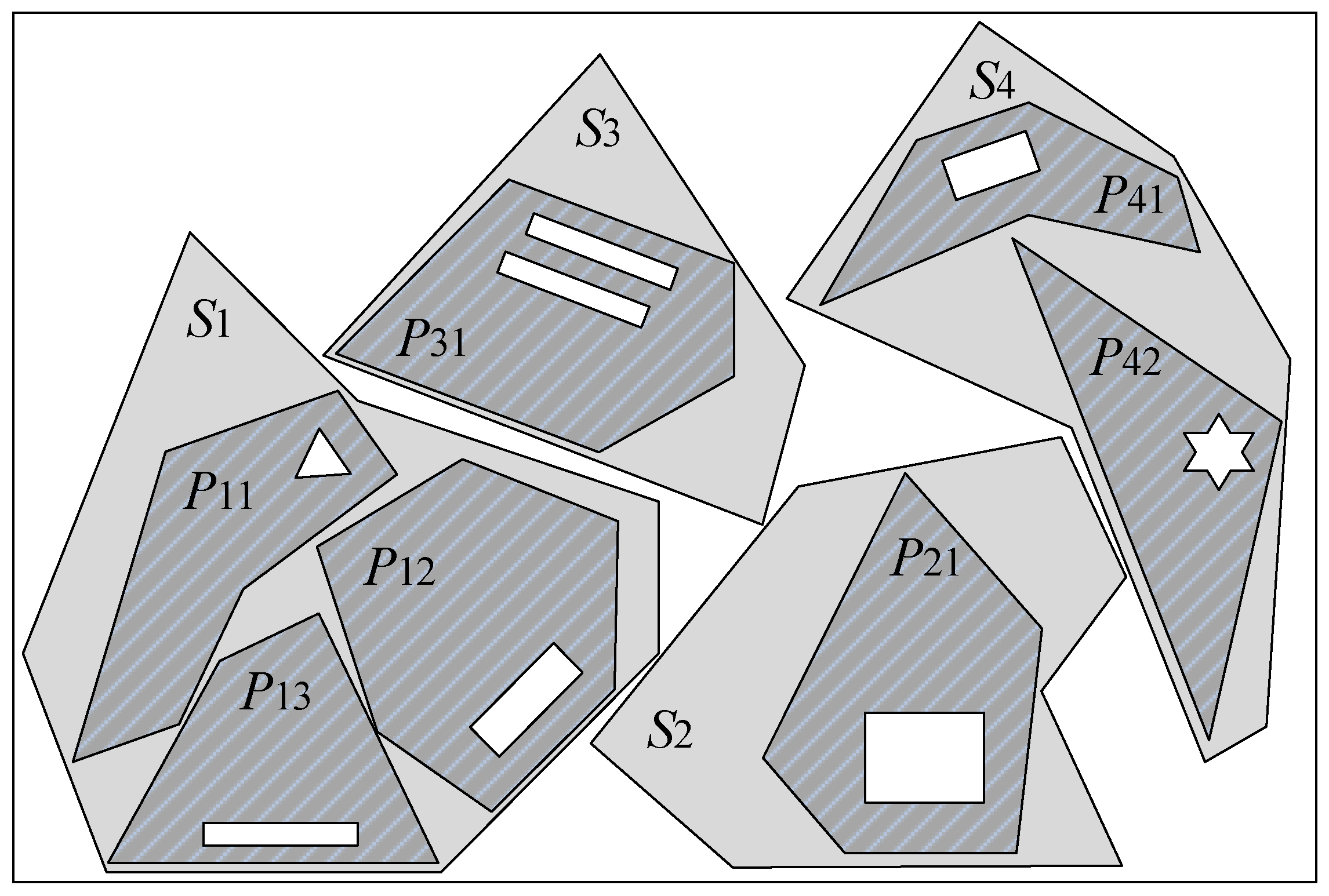
3. Description of the Problem of Combination Cutting of Plate Remainders

As mentioned in Section 1, it is expected that the appropriate nesting algorithm has identified the match between the parts to be cut and the remainders as well as the position of a part within the related remainder. If only one remainder is cut at a time, it will be laborious and time-consuming, because much time will be wasted on switching machines repeatedly and loading and unloading the remainders, which has a significant impact on the processing efficiency. Because plate remainders are always small, it is reliable to cut a batch of remainders packed on the CNC machine surface in advance at a time, followed by cutting another batch of remainders. The combination layout of various remainders makes cutting the remainders simultaneously possible. As shown in Figure 1, $S_i$ represents the plate remainder $i$. $P_{ij}$ represents the part $j$ in the plate remainder $S_i$. For example, $P_{11}$ is the first part to be cut in remainder $S_1$. There are seven parts to be cut. $P_{11}$, $P_{12}$, $P_{13}$, and $P_{21}$ are in the remainders $S_1$ and $S_2$. $P_{31}$, $P_{41}$ and $P_{42}$ are in the remainders $S_3$ and $S_4$. The four remainders packed on the surface of the CNC machine in advance are cut at the same time, which significantly increases processing effectiveness.

Solving the problem of combination cutting of plate remainders requires two steps. The combination layout optimization is the initial step. Layout optimization makes it possible to place more and closer plate remnants in the cutting region, which boosts single-cut output and shortens the cutting path. The second step is the optimization of the combination cutting path. By optimizing the laser head’s cutting path throughout the machining process, the idle travel of the laser head can be effectively decreased, reducing the cutting time and increasing machining productivity.

4. Optimization of the Combination Layout of the Plate Remainders

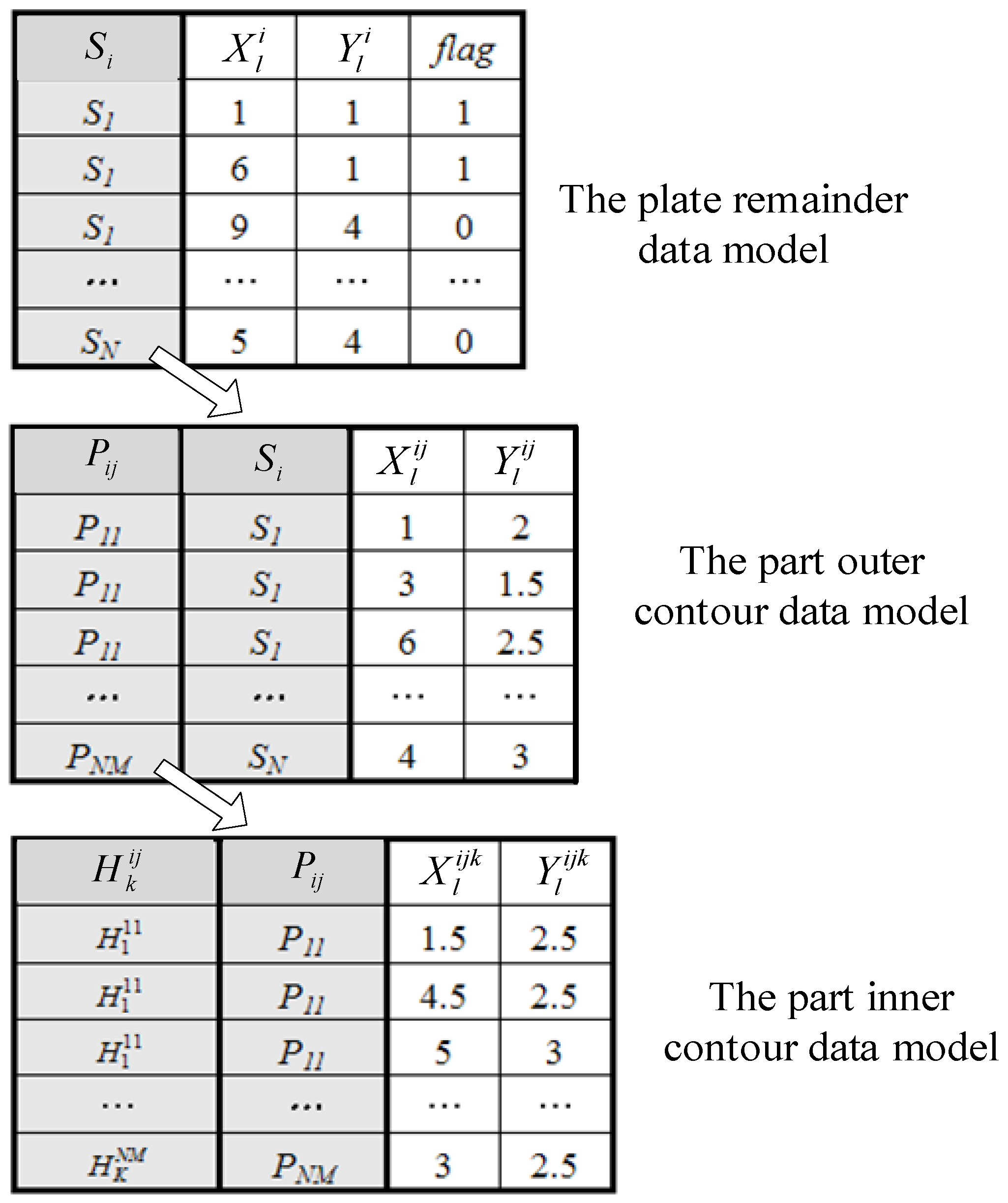
4.1. Graphical Data Model

According to the part-cutting constraint rule of inside-contour priority, all the inside contours of the parts that need to be cut must be identified to optimize the cutting path; however, it is difficult because of the coexistence of the plate-remainder contours, the part outer contours, and the part inner contours. To express the graph information, a three-layer graphical data model was proposed, as shown in Figure 2, which includes the plate-remainder data model, the part-outer-contour data model, and the part-inner-contour data model.

The variables are defined below.

$N$ represents the number of plate remainders.

$M$ denotes the number of parts to be cut.

$K$ signifies the number of inner contours of a part.

$l$ symbolizes the $l_{th}$ vertice of a plate remainder, a part, or an inner contour.

$H_k^{ij}$ represents the $k_{th}$ inner contour of $P_{ij}$.

$X_l^i$ and $Y_l^i$ denote the original $x$ and $y$ coordinates of the corresponding vertice of the remainder $S_i$.

$X_l^{ij}$ and $Y_l^{ij}$ symbolize the original $x$ and $y$ coordinates of the corresponding vertice of the part $P_{ij}$ in the remainder $S_i$.

$X_l^{ijk}$ and $Y_l^{ijk}$ represent the original $x$ and $y$ coordinates of the corresponding vertice of the $k_{th}$ inner contour of the part $P_{ij}$ in the remainder $S_i$.

$flag$ is 0 or 1. When the vertice is the reference point, $flag=1$; if not, $flag=0$. The transformation matrix of each plate remainder requires three reference points, which are also the vertices of the plate remainder.

The relationships between the plate-remainder data model, the part-outer-contour model, and the part-inner-contour model are established by $S_i$ and $P_{ij}$, respectively. The geometric contour data of the three levels are thus independent and related to each other. Any geometric contour data can be operated without influencing other geometric contour data at another level, and they can be rapidly associated with other data at another level. The model addresses the issue of quickly identifying the interior and external contours of parts and clearly describes the graphical geometric information.

4.2. The Combination Layout Optimization Method for Plate Remainders

Optimization of the combination layout of the plate remainders is a 2D irregular layout optimization problem; methods such as the NFP algorithm [11,14], an extended local search algorithm [10], and others that have been proposed to optimize the layout of two-dimensional irregular parts can also be used to optimize the combination layout of the plate remainders. To optimize the cutting path of parts to be cut in plate remainders, we must know the new position of the parts after layout; consequently, we can take the geometric contours of plate remainders as the outer contours of parts to be packed in an ordinary two-dimensional irregular-part layout problem. The genetic algorithm based on the gravity-center NFP method [11] was used to optimize the layout of the plate remainders. The details of the gravity-center NFP method can be found in [11]. The new geometric coordinates of plate remainders are obtained after layout. The part to be cut is always the internal figure in the remainder; the relative position between the part and the matching remainder is constant, and thus, the new geometric coordinates of the parts (also called the internal figures in the remainder) can be calculated using geometric transformation. Because just the geometric contours of the plate remainders were calculated during packing, the method can reduce the amount of calculation and speed up the solution.

4.2.1. The Coding Method of the Feasible Solution

The gravity-center NFP method is employed as the positioning strategy for the layout of the plate remainders in this research. The packing order of the plate remainders must be determined in order to determine the layout of the plate remainders; hence, this order is crucial. For convenience, we can record the sequence of the plate remainders as a layout plan. For example, if there are six remainders to be packed and the packing sequence is (3, 2, 5, 6, 1, 4), the layout pattern could be recorded as (3, 2, 5, 6, 1, 4). The method is the easiest and most straightforward way to communicate the layout idea; it is also more logical and true to life.

4.2.2. Fitness Function

The fitness function is established for the irregular layout of the plate remainders to reflect the quality of the solution, as illustrated in Formula (1):

$$f=A_{sum}/\left(W·L_{max}\right)$$

(1)

where $f$ is the fitness value, $A_{sum}$ is the total area of all plate remainders packed on the surface of the CNC machine, $W$ is the working area width of the cutting machine, and $L_{max}$ is the maximum length of the plate remainders packed in the cutting machine working area. Thus, the fitness value $f$ represents the utilization of the cutting machine working area corresponding to the packing sequence of the layout pattern. The higher the fitness value, the better the quality of the corresponding packing sequence (feasible solution).

4.2.3. Selection Operation

In genetic algorithms, gene selection is usually chosen based on an individual’s fitness value, and the gene of the individual with a high fitness value will have a great probability of being passed on to the next generation, allowing for the expansion of good genes over time during evolution and enhancing the fitness value of the individual. Roulette, random traversal sampling, local selection, tournament selection, and other approaches are examples of common selection methods. In this paper, the roulette method is used for individual selection. The probability of selecting an individual is proportional to its fitness value, and the probability is the ratio of the individual’s fitness value to the sum of the fitness values of all individuals, as shown in Formula (2).

$$p_i=f_i/{\displaystyle \sum }_{i=1}^n{f}_i$$

(2)

In Formula (2), $p_i$ is the probability that the $i_{th}$ individual is selected, and $f_i$ is the fitness value calculated by Formula (1).

During each round, a random number between (0,1) is generated and utilized as a selection pointer to identify the selected individual for subsequent crossover and mutation operations.

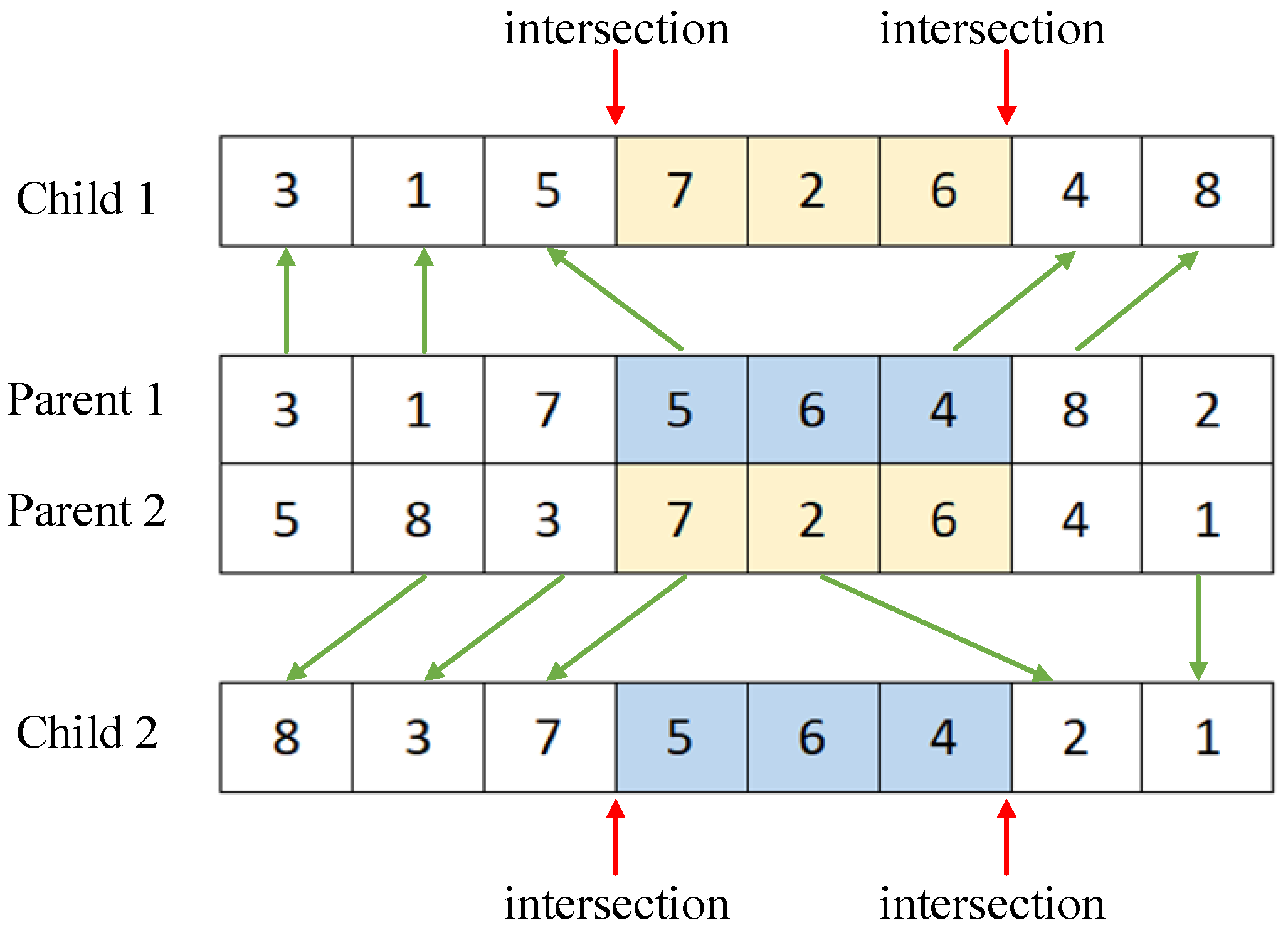
4.2.4. Crossover Operation

Sequential crossover, consistent crossover, rotating crossover, and other crossover techniques are frequently employed in genetic algorithms. The method of sequential crossover is used in this paper. The genes between the two intersections in the paternal individual remain unchanged, and the rest of the genes are filled according to the sequence of genes in the other paternal individual if the genes that have already been selected are no longer selected. Each time the procedure is used, two new offspring can be formed. For example, two paternal individuals are: (3,1,7,/5,6,4,/8,2) and (5,8,3,/7,2,6,/4,1), where “/” represents the two randomly generated intersections. According to the method (as illustrated in Figure 3), the progeny individuals are (8,3,7,5,6,4,2,1) and (3,1,5,7,2,6,4,8).

The crossover probability ${\rho }_c$ is used to decide whether to perform a crossover operation or not. In one round, if the probability of crossover is greater than Random [0, 1], the parents would produce new children Child1 and Child2 through the crossover; otherwise, no crossover operation is performed.

4.2.5. Mutation Operation

Exchange mutation and insertion mutation are two of the most frequently utilized mutation operation methods in genetic algorithms. Exchange mutation is the process of creating a new chromosome by swapping two randomly chosen gene locations on the existing chromosome. Insertion mutation obtains a new chromosome by randomly inserting the last gene into the existing chromosome. Both exchange mutation and insertion mutation aim to pack the sequence of some plate remainders. In this paper, we employ exchange mutation.

The mutation probability ${\rho }_m$ is used to decide whether to carry out a mutation operation or not. In one round, if the mutation probability is greater than Random [0, 1], the mutation operation will be performed; otherwise, no mutation operation is performed.

4.2.6. The Stock Layout Process Based on the Genetic Algorithm

The algorithm steps are as follows:

Step 1. Initialization. The $M$ initial individuals (the sequences of plate remainders to be packed) are generated. Let us initialize the evolutionary algebra $gn=0$ and set the maximum evolutionary algebra $GN$.

Step 2. Based on the method of gravity-center NFP, the layout pattern of each individual in the current population is acquired. The fitness value of each layout pattern is calculated, and the individual with the highest fitness value is considered to be the best individual in the population. The packing sequence of the best individual is chosen as the global optimal solution.

Step 3. To establish new populations, the methods indicated above are used to perform selection, crossover, and mutation operations on individuals in the present population.

Step 4. The gravity-center NFP method is used to determine each individual’s layout pattern in the new population. The fitness value of each layout pattern is calculated, and the individual with the highest fitness value is the best global individual. Let the global optimal solution be updated, and let $gn=gn+1$.

Step 5. Determining whether to stop evolution or not. If $gn\ge GN$, then the evolution ends and the best individual is produced; otherwise, the process returns to step 3.

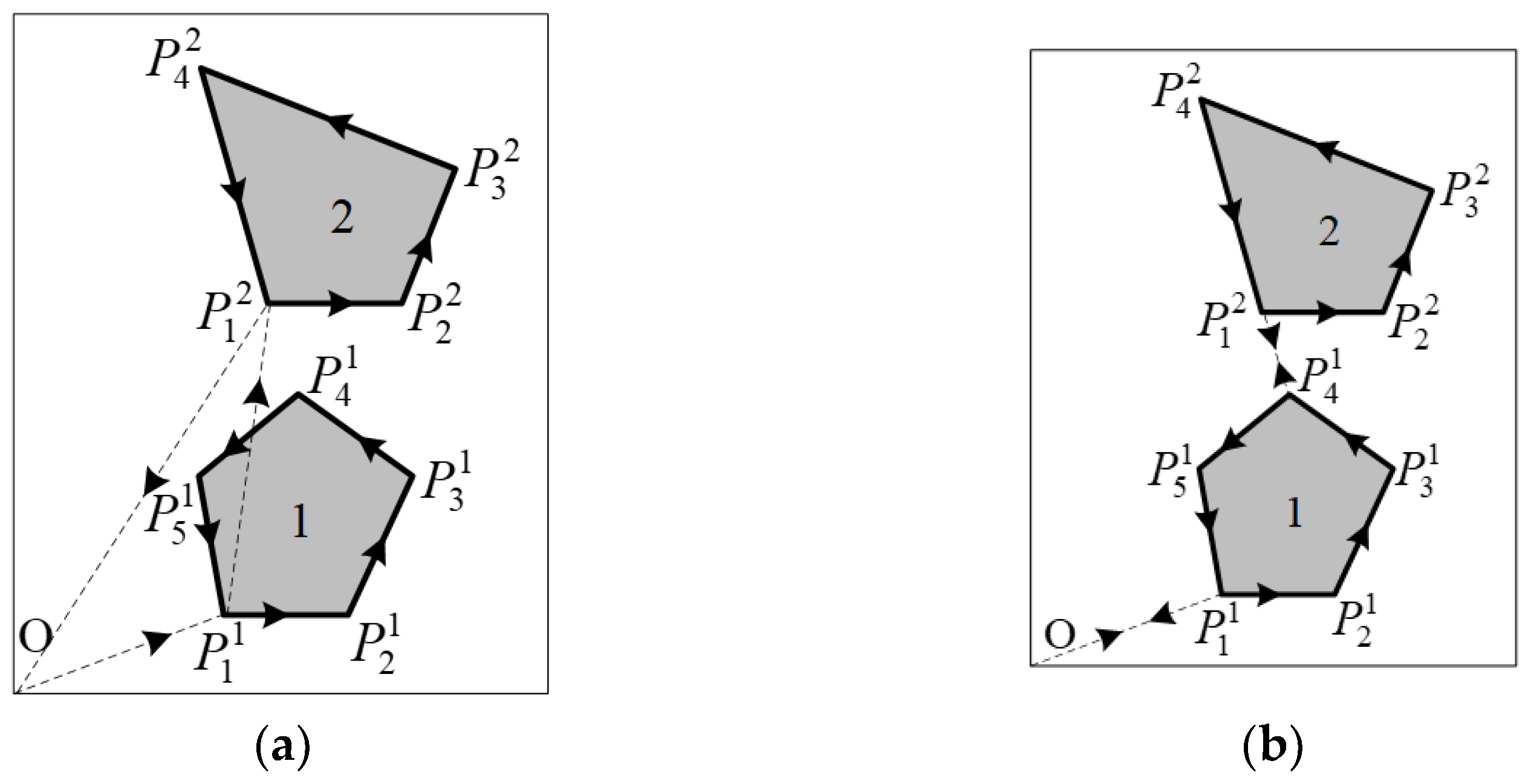
4.3. The Internal-Figure Geometric Transformation of Plate Remainders

After the combination layout of the plate remainders, the new geometric coordinates of the plate contours are obtained, and then the geometric coordinates of the internal figure of the remainder must be updated. The position of the plate remainders has varied during the layout process, but their shapes and sizes have remained the same. It is clear that the procedure is fundamentally a graphical geometric transformation. The figure before and the figure after layout are referred to as the old figure and the new figure, respectively. Based on 2D geometric figure transformation theory [28], the figure transformation equation is as follows:

$$A\times T=B$$

(3)

where $A$ and $B$ are the point set matrices of the old figure and the new figure, respectively, and $T$ is the transformation matrix.

Three vertices of $S_i$ are selected as reference points for ease of calculation, and $X_{Rh}^i$ and $Y_{Rh}^i$ represent the original $x$ and $y$ coordinates of the $h_{th}\left(h=1,2,3\right)$ reference point of the remainder $S_i$, respectively.

The original coordinate matrix before layout is obtained as follows:

$$A_i=\left[\begin{array}{c}{X}_{R1}^i Y_{R1}^i 1\\ X_{R2}^i Y_{R2}^i 1\\ X_{R3}^i Y_{R3}^i 1\end{array}\right]$$

(4)

The new coordinate matrix after layout is acquired as follows:

$$B_i=\left[\begin{array}{c}{X}_{R1}^i{}^{\prime } Y_{R1}^i{}^{\prime } 1\\ X_{R2}^i{}^{\prime } Y_{R2}^i{}^{\prime } 1\\ X_{R3}^i{}^{\prime } Y_{R3}^i{}^{\prime } 1\end{array}\right]$$

(5)

The transformation matrix is obtained as follows, as the plate remainder is only translated and rotated during the layout process.

$$T_i=\left[\begin{array}{c}a b 0\\ c d 0\\ l m 1\end{array}\right]$$

(6)

According to Formula (1), we can obtain

$$\left[\begin{array}{c}{X}_{R1}^i Y_{R1}^i 1\\ X_{R2}^i Y_{R2}^i 1\\ X_{R3}^i Y_{R3}^i 1\end{array}\right]\times \left[\begin{array}{c}a b 0\\ c d 0\\ l m 1\end{array}\right]=\left[\begin{array}{c}{X}_{R1}^i{}^{\prime } Y_{R1}^i{}^{\prime } 1\\ X_{R2}^i{}^{\prime } Y_{R2}^i{}^{\prime } 1\\ X_{R3}^i{}^{\prime } Y_{R3}^i{}^{\prime } 1\end{array}\right]$$

(7)

A standard system of linear equations is given in Formula (7). The six parameters $a$, $b$, $c$, $d$, $l$, and $m$ can be easily obtained (the solution process is abbreviated), and the geometric transformation matrix $T_i$ of the plate remainder $S_i$ is obtained. Because their relative position remains unchanged, the new geometric coordinates of the shape to be cut in the plate remainder $S_i$ can be derived by $T_i$. In the graphical data model, the original coordinate matrices of the outer and inner contour vertices of all parts in the plate remainder $S_i$ are recorded as $A_{iouter}$ and $A_{iinner}$, respectively, and their new coordinate matrices after layout correspondingly are recorded as $B_{iouter}$ and $B_{iinner}$, respectively. Using Formula (3), we can obtain

$$B_{iouter}=A_{iouter}\times T_i$$

(8)

$$B_{iinner}=A_{iinner}\times T_i$$

(9)

The transformation matrix of each remainder can be obtained based on Formula (7), after which the new geometric coordinates of a figure inside a plate remainder can be obtained using Formulas (8) and (9), and finally, the related geometric coordinates in the graphical data model are updated based on the calculation results.

5. Combination Cutting-Path Optimization of Plate Remainders

5.1. The Part-Cutting Constraint Rules

The mathematical model of cutting-path optimization was established for optimizing the combination cutting path. There are two constraint rules that must be followed during the cutting process in order to comply with the standards for the cutting of pieces [15].

1.

The rule of inside-contour priority

The rule of first cutting the inner contour and then cutting the outer contour has been widely accepted in the industry to reduce cutting distortion throughout the cutting process. A three-layer graphical data model is used to describe the geometric information of the graphs. The geometric data of the inner contours and the outer contours of a part in the model is hierarchical and interrelated, and can be immediately identified in the process of cutting-path optimization calculation.

2.

The rule of cross-cutting

The cross-cutting rule permits the laser head to cross-cut among different parts during the cutting process without being constrained by the serial cutting order. Most literature [41] follows the rule of serial cutting, with the laser head cutting parts one by one without cross-cutting. The contours of a part to be cut can be replaced by a punch point from the contours, simplifying the optimization problem of the cutting path to find the shortest distance among punch point sets, known as the TSP (Traveling Salesman Problem), which may lead to some disadvantages. As shown in Figure 4a, the vertices of the two parts to be cut in a sheet are ($P_1^1$, $P_2^1$, $P_3^1$, $P_4^1$, $P_5^1$) and ($P_1^2$, $P_2^2$, $P_3^2$, $P_4^2$), respectively. According to the rule of serial cutting, the points $P_1^1$ and $P_1^2$ can be selected as the punch points. The cutting path is O→$P_1^1$→[$P_2^1$→$P_3^1$→$P_4^1$→$P_1^1$→$P_1^1$]→$P_1^2$→[$P_2^2$→$P_3^2$→$P_4^2$→$P_1^2$]→O, and the idle travel (the distance traveled by the laser head in the idle state) is $S_{idle}=\overline{O{P}_1^1}+\overline{P_1^1{P}_1^2}+\overline{P_1^{2}O}$. In accordance with the rule of cross-cutting, the cutting path and the idle travel are O→$P_1^1$→[$P_2^1$→$P_3^1$→$P_4^1$]→$P_1^2$→[$P_2^2$→$P_3^2$→$P_4^2$→$P_1^2$]→$P_4^1$→[$P_1^1$→$P_1^1$]→O and $S_{idle}^{\prime }=\overline{O{P}_1^1}+\overline{P_4^1{P}_1^2}+\overline{P_1^2{P}_4^1}+\overline{P_1^{1}O}=2\overline{O{P}_1^1}+2\overline{P_4^1{P}_1^2}$, respectively (as shown in Figure 4b). Obviously, the latter is shorter, and it can be seen that the rule of serial cutting may occasionally prevent the optimization algorithm from discovering a solution that is relatively better. The rule of cross-cutting was proposed in this research to promote the optimization algorithm finding a better solution.

5.2. The Optimization Model of Cutting Path

The goal of cutting-path optimization is to shorten idle travel to improve processing efficiency. Due to the adoption of the rule of cross-cutting, it is necessary to distinguish between the internal and external contours of all parts to be cut into a group of line segments. Therefore, the cutting-path optimization problem is equivalently transformed into a cutting-sequence-planning problem for line segments.

It is clear from the two cases in

Table 1. Two examples of path transfer.

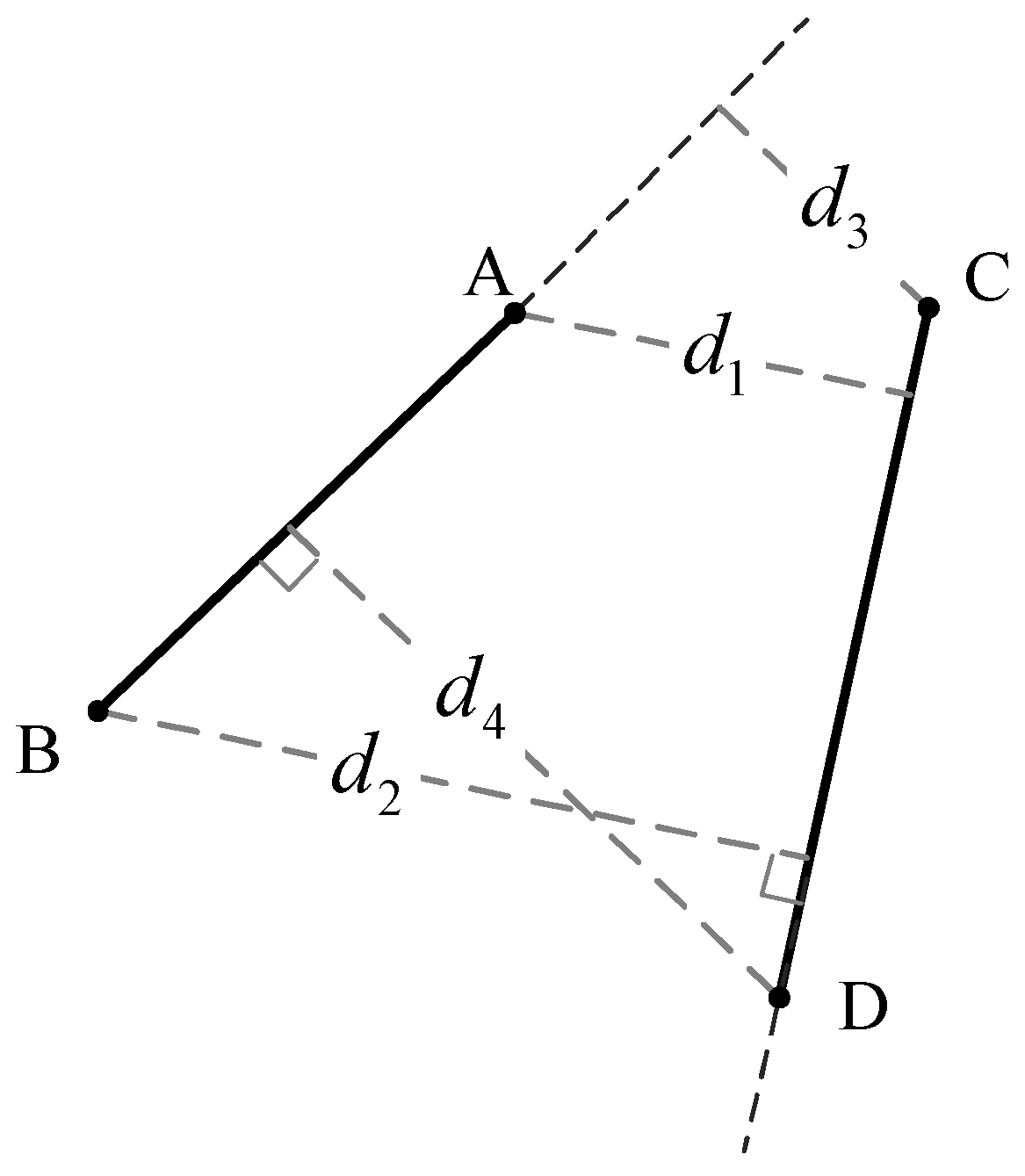
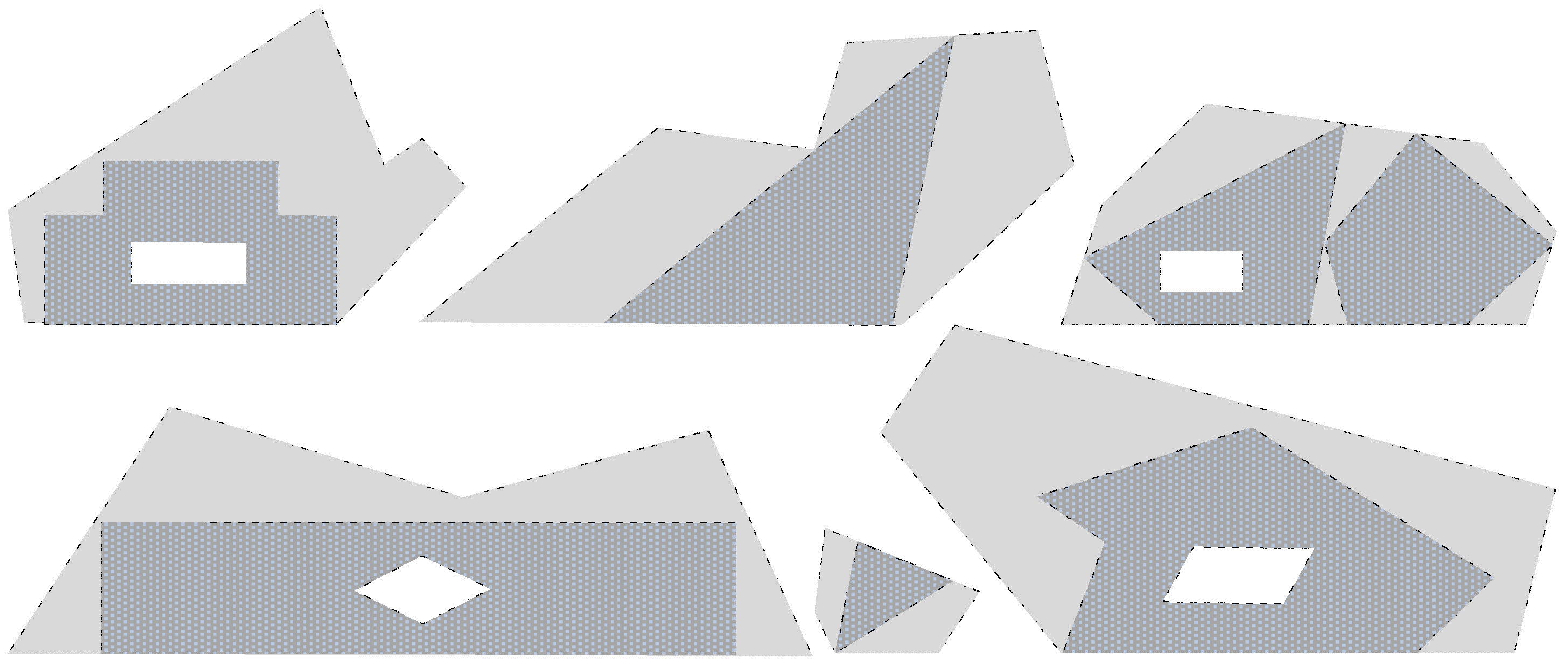
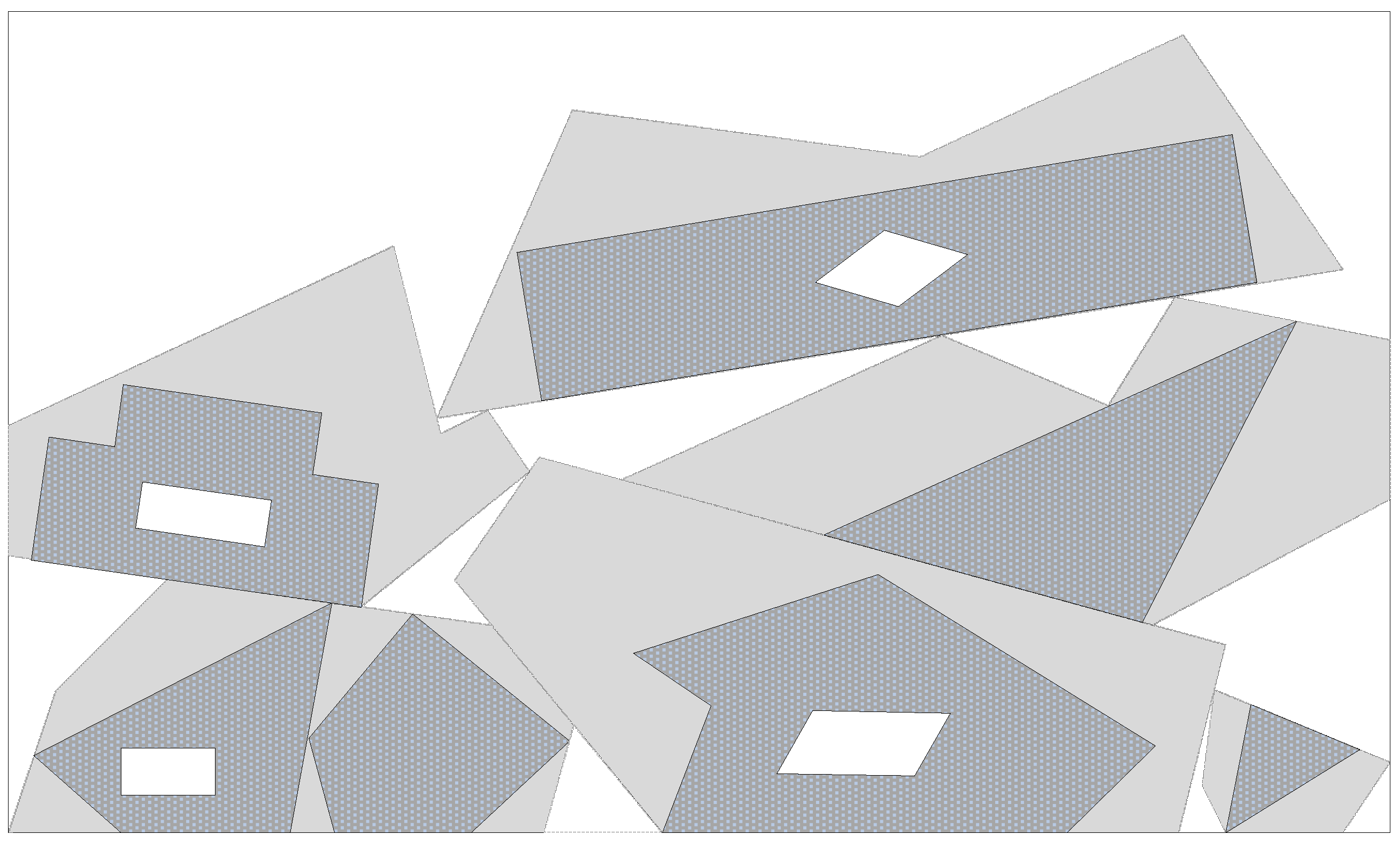
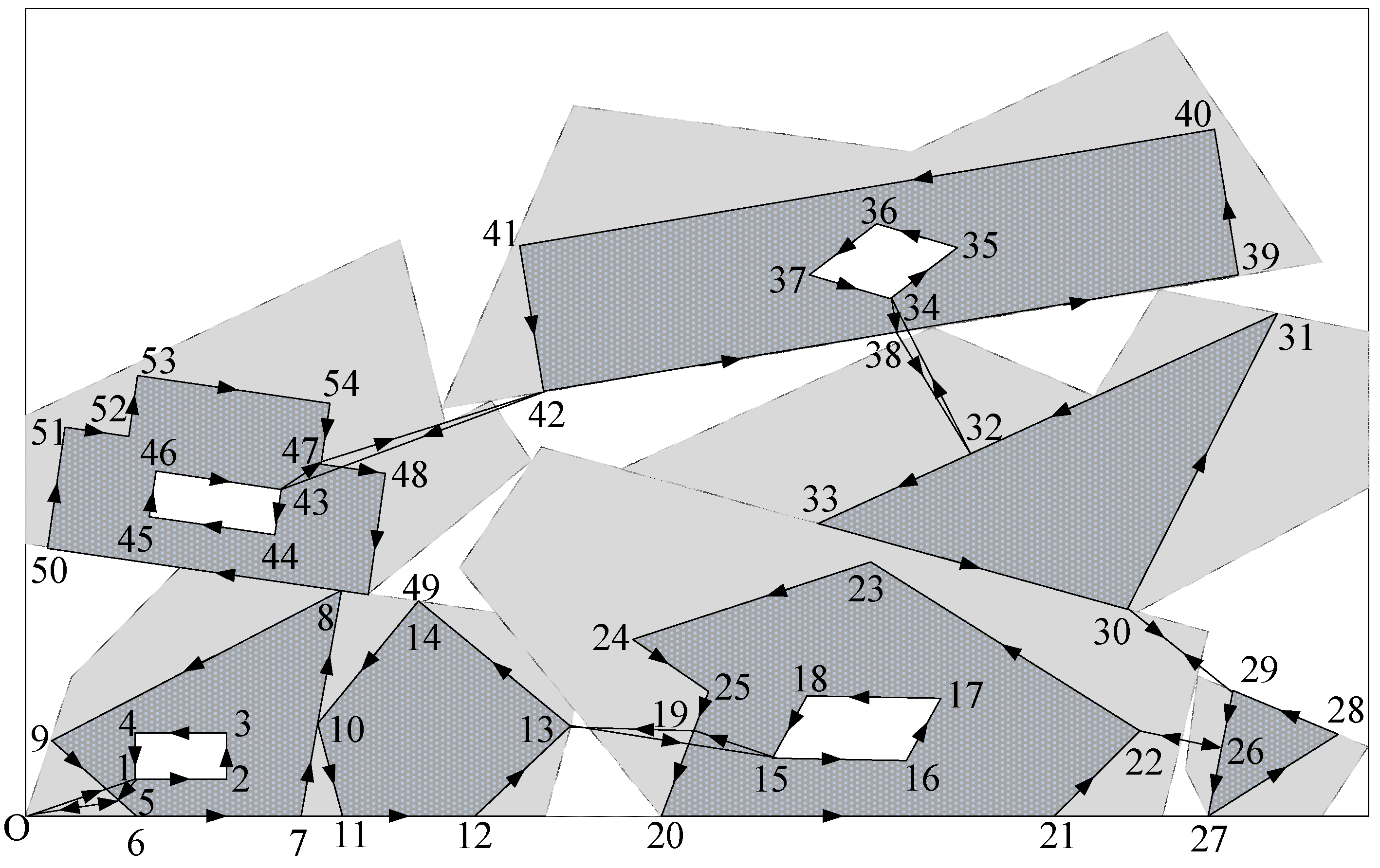
Example	Transfer by the Endpoint of a Segment	Transfer by the Shortest Distance between Segments	Transfer Path
example 1		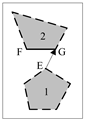	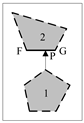EG > FP
example 2		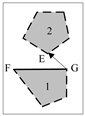	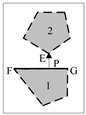EG > FP

that the path length transferred from the endpoint $E$ of a segment to one end of the other segment $FG$ is significantly greater than the path length transferred from $E$ to $P$, which is the foot point from A to the line segment $FG$. In order to reduce idle travel, the principle of transferring by the shortest distance between segments was adopted. The following equation can be used to determine the shortest distance between two line segments.

$$d_{min}=\min \left(d_1,d_2,d_3,d_4\right)$$

(10)

As is shown in Figure 5, $d_1$ is the shortest distance from the point $A$ to the line segment $CD$, $d_2$ is the shortest distance from the point $B$ to the line segment $CD$, $d_3$ is the shortest distance from the point $C$ to the line segment $AB$, and $d_4$ is the shortest distance from the point $D$ to the line segment $AB$.

The cutting sequence of each contour line segment is listed in

Table 2. Examples of laser head transfer path.

Order Number	Line Segment	The Coordinate of Endpoint 1	The Coordinate of Endpoint 2
1	$L_1$	$L{P}_{11}$($x_{11}$,$y_{11}$)	$L{P}_{12}$($x_{12}$,$y_{12}$)
2	$L_2$	$L{P}_{21}$($x_{21}$,$y_{21}$)	$L{P}_{22}$($x_{22}$,$y_{22}$)
3	$L_3$	$L{P}_{31}$($x_{31}$,$y_{31}$)	$L{P}_{32}$($x_{32}$,$y_{32}$)
4	$L_4$	$L{P}_{41}$($x_{41}$,$y_{41}$)	$L{P}_{42}$($x_{42}$,$y_{42}$)
…	…	……	……
Z	$L_Z$	$L{P}_{Z1}$($x_{Z1}$,$y_{Z1}$)	$L{P}_{Z2}$($x_{Z2}$,$y_{Z2}$)

, where Z is the total number of contour line segments and O (0, 0) is the laser head’s initial origin. The cutting path of the laser head is O→[LP₁₁→LP₁₂]→[LP₂₁→LP₂₂]→……→[LP_Z1→LP_Z2]→O.

The idle travel is

$$S_{empty}=\overline{OL{P}_{11}}+\overline{L{P}_{12}L{P}_{21}}+\overline{L{P}_{22}L{P}_{31}}+ \cdots +\overline{L{P}_{Z-1,2}L{P}_{Z1}}+\overline{L{P}_{Z2}O}$$

(11)

Therefore, the mathematical model of the cutting-path optimization is

$$min{S}_{empty}=\sqrt{x_{11}^2+y_{11}^2}+{\displaystyle \sum }_{i=1}^{Z-1}\sqrt{{(x_{i+1,1}-x_{i,2})}^2+{(y_{i+1,1}-y_{i,2})}^2} +\sqrt{x_{Z2}^2+y_{Z2}^2}$$

(12)

$$s.t. x_{ij}\ge 0 \left(i=1,2,\cdots ,Z;j=1,2\right)$$

$$y_{ij}\ge 0\left(i=1,2,\cdots ,Z;j=1,2\right)$$

5.3. The Optimization Algorithm for the Cutting Path

Cutting-path optimization is essentially a combinatorial NP (Non-deterministic Polynomial) optimization problem where each line segment’s cutting sequence is optimized. An ant colony algorithm, a heuristic technique based on simulated evolution that has been successfully employed in the optimal solution of many issues, was used to solve the issue in this study.

Table 3. The relative variables and their meanings of the algorithm.

Variable	Meaning
$NC$	the maximum number of iterations
$nc$	the current number of iterations
$u$	ant colony number
$Z$	the total number of part contour line segments
$\alpha$	pheromone importance coefficient
$\beta$	heuristic factor importance coefficient
$\rho$	pheromone evaporation coefficient
${\tau }_{min}$	the minimum value of pheromone
${\tau }_{max}$	the maximum value of pheromone
$PL{M}_{Z\times 4}$	the coordinate matrix of line segments
$NPL{M}_{2Z\times 4}$	the extended coordinate matrix of line segments (each line segment has two cutting starting points)
$Inf{o}_{2Z\times Z}$	the pheromone matrix of line segments
$Allowe{d}_{2Z\times 1}$	the selective-state matrix of line segments
$Pat{h}_{u\times Z}$	the order-number matrix of the ant colony path
$Path\_XY$	the coordinate matrix of the ant colony path
$S_{u\times 1}$	the idle-travel matrix of ant colony
$RCours{e}_{NC\times 1}$	the iteration-process matrix
$x$	the x-coordinate of ant current point
$y$	the y-coordinate of ant current point
$PathBes{t}_{1\times Z}$	the order-number vector of the globally optimal path
$S\left(k\right)$	the idle travel
$Y^{\prime }$	the single-iteration optimal solution of idle travel
$Y$	the global optimal solution of idle travel
$PathBest\_XY$	the coordinate matrix of the optimal path

shows the relative variables of the cutting-path optimization algorithm and their meanings.

The specific algorithm steps are as follows:

Step 1. Initialize the variables. Set the values for $NC$, $u$, $Info$, $\alpha$, $\beta$, $\rho$, ${\tau }_{min}$, and ${\tau }_{max}$, let $nc=1$, and then $NPLM$ can be obtained.

Step 2. The $n{c}_{\mathrm{th}}$ iteration. Let $Path$ and $S$ be zero matrices and $k=1$.

Step 3. Traverse the ant colony. Begin by setting the ant $k$ at the origin (which can be represented as a contour line segment with length 0), let $x=0$, $y=0$. Set values for the matrix $Allowed$ (if the segment $i$ was walked by an ant, $Allowed\left(i\right)=0$; otherwise, $Allowed\left(i\right)=1$), and set the number of selection $t=1$.

Step 4. Line selection. Calculate the distance matrix $Distanc{e}_{2Z\times 6}$ between the current line segment and other contour line segments and generated using Formula (8), and calculate the heuristic coefficient matrix $P{M}_{2Z\times 1}$ using Formula (13). The distance matrix’s six columns are the order number, the $x$ coordinate of the exit point, the $y$ coordinate of the exit point, the $x$ coordinate of the entry point, the $y$ coordinate of the entry point, and the transfer distance.

$$PM\left(i\right)=\{\begin{array}{l}1/Distance\left(i,6\right),Allowed\left(i\right)=1\\ 0,Allowed\left(i\right)=0\end{array}\left(i=1,2,\cdots ,2Z\right)$$

(13)

Calculate the probability matrix for the selection of line segment $P{K}_{2Z\times 1}$ according to Formula (14).

$$PK\left(j\right)=Info{(j,t)}^{\alpha }PM{(j)}^{\beta }\left(j=1,2,\cdots ,2Z\right)$$

(14)

According to the roulette rules, the line segment $h$ selected by the ants was randomly determined.

Step 5. Ant walks. Read the coordinates of the exit point and the entry point: $x_1=Distance\left(h,2\right)$, $y_1=Distance\left(h,3\right)$, $x_2=Distance\left(h,4\right)$, $y_2=Distance\left(h,5\right)$. If the exit point is not the endpoint of the line segment, add the remaining line segments to the matrices of $NPLM$ and $Allowed$; if the exit point is not the endpoint of the line segment, add one of the line segments to the matrices of $NPLM$ and $Allowed$.

The cumulative idle travel is

$$S\left(k\right)=S\left(k\right)+Distance\left(h,6\right)$$

(15)

Save the order number of paths and coordinate points to $Path$ and $Path\_XY$, respectively. Update the current coordinates of the ant: $x=x_2$, $y=y_2$, and the matrix is $Allowed$.

Step 6. Decide if the iteration needs to be stopped. Continue to step 4 if there are any more line segments left; otherwise, move on to step 7.

Step 7. Ant $k$ returns to the origin. The travel back to the origin is idle, which is accumulate into the idle travel.

Step 8. Determine whether the iteration of the ant colony has to be stopped. If so, proceed to step 3; if not, move on to step 9.

Step 9. Update the optimal solution. Find out the optimal solution of this iteration $Y^{\prime }$ and the optimal path matrices $PathBes{t}^{\prime }$ and $PathBest\_X{Y}^{\prime }$, and save $Y^{\prime }$ into $RCourse$. If $Y^{\prime }<Y$, update the global optimal solution and path matrices: $Y=Y^{\prime }$, $PathBest=PathBes{t}^{\prime }$, $PathBest\_XY=PathBest\_X{Y}^{\prime }$.

Step 10. Update the pheromone matrix using Formula (16), as well as the minimum and maximum values of pheromone concentration:

$$Info\left(i,j\right)=\left(1-\rho \right)\cdot Info\left(i,j\right)+\Delta {\tau }_{ij}^{best}$$

(16)

Step 11. Judge whether the algorithm iteration needs to be terminated. If $nc<NC$, let $nc=nc+1$, and go to step 2; otherwise, the iteration is over and the relevant calculation results are produced.

6. Simulation Experiment

6.1. The Optimization Experiment on the Combination Layout of Plate Remainders

To verify the feasibility and validity of the algorithm proposed in this paper, the algorithm programmed on the Visual C++ platform is put to the test on some instances and compared with the tree search algorithm proposed in the literature [9] and the TOPOS algorithm provided in the literature [10]. The best utilization ratio of plate using the tree search algorithm is from [10], which used the algorithm proposed in [9]. The algorithm’s relevant parameters are $M=60$, ${\rho }_c=0.7$, ${\rho }_m=0.1$, and $GN=60$. All instances are from the EURO Special Interest Group on Cutting and Packing (ESICUP), whose website is https://www.euro-online.org/websites/esicup/ (accessed on 9 June 2022). The average plate utilization ratio is calculated after 20 iterations of our algorithm.

Table 4. Comparison of the three algorithms (our algorithm, the tree search algorithm, and the TOPOS algorithm).

Instance	The Plate Utilization Ratio			Increased Utilization Ratio Compared to the Other Algorithms
	The Tree Search Algorithm (the Best)	TOPOS (the Best)	Our Algorithm (the Average)	The Tree Search Algorithm	TOPOS
Shapes0	56.99%	59.77%	60.38%	+3.39%	+0.61%
Shapes1	63.32%	65.40%	64.12%	+0.80%	−1.28%
Shapes2	68.57%	74.74%	77.59%	+9.02%	+2.85%
Shirts	78.13%	81.27%	81.68%	+3.55%	+0.41%
Trousers	78.80%	82.76%	83.62%	+4.82%	+0.86%

compares the average plate utilization ratio of our algorithm with the best plate utilization ratio of the other two algorithms.

Table 4 demonstrates our algorithm outperforms the other two algorithms on the five instances. Our algorithm surpasses the tree search algorithm by 1% to 9%, with an average improvement of 4.3%. With the exception of the instance of Shapes1, our algorithm can obtain better results than the TOPOS algorithm, improving the plate utilization ratio by 1% to 3%.

6.2. The Optimization Experiment of the Combination Cutting Path of Plate Remainders

By using the six plate remainders to be cut as an example, the feasibility and effectiveness of the method presented in this study were verified, as shown in Figure 6. Due to space limitations, the three-layer graphical data model for each plate remainder and its parts were omitted. The combination layout of the six plate remainders (as shown in Figure 7) was created using the optimization method for the combination layout and the internal-figure geometric transformation of plate remainders. The operation path of the laser head was optimized using the ant colony algorithm-based cutting-path optimization algorithm with parameters $u=80$, $\alpha =0.6$, $\beta =3.5$, $\rho =0.6$, $NC=100$. The optimization program was compiled by Matlab, and the best cutting path of the laser head (as shown in Figure 8) was obtained after running 20 times.

The best cutting path was O→[1→2→3→4→1]→[5→6→7]→[10→11→12→13]→[15→16→17→18→15]→[19→20→21→22]→[26→27→28→29]→[30→31→32]→[34→35→36→37→34]→[38→39→40→41→42]→[43→44→45→46→43]→[47→48→49→50→51→52→53→54→47]→[42→38]→[32→33→30]→[29→26]→[22→23→24→25→19]→[13→14→10]→[8→9→5]→O.

The best idle travel was:

$$\begin{array}{ll}{S}_{empty}& =\overline{0-1}+\overline{1-5}+\overline{5-0}+\overline{13-15}+\overline{15-19} +\overline{19-13}+2\times \overline{22-26}+2\times \overline{29-30}+\overline{32-34}+\overline{34-38}\\ & \hspace{1em}\hspace{1em}\hspace{1em}+\overline{38-32}+\overline{42-43}+\overline{43-47}+\overline{47-42}=7632 \mathrm{mm}\end{array}$$

(17)

In this simulation example, the idle travel achieved by the algorithm in this paper is shortened by 3993 mm compared to the traditional equivalent TSP algorithm (with which the idle travel is 11,625 mm), which greatly optimizes the cutting path of the laser head and improves the processing efficiency.

7. Conclusions

Cutting and packing problems arise from real-world production, such as cutting glass sheets into small rectangles or cloth into irregular shapes, which is a classic problem in operational research that has been actively researched for over sixty years. A substantial number of plate remainders will inevitably accumulate over the long-term production process in large-scale sheet-metal-manufacturing enterprises. The reuse of these irregular plate remainders is crucial for improving material utilization and reducing production costs. It is important to optimize the combination layout and cutting path for two-dimensional irregular plate remainders. The method proposed in this study can be used to solve the optimization problem of CNC laser combination cutting of irregular plate remainders, and it also has a certain reference value for other similar problems.

The cutting-path optimization aims to minimize the idle travel of the cutting path. The combination layout optimization and the combination cutting-path optimization of the plate remainders are the two key tasks completed in this article. The optimization of the combination layout of the plate remainders seeks to make the remainders close to each other but not overlapping as soon as possible. The gravity-center NFP method presented in [11] is applied to pack the plate remainders on the surface of the CNC machine, and then the genetic algorithm is used to optimize the layout pattern of plate remainders. The coordinates of parts to be cut in plate remainders after packing were acquired by geometric transformation with the aid of the three-layer graphic data correlation model. The internal and external contours of all the parts that need to be cut are distributed as a result of the rule of cross-cutting, and the cutting-path optimization problem is correspondingly transformed into a cutting-sequence-planning problem for line segments, which can be solved by the ant colony algorithm.

The algorithm for packing irregular shapes is put to the test in some instances to ensure its feasibility and validity, and a comparison with other algorithms is provided. It has been demonstrated that our algorithm outperforms the other two algorithms in most cases, improving the plate utilization ratio by an average of 4.3% and by 1% to 9% when compared to the tree search algorithm. The validity of the cutting-path optimization algorithm is also verified by taking six plate remainders to be cut as an example; the idle travel obtained by the algorithm in this paper is 7632 mm, which is decreased by 3993 mm when compared to the traditional equivalent TSP algorithm (for which the idle travel is 11,625 mm), significantly improving the cutting path of the laser head and the processing efficiency.

Although the feasibility and validity of the algorithm proposed in this paper have been verified, it is recommended that a wide range of situations be investigated in the future. The plate remainders in this research have no holes, but plate remainders with holes exist in real production and can be solved by our algorithm, because it is assumed that parts to be cut have been packed in the plate remainders. In addition, the plate remainders and the parts to be cut in this paper have vertices, but there are also the circular remainders and parts without vertices, which are not fully addressed by the method proposed in this paper, and they will be our future work’s focus. Because plate remainders are always small, if one part to be cut can be packed in several plate remainders and then the several shapes after cutting can be melted into a whole part, the utilization ratio of plate remainders will increase greatly, which is complex but meaningful and is a new problem to be solved.