Structural Fault Diagnosis Based on Static and Dynamic Response Parameters
Abstract
:1. Introduction
2. The Hybrid Sensitivity Method for Structural Fault Diagnosis
2.1. Static Displacement Sensitivity
2.2. Vibration Mode Sensitivity
2.3. The Hybrid Sensitivity
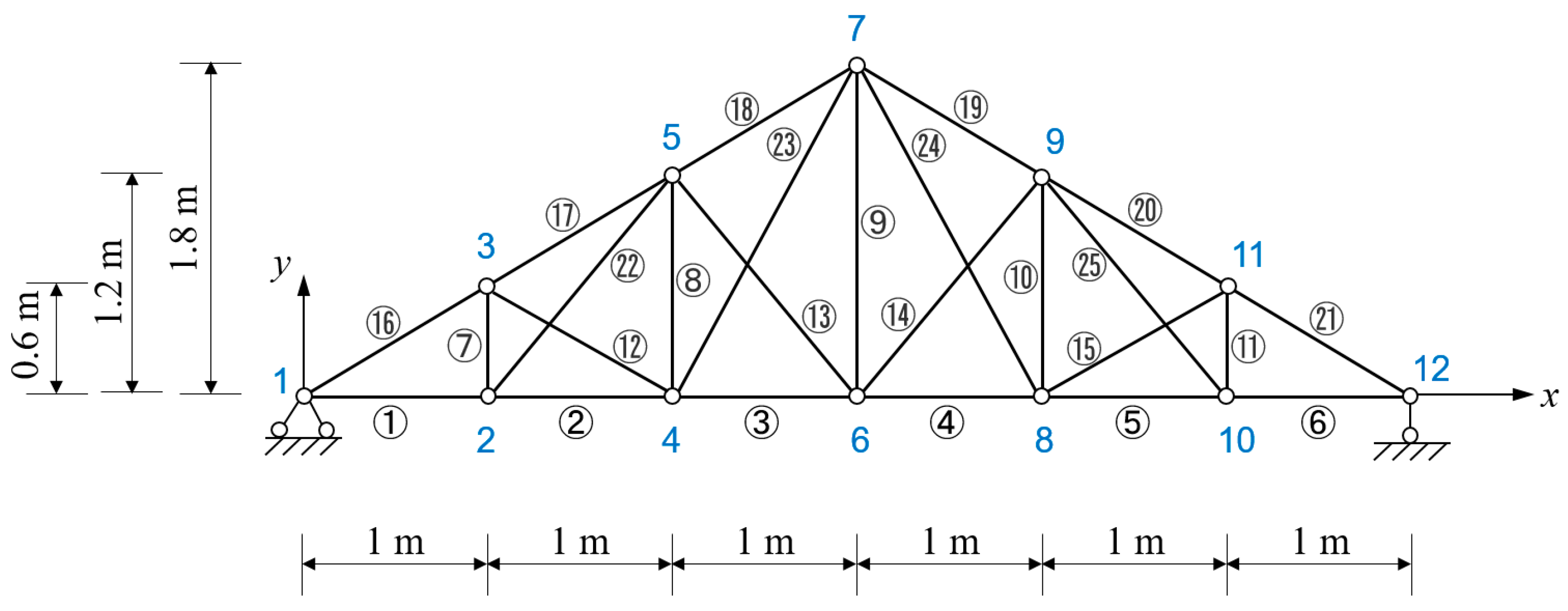
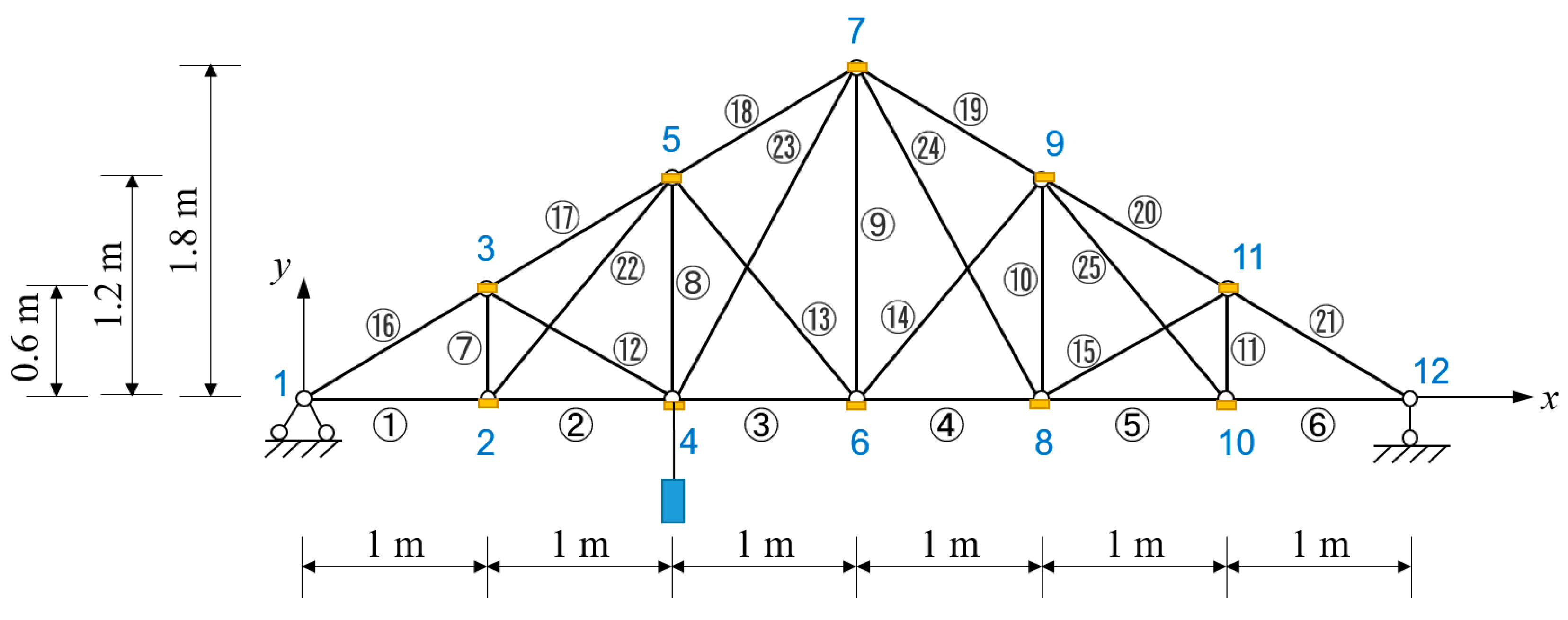
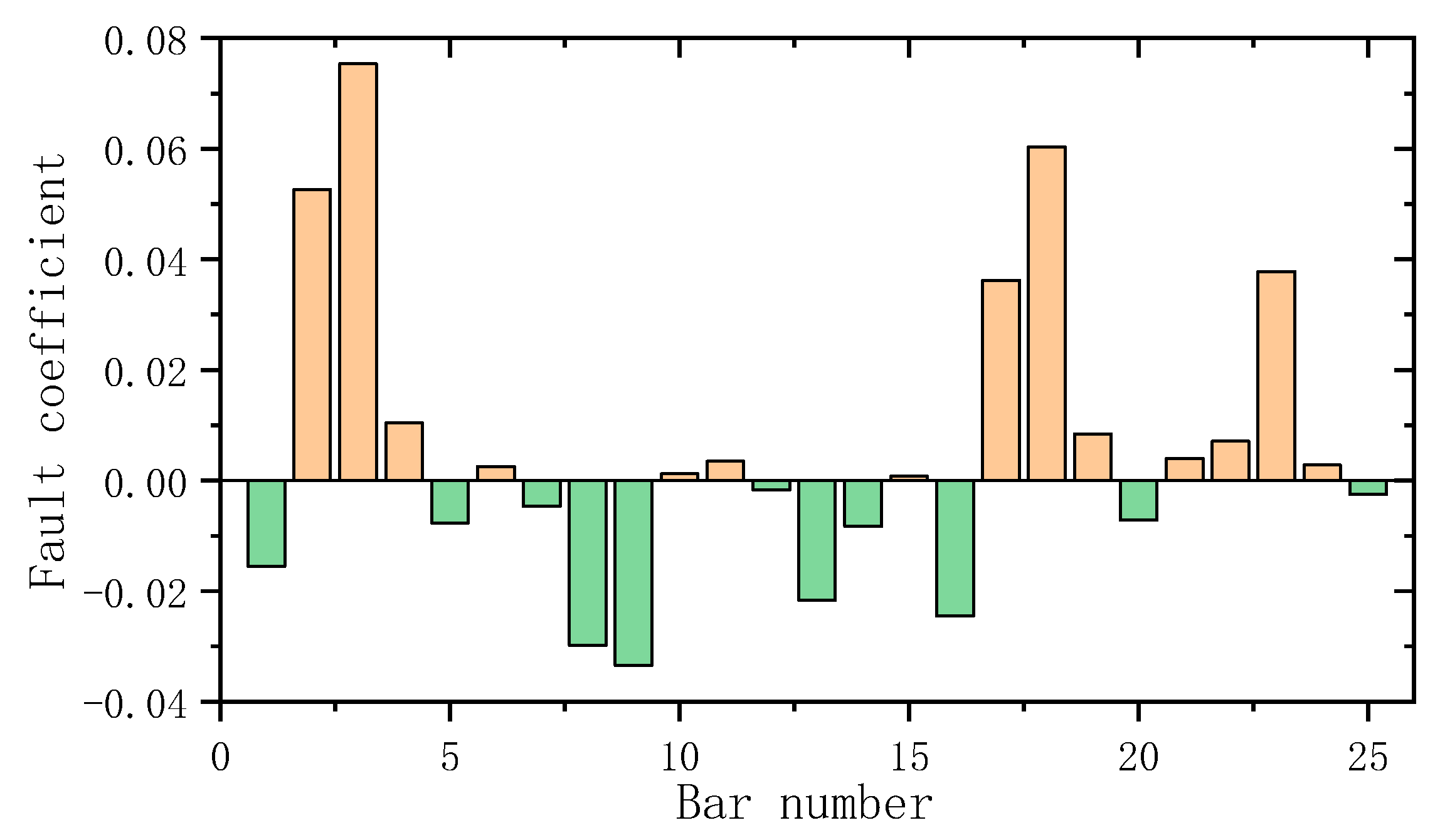
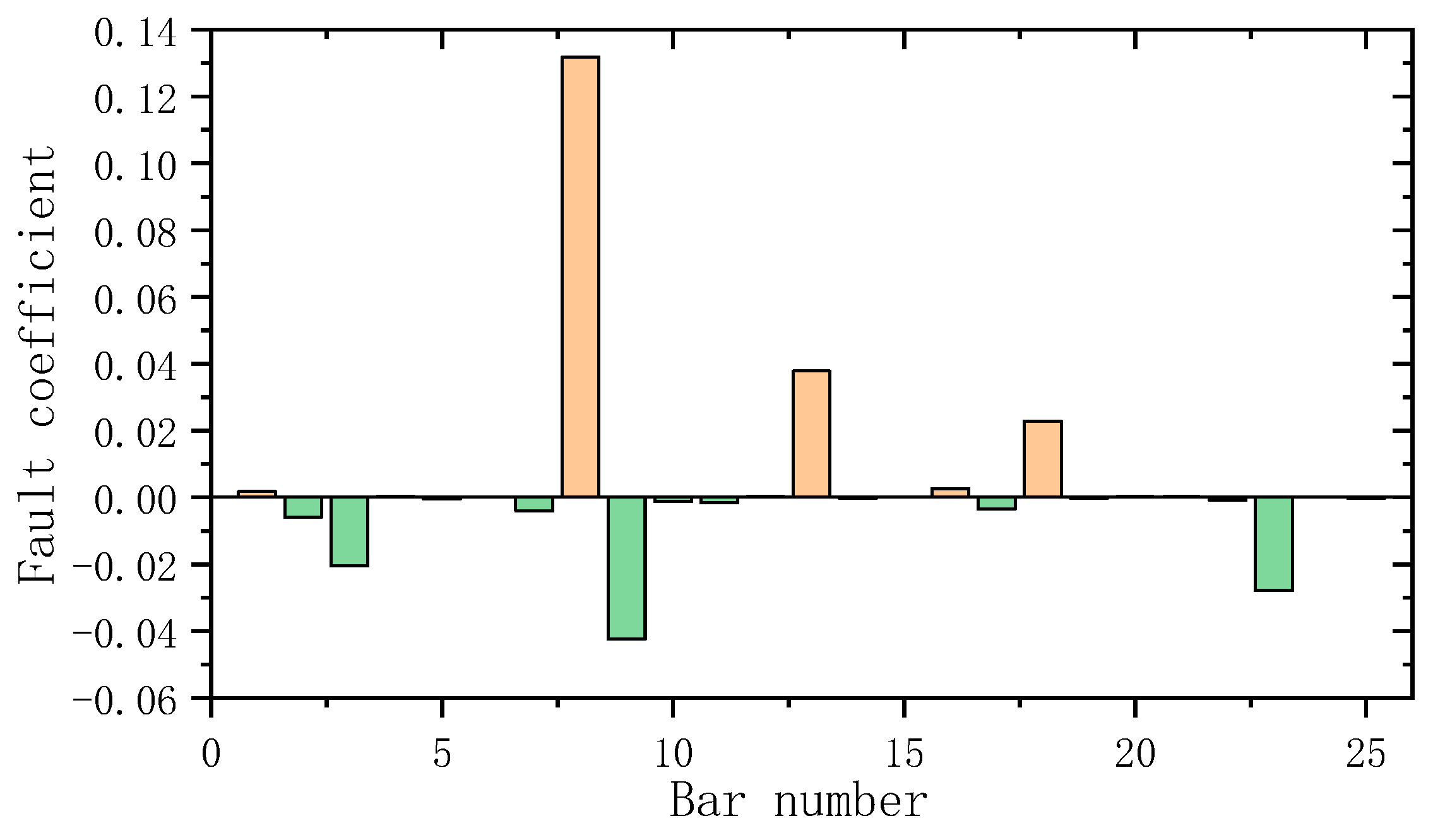
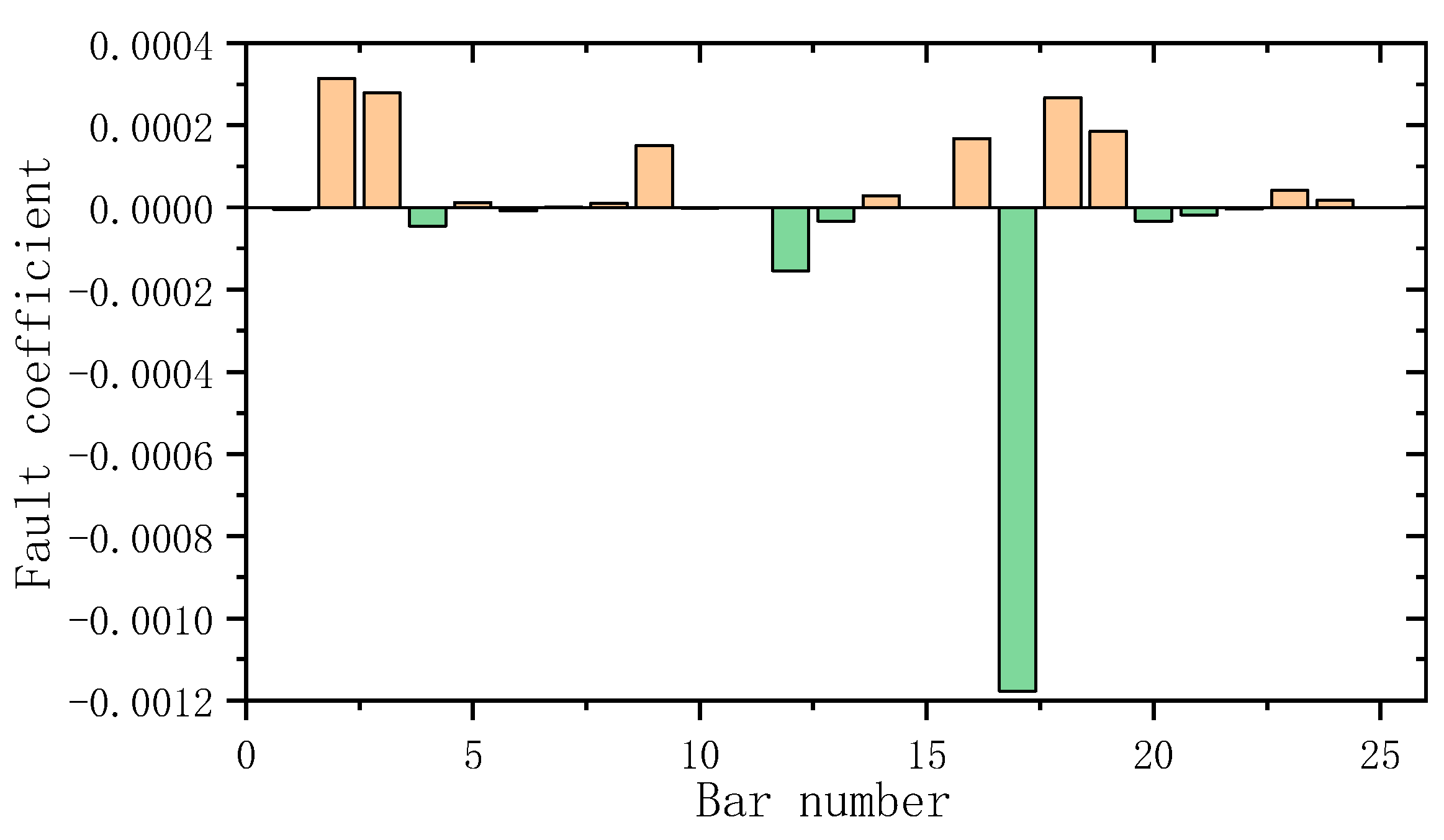
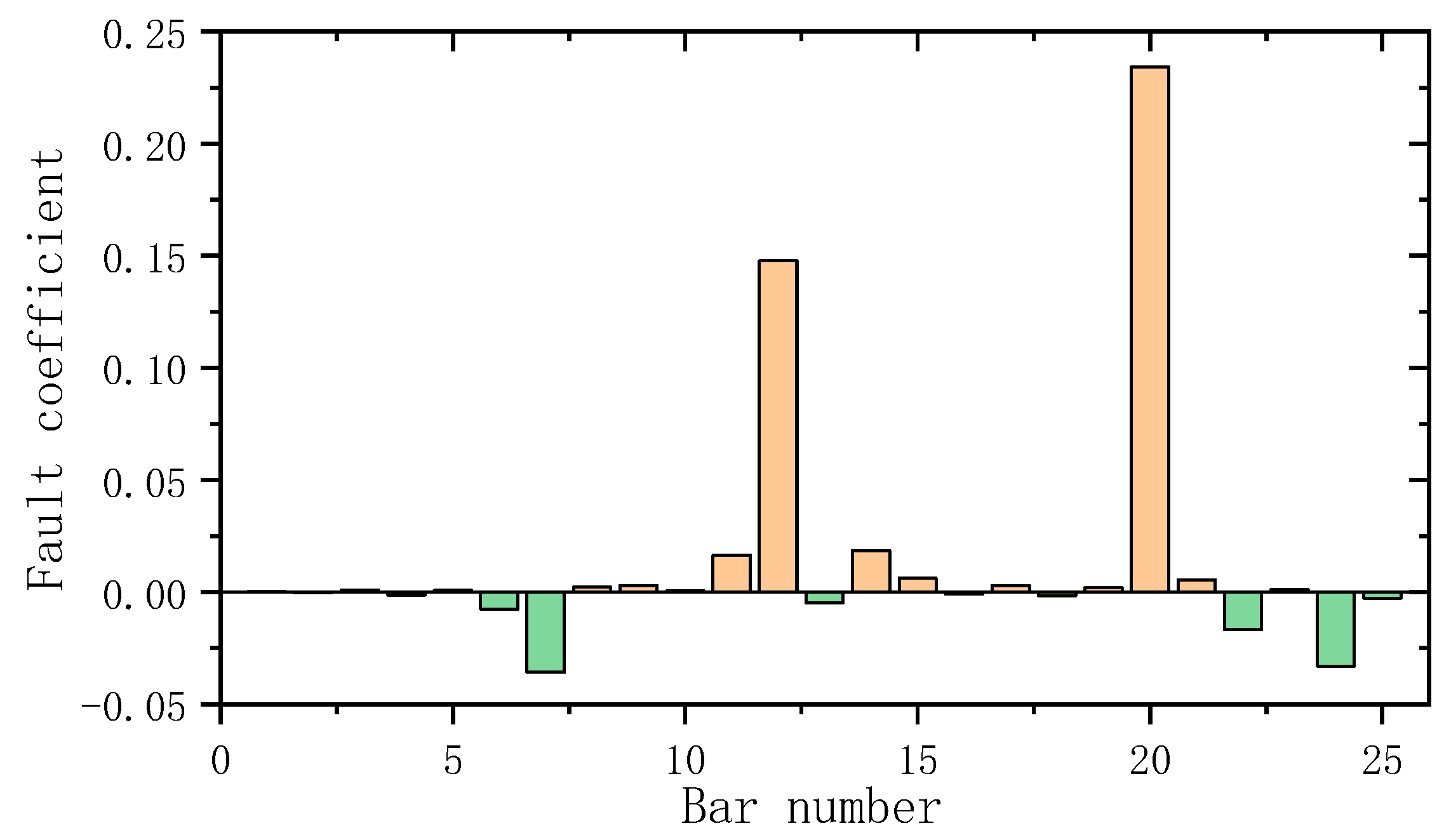
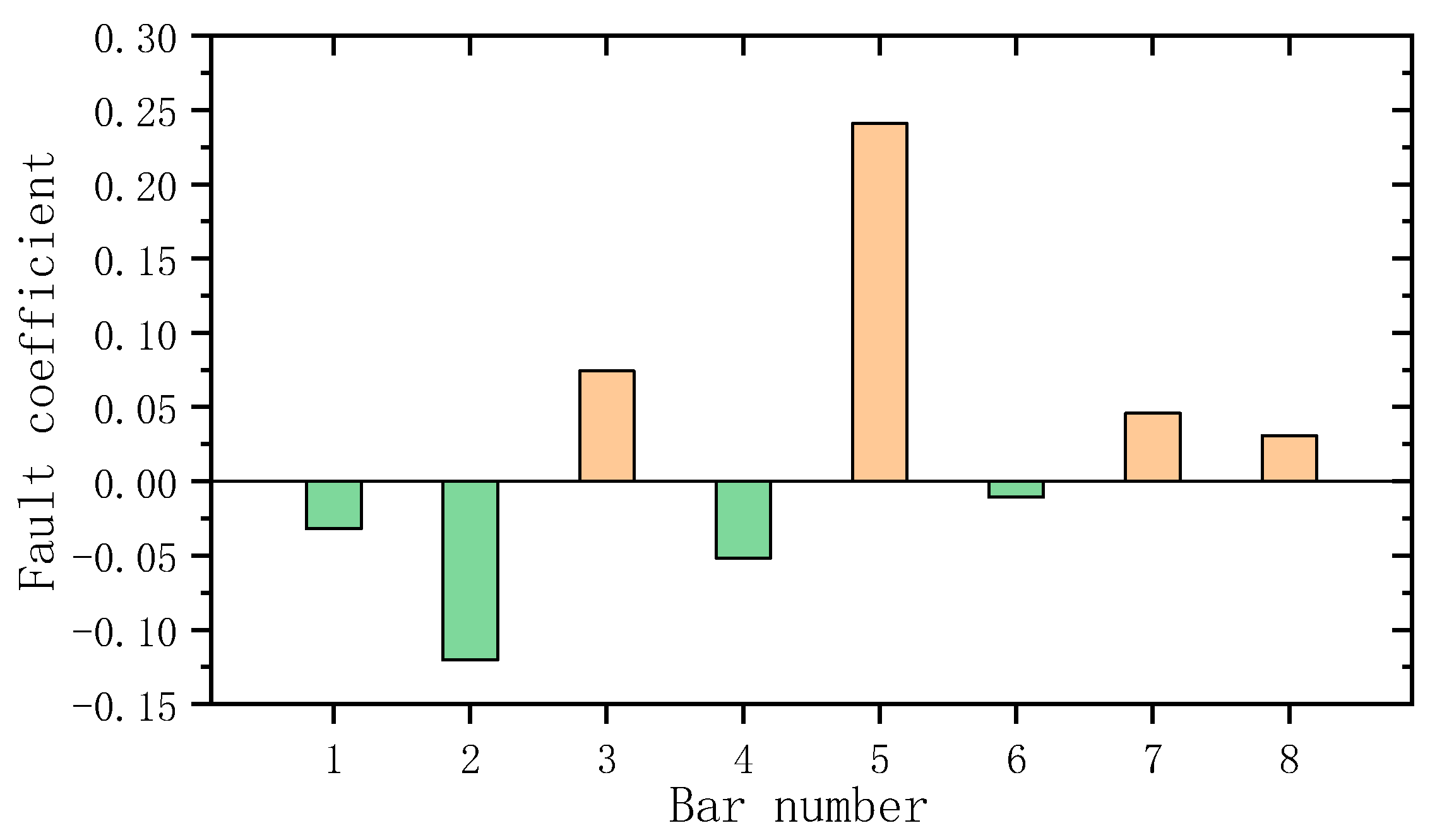
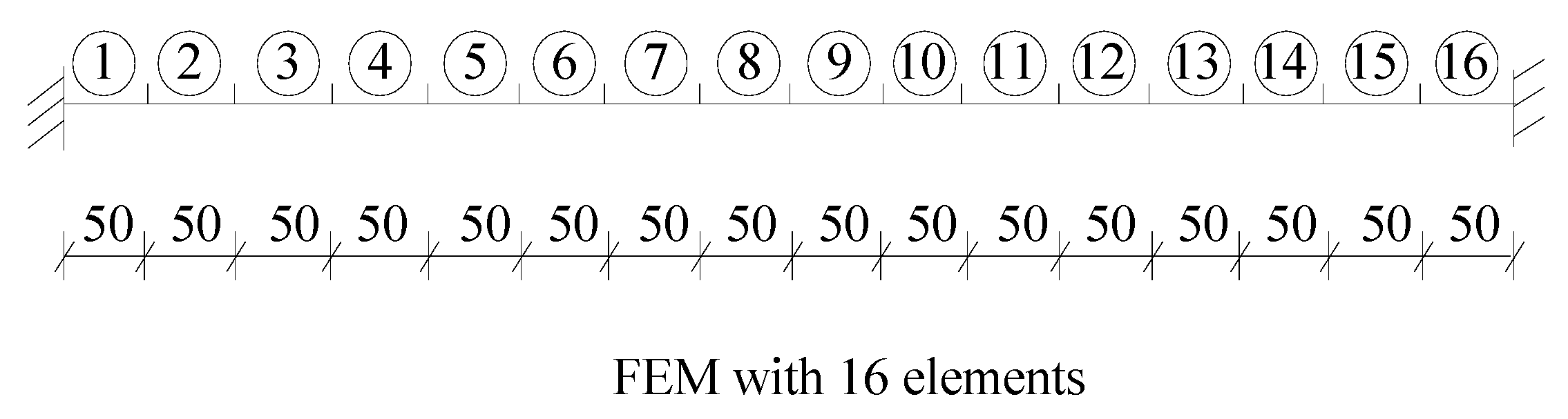
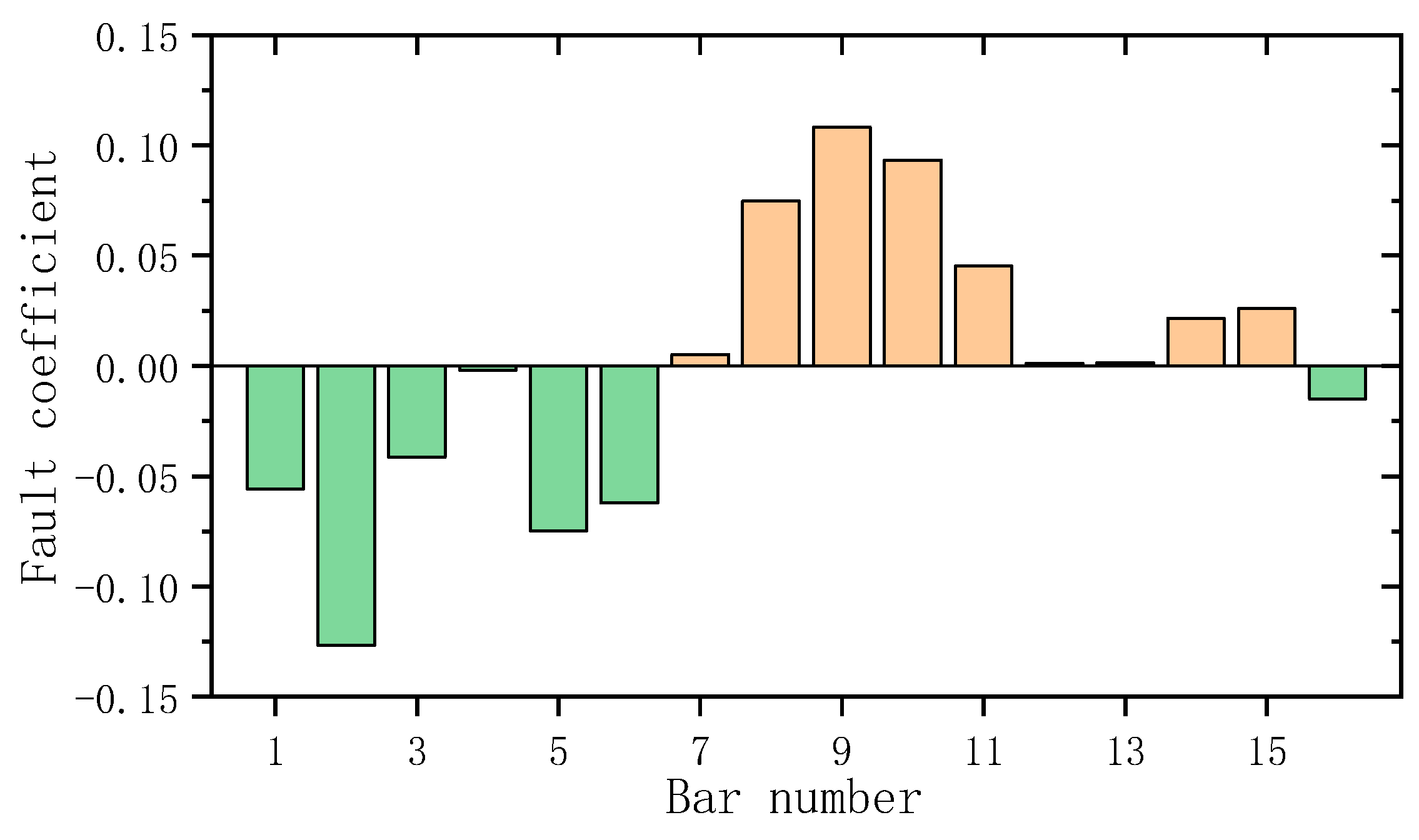
3. Numerical Example
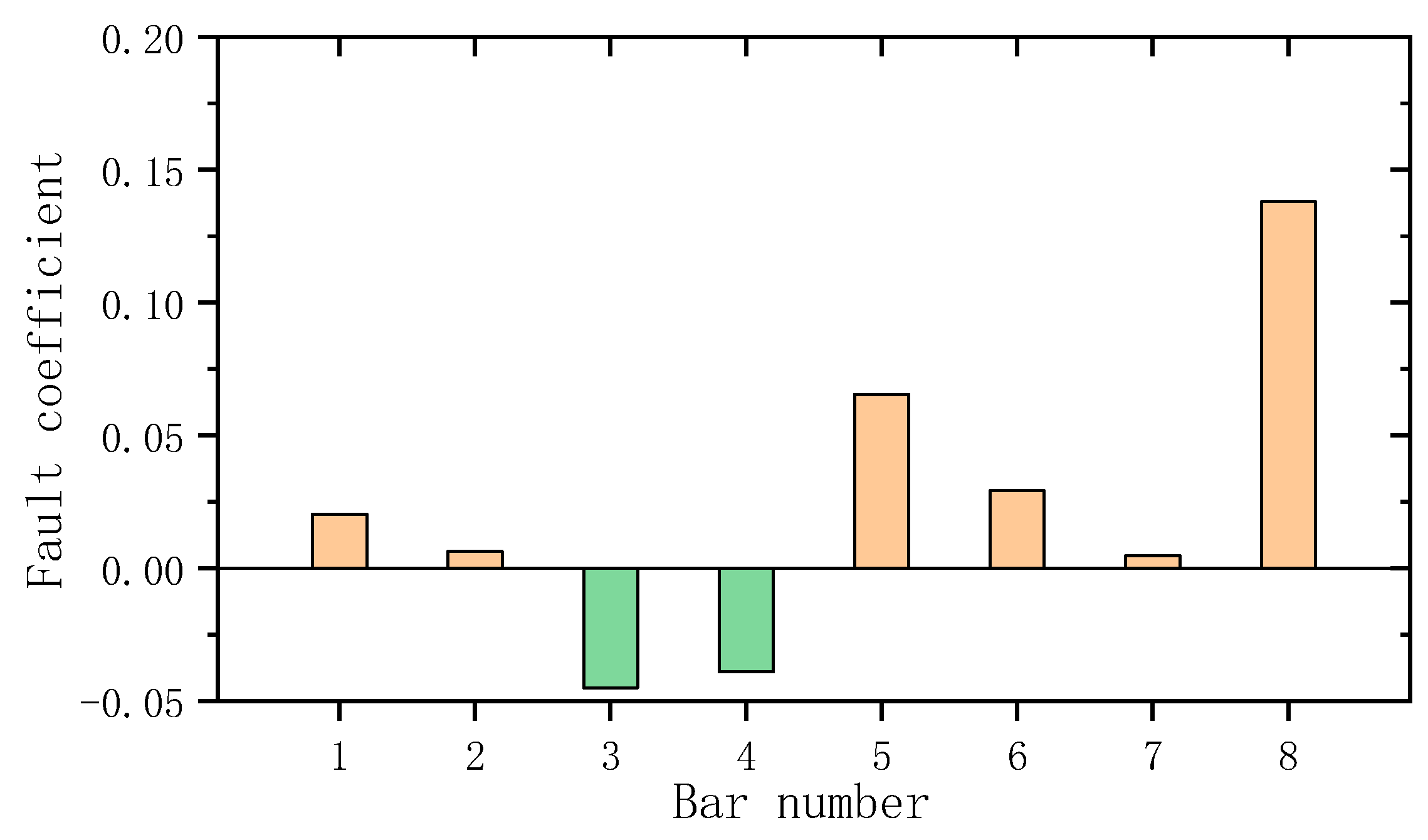
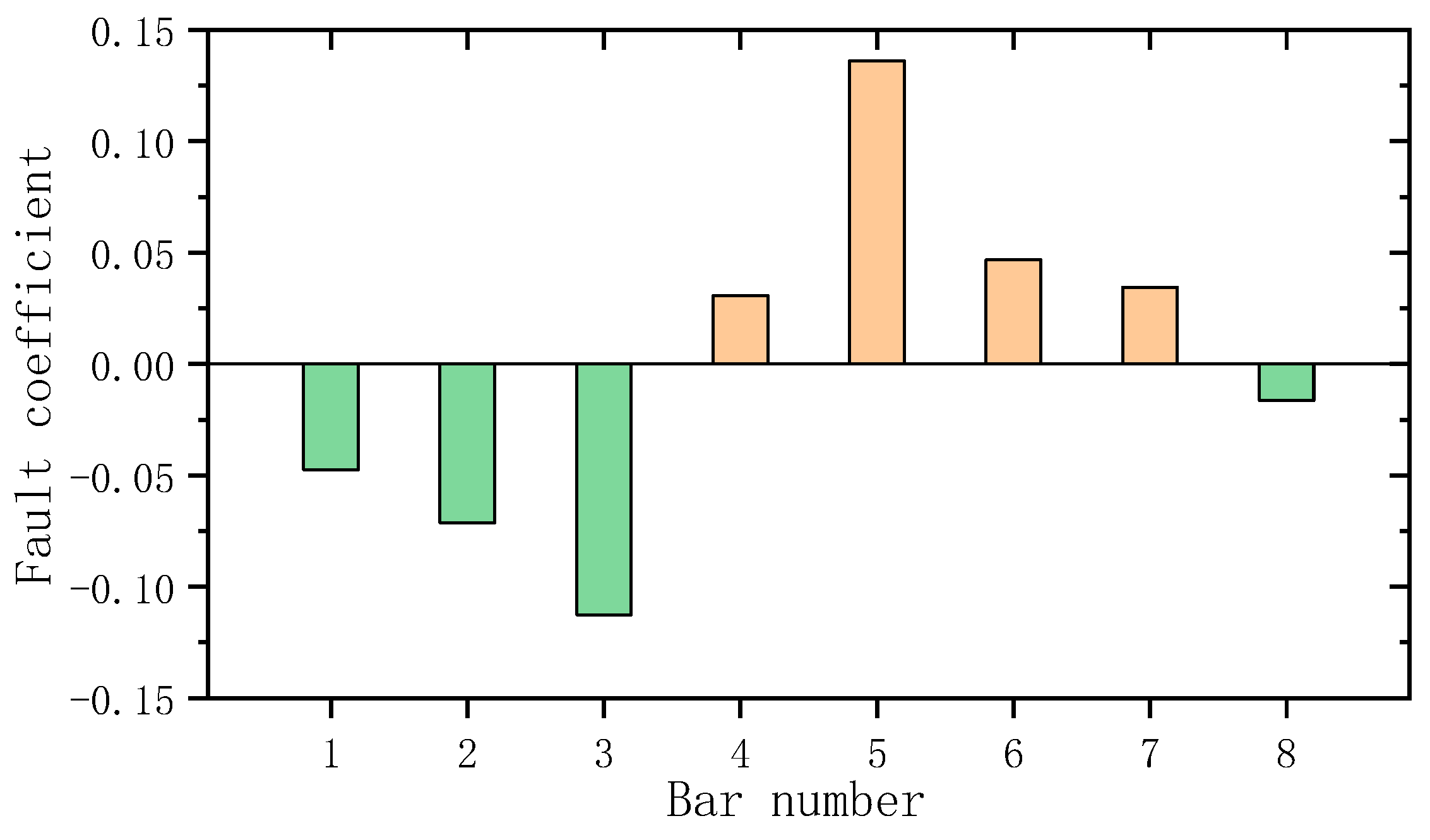
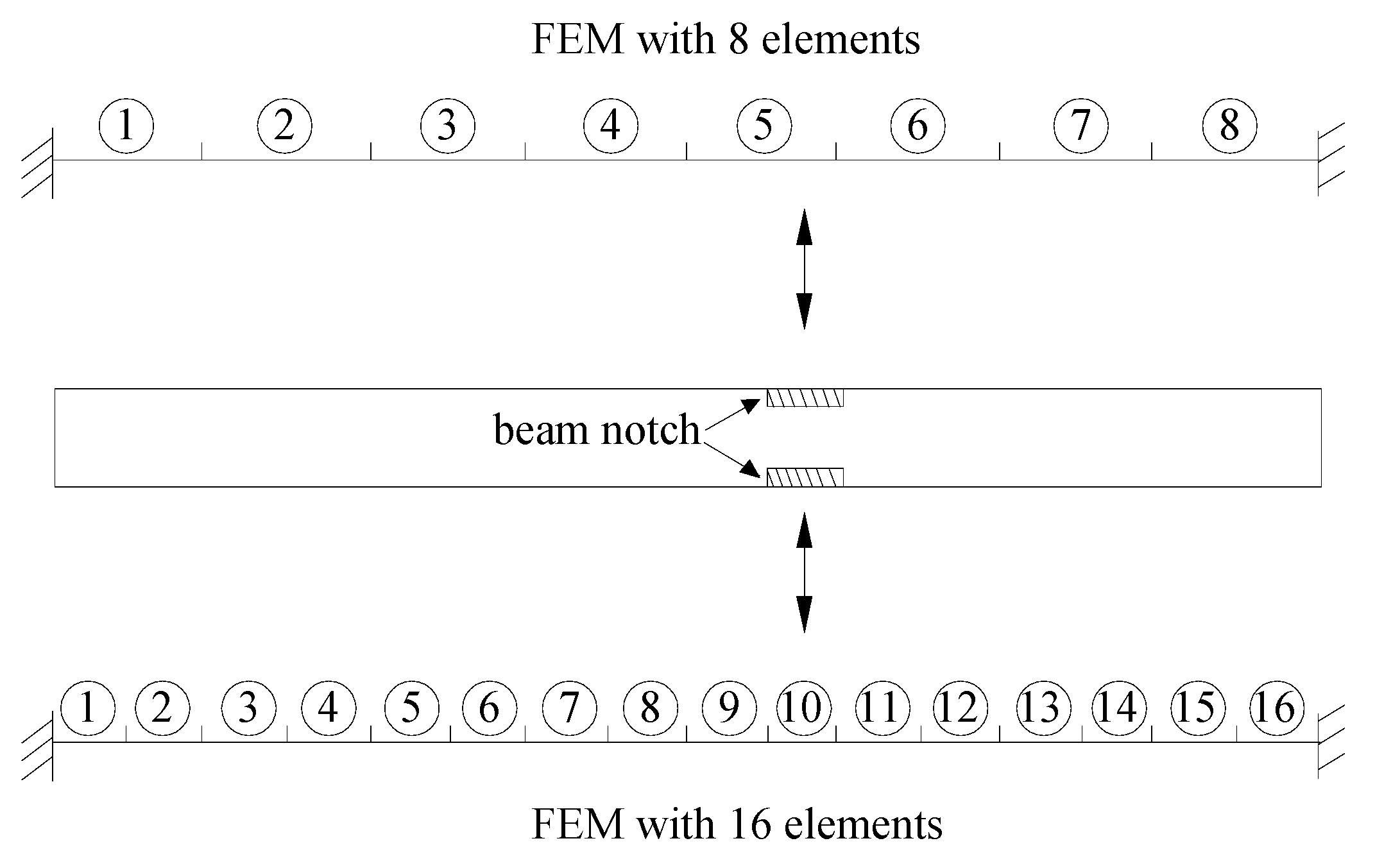
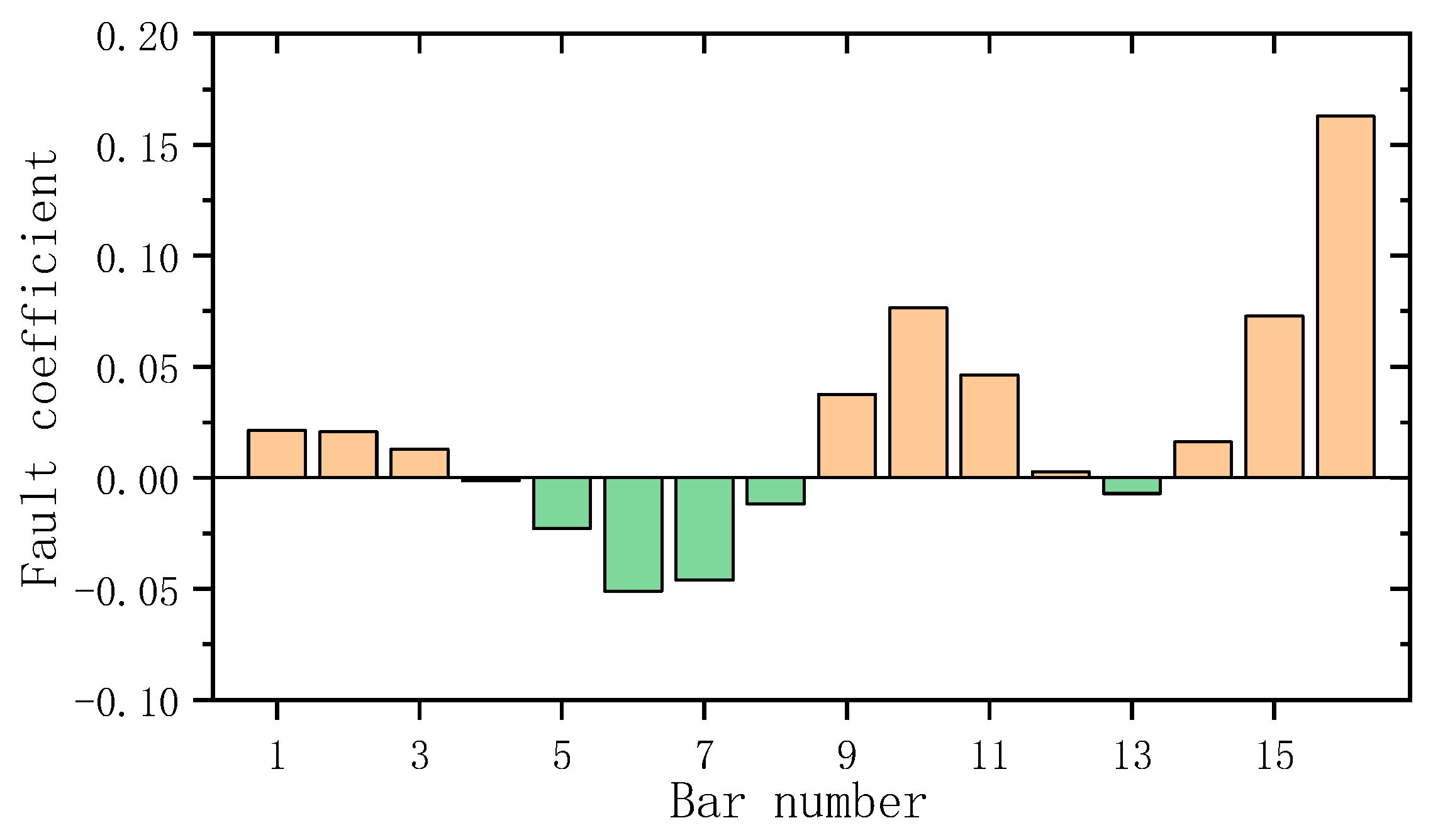
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Yang, Q.; Peng, X. Damage Identification for Shear-Type Structures Using the Change of Generalized Shear Energy. Coatings 2022, 12, 192. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, Q.; Peng, X. Structural Damage Assessment Using Multiple-Stage Dynamic Flexibility Analysis. Aerospace 2022, 9, 295. [Google Scholar] [CrossRef]
- Fang, R.; Wu, Y.; Wei, W.; Na, L.; Biao, Q.; Jiang, P.; Yang, Q. An Improved Static Residual Force Algorithm and Its Application in Cable Damage Identification for Cable-Stayed Bridges. Appl. Sci. 2022, 12, 2945. [Google Scholar] [CrossRef]
- Yang, Q.; Sun, B. Structural damage localization and quantification using static test data. Struct. Health Monit. 2010, 10, 381–389. [Google Scholar] [CrossRef]
- Yang, Q.W. Fast and Exact Algorithm for Structural Static Reanalysis Based on Flexibility Disassembly Perturbation. AIAA J. 2019, 57, 3599–3607. [Google Scholar] [CrossRef]
- Yang, Q.; Peng, X. A Fast Calculation Method for Sensitivity Analysis Using Matrix Decomposition Technique. Axioms 2023, 12, 179. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, C.; Li, N.; Luo, S.; Wang, W. Model-Free Method for Damage Localization of Grid Structure. Appl. Sci. 2019, 9, 3252. [Google Scholar] [CrossRef]
- Bakhtiari-Nejad, F.; Rahai, A.; Esfandiari, A. A structural damage detection method using static noisy data. Eng. Struct. 2005, 27, 1784–1793. [Google Scholar] [CrossRef]
- Abdo, M.A.B. Parametric study of using only static response in structural damage detection. Eng. Struct. 2012, 34, 124–131. [Google Scholar] [CrossRef]
- Tian, S.; Yang, Z.; Chen, X.; Xie, Y. Damage Detection Based on Static Strain Responses Using FBG in a Wind Turbine Blade. Sensors 2015, 15, 19992–20005. [Google Scholar] [CrossRef]
- Santos, J.; Cremona, C.; Orcesi, A.; Silveira, P.; Calado, L. Static-based early-damage detection using symbolic data analysis and unsupervised learning methods. Front. Struct. Civ. Eng. 2015, 9, 1–16. [Google Scholar] [CrossRef]
- Viola, E.; Bocchini, P. Non-destructive parametric system identification and damage detection in truss structures by static tests. Struct. Infrastruct. Eng. 2013, 9, 384–402. [Google Scholar] [CrossRef]
- Terlaje, A.S., III; Truman, K.Z. Parameter identification and damage detection using structural optimization and static response data. Adv. Struct. Eng. 2007, 10, 607–621. [Google Scholar] [CrossRef]
- Boumechra, N. Damage detection in beam and truss structures by the inverse analysis of the static response due to moving loads. Struct. Control. Health Monit. 2016, 24, e1972. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Q. Damage detection in beam-like structures using static shear energy redistribution. Front. Struct. Civ. Eng. 2022, 16, 1552–1564. [Google Scholar] [CrossRef]
- Chrysanidis, T. Experimental and numerical research on cracking characteristics of medium-reinforced prisms under variable uniaxial degrees of elongation. Eng. Fail. Anal. 2023, 145, 107014. [Google Scholar] [CrossRef]
- Lu, Z.; Law, S. Features of dynamic response sensitivity and its application in damage detection. J. Sound Vib. 2007, 303, 305–329. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection—A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Gentile, C.; Guidobaldi, M.; Saisi, A. One-year dynamic monitoring of a historic tower: Damage detection under changing environment. Meccanica 2016, 51, 2873–2889. [Google Scholar] [CrossRef]
- Cardoso, R.D.A.; Cury, A.; Barbosa, F. Automated real-time damage detection strategy using raw dynamic measurements. Eng. Struct. 2019, 196, 109364. [Google Scholar] [CrossRef]
- Yang, Q.W.; Peng, X. A highly efficient method for structural model reduction. Int. J. Numer. Methods Eng. 2022, 124, 513–533. [Google Scholar] [CrossRef]
- Yang, Q.; Peng, X. Sensitivity Analysis Using a Reduced Finite Element Model for Structural Damage Identification. Materials 2021, 14, 5514. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Yang, Q.-W. Sensor Placement and Structural Damage Evaluation by Improved Generalized Flexibility. IEEE Sensors J. 2021, 21, 11654–11664. [Google Scholar] [CrossRef]
- Weng, S.; Zhu, H.; Xia, Y.; Li, J.; Tian, W. A review on dynamic substructuring methods for model updating and damage detection of large-scale structures. Adv. Struct. Eng. 2019, 23, 584–600. [Google Scholar] [CrossRef]
- Meixedo, A.; Santos, J.; Ribeiro, D.; Calçada, R.; Todd, M. Damage detection in railway bridges using traffic-induced dynamic responses. Eng. Struct. 2021, 238, 112189. [Google Scholar] [CrossRef]
- Yang, Q.; Peng, X. An Exact Method for Calculating the Eigenvector Sensitivities. Appl. Sci. 2020, 10, 2577. [Google Scholar] [CrossRef]
- Yang, Q.; Sun, B.; Lu, C. An improved spectral decomposition flexibility perturbation method for finite element model updating. Adv. Mech. Eng. 2018, 10, 1687814018814920. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Qin, F.; Peng, X. Structural Fault Diagnosis Based on Static and Dynamic Response Parameters. Coatings 2023, 13, 920. https://doi.org/10.3390/coatings13050920
Yang Q, Qin F, Peng X. Structural Fault Diagnosis Based on Static and Dynamic Response Parameters. Coatings. 2023; 13(5):920. https://doi.org/10.3390/coatings13050920
Chicago/Turabian StyleYang, Qiuwei, Fengjiang Qin, and Xi Peng. 2023. "Structural Fault Diagnosis Based on Static and Dynamic Response Parameters" Coatings 13, no. 5: 920. https://doi.org/10.3390/coatings13050920





