Ring-Core Photonic Crystal Fiber Sensor Based on SPR for Extra-Wide Refractive Index Detection
Abstract
:1. Introduction
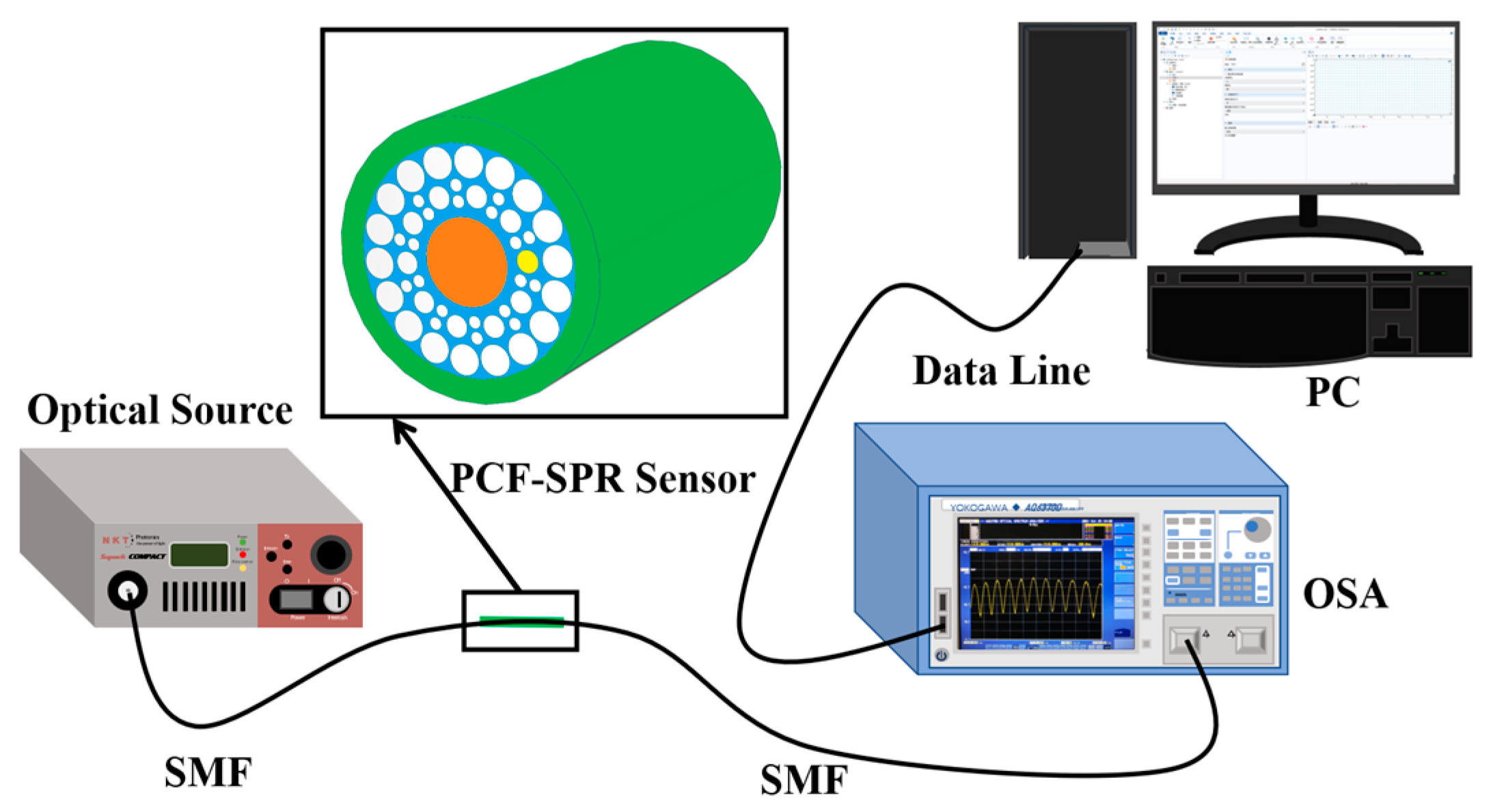
2. Numerical Modelling
3. Results and Discussion
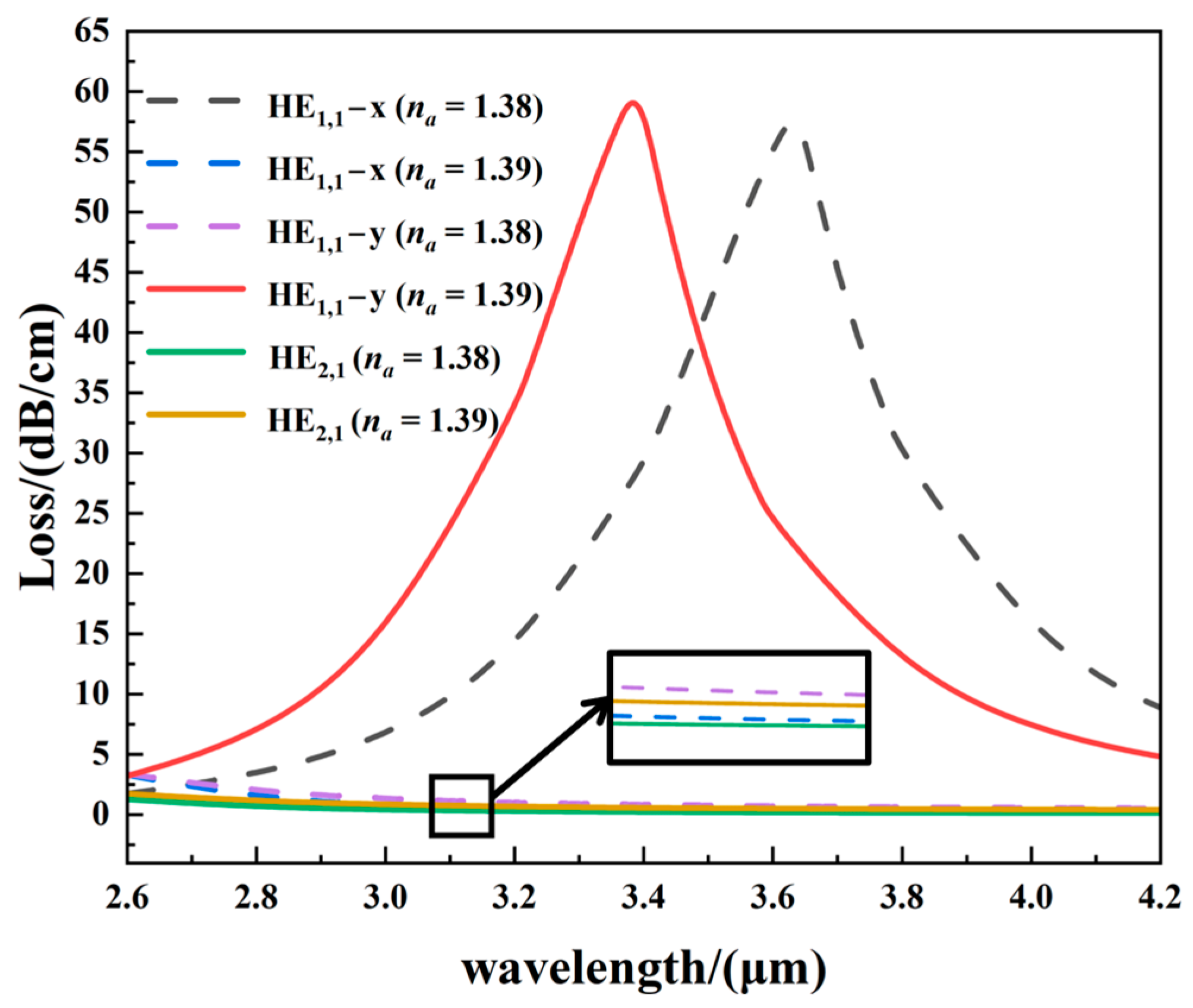
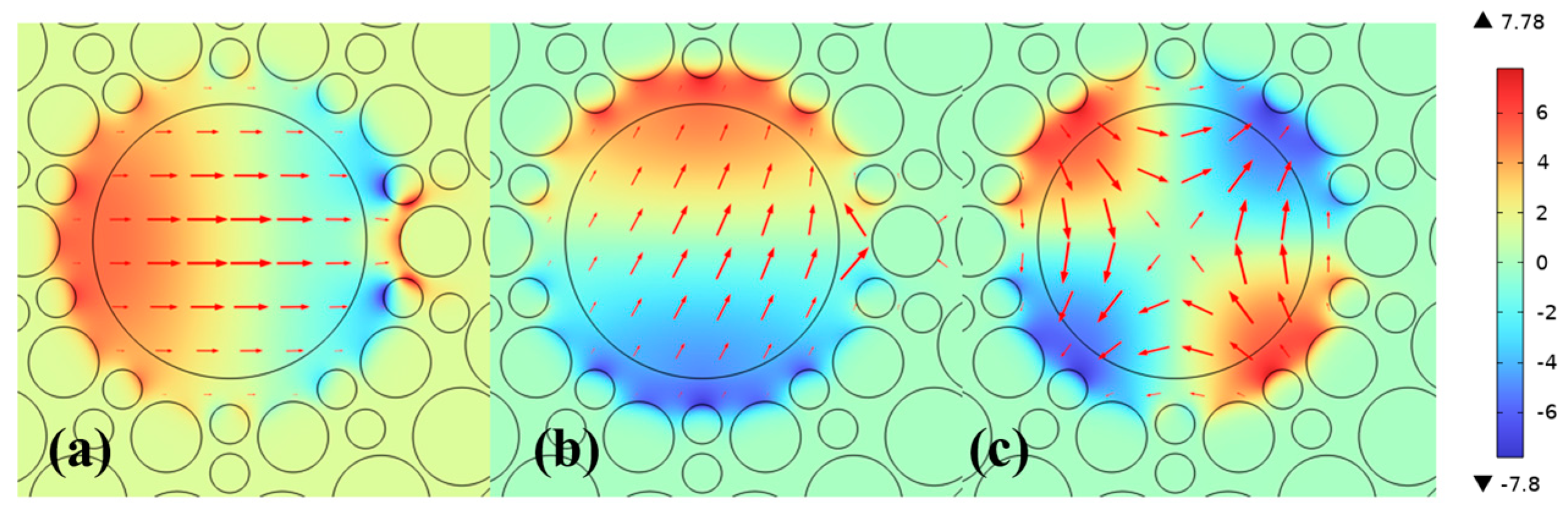
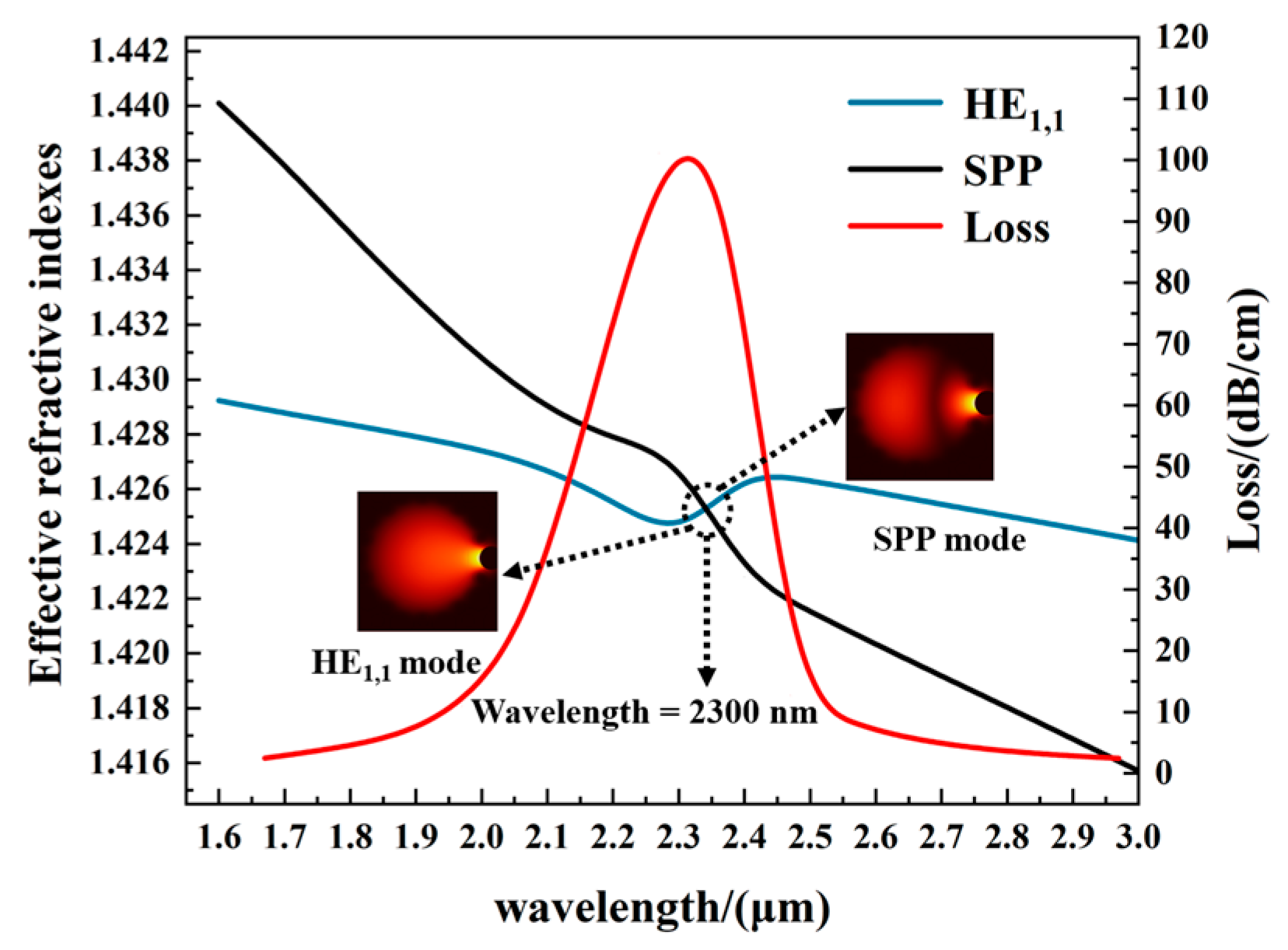
3.1. Coupling Characteristics
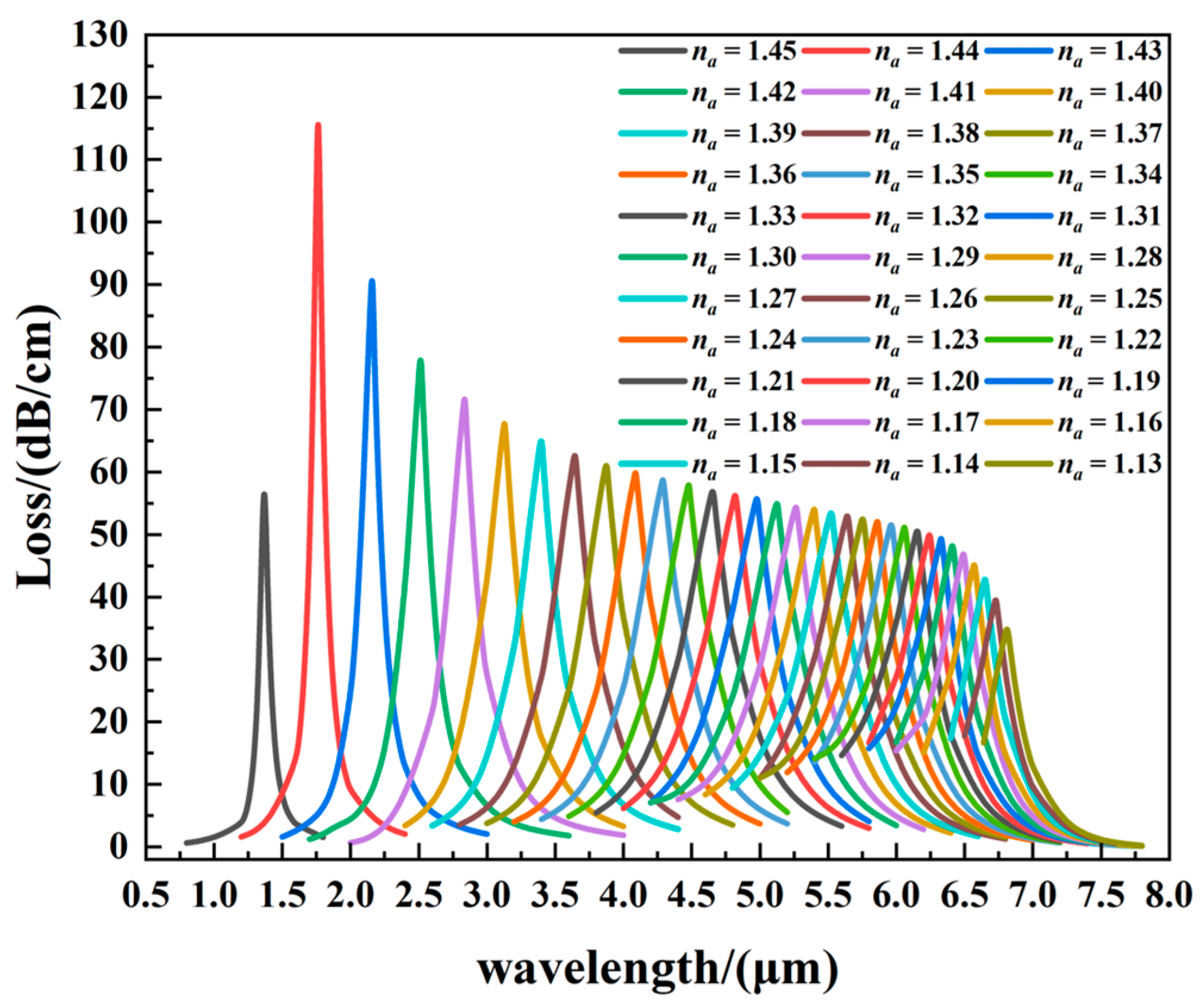
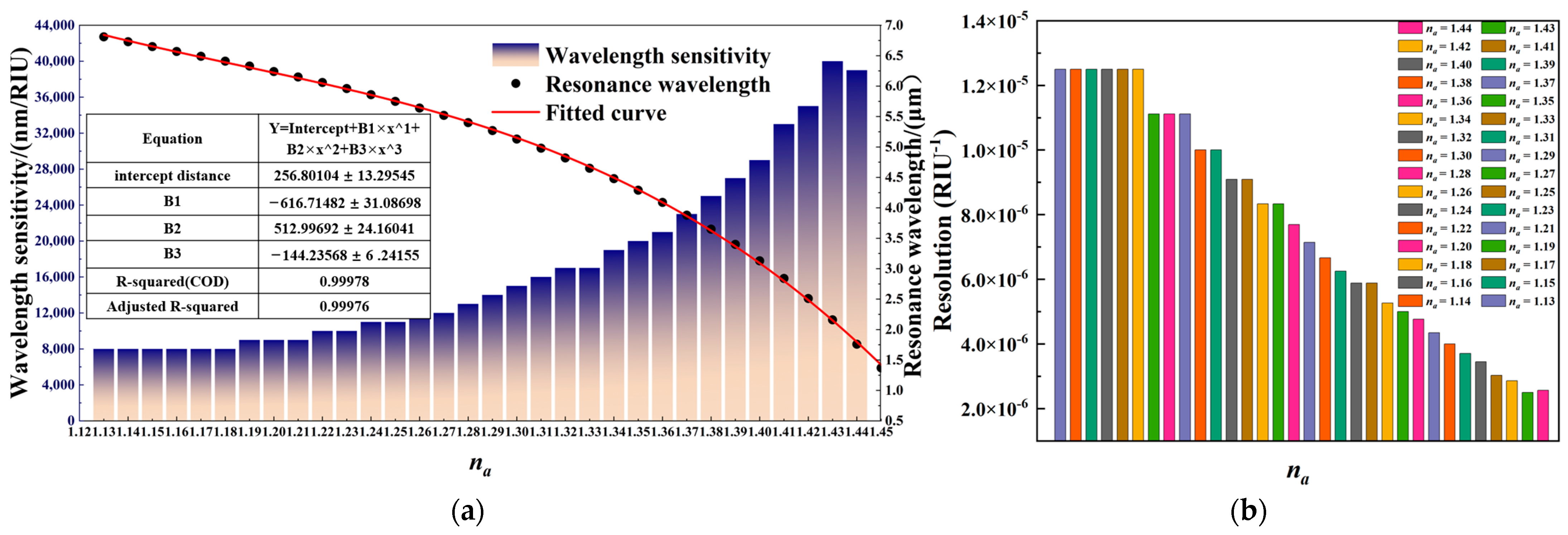
3.2. Wavelength Sensitivity and Resolution
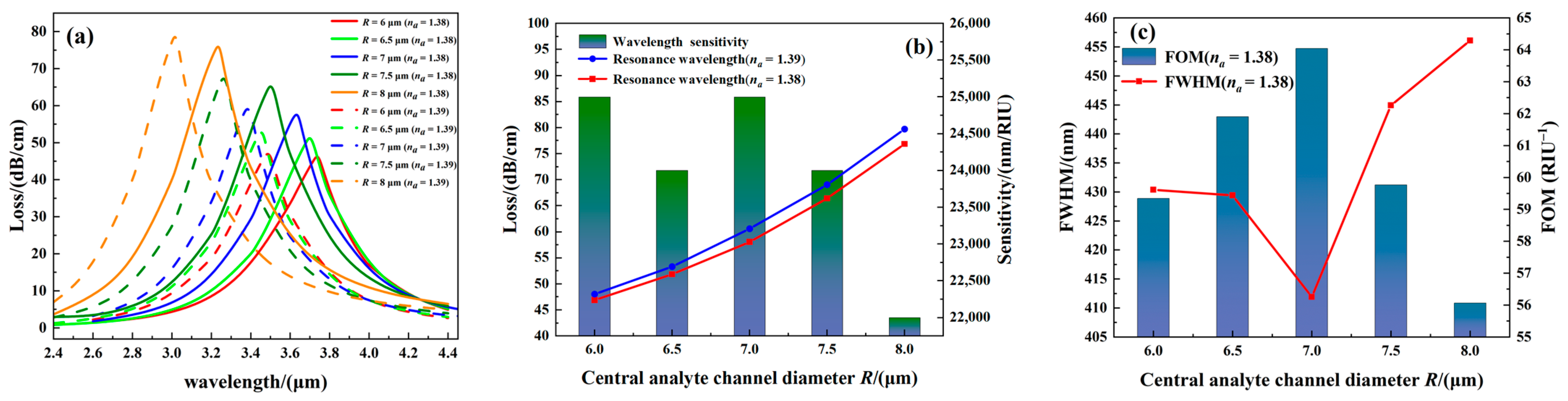
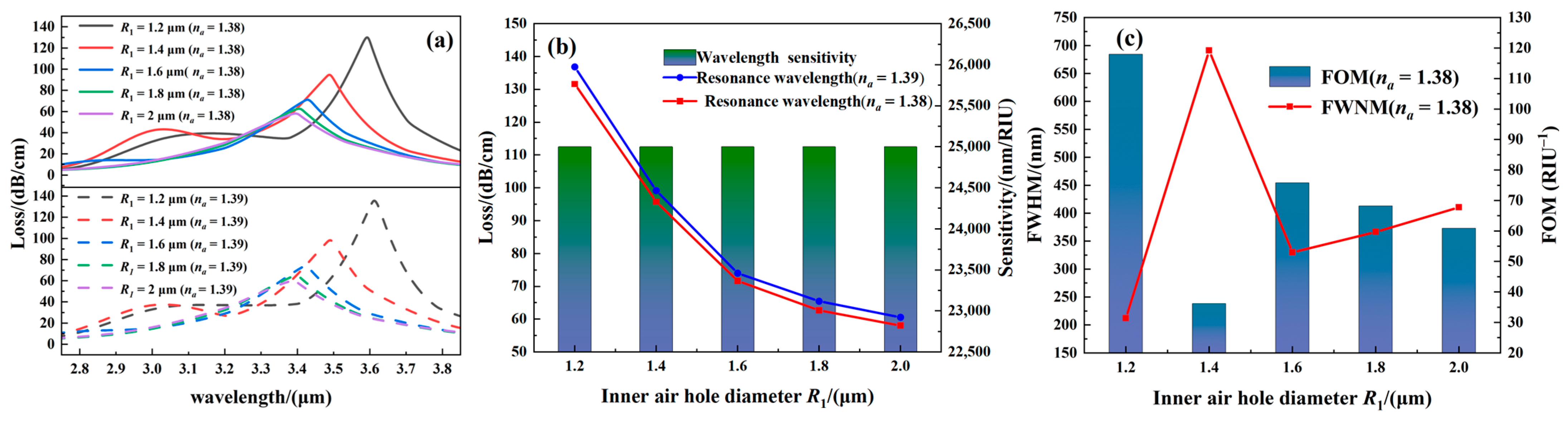
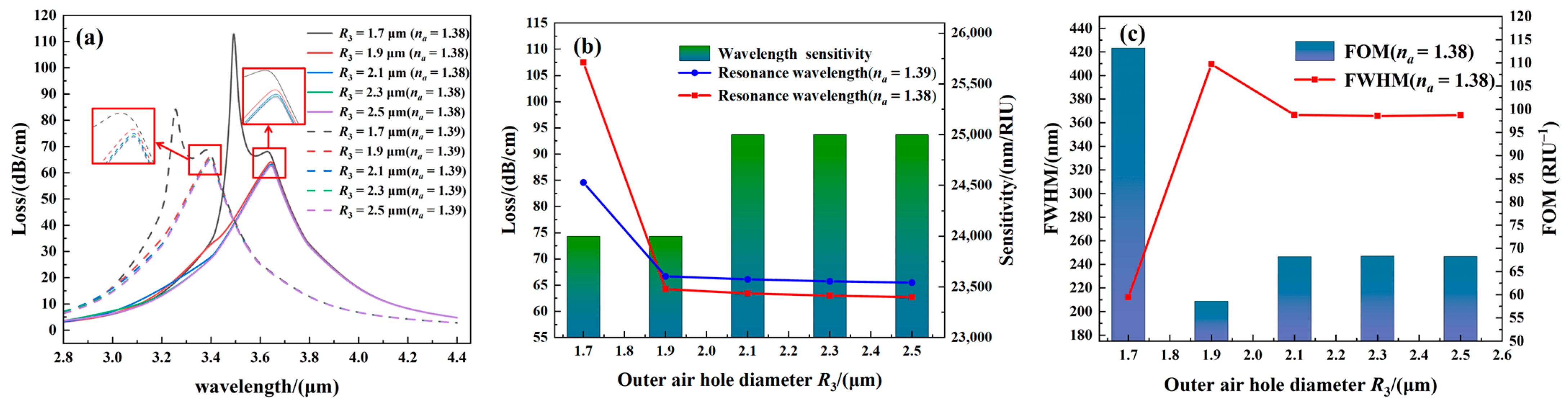
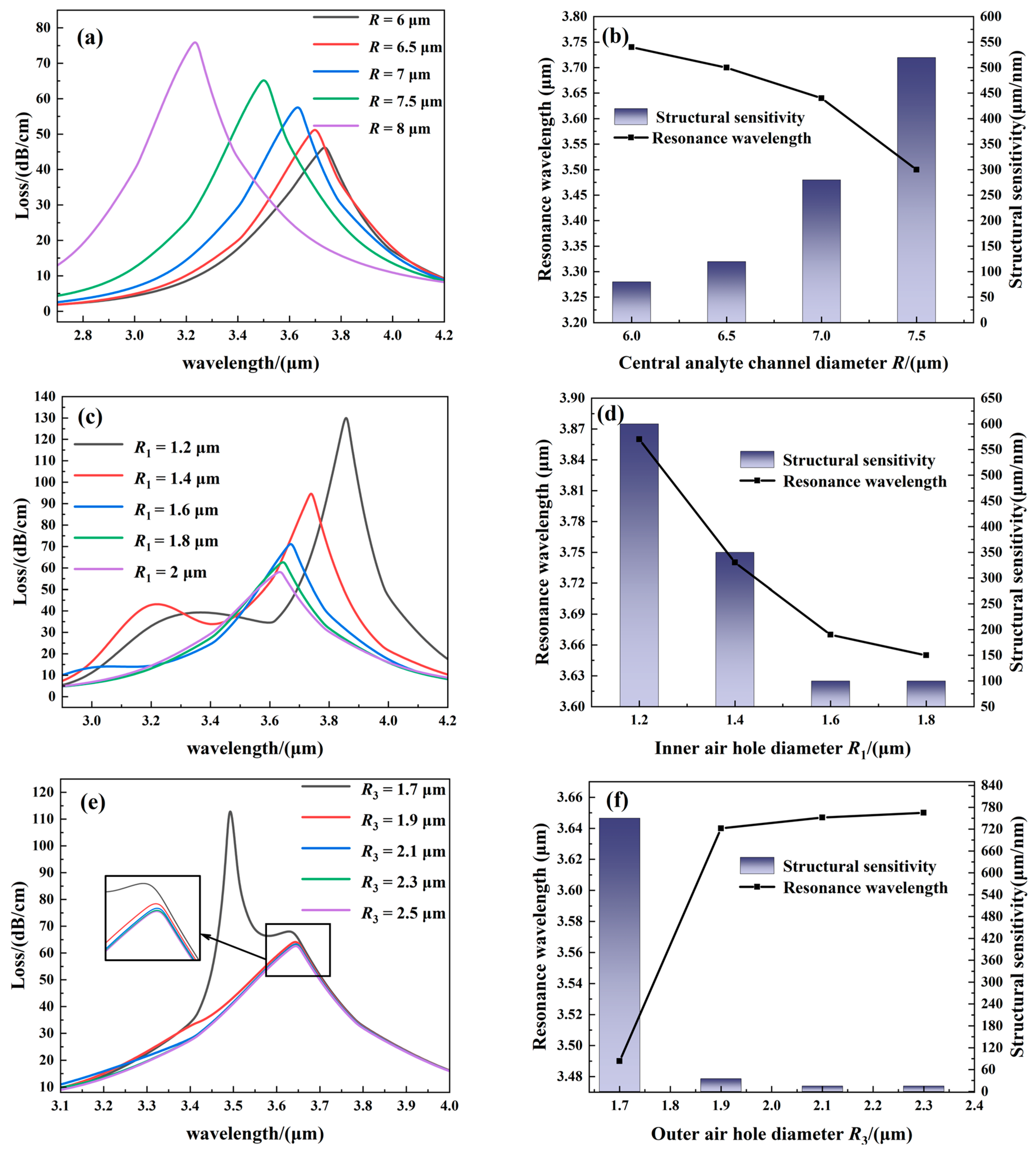
3.3. Structural Sensitivity
3.4. Amplitude Sensitivity
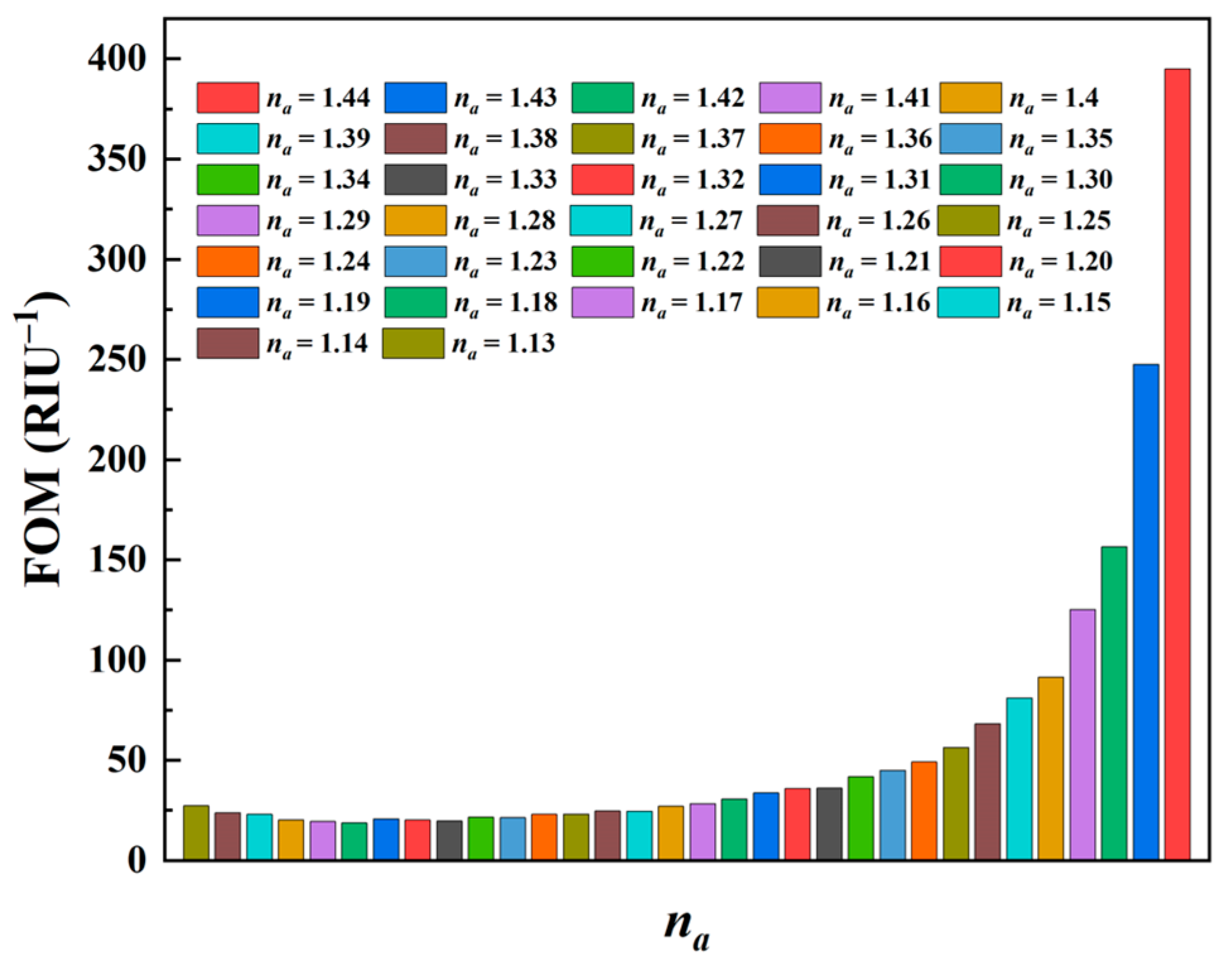
3.5. FOM
3.6. Comparison of Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Culshaw, B. Optical fiber sensor technologies: Opportunities and-perhaps-pitfalls. J. Light. Technol. 2004, 22, 39. [Google Scholar] [CrossRef]
- Chen, X.; Xia, L.; Li, C. Surface plasmon resonance sensor based on a novel D-shaped photonic crystal fiber for low refractive index detection. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Liu, W.; Hu, C.; Zhou, L.; Yi, Z.; Liu, C.; Lv, J.; Yang, L.; Chu, P.K. A square-lattice D-shaped photonic crystal fiber sensor based on SPR to detect analytes with large refractive indexes. Phys. E Low-Dimens. Syst. Nanostructures 2022, 138, 115106. [Google Scholar] [CrossRef]
- Liu, W.; Shi, Y.; Yi, Z.; Liu, C.; Wang, F.; Li, X.; Lv, J.; Yang, L.; Chu, P.K. Surface plasmon resonance chemical sensor composed of a microstructured optical fiber for the detection of an ultra-wide refractive index range and gas-liquid pollutants. Opt. Express 2021, 29, 40734–40747. [Google Scholar] [CrossRef]
- Liu, W.; Liu, C.; Wang, J.; Lv, J.; Lv, Y.; Yang, L.; An, N.; Yi, Z.; Liu, Q.; Hu, C. Surface plasmon resonance sensor composed of microstructured optical fibers for monitoring of external and internal environments in biological and environmental sensing. Results Phys. 2023, 47, 106365. [Google Scholar] [CrossRef]
- Liu, C.; Lü, J.; Liu, W.; Wang, F.; Chu, P.K. Overview of refractive index sensors comprising photonic crystal fibers based on the surface plasmon resonance effect. Chin. Opt. Lett. 2021, 19, 102202. [Google Scholar] [CrossRef]
- Hien, N.D. Optical properties of a single quantum well with Pöschl–Teller confinement potential. Phys. E Low-Dimens. Syst. Nanostructures 2023, 145, 115504. [Google Scholar] [CrossRef]
- Zhukova, L.; Salimgareev, D.; Lvov, A.; Yuzhakova, A.; Korsakov, A.; Belousov, D.; Lipustin, K.; Kondrashin, V. Highly transparent ceramics for the spectral range from 1.0 to 60.0 µm based on solid solutions of the system AgBr–AgI–TlI–TlBr. Chin. Opt. Lett. 2021, 19, 021602. [Google Scholar] [CrossRef]
- Butt, M.; Khonina, S.; Kazanskiy, N. Plasmonics: A necessity in the field of sensing—A review. Fiber Integr. Opt. 2021, 40, 14–47. [Google Scholar] [CrossRef]
- Jain, S.; Choudhary, K.; Kumar, S. Photonic crystal fiber-based SPR sensor for broad range of refractive index sensing applications. Opt. Fiber Technol. 2022, 73, 103030. [Google Scholar] [CrossRef]
- Singh, Y.; Raghuwanshi, S.K. Titanium dioxide (TiO2) coated optical fiber-based SPR sensor in near-infrared region with bimetallic structure for enhanced sensitivity. Optik 2021, 226, 165842. [Google Scholar] [CrossRef]
- Liu, W.; Hu, C.; Zhou, L.; Yi, Z.; Liu, C.; Lv, J.; Yang, L.; Chu, P.K. Ultra-sensitive hexagonal PCF-SPR sensor with a broad detection range. J. Mod. Opt. 2020, 67, 1545–1554. [Google Scholar] [CrossRef]
- Xiong, Y.; Shepherd, S.; Tibbs, J.; Bacon, A.; Liu, W.; Akin, L.D.; Ayupova, T.; Bhaskar, S.; Cunningham, B.T. Photonic crystal enhanced fluorescence: A review on design strategies and applications. Micromachines 2023, 14, 668. [Google Scholar] [CrossRef] [PubMed]
- Gauvreau, B.; Hassani, A.; Fehri, M.F.; Kabashin, A.; Skorobogatiy, M. Photonic bandgap fiber-based surface plasmon resonance sensors. Opt. Express 2007, 15, 11413–11426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hassani, A.; Skorobogatiy, M. Design criteria for microstructured-optical-fiber-based surface-plasmon-resonance sensors. J. Opt. Soc. Am. B 2007, 24, 1423–1429. [Google Scholar] [CrossRef]
- Wang, J.; Pei, L.; Wu, L.; Wang, J.; Ruan, Z.; Zheng, J. A polarization-independent SPR sensor based on photonic crystal fiber for low RI detection. Plasmonics 2020, 15, 327–333. [Google Scholar] [CrossRef]
- Liang, H.; Shen, T.; Feng, Y.; Liu, H.; Han, W. A D-Shaped photonic crystal fiber refractive index sensor coated with graphene and zinc oxide. Sensors 2020, 21, 71. [Google Scholar] [CrossRef]
- Ramani, U.; Kumar, H.; Singh, B.K.; Pandey, P.C. Design of surface plasmon resonance based both side polished photonic crystal fiber for highly efficient refractive index sensor. Optik 2021, 248, 168062. [Google Scholar] [CrossRef]
- Yang, H.; Wang, G.; Lu, Y.; Yao, J. Highly sensitive refractive index sensor based on SPR with silver and titanium dioxide coating. Opt. Quantum Electron. 2021, 53, 341. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Dinovitser, A.; Ng, B.W.-H.; Abbott, D. A gold coated plasmonic sensor for biomedical and biochemical analyte detection. In Proceedings of the 2018 43rd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Nagoya, Japan, 9–14 September 2018; pp. 1–2. [Google Scholar]
- Liu, W.; Hu, C.; Zhou, L.; Yi, Z.; Shi, Y.; Liu, C.; Lv, J.; Yang, L.; Chu, P.K. A highly sensitive D-type photonic crystal fiber infrared sensor with indium tin oxide based on surface plasmon resonance. Mod. Phys. Lett. B 2022, 36, 2150499. [Google Scholar] [CrossRef]
- Hossain, M.B.; Mahendiran, T.; Abdulrazak, L.F.; Mehedi, I.M.; Hossain, M.A.; Rana, M.M. Numerical analysis of gold coating based quasi D-shape dual core PCF SPR sensor. Opt. Quantum Electron. 2020, 52, 446. [Google Scholar] [CrossRef]
- Liu, W.; Wang, F.; Liu, C.; Yang, L.; Liu, Q.; Su, W.; Lv, J.; An, S.; Li, X.; Sun, T. A hollow dual-core PCF-SPR sensor with gold layers on the inner and outer surfaces of the thin cladding. Results Opt. 2020, 1, 100004. [Google Scholar] [CrossRef]
- Noman, A.A.; Haque, E.; Hossain, M.A.; Hai, N.H.; Namihira, Y.; Ahmed, F. Sensitivity enhancement of modified D-shaped microchannel PCF-based surface plasmon resonance sensor. Sensors 2020, 20, 6049. [Google Scholar] [CrossRef]
- Liu, C.; Fu, H.; Lv, Y.; Yi, Z.; Lin, J.; Lv, J.; Yang, L.; Chu, P.K. HE1, 1 mode-excited surface plasmon resonance for refractive index sensing by photonic crystal fibers with high sensitivity and long detection distance. Optik 2022, 265, 169471. [Google Scholar] [CrossRef]
- Zhou, X.; Cheng, T.; Li, S.; Suzuki, T.; Ohishi, Y. Practical sensing approach based on surface plasmon resonance in a photonic crystal fiber. OSA Contin. 2018, 1, 1332–1340. [Google Scholar] [CrossRef]
- Luan, N.; Yao, J. A hollow-core photonic crystal fiber-based SPR sensor with large detection range. IEEE Photonics J. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Paul, A.K.; Habib, M.S.; Hai, N.H.; Razzak, S.A. An air-core photonic crystal fiber based plasmonic sensor for high refractive index sensing. Opt. Commun. 2020, 464, 125556. [Google Scholar] [CrossRef]
- Rachana, M.; Charles, I.; Swarnakar, S.; Krishna, S.V.; Kumar, S. Recent advances in photonic crystal fiber-based sensors for biomedical applications. Opt. Fiber Technol. 2022, 74, 103085. [Google Scholar] [CrossRef]
- Mumtaz, F.; Roman, M.; Zhang, B.; Abbas, L.G.; Dai, Y.; Ashraf, M.A.; Fiaz, M.A.; Kumar, A. MXene (Ti3C2Tx) coated highly-sensitive D-shaped photonic crystal fiber based SPR-biosensor. Photonics Nanostructures-Fundam. Appl. 2022, 52, 101090. [Google Scholar] [CrossRef]
- Islam, M.R.; Iftekher, A.; Hasan, K.R.; Nayen, M.J.; Islam, S.B.; Islam, R.; Khan, R.L.; Moazzam, E.; Tasnim, Z. Surface plasmon resonance based highly sensitive gold coated PCF biosensor. Appl. Phys. A 2021, 127, 118. [Google Scholar] [CrossRef]
- Fan, Z.; Chu, S.; Zhang, X.; Meng, J.; Fan, Y.; Zhang, Y. Two Kinds of Liquid Crystal Filled PCFs Temperature and RI Sensors Based on SPR. IEEE Sens. J. 2023, 23, 5766–5772. [Google Scholar] [CrossRef]
- Pandey, S.K.; Singh, S.; Prajapati, Y. A novel PCF design with an ultra-flattened dispersion and low confinement loss by varying tiny air-hole concentration at core and cladding. Opt. Rev. 2021, 28, 304–313. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Yu, C.; Wang, M.; Feng, S.; Zhou, Q.; Chen, D.; Hu, L. Fabrication and laser behaviors of Yb3+ doped silica large mode area photonic crystal fiber prepared by sol–gel method. Opt. Mater. 2013, 35, 1752–1755. [Google Scholar] [CrossRef]
- Wang, S.; Feng, S.; Wang, M.; Yu, C.; Zhou, Q.; Li, H.; Tang, Y.; Chen, D.; Hu, L. Optical and laser properties of Yb3+-doped Al2O3–P2O5–SiO2 large-mode-area photonic crystal fiber prepared by the sol–gel method. Laser Phys. Lett. 2013, 10, 115802. [Google Scholar] [CrossRef]
- Xu, L.; Liu, C.; Shi, Y.; Yi, Z.; Lv, J.; Yang, L.; Wang, J.; Chu, P.K. High-sensitivity photonic crystal fiber methane sensor with a ring core based on surface plasmon resonance and orbital angular momentum theory. Optik 2023, 286, 170941. [Google Scholar] [CrossRef]
- Shakya, A.K.; Ramola, A.; Singh, S.; Van, V. Design of an ultra-sensitive bimetallic anisotropic PCF SPR biosensor for liquid analytes sensing. Opt. Express 2022, 30, 9233–9255. [Google Scholar] [CrossRef]
- Roh, S.; Chung, T.; Lee, B. Overview of the characteristics of micro-and nano-structured surface plasmon resonance sensors. Sensors 2011, 11, 1565–1588. [Google Scholar] [CrossRef] [Green Version]
- Kabashin, A.V.; Patskovsky, S.; Grigorenko, A.N. Phase and amplitude sensitivities in surface plasmon resonance bio and chemical sensing. Opt. Express 2009, 17, 21191–21204. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R.; Khan, M.M.I.; Siraz, S.; Mehjabin, F.; Rahman, M.; Islam, M.; Anzum, M.S.; Chowdhury, J.A.; Noor, F. Design and analysis of a QC-SPR-PCF sensor for multipurpose sensing with supremely high FOM. Appl. Nanosci. 2022, 12, 29–45. [Google Scholar] [CrossRef]
- Hoque, A.M.T.; Al-tabatabaie, K.F.; Ali, M.E.; Arshad, A.; Mitu, S.S.I.; Qureshi, K.K. U-grooved Selectively Coated and Highly Sensitive PCF-SPR Sensor for Broad Range Analyte RI Detection. IEEE Access 2023. [Google Scholar] [CrossRef]
- Irawan, D.; Ramadhan, K.; Fitmawati, F.; Hanto, D.; Widiyatmoko, B. High-Performance of Star-Photonics Crystal Fiber Based on Surface Plasmon Resonance Sensor. Indian J. Pure Appl. Phys. (IJPAP) 2022, 60, 727–733. [Google Scholar]
- Guo, Y.; Li, J.; Li, S.; Liu, Y.; Zhang, S.; Wang, J.; Wang, S.; Zhang, W.; Cheng, T.; Hao, R. Dual-polarized optical sensing of microstructure fiber with pentagonal-lattice based on surface plasmon resonance in the near-IR spectrum. Optik 2020, 202, 163671. [Google Scholar] [CrossRef]
- Fang, H.; Wei, C.; Yang, H.; Zhao, B.; Yuan, L.; Li, J. D-shaped photonic crystal fiber plasmonic sensor based on silver-titanium dioxide composite micro-grating. Plasmonics 2021, 16, 2049–2059. [Google Scholar] [CrossRef]
- Kaur, V.; Singh, S. Design of titanium nitride coated PCF-SPR sensor for liquid sensing applications. Opt. Fiber Technol. 2019, 48, 159–164. [Google Scholar] [CrossRef]



| Ref | Characteristic | RI Ranges | Wavelength Sensitivity Range (nm/RIU) | Resolution (RIU) |
|---|---|---|---|---|
| [41] | Solid−PCF | 1.29–1.40 | 600–12,500 | 8.0 × 10−6 |
| [42] | Solid−PCF | 1.30–1.39 | 1000–12,000 | 5.4 × 10−5 |
| [43] | Solid−PCF | 1.32–1.38 | X-pol:N/A—10,286 Y-pol:N/A—9464 | 9.72 × 10−6 |
| [44] | Solid−PCF | 1.33–1.40 | 2400–10,300 | 9.71 × 10−6 |
| [45] | Eccentric−core PCF | 1.385–1.40 | 5000–10,000 | 2.0 × 10−5 |
| This work | Ring−core PCF | 1.13–1.45 | 8000–40,000 | 2.5 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Wang, J.; Yang, L.; Lv, J.; Liu, W.; Liu, Q.; Chu, P.K.; Liu, C. Ring-Core Photonic Crystal Fiber Sensor Based on SPR for Extra-Wide Refractive Index Detection. Coatings 2023, 13, 1207. https://doi.org/10.3390/coatings13071207
He J, Wang J, Yang L, Lv J, Liu W, Liu Q, Chu PK, Liu C. Ring-Core Photonic Crystal Fiber Sensor Based on SPR for Extra-Wide Refractive Index Detection. Coatings. 2023; 13(7):1207. https://doi.org/10.3390/coatings13071207
Chicago/Turabian StyleHe, Jie, Jianxin Wang, Lin Yang, Jingwei Lv, Wei Liu, Qiang Liu, Paul K. Chu, and Chao Liu. 2023. "Ring-Core Photonic Crystal Fiber Sensor Based on SPR for Extra-Wide Refractive Index Detection" Coatings 13, no. 7: 1207. https://doi.org/10.3390/coatings13071207
APA StyleHe, J., Wang, J., Yang, L., Lv, J., Liu, W., Liu, Q., Chu, P. K., & Liu, C. (2023). Ring-Core Photonic Crystal Fiber Sensor Based on SPR for Extra-Wide Refractive Index Detection. Coatings, 13(7), 1207. https://doi.org/10.3390/coatings13071207







