The Spreading Characteristics of Droplets Impacting Wheat Leaves Based on the VOF Model
Abstract
:1. Introduction
2. Materials and Methods
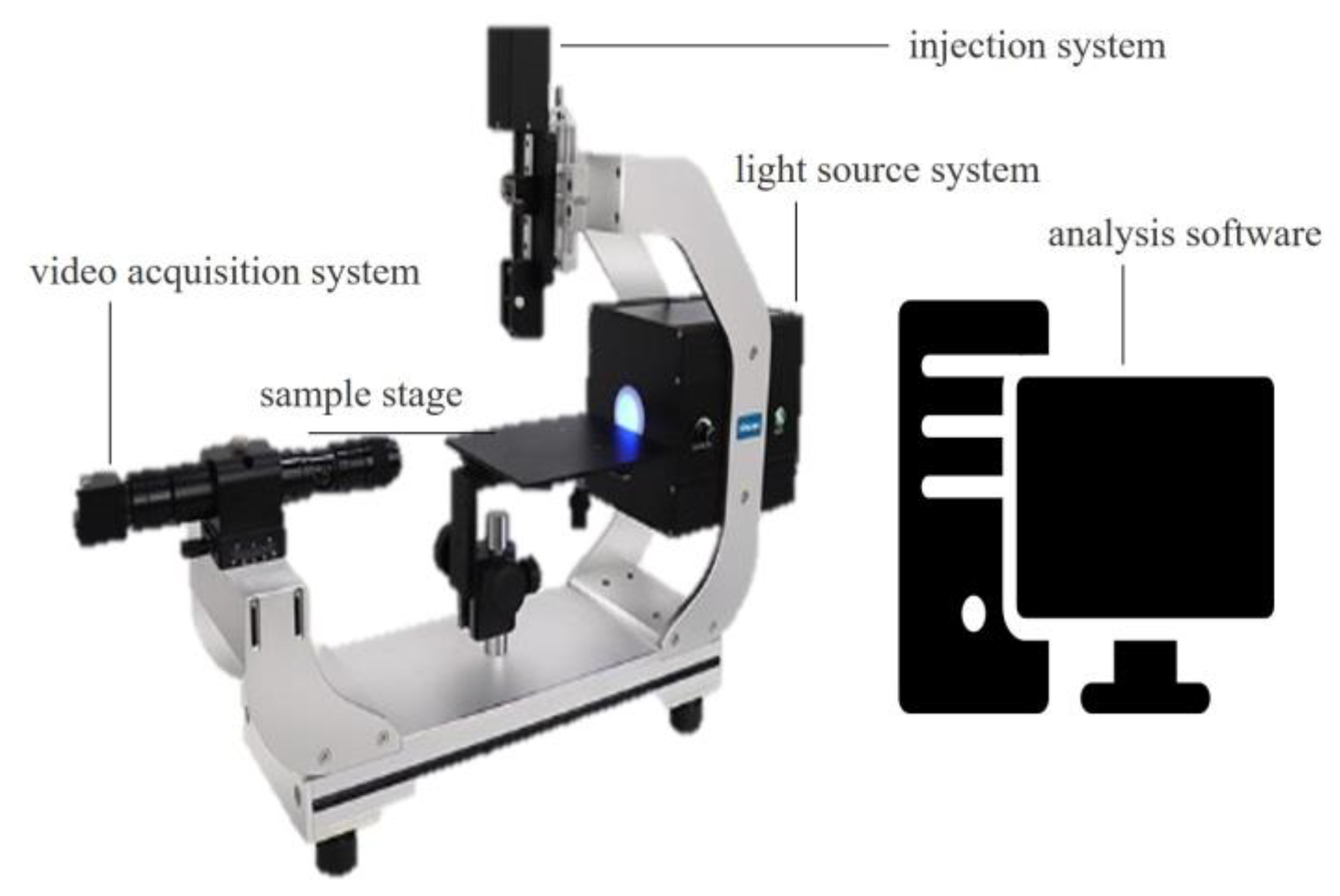
2.1. Experimental Principles
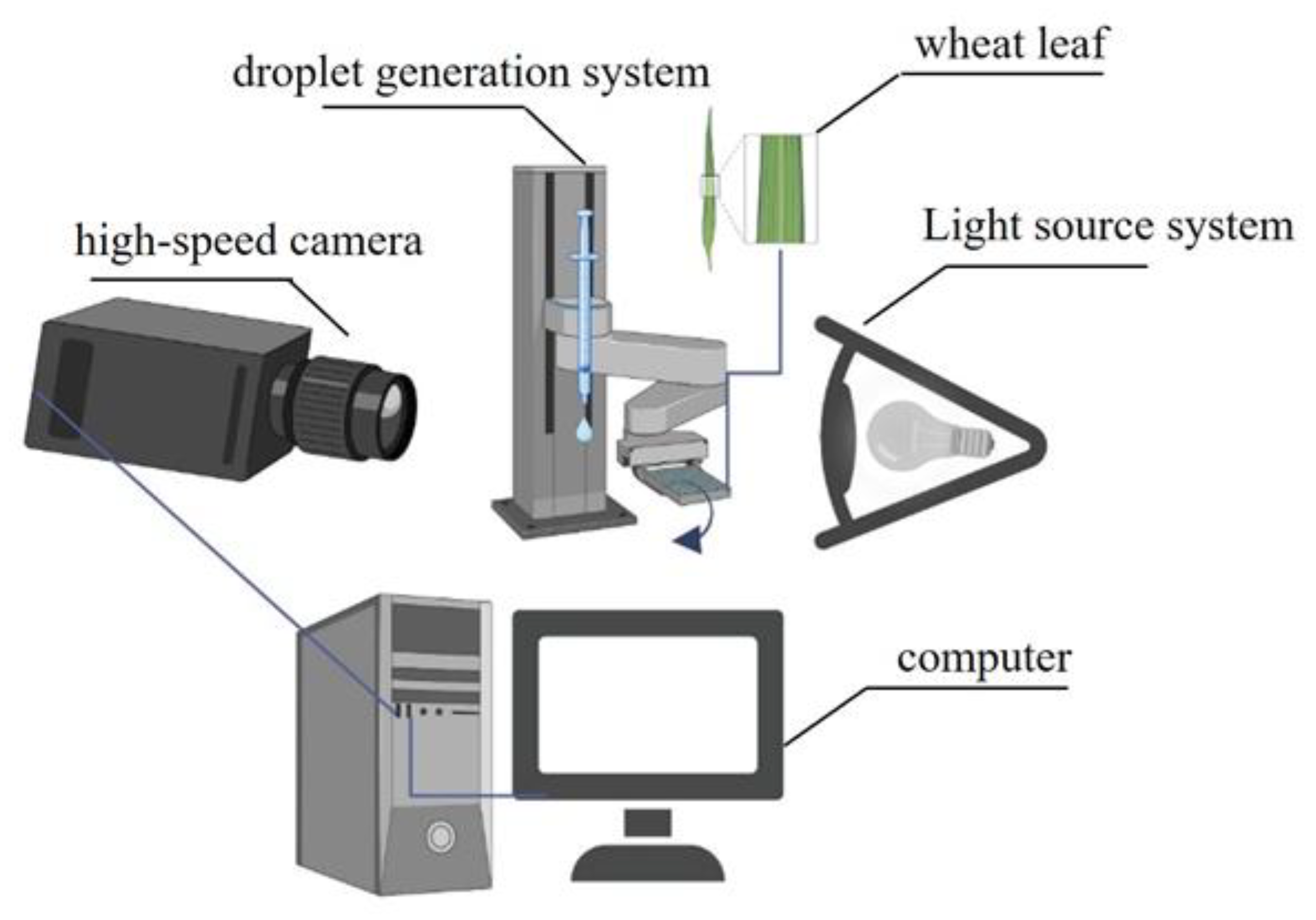
2.2. Visualization Test Scheme of Droplets Impacting Wheat Leaves
2.3. Experimental Materials
3. Numerical Model
3.1. Model Establishment
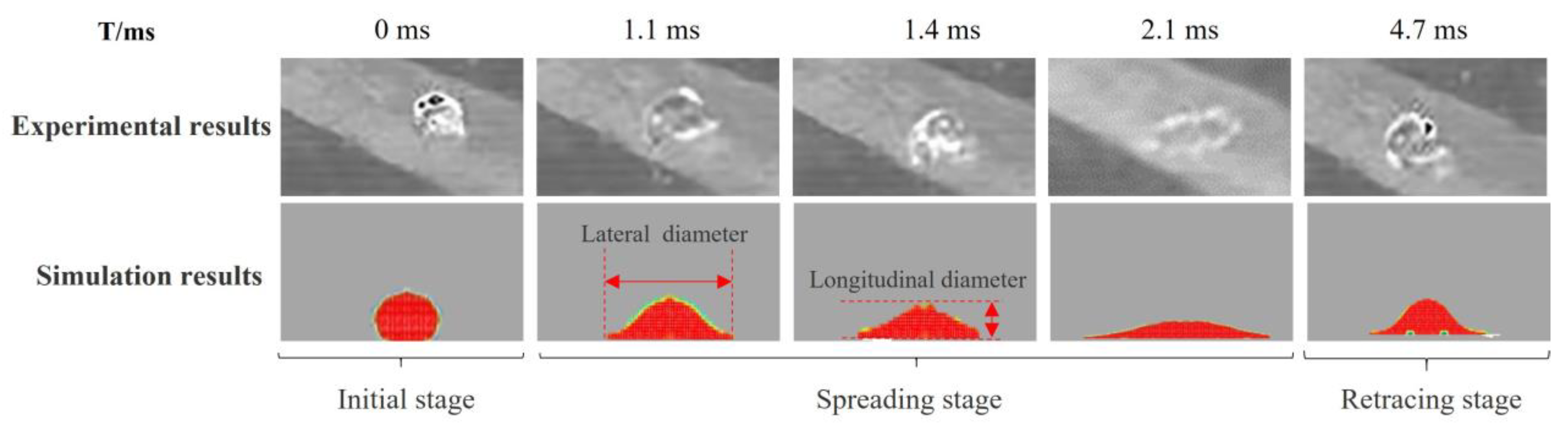
3.2. Model Verification
4. Results and Discussion
4.1. Spreading Characteristics of Droplets on a Wheat Leaf Surface
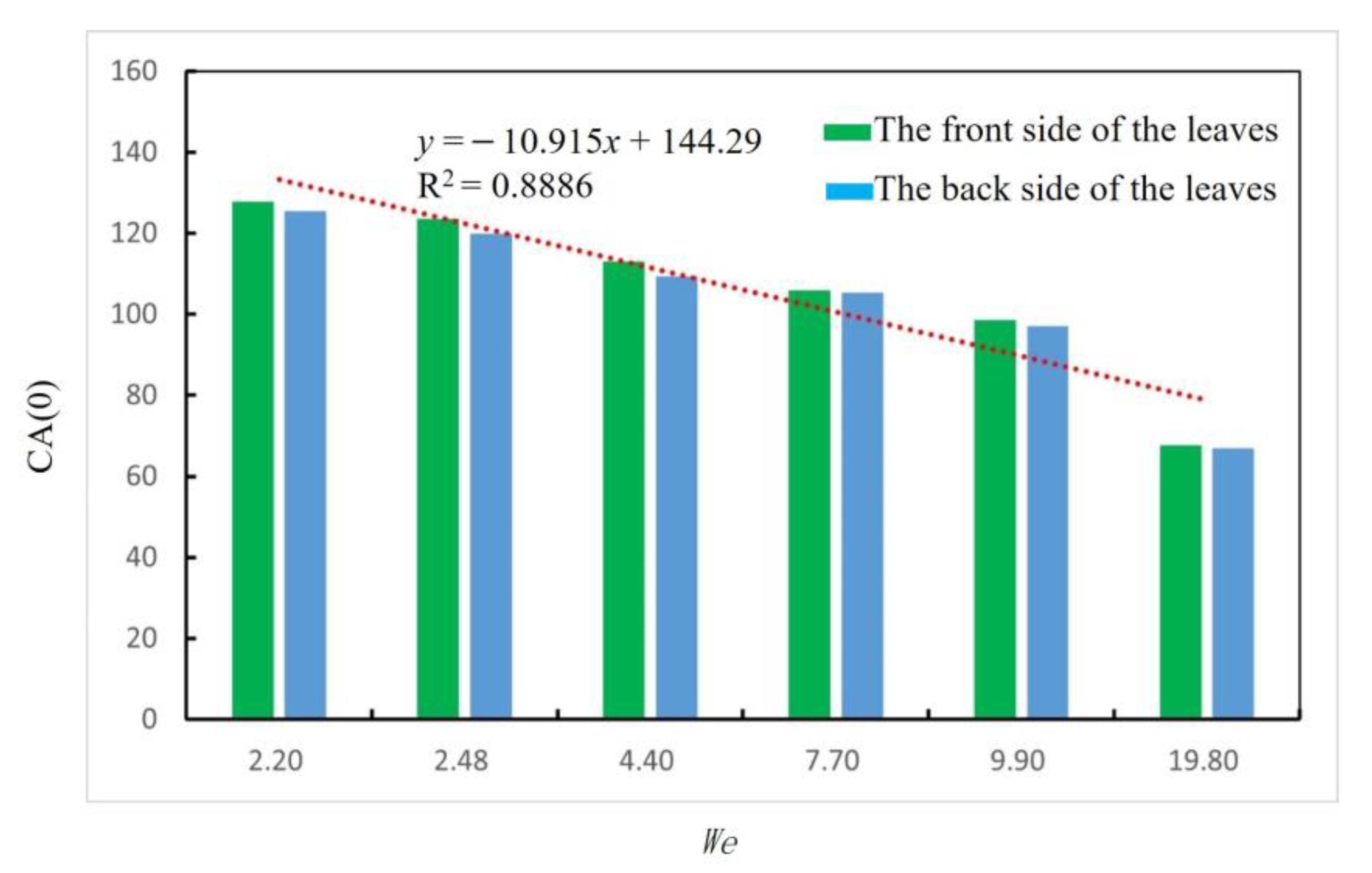
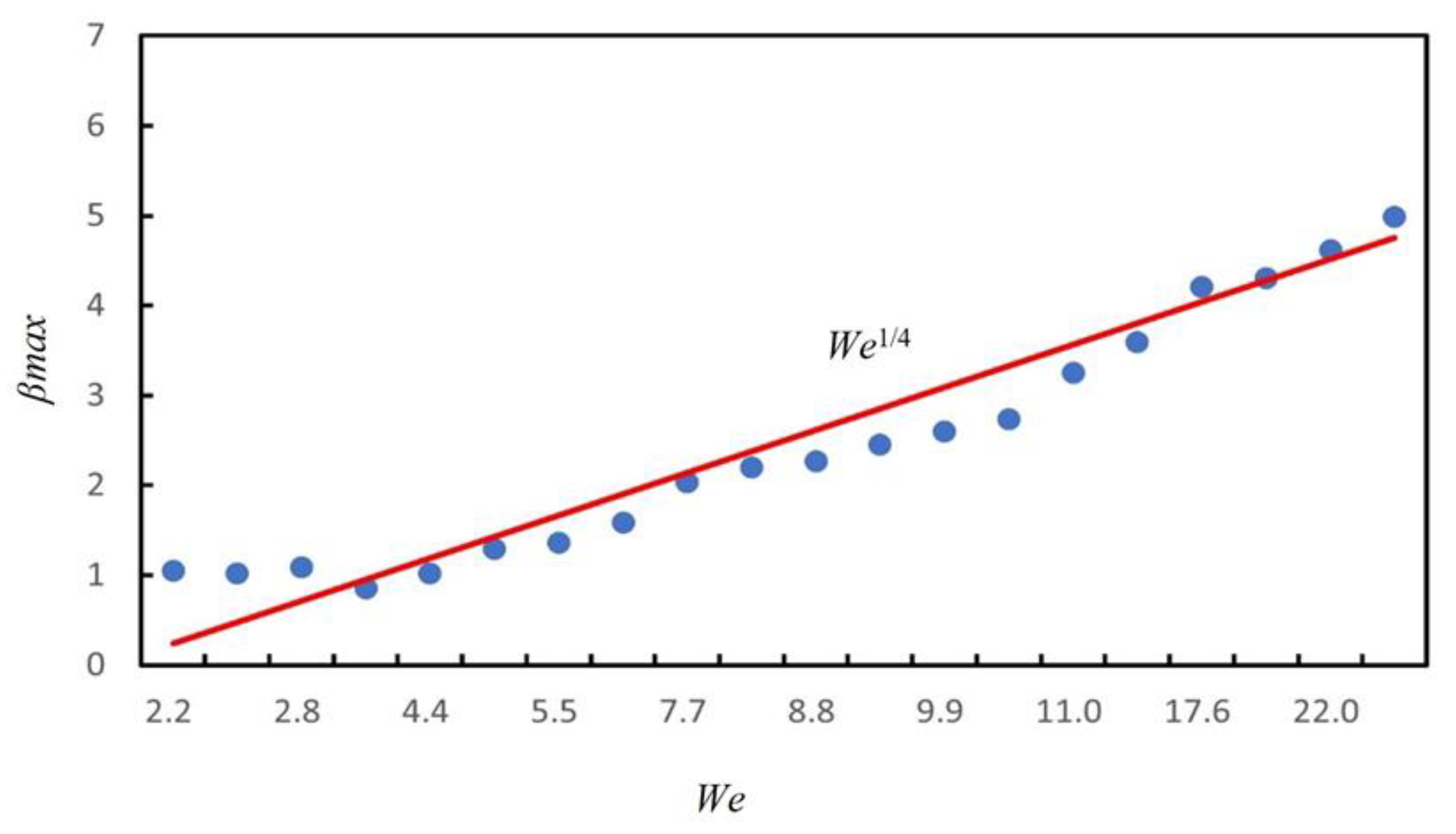
4.2. The Relationship between a Droplet’s Weber Number and Maximum Spreading Rate, βmax
5. Conclusions
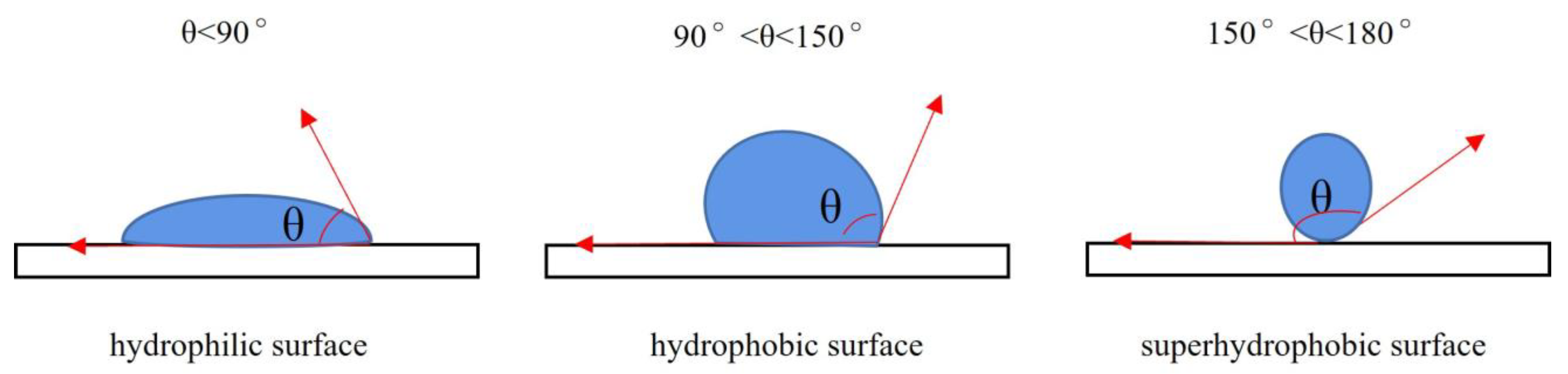
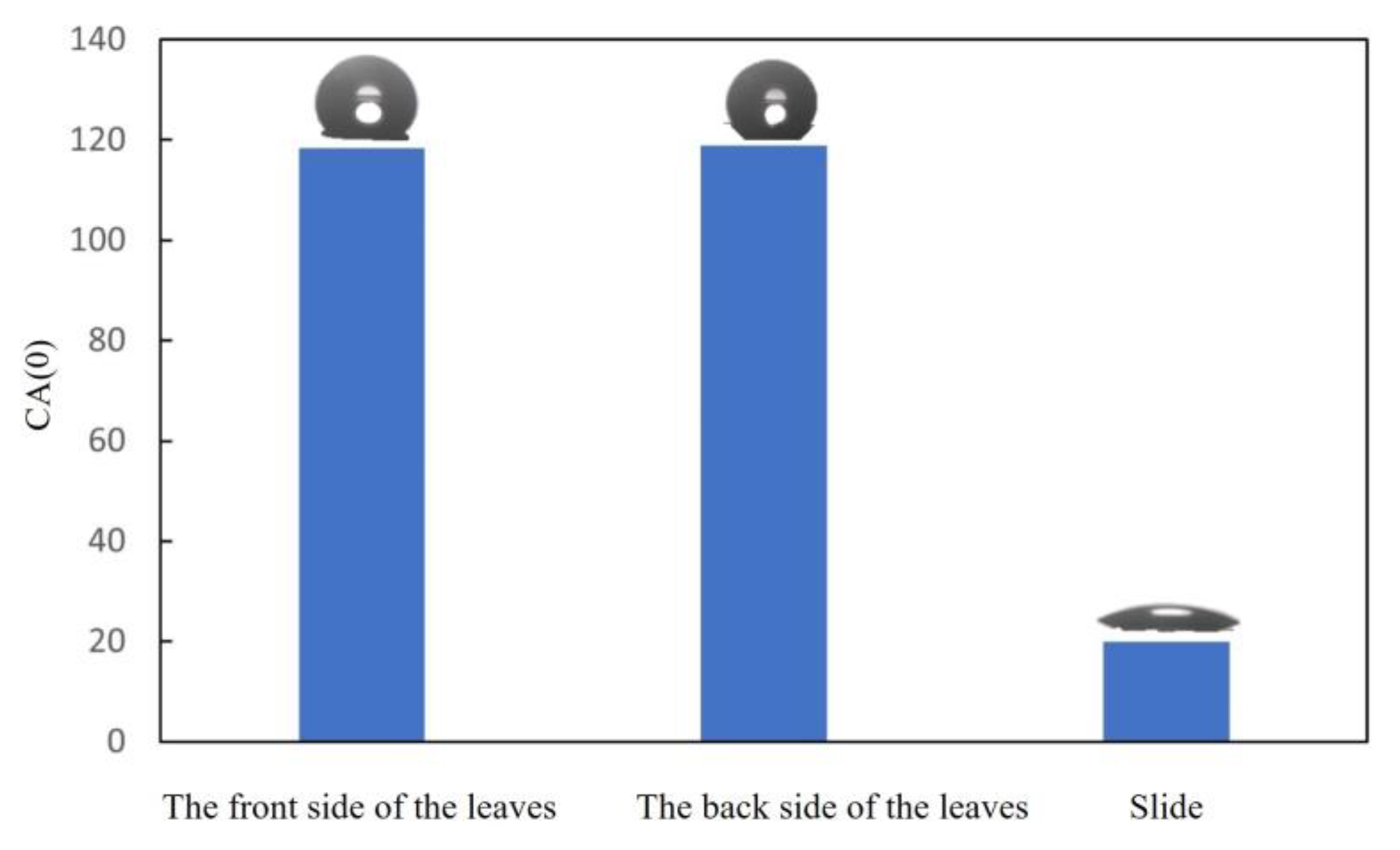
- When a droplet hits the front side and back side of a leaf (non-ridge), the contact angle does not differ greatly, and the contact angle gradually decreases as the droplet’s Weber number increases. When droplets hit the ridge on the back side of a wheat leaf, the droplets split in two.
- After a droplet hits the surface of a wheat leaf, the droplet will form a coronal droplet and then continue spreading to reach its maximum spreading diameter before retracting until it reaches a stable stage. As the Weber number of the droplet increases, its spreading time the droplet becomes longer.
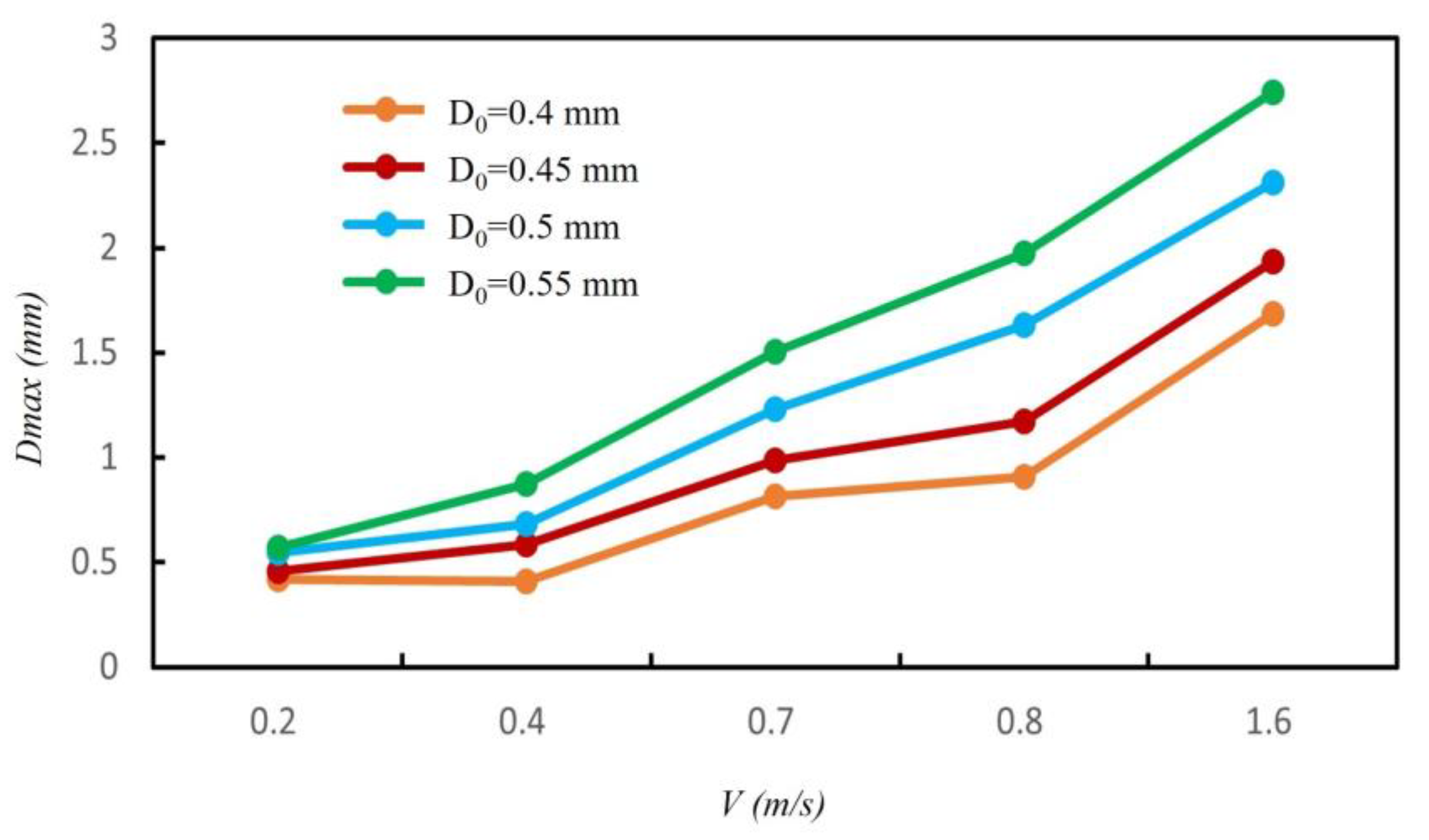
- With an increase in a droplet’s impact velocity, the droplet’s maximum spreading diameter gradually increases. As the initial diameter of the droplet increases, the maximum spreading diameter of the droplet also gradually increases. As the droplet velocity increases, the droplet diameter has an increasing influence on its maximum spreading diameter.
- The numerical simulation results show that the maximum spreading rate of droplets increases with an increase in the Weber number, which is consistent with βmax , which is also consistent with the existing theory. It is suggested that when creating a droplet-generating device, the Weber number of the droplets should be increased as much as possible while considering the droplet size to obtain the maximum droplet spreading diameter and improve the droplet utilization rate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tudi, M.; Daniel Ruan, H.; Wang, L.; Lyu, J.; Sadler, R.; Connell, D.; Chu, C.; Phung, D.T. Agriculture Development, Pesticide Application and Its Impact on the Environment. Int. J. Environ. Res. Public Health 2021, 18, 1112. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Wang, Z.; Meng, H.; Dong, B.; Deng, X.; Zhou, H. Formulation of Matrine Oil-Based Suspension Concentrate for Improving the Wetting of Droplets and Spraying Performance. Agronomy 2023, 13, 1895. [Google Scholar] [CrossRef]
- Ferguson, J.C.; Chechetto, R.G.; Adkins, S.W.; Hewitt, A.J.; Chauhan, B.S.; Kruger, G.R.; O’Donnell, C.C. Effect of spray droplet size on herbicide efficacy on four winter annual grasses. Crop Prot. 2018, 112, 118–124. [Google Scholar] [CrossRef]
- Xu, L.; Zhu, H.; Ozkan, H.E.; Bagley, W.E.; Krause, C.R. Droplet evaporation and spread on waxy and hairy leaves associated with type and concentration of adjuvants. Pest Manag. Sci. 2011, 67, 842–851. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Yang, P.; Wang, W.; Liu, Y.; Ge, X.; Tong, B. Spreading Behavior of Single Oil Droplet Impacting Surface with/without a Thin Liquid Film. Lubricants 2023, 11, 31. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Zhang, Z.; Han, L.; Li, Y.; Zhang, H.; Wongsuk, S.; Li, Y.; Wu, X.; He, X. Spray performance evaluation of a six-rotor unmanned aerial vehicle sprayer for pesticide application using an orchard operation mode in apple orchards. Pest Manag. Sci. 2022, 78, 2449–2466. [Google Scholar] [CrossRef]
- Srivastava, T.; Jena, S.K.; Kondaraju, S. Droplet Impact and Spreading on Inclined Surfaces. Langmuir 2021, 37, 13737–13745. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Wang, S. Droplet impact on cylindrical surfaces: Effects of surface wettability, initial impact velocity, and cylinder size. J. Colloid Interface Sci. 2020, 578, 207–217. [Google Scholar] [CrossRef]
- Guo, J.; Jin, L.; Yang, Y.; Cui, R.; Khan, N.M.; Li, M.; Zhang, Q.; Yue, X. Study on Dynamic Contact Behavior of Multi-Component Droplet and Dust Surface. Coatings 2023, 13, 1146. [Google Scholar] [CrossRef]
- Kim, H.Y.; Park, S.Y.; Min, K. Imaging the high-speed impact of microdrop on solid surface. Rev. Sci. Instrum. 2003, 74, 4930–4937. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Madden, L.V.; Reichard, D.L.; Fox, R.D.; Ellis, M.A. Motion Analysis of Drop Impaction on a Strawberry Surface. Agr. Forest Meteorol. 1991, 56, 67–92. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop impact dynamics: Splashing, spreading, receding, bouncing…. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Weisensee, P.B.; Tian, J.; Miljkovic, N.; King, W.P. Water droplet impact on elastic superhydrophobic surfaces. Sci. Rep. 2016, 6, 30328. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Zhu, L.; Bu, W.; Liang, Y. Superhydrophobic surfaces: From nature to biomimetic through VOF simulation. Micron 2018, 107, 94–100. [Google Scholar] [CrossRef]
- Elghobashi, S. Direct Numerical Simulation of Turbulent Flows Laden with Droplets or Bubbles. Annu. Rev. Fluid Mech. 2019, 51, 217–244. [Google Scholar] [CrossRef] [Green Version]
- Malgarinos, I.; Nikolopoulos, N.; Marengo, M.; Antonini, C.; Gavaises, M. VOF simulations of the contact angle dynamics during the drop spreading: Standard models and a new wetting force model. Adv. Colloid Interface Sci. 2014, 212, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Bristot, A.; Morvan, H.P.; Simmons, K.A. Evaluation of a Volume of Fluid Cfd Methodology for the Oil Film Thickness Estimation in an Aero-Engine Bearing Chamber. In Proceedings of the Asme Turbo Expo: Turbine Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; Volume 2c. [Google Scholar]
- Dai, S.; Wang, M.; Ou, M.; Zhou, H.; Jia, W.; Gao, R.; Wang, C.; Wang, G.; Li, Z.; Chen, H. Development and Experiment of an Online Measuring System for Spray Deposition. Agriculture 2022, 12, 1195. [Google Scholar] [CrossRef]
- Liang, C.; Feigl, K.A.; Tanner, F.X.; Case, W.R.; Windhab, E.J. Three-Dimensional Simulations of Drop Deformation and Breakup in Air Flow and Comparisons with Experimental Observations. At. Spray. 2018, 28, 621–641. [Google Scholar] [CrossRef]
- Wang, F.; Wang, L.; Chen, G. Analysis of Oil Droplet Deposition Characteristics and Determination of Impact State Criterion in Aero-Engine Bearing Chamber. Processes 2020, 8, 741. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, J.; Zhang, Z. Experimental and Numerical Investigation on the Dynamics of Impacting Droplet Spreading at Small Weber Numbers. Energies 2022, 15, 8181. [Google Scholar] [CrossRef]
- Li, B.; Fan, L.; Bai, J.; Xiang, H.; Yuan, Y. Water-Droplet Impact and Sliding Behaviors on Slippery Surfaces with Various Weber Numbers and Surface Inclinations. Coatings 2023, 13, 264. [Google Scholar] [CrossRef]
- Mundo, C.; Sommerfeld, M.; Tropea, C. On the modeling of liquid sprays impinging on surfaces. At. Spray. 1998, 8, 625–652. [Google Scholar] [CrossRef]
- Zheng, N.; Liu, H.L. Study On The Spring-Back Phenomenon And Maximum Spread Of Shear-Thinned Fluid Droplets On Hydrophobic Surfaces. Chin. J. Mech. 2022, 54, 1934–1942. [Google Scholar]
- Tang, C.; Qin, M.; Weng, X.; Zhang, X.; Zhang, P.; Li, J.; Huang, Z. Dynamics of droplet impact on solid surface with different roughness. Int. J. Multiph. Flow 2017, 96, 56–69. [Google Scholar] [CrossRef]
- Clanet, C.; Béguin, C.; Richard, D.; Quéré, D. Maximal deformation of an impacting drop. J. Fluid Mech. 2004, 517, 199–208. [Google Scholar] [CrossRef]
- Mehrizi, A.A.; Lin, S.; Sun, L.; Wang, Y.; Chen, L. Penetration and ligament formation of viscoelastic droplets impacting on the superhydrophobic mesh. Sci. Rep. 2022, 12, 11920. [Google Scholar] [CrossRef]
- Baumgartner, D.; Brenn, G.; Planchette, C. The Influence of Viscosity on the Outcome of Collisions between Liquid Droplets and Another Immiscible Liquid Jet. At. Spray. 2020, 30, 811–823. [Google Scholar] [CrossRef]
- Bordbar, A.; Taassob, A.; Khojasteh, D.; Marengo, M.; Kamali, R. Maximum Spreading and Rebound of a Droplet Impacting onto a Spherical Surface at Low Weber Numbers. Langmuir 2018, 34, 5149–5158. [Google Scholar] [CrossRef]
- Lee, C.; Kim, H.; Nam, Y. Drop Impact Dynamics on Oil-Infused Nanostructured Surfaces. Langmuir 2014, 30, 8400–8407. [Google Scholar] [CrossRef]
- Muschi, M.; Brudieu, B.; Teisseire, J.; Sauret, A. Drop impact dynamics on slippery liquid-infused porous surfaces: Influence of oil thickness. Soft Matter 2018, 14, 1100–1107. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Wang, Q.; Ying, Y.; You, Z.; Wang, S.; Chun, J.; Ma, X.; Wen, R. Droplet Spreading Characteristics on Ultra-Slippery Solid Hydrophilic Surfaces with Ultra-Low Contact Angle Hysteresis. Coatings 2022, 12, 755. [Google Scholar] [CrossRef]
- Rudman, M. Volume-tracking methods for interfacial flow calculations. Int. J. Numer. Methods Fluids 1997, 24, 671–691. [Google Scholar] [CrossRef]
- Song, M.; Hu, D.; Zheng, X.; Wang, L.; Yu, Z.; An, W.; Na, R.; Li, C.; Li, N.; Lu, Z.; et al. Enhancing Droplet Deposition on Wired and Curved Superhydrophobic Leaves. Acs Nano 2019, 13, 7966–7974. [Google Scholar] [CrossRef]
- Hu, Z.; Chu, F.; Lin, Y.; Wu, X. Contact Time of Droplet Impact on Inclined Ridged Superhydrophobic Surfaces. Langmuir 2022, 38, 1540–1549. [Google Scholar] [CrossRef]
- Laan, N.; de Bruin, K.G.; Bartolo, D.; Josserand, C.; Bonn, D. Maximum Diameter of Impacting Liquid Droplets. Phys. Rev. Appl. 2014, 2, 004018. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Zhao, B.; Zou, S.; Guo, J.; Wei, Z.; Chen, L. Impact of viscous droplets on different wettable surfaces: Impact phenomena, the maximum spreading factor, spreading time and post-impact oscillation. J. Colloid Interf. Sci. 2018, 516, 86–97. [Google Scholar] [CrossRef]
- Ukiwe, C.; Kwok, D.Y. On the maximum spreading diameter of impacting droplets on well-prepared solid surfaces. Langmuir 2005, 21, 666–673. [Google Scholar] [CrossRef]







| Droplet Parameter | Value |
|---|---|
| Density (ρ/kg·m−3) | 995.8 |
| Viscosity (μ/mPa·s) | 0.98 |
| Surface tension (σ/mN·m−1) | 73.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Wang, M.; Zhang, Y.; Wang, X.; Ni, J.; Zhu, Y.; Cao, W.; Jiang, X. The Spreading Characteristics of Droplets Impacting Wheat Leaves Based on the VOF Model. Coatings 2023, 13, 1415. https://doi.org/10.3390/coatings13081415
Liao Y, Wang M, Zhang Y, Wang X, Ni J, Zhu Y, Cao W, Jiang X. The Spreading Characteristics of Droplets Impacting Wheat Leaves Based on the VOF Model. Coatings. 2023; 13(8):1415. https://doi.org/10.3390/coatings13081415
Chicago/Turabian StyleLiao, Yaoyao, Mian Wang, Ying Zhang, Xingchen Wang, Jun Ni, Yan Zhu, Weixing Cao, and Xiaoping Jiang. 2023. "The Spreading Characteristics of Droplets Impacting Wheat Leaves Based on the VOF Model" Coatings 13, no. 8: 1415. https://doi.org/10.3390/coatings13081415
APA StyleLiao, Y., Wang, M., Zhang, Y., Wang, X., Ni, J., Zhu, Y., Cao, W., & Jiang, X. (2023). The Spreading Characteristics of Droplets Impacting Wheat Leaves Based on the VOF Model. Coatings, 13(8), 1415. https://doi.org/10.3390/coatings13081415







