Variable Velocity Coating Thickness Distribution Model for Super-Large Planar Robot Spraying
Abstract
1. Introduction
2. Description and Analysis of Problem
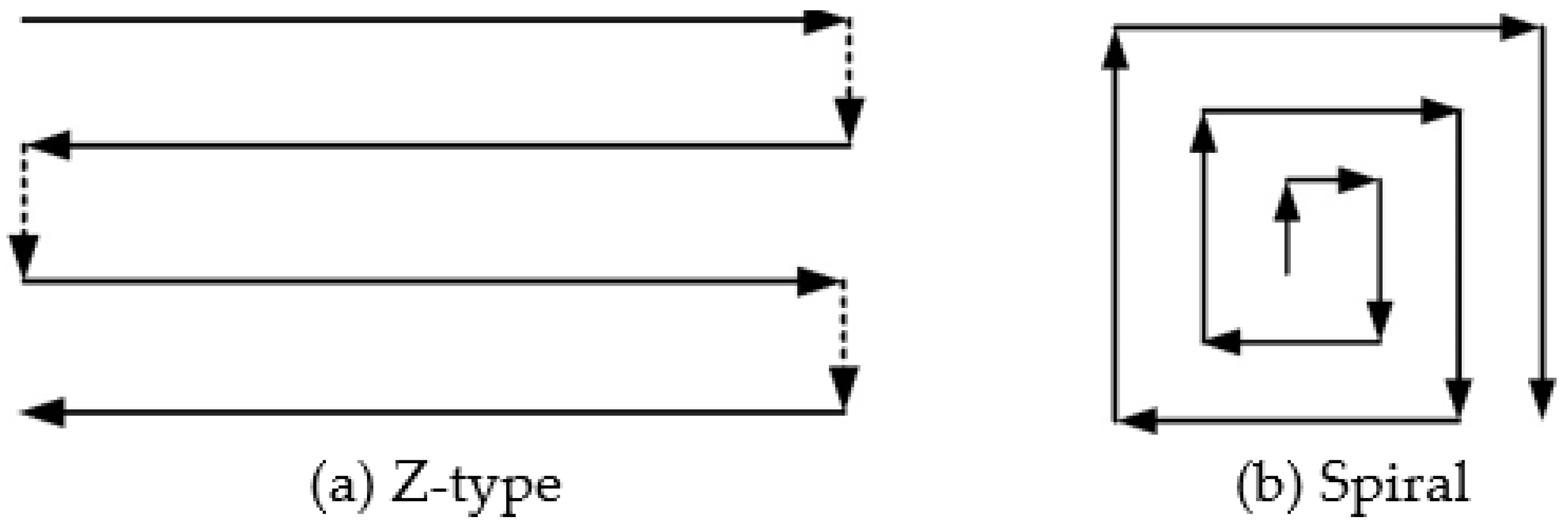
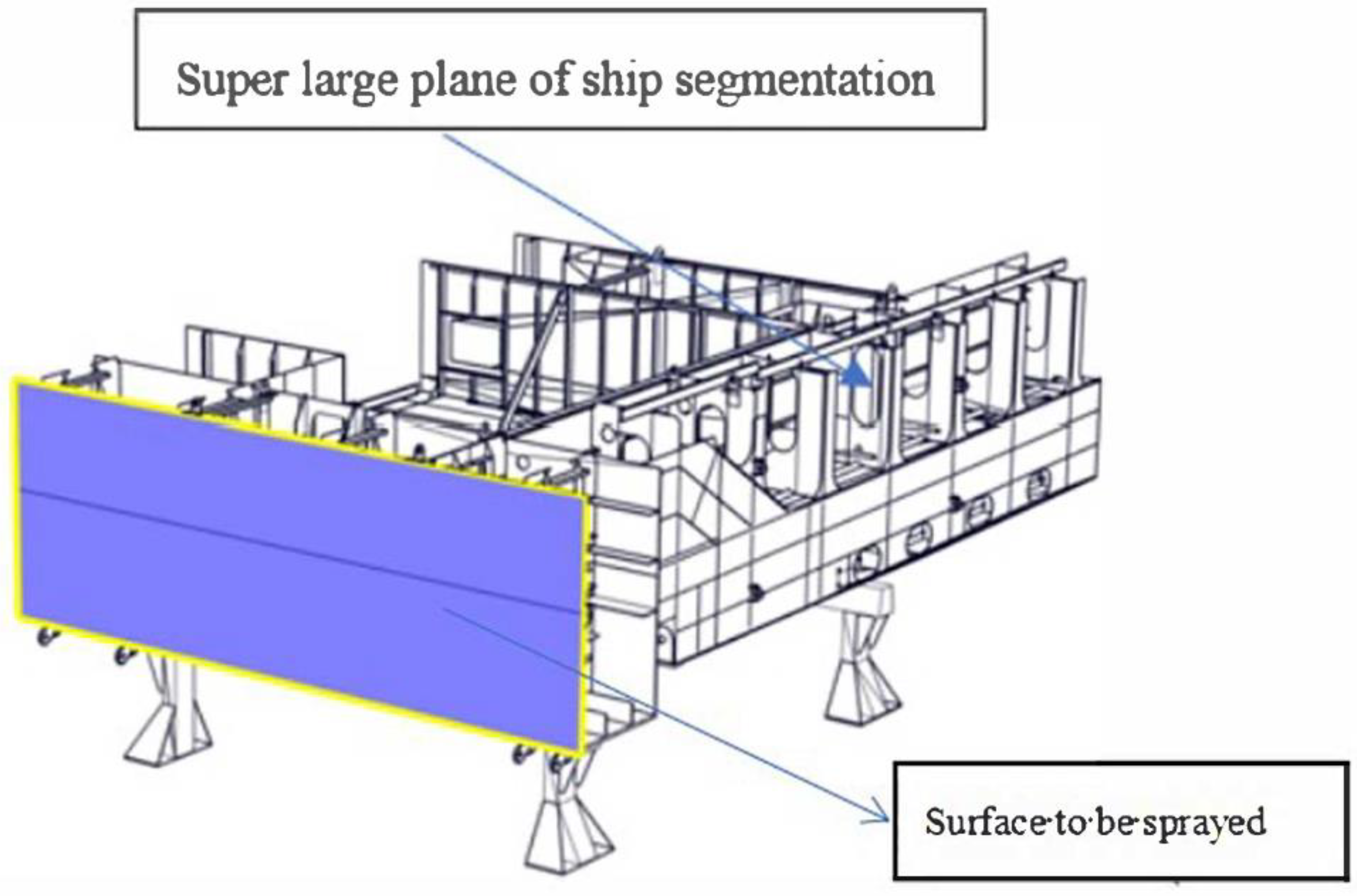
2.1. Selection of Spray Path in Subsection of Large Plane
2.2. The Consequences of Planning Spraying Speed without Considering Acceleration and Deceleration
3. Establishment of Mathematical Model
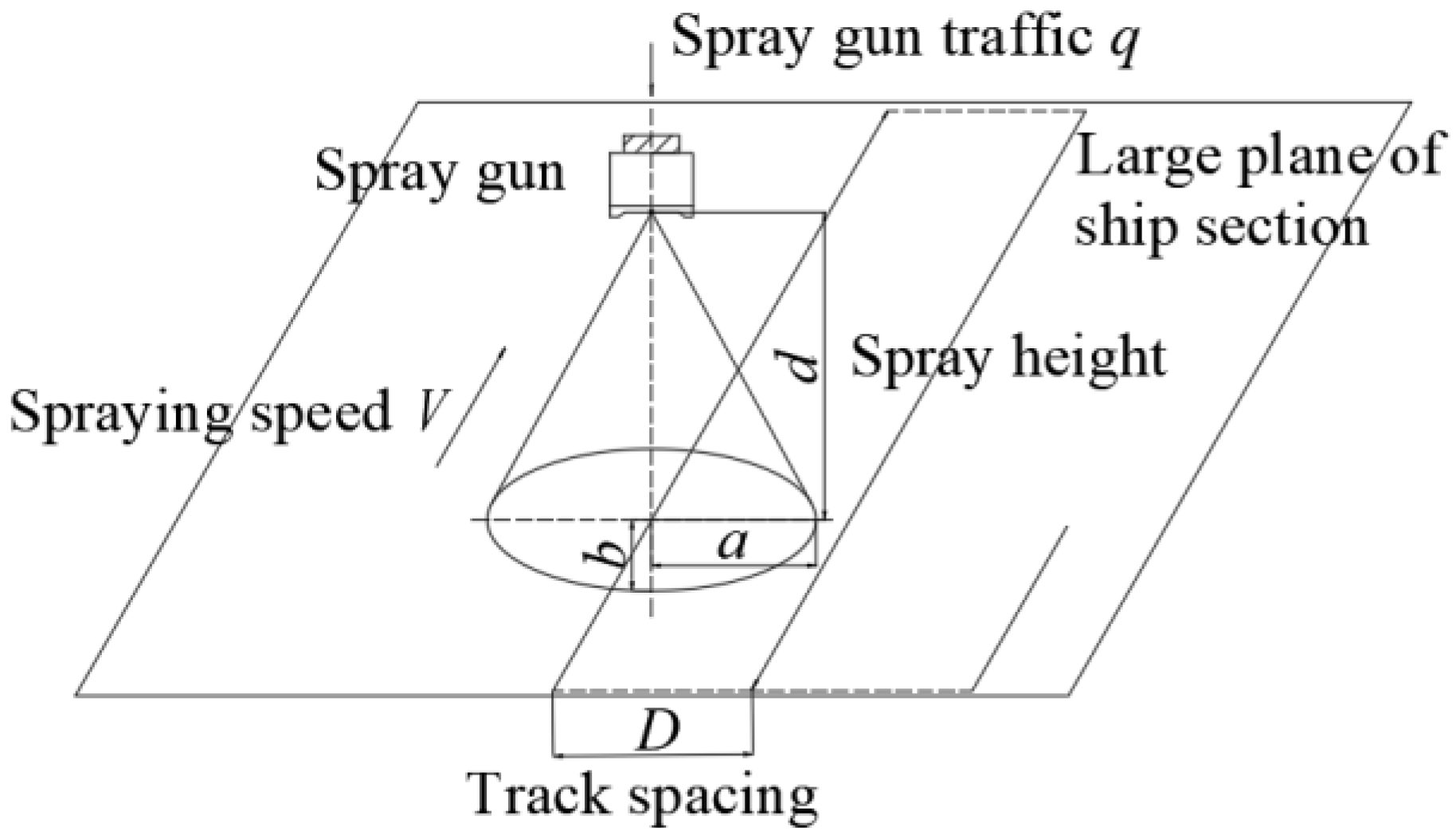
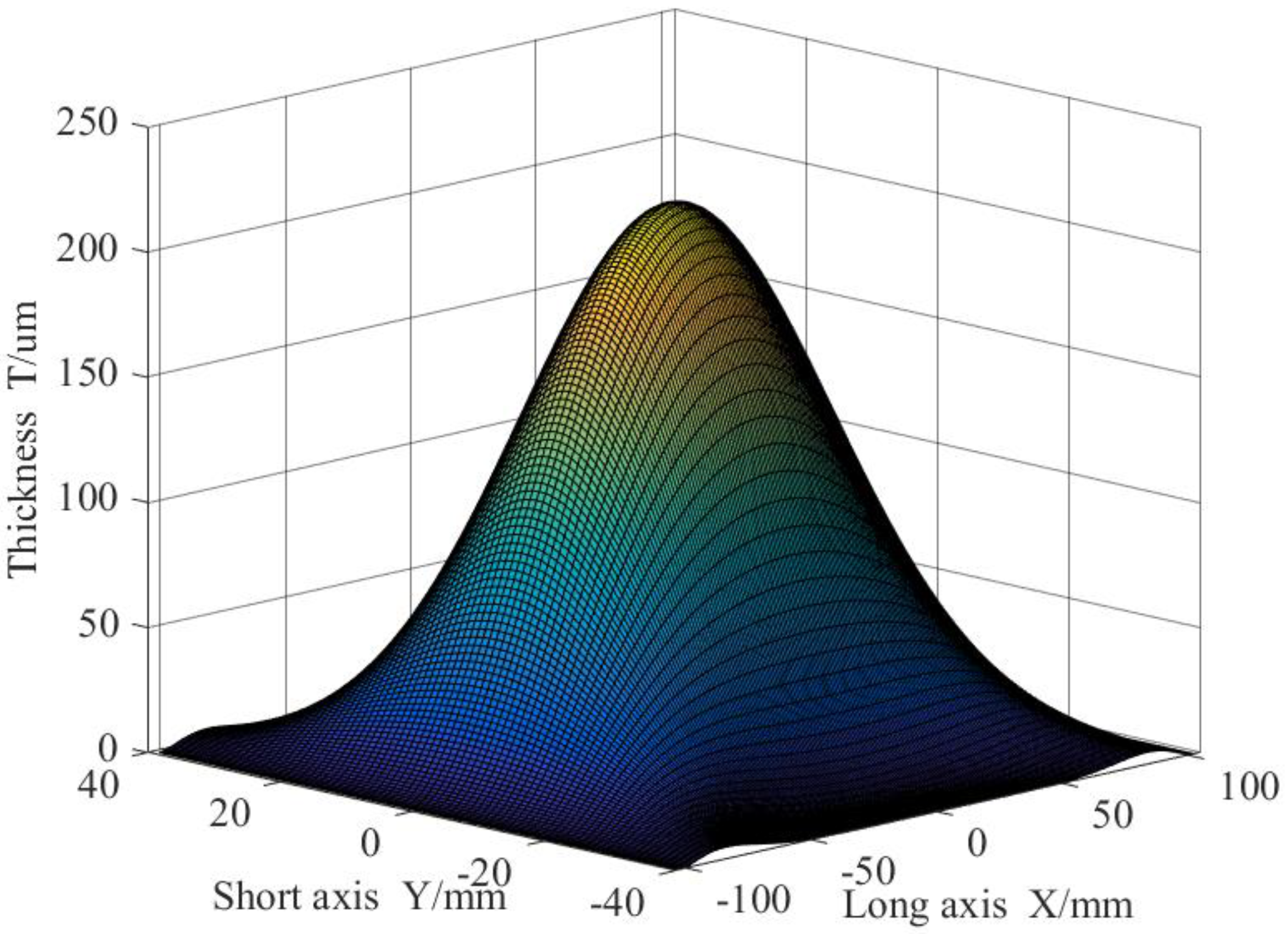
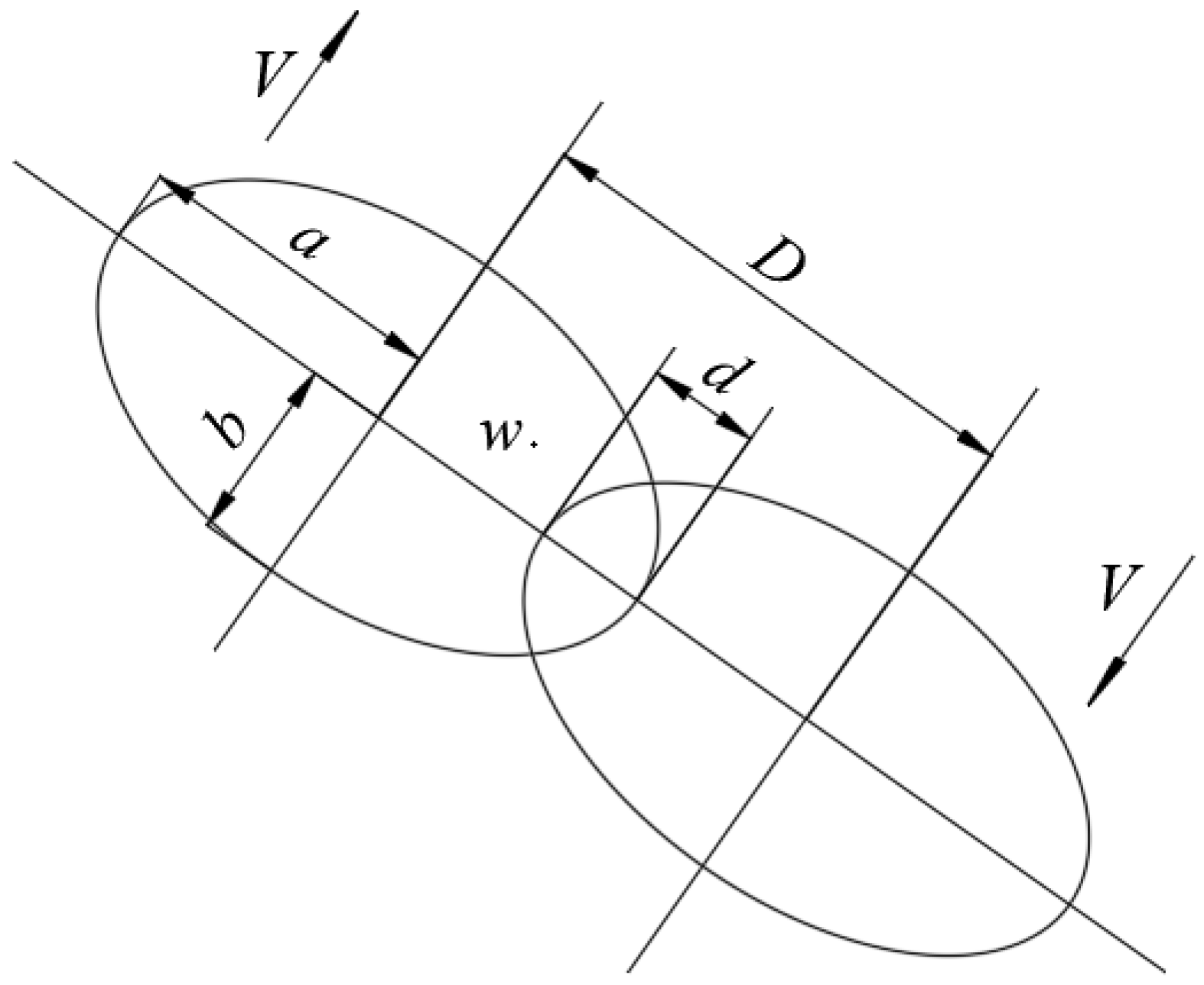
3.1. Static Spraying Model
3.2. Establishment of Dynamic Model of Spray Gun
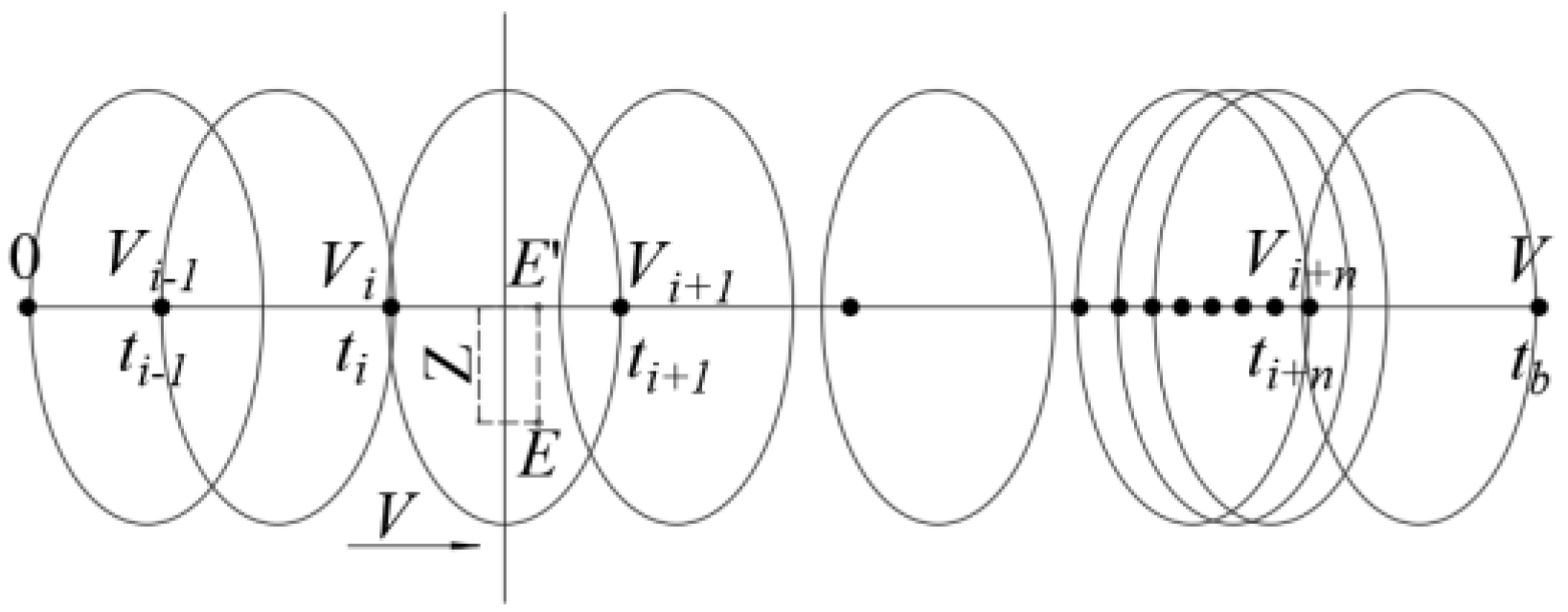
3.3. Optimization of Track Spacing and Spraying Speed of Paint Film Uniformity under Adjacent Spraying Tracks
3.4. Variable Flow Optimization of Spray Gun in the Acceleration and Deceleration Interval at the Beginning and End of Z-Shaped Spraying Trajectory
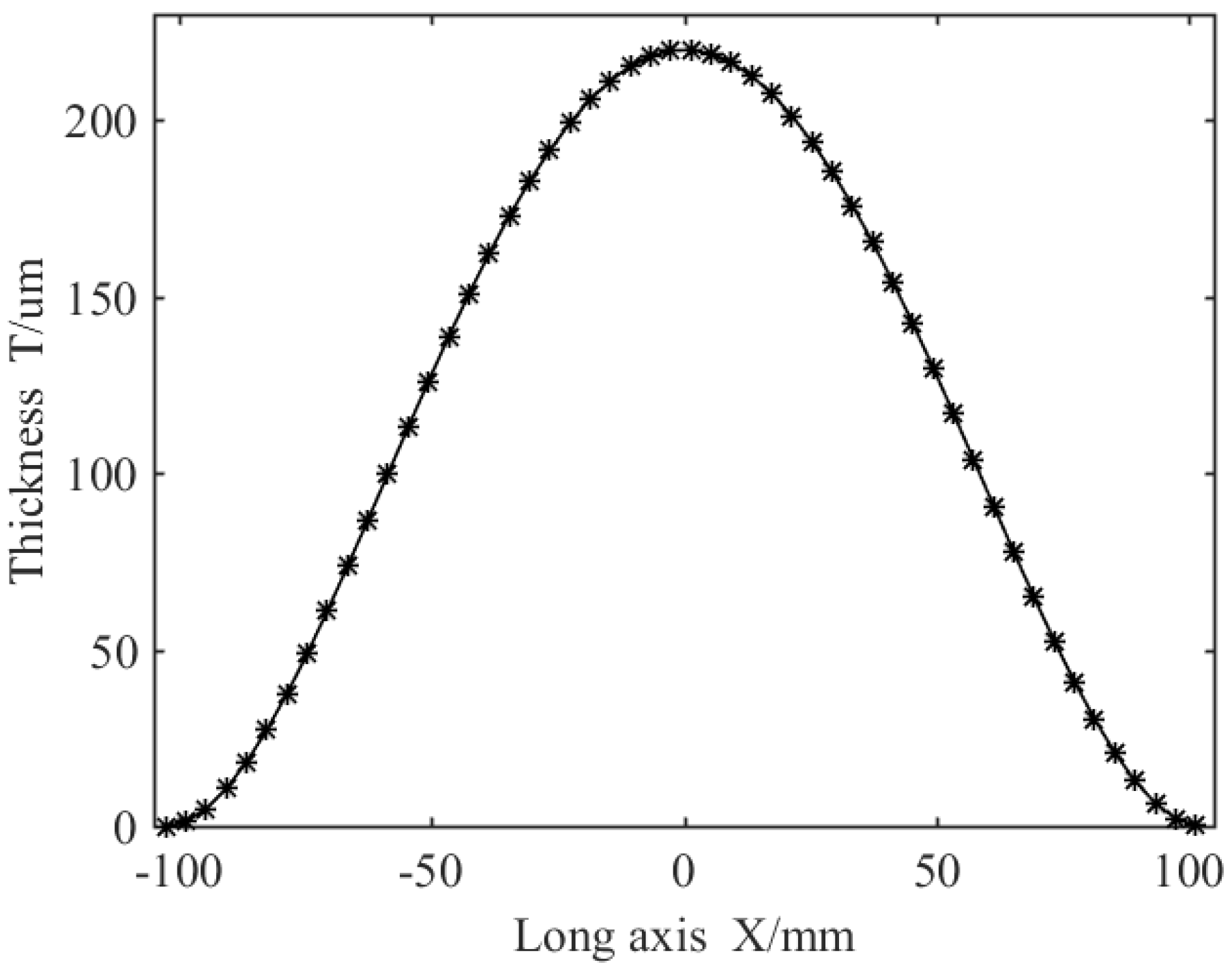
4. Numerical Simulation and Simulation Experiment
5. Experimental Verification
6. Conclusions
- (1)
- This study analyzed the pros and cons of two spraying trajectories, the Z-type and spiral spraying trajectories, based on the structure of a large plane of a ship segment. The research established the Z-type trajectory as the optimal spraying trajectory for a super-large plane of a ship segment.
- (2)
- The elliptic double beta model served as the static model prototype for the spray gun, with the goal of minimizing the coating thickness error. An optimization function was established for spraying speed and spraying trajectory spacing. The maximum uniformity of paint film coating thickness on a large plane of a ship segment was achieved when the acceleration and deceleration section were not taken into consideration.
- (3)
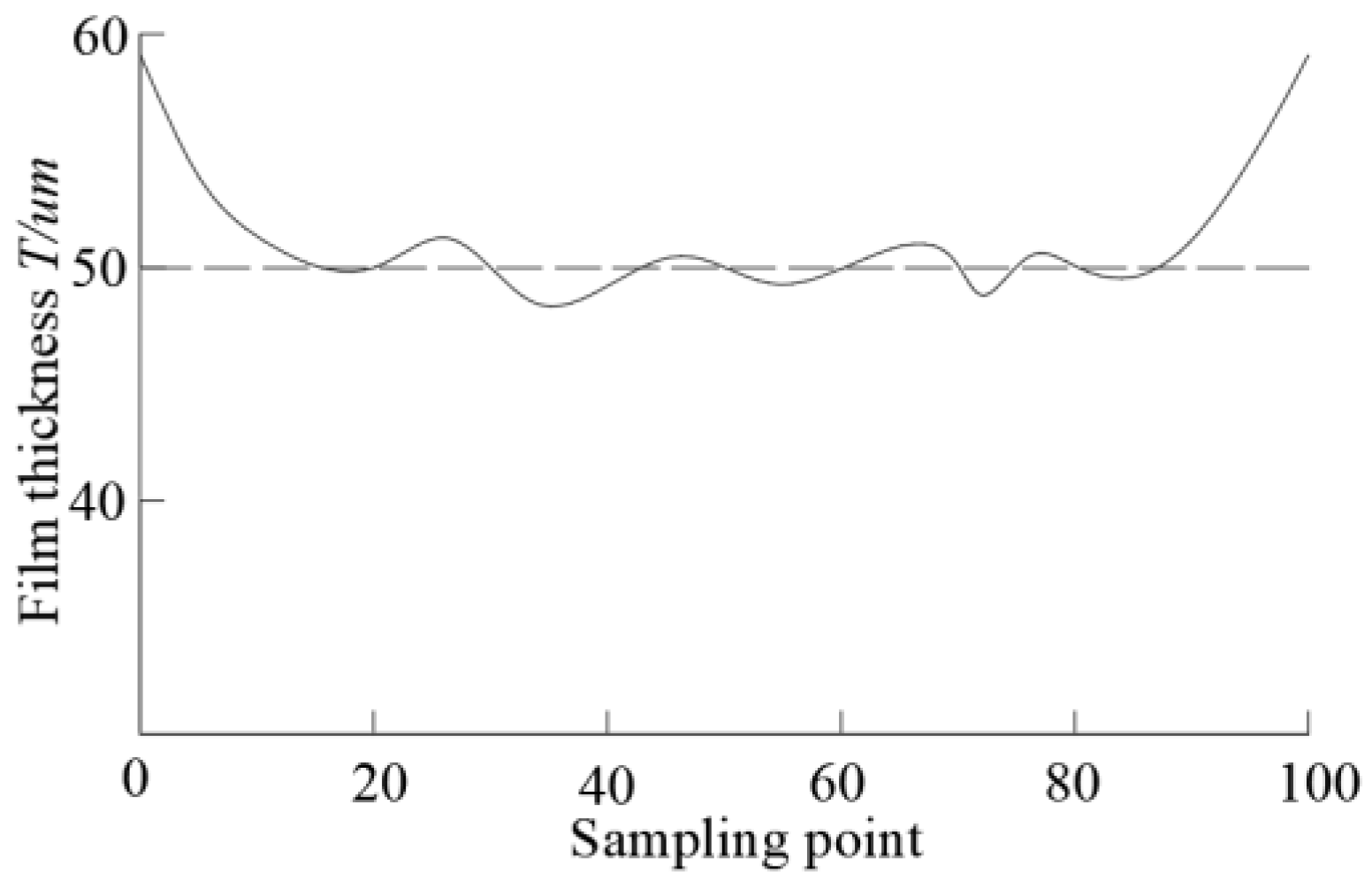
- The study assumed that the spraying trajectory follows a linear motion of equal acceleration and equal deceleration. Since the acceleration and deceleration sections are symmetric, only cases with equal-acceleration linear motion were considered. The velocity during the constant acceleration phase can be determined using the known spraying velocity, which leads to the mathematical model of the variable flow spray gun. This model enables the determination of a suitable spraying flow rate corresponding to any speed in the acceleration and deceleration sections. A numerical simulation was used to verify the effectiveness and feasibility of the proposed method. In this method, the uniformity of the film thickness can be increased by 10% in the acceleration and deceleration stage, which results in a uniform distribution of paint film thickness on the super-large plane of a ship segment.
- (4)
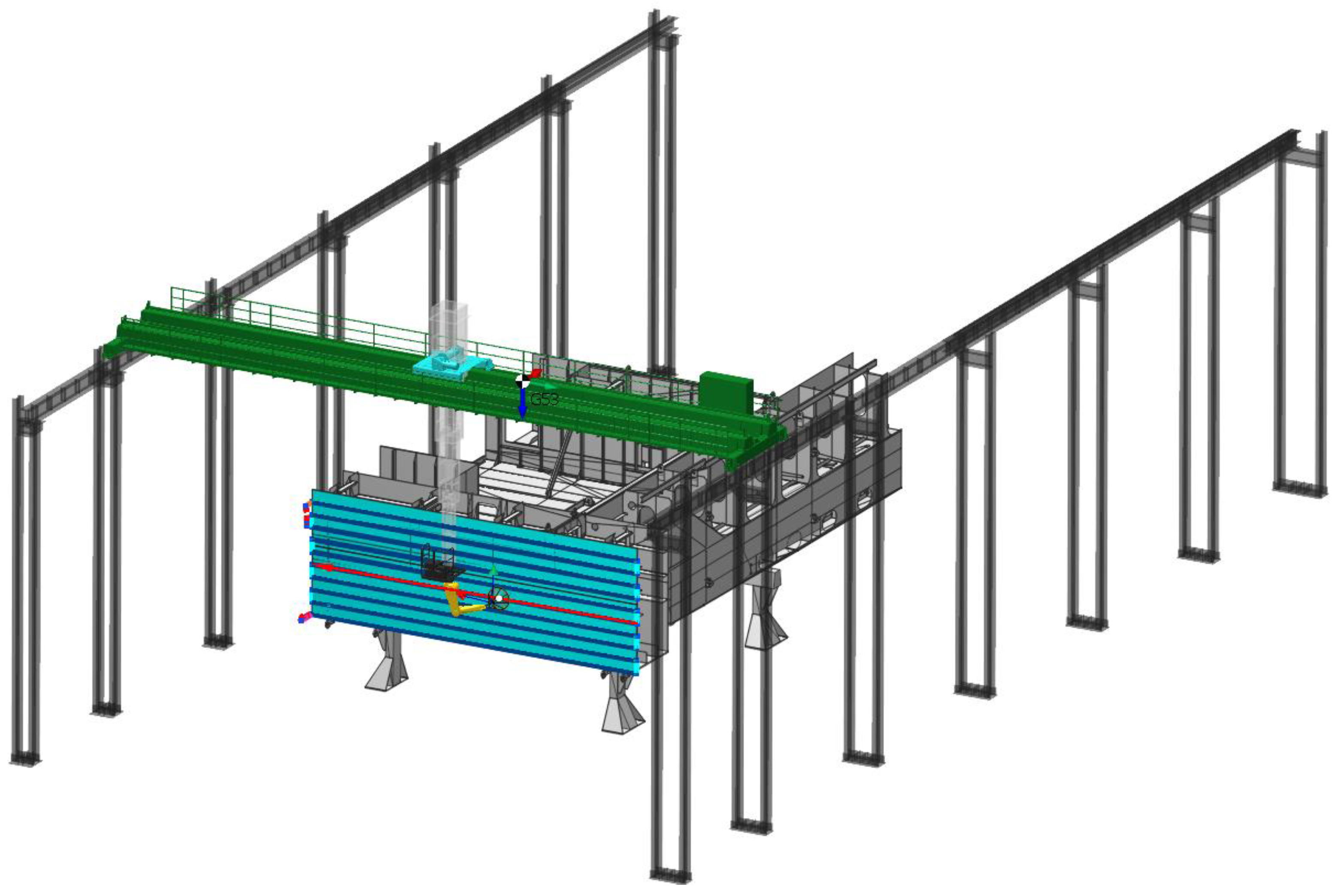
- For the spraying of complex structural ship segments, the structural design and control of the ship segmental spraying robot is the basis of the spraying method. However, the existing spraying robots have shortcomings such as a small space for movement, poor obstacle avoidance ability, and false linkage between the mechanical arm and the external axis. Therefore, it is particularly important to carry out the research and design of spraying robots for segmented structural surfaces and non-structural surfaces of ships in the future, so as to make up for the lack of segmented intelligent spraying equipment for ships.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Long, Z.; Li, X.T.; Shuai, T.; Wen, F.J.; Feng, W.R.; Lang, C.P. Review of Research State of Trajectory Planning for Industrial Robots. Mech. Sci. Technol. Aerosp. Eng. 2021, 6, 853–862. [Google Scholar]
- Ning, Y.; Meng, M. Analysis and Prospect of Spraying Robot Path Planning Method. Sci. Technol. Eng. 2019, 19, 19–27. [Google Scholar]
- Cai, Z.; Liang, H.; Quan, S.; Deng, S.; Zeng, C.; Zhang, F. Computer-aided robot trajectory auto-generation strategy in thermal spraying. J. Therm. Spray Technol. 2015, 24, 1235–1245. [Google Scholar] [CrossRef]
- Fang, D.; Zheng, Y.; Zhang, B.; Li, X.; Ju, P.; Li, H.; Zeng, C. Automatic robot trajectory for thermal-sprayed complex Surfaces. Adv. Mater. Sci. Eng. 2018, 2018, 8697056. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, Z.; Zeng, Q.; Liu, X.; Hu, X. Research on off-line programming system of marine spraying robot. Mach. Manuf. 2021, 59, 53–59. [Google Scholar]
- Chen, Q.; Zou, Y.; Zhang, T.; Zhou, Q. Development of Off—Line Programming System for Spray Robot. Mach. Tool Hydraul. 2013, 41, 122–124. [Google Scholar]
- Wang, X.; Sun, K. QT Develop Spraying Robot Off—Line Program Simulation System. Coal Mine Mach. 2016, 37, 188–190. [Google Scholar]
- Zeng, Y.; Yu, Y.; Liu, Y.; Liu, D. Parameter Optimization of Boundary-constrained Spray Trajectory for Irregular Plane. Mech. Sci. Technol. Aerosp. Eng. 2020, 39, 904–909. [Google Scholar]
- Ma, S.; Luo, X.; Li, A.; Zhou, Y. Painting parametric optimization using AMPSO algorithm on ship painting robots. Chin. J. Constr. Mach. 2016, 14, 125–130. [Google Scholar]
- Wang, Y.; Wang, G.; Li, B.; Yan, J.; Lu, D. Analysis of Coating Uniformity in Boundary Zone for Large-Size Surface Spraying. Mech. Sci. Technol. Aerosp. Eng. 2021, 9, 1–8. [Google Scholar]
- Lin, M.; Tang, Q.; Li, G.; Luo, Y.; Li, Y.; Fan, Q.; Yang, A.; Zhang, P. Research on Trajectory Planning of Plane Double-pass Spraying Based on Particle Swarm Algorithm. Mech. Eng. 2021, 6, 25–30. [Google Scholar]
- Xue-mei, L.I.U.; Tao, L.I.U.; Lian-sheng, Y.A.N.G. Spray Painting Film Thickness Distribution on Panel and Optimization of Width of Paint Film Overlay. Surf. Technol. 2018, 47, 116–125. [Google Scholar]
- Qingjun, Z.H.A.N.G.; Yin, X.I.E.; Song, W.U. Prediction of Wave Absorbing Coatings Thickness of Airborne Conformal Antenna Based on Orthogonal Experimental Design and Regression Analysis. Acta Armamentarii 2021, 10, 203–210. [Google Scholar]
- Xia, W.; Yu, S.R.; Liao, X.P. Paint deposition pattern modeling and estimation for robotic air spray painting on free-form surface using the curvature circle method. Ind. Robot. 2010, 37, 202–213. [Google Scholar] [CrossRef]
- Zhao, D.; Chen, W.; Tang, Y. Tool Path Planning of Spray Painting Robot Based on Genetic Algorithms. China Mech. Eng. 2008, 19, 777–792. [Google Scholar]
- Zhang, Y.; Huang, Y.; Gao, F.; Wang, W. New model for air spray gun of robotic spray-painting. Chin. J. Mech. Eng. 2006, 42, 226–233. [Google Scholar] [CrossRef]
- Guolei, W.A.N.G.; Qiang, Y.I.; Dongjing, M.I.A.O.; Ken, C.H.E.N.; Liqiang, W.A.N.G. Multivariable coating hickness distribution model for robotic spray painting. J. Tsinghua Univ. Sci. Technol. 2017, 57, 324–330. [Google Scholar]



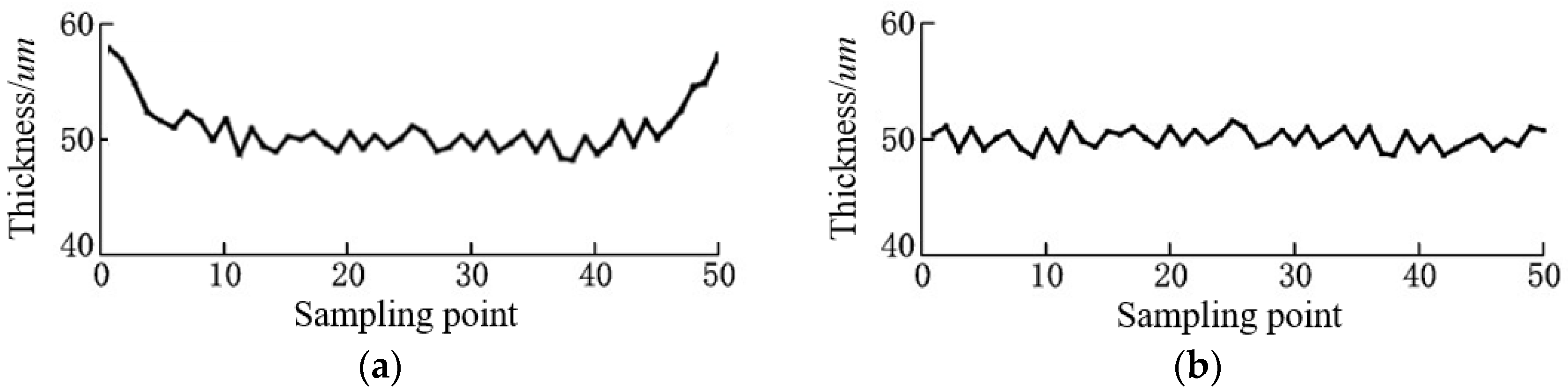


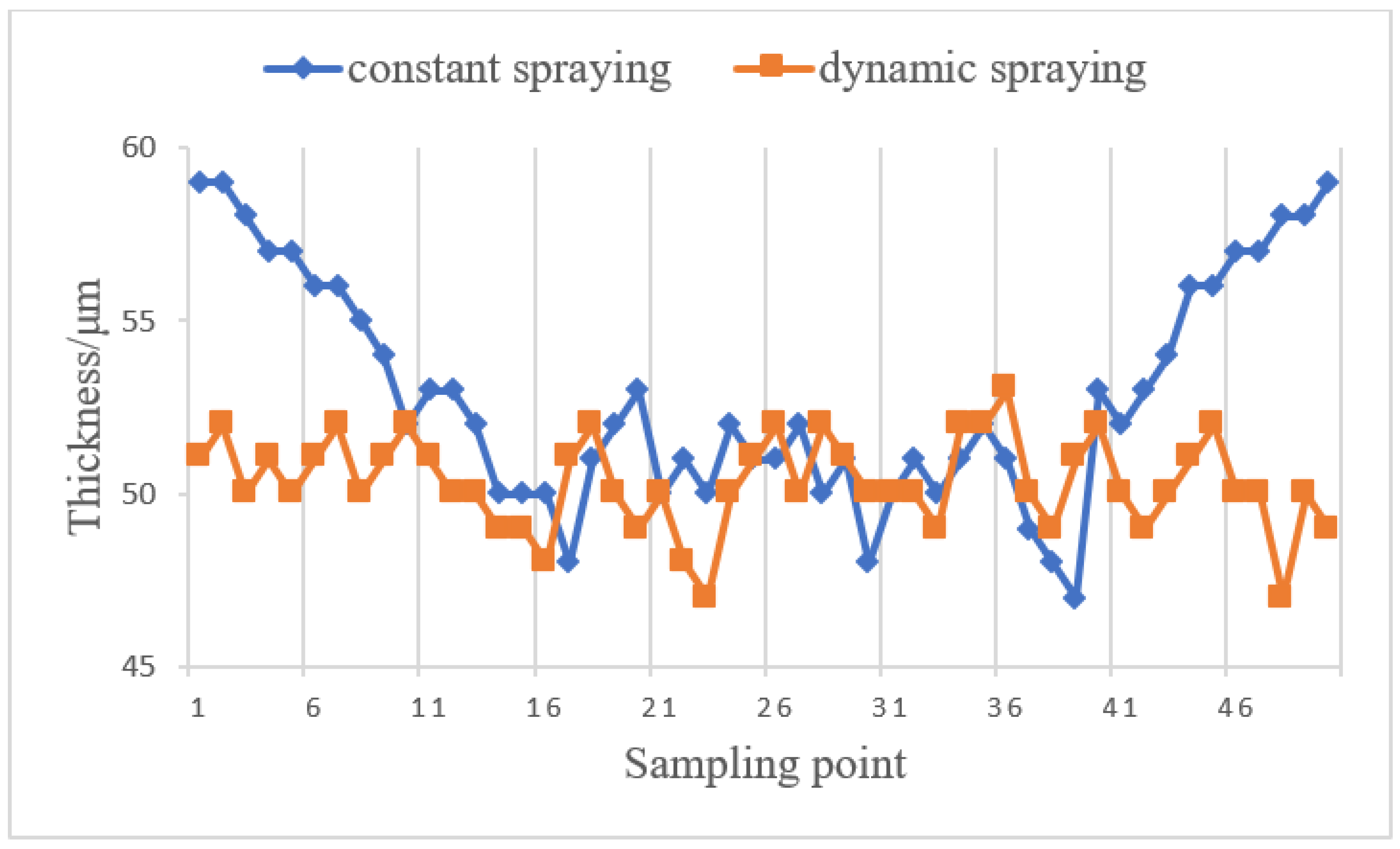
| DATA | |
|---|---|
| standard (target) values | 50 |
| mean thickness (constant spraying) | 52.86 |
| mean thickness (dynamic spraying) | 50.32 |
| rms thickness (constant spraying) | 3.24 |
| rms thickness (dynamic spraying) | 1.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, T.; Xu, J.; Cui, J.; Tao, L.; Xu, W.; Wang, Z.; Ji, J. Variable Velocity Coating Thickness Distribution Model for Super-Large Planar Robot Spraying. Coatings 2023, 13, 1434. https://doi.org/10.3390/coatings13081434
Shi T, Xu J, Cui J, Tao L, Xu W, Wang Z, Ji J. Variable Velocity Coating Thickness Distribution Model for Super-Large Planar Robot Spraying. Coatings. 2023; 13(8):1434. https://doi.org/10.3390/coatings13081434
Chicago/Turabian StyleShi, Tongjun, Jiangmin Xu, Jie Cui, Lei Tao, Weijia Xu, Ziqiang Wang, and Jianbo Ji. 2023. "Variable Velocity Coating Thickness Distribution Model for Super-Large Planar Robot Spraying" Coatings 13, no. 8: 1434. https://doi.org/10.3390/coatings13081434
APA StyleShi, T., Xu, J., Cui, J., Tao, L., Xu, W., Wang, Z., & Ji, J. (2023). Variable Velocity Coating Thickness Distribution Model for Super-Large Planar Robot Spraying. Coatings, 13(8), 1434. https://doi.org/10.3390/coatings13081434





