Initial Vacancy-Dependent High-Temperature Creep Behavior of Nanocrystalline Ni by Molecular Dynamics Simulation
Abstract
1. Introduction
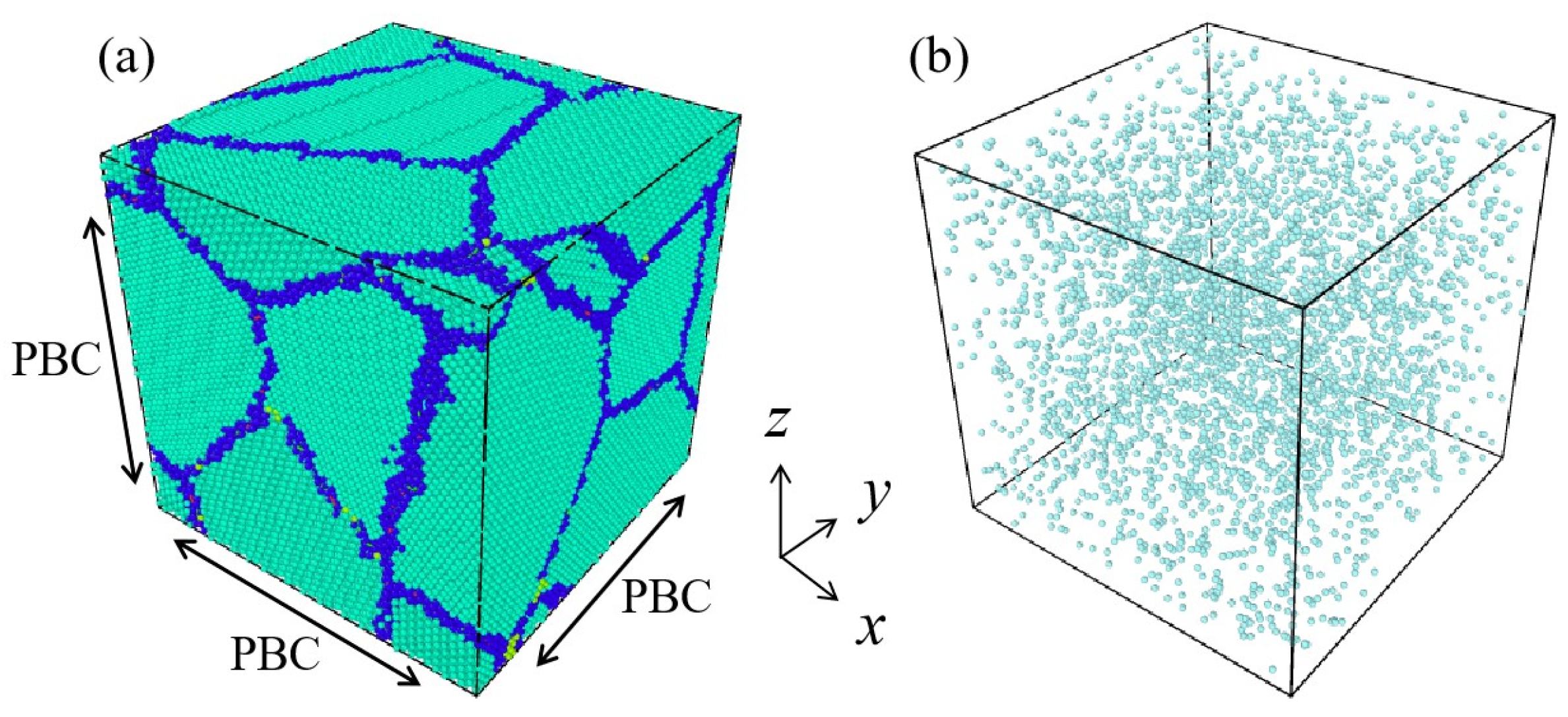
2. Simulation Model and Method
3. Results and Discussion
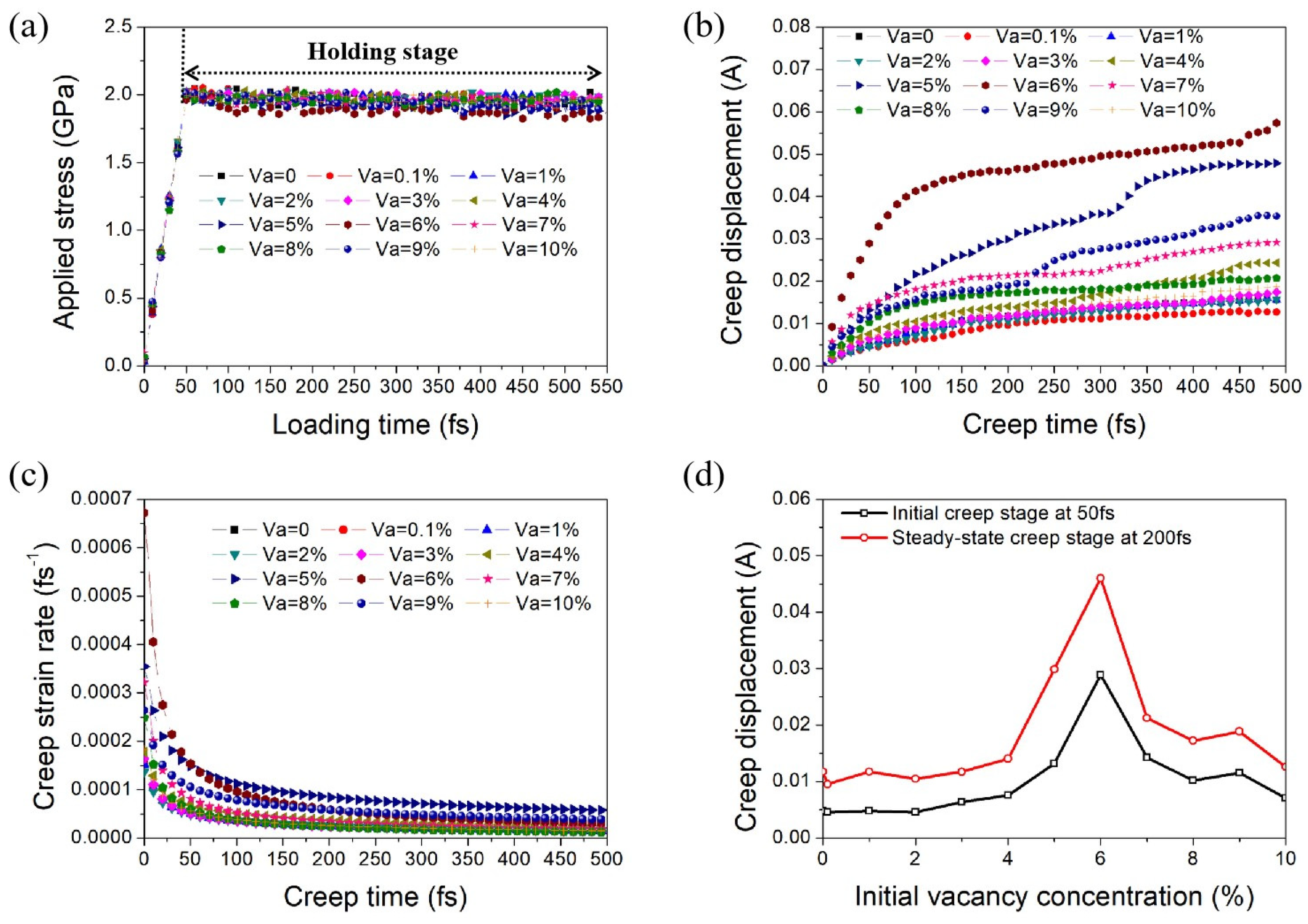
3.1. Creep Behavior of Nanocrystalline Ni with Initial Vacancies
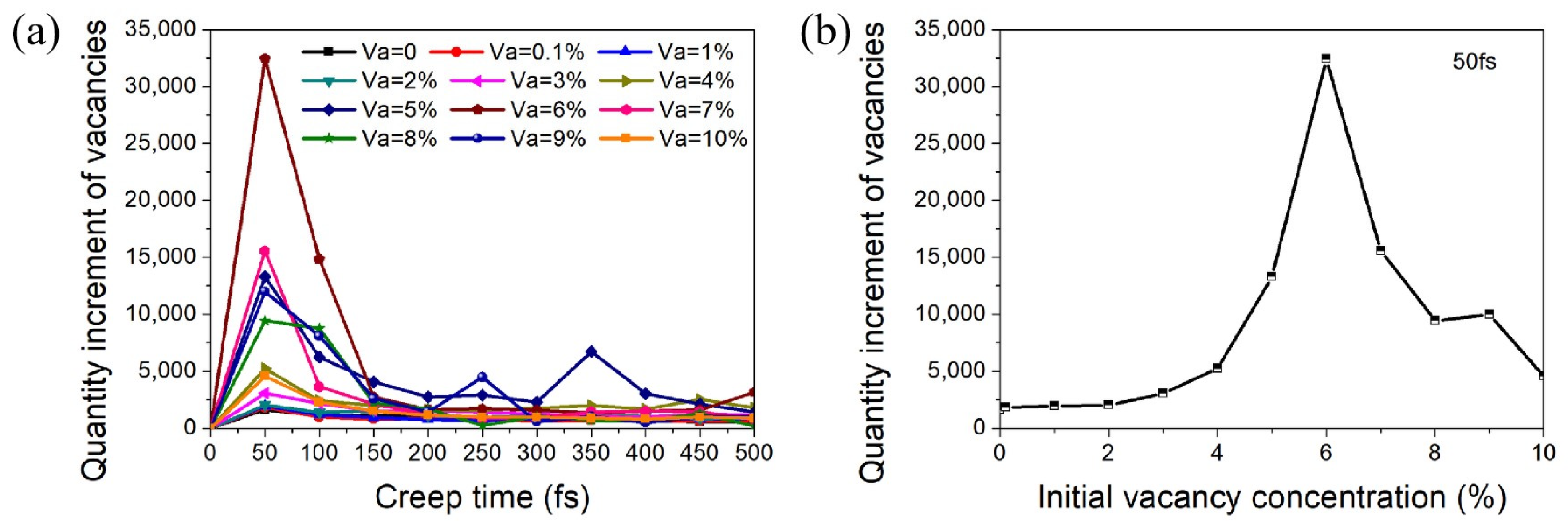
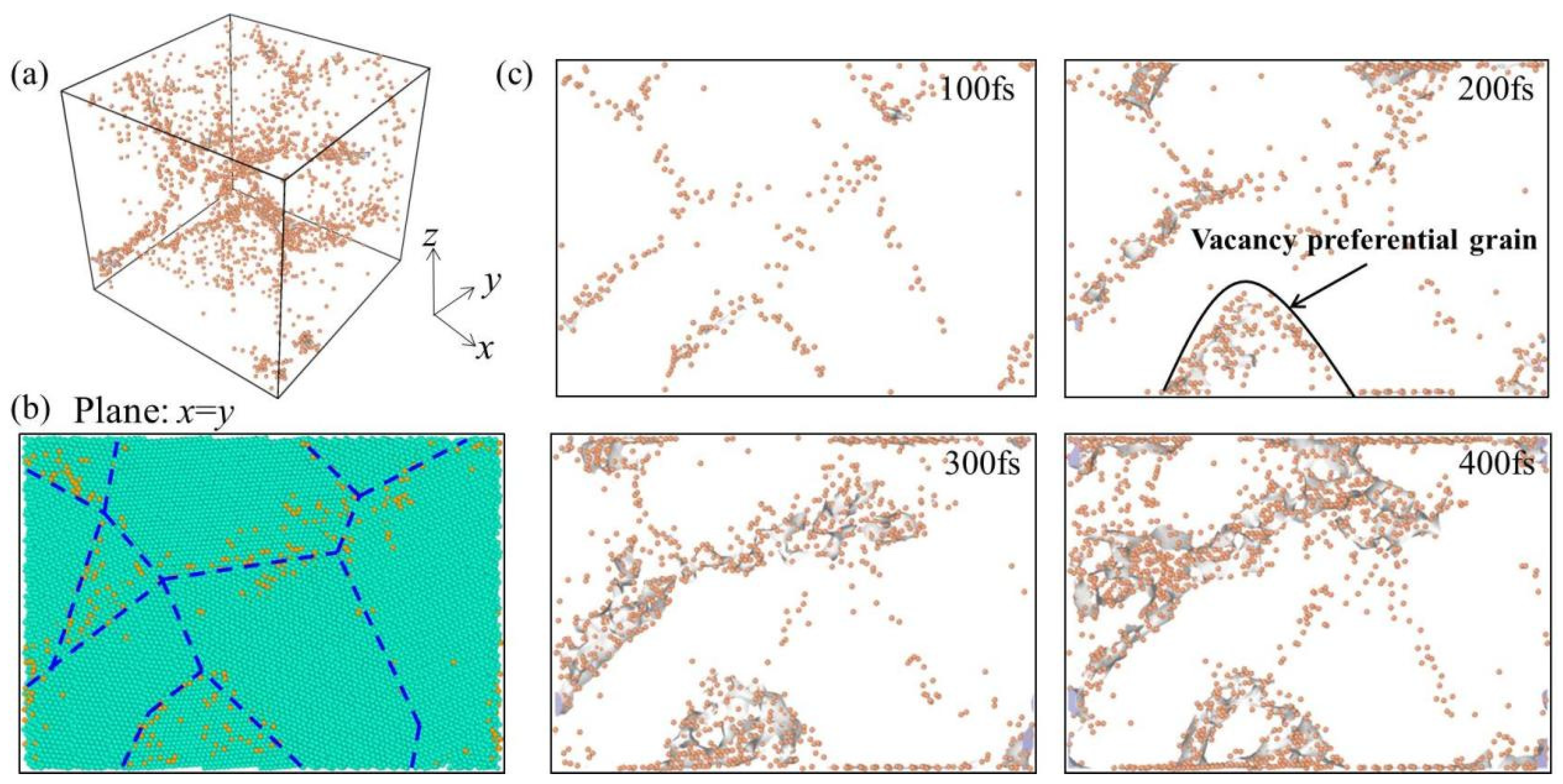
3.2. Characteristics of Deformation-Induced Vacancy Formation during Creep
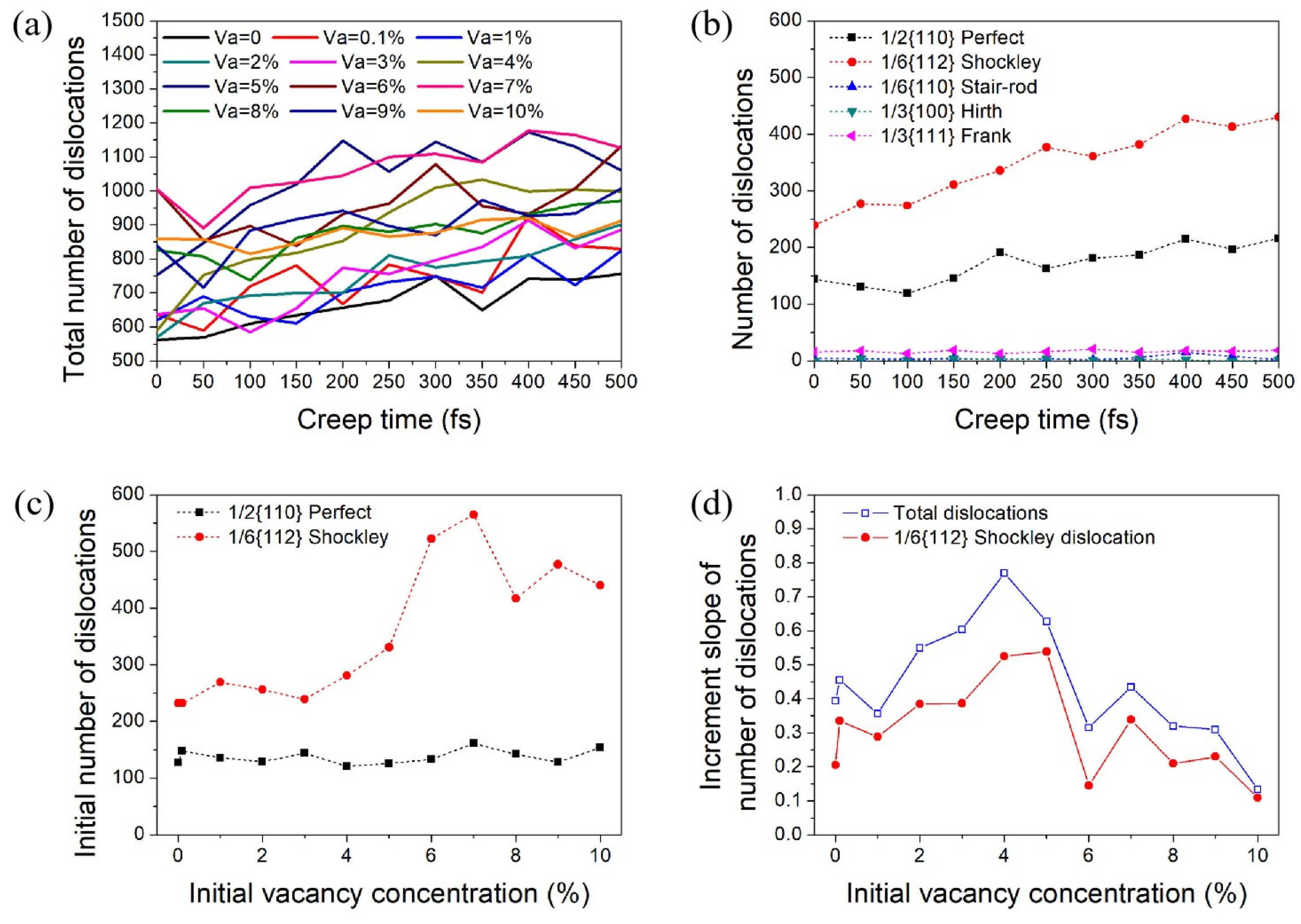
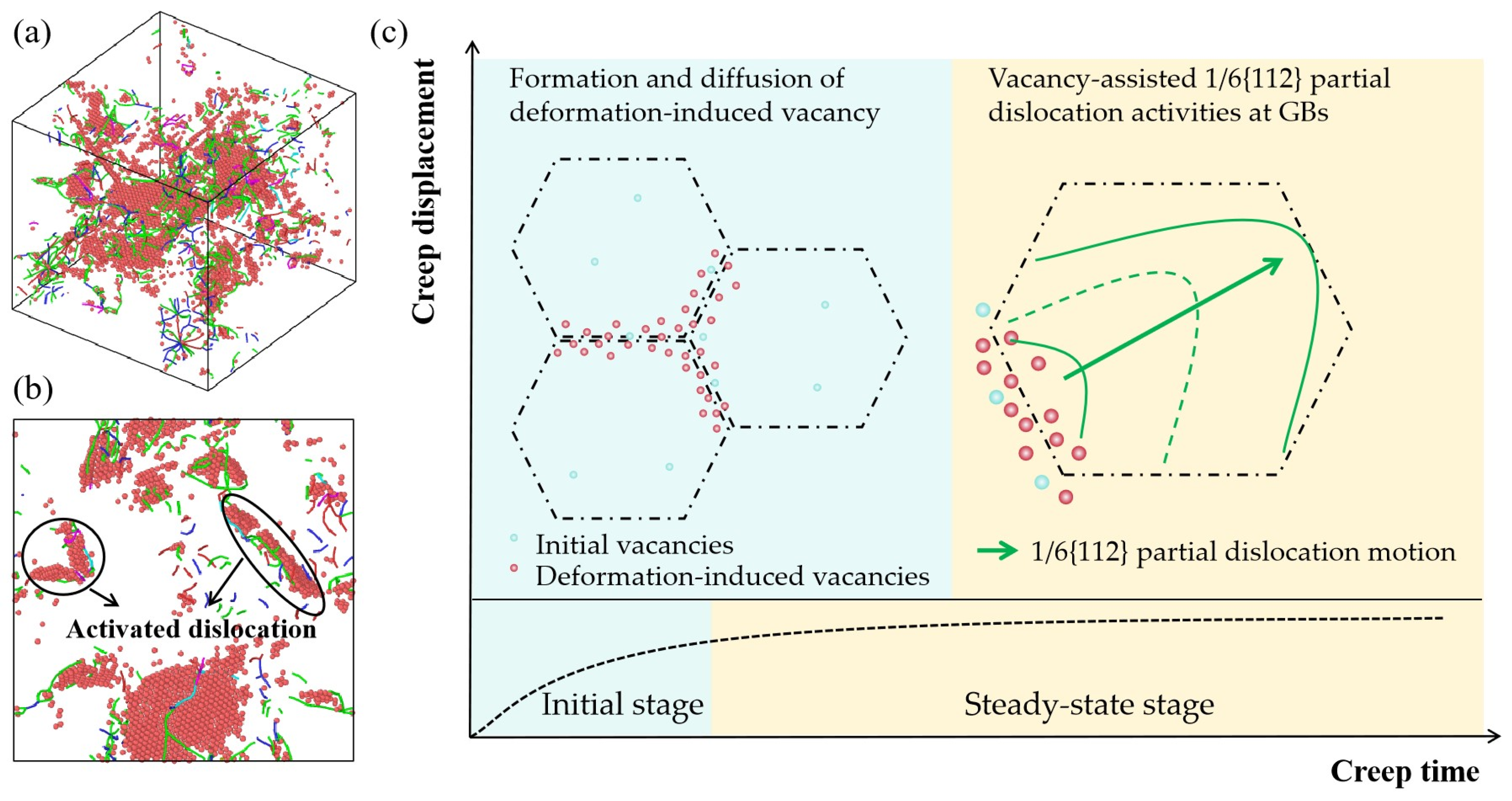
3.3. Influence of Initial Vacancy Concentration on Dislocation-Related Activities
3.4. Microstructural Evolution of Nanocrystalline Ni during Creep
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, T.; Li, J. Ultra-strength materials. Prog. Mater. Sci. 2010, 55, 710–757. [Google Scholar] [CrossRef]
- Liu, X.; Sun, L.; Zhu, L.; Liu, J.; Lu, K.; Lu, J. High-order hierarchical nanotwins with superior strength and ductility. Acta Mater. 2018, 149, 397–406. [Google Scholar] [CrossRef]
- Zhang, N.; Jin, S.; Sha, G.; Yu, J.; Cai, X.; Du, C.; Shen, T. Segregation induced hardening in annealed nanocrystalline Ni-Fe alloy. Mater. Sci. Eng. A 2018, 735, 354–360. [Google Scholar] [CrossRef]
- Li, Q.J.; Ma, E. When ‘smaller is stronger’no longer holds. Mater. Res. Lett. 2018, 6, 283–292. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, Z.; Wang, Y.; Zhou, Q.; Yang, T.; Li, Q.; Jia, Q.; Wang, H. Friction-induced rapid amorphization in a wear-resistant (CoCrNi)88Mo12 dual-phase medium-entropy alloy at cryogenic temperature. Compos. Part B Eng. 2023, 263, 110833. [Google Scholar] [CrossRef]
- Kale, C.; Srinivasan, S.; Hornbuckle, B.; Koju, R.; Darling, K.; Mishin, Y.; Solanki, K. An experimental and modeling investigation of tensile creep resistance of a stable nanocrystalline alloy. Acta Mater. 2020, 199, 141–154. [Google Scholar] [CrossRef]
- Meraj; Pal, S. The Effect of Temperature on Creep Behaviour of Porous (1 at.%) Nano Crystalline Nickel. Trans. Indian Inst. Met. 2015, 69, 277–282. [Google Scholar] [CrossRef]
- Nie, K.; Wu, W.-P.; Zhang, X.-L.; Yang, S.-M. Molecular dynamics study on the grain size, temperature, and stress dependence of creep behavior in nanocrystalline nickel. J. Mater. Sci. 2016, 52, 2180–2191. [Google Scholar] [CrossRef]
- Yang, X.-S.; Wang, Y.-J.; Zhai, H.-R.; Wang, G.-Y.; Su, Y.-J.; Dai, L.; Ogata, S.; Zhang, T.-Y. Time-, stress-, and temperature-dependent deformation in nanostructured copper: Creep tests and simulations. J. Mech. Phys. Solids 2016, 94, 191–206. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Ishii, A.; Ogata, S. Transition of creep mechanism in nanocrystalline metals. Phys. Rev. B 2011, 84, 224102. [Google Scholar] [CrossRef]
- Coble, R.L. A Model for Boundary Diffusion Controlled Creep in Polycrystalline Materials. J. Appl. Phys. 1963, 34, 1679–1682. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. Steady-state diffusional creep. Philos. Mag. 1967, 16, 231–237. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, B.; He, C.; Xie, L.; Peng, Q. Shift of Creep Mechanism in Nanocrystalline NiAl Alloy. Materials 2019, 12, 2508. [Google Scholar] [CrossRef]
- Yuasa, M.; Matsumoto, H.; Hakamada, M.; Mabuchi, M. Effects of Vacancies on Deformation Behavior in Nanocrystalline Nickel. Mater. Trans. 2008, 49, 2315–2321. [Google Scholar] [CrossRef]
- Islam, Z.; Wang, B.; Hattar, K.; Gao, H.; Haque, A. Departing from the mutual exclusiveness of strength and ductility in nanocrystalline metals with vacancy induced plasticity. Scr. Mater. 2018, 157, 39–43. [Google Scholar] [CrossRef]
- Ford, J.; Wheeler, J.; Movchan, A. Computer simulation of grain-boundary diffusion creep. Acta Mater. 2002, 50, 3941–3955. [Google Scholar] [CrossRef]
- Millett, P.C.; Desai, T.; Yamakov, V.; Wolf, D. Atomistic simulations of diffusional creep in a nanocrystalline body-centered cubic material. Acta Mater. 2008, 56, 3688–3698. [Google Scholar] [CrossRef]
- Zhao, F.; Zhang, J.; He, C.; Zhang, Y.; Gao, X.; Xie, L. Molecular dynamics simulation on creep behavior of nanocrystalline TiAl alloy. Nanomaterials 2020, 10, 1693. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Li, X. Atomistic simulations of high-temperature creep in nanotwinned TiAl alloys. Extrem. Mech. Lett. 2021, 44, 101253. [Google Scholar] [CrossRef]
- Yang, C.; Yin, C.; Wu, Y.; Zhou, Q.; Liu, X. Atomic insights into the deformation mechanism of an amorphous wrapped nanolamellar heterostructure and its effect on self-lubrication. J. Mater. Res. Technol. 2023, 26, 4206–4218. [Google Scholar] [CrossRef]
- Zhou, Q.; Luo, D.; Hua, D.; Ye, W.; Li, S.; Zou, Q.; Chen, Z.; Wang, H. Design and characterization of metallic glass/graphene multilayer with excellent nanowear properties. Friction 2022, 10, 1913–1926. [Google Scholar] [CrossRef]
- Shi, Y.; Ye, W.; Hua, D.; Zhou, Q.; Huang, Z.; Liu, Y.; Li, S.; Guo, T.; Chen, Y.; Eder, S.J.; et al. Interfacial engineering for enhanced mechanical performance: High-entropy alloy/graphene nanocomposites. Mater. Today Phys. 2023, 38, 101220. [Google Scholar] [CrossRef]
- Yao, H.; Ye, T.; Yu, W.; Wang, P.; Wu, J.; Wu, Y.; Chen, P. Atomic-scale investigation of creep behavior and deformation mechanism in nanocrystalline FeCrAl alloys. Mater. Des. 2021, 206, 109766. [Google Scholar] [CrossRef]
- Pal, S.; Meraj, M. Investigation of reorganization of a nanocrystalline grain boundary network during biaxial creep deformation of nanocrystalline Ni using molecular dynamics simulation. J. Mol. Model. 2019, 25, 282. [Google Scholar] [CrossRef]
- Pal, S.; Mishra, S.; Meraj; Mondal, A.; Ray, B. On the comparison of interrupted and continuous creep behaviour of nanocrystalline copper: A molecular dynamics approach. Mater. Lett. 2018, 229, 256–260. [Google Scholar] [CrossRef]
- Weertman, J.R. Retaining the Nano in Nanocrystalline Alloys. Science 2012, 337, 921–922. [Google Scholar] [CrossRef]
- Pal, S.; Meraj; Deng, C. Effect of Zr addition on creep properties of ultra-fine grained nanocrystalline Ni studied by molecular dynamics simulations. Comput. Mater. Sci. 2017, 126, 382–392. [Google Scholar] [CrossRef]
- Li, G.; Zhang, F.; Zhu, D.; Wang, L. Segregation thickness effect on the mechanical behaviors of nanocrystalline Ni-doped W alloy. Phys. Lett. A 2021, 409, 127513. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Etesami, S.A.; Asadi, E. Molecular dynamics for near melting temperatures simulations of metals using modified embedded-atom method. J. Phys. Chem. Solids 2018, 112, 61–72. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 1998, 57, 7192–7205. [Google Scholar] [CrossRef]
- Shimizu, F.; Ogata, S.; Li, J. Theory of Shear Banding in Metallic Glasses and Molecular Dynamics Calculations. Mater. Trans. 2007, 48, 2923–2927. [Google Scholar] [CrossRef]
- Herring, C. Diffusional Viscosity of a Polycrystalline Solid. J. Appl. Phys. 1950, 21, 437–445. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Shao, W.; Shi, Y.; Zhou, Q. Initial Vacancy-Dependent High-Temperature Creep Behavior of Nanocrystalline Ni by Molecular Dynamics Simulation. Coatings 2024, 14, 63. https://doi.org/10.3390/coatings14010063
Cui Y, Shao W, Shi Y, Zhou Q. Initial Vacancy-Dependent High-Temperature Creep Behavior of Nanocrystalline Ni by Molecular Dynamics Simulation. Coatings. 2024; 14(1):63. https://doi.org/10.3390/coatings14010063
Chicago/Turabian StyleCui, Yan, Weidong Shao, Yeran Shi, and Qing Zhou. 2024. "Initial Vacancy-Dependent High-Temperature Creep Behavior of Nanocrystalline Ni by Molecular Dynamics Simulation" Coatings 14, no. 1: 63. https://doi.org/10.3390/coatings14010063
APA StyleCui, Y., Shao, W., Shi, Y., & Zhou, Q. (2024). Initial Vacancy-Dependent High-Temperature Creep Behavior of Nanocrystalline Ni by Molecular Dynamics Simulation. Coatings, 14(1), 63. https://doi.org/10.3390/coatings14010063






