Research Progress on Numerical Simulation of the Deposition and Deformation Behavior of Cold Spray Particles
Abstract
1. Introduction
2. Commonly Used Material Constitutive Models and Alloy Property Parameters for Cold Spraying
2.1. Material Modeling Methods and Parameters of Commonly Used Cold Spraying Materials
2.2. Common Constitutive Models of Materials
2.2.1. Johnson–Cook Plasticity (JC) Model
2.2.2. Zerilli–Armstrong (ZA) Model
2.2.3. Preston–Tonks–Wallace (PTW) Model
2.2.4. Mechanical Threshold Stress Model (MTS)
2.2.5. Modified Johnson–Cook Model
3. Common Finite Element Simulation Software and Methods for Simulating Particle Deposition and Deformation Behavior in Cold Spray Coating
3.1. ALE Method
3.2. SPH Method
3.3. Euler Method
3.4. Other Common Methods
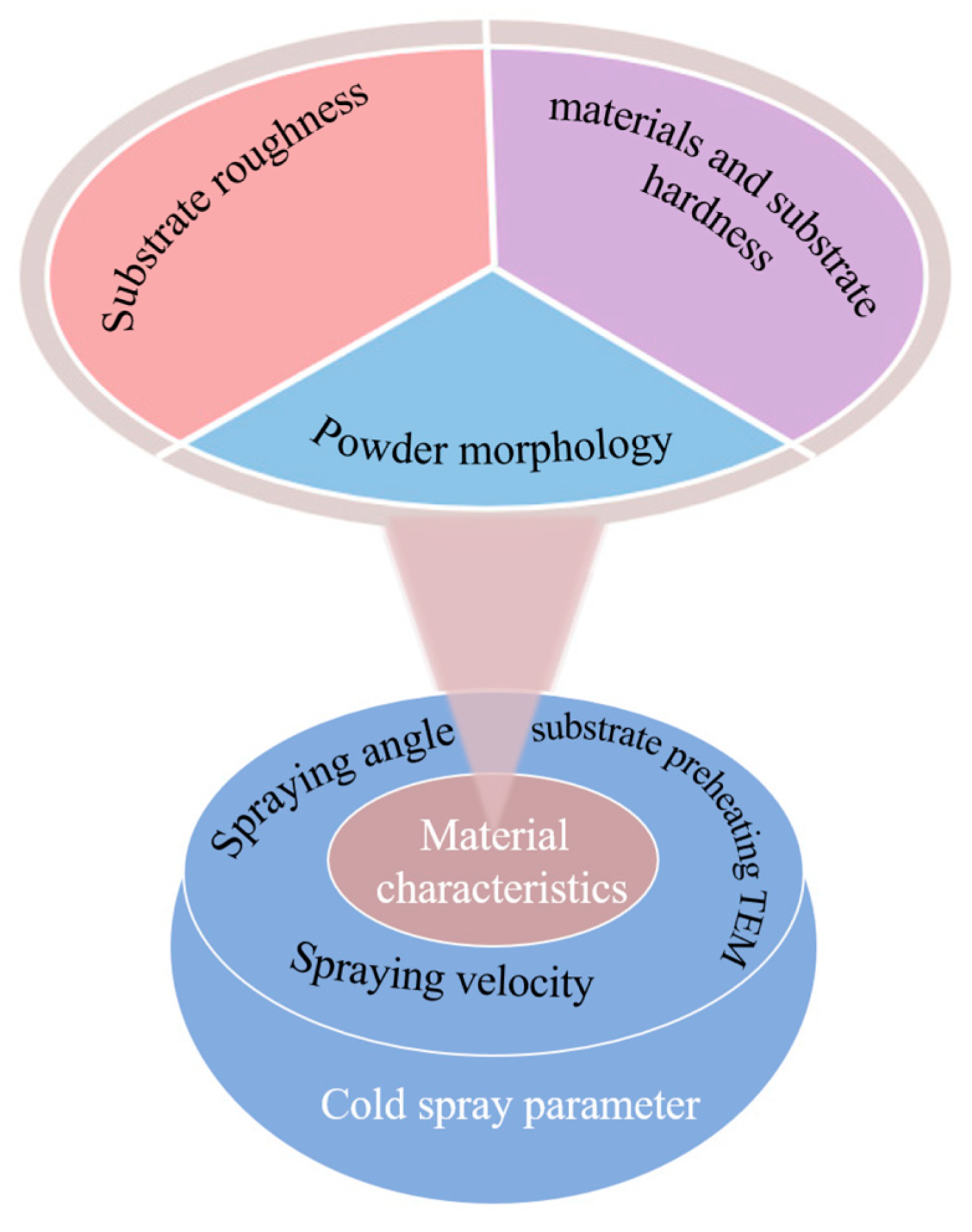
4. Factors Influencing the Simulated Depositional Binding and Deformation Behavior of Particles
4.1. Material Characteristics
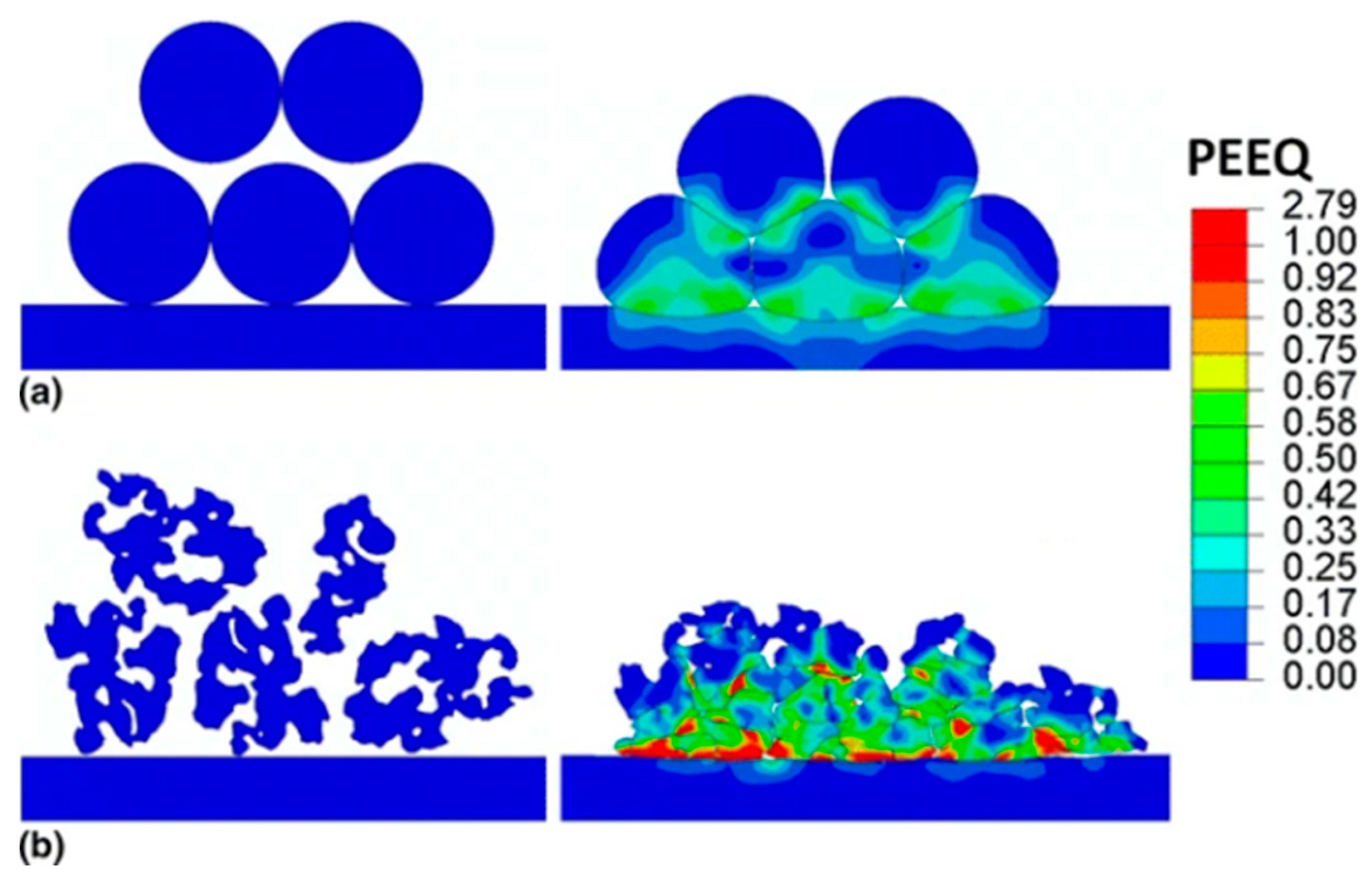
4.1.1. Particle Morphology
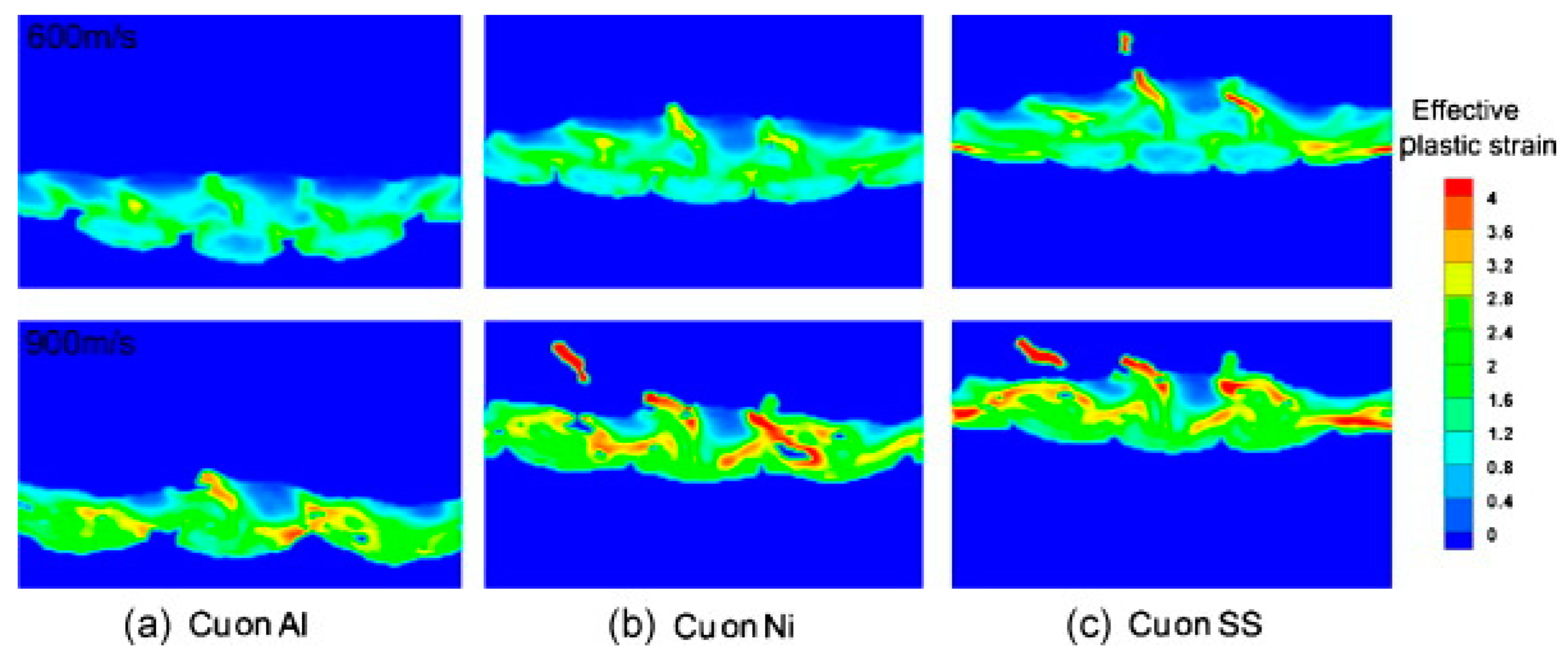
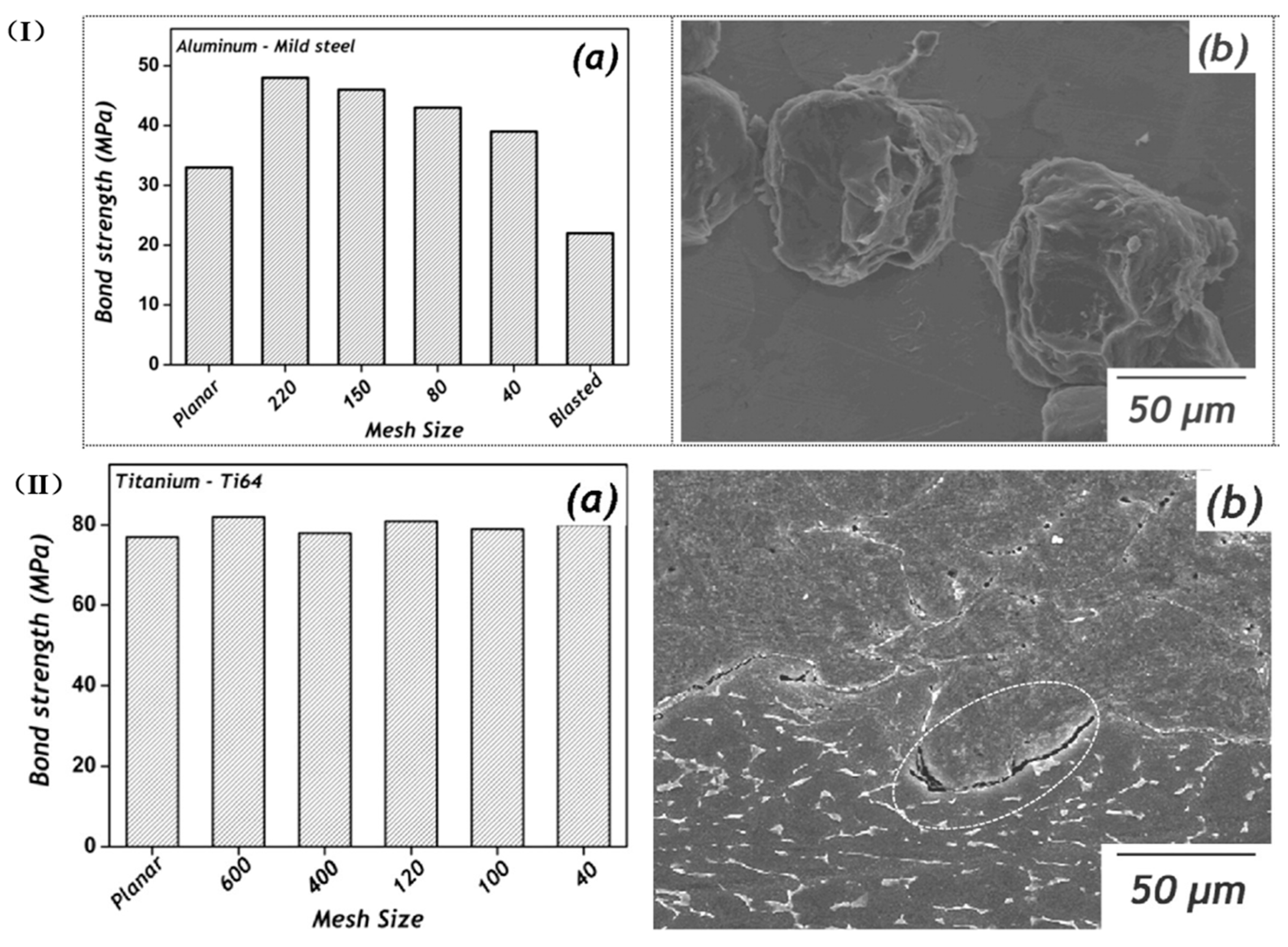
4.1.2. Particle/Substrate Hardness
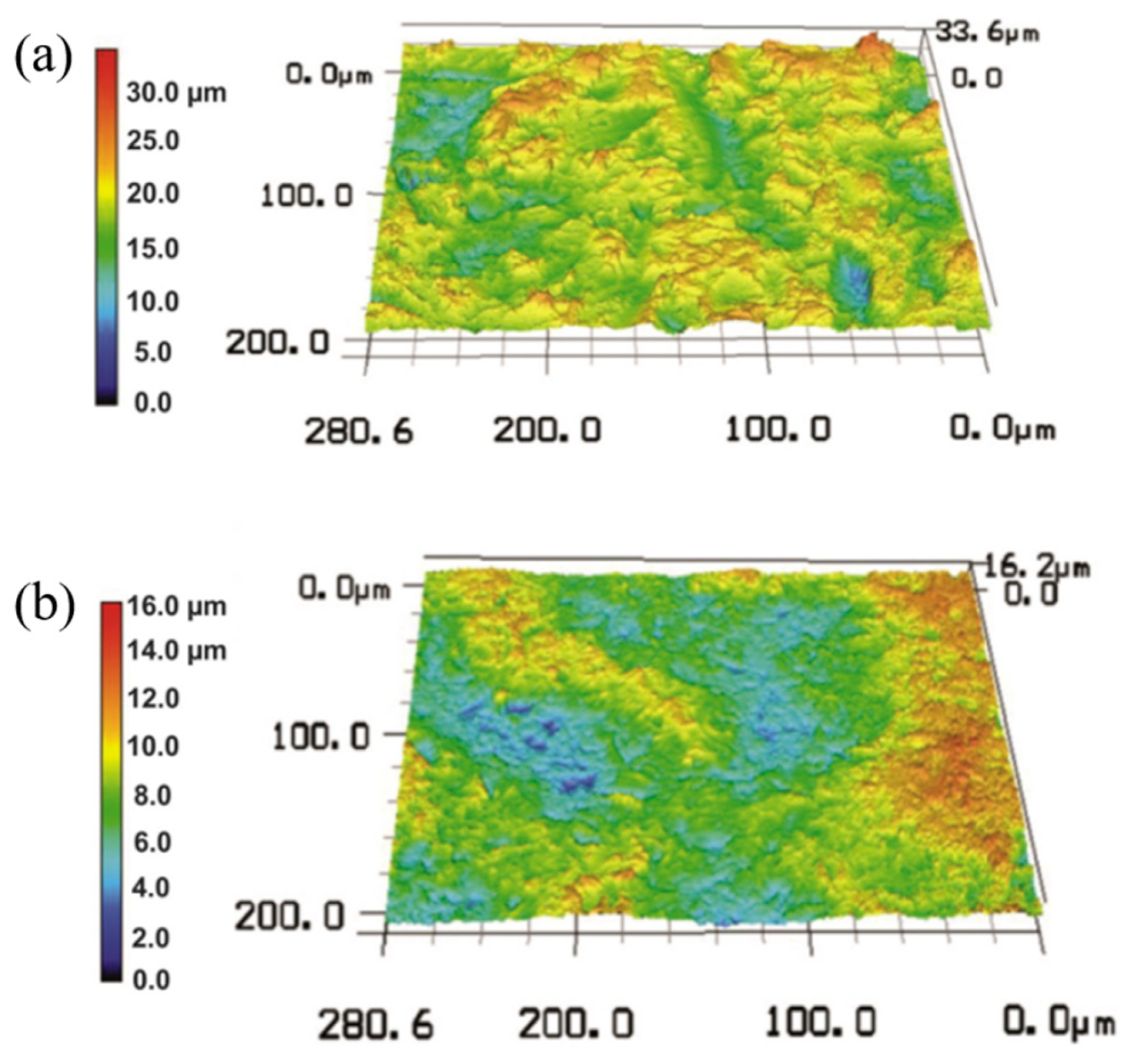
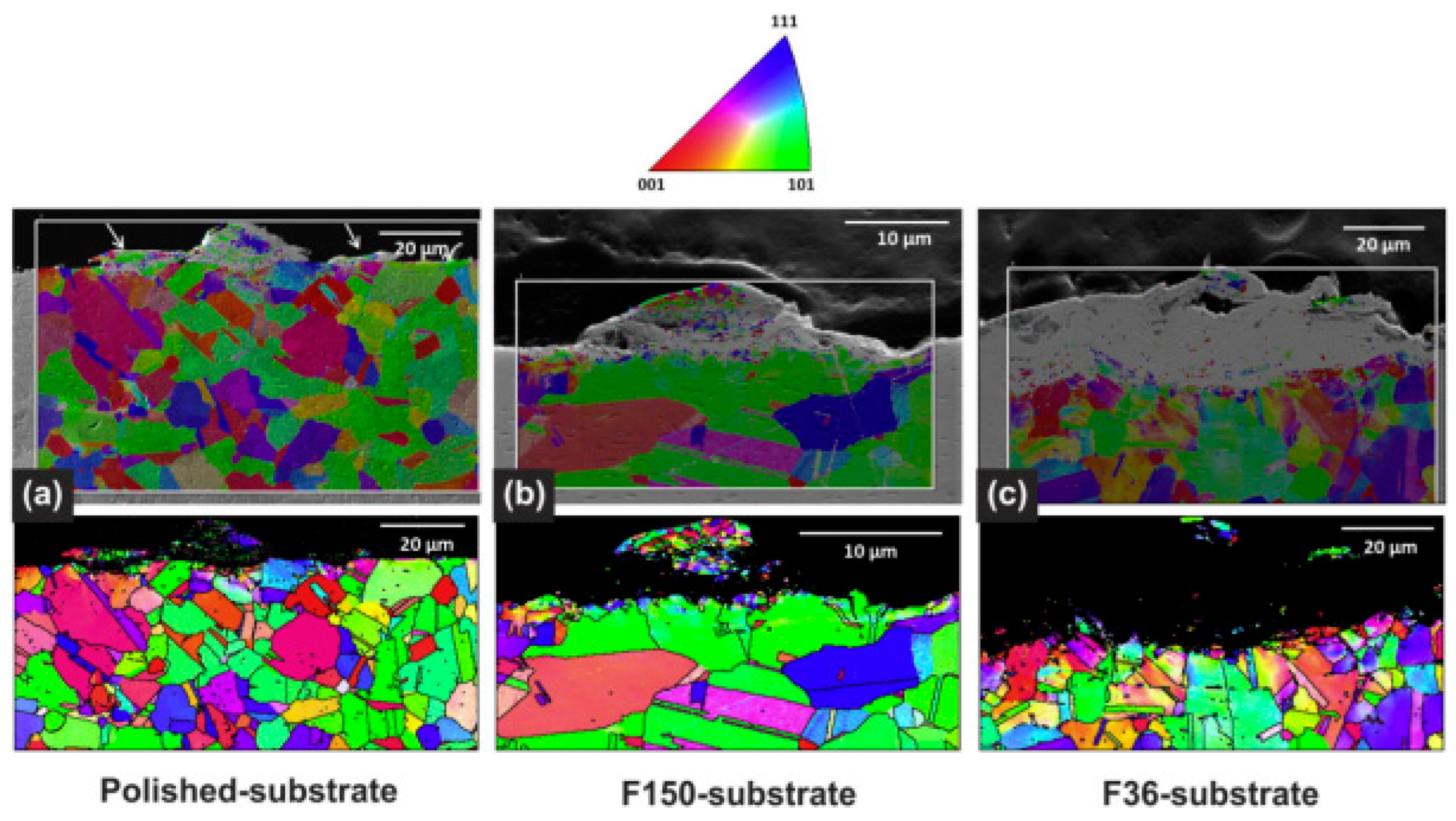
4.1.3. Substrate Roughness
4.2. Cold Spray Parameter Factors
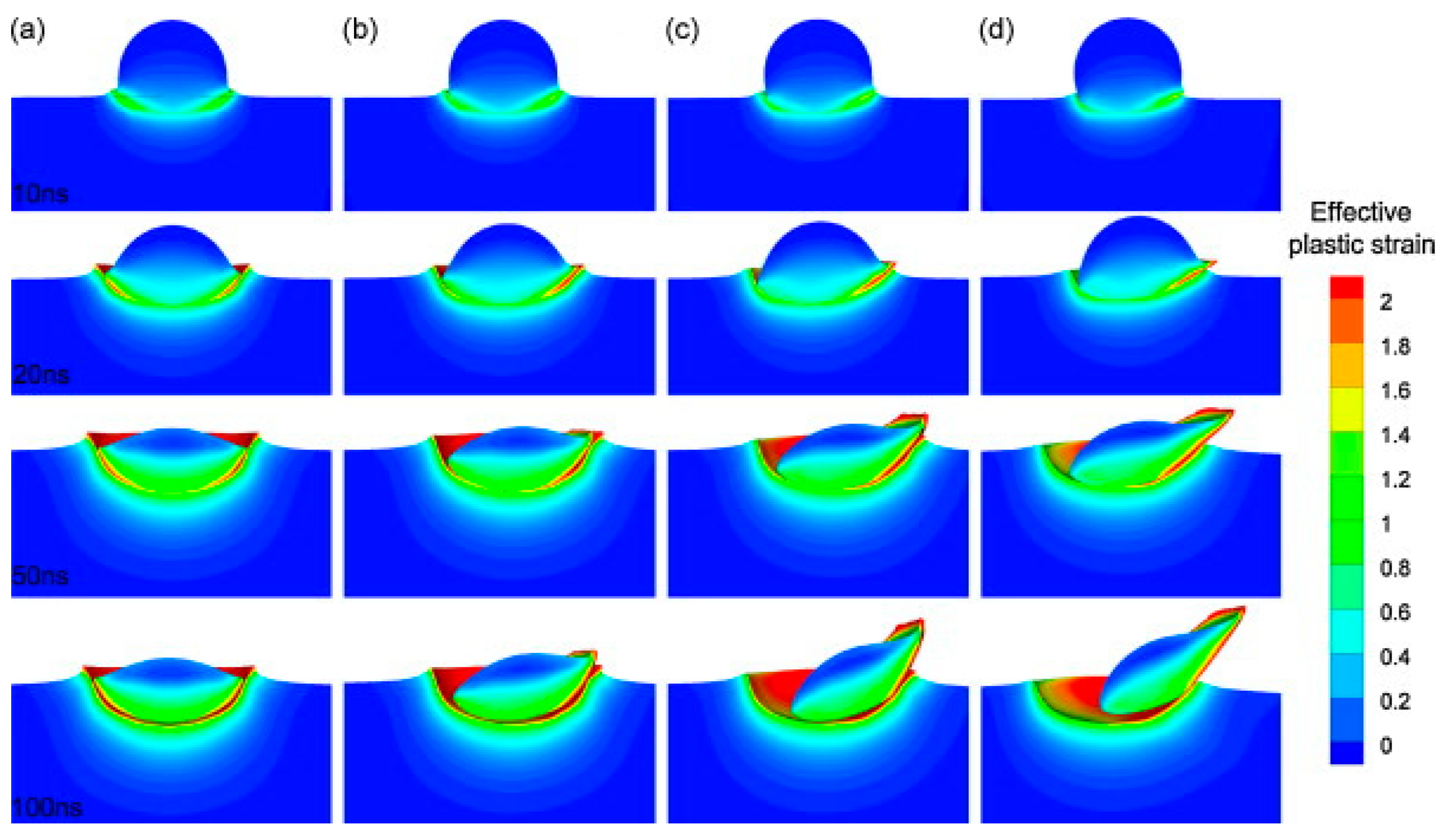
4.2.1. Cold Spraying Velocity
4.2.2. Preheating Temperature
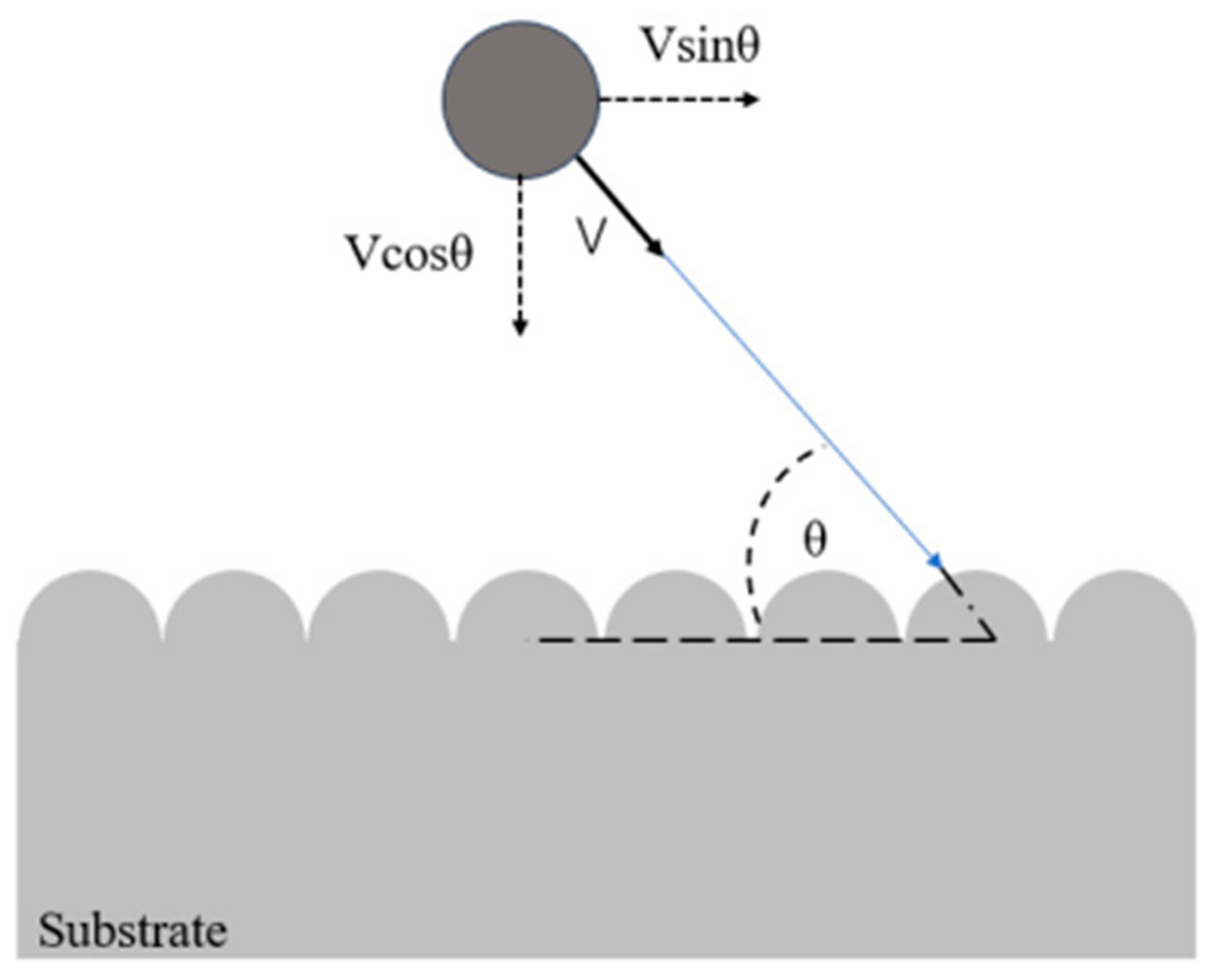
4.2.3. Spraying Angle
5. Conclusions and Outlook
5.1. Conclusions
5.2. Outlook
- So far, many studies have focused on the ideal cold spray deposition of spherical particles on the surface of a smooth substrate. However, the situation involves irregular particle morphology, varying particle size, and coarse surface substrates. So, the actual simulation of the situation is difficult; although there are studies in this area, the number of studies is still relatively small.
- Most studies primarily concentrate on simulating the initial layer of particle impact substrate coating. While the initial layer is crucial, successful coating preparation requires equal attention to the same material’s second layer and multi-layer particle combinations. Regrettably, research in this area remains limited.
- Considerable progress has been made in numerically simulating cold spraying at the macroscopic level. However, there has been little simulation at the microscopic level, particularly in addressing the internal organization of particles/substrate and how it changes after a collision. Furthermore, the impact of particle organization on coating properties after deposition has not been thoroughly investigated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oyinbo, S.T.; Jen, T.-C. Investigation of the process parameters and restitution coefficient of ductile materials during cold gas dynamic spray (CGDS) using finite element analysis. Addit. Manuf. 2020, 31, 100986. [Google Scholar] [CrossRef]
- Papyrin, A. Cold Spray Technology. Adv. Mater. Process. 2001, 159, 49. [Google Scholar]
- Yin, S.; Cavaliere, P.; Aldwell, B.; Jenkins, R.; Liao, H.; Li, W.; Lupoi, R. Cold spray additive manufacturing and repair: Fundamentals and applications. Addit. Manuf. 2018, 21, 628–650. [Google Scholar] [CrossRef]
- Yu, T.; Chen, M.; Wu, Z. Experimental and numerical study of deposition mechanisms for cold spray additive manufacturing process. Chin. J. Aeronaut. 2022, 35, 276–290. [Google Scholar] [CrossRef]
- Gärtner, F.; Schmidt, T.; Stoltenhoff, T.; Kreye, H. Recent Developments and Potential Applications of Cold Spraying. Adv. Eng. Mater. 2006, 8, 611–618. [Google Scholar] [CrossRef]
- Irissou, E.; Legoux, J.-G.; Ryabinin, A.N.; Jodoin, B.; Moreau, C. Review on Cold Spray Process and Technology: Part I—Intellectual Property. J. Therm. Spray Technol. 2008, 17, 495–516. [Google Scholar] [CrossRef]
- Assadi, H.; Kreye, H.; Gärtner, F.; Klassen, T. Cold spraying—A materials perspective. Acta Mater. 2016, 116, 382–407. [Google Scholar] [CrossRef]
- Fardan, A.; Berndt, C.C.; Ahmed, R. Numerical modelling of particle impact and residual stresses in cold sprayed coatings: A review. Surf. Coat. Technol. 2021, 409, 126835. [Google Scholar] [CrossRef]
- Hassani-Gangaraj, M.; Veysset, D.; Champagne, V.K.; Nelson, K.A.; Schuh, C.A. Adiabatic shear instability is not necessary for adhesion in cold spray. Acta Mater. 2018, 158, 430–439. [Google Scholar] [CrossRef]
- Assadi, H.; Gärtner, F.; Stoltenhoff, T.; Kreye, H. Bonding mechanism in cold gas spraying. Acta Mater. 2003, 51, 4379–4394. [Google Scholar] [CrossRef]
- Khodabakhshi, F.; Marzbanrad, B.; Jahed, H.; Gerlich, A.P. Interfacial bonding mechanisms between aluminum and titanium during cold gas spraying followed by friction-stir modification. Appl. Surf. Sci. 2018, 462, 739–752. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, M.X. Review on Recent Research and Development of Cold Spray Technologies. Key Eng. Mater. 2013, 533, 1–52. [Google Scholar] [CrossRef]
- Yildirim, B.; Fukanuma, H.; Ando, T.; Gouldstone, A.; Müftü, S. A Numerical Investigation Into Cold Spray Bonding Processes. J. Tribol. 2014, 137, 011102. [Google Scholar] [CrossRef]
- Li, W.-Y.; Liao, H.; Li, C.-J.; Bang, H.-S.; Coddet, C. Numerical simulation of deformation behavior of Al particles impacting on Al substrate and effect of surface oxide films on interfacial bonding in cold spraying. Appl. Surf. Sci. 2007, 253, 5084–5091. [Google Scholar] [CrossRef]
- Wang, F. Deposition characteristic of Al particles on Mg alloy micro-channel substrate by cold spray. Int. J. Adv. Manuf. Technol. 2016, 91, 791–802. [Google Scholar] [CrossRef]
- Cloutman, L.D. SPH (Smoothed Particle Hydrodynamics) Simulations of Hypervelocity Impacts; Lawrence Livermore National Lab.: Livermore, CA, USA, 1991. [Google Scholar]
- Wang, Q.; Luo, X.; Tsutsumi, S.; Sasaki, T.; Li, C.; Ma, N. Measurement and analysis of cold spray residual stress using arbitrary Lagrangian–Eulerian method. Addit. Manuf. 2020, 35, 101296. [Google Scholar] [CrossRef]
- Chen, Q.; Xie, W.; Champagne, V.K.; Nardi, A.; Lee, J.-H.; Müftü, S. On adiabatic shear instability in impacts of micron-scale Al-6061 particles with sapphire and Al-6061 substrates. Int. J. Plast. 2023, 166, 103630. [Google Scholar] [CrossRef]
- Li, W.Y.; Yu, M.; Wang, F.F.; Yin, S.; Liao, H.L. A Generalized Critical Velocity Window Based on Material Property for Cold Spraying by Eulerian Method. J. Therm. Spray Technol. 2014, 23, 557–566. [Google Scholar] [CrossRef]
- Yu, M.; Li, W.Y.; Wang, F.F.; Liao, H.L. Finite Element Simulation of Impacting Behavior of Particles in Cold Spraying by Eulerian Approach. J. Therm. Spray Technol. 2012, 21, 745–752. [Google Scholar] [CrossRef]
- Cavaliere, P.; Silvello, A. Finite element analyses of pure Ni cold spray particles impact related to coating crack behaviour. Surf. Eng. 2018, 34, 361–368. [Google Scholar] [CrossRef]
- Zhou, H.; Li, C.; Bennett, C.; Tanvir, H.; Li, C. Numerical Analysis of Deformation Behavior and Interface Bonding of Ti6Al4V Particle After Subsequent Impact During Cold Spraying. J. Therm. Spray Technol. 2021, 30, 1093–1106. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Johnson, G.R. A Constitutive Model and Date for Metals Subject to Large Strains, High Strain Rate and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- Henao, J.; Bolelli, G.; Concustell, A.; Lusvarghi, L.; Dosta, S.; Cano, I.G.; Guilemany, J.M. Deposition behavior of cold-sprayed metallic glass particles onto different substrates. Surf. Coat. Technol. 2018, 349, 13–23. [Google Scholar] [CrossRef]
- Abed, F.H.; Voyiadjis, G.Z. A consistent modified Zerilli-Armstrong flow stress model for BCC and FCC metals for elevated temperatures. Acta Mech. 2005, 175, 1–18. [Google Scholar] [CrossRef]
- Cormier, Y.; Dupuis, P.; Jodoin, B.; Ghaei, A. Finite Element Analysis and Failure Mode Characterization of Pyramidal Fin Arrays Produced by Masked Cold Gas Dynamic Spray. J. Therm. Spray Technol. 2015, 24, 1549–1565. [Google Scholar] [CrossRef]
- Zhang, B.; Shim, V.P.W. Effect of strain rate on microstructure of polycrystalline oxygen-free high conductivity copper severely deformed at liquid nitrogen temperature. Acta Mater. 2010, 58, 6810–6827. [Google Scholar] [CrossRef]
- Chakrabarty, R.; Song, J. A modified Johnson-Cook material model with strain gradient plasticity consideration for numerical simulation of cold spray process. Surf. Coat. Technol. 2020, 397, 125981. [Google Scholar] [CrossRef]
- Feng, W.; Ming, Z. Simulation of Particle Deposition Behavior in Cold-Sprayed Mg Anticorrosion Coating. Mater. Manuf. Process. 2015, 31, 1483–1489. [Google Scholar] [CrossRef]
- Grujicic, M.; Zhao, C.L.; DeRosset, W.S.; Helfritch, D. Adiabatic shear instability based mechanism for particles/substrate bonding in the cold-gas dynamic-spray process. Mater. Des. 2004, 25, 681–688. [Google Scholar] [CrossRef]
- Yin, S.; Wang, X.-F.; Li, W.-Y.; Xu, B.-P. Numerical Investigation on Effects of Interactions Between Particles on Coating Formation in Cold Spraying. J. Therm. Spray Technol. 2009, 18, 686–693. [Google Scholar] [CrossRef]
- Li, C.-J.; Li, W.-Y. Deposition characteristics of titanium coating in cold spraying. Surf. Coat. Technol. 2003, 167, 278–283. [Google Scholar] [CrossRef]
- King, P.C.; Bae, G.; Zahiri, S.H.; Jahedi, M.; Lee, C. An Experimental and Finite Element Study of Cold Spray Copper Impact onto Two Aluminum Substrates. J. Therm. Spray Technol. 2010, 19, 620–634. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.-F.; Yin, S.; Xu, S.-L. Influence of Particle Initial Temperature on High Velocity Impact Process in Cold Spraying. Procedia Environ. Sci. 2012, 12, 298–304. [Google Scholar] [CrossRef]
- Suo, X.K.; Liu, T.K.; Li, W.Y.; Suo, Q.L.; Planche, M.P.; Liao, H.L. Numerical study on the effect of nozzle dimension on particle distribution in cold spraying. Surf. Coat. Technol. 2013, 220, 107–111. [Google Scholar] [CrossRef]
- Li, W.-Y.; Zhang, C.; Li, C.-J.; Liao, H. Modeling Aspects of High Velocity Impact of Particles in Cold Spraying by Explicit Finite Element Analysis. J. Therm. Spray Technol. 2009, 18, 921–933. [Google Scholar] [CrossRef]
- Yildirim, B.; Muftu, S.; Gouldstone, A. Modeling of high velocity impact of spherical particles. Wear 2011, 270, 703–713. [Google Scholar] [CrossRef]
- Wu, Q.; Su, J.; Zhao, W.; Li, J.; Zhang, K.; Wang, L. Determination of Critical Velocity of Cold-Sprayed NiCoCrAlY Coating via Arbitary Lagrangian-Eulerian (ALE) Method of Finite Element Simulation. Coatings 2023, 13, 1992. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. Numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 12. [Google Scholar] [CrossRef]
- Saleh, M.; Luzin, V.; Spencer, K. Analysis of the residual stress and bonding mechanism in the cold spray technique using experimental and numerical methods. Surf. Coat. Technol. 2014, 252, 15–28. [Google Scholar] [CrossRef]
- Lemiale, V.; King, P.C.; Rudman, M.; Prakash, M.; Cleary, P.W.; Jahedi, M.Z.; Gulizia, S. Temperature and strain rate effects in cold spray investigated by smoothed particle hydrodynamics. Surf. Coat. Technol. 2014, 254, 121–130. [Google Scholar] [CrossRef]
- Li, W.-Y.; Yin, S.; Wang, X.-F. Numerical investigations of the effect of oblique impact on particle deformation in cold spraying by the SPH method. Appl. Surf. Sci. 2010, 256, 3725–3734. [Google Scholar] [CrossRef]
- Abubakar, A.A. A hybrid computational approach for modeling cold spray deposition. Eng. Sci. Technol. Int. J. 2023, 48, 101579. [Google Scholar] [CrossRef]
- Christoulis, D.K.; Jeandin, M.; Irissou, E.; Legoux, J.-G.; Knapp, W. Laser-Assisted Cold Spray (LACS); Dumitras, D.C., Ed.; Nd YAG Laser, InTech: New York, NY, USA, 2012; pp. 59–96. [Google Scholar] [CrossRef]
- Gnanasekaran, B.; Liu, G.-R.; Fu, Y.; Wang, G.; Niu, W.; Lin, T. A Smoothed Particle Hydrodynamics (SPH) procedure for simulating cold spray process—A study using particles. Surf. Coat. Technol. 2019, 377, 124812. [Google Scholar] [CrossRef]
- Yin, S.; Wang, X.-F.; Xu, B.-P.; Li, W.-Y. Examination on the Calculation Method for Modeling the Multi-Particle Impact Process in Cold Spraying. J. Therm. Spray Technol. 2010, 19, 1032–1041. [Google Scholar] [CrossRef]
- Manap, A.; Nooririnah, O.; Misran, H.; Okabe, T.; Ogawa, K. Experimental and SPH study of cold spray impact between similar and dissimilar metals. Surf. Eng. 2014, 30, 335–341. [Google Scholar] [CrossRef]
- Schmidt, T.; Gärtner, F.; Assadi, H.; Kreye, H. Development of a generalized parameter window for cold spray deposition. Acta Mater. 2006, 54, 729–742. [Google Scholar] [CrossRef]
- Li, W.-Y.; Liao, H.; Li, C.-J.; Li, G.; Coddet, C.; Wang, X. On high velocity impact of micro-sized metallic particles in cold spraying. Appl. Surf. Sci. 2006, 253, 2852–2862. [Google Scholar] [CrossRef]
- Wang, F.F.; Li, W.Y.; Yu, M.; Liao, H.L. Prediction of Critical Velocity During Cold Spraying Based on a Coupled Thermomechanical Eulerian Model. J. Therm. Spray Technol. 2014, 23, 60–67. [Google Scholar] [CrossRef]
- Yu, M.; Li, W.Y.; Wang, F.F.; Suo, X.K.; Liao, H.L. Effect of particle and substrate preheating on particle deformation behavior in cold spraying. Surf. Coat. Technol. 2013, 220, 174–178. [Google Scholar] [CrossRef]
- Schmidt, T.; Assadi, H.; Gärtner, F.; Richter, H.; Stoltenhoff, T.; Kreye, H.; Klassen, T. From Particle Acceleration to Impact and Bonding in Cold Spraying. J. Therm. Spray Technol. 2009, 18, 794–808. [Google Scholar] [CrossRef]
- Ardeshiri Lordejani, A.; Colzani, D.; Guagliano, M.; Bagherifard, S. An inclusive numerical framework to assess the role of feedstock features on the quality of cold spray deposits. Mater. Des. 2022, 224, 111374. [Google Scholar] [CrossRef]
- Oyinbo, S.T.; Jen, T.-C. Feasibility of numerical simulation methods on the Cold Gas Dynamic Spray (CGDS) Deposition process for ductile materials. Manuf. Rev. 2020, 7, 24. [Google Scholar] [CrossRef]
- Heydari Astaraee, A.; Colombo, C.; Bagherifard, S. Numerical Modeling of Bond Formation in Polymer Surface Metallization Using Cold Spray. J. Therm. Spray Technol. 2021, 30, 1765–1776. [Google Scholar] [CrossRef]
- Nélias, D.; Xie, J.; Walter-Le Berre, H.; Ichikawa, Y.; Ogawa, K. Simulation of the Cold Spray Deposition Process for Aluminum and Copper using Lagrangian, ALE and CEL Methods. In Thermomechanical Industrial Processes: Modeling and Numerical Simulation; Wiley-Blackwell: Hoboken, NJ, USA, 2014; pp. 321–358. [Google Scholar]
- Malama, T.; Hamweendo, A.; Botef, I. Molecular Dynamics Simulation of Ti and Ni Particles on Ti Substrate in the Cold Gas Dynamic Spray (CGDS) Process. Mater. Sci. Forum 2015, 828–829, 453–460. [Google Scholar] [CrossRef]
- Joshi, A.; James, S. Molecular dynamics simulation study of cold spray process. J. Manuf. Process. 2018, 33, 136–143. [Google Scholar] [CrossRef]
- Sun, C.; Zhou, X.; Xie, C.; Liu, B. Investigating hard/soft combinations of cold spraying by Eulerian approach. Surf. Eng. 2020, 36, 1049–1057. [Google Scholar] [CrossRef]
- Li, W.; Yang, K.; Zhang, D.; Zhou, X. Residual Stress Analysis of Cold-Sprayed Copper Coatings by Numerical Simulation. J. Therm. Spray Technol. 2015, 25, 131–142. [Google Scholar] [CrossRef]
- Van Steenkiste, T.H.; Smith, J.R.; Teets, R.E. Aluminum coatings via kinetic spray with relatively large powder particles. Surf. Coat. Technol. 2002, 154, 237–252. [Google Scholar] [CrossRef]
- Gärtner, F.; Stoltenhoff, T.; Schmidt, T.; Kreye, H. The Cold Spray Process and Its Potential for Industrial Applications. J. Therm. Spray Technol. 2006, 15, 223–232. [Google Scholar] [CrossRef]
- Ning, X.-J.; Jang, J.-H.; Kim, H.-J. The effects of powder properties on in-flight particle velocity and deposition process during low pressure cold spray process. Appl. Surf. Sci. 2007, 253, 7449–7455. [Google Scholar] [CrossRef]
- Mauer, G.; Singh, R.; Rauwald, K.H.; Schrüfer, S.; Wilson, S.; Vaßen, R. Diagnostics of Cold-Sprayed Particle Velocities Approaching Critical Deposition Conditions. J. Therm. Spray Technol. 2017, 26, 1423–1433. [Google Scholar] [CrossRef]
- Yin, S.; Meyer, M.; Li, W.; Liao, H.; Lupoi, R. Gas Flow, Particle Acceleration, and Heat Transfer in Cold Spray: A review. J. Therm. Spray Technol. 2016, 25, 874–896. [Google Scholar] [CrossRef]
- Luo, X.-T.; Li, Y.-J.; Li, C.-J. A comparison of cold spray deposition behavior between gas atomized and dendritic porous electrolytic Ni powders under the same spray conditions. Mater. Lett. 2016, 163, 58–60. [Google Scholar] [CrossRef]
- MacDonald, D.; Fernández, R.; Delloro, F.; Jodoin, B. Cold Spraying of Armstrong Process Titanium Powder for Additive Manufacturing. J. Therm. Spray Technol. 2017, 26, 598–609. [Google Scholar] [CrossRef]
- Munagala, V.N.V.; Akinyi, V.; Vo, P.; Chromik, R.R. Influence of Powder Morphology and Microstructure on the Cold Spray and Mechanical Properties of Ti6Al4V Coatings. J. Therm. Spray Technol. 2018, 27, 827–842. [Google Scholar] [CrossRef]
- Qiu, X.; Tariq, N.u.H.; Qi, L.; Tang, J.-R.; Cui, X.-Y.; Du, H.; Wang, J.-Q.; Xiong, T.-Y. Influence of particulate morphology on microstructure and tribological properties of cold sprayed A380/Al2O3 composite coatings. J. Mater. Sci. Technol. 2020, 44, 9–18. [Google Scholar] [CrossRef]
- Yin, S.; Wang, X.-F.; Li, W.Y.; Jie, H.-E. Effect of substrate hardness on the deformation behavior of subsequently incident particles in cold spraying. Appl. Surf. Sci. 2011, 257, 7560–7565. [Google Scholar] [CrossRef]
- Ziemian, C.W.; Sharma, M.M.; Bouffard, B.D.; Nissley, T.; Eden, T.J. Effect of substrate surface roughening and cold spray coating on the fatigue life of AA2024 specimens. Mater. Des. 2014, 54, 212–221. [Google Scholar] [CrossRef]
- Blochet, Q.; Delloro, F.; N’Guyen, F.; Jeulin, D.; Borit, F.; Jeandin, M. Effect of the Cold-Sprayed Aluminum Coating-Substrate Interface Morphology on Bond Strength for Aircraft Repair Application. J. Therm. Spray Technol. 2017, 26, 671–686. [Google Scholar] [CrossRef]
- Richer, P.; Jodoin, B.; Ajdelsztajn, L.; Lavernia, E.J. Substrate Roughness and Thickness Effects on Cold Spray Nanocrystalline Al-Mg Coatings. J. Therm. Spray Technol. 2006, 15, 246–254. [Google Scholar] [CrossRef]
- Singh, R.; Rauwald, K.H.; Wessel, E.; Mauer, G.; Schruefer, S.; Barth, A.; Wilson, S.; Vassen, R. Effects of substrate roughness and spray-angle on deposition behavior of cold-sprayed Inconel 718. Surf. Coat. Technol. 2017, 319, 249–259. [Google Scholar] [CrossRef]
- Kumar, S.; Bae, G.; Lee, C. Influence of substrate roughness on bonding mechanism in cold spray. Surf. Coat. Technol. 2016, 304, 592–605. [Google Scholar] [CrossRef]
- Jiang, S.; Zhou, H.; Li, X.; Wang, Y. Numerical simulation of substrate roughness on the interface bonding of cold-sprayed Ti6Al4V. China Surface Engineering 2022, 35, 262–272. (In Chinese) [Google Scholar]
- Zhou, X.; Su, X.; Cui, H.; Guo, H.; Wu, X.; Zhang, J. Effect of material properties of cold-sprayed particles on its impacting behavior. Acta Metallurgica Sinica 2008, 44, 1286–1291. (In Chinese) [Google Scholar]
- Meng, F.; Yue, S.; Song, J. Quantitative prediction of critical velocity and deposition efficiency in cold-spray: A finite-element study. Scr. Mater. 2015, 107, 83–87. [Google Scholar] [CrossRef]
- Li, W.Y.; Yang, K.; Yin, S.; Guo, X.P. Numerical Analysis of Cold Spray Particles Impacting Behavior by the Eulerian Method: A Review. J. Therm. Spray Technol. 2016, 25, 1441–1460. [Google Scholar] [CrossRef]
- Li, W.Y.; Zhang, D.D.; Huang, C.J.; Yin, S.; Yu, M.; Wang, F.F.; Liao, H.L. Modelling of impact behaviour of cold spray particles: Review. Surf. Eng. 2014, 30, 299–308. [Google Scholar] [CrossRef]
- Yin, S.; Wang, X.; Suo, X.; Liao, H.; Guo, Z.; Li, W.; Coddet, C. Deposition behavior of thermally softened copper particles in cold spraying. Acta Mater. 2013, 61, 5105–5118. [Google Scholar] [CrossRef]
- Sun, W.; Tan, A.W.Y.; Bhowmik, A.; Marinescu, I.; Song, X.; Zhai, W.; Li, F.; Liu, E. Deposition characteristics of cold sprayed Inconel 718 particles on Inconel 718 substrates with different surface conditions. Mater. Sci. Eng. A 2018, 720, 75–84. [Google Scholar] [CrossRef]
- Yin, S.; Suo, X.; Xie, Y.; Li, W.; Lupoi, R.; Liao, H. Effect of substrate temperature on interfacial bonding for cold spray of Ni onto Cu. J. Mater. Sci. 2015, 50, 7448–7457. [Google Scholar] [CrossRef]
- Seng, D.H.L.; Zhang, Z.; Zhang, Z.-Q.; Meng, T.L.; Teo, S.L.; Tan, B.H.; Loi, Q.; Pan, J. Influence of spray angle in cold spray deposition of Ti-6Al-4V coatings on Al6061-T6 substrates. Surf. Coat. Technol. 2022, 432, 128068. [Google Scholar] [CrossRef]
- Binder, K.; Gottschalk, J.; Kollenda, M.; Gärtner, F.; Klassen, T. Influence of Impact Angle and Gas Temperature on Mechanical Properties of Titanium Cold Spray Deposits. J. Therm. Spray Technol. 2011, 20, 234–242. [Google Scholar] [CrossRef]
- Li, C.J.; Li, W.Y.; Wang, Y.Y.; Fukanuma, H. Effect of Spray Angle on Deposition Characteristics in Cold Spraying. In Proceedings of the ITSC2003, Orlando, FL, USA, 5–8 May 2003; pp. 91–96. [Google Scholar]
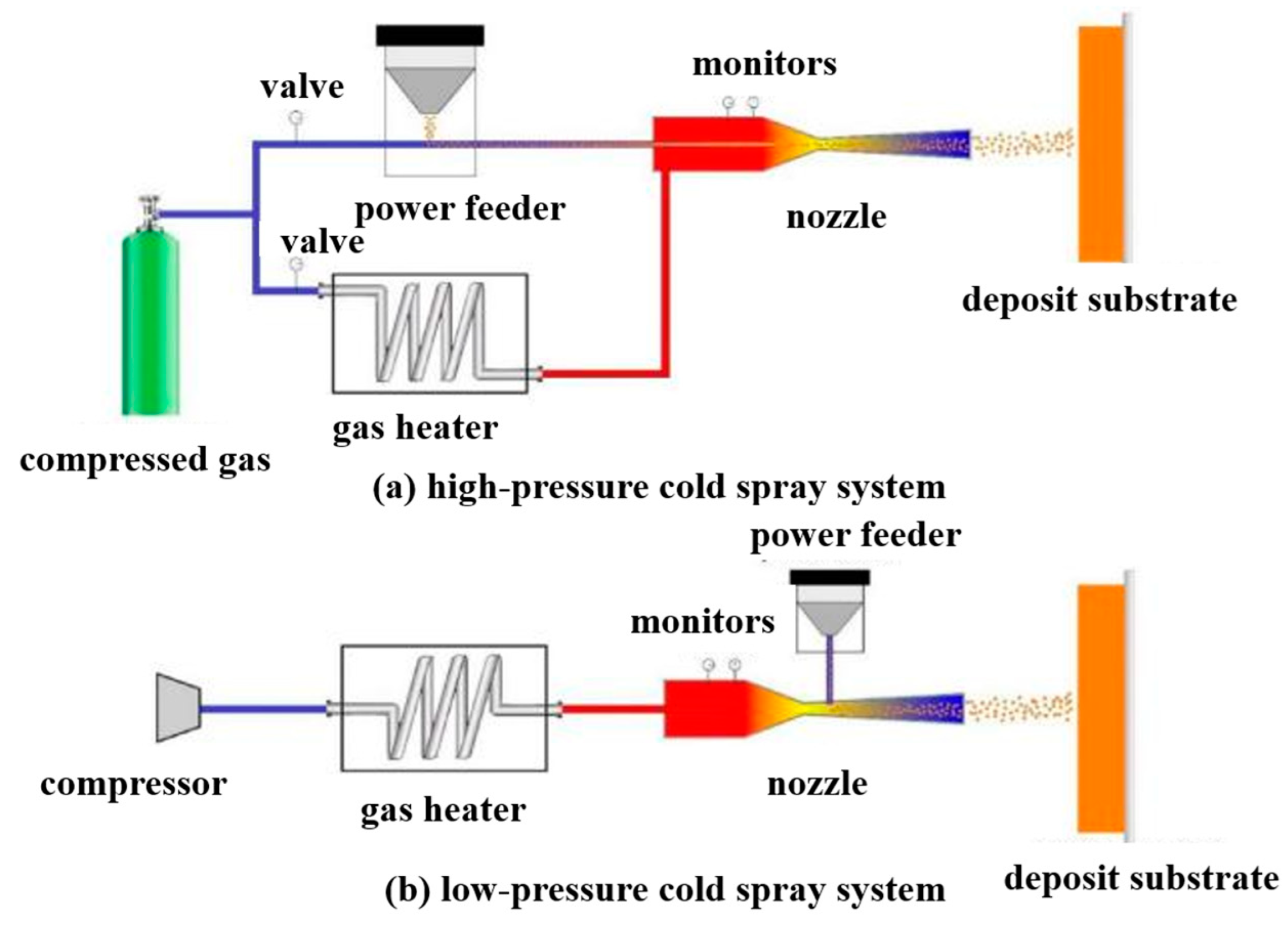



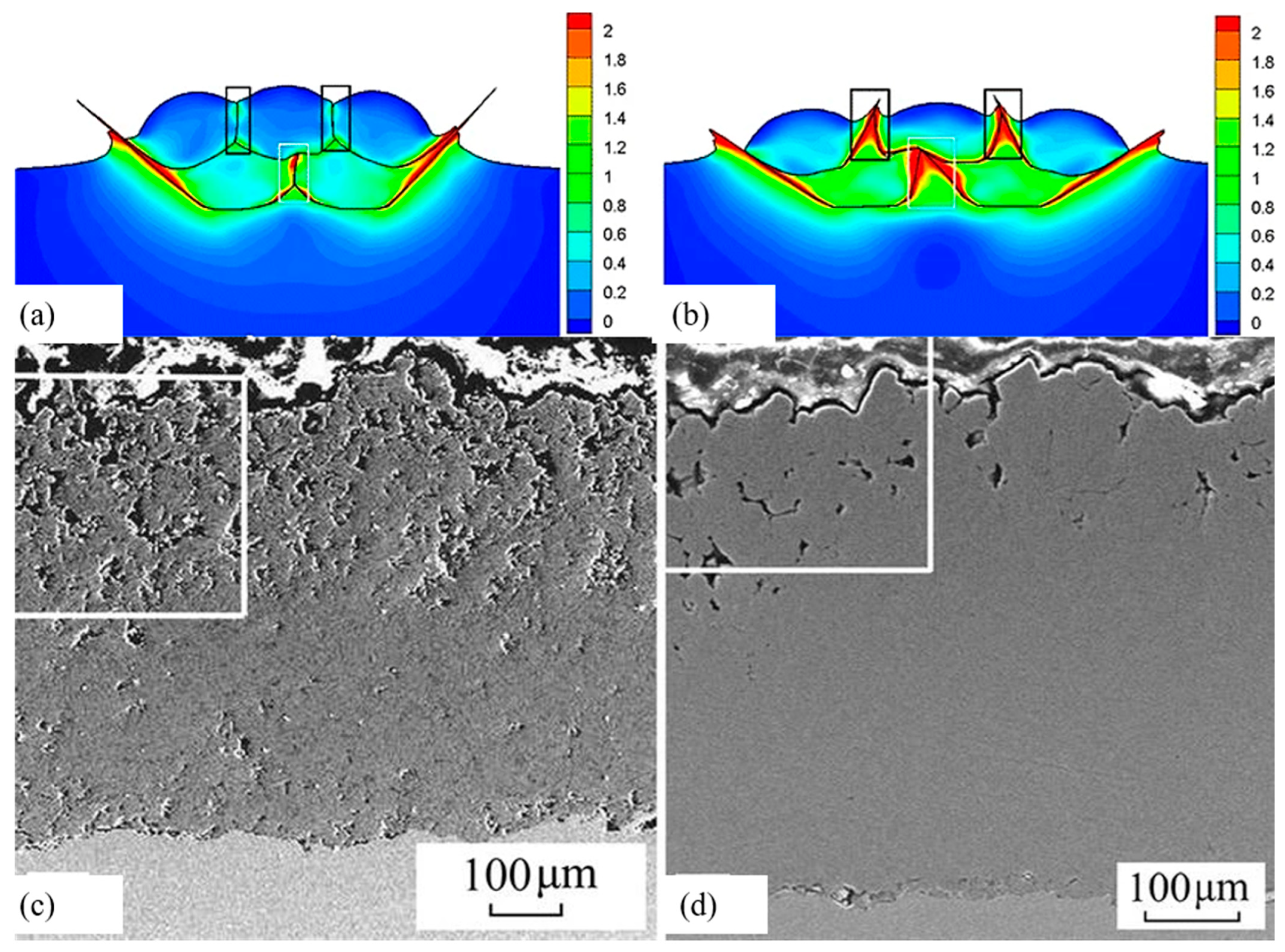

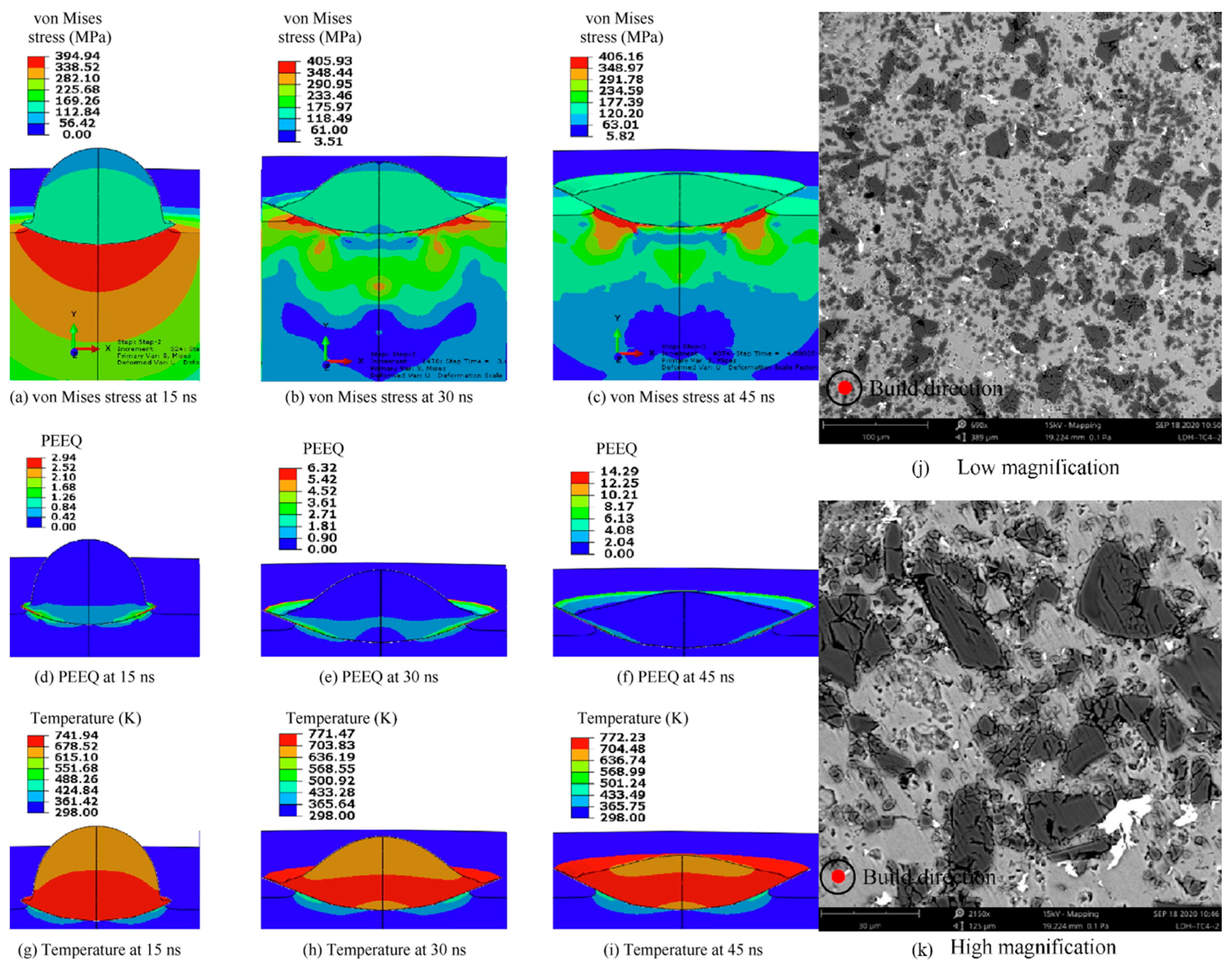

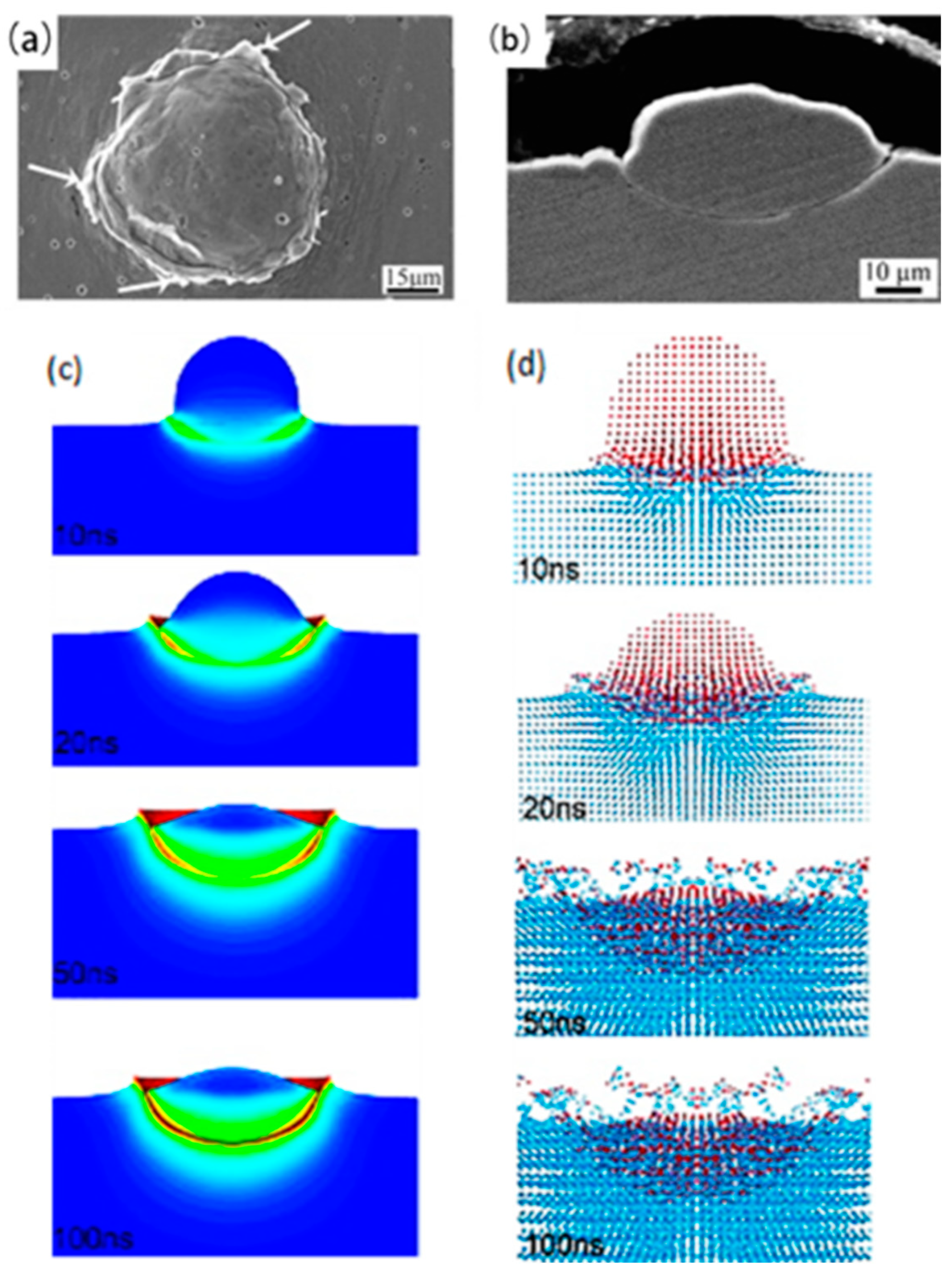
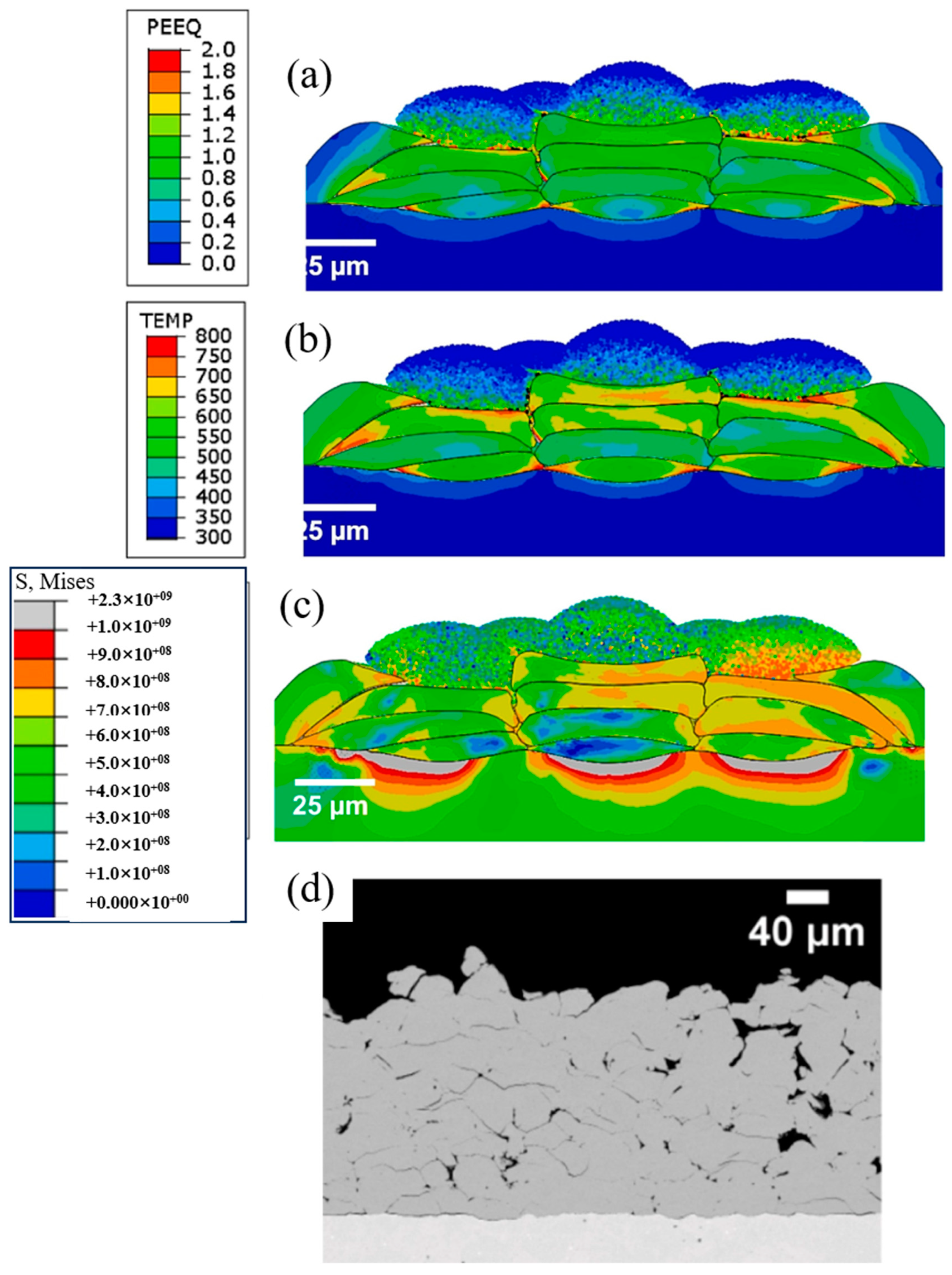

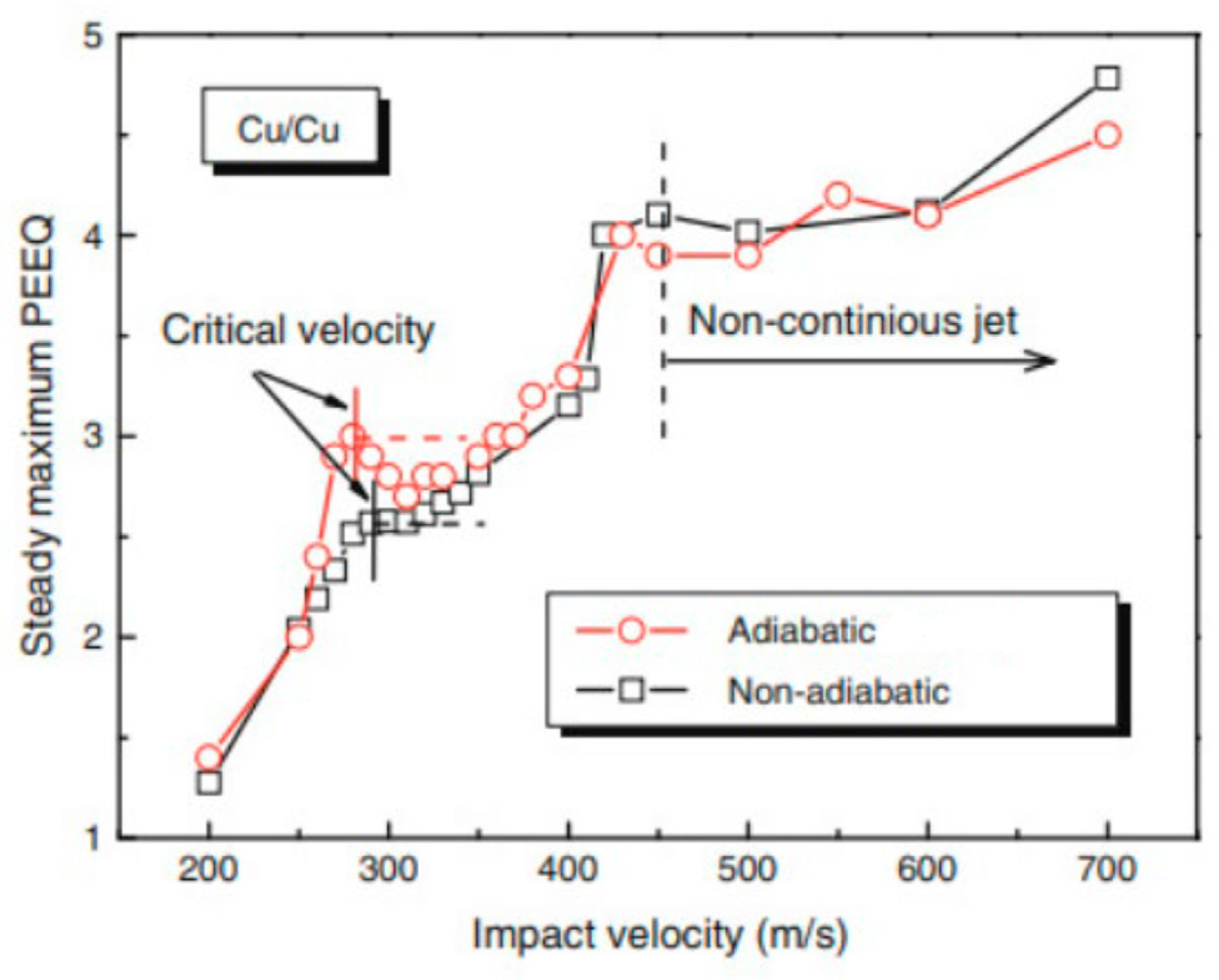








| Material Property | Cu | Al | Fe | Ni | Ti | Ti6Al4V | Mg Alloy |
|---|---|---|---|---|---|---|---|
| Density (kg/m3) | 8930 | 2700 | 7870 | 8890 | 4510 | 4428 | 1780 |
| Young’s modulus (GPa) | 110 | 68 | 200 | 205 | 116 | 110 | 45 |
| Poisson’s ratio | 0.35 | 0.33 | 0.33 | 0.31 | 0.34 | 0.36 | 0.35 |
| Specific heat (J/(kg k)) | 385 | 900 | 444 | 460 | 528 | 560 | 250 |
| Heat conduction (W/mK) | 385 | 210 | 76.2 | 61 | 60 | 13 | 96 |
| Johnson–Cook model parameter | |||||||
| A (MPa) | 150 | 265 | 175 | 163 | 807 | 1098 | 170 |
| B (MPa) | 305 | 426 | 388 | 648 | 482 | 1092 | 235 |
| C | 0.034 | 0.015 | 0.06 | 0.006 | 0.0194 | 0.014 | 0.013 |
| n | 0.096 | 0.34 | 0.32 | 0.33 | 0.319 | 0.93 | 0.15 |
| m | 1.09 | 1 | 0.55 | 1.44 | 0.655 | 1.1 | 1 |
| Tm (K) | 1356 | 933 | 1809 | 1723 | 1923 | 1356 | 903 |
| Numerical Simulation Methods | Advantage | Disadvantage | Characteristic | References |
|---|---|---|---|---|
| Lagrange method | The operation is simple, and the contact interface can be tracked for easy analysis. | When the mesh deformation is large, the program is easy to terminate, and the particles are prone to rebound. | The delineated mesh moves with the material’s deformation. When the deformation is small, the calculation time is short, and the accuracy is high, which is used for solid analysis. | [4,31,34] |
| Euler method | Large deformations can be simulated without mesh limitations and with high computational accuracy. | Calculations are slow; particle/particle and particle/substrate interfaces cannot be traced. | The material can flow freely within the set mesh used for fluid analysis. | [20,61,62] |
| CEL method (coupled Lagrange–Euler method) | Ability to simulate extreme deformation of particles and track interfaces with high computational accuracy. | Calculations are terminated due to distortion of the substrate mesh, the results of particles and substrate cannot be monitored simultaneously, and the calculations are slower. | Combines both Lagrange and Euler features | [58] |
| ALE method (arbitrary Lagrange–Euler method) | It can effectively solve the problem of computation termination due to mesh distortion in Lagrange, and the computation speed is fast. | Low computational accuracy, failure to solve the problem of particle rebound in the Lagrange, cumbersome parameterization, and unrealistic jet bands generated by particles impacting the substrate | Adaptive changes when the mesh is distorted | [14,15,17,39] |
| SPH method (Smooth Particle Hydrodynamics) | Extreme deformations can be simulated without mesh limitation, and the calculation accuracy is high when the deformation is large. | Uneven particle mass leads to unstable stretching between particles, slower calculation speed, and low calculation accuracy when the deformation amount is small. | Modeling material characteristics with a series of particle combinations | [42,43,44] |
| MD method (molecular dynamics method) | can simulate the microscopic mechanisms of particles upon impact with the substrate. | It is not easy to simulate large-scale particles. | Simulates interactions between atoms or molecules; the smaller the particle size, the higher the accuracy. | [59,60] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Liu, J.; Li, H.; Wu, Z.; Zhong, Y.; Ramachandran, C.S.; Cheng, Y.; Wang, Q. Research Progress on Numerical Simulation of the Deposition and Deformation Behavior of Cold Spray Particles. Coatings 2024, 14, 913. https://doi.org/10.3390/coatings14070913
Liu Z, Liu J, Li H, Wu Z, Zhong Y, Ramachandran CS, Cheng Y, Wang Q. Research Progress on Numerical Simulation of the Deposition and Deformation Behavior of Cold Spray Particles. Coatings. 2024; 14(7):913. https://doi.org/10.3390/coatings14070913
Chicago/Turabian StyleLiu, Zhihao, Jianwu Liu, Haifeng Li, Zizhao Wu, Yuan Zhong, Chidambaram Seshadri Ramachandran, Yingliang Cheng, and Qun Wang. 2024. "Research Progress on Numerical Simulation of the Deposition and Deformation Behavior of Cold Spray Particles" Coatings 14, no. 7: 913. https://doi.org/10.3390/coatings14070913
APA StyleLiu, Z., Liu, J., Li, H., Wu, Z., Zhong, Y., Ramachandran, C. S., Cheng, Y., & Wang, Q. (2024). Research Progress on Numerical Simulation of the Deposition and Deformation Behavior of Cold Spray Particles. Coatings, 14(7), 913. https://doi.org/10.3390/coatings14070913






